Специалист по Computer Science Александр Панов об искусственном интеллекте, целенаправленном действии и вычислительной модели неокортекса.

Курс представляет собой букет из трёх очень старых и трёх очень новых идей. Основной объект — число целых (т.е. с целыми координатами) точек в многограннике. Зачем нужны целые точки? Несколько примеров: многогранник Ньютона, Теорема Бриона — для начала без доказательства, просто в качестве фокуса, а также подсчёт целых метрических ленточных графов. Число целых точек в выпуклом многограннике ведёт себя как полином. Согласно конструкции, в полином, вычисляющий число целых точек, имеет смысл подставлять лишь положительные числа. Чтобы придать смысл отрицательной подстановке, нужны виртуальные многогранники. Двойственность Эрхарта и её естественное обобщение. Секрет фокуса Бриона.

Вот три тесно связанные между собой задачи, которые мы будем обсуждать: Как распрямить плотницкую линейку? Можно ли нарисовать на сфере правильно раскрашенный граф? Верна ли старая гипотеза А. Д. Александрова о характеризации сферы? Попутно будет сформулировано много задач разного уровня сложности (именно исследовательских задач, а не упражнений!). Часть из них — для умеющих и любящих программировать. В курсе будет много картинок.

Теорема о существовании и единственности выпуклого многогранника с данными направлениями и площадями его граней, открытая Минковским в 1897 году, наряду с теоремами Эйлера, Коши, А. Д. Александрова, является одной из фундаментальных теорем о многогранниках. Рассказано о нескольких приложениях этой замечательной теоремы.

Лекцию читает Долбилин Николай Петрович, профессор, доктор физико-математических наук. Летняя школа «Современная математика», г. Дубна. 28 июля 2008 г.

Параллелоэдром (это понятие и сам термин были введены великим кристаллографом Е.С. Федоровым для нужд кристаллографии) называют многогранник, параллельными копиями которого можно заполнить пространство. Обычный строительный кирпич является очевидно частным случаем параллелоэдра. Как и кирпич, любой параллелоэдр имеет попарно параллельные грани, чем объясняется его труднопроизносимое название. Многомерный параллелоэдр имеет многочисленные приложения в геометрии чисел, в теории кодирования, комбинаторной геометрии и т.д. В лекции будет рассказано в первую очередь о двух замечательных теоремах Минковского о свойствах параллелоэдров, а также об открытой проблеме Вороного, которой в этом году исполнился 101 год, и кое о чем еще.

Сергей Ландо, докт. физ.-мат. наук, профессор факультета математики Высшей школы экономики, стоял у истоков возникновения факультета математики и исполнял обязанности декана с момента создания факультета в 2007 году до весны 2015 года. Людмила Сапченко расспросила Сергея Константиновича о его научной деятельности, о том, какое место занимают математические науки в современном мире, как создавался факультет, какие задачи ставятся перед факультетом в настоящее время.

Рассмотрим прямоугольник, составленный из маленьких правильных шестиугольных плиток. Подкинем для каждой из этих плиток монетку, и, если выпадет орел, объявим ее открытой, а иначе закрытой. С какой вероятностью от левого края прямоугольника до правого можно дойти путем, проходящим только по открытым плиткам? Этим и многими другими схожими вопросами занимается теория протекания. Ответ на вопрос о вероятности пробоя дается (на первый взгляд пугающей) формулой Карди, предсказанной им в 1991 г. из соображений конформной теории поля. Строго эта формула — в гораздо более приятно выглядящей переформулировке Л. Карлесона — была доказана лишь десять лет спустя С. К. Смирновым в его работах 2001-го года (одних из тех, за которые в 2010-м он получил премию Филдса). В нашем курсе мы, хоть и не в деталях, обсудим доказательство этой формулы — опирающееся на такую удивительную вещь, как дискретный комплексный анализ.

В этом курсе будет рассказано о подстановочных системах довольно общего вида и о связанных с ними геометрических конструкциях, называемых фракталами Рози. Например, слово Трибоначчи 121312112131… состоит из цифр {1,2,3} и получается с помощью подстановки 1→12, 2→13, 3→1. Оказывается, что оно в некотором смысле устроено так же, как двумерный тор, разбитый на три части с фрактальной границей. (В то, что на первом рисунке изображена развёртка тора, трудно поверить, но тем не менее это так, и вторая картинка это иллюстрирует).

Известна олимпиадная задача: На плоском столе лежат монеты (выпуклые фигуры). Тогда одну из них можно стащить со стола, не задевая остальных. Долгое время математики пытались доказать пространственный аналог этого утверждения, пока не был построен контрпример! Возникла идея: в малом зерне часто нет трещины, трещина за границу зерна не вырастает, а трещины друг друга держат. Эта идея теоретически позволяет создавать композиты в которых не растут трещины, в частности, броню из керамики.

Рассмотрим s-порожденную группу (s<1) с тождеством x^n=1. Будет ли она конечна? Ответ положителен при n=2 (легкое упражнение), при n=3 (это уровень сложной задачи студенческой олимпиады), при n=4 (проблема стояла около 40 лет) при n=6 (проблема стояла около 50 лет). При n=5 ничего не известно! В середине 20 века П. С. Новиковым и С. И. Адяном было показано, что если n нечетное число ≥661 то такая группа может быть бесконечна. А. И. Мальцев рассматривал этот результат как основное событие алгебры 20 века (эту точку зрения разделяет, в частности, И. Рипс, чьи исследования были вдохновлены работами П. С. Новикова-С. И. Адяна). Недавно С. И. Адян улучшил оценку до 101.

Дифференциальные 1-формы можно рассматривать как многозначные функции. Они приводят к глубоким топологическим задачам и имеют нетривиальные приложения в физике твёрдого тела. Лекцию читает Новиков Сергей Петрович, академик РАН, доктор физико-математических наук, профессор.

Из курса математического анализа известно, что если функция имеет n производных, то n-я производная может даже не быть непрерывной; если функция имеет все производные, то она может все-таки не разлагаться в ряд Тейлора: он может расходиться или сходиться к другой функции. Удивительная особенность функций комплексного переменного состоит в том, что одна только дифференцируемость функции во всех точках ее области определения обеспечивает, что функция имеет все производные и разлагается в ряд Тейлора. Этот факт доказывается с использованием интегрального исчисления функций комплексного переменного, хотя по своей форме он относится к дифференциальному исчислению. В лекциях будет предложено другое доказательство того же факта. Оно обходится без специфического комплексного интегрирования и вообще опирается на “вещественные” сведения.

Лекцию читает Новиков Сергей Петрович, академик РАН, доктор физико-математических наук, профессор. Летняя школа «Современная математика», г. Дубна 21 июля 2005 г.

Курс посвящён обобщению понятия вращения евклидова пространства. Оказывается, что с каждым евклидовым пространством можно связать новое пространство, объекты которого называются спинорами. Между исходным пространством и пространством спиноров имеется замечательная связь: всякому вращению исходного пространства можно сопоставить преобразование пространства спиноров, определённое однозначно с точностью до знака. Получаемые таким образом преобразования пространства спиноров образуют группу, называемую спинорной группой.

Квазипериодические функции: что это такое, откуда возникают, проблемы их изучения, как появляется топология и динамические системы. Лекцию читает Новиков Сергей Петрович, академик РАН, доктор физико-математических наук, профессор.

Лекцию читает Новиков Сергей Петрович, академик РАН, доктор физико-математических наук, профессор. Летняя школа «Современная математика», г. Дубна. 20 июля 2003 г.

В совместной работе с И. Дынниковым мы предложили дискретный вариант комплексного анализа, который стартует с решётки правильных треугольников на плоскости. Нам представляется, что этот подход лучше обычного подхода, использующего квадратную решётку.

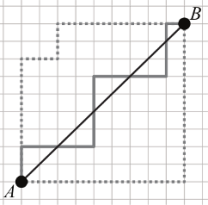
Математик Мишель Рудольф-Лилит из Национального центра научных исследований Франции описала особенности окружностей, начерченных в дискретном пространстве, в качестве примера которого ученый рассмотрела пересечения улиц и проспектов Манхэттена — центрального района Нью-Йорка. Оказалось, что можно аналитически описать несколько алгоритмов, следуя которым, гипотетический таксист проедет вдоль линии, максимально приближенной к идеальной окружности, а при достаточно большом ее радиусе можно с хорошей точностью измерить число π.

Рассмотрим конечный связный граф. Сколько в нем остовных деревьев — деревьев, содержащих все вершины графа? А какая их доля содержит данный набор ребер? Цель нашего курса — дать элементарное введение в теорию детерминантных процессов. Мы планируем обсудить недавние достижения и сформулировать нерешенные проблемы. Программа занятий: детерминанты и пфаффианы; остовные деревья; случайные матрицы; мультипликативные функционалы.