Математик Мишель Рудольф-Лилит из Национального центра научных исследований Франции описала особенности окружностей, начерченных в дискретном пространстве, в качестве примера которого ученый рассмотрела пересечения улиц и проспектов Манхэттена — центрального района Нью-Йорка. Оказалось, что можно аналитически описать несколько алгоритмов, следуя которым, гипотетический таксист проедет вдоль линии, максимально приближенной к идеальной окружности, а при достаточно большом ее радиусе можно с хорошей точностью измерить число
 .
. Исследование в виде препринта опубликовано на
arXiv.org.
В математике есть понятие «норма», простейший смысл которого — это расстояние (или, точнее, длина вектора) в некотором пространстве. В жизни мы чаще всего пользуемся евклидовой нормой, которая для плоскости очень похожа на теорему Пифагора. Чтобы найти расстояние от некоторого центра с координатами

до точки с координатами
 ,
, проведем в эту точку вектор
 .
. Квадрат его нормы

и будет равен квадрату расстояния до точки
 .
.
Но как быть, если мы находимся в дискретном пространстве? Например, как рассказывает Рудольф-Лилит, все в том же Манхэттене расстояние от одной точки до другой по прямой может быть 4,3 мили, но на самом деле кратчайший маршрут составит около 6 миль, ведь ехать можно только по улицам и проспектам, которые пересекаются под прямым углом. В этом случае пространство можно задать как множество точек, соответствующее перекресткам. Тогда любой маршрут будет задаваться линией, которую мы проведем по этим точкам, причем использовать диагонали нельзя.
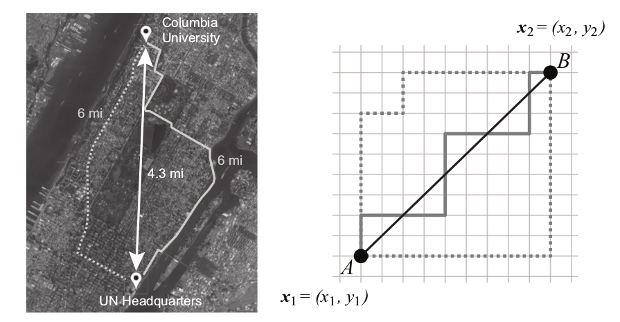 Из-за перпендикулярного расположения улиц и проспектов на Манхэттене реальные расстояние для таксистов почти никогда не равняются «прямым». Michelle Rudolph-Lilith/ arXiv.org |
Для такого пространства уже не имеет смысла использовать евклидову (или
 )
) норму, так как она не дает представления о реальной длине маршрута. Вместо этого подойдет норма

(ее, кстати, называют «манхэттенской»), которая для нашего же вектора

будет определена как
 .
. У этой нормы есть ряд отличительных особенностей. Например, в евклидовом пространстве (с

нормой) для любой пары точек есть только один кратчайший маршрут — отрезок, соединяющий эти две точки. В дискретном пространстве вы такой отрезок провести не можете, и кратчайших маршрутов в этом случае будет множество. Например, можно сначала переместиться на

по проспекту, потом повернуть, и сместиться на

по улице, а можно двигаться зигзагом и сворачивать на каждом перекрестке влево-вправо. Легко убедиться, что пройденное расстояние будет одинаковым.
Вопрос, который поднимает математик в своей работе, состоит в том, как правильно задать окружность в дискретном множестве точек, и можно ли с помощью таких окружностей точно определить число
 ?
? Первая проблема тесно связана, например, с компьютерной графикой, где все окружности (и кривые линии в целом) нужно отрисовывать на дискретном пространстве пикселей, то есть растеризовать. Разумеется, сама прикладная задача давно решена, однако ряд математических свойств этих решений остался неизученным.
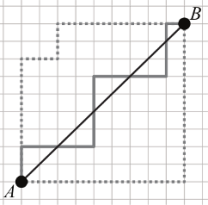
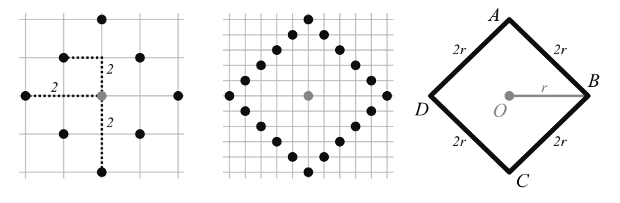 Так выглядит «окружность», заданная на дискретном пространстве точек, и определенная с помощью  нормы. Michelle Rudolph-Lilith/ arXiv.org |
Прежде, чем перейти к выводу необходимых соотношений, Рудольф-Лилит напомнила, что результат может зависеть от того, как именно мы определим понятие окружности. Так, если следовать «школьному» определению (на самом деле, авторства Евклида), согласно которому окружность — это множество точек, лежащих на равном расстоянии от выбранного центра, то для дискретного пространства эта линия будет выглядеть очень непривычно: это будет квадрат, повернутый на 45 градусов. Тогда

норма векторов, проведенных во все его точки, действительно будет одинакова и если для такой «окружности» определить число

как отношение длины окружности к диаметру, оно будет равно 4, а не 3,14... .
Чтобы избежать непонимания, автор подчеркнула, что изучаться будет именно привычная нам окружность, которую для центра в

и радиуса

можно задать параметрически как множество точек, удовлетворяющих
 .
. «Дискретная» окружность тогда будет задаваться как множество точек в дискретном пространстве, лежащих как можно ближе к «настоящей» окружности. Автор приводит широко используемые алгоритмы, в частности mid-point и signum, которые давно и успешно используются для черчения таких дискретных окружностей. Рудольф-Лилит отмечает, что «таксисту будет несложно прокатить пассажира „по кругу“, в уме вычисляя, куда повернуть на том или ином перекрестке».
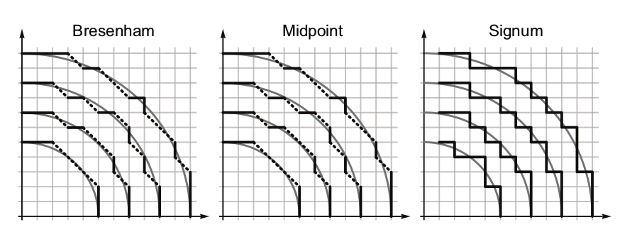 Некоторые алгоритмы растеризации окружности. Michelle Rudolph-Lilith/ arXiv.org |
С точки зрения математика гораздо интереснее понять, можно ли с помощью построения такой окружности точно вычислить знаменитое число
 .
. Кажется, что при увеличении радиуса окружности, мы должны все точнее приближать
 ,
, однако в математике известны похожие задачи, где в любом бесконечном пределе все равно не удается приблизить одно расстояние другим: сколько бы перекрестков не было по пути, вам никогда не превратить 6 миль в 4,3, так уж устроено дискретное пространство.
Тем не менее, автор показывает, что с увеличением радиуса воображаемой окружности точность определения числа

через отношение длины окружности к диаметру растет. Для окружности радиусом в десять перекрестков можно определить

с точностью до третьего знака после запятой, а для радиуса в 1000000 перекрестков — до девятого знака. Рудольф-Лилит не только сделала численное моделирование, но получила необходимые аналитические выражения, которые показывают справедливость ее утверждений в предельном переходе к бесконечному радиусу.
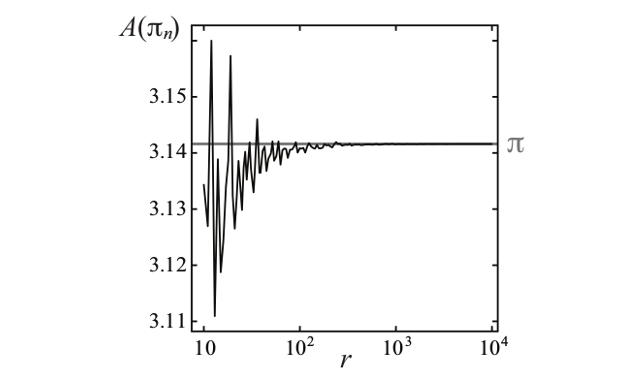 Сходимость числа  в зависимости от радиуса дискретной окружности. Michelle Rudolph-Lilith/ arXiv.org |
Математик в заключении признается, что удивлена, что несмотря на особенности дискретного пространства улиц Нью-Йорка, удается воспроизвести

— фундаментальную константу для евклидовой окружности. «Теперь, сидя в такси, мы будем не только слушать размышления водителя вслух, но и гадать, какие еще сюрпризы нам приподнесет город, который никогда не спит».
Число

— один из любимых объектов математиков. Эту
иррациональную константу можно измерить многими, часто неординарными способами: например,
бросая иголки на стол или
стреляя 200 раз из дробовика Mossberg 500. А четырнадцатого марта (03/14 в формате дат, принятом в США) по всему миру традиционно отмечается
день числа 
.
Тарас Молотилин
N+1







 Математик Илья Щуров о десятичных дробях, трансцендентности и иррациональности числа Пи.
Математик Илья Щуров о десятичных дробях, трансцендентности и иррациональности числа Пи.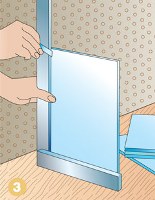 В школе мы несколько лет подряд прилежно изучаем геометрию. Но не зря ли мы тратим время? Чем может помочь геометрия в жизни? Измерить расстояние от точки до точки, вычислить площадь или объём предмета и только? Нет, конечно. Законы геометрии применимы буквально на каждом шагу. Просто нужно знать, как ими воспользоваться.
В школе мы несколько лет подряд прилежно изучаем геометрию. Но не зря ли мы тратим время? Чем может помочь геометрия в жизни? Измерить расстояние от точки до точки, вычислить площадь или объём предмета и только? Нет, конечно. Законы геометрии применимы буквально на каждом шагу. Просто нужно знать, как ими воспользоваться. В журнале «Квантик» № 5, 2016 была опубликована задача:«Робот-пылесос, имеющий форму круга, проехал по плоскому полу. Для каждой точки граничной окружности робота можно указать прямую, на которой эта точка оставалась в течение всего времени движения. Обязательно ли и центр робота оставался на некоторой прямой в течение всего времени движения?» Удивительно, но ответ отрицателен — центр мог двигаться не по прямой! Мы дадим несколько решений, начнём издалека, зато узнаем по дороге много интересного.
В журнале «Квантик» № 5, 2016 была опубликована задача:«Робот-пылесос, имеющий форму круга, проехал по плоскому полу. Для каждой точки граничной окружности робота можно указать прямую, на которой эта точка оставалась в течение всего времени движения. Обязательно ли и центр робота оставался на некоторой прямой в течение всего времени движения?» Удивительно, но ответ отрицателен — центр мог двигаться не по прямой! Мы дадим несколько решений, начнём издалека, зато узнаем по дороге много интересного. Математики из Вашингтонского университета в Ботелле открыли новый тип пятиугольных паркетов — выпуклых пятиугольников, которыми можно замостить плоскость без пробелов и наложений. Ранее было известно только 14 типов таких пятиугольников, последний из которых был открыт 30 лет назад.
Математики из Вашингтонского университета в Ботелле открыли новый тип пятиугольных паркетов — выпуклых пятиугольников, которыми можно замостить плоскость без пробелов и наложений. Ранее было известно только 14 типов таких пятиугольников, последний из которых был открыт 30 лет назад. Эссе Пола Локхарда «Плач математика» о преподавании математики в средней школе. Хотя в сочинении говорится об американской современной средней школе, многие проблемы, идентифицируемые Локхардом, относятся к любой стране мира, за исключением, возможно, Эльдорадо, которой нет. Еще менее привязаны к американской реальности размышления автора о том, что такое математика и как она должна преподаваться. Даже если вы не математик и не имеете отношения к преподаванию, думаю, вы найдете это эссе интересным, а возможно, и сделаете для себя несколько небольших открытий и сломаете кое-какие стереотипы. В конце концов, вы ведь учили математику в школе!
Эссе Пола Локхарда «Плач математика» о преподавании математики в средней школе. Хотя в сочинении говорится об американской современной средней школе, многие проблемы, идентифицируемые Локхардом, относятся к любой стране мира, за исключением, возможно, Эльдорадо, которой нет. Еще менее привязаны к американской реальности размышления автора о том, что такое математика и как она должна преподаваться. Даже если вы не математик и не имеете отношения к преподаванию, думаю, вы найдете это эссе интересным, а возможно, и сделаете для себя несколько небольших открытий и сломаете кое-какие стереотипы. В конце концов, вы ведь учили математику в школе! Генно-инженерные эксперименты показали, что количество пальцев у мышей зависит от двух взаимодействующих систем генов-регуляторов. По мере отключения этих генов пальцы становятся многочисленнее, короче и тоньше, а их концы соединяются костно-хрящевой дугой, так что в итоге кисть начинает напоминать плавник примитивной рыбы. Новые данные согласуются с гипотезой о том, что развитие пальцев основано на реакционно-диффузионном механизме самоорганизации, придуманном Аланом Тьюрингом в 1952 году.
Генно-инженерные эксперименты показали, что количество пальцев у мышей зависит от двух взаимодействующих систем генов-регуляторов. По мере отключения этих генов пальцы становятся многочисленнее, короче и тоньше, а их концы соединяются костно-хрящевой дугой, так что в итоге кисть начинает напоминать плавник примитивной рыбы. Новые данные согласуются с гипотезой о том, что развитие пальцев основано на реакционно-диффузионном механизме самоорганизации, придуманном Аланом Тьюрингом в 1952 году.