Число Пи
Программа курса:
- История. Первые оценки. Проблема соизмеримости длины окружности с ее диаметром.
- Бесконечные ряды, произведения и другие выражения для
 . Сходимость и ее качество. Выражения, содержащие . Сходимость и ее качество. Выражения, содержащие  . .
- Последовательности, быстро сходящиеся к
 . Современные методы вычисления . Современные методы вычисления  , использование компьютеров. , использование компьютеров.
- Об иррациональности и трансцендентности
 и некоторых других чисел. и некоторых других чисел.
Предварительных знаний для понимания курса не требуется.
Шабат Георгий Борисович, доктор физико-математических наук.
Летняя школа «Современная математика», г. Дубна
25 июля 2005 г.
Похожее
-
Александр Буфетов
Традиция отмечать неофициальный день числа Пи зародилась в Соединенных Штатах почти 30 лет назад, когда известный американский физик Ларри Шоу обратил внимание на то, что 14 марта совпадает с первыми тремя цифрами знаменитой "архимедовой константы" — 3,14. На следующий год, с подачи Шоу, в этот день посетителей музея начали угощать пирогами (из-за сходного звучания слов "пирог" и "Пи" английском языке "pi" — "pie"), после чего к ежегодному отмечанию этой даты постепенно присоединились физики и математики со всего мира.
-
Наталья Карпушина

Знаете ли вы, почему в окружности 360 градусов, а не 180 или, скажем, не 300? Откуда пошла традиция делить окружность на равные части и почему было выбрано именно такое их число? Оказывается, этому делению мы обязаны вавилонянам. Считается, что они же изобрели простейший инструмент для измерения углов − транспортир. Но вот вопрос: как же древние сумели разделить окружность на равные части, не владея техникой геометрических построений и располагая лишь примитивными инструментами?
-
Алексей Белов

Всем говорят в школе, что число π иррационально и даже — трансцендентно, т. е. не является корнем многочлена с целыми коэффициентами. Имеется изящное и вполне элементарное доказательство Эрмита иррациональности числа π (требующее только знания интегрирования по частям — понимания как вычислить интеграл ∫ x^k sin(x)dx в пределах от a до b). Наша цель — доказательство теоремы Линдемана–Веерштрасса (если α_i линейно независимые над Q алгебраические числа, то e^(α_i) алгебраически независимы), а также теоремы Гельфонда (если числа α ≠ 0,1; β ∉ Q алгебраические, то αβ есть число трансцендентное).
-
Георгий Шабат

Детские рисунки (dessins d'enfants) – термин, введённый Александром Гротендиком в 70-е годы прошлого века. С «детской» точки зрения этот термин означает граф, вложенный в поверхность; с взрослой – это объект, в котором закодированы различные структуры, относящиеся к далёким друг от друга областям математики. Под подсчётом детских рисунков понимается подсчёт количества детских рисунков ограниченной сложности, которая будет определена. В последние годы были получены замечательные результаты о количествах детских рисунков. Элементарная часть этих результатов будет изложена в курсе.
-
Георгий Шабат

Предполагается прочесть четыре лекции. Первые две будут популярны и общепонятны, а третья и четвёртая будут содержать довольно поверхностные обзоры некоторых перспективных направлений современной математики. 1. О геометрии над конечными полями. 2. Группы Шевалле и группы перестановок. 3. Линейная алгебра над F1 и гомотопическая топология. 4. Разное. Обобщённые кольца Дурова и F∅, F±1, F∞√1. Анализ на множестве корней из единицы (по Хабиро, Концевичу, Манину). О геометрии Аракелова. О тропической математике.
-
Георгий Шабат
Мы сейчас знаем о строении Вселенной примерно столько же, сколько древние люди знали о поверхности Земли. Точнее, мы знаем, что небольшая часть Вселенной, доступная нашим наблюдениям, устроена так же, как небольшая часть трёхмерного евклидова пространства. Иначе говоря, мы живём на трёхмерном многообразии (3-многообразии). Кругосветным путешествиям и построениям полных атласов может предшествовать априорная классификация маломерных многообразий — вопрос о том, где мы “на самом деле” живём заменяется на вопрос где мы могли бы жить? Эта классификация (требующая некоторых естественных ограничений на многообразия) тривиальна в размерности 1, допускает красивый полный ответ в размерности 2, полученный в XIX веке, и составляет исключительно трудную проблему в размерности 3. В этой проблеме совсем недавно достигнуты замечательные результаты, обзор которых и составляет цель курса.
-
Илья Щуров

Математик Илья Щуров о десятичных дробях, трансцендентности и иррациональности числа Пи.
-
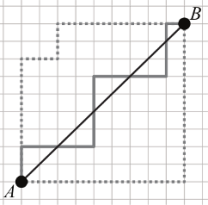
Математик Мишель Рудольф-Лилит из Национального центра научных исследований Франции описала особенности окружностей, начерченных в дискретном пространстве, в качестве примера которого ученый рассмотрела пересечения улиц и проспектов Манхэттена — центрального района Нью-Йорка. Оказалось, что можно аналитически описать несколько алгоритмов, следуя которым, гипотетический таксист проедет вдоль линии, максимально приближенной к идеальной окружности, а при достаточно большом ее радиусе можно с хорошей точностью измерить число π.
-

Ученые из Оксфордского университета заявили, что самым ранним известным употреблением цифры 0 для обозначения отсутствия значения разряда (как в числе 101) следует считать текст индийского манускрипта Бахшали.
-
BBC

Как «единица» помогла построить первые города и великие империи? Как вдохновляла выдающиеся умы человечества? Какую роль в появлении денег она сыграла? Как «единица» объединилась с нулем, чтобы править современным миром? История единицы неразрывно связана с историей европейской цивилизации. Терри Джонс отправляется в юмористическое путешествие с целью собрать воедино удивительную историю нашего самого простого числа. С помощью компьютерной графики в этой программе единица оживает в самых различных испостасях. Из истории единицы становится ясно, откуда появились современные числа, и каким образом изобретение нуля спасло нас от необходимости сегодня использовать римские цифры.
Далее >>>
|
|


 Знаете ли вы, почему в окружности 360 градусов, а не 180 или, скажем, не 300? Откуда пошла традиция делить окружность на равные части и почему было выбрано именно такое их число? Оказывается, этому делению мы обязаны вавилонянам. Считается, что они же изобрели простейший инструмент для измерения углов − транспортир. Но вот вопрос: как же древние сумели разделить окружность на равные части, не владея техникой геометрических построений и располагая лишь примитивными инструментами?
Знаете ли вы, почему в окружности 360 градусов, а не 180 или, скажем, не 300? Откуда пошла традиция делить окружность на равные части и почему было выбрано именно такое их число? Оказывается, этому делению мы обязаны вавилонянам. Считается, что они же изобрели простейший инструмент для измерения углов − транспортир. Но вот вопрос: как же древние сумели разделить окружность на равные части, не владея техникой геометрических построений и располагая лишь примитивными инструментами? Всем говорят в школе, что число π иррационально и даже — трансцендентно, т. е. не является корнем многочлена с целыми коэффициентами. Имеется изящное и вполне элементарное доказательство Эрмита иррациональности числа π (требующее только знания интегрирования по частям — понимания как вычислить интеграл ∫ x^k sin(x)dx в пределах от a до b). Наша цель — доказательство теоремы Линдемана–Веерштрасса (если α_i линейно независимые над Q алгебраические числа, то e^(α_i) алгебраически независимы), а также теоремы Гельфонда (если числа α ≠ 0,1; β ∉ Q алгебраические, то αβ есть число трансцендентное).
Всем говорят в школе, что число π иррационально и даже — трансцендентно, т. е. не является корнем многочлена с целыми коэффициентами. Имеется изящное и вполне элементарное доказательство Эрмита иррациональности числа π (требующее только знания интегрирования по частям — понимания как вычислить интеграл ∫ x^k sin(x)dx в пределах от a до b). Наша цель — доказательство теоремы Линдемана–Веерштрасса (если α_i линейно независимые над Q алгебраические числа, то e^(α_i) алгебраически независимы), а также теоремы Гельфонда (если числа α ≠ 0,1; β ∉ Q алгебраические, то αβ есть число трансцендентное). Детские рисунки (dessins d'enfants) – термин, введённый Александром Гротендиком в 70-е годы прошлого века. С «детской» точки зрения этот термин означает граф, вложенный в поверхность; с взрослой – это объект, в котором закодированы различные структуры, относящиеся к далёким друг от друга областям математики. Под подсчётом детских рисунков понимается подсчёт количества детских рисунков ограниченной сложности, которая будет определена. В последние годы были получены замечательные результаты о количествах детских рисунков. Элементарная часть этих результатов будет изложена в курсе.
Детские рисунки (dessins d'enfants) – термин, введённый Александром Гротендиком в 70-е годы прошлого века. С «детской» точки зрения этот термин означает граф, вложенный в поверхность; с взрослой – это объект, в котором закодированы различные структуры, относящиеся к далёким друг от друга областям математики. Под подсчётом детских рисунков понимается подсчёт количества детских рисунков ограниченной сложности, которая будет определена. В последние годы были получены замечательные результаты о количествах детских рисунков. Элементарная часть этих результатов будет изложена в курсе. Предполагается прочесть четыре лекции. Первые две будут популярны и общепонятны, а третья и четвёртая будут содержать довольно поверхностные обзоры некоторых перспективных направлений современной математики. 1. О геометрии над конечными полями. 2. Группы Шевалле и группы перестановок. 3. Линейная алгебра над F1 и гомотопическая топология. 4. Разное. Обобщённые кольца Дурова и F∅, F±1, F∞√1. Анализ на множестве корней из единицы (по Хабиро, Концевичу, Манину). О геометрии Аракелова. О тропической математике.
Предполагается прочесть четыре лекции. Первые две будут популярны и общепонятны, а третья и четвёртая будут содержать довольно поверхностные обзоры некоторых перспективных направлений современной математики. 1. О геометрии над конечными полями. 2. Группы Шевалле и группы перестановок. 3. Линейная алгебра над F1 и гомотопическая топология. 4. Разное. Обобщённые кольца Дурова и F∅, F±1, F∞√1. Анализ на множестве корней из единицы (по Хабиро, Концевичу, Манину). О геометрии Аракелова. О тропической математике. Математик Илья Щуров о десятичных дробях, трансцендентности и иррациональности числа Пи.
Математик Илья Щуров о десятичных дробях, трансцендентности и иррациональности числа Пи. Математик Мишель Рудольф-Лилит из Национального центра научных исследований Франции описала особенности окружностей, начерченных в дискретном пространстве, в качестве примера которого ученый рассмотрела пересечения улиц и проспектов Манхэттена — центрального района Нью-Йорка. Оказалось, что можно аналитически описать несколько алгоритмов, следуя которым, гипотетический таксист проедет вдоль линии, максимально приближенной к идеальной окружности, а при достаточно большом ее радиусе можно с хорошей точностью измерить число π.
Математик Мишель Рудольф-Лилит из Национального центра научных исследований Франции описала особенности окружностей, начерченных в дискретном пространстве, в качестве примера которого ученый рассмотрела пересечения улиц и проспектов Манхэттена — центрального района Нью-Йорка. Оказалось, что можно аналитически описать несколько алгоритмов, следуя которым, гипотетический таксист проедет вдоль линии, максимально приближенной к идеальной окружности, а при достаточно большом ее радиусе можно с хорошей точностью измерить число π. Ученые из Оксфордского университета заявили, что самым ранним известным употреблением цифры 0 для обозначения отсутствия значения разряда (как в числе 101) следует считать текст индийского манускрипта Бахшали.
Ученые из Оксфордского университета заявили, что самым ранним известным употреблением цифры 0 для обозначения отсутствия значения разряда (как в числе 101) следует считать текст индийского манускрипта Бахшали. Как «единица» помогла построить первые города и великие империи? Как вдохновляла выдающиеся умы человечества? Какую роль в появлении денег она сыграла? Как «единица» объединилась с нулем, чтобы править современным миром? История единицы неразрывно связана с историей европейской цивилизации. Терри Джонс отправляется в юмористическое путешествие с целью собрать воедино удивительную историю нашего самого простого числа. С помощью компьютерной графики в этой программе единица оживает в самых различных испостасях. Из истории единицы становится ясно, откуда появились современные числа, и каким образом изобретение нуля спасло нас от необходимости сегодня использовать римские цифры.
Как «единица» помогла построить первые города и великие империи? Как вдохновляла выдающиеся умы человечества? Какую роль в появлении денег она сыграла? Как «единица» объединилась с нулем, чтобы править современным миром? История единицы неразрывно связана с историей европейской цивилизации. Терри Джонс отправляется в юмористическое путешествие с целью собрать воедино удивительную историю нашего самого простого числа. С помощью компьютерной графики в этой программе единица оживает в самых различных испостасях. Из истории единицы становится ясно, откуда появились современные числа, и каким образом изобретение нуля спасло нас от необходимости сегодня использовать римские цифры.