|
||
|
|
||
| Главная ≫ Инфотека ≫ Математика ≫ Теорема Коперника и робот-пылесос |
Теорема Коперника и робот-пылесос
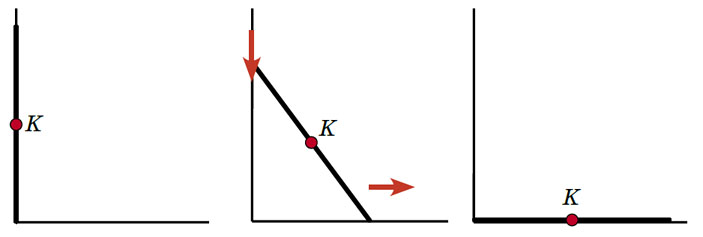
В журнале «Квантик» № 5, 2016 была опубликована следующая задача: «Робот-пылесос, имеющий форму круга, проехал по плоскому полу. Для каждой точки граничной окружности робота можно указать прямую, на которой эта точка оставалась в течение всего времени движения. Обязательно ли и центр робота оставался на некоторой прямой в течение всего времени движения?» Удивительно, но ответ отрицателен — центр мог двигаться не по прямой! Мы дадим несколько решений, начнём издалека, зато узнаем по дороге много интересного. Квантик на лестницеПусть к стене вертикально приставлена лестница, на середине которой неподвижно сидит Квантик (вид сбоку показан на рисунке 1). Лестница съезжает — нижний конец движется по полу вправо, а верхний движется по стене вниз (рис. 2), — пока не ляжет на пол (рис. 3). По какой линии движется Квантик?
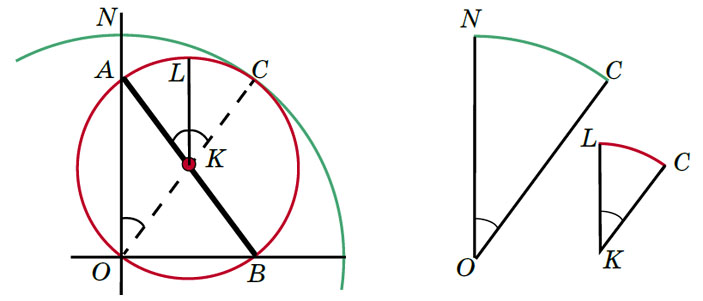
Пусть О — точка под лестницей, в которой стыкуются стена и пол. Заметим, что и в начале, и в конце пути Квантик находится от точки O на одном и том же расстоянии, равном половине длины лестницы. А что будет в любом промежуточном положении (рис. 4)? Достроим треугольник AOB до прямоугольника OACB. Квантик находится в точке пересечения диагоналей этого прямоугольника (рис. 5). Так как диагонали равны и точкой пересечения делятся пополам, OK — это половина AB. Получается, что расстояние от Квантика до точки O всегда одно и то же.
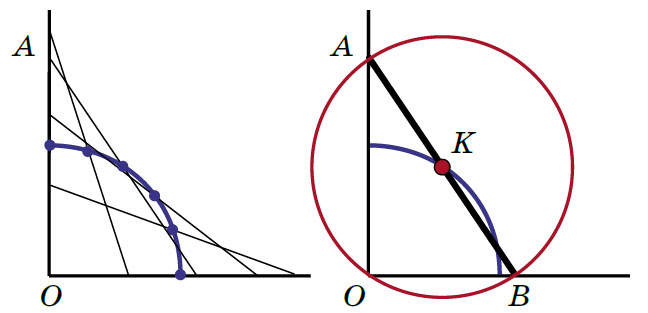
Значит, Квантик всё время находится на окружности с центром в точке O и радиусом длиной в половину лестницы, более точно — на четверти этой окружности (синяя линия на рисунке 6). В каждой ли точке этой линии Квантик побывает? Очевидно, что да: Квантик движется «непрерывно» и не может «пропустить» какую-то точку синей дуги. Можно даже для каждой точки K на дуге нарисовать соответствующее положение лестницы: продлеваем OK до OC (удваивая) и достраиваем до прямоугольника. Итак, путь Квантика — четверть окружности (рис. 6).
Но при чём здесь задача о круглом пылесосе? Прикрепим к лестнице пылесос, ограниченный красной окружностью (рис. 7) так, чтобы лестница была диаметром этой окружности (Квантик тогда сидит в её центре). Вместе со съезжающей лестницей-диаметром будет двигаться и окружность. При этом две точки окружности — концы лестницы, — будут перемещаться по прямым (стене и полу), а центр окружности (Квантик) — не по прямой, а по дуге! Одна окружность катится по другой
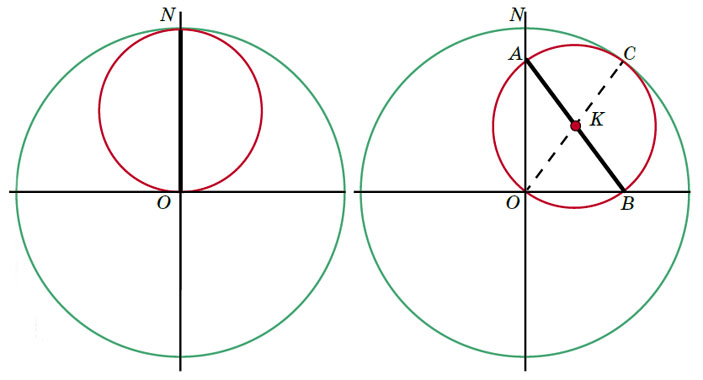
Оказывается, и остальные точки красной окружности будут двигаться по прямым. Чтобы доказать это, нам понадобится ещё одна окружность — с центром в точке O и радиусом, равным длине лестницы (она отмечена зелёным на рисунке 8). Сейчас мы докажем, что красная окружность будет просто катиться по зелёной (без проскальзывания). Рассмотрим, например, положение красной окружности, изображённое на рисунке 9: лестница NO переехала в положение AB, Квантик сидит в точке K (заметьте, что красная окружность всегда проходит через O). Удвоим отрезок OK, продлив его до OC. Точка С окажется одновременно и на красной, и на зелёной окружностях. Отметим середину L дуги AC (рис. 10). Ясно, что углы LKC и NOC равны (так как NO и LK параллельны). Поскольку радиус красной окружности в два раза меньше радиуса зелёной, красная дуга LC в два раза короче зелёной дуги NC (рис. 11). Но тогда вдвое большая, чем LC, красная дуга AC равна зелёной дуге NC.
Это и значит, что красная окружность катится по зелёной, не проскальзывая: зелёное расстояние от точки N до точки касания окружностей всегда равно красному расстоянию от A до точки касания. Но если какая-то точка красной окружности движется по прямой, то и остальные тоже — ведь красная окружность равномерно катится по зелёной, и все точки красной окружности равноправны. Чтобы узнать, по какой именно прямой движется конкретная точка X красной окружности, можно дождаться, когда X попадёт на зелёную окружность, и в этот момент соединить прямой O и Х. Мы доказали теорему Коперника: если окружность катится по внутренней стороне вдвое большей окружности, то каждая точка катящейся окружности всё время остаётся на некоторой прямой. Решение в движении смотрите в мультфильме «Котёнок на лестнице». Пылесос едет и вращается
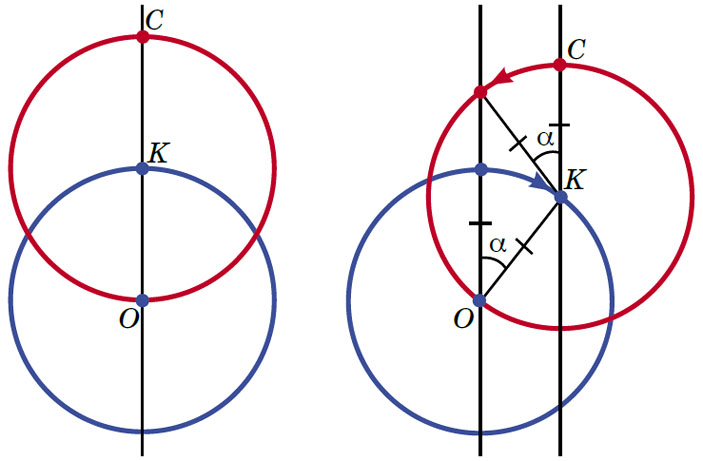
Приведём более короткое решение исходной задачи — опишем другим способом, как должен двигаться пылесос (ограниченный красной окружностью). Нарисуем на столе синюю окружность с центром в точке O и такого же радиуса, как у пылесоса. Запустим пылесос так, чтобы его центр K двигался равномерно по синей окружности, а сам пылесос при этом вращался: если центр пылесоса поворачивается вокруг O на некий угол, то сам пылесос поворачивается вокруг своего центра на тот же самый угол в обратную сторону. При таком движении все точки красной окружности равноправны — достаточно про любую из них доказать, что она движется вдоль некоторой прямой. Пусть пылесос стартовал из положения, показанного на рисунке 12. Докажем, что точка C пылесоса (его верхняя точка в стартовом положении) движется по прямой, проходящей через O.
Пусть центр пылесоса (K) повернулся на угол α вокруг О (по часовой стрелке). Если бы пылесос не вращался вокруг своего центра, точка C по-прежнему находилась бы над K, то есть на вертикальной прямой, проходящей через K (эта воображаемая ситуация показана на рисунке 13). Но надо ещё повернуть точку C на угол α в обратную сторону. Где окажется C после этого? Поскольку точка K синей окружности, лежавшая над её центром, повернувшись на угол α по часовой стрелке, переехала с левой вертикальной прямой на правую, то точка C, лежащая над центром точно такой же красной окружности, повернувшись на тот же самый угол α против часовой стрелки, переедет с правой вертикальной прямой на левую! Задача решена. Интересный факт
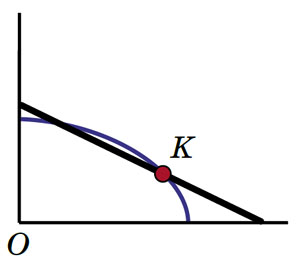
Вернёмся к задаче про Квантика. А что, если он будет сидеть не на середине лестницы, а в какой-то другой её точке (не на концах)? Тогда траектория Квантика будет четвертью эллипса (рис. 14). Много других интересных фактов можно найти в книге Н. Б. Васильева и В. Л. Гутенмахера «Прямые и кривые» (М.: МЦНМО, 2016), по мотивам введения к которой и написана эта статья.
Художник: Мария Усеинова Сергей Дориченко
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Математика ≫ Теорема Коперника и робот-пылесос |
|
[time: 7 ms; queries: 7]
11 Мар 2026 01:18:50 GMT+3 |


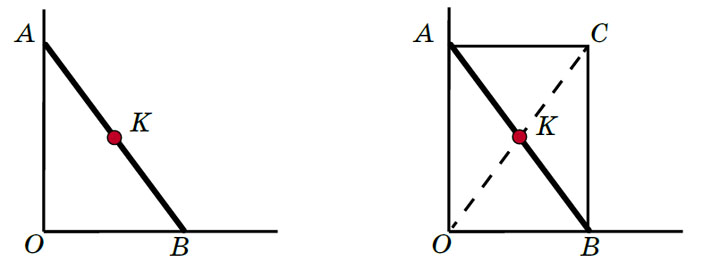


 В 1850 году преподобный Томас Киркман, британский математик и настоятель прихода в Ланкашире, сформулировал невинно выглядящую головоломку в развлекательном журнале для любителей математики. Задачка выглядит простой, но если попробовать её решить, то сразу понимаешь, что это не так. В силу своей ложной простоты задача быстро стала знаменитой. Свои решения присылали любители математики, а учёные публиковали научные статьи с попыткой сформулировать общее решение для проблемы. В результате, эта головоломка помогла сформировать новое направление математики.
В 1850 году преподобный Томас Киркман, британский математик и настоятель прихода в Ланкашире, сформулировал невинно выглядящую головоломку в развлекательном журнале для любителей математики. Задачка выглядит простой, но если попробовать её решить, то сразу понимаешь, что это не так. В силу своей ложной простоты задача быстро стала знаменитой. Свои решения присылали любители математики, а учёные публиковали научные статьи с попыткой сформулировать общее решение для проблемы. В результате, эта головоломка помогла сформировать новое направление математики. 8 августа 1900 года Давид Гильберт сделал на Втором Математическом конгрессе доклад, представив слушателям ставший с тех пор знаменитым список проблем столетия. За прошедшие сто с лишним лет большая их часть была решена – и, что важнее, в ходе их решения появились новые сюжеты и новое понимание. Я собираюсь затронуть несколько из них и обсудить, в каком контексте они формулировались и куда продвинулось наше понимание за эти сто лет. Этот курс предполагается обзорным и адресованным школьникам (в частности, он не предполагает предварительных сведений).
8 августа 1900 года Давид Гильберт сделал на Втором Математическом конгрессе доклад, представив слушателям ставший с тех пор знаменитым список проблем столетия. За прошедшие сто с лишним лет большая их часть была решена – и, что важнее, в ходе их решения появились новые сюжеты и новое понимание. Я собираюсь затронуть несколько из них и обсудить, в каком контексте они формулировались и куда продвинулось наше понимание за эти сто лет. Этот курс предполагается обзорным и адресованным школьникам (в частности, он не предполагает предварительных сведений).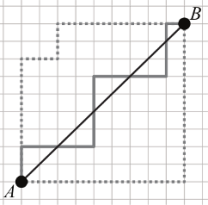 Математик Мишель Рудольф-Лилит из Национального центра научных исследований Франции описала особенности окружностей, начерченных в дискретном пространстве, в качестве примера которого ученый рассмотрела пересечения улиц и проспектов Манхэттена — центрального района Нью-Йорка. Оказалось, что можно аналитически описать несколько алгоритмов, следуя которым, гипотетический таксист проедет вдоль линии, максимально приближенной к идеальной окружности, а при достаточно большом ее радиусе можно с хорошей точностью измерить число π.
Математик Мишель Рудольф-Лилит из Национального центра научных исследований Франции описала особенности окружностей, начерченных в дискретном пространстве, в качестве примера которого ученый рассмотрела пересечения улиц и проспектов Манхэттена — центрального района Нью-Йорка. Оказалось, что можно аналитически описать несколько алгоритмов, следуя которым, гипотетический таксист проедет вдоль линии, максимально приближенной к идеальной окружности, а при достаточно большом ее радиусе можно с хорошей точностью измерить число π.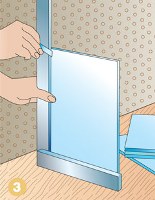 В школе мы несколько лет подряд прилежно изучаем геометрию. Но не зря ли мы тратим время? Чем может помочь геометрия в жизни? Измерить расстояние от точки до точки, вычислить площадь или объём предмета и только? Нет, конечно. Законы геометрии применимы буквально на каждом шагу. Просто нужно знать, как ими воспользоваться.
В школе мы несколько лет подряд прилежно изучаем геометрию. Но не зря ли мы тратим время? Чем может помочь геометрия в жизни? Измерить расстояние от точки до точки, вычислить площадь или объём предмета и только? Нет, конечно. Законы геометрии применимы буквально на каждом шагу. Просто нужно знать, как ими воспользоваться. Математики из Вашингтонского университета в Ботелле открыли новый тип пятиугольных паркетов — выпуклых пятиугольников, которыми можно замостить плоскость без пробелов и наложений. Ранее было известно только 14 типов таких пятиугольников, последний из которых был открыт 30 лет назад.
Математики из Вашингтонского университета в Ботелле открыли новый тип пятиугольных паркетов — выпуклых пятиугольников, которыми можно замостить плоскость без пробелов и наложений. Ранее было известно только 14 типов таких пятиугольников, последний из которых был открыт 30 лет назад.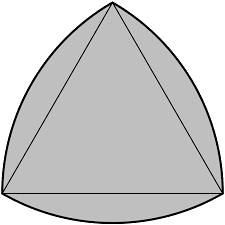 Почему крышки люков делают круглыми? Что такое фигура постоянной ширины? Какими интересными свойствами обладает треугольник Рело и как его построить? Почему английская 20-пенсовая монета имеет такую необычную форму? Как и чем сверлят квадратные отверстия? Что представляют собой фигуры постоянной ширины в трёхмерном пространстве и какая открытая математическая проблема с ними связана?
Почему крышки люков делают круглыми? Что такое фигура постоянной ширины? Какими интересными свойствами обладает треугольник Рело и как его построить? Почему английская 20-пенсовая монета имеет такую необычную форму? Как и чем сверлят квадратные отверстия? Что представляют собой фигуры постоянной ширины в трёхмерном пространстве и какая открытая математическая проблема с ними связана? Лекцию читает Арнольд Владимир Игоревич (1937–2010), доктор физико-математических наук, профессор, академик РАН. Летняя школа «Современная математика», г. Дубна, 20 июля 2007 г.
Лекцию читает Арнольд Владимир Игоревич (1937–2010), доктор физико-математических наук, профессор, академик РАН. Летняя школа «Современная математика», г. Дубна, 20 июля 2007 г.