Тематику дифференциальных уравнений, безусловно, надо расширять, иначе «молодые побеги» — хаос, аттракторы, солитоны — будут расти сквозь асфальт. С другой стороны, базовые курсы нуждаются в резком сокращении, поскольку для самих дифуров не так много места остается в этой жизни. Из-за информационного переполнения. При этом стандартных мер недостает. Единственное средство — тривиализация дисциплины. Математика, как и человек, — иногда надувает щеки, наряжается и творит мифы. Поэтому в дифурах немало лишнего, вычурного, случайного — и одно лишь наведение порядка высвобождает массу свободного места. Данный мини-курс адресован «всем», поскольку преподносит некую общую часть. Не простую и не сложную, но дающую представление об основах и позволяющую при необходимости быстро войти в предмет и двигаться дальше.

ТФКП — теория функций комплексной переменной, эквивалент «теории аналитических функций». Математическая дисциплина второго круга образования — не в каждом техническом ВУЗе преподаётся. А жаль. Потому что ТФКП необыкновенно красива и в своей основе достаточно проста. Ибо в римановы пространства и конформные преобразования не обязательно заглядывать без особой надобности. Но и без них в лучах «аналитических функций» многое в нижележащих слоях математики озаряется буквально волшебным светом. Проясняется и упрощается. Вскрываются внутренние механизмы, обнажаются загадки. Поэтому ТФКП, по крайней мере в «данном исполнении», можно рекомендовать для самообразования. Простое изложение может оказаться полезным и при углублённом изучении предмета, когда подробности мешают видеть общую картину.

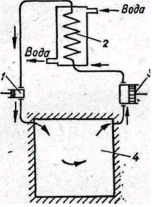
Воздух как хладагент безвреден, общедоступен, безопасен и почти нейтрален к металлам и смазочным маслам, поэтому его применение в холодильной технике весьма удобно. Однако его недостатком является малая объемная холодопроизводительность.

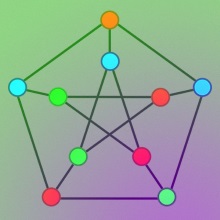
Несколько дней назад сообщество математиков — специалистов в теории графов было взволновано сообщением о том, что выдвинутая Стефеном Хидетниеми (Stephen T. Hedetniemi) в 1966 году гипотеза оказалась неверной. Оказывается, хроматическое число тензорного произведения двух графов может быть меньше минимума хроматических чисел сомножителей, а не всегда равно этому минимуму, как когда-то предположил Хидетниеми. Как построить контрпример к этой гипотезе, придумал молодой московский математик Ярослав Шитов.

Четыре тысячи лет назад жители Вавилонии изобрели умножение. А в марте этого года математики усовершенствовали его. 18 марта 2019 два исследователя описали самый быстрый из известных методов перемножения двух очень больших чисел. Работа отмечает кульминацию давнишнего поиска наиболее эффективной процедуры выполнения одной из базовых операций математики. «Все думают, что метод умножения, который они учили в школе, наилучший, но на самом деле в этой области идут активные исследования», — говорит Йорис ван дер Хувен, математик из Французского национального центра научных исследований, один из соавторов работы.

Лекция посвящена тому, как последние открытия повлияли на наше представление о макромире и какие вопросы встали на повестку дня. Эволюция вселенной в первые мгновения после большого взрыва. Темная материя и темная энергия. Вещество и антивещество. Законы сохранения и барионное число. Как объяснить неоднородность вселенной. Теория инфляционной вселенной. Флуктуации вакуума. Реликтовые гравитационные волны.

Словарь отвечает на многие вопросы из области техники, рассказывает об истории ее развития и научно-техническом прогрессе, об известных ученых и наиболее выдающихся открытиях. Книга охватывает большой круг знаний — от космической техники до техники кино и телевидения, рассказывает о многих профессиях. В ней содержатся практические советы юным техникам. Для школьников среднего и старшего возраста.

Если концепция мультивселенной кажется странной, так это потому, что нам нужно поменять наши представления о времени и пространстве.

Попробуйте выведать у физика, что такое время. Это вам очевидно, что время это последовательность событий и оно течет вперед. Чем больше вы знаете и чем глубже погружаетесь, тем менее это становится очевидным. Описание того, что такое время, все больше схлопывается к тому, что время — это буквочка t, которая участвует в таких-то математических уравнениях. По мере движения к все более фундаментальному уровню математика становится все более сложной, а словесно-описательный багаж начинает все больше вырождаться. В пределе, предполагает Макс, у Общей Теории Всего нет багажа. Физика пытается найти уравнения для нашего мира, исходя из наблюдений и экспериментальных данных. Макс предлагает рассмотреть “Физику Наоборот” — вы задаете уравнения, какой мир вы получаете?

Возьмем наш любимый iPhone. У меня он уже три или четыре года, и он берет на себя целую кучу функций моего мозга. То, что раньше делал мой мозг, теперь делает мой iPhone. Возьмем память: сколько людей используют свой мозг, чтобы запоминать номера телефонов? Уж точно не я! Я хочу поговорить с вами о новом взгляде на сознание. То, что я называю расширенным сознанием, — это идея о том, что технологии, которые мы используем, становится частью нашего сознания, распространяя его, и значит нас самих.

Миллиарды нейронов у нас в мозге постоянно трудятся над созданием сознательного опыта, восприятия мира вокруг и внутри вас. Как это происходит? Нейроученый Анил Сет считает, что все мы постоянно галлюцинируем, а когда наши галлюцинации совпадают, мы называем это реальностью. Возможно, его выступление заставит вас задуматься о самой природе существования.

Экзистенциализм. Хайдеггер: особенность человеческого существования Dasein. Экзистенциализм Сартра. Философия жизни. Структурализм. Постструктурализм. Фердинанд де Соссюр: язык есть пучок различий. Жак Деррида и Жан Лиотар.

Определение метафизики. Метафизика vs Позитивизм. Верификация и фальсификация. Логический позитивизм и Людвиг Витгенштейн. Критика субъектоцентризма. Структурализм. Детрансцендирование и имманентизм в философии. Критика субъект-объектного дуализма. Феноменология Гуссерля и интенциональность. Мартин Хайдеггер: не субъект, но Dasein. Мишель Фуко: смерть субъекта.

RSA (аббревиатура от фамилий Rivest, Shamir и Adleman) — криптографический алгоритм с открытым ключом, основывающийся на вычислительной сложности задачи факторизации больших целых чисел. Алгоритм используется в большом числе криптографических приложений, включая PGP, S/MIME, TLS/SSL, IPSEC/IKE и других.

Вычислимая функция f:N→N называется доказуемо рекурсивной в данной формальной теории T, если существует алгоритм её вычисления такой, что в T можно доказать утверждение «для любого x существует y такой, что f(x)=y». В математической логике такие функции изучаются по двум причинам. Во-первых, для данной программы нас часто интересует доказательство её корректности, в частности вопрос о том, завершает ли она работу при любых исходных данных. С другой стороны, варьируя функцию f мы можем ставить для теории T сколь угодно сложные (вплоть до невыполнимости) задачи на доказательство. Тем самым, доказуемо рекурсивные функции могут быть использованы для изучения различных формальных теорий. Такой подход приводит к наиболее впечатляющим на сегодняшний день примерам недоказуемых комбинаторных утверждений. Мы начнем с понятия машины Тьюринга и вычислимой функции. Разберемся, как формальная арифметика может говорить о вычислениях. Поймем, что для любых разумных систем аксиом T их запас доказуемо рекурсивных функций никак не может исчерпывать все вычислимые всюду определенные функции. Отсюда выведем первую теорему Гёделя о неполноте.

Если представлять себе выдающиеся произведения научной литературы как горные маршруты, уводящие в небо, то наш небольшой курс — не более чем прогулка с видом на далекие белоснежные вершины. Мы собираемся просмотреть видимые начала одного из красивейших маршрутов, уводящего далеко за облака, к высоким перевалам и вершинам классической механики. Очень скоро вчерашние школьники сами выйдут на этот маршрут, а пока… давайте немного потренируемся.

Я приведу два весьма важных с прикладной точки зрения примера задач, которые тесно связаны с фундаментальными теоретическими вопросами. 1. Равномерное распределение точек в многомерном единичном кубе. Как понимать «равномерное»? Существует несколько подходов. Подход, который мы обсудим в деталях, ведет к понятию дискрепанса. Оказывается, что это понятие тесно связано с численным интегрированием функции многих переменных. 2. Экономное представление функций. В реальной жизни многие сигналы могут быть приближенно представлены в виде линейной комбинации небольшого числа базисных функций. Например, это относится к музыке, где можно использовать тригонометрическую систему в качестве источника базисных функций. Такие представления называются «разреженными». Возникает естественный вопрос. Как строить разреженные приближения?

Чем определяется успех на математических олимпиадах? Коррелируют ли олимпиадные успехи с будущими научными достижениями? Какие навыки необходимы для того, чтобы стать настоящим учёным? Рассказывает Алексей Савватеев, математик и матэкономист, доктор физико-математических наук, научный руководитель Кавказского Математического Центра АГУ, ректор Университета Дмитрия Пожарского, профессор МФТИ, научный руководитель ЦДПО РЭШ, ведущий научный сотрудник ЦЭМИ РАН, популяризатор математики среди детей и взрослых.

Общая постановка такова. Пусть P(x_1,…,x_n) — некоммутативный многочлен от матриц порядка n. Каким может быть множество его значений? И. Капланский и И. В. Львов поставили вопрос о том, что множество значений полилинейного многочлена есть векторное пространство (в этом случае оно совпадает либо с нулем, либо с пространством всех матриц, либо с пространством бесследовых матриц, либо со скалярными матрицами). Решение проблемы Капланского для матриц второго порядка над квадратично замкнутым полем оказалось весьма нетривиальным и глубоким. Вопросы, связанные с уравнениями в матрицах, помимо прикладного значения имеют отношение к конструкции алгебраически замкнутого тела, к теореме о свободе: если добавить новую некоммутативную переменную и соотношение, где та участвует, то это не приведет к появлению новых соотношений. Имеется ряд глубоких проблем, относящихся к множеству значений слов в группе — в частности, в матрицах второго порядка.

Рассматривается дискретный аналог броуновского движения. Именно свойства этого блуждания являются целью лекций с последующим переходом к броуновскому движению (винеровскому процессу). Применяя вероятностный подход мы вводим прежде всего основные характеристики: вероятностное пространство (Ω,F,P), случайные величины, математические ожидания и др. Далее рассматриваются фундаментальные свойства случайных блужданий: закон больших чисел, теорема Муавра-Лапласа, усиленный закон больших чисел, закон повторного логарифма и др. На примерах будет показано как вероятностная комбинаторика и свойства случайных блужданий приводят к результатам, слабо поддающихся интуиции.