Решения

• Глава 1
• Глава 2
• Глава 3
• Глава 4
• Глава 5
• Глава 6
• Глава 7
• Глава 9
• Глава 11

Глава 1

Кто Джон? Для того чтобы узнать, кого из двух братьев-близнецов зовут Джон, нужно спросить одного из них: «Джон говорит правду?». Если в ответ на этот вопрос последует «да», то независимо от того, лжет ли спрошенный близнец или говорит всегда только правду, он должен быть Джоном. Если же он ответит «нет», то Джоном зовут его брата. Доказать это можно следующим образом.

Если спрошенный близнец отвечает «да», то он тем самым утверждает, что Джон говорит правду. Если это утверждение истинно, то Джон действительно говорит правду, а так как говорящий изрек истину, то его и должны звать Джоном. Если же высказанное утверждение ложно, то Джон в действительности не говорит правду. Значит, Джон лжет, как лжет и спрошенный близнец. Следовательно, и в этом случае спрошенного должны звать Джоном. Тем самым доказано, что независимо от того, говорит ли тот, к кому мы обращаемся с вопросом, всегда только правду или лжет, он должен быть Джоном (в предположении, что на наш вопрос он ответил «да»).

Если же спрошенный нами ответит «нет», то тем самым он утверждает, что Джон говорит неправду. Если это утверждение истинно, то Джон не говорит правду, а если ложно, то Джон говорит правду. И в том и в другом случае спрошенный близнец поступает не так, как Джон. Следовательно, он должен быть братом Джона. Таким образом, «нет» в ответ на заданный вопрос означает, что спрошенного зовут не Джон.

Разумеется, вопрос «Лжет ли Джон?» ничуть не хуже. «Да» в ответ на этот вопрос означает, что спрошенный близнец не Джон, а «нет» – что его зовут Джон.

Мне удалось придумать только эти два вопроса в три слова, которые позволяют решить задачу. Интересно, есть ли другие?

* * *

Во второй задаче (найти вопрос из трех слов, позволяющий установить, не лжет ли Джон) достаточно просто спросить: «Вы не Джон?»

Предположим, что близнец, к которому мы обращаемся, отвечает «да». Он либо говорит правду, либо лжет. Предположим, что выбранный нами близнец говорит правду. Тогда его действительно зовут Джон, а так как он говорит правду, то Джон всегда говорит только правду.

Предположим теперь, что близнец, к которому мы обращаемся, лжет. Тогда в действительности его зовут не Джон (раз он утверждает, что его зовут Джон). Значит, он лжет и его зовут не Джон, поэтому Джоном должен быть тот из братьев, кто всегда говорит только правду. Тем самым доказано, что если близнец, к которому мы обращаемся с вопросом, отвечает «да», то независимо от того, лжет ли он или говорит правду, того, кто всегда говорит только правду, зовут Джоном.

Предположим теперь, что в ответ на наш вопрос мы услышали «нет». Близнец, к которому мы обратились, либо лжет, либо всегда говорит только правду. Предположим, что он говорит правду. Тогда он действительно не Джон и Джоном зовут другого брата, а поскольку другой брат всегда говорит только правду, Джоном зовут того из двух братьев, кто лжет.

Предположим теперь, что близнец, к которому мы обратились, лжет. Тогда (поскольку лжец утверждает, что он не Джон) его настоящее имя должно быть Джон, поэтому Джоном в данном случае зовут лжеца. Тем самым доказано, что если близнец, к которому мы обращаемся с вопросом, отвечает «нет», то независимо от того, лжет он или говорит правду, того, кто лжет, зовут Джоном.

Между решениями двух задач, которые решали Алиса и ее гости, имеется замечательная симметрия. Для того чтобы узнать, не зовут ли того из близнецов, к которому вы обращаетесь, Джоном, ему необходимо задать вопрос: «Лжет ли Джон?». Для того чтобы выяснить, лжет ли Джон, необходимо задать вопрос: «Вы не Джон?».

Глава 2

1. История первая. По существу, Болванщик заявил, что варенье украли либо Мартовский Заяц, либо Соня. Если Болванщик солгал, то ни Мартовский Заяц, ни Соня не украли варенье. Но тогда Мартовский Заяц, поскольку он не украл варенье, дал правдивые показания. Следовательно, если Болванщик лгал, то Мартовский Заяц не лгал, поэтому Болванщик и Мартовский Заяц не могли лгать одновременно. Следовательно, когда Соня показала, что по крайней мере один из ее соседей, то есть либо Мартовский Заяц, либо Болванщик, не лгали, она сказала правду. Но из условий задачи мы знаем, что Соня и Мартовский Заяц не могли дать правдивые показания одновременно. Так как Соня сказала правду, Мартовский Заяц не мог дать правдивые показания. Значит, Мартовский Заяц солгал. Его показания ложны. Следовательно, варенье украл Мартовский Заяц.

2. История вторая. Предположим, что муку украл Мартовский Заяц. Так как тот, кто похитил муку, дал правдивые показания, Мартовский Заяц на суде сказал правду, то есть муку украл Болванщик. Но мы твердо знаем, что муку украл только один из трех обитателей домика. Следовательно, Мартовский Заяц не мог украсть муку. Значит, Мартовский Заяц невиновен. Но поскольку двое из трех подсудимых дали ложные показания на суде, Мартовский Заяц в своем выступлении на суде солгал. Неверно, что муку украл Болванщик (как утверждал Мартовский Заяц). Следовательно, ни Мартовский Заяц, ни Болванщик не могли украсть муку. Значит, муку должна была украсть Соня.

3. История третья. Если бы кухарка украла перец, то она заведомо знала бы об этом. Следовательно, давая показания на суде (когда она заявила, что знает, кто украл перец), она сказала бы правду. Между тем мы твердо знаем, что те, кто крадет перец, никогда не говорят правды. Следовательно, кухарка Герцогини невиновна.

4. Кто же украл перец? Если перец украл Мартовский Заяц, то он лгал (потому что те, кто крадет перец, всегда лгут). Следовательно, его утверждение о Болванщике ложно. Значит, Болванщик тоже украл перец. Но из условий задачи нам известно, что перец украл кто-то один. Следовательно, Мартовский Заяц не мог украсть перец. Так как Мартовский Заяц невиновен, его заявление на суде истинно. Значит, то, что он сказал о Болванщике, истинно. Следовательно, Болванщик также невиновен. В свою очередь это означает, что Болванщик сказал правду, поэтому Соня также невиновна. Таким образом, никто из троих подозреваемых не крал перец.

5. Так кто же все-таки украл перец? Предположим, что Грифон был бы виновен. Это означало бы, что, выступая на суде, он солгал. Следовательно, Черепаха Квази не невиновен (как утверждал Грифон), а виновен. Но тогда виновных было бы двое, хотя перец (как говорилось в предыдущей задаче) украл кто-то один. Значит, Грифон невиновен. Но тогда на суде он сказал правду, поэтому Черепаха Квази невиновен. Следовательно, Черепаха Квази на суде сказал правду: виновен Омар.

6. Метазадача. Те из вас, кто читал «Приключения Алисы в Стране Чудес», должно быть, помнят, что Омар (в отличие от Грифона и Черепахи Квази) не входит в число действующих лиц знаменитой сказки Льюиса Кэрролла. Он фигурирует лишь в стихотворении «Это голос Омара», которое читает Алиса.

7. История четвертая. Предположим, что сахар украла Герцогиня. Значит, выступая на суде, она лгала. Следовательно, ее утверждение о том, что кухарка не крала сахар, ложно. Иначе говоря, кухарка также должна была бы украсть сахар. Но как нам достоверно известно, сахар украден только одной из двух обвиняемых. Следовательно, Герцогиня не могла украсть сахар. Значит, сахар украла кухарка. (Заметим, кстати, что обе обвиняемые лгали.)

8. История пятая. Если соль съел Чеширский Кот, то все трое обвиняемых лгут, что противоречит условиям задачи. Если соль съел Ящерка Билль, то все трое всегда говорят только правду, что также противоречит условиям задачи. Следовательно, соль съела Гусеница (поэтому первые два заявления ложны, а третье истинно).

9. История шестая. Если сковороду украл Лягушонок, то он и Валет Червей оба лгали, что по условиям задачи исключается. Если сковороду украл Лакей-Лещ, то он и Валет Червей оба лгали, что по условиям задачи также исключается. Следовательно, сковороду украл Валет Червей (как ни смешно, но в своем выступлении на суде он сказал правду, как и Лакей-Лещ).

10. История седьмая. Чеширский Кот не мог украсть поваренную книгу, так как в этом случае вор говорил бы правду. Следовательно, Чеширский Кот не крал поваренную книгу (а Кот и Герцогиня лгали вдвоем на суде). Если бы поваренную книгу похитила кухарка, то лгали бы все трое обвиняемых, что противоречит условиям задачи. Значит, поваренную книгу украла Герцогиня (поэтому Герцогиня лжет, Чеширский Кот лжет, а кухарка всегда говорит только правду).

11. Продолжение седьмой истории. Чеширский Кот не мог украсть поваренную книгу по той же причине, что и в предыдущей задаче. Предположим, что поваренную книгу украла Герцогиня. Тогда Чеширский Кот лжет, а кухарка говорит правду, что противоречит условию задачи (если поваренную книгу украла Герцогиня, то двое других обвиняемых либо оба лгут, либо говорят правду). Следовательно, Герцогиня не похищала поваренную книгу. Ее украла кухарка. (Двое других обвиняемых либо оба лгут, либо оба говорят правду – в действительности оба лгут. Все трое – лжецы.)

12. История восьмая. Прежде всего заметим, что Соня не могла украсть масло (тот, кто украл масло, говорит правду, а Соня на суде показала, что украла молоко). Следовательно, молоко украла не Соня. Значит, масло украл либо Мартовский Заяц, либо Болванщик. Если бы масло украл Мартовский Заяц, то его утверждение о том, что масло украл Болванщик, было бы истинным (напомним, что тот, кто украл масло, говорит правду). Но тогда масло должен был бы украсть Болванщик, а это противоречит условиям задачи (масло украл кто-то один из обвиняемых). Значит, масло украл не Мартовский Заяц. Но тогда масло украл Болванщик. Следовательно, его заявление на суде истинно и яйца украла_> Соня. Значит, Мартовский Заяц украл молоко.

Итак, Мартовский Заяц украл молоко, Болванщик украл масло (и всегда говорит только правду), а Соня украла яйца (и всегда лжет).

13. История девятая и последняя. Если бы Белый Кролик разбирался получше в логике, то он никогда бы не сказал, что Билль говорит правду, а Валет лжет, поскольку логически невозможно, чтобы Билль говорил правду, а Валет лгал! Иначе говоря, я утверждаю, что если Билль говорит правду, то Валету не остается ничего другого, как говорить правду. Позвольте мне доказать это.

Предположим, что Ящерка Билль говорит правду. Тогда его показания на суде истинны. Значит, либо Мартовский Заяц, либо Соня говорит правду (возможно, что правду говорят оба). Предположим, что правду говорит Мартовский Заяц. Тогда кухарка должна говорить правду (напомним, что, как показал на суде Мартовский Заяц, кухарка и Чеширский Кот говорят правду). С другой стороны, если Соня говорит правду, то кухарка должна опять-таки говорить правду (ибо так утверждала в своих показаниях на суде Соня). Таким образом, и в том и в другом случае (говорит ли правду Мартовский Заяц или Соня) кухарка должна говорить правду. Но либо Мартовский Заяц, либо Соня говорит правду. Следовательно, в любом случае кухарка должна говорить правду. Это доказывает, что кухарка говорит правду (разумеется, в предположении, которое мы разделяем, что Ящерка Билль сказал правду). Кроме того, Мартовский Заяц показал (и это подтвердила кухарка), что Чеширский Кот говорит правду, а Соня показала (и ее слова также подтвердила кухарка), что Гусеница говорит правду,… Следовательно, либо Чеширский Кот, либо Гусеница говорит правду (поскольку либо Мартовский Заяц, либо Соня говорит правду; если правду говорит Мартовский Заяц, то не лжет Чеширский Кот; если же правду говорит Соня, то не лжет Гусеница). Но в своих показаниях на суде Болванщик утверждал, что либо Чеширский Кот, либо Гусеница говорит правду, поэтому сам Болванщик говорит правду. Значит, и кухарка, и Болванщик говорят правду. Именно это и утверждал Валет Червей. Таким образом, Валет Червей говорит правду (разумеется, при условии, что Ящерка Билль говорит правду).

Итак, мы доказали, что если Ящерка Билль говорит правду, то Валет Червей не может не говорить только правду. Значит, Белый Кролик лгал, когда утверждал, что Билль говорит правду, а Валет лжет. Итак, Белый Кролик – лжец.

Обратимся теперь к показаниям Алисы (их истинность не вызывает сомнений). Алиса сказала, что Белый Кролик и Герцогиня либо оба говорят правду, либо оба лгут. Говорить правду они оба не могут (так как Белый Кролик лжет). Следовательно, они могут только лгать вдвоем. Но коль скоро Герцогиня лжет, то крендели украл не кто иной, как Грифон.

Глава 3

14. Гусеница и Ящерка Билль. Гусеница считает, что и она, и Ящерка Билль не в своем уме. Если бы Гусеница была в здравом уме, то мнение о том, что и она, и Ящерка Билль не в своем уме, было бы ложно. Следовательно, Гусеница (будучи в здравом уме) не могла бы придерживаться этого ложного мнения. Значит, Гусеница не в своем уме. Но коль скоро она не в своем уме, то ее представление об окружающих превратно. Следовательно, неверно, что и Гусеница, и Ящерка Билль не в своем уме. Значит, другой партнер (Ящерка Билль) должен быть в здравом рассудке.

Итак, Гусеница не в своем уме, а Ящерка Билль в здравом рассудке.

15. Кухарка и Кот. Если бы кухарка была не в своем уме, то ее мнение о том, что по крайней мере один из двух – либо она, либо Чеширский Кот – не в своем уме, было бы истинным. Но тогда мы имели бы человека, который, будучи не в своем уме, придерживается здравых суждений, что противоречит условиям задачи. Следовательно, кухарка должна быть в здравом рассудке. А поскольку она в здравом уме, то ее суждения истинны, и поэтому один из двух – либо она, либо Чеширский Кот – не в своем уме. Поскольку этот «один» не кухарка, им должен быть Чеширский Кот.

Итак, кухарка в здравом рассудке, а Чеширский Кот не в своем уме.

16. Лакей-Лещ иЛягушонок. Приведенные в условиях задачи сведения не позволяют определить, в здравом ли рассудке или не в своем уме Лакей-Лещ, но мы докажем, что Лягушонок должен быть в здравом рассудке. Будем рассуждать следующим образом.

Имеются две возможности: либо Лакей-Лещ в здравом рассудке, либо он не в своем уме. Покажем, что и в том и в другом случае Лягушонок должен быть в здравом рассудке.

Предположим, что Лакей-Лещ в здравом рассудке. Тогда он судит обо всем правильно. Значит, Лягушонок действительно во всем схож с Лакеем-Лещом. Следовательно, Лягушонок в здравом рассудке.

С другой стороны, предположим, что Лакей-Лещ не в своем уме. Тогда он обо всем судит превратно, поэтому Лягушонок совершенно несхож с Лакеем-Лещом. Так как Лакей-Лещ не в своем уме, то Лягушонок в противоположность ему должен быть в здравом рассудке.

Итак, в любом случае (в здравом ли рассудке Лакей-Лещ или не своем уме) Лягушонок должен быть в здравом уме.

А что если бы Лакей-Лещ считал Лягушонка не во всем схожим, а во всем несхожим с собой? Каким был бы тогда Лакей-Лещ – в здравом рассудке или не в своем уме?

Ответ: Лягушонок в таком случае должен был быть не в своем уме. Доказательство этого утверждения я предоставляю читателю в качестве самостоятельного упражнения.

17. Король и Королева Бубен. Никто из этой августейшей четы не может думать о себе, что он не в своем уме. Действительно, человек в здравом рассудке знает в соответствии с истиной, что он в своем уме, а безумец ошибочно полагает, что он в своем уме. Следовательно, Королева в действительности не думает, что она не в своем уме. Значит, не в своем уме Король, который считает, что Королева так думает.

Данные задачи не позволяют утверждать что-либо относительно того, в своем ли уме Королева Бубен.

18. Мартовский Заяц, Болванщик и Соня. Предположим, что Болванщик в своем уме. Тогда он обо всем судит здраво. Значит, Мартовский Заяц не думает, что все три участника безумного чаепития в своем уме. Следовательно, Мартовский Заяц должен быть в своем уме потому, что если бы он был не в своем уме, то разделял бы ложное мнение о том, что все три участника безумного чаепития в своем уме. Но тогда, Соня, считающая, что Мартовский Заяц в здравом рассудке, сама должна быть в своем уме. Значит, все три участника безумного чаепития должны быть в своем уме. Как же в таком случае мог Мартовский Заяц не признавать истинным утверждение о том, что все три участника безумного чаепития в своем уме? Полученное противоречие доказывает, что предположение о том, будто Болванщик в своем уме, ложно: в действительности Болванщик должен быть не в своем уме.

Так как Болванщик должен быть не в своем уме, он судит обо всем превратно, и поэтому Мартовский Заяц думает, что все три участника безумного чаепития в здравом рассудке. Разумеется, Мартовский Заяц заблуждается (так как Болванщик не в своем уме), поэтому Мартовский Заяц также не в своем уме. Но тогда и Соня, считающая, что Мартовский Заяц в здравом рассудке, также не в своем уме.

Итак, все трое участников безумного чаепития не в своем уме (что, впрочем, не слишком удивительно!).

19. Грифон, Черепаха Квази и Омар. Прежде всего Грифон и Черепаха Квази должны быть «одинаковыми», то есть либо оба не в своем уме, либо оба в здравом рассудке, так как Черепаха Квази считает, что Грифон в своем уме. Если Черепаха Квази в здравом рассудке, то это означает, что Грифон в своем уме. Если же Черепаха Квази не в своем уме, то он судит обо всем превратно. Значит, Грифон в действительности не в здравом рассудке, а безумен. Таким образом, Грифок и Черепаха Квази оба не в своем уме.

Докажем теперь, что Омар не в своем уме. Будем рассуждать от противного: предположим, что он в своем уме. Тогда Омар обо всем судит здраво и, следовательно, Грифон действительно считает, что ровно один из троих (Грифон, Черепаха Квази и Омар) в своем уме. Но это невозможно, так как если Грифон в своем уме, то Черепаха Квази (равно как и Омар) в своем уме, поэтому утверждение о том, что ровно один из них в своем уме, ложно (так как в своем уме все трое). Следовательно, Грифон, будучи в здравом рассудке, так думать не мог. С другой стороны, если Грифон в своем уме, то утверждение о том, что ровно один из троих (а именно Омар, так как Черепаха Квази не в своем уме) в здравом рассудке, истинно. Но существо, которое не в своем уме, не может мыслить истинными суждениями. Следовательно, предположение о том, что Омар в своем уме, приводит к противоречию. Значит, Омар не может быть в здравом рассудке: он должен быть не в своем уме.

Итак, мы знаем, что Омар не в здравом рассудке. Значит, в действительности неверно, будто Грифон считает, что разумен ровно один из троих (Грифон, Черепаха Квази и Омар). Если Грифон не в своем уме, то Черепаха Квази также не в своем уме, и, таким образом, все трое не в своем уме. Следовательно, утверждение о том, что не в своем уме ровно один из троих, ложно. Это означает, что Грифон, будучи не в своем уме, должен принимать за истинные все ложные утверждения, в частности утверждение о том, что ровно один из троих в здравом рассудке, хотя, как мы уже доказали, он так не думает. Полученное противоречие показывает, что Грифон не может быть не в своем уме. Следовательно, Грифон в здравом рассудке и Черепаха Квази (будучи таким же безумным или здравомыслящим), как Грифон, должен быть в своем уме.

Ответ: Омар не в своем уме, Грифон и Черепаха Квази оба в здравом рассудке.

20. Король и Королева Червей. Королева Пик думает, что Король Пик думает, что она не в своем уме. Если она в здравом рассудке, то Король действительно думает, что она не в своем уме, а это означает, что не в своем уме должен быть Король. Если же Королева не в своем уме, то Король в действительности не думает, что она не в своем уме, а если бы он был в здравом рассудке, то думал бы. Поэтому и в этом случае Король не в своем уме. Итак, в любом случае Король должен быть не в своем уме. Что же касается Королевы Пик, то она может быть и в здравом рассудке, и не в своем уме.

21. Король и Королева Треф. Не может быть, чтобы Король (Треф) думал, что Королева (Треф) думает, что Король думает, что Королева не в своем уме. Действительно, предположим, что Король так думает. Тогда Королева думает, что Король думает, что она не в своем уме. Но, как было показано в предыдущей задаче, это означает, что не в своем уме Король. Таким образом, если Король в своем уме, то он не в своем уме. Следовательно, Король не может быть в своем уме – Король безумен. Значит, он превратно судит обо всем и Королева в действительности не думает, что Король думает, что она не в своем уме. Но Королева либо в своем уме, либо безумна. Если она в своем уме, то здраво судит обо всем. Значит, верно, что Король не думает, что она не в своем уме, поэтому Король думает, что Королева в здравом рассудке. Но тогда Король мыслит здраво, и мы опять приходим к противоречию: безумный Король мыслит в соответствии с истиной. С другой стороны, если Королева не в своем уме, то она судит обо всем превратно, поэтому Король в действительности думает, что она не в своем уме. Тем самым Король должен был бы быть в здравом рассудке, между тем как он не в своем уме. Итак, и в одном и в другом случае мы приходим к противоречию.

Оно доказывает просто невозможность такого положения, при котором Король думает, что Королева думает, что она не в своем уме. Таким образом, если бы Герцогиня задала Алисе логическую задачу, то это, несомненно, свидетельствовало бы о том, что Герцогиня не в своем уме. Но в действительности Герцогиня не задавала Алисе такой задачи. Она лишь спросила у Алисы:

– А что бы ты сказала, если бы я сообщила тебе, что…

22. Королева Червей. Все, что мы доказали в предыдущей задаче, применимо не только к Королю и Королеве Треф, но и к Королю и Королеве Червей. Действительно, невозможно, чтобы Король Червей думал, что Королева Червей думает, что Король Червей думает, что она не в своем уме. Так как Королева Червей действительно думает, что Король так думает, то она не в своем уме. Что же касается Короля, то данные задачи не позволяют определить, в своем ли он уме.

23. Додо, Попугайчик Лори и Орленок. Так как Лори думает, что Додо не в своем уме, то Лори и Додо совсем несхожи (если Лори в здравом рассудке, то Додо не в своем уме; если Лори не в своем уме, то Додо в действительности не безумец, а пребывает в здравом рассудке). Так как Орленок думает, что Додо в здравом рассудке, то Орленок совсем несхож с Лори (который думает, что Додо не в своем уме). Следовательно, Орленок схож с Лори. (То же самое можно доказать иначе: если Орленок в своем уме, то Додо в действительности в здравом рассудке, а если Орленок не в своем уме, то Додо в действительности не в здравом рассудке, а не в своем уме.) Следовательно, Орленок и Додо схожи между собой, а Лори несхож с ними обоими. Так как Лори несхож с Орленком, то Лори должен думать, что Орленок не в своем уме. Значит, Додо судит здраво, поэтому Додо в своем уме.

24. Валет Червей. Докажем, что если Семерка не в своем уме, то Шестерка должен быть в здравом рассудке и, следовательно, Валет Червей здраво рассудил, думая, что Шестерка и Семерка не могут быть оба не в своем уме.

Предположим, что не в своем уме Семерка. Тогда то, что Семерка думает о Пятерке, ложно, поэтому Пятерка в здравом рассудке. Следовательно, Пятерка судит обо всем здраво, поэтому Туз и Четверка либо оба не в своем уме, либо оба в здравом рассудке. Но Туз и Четверка не могут быть оба не в своем уме. (Если бы Четверка был не в своем уме, то он судил бы обо всем превратно. Тогда Тройка и Двойка были бы оба не в своем уме, между тем как безумие Тройки означало бы, что Туз скорее в здравом разуме, чем не в своем уме. Следовательно, если Четверка не в своем уме, то Туз должен быть в здравом рассудке, поэтому Туз и Четверка не могут быть оба не в своем уме.) Таким образом, Туз и Четверка оба в здравом рассудке. А так как Четверка в здравом рассудке, Тройка и Двойка не могут быть оба не в своем уме – по крайней мере один из них в здравом рассудке. Но Тройка не может быть в здравом рассудке, так как он думает, что Туз не в своем уме. Следовательно, в здравом рассудке должен быть Двойка. Значит, Туз и Двойка оба в здравом уме. Стало быть, Шестерка судит здраво, поэтому он должен быть в здравом уме.

Итак, мы доказали, что если Семерка не в своем уме, то Шестерка должен быть в здравом рассудке. Следовательно, не может быть, чтобы Семерка и Шестерка оба были не в своем уме. Так как Валет думает, что они не могут быть оба не в своем уме, сам Валет должен быть в здравом рассудке.

25. Оценка Грифона. В задаче 15 мы доказали, что кухарка в здравом уме. Следовательно, если то, о чем поведала Герцогиня Алисе, было правильно, кухарка была бы в здравом уме. Но Герцогиня сообщает Алисе, что кухарка считает, что она, Герцогиня, не в своем уме. Следовательно, Герцогиня должна была бы быть не в своем уме (поскольку кухарка, будучи в здравом уме, считает, что Герцогиня не в своем уме). Значит, если бы то, о чем Герцогиня рассказала Алисе, было истинно, то Герцогиня должна была бы быть не в своем уме, но тогда ее рассказ не соответствовал бы истине. Таким образом, если бы то, о чем поведала Герцогиня Алисе, было верно, то мы пришли бы к противоречию. Следовательно, то, о чем рассказала Герцогиня, неверно.

Заметим, кстати, что приведенное выше рассуждение отнюдь не предназначается для доказательства безумия Герцогини: у нас кет причин думать, что Герцогиня не в своем уме. Мы доказали лишь, что если бы ее история была правдива, то Герцогиня должна была бы быть не в своем уме. Следовательно, рассказанная Герцогиней история не соответствует истинному положению вещей. Но это отнюдь не означает, что Герцогиня обо всем судит превратно. Мы доказали лишь то, что кое о чем она судит превратно!

Глава 4

26. Сколько кренделей у каждого? Назовем одной порцией все крендельки, которые достались Соне, сколько бы их ни было. Тогда Соне досталась 1 порция. Мартовскому Зайцу досталось вдвое больше крендельков, чем Соне (потому что Соню Болванщик посадил на такое место, где крендельков было вдвое меньше, чем у Мартовского Зайца), то есть Мартовскому Зайцу досталось 2 порции. Сам Болванщик сел на такое место, где крендельков было втрое больше, чем у Мартовского Зайца, поэтому Болванщику досталось 6 порций. Так как у Болванщика оказалось 6 порций, а у Сони только 1 порция, Болванщику досталось на 5 порций больше, чем Соне. Кроме того, известно, что у Болванщика оказалось на 20 кренделей больше, чем у Сони. Следовательно, 5 порций крендельков соответствует 20 кренделькам и 1 порцию составляют 4 кренделька. Таким образом, Соне досталось 4 кренделька, Мартовскому Зайцу – 8 крендельков и Болванщику – 24 кренделька, то есть на 20 крендельков больше, чем Соне.

27. Возмездие. После того как Мартовский Заяц съел 5/16 кренделей, на тарелке осталось 11/16. Соня съела 7/11 оставшихся кренделей, то есть 7/11 от 11/16. Так как 7/11 × 11/16 = 7/16, Соня съела 7/16 всех кренделей. Вместе с Мартовским Зайцем, съевшим 5/16 всех кренделей, они съели вдвоем 7/16 + /16 = 12/16, то есть 12/16 всех кренделей. Болванщику они оставили 4/16, или 1/4, кренделей. Поскольку Болванщику досталось 8 кренделей, эти 8 кренделей составляют 1/4 всех кренделей. Следовательно, всего было 32 кренделя. От 32 кренделей Vie составляет 2 кренделя, а 5/16 – 10 кренделей. Следовательно, Мартовский Заяц съел 10 кренделей, после чего на тарелке осталось 22 кренделя. Затем Соня съела 7/11 от 22 оставшихся кренделей, что составляет 14 кренделей (так как 1/11 от 22 кренделей равна 2 кренделям, а 7/11 – 14 кренделям). На тарелке осталось 8 кренделей для Болванщика, так что все сходится.

28. Сколько фаворитов? Эта задача, обычно решаемая с помощью алгебры, очень проста, если подойти к ней следующим образом. Раздадим сначала по 3 кренделя каждому из 30 гостей Королевы. У нас останется 10 кренделей. При этом все нефавориты получат все крендели, которые им причитаются, а каждому из фаворитов еще предстоит получить по 1 кренделю. Следовательно, все оставшиеся крендели предназначаются фаворитам – по 1 кренделю каждому фавориту. Значит, фаворитов должно быть 10.

Проверка. Каждый из 10 фаворитов должен получить по 4 кренделя, что составляет 40 кренделей на всех фаворитов. Каждый из остальных 20 гостей получит по 3 кренделя, что составляет еще 60 кренделей. 40 + 60 = 100. Следовательно, наше решение правильно.

29. Крендели и крендельки. Так как каждый крендель стоит столько, сколько один кренделек, то 7 кренделей стоят столько же, сколько 21 кренделек, а 7 кренделей и 4 кренделька – столько же, сколько 25 крендельков. С другой стороны, 4 кренделя и 7 крендельков стоят столько, сколько 19 крендельков (так как 4 кренделя стоят столько же, сколько 12 крендельков). Таким образом, разность в стоимости 25 и 19 крендельков составляет 12 центов. Значит, 6 крендельков (25 – 19 = 6) стоят 12 центов, 1 кренделек – 2 цента, а 1 крендель – 6 центов.

Проверка. 4 кренделя и 7 крендельков стоят 24 + 14 = 38 центов, а 7 кренделей и 4 кренделька стоят 42 + 8 = 50 центов, то есть действительно на 12 центов дороже, чем в первом случае.

30. В гостях у Герцогини, кухарки и Чеширского Кота. Чеширский Кот должен обнаружить на подносе 2 кренделя: после того как он съест половину кренделей и еще 1 крендель, на подносе не останется ничего. Соня должна обнаружить на подносе 6 кренделей: после того как она съест половину кренделей и еще 1 крендель, на подносе останется 2 кренделя для Чеширского Кота. Мартовский Заяц увидел на подносе 14 кренделей: после того как он съел 7 кренделей и еще 1 крендель, на подносе осталось 6 кренделей. Болванщик увидел 30 кренделей: после того как он съел 15 кренделей и еще 1 крендель, на подносе осталось 14 кренделей.

Таким образом, скачала на подносе было 30 кренделей.

31. Сколько дней работал садовник? Работая добросовестно, садовник может заработать самое большее 3 – 26 = 78 кренделей. Он заработал только 62 кренделя. Значит, 16 кренделей он не получил из-за того, что отлынивал от работы. Каждый день, который садовник отлынивал от работы, он теряет 4 кренделя (разность между 3 кренделями, которые мог бы получить за добросовестную работу, и 1 кренделем, который взыскивается с него за безделье). Следовательно, садовник отлынивал от работы 4 дня и работал добросовестно 22 дня.

Проверка. За 22 добросовестно отработанных дня садовник заработал 66 кренделей. За 4 дня, которые он отлынивал от работы, садовник вернул 4 кренделя.

Таким образом, всего он получил 62 кренделя.

32. В котором часу? Неправильный ответ, который обычно приходится слышать: в 6 часов. Правильный ответ: в 5 часов.

В 5 часов первый удар часов Королевы совпадает с первым ударом часов Короля. Второй удар часов Королевы приходится по времени на третий удар часов Короля. Третий удар часов Королевы совпадает с пятым ударом часов Короля. На этом бой часов Короля заканчивается, а часы Королевы еще должны пробить 2 раза.

33. Сколько человек заблудилось в горах? Назовем одной порцией количество припасов, которое один человек съедает за день. У 9 человек первоначально было 45 порций (запас провизии на 5 дней). На второй день у них осталось только 36 порций. На второй же день они повстречали вторую группу, и 36 оставшихся порций хватило всем на 3 дня. Следовательно, всего должно было быть 12 человек.

Значит, во второй группе было 3 человека.

34. Сколько пролито воды? На пятый день, когда вода была пролита, ее оставалось на 8 дней. Пролитой воды хватило бы погибшему на 8 дней. Следовательно, пролито было 8 кварт воды.

35. Скоро ли на свободу? Когда тюремный надзиратель станет вдвое старше узника, разность их возрастов будет равна возрасту узника. Но разность возрастов не зависит от времени и по истечении срока заключения будет такой же, как сейчас, то есть равной 29 годам. Следовательно, в день выхода на свободу узнику исполнится 29 лет, а тюремному надзирателю, который вдвое старше, 58 лет.

Таким образом, узнику осталось провести в темнице еще 4 года.

36. Долго ли выбраться из колодца? Те, кто думают, что лягушка выберется из колодца за 30 дней, ошибаются: лягушка могла бы выбраться из колодца к вечеру на 28-й день. Действительно, утром на 2-й день лягушка находится на высоте 1 фут над дном колодца, утром на 3-й день – на высоте 2 фута и т. д. Наконец, утром на 28-й день лягушка находится на высоте 27 футов над дном колодца. К вечеру того же дня она достигнет верха и вылезет из колодца, после чего ей уже не придется соскальзывать вниз.

37. Успеет ли велосипедист на поезд? Велосипедист рассуждал неверно: он усреднял расстояния, а не время. Если бы со скоростью 4 мили в час, 8 миль в час и 12 миль в час он двигался одно и то же время, то его средняя скорость действительно составила бы 8 миль в час, но большую часть времени он затратил на подъем в гору (со скоростью 4 мили в час), а меньшую – на спуск под гору (со скоростью 12 миль в час).

Нетрудно подсчитать, сколько времени он пробыл в пути. Подъем в гору занял у него 1 ч, полчаса (или 30 мин) он затратил на передвижение по ровному участку дороги и треть часа (или 20 мин) на спуск под гору. Всего в пути он пробыл 1 ч 50 мин, опоздав к поезду на 20 мин.

38. Не опоздал ли пассажир на поезд? На первую станцию пассажир прибыл через минуту после того, как ушел поезд. Десять миль в час – это одна миля за 6 мин или полторы мили за 9 мин. Таким образом, на следующую станцию поезд прибыл через 8 мин после того, как пассажир прибыл на первую станцию. На следующей станции поезд стоял 14 1/2 мин, поэтому у пассажира было в запасе 22 1/2 мин, чтобы успеть сесть на поезд на следующей станции. Четыре мили в час – это 1 миля за 15 мин, или полторы мили за 22 1/2 мин. На следующую станцию пассажир прибудет как раз вовремя, чтобы успеть сесть на поезд.

39. Далеко ли до школы? Разница во времени между опозданием на 5 мин и приходом за 10 мин до начала урока составляет 15 мин. Следовательно, если мальчик будет идти в школу со скоростью 5 миль в час, то он сэкономит 15 мин (по сравнению с тем, сколько он затратил бы на дорогу, если бы шел со скоростью 4 мили в час). Пять миль в час – это одна миля за 12 мин, а 4 мили в час – это 1 миля за 15 мин. Следовательно, идя быстрее, мальчик экономит по 3 мин на каждой миле, а 15 мин – на расстоянии 5 миль.

Значит, школа находится в 5 милях от дома.

Проверка. Идя со скоростью 5 миль в час, мальчик затрачивает на дорогу один час, а идя со скоростью 4 мили в час, – час с четвертью (за час он проходит первые 4 мили, а за четверть часа – последнюю милю), то есть 1 ч 15 мин. Разница по времени действительно составляет 15 мин.

40. Разве не печально? История действительно немного печальная, так как при подсчете барышей и убытков торговец произведениями искусства просчитался: в тот день он не только ничего не заработал, но и потерпел убыток в 20 долларов.

Попробуем разобраться, почему так получилось. Первую картину он продал с 10 %-ной прибылью. От продажи ее он выручил 990 долларов. За сколько он купил ее? Так как прибыль составляет 10 % не от 990 долларов, а от первоначальной стоимости картины, то 990 долларов – это 110 % от первоначальной стоимости картины, или 11/10. Следовательно, за картину торговец заплатил 10/11 от 990, то есть 990 долларов.

[Проверка. За картину торговец заплатил 900 долларов, 10 % от 900 составляют 90 долларов, поэтому от продажи картины он выручил 990 долларов, получив при этом прибыль 90 долларов.]

А как обстоит дело со второй картиной? От продажи ее торговец потерял 10 % от ее первоначальной стоимости, поэтому вторую картину он продал за 90 %, или 9/10, от ее первоначальной стоимости. Следовательно, при покупке второй картины торговец заплатил за нее 10/9 от 990 долларов, то есть 1100 долларов.

[Проверка. За вторую картину торговец заплатил 1100 долларов, 10 % от 1100 составляют 110 долларов, поэтому он продал ее за 1100 – 110 = 990 долларов.]

Таким образом, от продажи второй картины он потерпел убыток в ПО долларов, а от продажи первой картины получил прибыль всего 90 долларов. Следовательно, в тот день он потерял всего 20 долларов.

41. Кто старше? Прежде всего вычислим, через сколько дней часы Болванщика и Мартовского Зайца покажут одно и то же время. Так как часы Мартовского Зайца отстают с такой же скоростью, с какой спешат часы Болванщика, то в следующий раз они покажут одно и то же время, когда часы Болванщика уйдут вперед на 6 ч, а часы Мартовского Зайца отстанут на 6 ч. (На тех и других часах будет 6 ч, причем и те и другие часы будут показывать неверное время.) За сколько дней часы Болванщика уйдут вперед на 6 ч. За час они уходят вперед на 10 с, за 6 ч – на 1 мин, за сутки – на 4 мин, за 15 суток – на 1 ч, за 90 суток (дней на календаре) – на 6 ч. Таким образом, через 90 дней на часах Болванщика и Мартовского Зайца стрелки снова будут показывать одно и то же время.

Нам неизвестно, в какой из дней января Болванщик и Мартовский Заяц поставили на своих часах точное время.

Но если бы это произошло в любой из дней, кроме 1 января, то день, когда часы Болванщика и Мартовского Зайца в следующей раз покажут одно и то же время (а это событие, как мы установили, произойдет через 90 дней), пришелся бы не на март, а на апрель (или даже на май). Следовательно, Болванщик и Мартовский Заяц могли сверить свои часы только 1 января. Но даже в этом случае их часы покажут в следующий раз одно и то же время в марте только при условии, если год високосный! (В этом читатель без труда убедится с помощью календаря: через 90 дней после 1 января в обычный год наступает 1 апреля, а в високосный год – 31 марта!) Тем самым доказано, что 21 день рождения Мартовского Зайца приходится на високосный год. Следовательно, Мартовский Заяц мог родиться в 1843, а не в 1842 году или 1844 году. (Через 21 год после 1843 года наступает високосный 1864 год.) По условиям задачи только один из двух (либо Мартовский Заяц, либо Болванщик) родился в 1842 году. Следовательно, в 1842 году родился Болванщик. Значит, Болванщик старше Мартовского Зайца.

Глава 5

42. Появление первого шпиона. C заведомо не может быть рыцарем, так как ни один рыцарь не стал бы лгать и утверждать, будто он шпион. Следовательно, C либо лжец, либо шпион. Предположим, что C шпион. Тогда показание A ложно, значит, A шпион (A не может быть шпионом, так как шпион C) и рыцарем может быть только B. Но если B рыцарь, то как он мог дать ложные показания, утверждая, будто A рыцарь? Следовательно, предположение о том, что Сшпиои, приводит к противоречию. Значит, C лжец. Тогда показание B ложно, поэтому B либо лжец, либо шпион. Но так как лжец B, то шпионом должен быть A. Следовательно, A может быть только рыцарем.

Итак, A рыцарь, B шпион и C лжец.

43. Глупый шпион. Ложное заявление, изобличающее шпиона, могло быть, например, таким: «Я лжец».

Рыцарь никогда не лжет и поэтому не станет утверждать о себе, будто он лжец. С другой стороны, лжец никогда не говорит правды и не станет признаваться, что он лжец. Только шпион может сделать ложное признание, будто он лжец.

44. Еще один глупый шпион. Истинное заявление, изобличающее шпиона, могло быть, например, таким: «Я не рыцарь». Действительно, ни рыцарь, ни лжец не могли бы сказать о себе такое. Рыцарь никогда не лжет и не станет утверждать, будто он не рыцарь. Лжец всегда лжет и не станет признаваться, что он не рыцарь. Значит, такое заявление мог бы сделать только шпион.

45. Хитрый шпион. Если бы A ответил на вопрос судьи «да», то тем самым он изобличил себя как шпиона, так как судья (вместе с присяжными) мог бы рассуждать следующим образом:

«Предположим, что B шпион. Тогда все трое обвиняемых дали бы правдивые показания, что невозможно, так как один из них лжец. Следовательно, B не может быть шпионом. Значит, его показание ложно, поэтому B лжец. Показание C также ложно, а поскольку C не лжец (ибо лжец B), то он шпион».

Таким образом, если бы на вопрос судьи C ответил «да», то он был бы изобличен как шпион. Зная это, C благоразумно ответил «нет», лишив тем самым суд возможности установить, шпион он или коренной житель. (Суду удалось лишь установить, что либо C рыцарь, а B шпион, либо C лжец, а A шпион, либо C шпион.)

46. Кто Мердок? Так как A утверждает, что он шпион, то A либо лжец, либо шпион. Аналогичным образом, так как C утверждает, что он шпион, C либо лжец, либо шпион. Следовательно, из двух подсудимых A и C один лжец, а другой шпион. Значит, B рыцарь и дал на суде правдивые показания: A шпион.

47. Возвращение Мердока. Если A Мердок, то все три показания истинны, что невозможно, так как один из троих подсудимых лжец. Если C Мердок, то все три показания ложны, что также невозможно, так как один из троих подсудимых рыцарь. Следовательно, Мердоком должен быть B.

48. Более интересный случай. Задачу невозможно было бы решить, если бы в условиях не было ссылки на то, что суд изобличил шпиона, после того как на него указал C: ведь мы знаем, что суд смог установить, кто из троих шпион, и это весьма важная «зацепка»!

Предположим, что C обвинил A в том, что тот шпион. Располагая этими данными, судья не мог бы решить, кто шпион, поскольку они позволяют лишь утверждать, что либо A шпион, B лжец и C рыцарь либо B шпион, A рыцарь и C лжец, либо C шпион, A лжец и B рыцарь.

Таким образом, если C указал на A как на шпиона, то судья не мог бы изобличить настоящего шпиона.

Посмотрим теперь, что произошло бы, если бы C указал на B. Тогда B обвиняли бы в том, что он шпион, двое: A и C. Выдвинутые A и C обвинения либо оба истинны, либо оба ложны. Если бы они были оба истинны, то B действительно был бы шпионом, а так как A и C оба сказали правду, они оба должны были бы быть рыцарями («вакансия» шпиона занята B). Но по условиям задачи среди подсудимых A, B и C не может быть двух рыцарей. Следовательно, предъявленные B обвинения в шпионаже ложны. Значит, B не шпион. Мог бы A быть шпионом? Нет, так как если бы A был шпионом, то взаимные обвинения B и C в шпионаже были бы ложны. Следовательно, В и С были бы (оба) лжецами (что противоречит условиям задачи.) Остается единственно возможный случай: шпион С (В, обвинивший C в шпионаже, рыцарь, а A, обвинивший B, лжец).

Итак, если C указал на A как на шпиона, то судья не смог бы установить, кто из троих в действительности шпион. Но если C указал на B, то судья смог бы решить что шпион C. А так как судья знал, на кого показал A, то C должен был указать на B, и судья на основании полученных данных изобличил C в шпионаже.

49. Еще более интересный случай. Мыне знаем, что ответили A и B, поэтому нам необходимо рассмотреть четыре возможных случая:

1) A и B оба сказали «да»:

2) A сказал «нет», B сказал «да»;

3) A сказал «да», B сказал «нет»;

4) A и B оба сказали «нет».

Все эти четыре случая встретятся нам и в следующих двух задачах, поэтому мы тщательно проанализируем их сейчас.

Случай 1: А и В оба сказали «да». Так как A утверждает, что он шпион, то A либо лжец, либо шпион (рыцарь не станет называть себя шпионом). Если A лжец, то он солгал и в том случае, когда утверждал, что занимается шпионажем. Следовательно, B солгал, утверждая, что A сказал правду. Значит, B не рыцарь, а поскольку A лжец, то B шпион, и, наконец, C должен быть рыцарем. Таким образом, если A лжец, то B шпион, а C рыцарь.

Предположим теперь, что A шпион. Тогда он сказал правду, поэтому B, утверждая, что A сказал правду, не погрешил против истины. Следовательно, B должен быть рыцарем. Но тогда C может быть только рыцарем. Таким образом, если A лжец, то B шпион, а C рыцарь. Запишем оба возможных варианта (1а и 1б) случая 1 в следующем виде: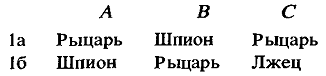

Случай 2: А сказал «нет», В сказал «да». Так как A отрицает, что он шпион, то A либо рыцарь, либо шпион (лжец солгал бы и сказал бы о себе, что он шпион). Если A рыцарь, то он сказал правду. Значит, B также сказал правду, когда заявил, что A сказал правду, поэтому B не может быть лжецом.

Следовательно, B должен быть шпионом. Но тогда C может быть только лжецом.

Если A шпион, то он солгал. Следовательно, B также солгал, когда утверждал, что A сказал правду. Значит, B лжец, и тогда C может быть только рыцарем. Оба возможных варианта случая 2 (2а и 26) запишем в следующем виде: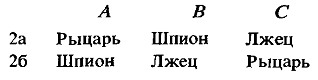

Случай 3: A сказал «да», В сказал «нет». Так как A утверждает о себе, что он шпион, то (как и в случае 1) A должен быть лжецом или шпионом. Если A лжец, то он солгал, но тогда B сказал правду. Значит, либо B рыцарь (и C шпион), либо B шпион (и C рыцарь). Если A шпион, то он сказал правду, но тогда B солгал. Значит, B лжец и C рыцарь. Таким образом, в случае 3 возможны три варианта:

Случай 4: A и B оба сказали «нет». Так как A отрицает, что он шпион, то (как в случае 2) A либо рыцарь, либо шпион. Предположим, что A рыцарь. Тогда A сказал правду, а B солгал. Следовательно, B лжец (а C шпион) или B шпион (а C лжец). Предположим, что A шпион. Тогда он сказал правду. Значит, B также сказал правду, поэтому B рыцарь (а C лжец). Таким образом, в случае 4 возможны три варианта (как и в случае 3):

Для удобства сведем все четыре случая в одну таблицу.

Обратимся снова к условиям задачи. После того как A и B ответили на вопросы судьи, тот сумел установить, что C не шпион. В случае 3 судья не мог бы установить, шпион ли C или рыцарь. В случае 4 судья не смог бы установить, шпион ли C или лжец. Но судья со всей определенностью заявил, что C не шпион. Значит, случаи 3 и 4 отпадают и остается либо случай 1, либо случай 2.

Когда судья утверждает, что C не шпион, ему известно, что A сказал правду. Тем самым судье известно, что A либо рыцарь, либо шпион. В случае 2 судья не смог бы определить, рыцарь ли A или шпион, и установить, кто шпион. Таким образом, остается только случай 1: судья знал, что A не мог быть лжецом (так как A сказал правду). Следовательно, A должен был быть шпионом.

50. Такой же интересный случай. Поскольку судья задал подсудимым A и B одинаковые вопросы, как и в предыдущей задаче, мы можем воспользоваться уже знакомой нам таблицей.

Рассмотрим тот момент судебного заседания, когда судья спросил подсудимого C, шпион ли тот. В этот момент судья не мог утверждать ни об одном из трех подсудимых, что тот заведомо не шпион, поскольку в противном случае судье пришлось бы освободить невиновного из-под стражи. Тем самым случаи 1 и 2 отпадают, так как в каждом из них судья бы знал, что C либо рыцарь, либо лжец, и освободил бы C. Следовательно, нам остается рассмотреть случаи 3 и 4.

Как мог рассуждать судья, выслушав ответ подсудимого C? В случае 3 судье известно, что C либо шпион, либо рыцарь. Если бы C на вопрос судьи ответил «нет», то судья не узнал бы ничего нового и не мог бы никого изобличить. Но если бы C ответил «да», то судья мог бы с уверенностью утверждать, что C шпион, так как рыцарь не мог бы сказать о себе, будто он шпион. Таким образом, в случае 3 как шпион был изобличен C.

В случае 4 судье известно, что C либо шпион, либо лжец. Если бы C ответил «да», то судья не мог бы утверждать, что C шпион (так ответить мог бы и лжец, и шпион). Но если бы C ответил «нет», то судья установил бы, что C шпион, поскольку лжец не способен сказать правду и признаться, что он не шпион. Таким образом, в случае 4 C был бы также изобличен как шпион.

Интересно отметить, что ни вы, дорогой читатель, ни я не можем сказать, какой из двух случаев (3 или 4) имеет место в действительности, как не можем узнать, что ответил («да» или «нет») C судье. Нам известно лишь, что судья смог определить, кто из обвиняемых шпион, поэтому либо все происходило, как в случае 3, и C ответил «да», либо все происходило, как в случае 4, и C ответил «нет». И в том и в другом случае C был изобличен как шпион, поэтому мы можем с уверенностью сказать, что C шпион.

51. Самый интересный случай из всех. Воспользуемся той же таблицей, которой мы пользовались при решении двух предыдущих задач.

1-й шаг. После того как B ответил на вопрос судьи, тот освободил одного из обвиняемых из-под стражи. В случаях 3 или 4 шпионом мог бы быть любой из трех подсудимых, и судья не мог бы снять обвинение ни с одного из них. Следовательно, в действительности нам необходимо обратиться к случаям 1 и 2. В этих двух случаях C не может быть шпионом, а каждый из двух остальных обвиняемых может, поэтому судья отпустил на свободу C. Таким образом, нам известно, что C был освобожден из-под стражи и что имеет место либо случай 1, либо случай 2, а о случаях 3 и 4 мы можем теперь полностью забыть.

После того как C покинул зал суда, судья спросил, обращаясь либо к A, либо к B (к кому именно, мы не знаем), не шпион ли его сосед по скамье подсудимых, и получил ответ «да» или «нет» (но какой именно, мы также не знаем). В случае 1 существуют 4 возможных варианта, в случае 2 – еще 4 варианта, что составляет вместе 8 вариантов. Половину из них можно исключить на основании того, что судья, получив ответ, смог решить, кто из двух (A или B) шпион.

Рассмотрим случай 1. Предположим, что судья задал вопрос подсудимому A. Если бы тот ответил «да» (признав тем самым, что шпион B), то судья мог бы исключить случай 1а, так как если A лжец и B шпион, то A, утверждая, что B шпион, не мог бы сказать правду. Исключив из этих соображений случай 1а, судья знал бы, что единственно возможным остается случай 16 и что A шпион. Если бы A ответил «нет», то судья не сумел бы изобличить шпиона, поскольку A мог бы оказаться либо лжецом (который солгал, утверждая, что B не шпион), либо шпионом (который сказал правду, утверждая, что B не шпион). Следовательно, в данной задаче A не мог ответить судье «нет». Таким образом, если судья обратился с вопросом к A, то A ответил «да» и был изобличен как шпион. Предположим теперь, что судья обратился к B и спросил того, шпион ли A. Если бы B ответил «да», то судья не смог бы изобличить шпиона (в чем читатель без труда убедится, рассмотрев оба варианта 1а и 1б: ни в одном из них B не мог бы ответить «нет»). Но если бы B ответил «нет», то судья пришел бы к выводу, что B шпион (случай 16 пришлось бы отбросить, так как в противном случае рыцарь B отрицал бы, что шпион A – шпион). Таким образом, на вопрос судьи подсудимый B ответил бы «нет» и был бы изобличен как шпион. На этом анализ случая 1 завершается.

Случай 2 может быть проанализирован аналогичным образом, и мы приводим лишь общий ход доказательства; предоставляя читателю самостоятельно восполнить недостающие подробности. Итак, в случае 2, если бы вопрос был задан подсудимому A, то для того, чтобы судья мог изобличить шпиона, тот должен был бы ответить «нет». При этом шпионом оказался бы сам A. Если бы вопрос был задай подсудимому B, то для того, чтобы судья мог изобличить шпиона, тот должен был бы ответить «да». Проверку этих утверждений мы предоставляем читателю (как я уже говорил, они лишь несущественно отличаются от приведенных выше рассуждений для случая 1).

Попытаемся теперь систематизировать все, что нам удалось узнать до сих пор.

В случае 1 либо судья адресовал свой третий вопрос подсудимому A, и тот, ответив «да», изобличил себя как шпиона, либо обратился с вопросом к подсудимому B, и тот, ответив «нет», изобличил себя как шпиона. В случае 2 либо судья задал свой третий вопрос подсудимому A, и тот, ответив «нет», выдал себя как шпиона, либо судья адресовал свой третий вопрос подсудимому B, и тот, ответив «да», изобличил себя как шпиона.

Таким образом, всего существуют четыре варианта:

2-й шаг. До сих пор мы могли обходиться без дополнительной информации о двух приятелях мистера Энтони. Известно, что они либо оба решили задачу, либо оба не решили ее. Докажем, что они могли оба решить задачу.

Начнем с первого приятеля. Если бы мистер Энтони ответил ему утвердительно, то приятель понял бы, что имеет дело со случаем 1а и что шпион A. Если бы мистер Энтони ответил приятелю отрицательно, то тот не смог бы различить, имеет ли он дело со случаями 1б, 2а или 2б, и выяснить, кто из двух, A или B, шпион. Следовательно, первый приятель мог решить задачу только при одном условии: если мистер Энтони ответил на его вопрос утвердительно и имеет место случай 1а.

Обратимся теперь ко второму приятелю. Если бы мистер Энтони ответил ему утвердительно, то этот приятель понял бы, что имеет дело со случаем 2а и что A шпион. Но если бы мистер Энтони ответил ему отрицательно, то второй приятель не мог бы решить задачу. Таким образом, второй приятель мог бы решить задачу только в случае 2а при условии, что мистер Энтони ответил на его вопрос утвердительно. Но случаи 1а и 2а не могут иметь место одновременно. Следовательно, мистер Энтони не мог утвердительно ответить на вопросы обоих своих приятелей, поэтому неверно, что его приятели оба решили задачу. Следовательно, они оба не решили задачу (так как известно, что они либо оба решили, либо оба не решили задачу) и мистер Энтони ни одному из них не ответил на вопрос утвердительно. Тем самым случаи 1а и 2а отпадают, поэтому B должен быть шпионом.

Глава 6

52. Первый вопрос. Алиса ошиблась, записав одиннадцать тысяч одиннадцать сотен и одиннадцать как 11111, что неверно! Число 11111 – это одиннадцать тысяч одна сотня и одиннадцать! Для того чтобы понять, как правильно записать делимое, сложим одиннадцать тысяч, одиннадцать сотен и одиннадцать «столбиком»: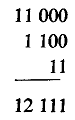

Мы видим, что одиннадцать тысяч одиннадцать сотен и одиннадцать – это 12111, то есть число, делящееся на 3 без остатка.

53. Еще одна задача на деление. Миллион, умноженный на четверть, равен четверти миллиона, а миллион, деленный на четверть, равен числу, четверть которого равна одному миллиону, то есть четырем миллионам.

Таким образом, правильный ответ на вопрос Черной Королевы: четыре миллиона.

54. Задача на сложение и вычитание. Обычно на вопрос задачи отвечают: «Четыре шиллинга». Но если бы бутылка стоила 4 шиллинга, то вино, которое стоит на 26 шиллингов дороже, стоило бы 30 шиллингов, а вино и бутылка вместе стоили бы 34 шиллинга.

Правильный ответ: бутылка стоит 2 шиллинга, вино стоит 28 шиллингов.

55. Во сне или наяву? Если бы Черный Король накануне в 10 ч вечера бодрствовал, то не мог бы вопреки истине считать, что он и Черная Королева почивают. Следовательно, Черный Король в это время спал. Но поскольку во сне он об всем судит превратно, то Черный Король ошибочно считал, что почивает и Королева. Следовательно, вчера в 10 ч вечера Черная Королева бодрствовала.

56. Во сне или наяву? В указанное время Король либо спал, либо бодрствовал. Предположим, что он не спал. Наяву Король обо всем судит здраво. Значит, Черная Королева спала. Но во сне она обо всем судит превратно, поэтому Черная Королева считала, что Король спит. Предположим теперь, что Король спал. Во сне он обо всем судит превратно, поэтому Черная Королева бодрствовала. Наяву Черная Королева обо всем судит здраво, поэтому считала, что Король спит.

Итак, независимо от того, спал Король или бодрствовал, Королева думала, что Король спит.

57. Сколько погремушек? Если Траляля проиграет пари, то у него будет половина от общего числа погремушек (или, что то же, столько же погремушек, сколько их у Труляля), поэтому до заключения пари у Траляля на одну погремушку больше, чем у Труляля. Если же Траляля выиграет пари, то у него будет на две погремушки больше, чем половина от общего числа погремушек. Кроме того, после выигрыша у Траляля окажется 2/3 от общего числа погремушек (или, что то же, вдвое больше погремушек, чем у Труляля), что на 1/6 от общего числа погремушек больше, чем половина от общего числа погремушек (1/2 – 1/3 = 1/6). Следовательно, приращение в 1/6 над половиной от общего числа погремушек то же самое, что приращение в 2 погремушки над половиной от общего числа погремушек. Значит, общее число погремушек равно 12, поэтому у Траляля 7 погремушек, а у Труляля 5.

Проверка. Если Траляля проигрывает пари, то у каждого из братцев становится по 6 погремушек. Если же Траляля выигрывает пари, то у него становится вдвое больше погремушек, чем у Труляля, – 8 против 4.

58. Сколько братьев и сестер? В семье Алисы и Тони четверо мальчиков и три девочки. У Тони три брата и три сестры, у Алисы четыре брата и две сестры.

59. Не по адресу. Утверждение о ровно трех письмах (из четырех), отправленных по адресу, означает то же самое, что утверждение о ровно одном письме, отправленном не по адресу. Следовательно, «выбирать» приходится между двумя случаями: когда по правильным адресам отправлены ровно три письма и ровно два письма. Но отправить по адресу ровно три письма невозможно, так как если три письма из четырех отправлены по адресу, то и четвертое письмо непременно отправлено по адресу. Следовательно, Королева отправила по адресу и не по адресу ровно по два письма.

60. Много ли земли? Обычно на вопрос задачи дают неправильный ответ: 11 акров. Если бы фермер действительно владел первоначально 11 акрами земли, то сборщик налогов отрезал бы у него l/10 акра (что составляет 1/10 от 11 акров), и у фермера осталось бы 9 9/10 акра вместо 10, как того требуют условия задачи. Таким образом, 11 акров не могут быть правильным ответом.

Как получить правильный ответ? Подойдем к решению задачи следующим образом. После того как сборщик налогов отрезал 1/10 участка, у фермера осталось 9/10 первоначальной площади участка. Таким образом, 1/10 первоначального участка составляют 10 акров. Это означает, что, умножив первоначальную площадь участка на 9/10, мы получим площадь урезанного участка, то есть 10 акров. Следовательно, для того чтобы от площади урезанного участка вернуться к площади исходного участка, площадь урезанного участка необходимо разделить на 9/10! Как известно, разделить на 9/10 то же самое, что умножить на 10/9, поэтому, умножив 10 акров на 10/9, мы получаем 100/9, или 11 1/9» акра.

Проверка. Площадь исходного участка 11 1/9 акра. Одна десятая от 11 1/9 составляет 1 1/9. После отрезания 1 1/9 акра остается участок площадью ровно 10 акров.

61. Еще одна задача об участке земли. Приведем все дроби к общему знаменателю (равному 60): 1/3 + 1/4 + 1/5 = 20/60 +15/60 + 12/60 = 47/60. Кукуруза занимает 13/60 всей площади. Следовательно, 13/60 участка составляют 26 акров, а так как 13 – половина от 26, то 60 – половина всей площади в акрах.

Таким образом, у фермера было 120 акров земли.

Проверка. Треть от 120 равна 40 (на 40 акрах фермер разводил тыкву). Четверть от 120 составляет 30 (30 акров отведено под горох). Одна пятая от 120 равна 24 (на 24 акрах посеяна фасоль). Так как 40 + 30 + 24 = 94, кукуруза занимает остальные 120 – 94 = 26 акров.

62. Часы бьют двенадцать. Шестой удар отделен от первого пятью промежутками времени (паузами). В сумме эти пять пауз длятся 30 с, поэтому пауза между двумя последовательными ударами составляет 6 с (а не 5, как ошибочно полагают некоторые!). Двенадцатый удар отделен от первого 11 паузами. Следовательно, 12 ударов часы пробьют за 66 с.

63. Двенадцатый и последний. Предположим, что Алиса ответила «да». Тогда Королева могла бы по своему усмотрению считать, что Алиса провалилась или выдержала экзамен. Если бы Королева сочла, что Алиса провалилась на экзамене и та осмелилась спросить почему, последовал бы ответ:

– Потому что ты ответила неправильно. Ведь ты сказала, что выдержала экзамен, тогда как в действительности провалилась. А поскольку на последний вопрос ты ответила неправильно, то не выдержала и весь экзамен!

С тем же основанием Черная Королева могла считать, что Алиса успешно выдержала экзамен, и сказать:

– Ты предсказала, что выдержишь экзамен, а так как ты действительно выдержала его, твое предсказание правильно. Значит, и на последний вопрос ты ответила правильно, поэтому я считаю, что ты успешно выдержала экзамен. (Разумеется, и в том и в другом случае в рассуждениях Королевы есть порочный круг, но каждое рассуждение ничуть не хуже другого!)

Вместе с тем, если Алиса ответила «нет», Черная Королева не может считать экзамен ни сданным, ни несданным. Если Королева сочтет, что Алиса успешно выдержала экзамен, то предсказание (ответ) Алисы окажется неверным, а за неправильный ответ (четвертый по счету!) экзамен по всем правилам следует считать несданным! Если же Королева сочтет, что Алиса провалилась на экзамене, то предсказание Алисы окажется правильным, а последний правильный ответ по всем правилам решает исход экзамена в пользу Алисы! Следовательно, Королева не может считать, ни что экзамен выдержан, ни что экзамен не сдан, не впадая при этом в противоречие!

Как я уже говорил, Алису в большей степени интересовало, чтобы не провалиться на экзамене, чем чтобы успешно сдать его, поэтому на последний вопрос она ответила «нет», чем полностью лишила Королеву возможности оценивать результаты экзамена.

Глава 7

64. Первый раунд (Красное н черное). Если внезапно заговоривший братец сказал правду, то его звали бы Траляля и в кармане у него была бы черная карта. Но тот, у кого в кармане карта черной масти, не может говорить правду. Следовательно, он лжет. Значит, в кармане у него действительно карта черной масти, а поскольку его высказывание ложно, то перед Алисой не Траляля с картой черной масти в кармане, а Труляля с картой черной масти в кармане.

65. Второй раунд (Красное и черное). Говоривший, по существу, утверждает, что он не Траляля с картой красной масти в кармане. Высказанное им утверждение должно быть истинным, ибо если бы он был Траляля с картой красной масти в кармане, то (так как у него карта красной масти) он не мог бы лгать и утверждать, будто он не Траляля с картой красной масти в кармане. Следовательно, верно, что он не Траляля с картой красной масти. Так как его утверждение истинно, то в действительности у него в кармане должна быть карта красной масти. А поскольку его утверждение (о том, что он не Траляля с картой красной масти) истинно, то он должен быть Труляля с картой красной масти.

66. Третий раунд (Красное и черное). «Либо – либо» означает «по крайней мере одно из двух» (а может быть, и то и другое). Следовательно, если бы у вышедшего из домика братца была карта черной масти, то было бы верно, что либо он Траляля, либо у него карта черной масти. Но это означало бы, что обладатель карты черной масти высказал истинное утверждение. Так как это невозможно, то у говорившего не может быть карты черной масти. Следовательно, у него должна быть карта красной масти, а его утверждение должно быть истинным. В свою очередь это означает, что либо его зовут Траляля, либо у него карта черной масти. Поскольку вторая альтернатива по доказанному выше не выполняется, наш герой Траляля с красной картой в кармане.

67. Четвертый раунд (Красное и черное). На этот раз невозможно определить, какой масти (красной или черной) карта того, кто вышел из домика, но и в том и в другом случае это должен быть Траляля. Предположим, что у него карта красной масти. Тогда он говорит правду. Следовательно, перед Алисой либо Траляля с картой черной масти, либо Труляля с картой красной масти. Первый вариант отпадает (так как у нашего героя карта красной масти). Остается второй вариант, поэтому перед Алисой не кто иной, как Труляля.

С другой стороны, предположим, что у него карта черной масти. Тогда высказанное им утверждение ложно. Значит, он не может быть ни Траляля с картой черной масти, ни Труляля с картой красной масти. Следовательно, он либо Траляля с картой красной масти, либо Труляля с картой черной масти. Первая альтернатива отпадает (так как по доказанному у него в кармане карта черной масти). Остается вторая альтернатива: перед Алисой Труляля, как и в разобранном выше случае.

68. Пятый раунд (Красное и черное). Предположим, что у говорившего красная карта. Тогда высказанное им утверждение истинно. Значит, перед Алисой должен быть Труляля. Предположим теперь, что у говорившего черная карта. Тогда высказанное им утверждение ложно. Значит, у Траляля не черная карта. Вместе с тем у того, кто вышел из домика, в кармане черная карта. Следовательно, он не может быть Траляля и его в этом случае зовут Труляля.

Итак, и в том и в другом случае из домика на этот раз вышел Труляля.

69. Шестой раунд (Красное и черное). Если бы у первого братца была карта красной масти, то мы пришли бы к следующему противоречию. Предположим, что у первого братца карта красной масти. Тогда высказанное им утверждение истинно. Следовательно, второго братца зовут Труляля, а его самого Траляля. Таким образом, первый братец Траляля с картой красной масти. Если это так, то утверждение высказанное вторым братцем, истинно. Но тогда как мог лгать первый братец, который говорит правду, утверждая, будто его братец Труляля с картой черной масти? Следовательно, у первого братца не может быть карты красной масти: у него должна быть карта черной масти. Так как у первого братца карта не красной масти, то высказанное вторым братцем утверждение не может быть истинным. Значит, и у второго братца карта черной масти. Если бы второго братца звали Труляля, то он был бы Труляля с картой черной масти. Тогда первый братец сказал бы правду. Но первый братец солгал (так как у него карта черной масти). Следовательно, второго братца зовут не Труляля. Значит, Труляля зовут первого братца.

70. Первый раунд (Оранжевое и пурпурное). Говоривший не мог быть Траляля с картой оранжевой масти, ибо в противном случае он сказал бы правду, заявив: «У меня карта оранжевой масти».

Говоривший не мог быть и Траляля с картой пурпурной масти, ибо в противном случае он солгал бы, утверждая: «У меня карта оранжевой масти».

Следовательно, говорившего звали не Траляля. Значит, это был Труляля (либо с картой пурпурной масти и говорящий правду, либо с картой оранжевой масти и лгущий).

71. Второй раунд (Оранжевое и пурпурное). Полезный принцип, которым мы воспользуемся в этой и некоторых других задачах, состоит в следующем: если у братцев две карты одной масти, то один из братцев лжет, а другой говорит правду. (Если бы у них были карты оранжевой масти, то Траляля говорил бы правду, а Труляля лгал бы. Если бы у них были карты пурпурной масти, то Труляля говорил бы правду, а Траляля лгал.) С другой стороны, если карты различных мастей, то братцы либо оба лгут, либо оба говорят правду.

Зная это, обратимся к нашей задаче. Так как оба братца утверждают, что их зовут Траляля, то один из них лжет, а другой говорит правду. Следовательно, обе карты должны быть одной масти. Предположим, что обе карты пурпурной масти. Тогда второе утверждение первого братца ложно. Значит, ложно и его первое утверждение. Следовательно, его зовут Труляля, и мы приходим к заключению, что Труляля с пурпурной картой лжет, а это невозможно. Значит, обе карты оранжевой масти. Тогда второе утверждение первого братца истинно. Следовательно, истинно и его первое утверждение, поэтому первого братца зовут Траляля.

Итак, первый братец – это Траляля, второй – Труляля и у обоих карты оранжевой масти.

72. Третий раунд (Оранжевое и пурпурное). Взглянув на первые два утверждения, нетрудно заметить, что они либо оба истинны, либо оба ложны. Следовательно (если воспользоваться принципом, приведенным в начале решения предыдущей задачи), карты у братцев различных мастей. В свою очередь это означает, что первый братец солгал, когда утверждал, будто у них карты одной масти. Следовательно, первый братец солгал и когда утверждал, будто его зовут Труляля. Значит, его зовут Траляля.

73. Четвертый раунд (Оранжевое и пурпурное). Так как братцы высказали противоречащие утверждения, то один из них лжет, а другой говорит правду. Следовательно (все тот же принцип!), у них должны быть карты одной масти. Если обе карты пурпурной масти, то первый братец говорит правду. Следовательно, это Труляля (потому что у него карта пурпурной масти и он говорит правду). Если обе карты оранжевой масти, то первый братец лжет. Следовательно, это опять Труляля (потому что у него карта оранжевой масти и он лжет). Итак, и в том и в другом случае первого братца зовут Труляля.

74. Пятый раунд (оранжевое и пурпурное). Первое утверждение первого братца согласуется с утверждением второго братца. Следовательно, братцы либо оба лгут, либо оба говорят правду. Значит, карты у них различных мастей (все тот же принцип!). Таким образом, верно, что по крайней мере одна карта пурпурной масти и первый братец говорит правду. Следовательно, его второе утверждение также истинно, поэтому его зовут Траляля. (Кроме того, у Траляля карта оранжевой масти, а у Труляля пурпурной.)

75. Шестой раунд (Оранжевое и пурпурное). Братцы противоречат друг другу, поэтому один из них лжет, а другой говорит правду. Следовательно, карты у них (все тот же принцип!) должны быть различных мастей.

Значит, правду говорит первый братец (его утверждение истинно).

76. Кто есть кто? На оборотной стороне знака начерчен либо квадрат, либо круг. Предположим, что начерчен квадрат. Тогда квадрат означает «да», а круг – «нет». Следовательно, второй братец отвечает на вопрос «нет», то есть лжет! Предположим теперь, что на оборотной стороне знака начерчен круг. Тогда круг означает «да» и второй братец отвечает иа вопрос «да», то есть снова лжет, поскольку на оборотной стороне знака начерчен не квадрат! Следовательно, второй брат солгал, поэтому его зовут Труляля.

77. О чем спросила Алиса? Вопросов, которые удовлетворяли бы условиям задачи, можно придумать много. Простейший из тех, которые приходят мне в голову, такой: «Ваша карта красной масти?».

Какой бы знак ни был начерчен на оборотной стороне «знака», ответ должен означать «да» потому, что тот, у кого карта красной – масти, всегда говорит правду и поэтому в ответ на заданный вопрос скажет «да», а тот, у кого карта черной масти, всегда лжет и поэтому скажет, будто у него карта красной масти. Следовательно, ответ второго братца означает «да». Предположим, что он ответит, нарисовав в воздухе квадрат. Тогда квадрат означает «да». Значит, приз у второго братца. Если же в ответ на вопрос он нарисует круг, то круг, а не квадрат означает «да». Значит, приз у первого братца.

Кратко можно сказать, что если второй братец нарисует в воздухе квадрат, то приз у него, а если круг, то приз у другого братца.

Глава 9

Во всех решениях этой главы A означает первого подсудимого, B – второго и C – третьего.

78. Кто виновен? Из условий задачи известно, что виновный дал ложные показания. Если бы B был виновен, то он сказал бы правду, когда признал виновным себя. Следовательно, B не может быть виновным. Если бы A был виновен, то все трое подсудимых дали бы ложные показания (так как A обвинил B или C, которые оба невиновны; B признал виновным самого себя, а он невиновен, и C либо признал виновным самого себя, тогда как C невиновен, либо обвинил A, который также невиновен). Но поскольку известно, что не все подсудимые дали ложные показания, то A также не может быть виновен. Следовательно, виновен подсудимый C.

79.Второй отчет о судебном процессе. О чем мог узнать Белый Король от Белого Рыцаря, что позволило ему установить виновного? Если бы Белый Рыцарь сообщил Белому Королю, что все трое подсудимых дали ложные показания, то Белый Король не мог бы найти виновного. Действительно, A мог быть виновен и обвинять B, а B и C могли обвинять друг друга (при этом все трое лгали бы); либо B мог быть виновен и обвинять C, а A и C могли обвинять друг друга (при этом все трое опять лгали бы); либо C мог быть виновен и обвинять A, а A и B могли обвинять друг друга. Следовательно, Белый Король не мог узнать от Белого Рыцаря, что все трое обвиняемых лгали на суде.

Мог бы Белый Король установить, кто виновен, если бы Белый Рыцарь сказал ему, что на суде лгали ровно двое из подсудимых, и указал тех, кто лгал? Нет. Предположим, например, что Белый Рыцарь сказал Белому Королю: «А говорил правду, B и C лгали». Тогда кем бы ни был тот, кого A назвал виновным, он должен был бы быть виновным (ведь A говорил правду), а B и C оба лгали и обвиняли A (или, быть может, B обвинял C, а C обвинял A). С другой стороны, A мог обвинять C, а подсудимые B и C могли бы обвинять A, тогда виновен был бы C. Таким образом, если бы A был единственным подсудимым, сказавшим на суде правду, то ни B, ни C не могли бы быть виновными. Аналогичным образом, если бы B был единственным подсудимым, сказавшим на суде правду, то ни A, ни C не могли бы быть виновными, а если бы правду на суде сказал только C, то ни A, ни B не могли бы быть виновными. Следовательно, если бы Белый Рыцарь сообщил Белому Королю, что на суде сказал правду только один из подсудимых (либо A, либо B, либо C), то Белый Король не смог бы установить виновного. Значит, Белый Рыцарь не говорил Белому Королю, что правду сказал на суде только один из подсудимых (либо A, либо B, либо C).

Мог Белый Рыцарь сообщить Белому Королю, что все трое подсудимых говорили на суде правду? Нет, это невозможно, так как виновный заведомо лгал (ведь он обвинял кого-то из двух других подсудимых, тогда как те были невиновны).

Остается единственно возможный вариант: на суде лгал ровно один подсудимый. Но если лгал ровно один подсудимый, то именно он и должен быть виновен, так как если бы солгал кто-нибудь из невиновных, то давших ложные показания было бы двое: один невиновный и виновный. Итак, Белый Король мог услышать от Белого Рыцаря один из трех вариантов.

Вариант 1. A лгал, B говорил правду, C говорил правду.

Вариант 2. A говорил правду, B лгал, C говорил правду.

Вариант 3. A говорил правду, B говорил правду, C лгал.

Теперь нам ясно, каким образом Белый Король узнал, кто был виновен, но каким образом мы можем установить, какой из трех вариантов Белый Рыцарь сообщил Белому Королю? Как известно, Шалтай-Болтай либо спросил Белого Рыцаря, были ли ложны показания двух подсудимых подряд, либо были ли истинны показания двух подсудимых подряд. Первый вопрос не имел бы смысла (так как из трех показаний только одно ложное), поскольку на него Белый Рыцарь ответил бы отрицательно и это не позволило бы Шалтаю-Болтаю установить, какой из трех вариантов был сообщен Белому Королю Белым Рыцарем. Значит, Шалтай-Болтай спросил, были ли истинны показания двух каких-нибудь подсудимых подряд. Если в ответ на его вопрос Белый Король сказал «да», то Шалтай-Болтай исключил бы вариант 2, но так и не смог бы установить виновного. Но раз Шалтай-Болтай определил, кто виновен, то это означает, что в ответ на его вопрос Белый Рыцарь ответил? «нет». Такой ответ позволил Шалтаю-Болтаю понять, что вариант 2 единственно возможный. Следовательно, виновен подсудимый C.

80. Следующий судебный процесс. Это очень простая задача. Так как A сказал правду и обвинил одного из двух других подсудимых, то либо B, либо C должен быть виновен. Следовательно, A невиновен. Если бы каждый из подсудимых обвинял не того, на кого он указал на самом деле, а другого, то B сказал бы правду. Так как мы знаем, что A невиновен, то на процессе B обвинил C. Следовательно, C виновен.

81. Судебный процесс, следующий за следующим. Так как A говорил правду и обвинял либо B, либо C, то либо B, либо C виновен, а A невиновен.

Белый Рыцарь сказал Белому Королю, что C либо лгал, либо говорил правду. Если бы Белому Королю было сказано, что C лгал, то Белый Король не мог бы установить, кто из трех подсудимых виновен, так как либо C мог быть виновным и ложно обвинять A (или B), либо B мог быть виновным и C мог ложно обвинять A. Таким образом, если известно, что C лгал, то не существует способа, позволяющего установить, кто виновен: B или C. С другой стороны, если известно, что C говорил правду, то он не мог обвинять A (поскольку тот невиновен). Следовательно, C обвинял B, а так как C говорил правду, B должен быть виновен. Таким образом, Бармаглот должен был сказать Белому Рыцарю, что C говорил правду. Тогда Белый Рыцарь смог бы установить, что виновным должен быть B.

82. Еще один судебный процесс. Как и в предыдущей задаче, поскольку A говорил правду и обвинял одного из двух подсудимых, A должен быть невиновен. Если Белый Рыцарь узнал от Бармаглота, что C говорил правду, то без всякой дополнительной информации Белый Рыцарь знал бы, что B виновен (как мы видели в решении предыдущей задачи). Но, как известно, Белый Рыцарь не мог без дополнительной информации определить, кто из трех подсудимых виновен. Следовательно, Бармаглот должен был сказать ему, что C лгал. Затем Белый Рыцарь узнал, кого обвинял подсудимый C, и это позволило ему узнать, кто виновен. Если бы Белый Рыцарь узнал от Бармаглота, что C обвинял подсудимого A, то Белый Рыцарь не смог бы определить, кто виновен: B или C. Именно поэтому Белому Рыцарю так важно было услышать от Бармаглота, что C обвинял подсудимого B: это означало, что B должен быть невиновен (так как C лгал), а поскольку A также невиновен, то виновен должен быть C.

83. Еще один случай. Существует 8 вариантов показаний, которые дали в ходе процесса подсудимые А, В и C. Действительно, A мог выступить с двумя вариантами показаний, каждый из которых мог сочетаться с двумя вариантами показаний подсудимого B, поэтому существуют 4 варианта показаний подсудимых A и B. (Перечислим эти варианты: 1) A и B оба признали себя виновными; 2) A признал себя виновным, B заявил о своей невиновности; 3) A заявил о своей невиновности, B признал себя виновным; 4) A и B оба заявили о своей невиновности.) Каждый из четырех вариантов показаний подсудимых A и B приходится на два варианта показаний подсудимого C, поэтому общее число показаний подсудимых A, B и C достигает 8.

В каждом из 8 вариантов показаний подсудимых виновным (по крайней мере в принципе) может быть любой из троих. Следовательно, общее число вариантов всего «расклада» (под «раскладом» мы условимся понимать набор из показаний каждого их троих подсудимых и его фактической виновности или невиновности) достигает 24. Разумеется, если бы мы знали, какой из 24 вариантов соответствует действительности, то нам было бы известно, кто лгал и кто говорил правду. Составим поэтому сводную таблицу всех 24 вариантов расклада. Она понадобится нам для решения не только этой задачи, но и одной из следующих задач. Все необходимые пояснения приведены после таблицы.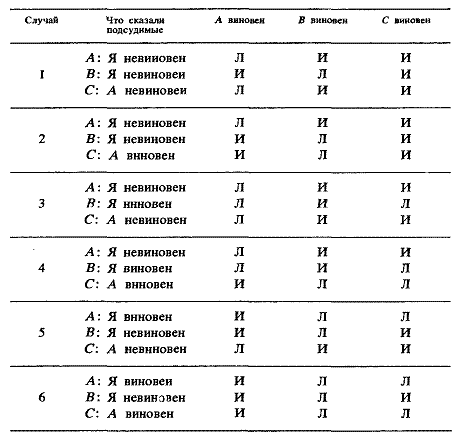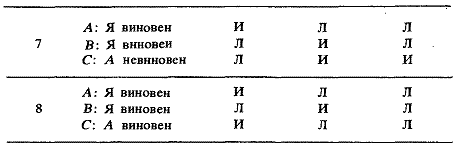

Буквы «Л» и «И» (от слов «Ложь» и «Истина») указывают, говорит ли правду (И) или лжет (Л) соответствующий подсудимый. В случае 5В (на пересечении полосы 5 и столбца «В виновен») мы видим, что A лжет, B лжет, а C говорит правду. (Под случаем 5B мы понимаем такой вариант, когда A признал виновным себя, B заявил о своей невиновности, C показал, что A невиновен, а в действительности виновен В.)

Другие примеры: в случае 8C все трое подсудимых лгали; в случае 3B все трое говорили правду; в случае 4C подсудимый A говорил правду, а B и C лгали.

Бармаглот, после того как ему стало известно, что именно сказал каждый подсудимый, а также что по крайней мере одно показание правдиво и по крайней мере одно ложно, сумел установить, кто виновен. Что из того, о чем мог сообщить Белый Рыцарь, позволило Бармаглоту установить, кто виновен? Предположим, Бармаглот узнал от Белого Рыцаря, что A заявил о своей невиновности, B заявил о своей невиновности, а C заявил о невиновности A (тем самым мы оказываемся в пределах случая 1). Располагая такой информацией, Бармаглот мог бы исключить виновность подсудимого C (так как в случае 1C все трое подсудимых лгали), но, пожалуй, не мог бы установить, кто виновен: A или B (так как в случае 1C по крайней мере одно показание правдиво и по крайней мере одно ложно; аналогичная картина наблюдается в случае 1В). Следовательно, Белый Рыцарь не мог сообщить Бармаглоту эту информацию (так как Бармаглот установил, кто виновен). А как обстояло бы дело в случае 2 (A заявил о своей невиновности, B заявил о своей невиновности, а C заявил о виновности A)? И в этом случае Бармаглот не смог бы определить, кто виновен (поскольку мог представиться и случай 2А, и случай 2В). С иной ситуацией мы сталкиваемся в случае 3, когда по крайней мере одно правдивое и по крайней мере одно ложное показание возможны только в подслучае 3C. Следовательно, если бы Белый Рыцарь сообщил Бармаглоту, что A заявил о своей невиновности, B заявил о своей невиновности, а C заявил о невиновности A, то Бармаглот путем умозаключений пришел бы к выводу, что C виновен. Поэтому не исключено, что Белый Рыцарь сообщил Бармаглоту именно эту информацию. Проанализировав остальные случаи (4, 5, 6, 7 и 8), читатель обнаружит, что только в случае 6 (помимо уже известного нам случая 3) Бармаглот мог бы установить, кто из троих подсудимых виновен. Как и в случае 3, виновным был бы подсудимый С.

Таким образом, к какому бы из двух случаев (случаю 3 или случаю 6) ни относились показания подсудимых, о которых поведал Бармаглоту Белый Рыцарь, и в том и в другом случае виновным (по счастливому для нас стечению обстоятельств) оказался бы подсудимый C.

84. И еще один случай. Мы знаем, что A обвинил B, но нам неизвестно, что сказали B или C. Предположим, мы располагали бы дополнительной информацией о том, что виновный – единственный из троих подсудимых, который дал ложные показания. Тогда виновным мог бы быть любой из троих подсудимых. Установить, кто именно из троих виновен, не представлялось бы никакой возможности. С другой стороны, если бы иам было известно, что виновный – единственный из подсудимых, который говорил правду, то мы могли бы заключить, что A не может быть виновен (так как если бы A был виновен, то, обвиняя B, сказал бы правду, а это в свою очередь означало бы, что B виновен) и B не может быть виновен (так как если бы B был виновен, то A был бы невиновен и, следовательно, сказал бы правду о B). Значит, виновным должен был бы быть C.

Таким образом, Черная Королева могла почерпнуть из беседы с Белым Рыцарем только то, что виновный – единственный из подсудимых, который дал правдивые показания (в противном случае Черная Королева не могла бы установить, кто виновен).

Итак, виновен C.

85. А что сказали бы вы? Предположим, Белый Рыцарь сказал Шалтаю-Болтаю, что все трое подсудимых лгали. Тогда Шалтай-Болтай не смог бы отдать предпочтение одному из двух вариантов: либо C виновен и обвинил A, либо A виновен и обвинил C (так как и в том и в другом случае все трое подсудимых лгали).

Шалтай-Болтай не мог узнать от Белого Рыцаря, что все трое подсудимых говорили правду, так как все трое не могли говорить правду (поскольку и A, и B обвиняли B, а C обвинял кого-то другого).

Если бы Белый Рыцарь сообщил Шалтаю-Болтаю, что ровно двое подсудимых солгали, то тот знал бы, что солгали подсудимые A и B (потому что если бы любой из них сказал правду, то и другой также сказал бы правду), а C сказал правду. Но тогда либо C обвинил самого себя и был виновен, либо C обвинил A и A был виновен, но установить, какой из этих двух вариантов соответствует действительности, было бы невозможно. Следовательно, в этом случае Шалтай-Болтай не мог бы определить, кто из подсудимых виновен.

Шалтай-Болтай мог бы установить виновного только в одном случае: если Белый Рыцарь сообщил ему, что ровно два показания были правдивыми. Это означало бы, что A и B оба сказали правду (поскольку их показания согласуются, то если бы одно из них было ложно, то и другое было бы ложно, но тогда мы имели бы два ложных показания), а C солгал. Так как A и B оба сказали правду и обвинили B, подсудимый B должен быть виновен.

86. Что стало с Козлом? Из того, что Козел солгал, не следует, ни что он виновен, ни что он невиновен. Следовательно, даже если суд установил, что Козел дал ложные показания, Козла могли и признать виновным (на основании других данных, о которых нам ничего не известно), и освободить из-под стражи (опять-таки на основании дополнительных данных) или не сделать ни того ни другого. Что именно решил суд, мы не знаем. С другой стороны, если бы Жук и Комар дали правдивые показания, то это означало бы, что Козел виновен, так как оба насекомых обвиняли одно и то же существо (поскольку они говорили правду) и ни Жук, ни Комар не обвиняли себя. Следовательно, зазеркальные насекомые должны были обвинять Козла. Господину в белой бумаге должно было стать известно, что оба насекомых дали правдивые показания, иначе он не смог бы восстановить, какой приговор вынес суд. Но если Белый Рыцарь сообщил ему, что Жук и Комар сказали правду, то Господин в белой бумаге узнал, что суд признал виновным Козла.

87. Самое запутанное дело. Для того чтобы решить эту замечательную задачу, нам понадобится таблица, которой мы воспользовались при решении задачи 83.

Прежде всего заметим, что Бармаглот смог решить задачу, зная, к какому из восьми случаев относится данный казус (то есть что показал каждый из подсудимых), и зная, что по крайней мере один подсудимый говорил правду. Полученные сведения позволили Бармаглоту исключить случаи 4, 6, 7 и 8. Действительно, в случае 4 имеются два варианта (4A и 4C), в каждом из которых правдивые показания дал не более чем один подсудимый. В случае 6 имеются два варианта (6B и 6C), в случае 7 – также два варианта (7A и 7C) и в случае 8 – два варианта (8B и 8C). Таким образом, ни в одном из четырех случаев 4, 6, 7 и 8 Бармаглот не мог бы определить, кто из подсудимых виновен. С другой стороны, в случае 1 вариант 1A – единственный, в котором имеется самое большее одно правдивое показание. В случае 2 имеется один единственно приемлемый вариант – 2B, в случае 3 – вариант 3 Л и в случае 5 – вариант 5B. Тем самым мы можем утверждать, что действительности соответствует один из случаев 1, 2, 3 и 5.

Труляля было сказано, что Бармаглот решил задачу. Следовательно, Труляля было известно, что показания на суде соответствуют либо случаю 1, либо случаю 2, либо случаю 3, либо случаю 5. Если бы Белый Рыцарь сообщил Труляля, что A заявил о своей виновности, то это позволило бы Труляля исключить случаи 1, 2 и 3, после чего он бы знал, что случай 5 единственно возможный. Это означало бы, что B виновен (так как в случае 5 речь могла бы идти только о варианте 5B, в котором среди показаний было не более одного правдивого). Но тогда Труляля решил бы задачу, а мы знаем, что он не решил задачу. Следовательно, Белый Рыцарь не мог сообщить ему, что A заявил о своей виновности, а сказал, что A заявил о своей невиновности. Следовательно, происходившее на процессе относилось не к случаю 5. Определить же, к какому из случаев, 1, 2 или 3, относились данные на суде показания, Труляля не мог. Следовательно, он не знал, кто из подсудимых виновен: A или B. Тем не менее круг поисков сузился: мы знаем, что речь может идти только о случаях 1, 2 или 3.

Обратимся теперь к Траляля. Белый Рыцарь сказал о Бармаглоте, поэтому Траляля знал, что речь может идти только о случаях 1, 2, 3 и 5, но ему не было сказано о Труляля, поэтому он не мог исключить случай 5. Известно, что Траляля задал вопрос о показаниях подсудимых B или C, но мы не знаем, кто именно его интересовал. Предположим, что Траляля спросил о показаниях подсудимого B. Если Белый Рыцарь сообщил Траляля, что B признан виновным, то Траляля исключил бы случаи 1, 2 и 5 и у него остался бы случай 3. Но тогда он решил бы задачу (придя к заключению, что виновен A). Как известно, в действительности Траляля не решил задачу. Следовательно, если Траляля задал вопрос о показаниях подсудимого B, то ему сказали, что B заявил о своей невиновности. Итак, мы знаем, что если Траляля интересовался показаниями подсудимого B, то на процессе имел место случай 1 или 2.

Предположим, что Траляля поинтересовался показаниями подсудимого C. Если бы Траляля было сказано, что C обвинял подсудимого A, то Траляля исключил бы случаи 1, 3 и 5 и решил бы задачу (придя к заключению, что виновен B). Но Траляля не решил задачу. Значит, ему было сказано, что C заявил о невиновности подсудимого A. Такое могло произойти в случаях 1 или 3, и A должен быть виновен (хотя Траляля об этом и не знал, потому что имевшиеся у него неполные данные не позволяли исключить случай 5, в котором виновен был бы B).

Мы видим, что если бы Траляля спросил о показаниях подсудимого B, то (поскольку Траляля не решил задачу) имел бы место либо случай 1, либо случай 2. Если бы Траляля поинтересовался бы показаниями подсудимого C, то имел бы место случай 1 или случай 3. Шалтай-Болтай осведомился, о чьих показаниях спрашивал Траляля: подсудимого B или C. Если бы Шалтай-Болтай узнал, что Траляля интересовали показания подсудимого B, то он установил бы, что речь может идти только о случаях 1 или 2, и, следовательно, не мог бы сказать, кто из двух подсудимых, A или B, виновен. Но Шалтай-Болтай решил задачу. Следовательно, он должен был узнать, что Траляля спрашивал о показаниях подсудимого C. Этим Шалтай-Болтай сузил круг поисков до двух случаев 1 или 3, а в каждом из них виновен подсудимый A.

Тем самым виновность подсудимого A доказана.

Глава 11

88. Всего лишь один вопрос. Действительно следуют. Рассмотрим сначала утверждение 1. Предположим, некто убежден, что он бодрствует. В действительности он либо бодрствует, либо не бодрствует. Предположим, что он бодрствует. Тогда его убеждение правильно, но всякий, кто придерживается наяву правильных убеждений, должен принадлежать к типу A. С другой стороны, предположим, что он спит. Тогда его убеждение ложно, а всякий, кто придерживается во сне ложных убеждений, должен принадлежать к типу A. Следовательно, персона, о которой идет речь, бодрствует ли она или спит, должна принадлежать к типу A. Тем самым утверждение 1 доказано.

Перейдем теперь к утверждению 2. Предположим, некто убежден, что принадлежит к типу A. Если он действительно принадлежит к типу A, то его убеждение правильно, а те, кто принадлежит к типу A, могут придерживаться правильных убеждений только наяву. С другой стороны, если в действительности он принадлежит к типу B, то его убеждение ложно, а те, кто принадлежит к типу B, могут придерживаться ложных убеждений только наяву.

И в том и в другом случае интересующая нас персона бодрствует. Тем самым утверждение 2 доказано.