Математики придумывают многомерные пространства, строят модели, которые, казалось бы, никакого отношения к нашей жизни не имеют. Но многие эти умозрительные вещи имеют практическое применение. Так, первые модемы использовали коды в восьмимерном пространстве. Именно это позволило нам сегодня пользоваться интернетом.

Почему домохозяйки трясут баночки с горохом? Какая упаковка шаров является наиболее плотной в пространствах различных размерностей? Что такое «kissing number» и был ли прав Ньютон, не захотев согласиться на число 13? Какое практическое применение нашло решение задачи о наиболее плотной упаковке шаров в 8-мерном пространстве в 20 веке? Рассказывает Николай Николаевич Андреев кандидат физико-математических наук, заведующий лабораторией популяризации и пропаганды математики Математического института им. В. А. Стеклова РАН.

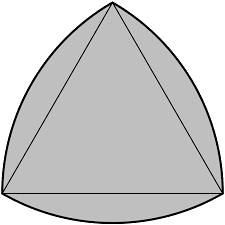
Почему крышки люков делают круглыми? Что такое фигура постоянной ширины? Какими интересными свойствами обладает треугольник Рело и как его построить? Почему английская 20-пенсовая монета имеет такую необычную форму? Как и чем сверлят квадратные отверстия? Что представляют собой фигуры постоянной ширины в трёхмерном пространстве и какая открытая математическая проблема с ними связана?

Ученый-популяризатор Николай Андреев создал сайт «Математические этюды», в котором собирает научно-популярные рассказы о современных задачах математики и визуализации математических сюжетов: почему у икосаэдра столько же граней, сколько вершин у додекаэдра, что будет, если зажечь лампочку в фокусе параболы, и какое отношение к квадрату суммы имеет Жан-Жак Руссо.

В школе мы несколько лет подряд прилежно изучаем геометрию. Но не зря ли мы тратим время? Чем может помочь геометрия в жизни? Измерить расстояние от точки до точки, вычислить площадь или объём предмета и только? Нет, конечно. Законы геометрии применимы буквально на каждом шагу. Просто нужно знать, как ими воспользоваться.

Математика — самый точный и универсальный язык науки, но можно ли с помощью цифр объяснить человеческие чувства? Формулы любви, семена хаоса и романтические дифференциальные уравнения — публикуем главу из книги одного из лучших преподавателей математики в мире — Стивена Строгаца «Удовольствие от Х», выпущенную издательством «Манн, Иванов и Фербер».

Давайте рассмотрим последовательность чисел, первое из которых равно 1, а каждое последующее вдвое больше: 1, 2, 4, 8, 16, … Называется она вполне ожидаемо: последовательность степеней двойки. Казалось бы, ничего выдающегося в ней нет — последовательность как последовательность, не лучше и не хуже других. Тем не менее, она обладает весьма примечательными свойствами.

Нам так и не удалось найти первоисточник этого широко распространённого поверья: ни один лист бумаги нельзя сложить вдвое больше семи (по некоторым данным — восьми) раз. Между тем текущий рекорд складывания – 12 раз. И что удивительнее, принадлежит он девушке, математически обосновавшей эту «загадку бумажного листа».

Лекция математика Алексея Владимировича Савватеева в СУНЦ МГУ про великие математические революции и нерешенные задачи, многие из которых уже решены, а некоторые — ждут своих героев. Для старших и "продвинутых" школьников, интересующихся математикой.

Представьте себе, что на стол высыпана кучка совершенно одинаковых по виду монет, но вам сказали, что одна из этих монет — фальшивая. Она отличается от остальных монет по весу, но вам не сообщили, легче она или тяжелее. В вашем распоряжении имеются чашечные весы без гирь. Как нужно действовать, чтобы выделить эту монету и выяснить её тип (то есть узнать, легче она или тяжелее) за минимальное число взвешиваний?