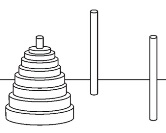
Давайте рассмотрим последовательность чисел, первое из которых равно 1, а каждое последующее вдвое больше: 1, 2, 4, 8, 16, … Используя показатели степени, ее можно записать в эквивалентном виде: 2⁰, 2¹, 2², 2³, 2⁴, … Называется она вполне ожидаемо: последовательность степеней двойки. Казалось бы, ничего выдающегося в ней нет — последовательность как последовательность, не лучше и не хуже других. Тем не менее, она обладает весьма примечательными свойствами.

Несомненно, многие читатели встречали ее в классической истории об изобретателе шахмат, который попросил у правителя в награду за первую клетку шахматной доски одно пшеничное зерно, за вторую — два, за третью — четыре, и так далее, всё время удваивая число зерен. Понятно, что суммарное их количество равно

S = 2⁰ + 2¹ + 2² + 2³ + 2⁴ + … + 2⁶³. (1)

Но так как эта сумма неимоверно велика и во много раз превосходит годовой урожай зерновых по всему миру, вышло, что мудрец ободрал правителя как липку.¹

Однако зададимся сейчас другим вопросом: как с наименьшими затратами труда подсчитать величину S? Обладатели калькулятора (или, паче того, компьютера) вполне могут за обозримое время выполнить перемножения, а затем сложить полученные 64 числа, получив ответ: 18 446 744 073 709 551 615. А поскольку объем вычислений немалый, то и вероятность ошибки весьма велика.

Кто похитрей, могут углядеть в этой последовательности геометрическую прогрессию. Не знакомые же с этим понятием (или те, кто попросту забыл стандартную формулу суммы геометрической прогрессии) могут использовать следующие рассуждения. Давайте-ка умножим обе части равенства (1) на 2. Так как при удвоении степени двойки ее показатель увеличивается на 1, то получим

2S = 2¹ + 2² + 2³ + 2⁴ + … + 2⁶⁴. (2)

Теперь из (2) вычтем (1). В левой части, понятное дело, получится 2S – S = S. В правой же части произойдет массовое взаимное уничтожение почти всех степеней двойки — от 2¹ до 2⁶³ включительно, и останется лишь 2⁶⁴ – 2⁰ = 2⁶⁴ – 1. Итак:

S = 2⁶⁴ – 1.

Что ж, выражение заметно упростилось, и теперь, имея калькулятор, позволяющий возводить в степень, можно найти значение этой величины без малейших проблем.

А если и калькулятора нет — как быть? Перемножать в столбик 64 двойки? Еще чего не хватало! Опытный инженер или математик-прикладник, для которого главный фактор — время, сумел бы быстро оценить ответ, т.е. найти его приближенно с приемлемой точностью. Как правило, в быту (да и в большинстве естественных наук) вполне допустима погрешность в 2–3%, а если она не превосходит 1% — то это просто великолепно! Оказывается, подсчитать наши зерна с такой погрешностью можно вообще без калькулятора, и всего за несколько минут. Как? Сейчас увидите.

Итак, надо возможно точней найти произведение 64 двоек (единицу в силу ее ничтожности отбросим сразу). Разобьем их на отдельную группу из 4 двоек и еще на 6 групп по 10 двоек. Произведение двоек в отдельной группе равно 2⁴ = 16. А произведение 10 двоек в каждой из остальных групп равно 2¹⁰ = 1024 (убедитесь, кто сомневается!). Но 1024 — это около 1000, т.е. 10³. Поэтому S должно быть близко к произведению числа 16 на 6 чисел, каждое из которых равно 10³, т.е. S ≈ 16·10¹⁸ (ибо 18 = 3·6). Правда, погрешность здесь все же великовата: ведь 6 раз при замене 1024 на 1000 мы ошибались в 1,024 раза, а всего мы ошиблись, как легко видеть, в 1,024⁶ раз. Так что теперь — дополнительно перемножать 1,024 шесть раз само на себя? Нет уж, обойдемся! Известно, что для числа х, которое во много раз меньше 1, с высокой точностью справедлива следующая приближенная формула: (1 + x)ⁿ ≈ 1 + xn.

Поэтому 1,024⁶ = (1 + 0,24)⁶ ≈ 1 + 0,24·6 = 1,144. Посему надо найденное нами число 16·10¹⁸ умножить на число 1,144, в результате чего получится 18 304 000 000 000 000 000, а это отличается от правильного ответа менее чем на 1%. Чего мы и добивались!

В данном случае нам крупно повезло: одна из степеней двойки (а именно — десятая) оказалась весьма близка к одной из степеней десятки (а именно — третьей). Это позволяет нам быстро оценивать значение любой степени двойки, не обязательно 64-й. Среди степеней других чисел подобное встречается нечасто. Например, 5¹⁰ отличается от 10⁷ также в 1,024 раза, но… в меньшую сторону.² Впрочем, это того же поля ягода: поскольку 2¹⁰·5¹⁰ = 10¹⁰, то во сколько раз 2¹⁰ превосходит 10³, во столько же раз 5¹⁰ меньше, чем 10⁷.

Другая интересная особенность рассматриваемой последовательности заключается в том, что любое натуральное число можно построить из различных степеней двойки, причем единственным способом. Например, для номера текущего года имеем

2012 = 2² + 2³ + 2⁴ + 2⁶ + 2⁷ + 2⁸ + 2⁹ + 2¹⁰.

Доказать эти возможность и единственность не составляет особого труда. Начнем с возможности. Пусть нам надо представить в виде суммы различных степеней двойки некоторое натуральное число N. Сначала запишем его в виде суммы N единиц. Так как единица — это 2⁰, то первоначально N есть сумма одинаковых степеней двойки. Затем начнем объединять их по парам. Сумма двух чисел, равных 2⁰, — это 2¹, так что в результате получится заведомо меньшее количество слагаемых, равных 2¹, и, возможно, одно число 2⁰, если ему не нашлось пары. Далее попарно объединяем одинаковые слагаемые 2¹, получая еще меньшее количество чисел 2² (здесь тоже возможно появление непарной степени двойки 2¹). Затем снова объединяем равные слагаемые попарно, и так далее. Рано или поздно процесс завершится, ибо количество одинаковых степеней двойки после каждого объединения уменьшается. Когда оно станет равным 1 — дело кончено. Осталось сложить все получившиеся непарные степени двойки — и представление готово.

Что касается доказательства единственности представления, то здесь хорошо подходит метод «от противного». Пусть одно и то же число N удалось представить в виде двух наборов различных степеней двойки, которые не полностью совпадают (т. е. имеются степени двойки, входящие в один набор, но не входящие в другой, и наоборот). Для начала отбросим все совпадающие степени двойки из обоих наборов (если таковые имеются). Получатся два представления одного и того же числа (меньшего или равного N) в виде суммы различных степеней двойки, причем все степени в представлениях различны. В каждом из представлений выделим наибольшую степень. В силу изложенного выше, для двух представлений эти степени различны. То представление, для которого эта степень больше, назовем первым, другое — вторым. Итак, пусть в первом представлении наибольшая степень равна 2^m, тогда во втором она, очевидно, не превышает 2^m–1. Но поскольку (и мы с этим уже сталкивались выше, подсчитывая зерна на шахматной доске) справедливо равенство

2^m = (2^m–1 + 2^m–2 + … + 2⁰) + 1,

то 2^m строго больше суммы всех степеней двойки, не превосходящих 2^m–1. По этой причине уже наибольшая степень двойки, входящая в первое представление, наверняка больше суммы всех степеней двойки, входящих во второе представление. Противоречие!

Фактически мы только что обосновали возможность записи чисел в двоичной системе счисления. Как известно, в ней используются лишь две цифры — ноль и единица, и каждое натуральное число записывается в двоичной системе единственным способом (например, упомянутое выше 2012 — как 11 111 011 100). Если пронумеровать разряды (двоичные цифры) справа налево, начиная с нуля, то номера тех разрядов, в которых стоят единицы, как раз и будут показателями степеней двоек, входящих в представление.³

Менее известно следующее свойство множества целых неотрицательных степеней двойки. Давайте некоторым из них произвольным образом присвоим знак «минус», т. е. из положительных сделаем отрицательными. Единственное требование — чтобы в результате и положительных, и отрицательных чисел оказалось бесконечное количество. Например, можно присвоить знак «минус» каждой пятой степени двойки или, допустим, оставить положительными только числа 2¹⁰, 2¹⁰⁰, 2¹⁰⁰⁰, и так далее — вариантов здесь сколько угодно.

Как ни удивительно, но любое целое число можно (и притом единственным способом) представить в виде суммы различных слагаемых нашей «положительно-отрицательной» последовательности.⁴ И доказать это не очень-то сложно (например, индукцией по показателям степеней двоек). Главная идея доказательства — наличие сколь угодно больших по абсолютной величине как положительных, так и отрицательных слагаемых. Попробуйте выполнить доказательство сами.

Интересно понаблюдать за последними цифрами членов последовательности степеней двойки. Так как каждое последующее число последовательности получается удвоением предыдущего, то последняя цифра каждого из них полностью определяется последней цифрой предыдущего числа. А так как различных цифр ограниченное количество, последовательность последних цифр степеней двойки просто обязана быть периодической! Длина периода, естественно, не превышает 10 (поскольку именно столько цифр мы используем), но это сильно завышенное значение. Попробуем оценить его, не выписывая пока саму последовательность. Ясно, что последние цифры всех степеней двойки, начиная с 2¹, четные. Кроме того, среди них не может быть нуля — потому что число, оканчивающееся нулем, делится на 5, в чем заподозрить степени двойки никак нельзя. А так как четных цифр без нуля имеется всего четыре, то и длина периода не превосходит 4.

Проверка показывает, что так оно и есть, причем периодичность проявляется почти сразу: 1, 2, 4, 8, 6, 2, 4, 8, 6, … — в полном соответствии с теорией!

Не менее успешно можно оценить и длину периода последней пары цифр последовательности степеней двойки. Так как все степени двойки, начиная с 2², делятся на 4, то и числа, образованные их последними двумя цифрами, делятся на 4. Не более чем двузначных чисел, делящихся на 4, имеется всего 25 (для однозначных чисел предпоследней цифрой считаем ноль), но из них надо выбросить пять чисел, оканчивающихся нулем: 00, 20, 40, 60 и 80. Так что период может содержать не более 25 – 5 = 20 чисел. Проверка показывает, что так и есть, начинается период с числа 2² и содержит пары цифр: 04, 08, 16, 32, 64, 28, 56, 12, 24, 48, 96, 92, 84, 68, 36, 72, 44, 88, 76, 52, а затем опять 04 и так далее.

Аналогично можно доказать, что длина периода последних m цифр последовательности степеней двойки не превышает 4·5^m–1 (более того — на самом деле она равна 4·5^m–1, но доказать это значительно сложнее).

Итак, на последние цифры степеней двойки наложены довольно жесткие ограничения. А как насчет первых цифр? Здесь ситуация практически противоположная. Оказывается, для любого набора цифр (первая из которых — не ноль) найдется степень двойки, начинающаяся с этого набора цифр. И таких степеней двойки бесконечно много! Например, существует бесконечное количество степеней двойки, начинающихся с цифр 2012 или, скажем, 3 333 333 333 333 333 333 333.

А если рассмотреть только одну самую первую цифру различных степеней двойки — какие значения она может принимать? Нетрудно убедиться, что любые — от 1 до 9 включительно (нуля среди них, естественно, нет). Но какие из них встречаются чаще, а какие реже? Как-то сразу не видно причин, по которым одна цифра должна встречаться чаще другой. Однако более глубокие размышления показывают, что как раз равной встречаемости цифр ожидать не приходится. Действительно, если первая цифра какой-либо степени двойки есть 5, 6, 7, 8 или 9, то первая цифра следующей за ней степени двойки будет обязательно единицей! Поэтому должен иметь место «перекос», по крайней мере, в сторону единицы. Следовательно, вряд ли и остальные цифры будут «равнопредставленными».

Практика (а именно — прямой компьютерный расчет для первых нескольких десятков тысяч степеней двойки) подтверждает наши подозрения. Вот какова относительная доля первых цифр степеней двойки с округлением до 4 знаков после запятой:

1 — 0,3010
2 — 0,1761
3 — 0,1249
4 — 0,0969
5 — 0,0792
6 — 0,0669
7 — 0,0580
8 — 0,0512
9 — 0,0458

Как видим, с ростом цифр эта величина убывает (и потому та же единица примерно в 6,5 раз чаще бывает первой цифрой степеней двойки, чем девятка). Как ни покажется странным, но практически такое же соотношение количеств первых цифр будет иметь место почти для любой последовательности степеней — не только двойки, но, скажем, и тройки, пятерки, восьмерки и вообще почти любого числа, в том числе и нецелого (исключение составляют лишь некоторые «особые» числа). Причины этого весьма глубоки и непросты, и для их уяснения надо знать логарифмы. Для тех, кто с ними знаком, приоткроем завесу: оказывается, относительная доля степеней двойки ⁵, десятичная запись которых начинается с цифры F (для F = 1, 2, …, 9), составляет lg (F + 1) – lg (F), где lg — так называемый десятичный логарифм, равный показателю степени, в которую надо возвести число 10, чтобы получить число, стоящее под знаком логарифма.⁶

Используя упомянутую выше связь между степенями двойки и пятерки, А. Канель обнаружил интересное явление. Давайте из последовательности первых цифр степеней двойки (1, 2, 4, 8, 1, 3, 6, 1, 2, 5, …) выберем несколько цифр подряд и запишем их в обратном порядке. Оказывается, эти цифры непременно встретятся тоже подряд, начиная с некоторого места, в последовательности первых цифр степеней пятерки.⁷

Степени двойки также являются своеобразным «генератором» для производства широко известных совершенных чисел, которые равны сумме всех своих делителей, за исключением себя самого. Например, у числа 6 четыре делителя: 1, 2, 3 и 6. Отбросим тот, который равен самому числу 6. Осталось три делителя, сумма которых как раз равна 1 + 2 + 3 = 6. Поэтому 6 — совершенное число.

Для получения совершенного числа возьмем две последовательные степени двойки: 2^n–1 и 2ⁿ. Уменьшим большую из них на 1, получим 2ⁿ – 1. Оказывается, если это — простое число, то, домножив его на предыдущую степень двойки, мы образуем совершенное число 2^n–1 (2ⁿ – 1). Например, при п = 3 получаем исходные числа 4 и 8. Так как 8 – 1 = 7 — простое число, то 4·7 = 28 — совершенное число.⁸ Более того — в свое время Леонард Эйлер доказал, что все четные совершенные числа имеют именно такой вид. Нечетные совершенные числа пока не обнаружены (и мало кто верит в их существование).

Тесную связь имеют степени двойки с так называемыми числами Каталана, последовательность которых имеет вид 1, 1, 2, 5, 14, 42, 132, 429… Они часто возникают при решении различных комбинаторных задач. Например, сколькими способами можно разбить выпуклый n-угольник на треугольники непересекающимися диагоналями? Всё тот же Эйлер выяснил, что это значение равно (n – 1)-му числу Каталана (обозначим его K_n–1), и он же выяснил, что K_n = K_n–1·(4n – 6)/n. Последовательность чисел Каталана имеет множество любопытных свойств, и одно из них (как раз связанное с темой этой статьи) заключается в том, что порядковые номера всех нечетных чисел Каталана являются степенями двойки!

Степени двойки нередко встречаются в различных задачах, причем не только в условиях, но и в ответах. Возьмем, например, популярную когда-то (да и поныне не забытую) Ханойскую башню. Так называлась игра-головоломка, придуманная в XIX веке французским математиком Э. Люка. Она содержит три стержня, на один из которых надето n дисков с отверстием в середине каждого. Диаметры всех дисков различны, и они расположены в порядке убывания снизу вверх, т. е. самый большой диск — внизу (см. рисунок). Получилась как бы башня из дисков.

Требуется перенести эту башню на другой стержень, соблюдая такие правила: перекладывать диски строго по одному (снимая верхний диск с любого стержня) и всегда класть только меньший диск на больший, но не наоборот. Спрашивается: какое наименьшее число ходов для этого потребуется? (Ходом мы называем снятие диска с одного стержня и надевание его на другой.) Ответ: оно равно 2ⁿ – 1, что легко доказывается по индукции.

Пусть для n дисков потребное наименьшее число ходов равно X_n. Найдем X_n+1. В процессе работы рано или поздно придется снимать самый большой диск со стержня, на который первоначально были надеты все диски. Так как этот диск можно надевать только на пустой стержень (иначе он «придавит» меньший диск, что запрещено), то все верхние n дисков придется предварительно перенести на третий стержень. Для этого потребуется не меньше X_n ходов. Далее переносим наибольший диск на пустой стержень — вот еще один ход. Наконец, чтобы сверху его «притиснуть» меньшими n дисками, опять потребуется не меньше X_n ходов. Итак, X_n+1 ≥ X_n + 1 + X_n = 2X_n + 1. С другой стороны, описанные выше действия показывают, как можно справиться с задачей именно 2X_n + 1 ходами. Поэтому окончательно X_n+1 =2X_n + 1. Получено рекуррентное соотношение, но для того чтобы его привести к «нормальному» виду, надо еще найти X₁. Ну, это проще простого: X₁ = 1 (меньше просто не бывает!). Не составляет труда, основываясь на этих данных, выяснить, что X_n = 2ⁿ – 1.

Вот еще одна интересная задача:

Найдите все натуральные числа, которые нельзя представить в виде суммы нескольких (не менее двух) последовательных натуральных чисел.

Давайте проверим сначала наименьшие числа. Ясно, что число 1 в указанном виде непредставимо. Зато все нечетные, которые больше 1, представить, конечно, можно. В самом деле, любое нечетное число, большее 1, можно записать как 2k + 1 (k — натуральное), что есть сумма двух последовательных натуральных чисел: 2k + 1 = k + (k + 1).

А как обстоят дела с четными числами? Легко убедиться, что числа 2 и 4 нельзя представить в требуемом виде. Может, и для всех четных чисел так? Увы, следующее же четное число опровергает наше предположение: 6 = 1 + 2 + 3. Зато число 8 опять не поддается. Правда, следующие числа вновь уступают натиску: 10 = 1 + 2 + 3 + 4, 12 = 3 + 4 + 5, 14 = 2 + 3 + 4 + 5, а вот 16 — вновь непредставимо.

Что ж, накопленная информация позволяет сделать предварительные выводы. Обратите внимание: не удалось представить в указанном виде только степени двойки. Верно ли это для остальных чисел? Оказывается, да! В самом деле, рассмотрим сумму всех натуральных чисел от m до n включительно. Так как всего их, по условию, не меньше двух, то n > m. Как известно, сумма последовательных членов арифметической прогрессии (а ведь именно с ней мы имеем дело!) равна произведению полусуммы первого и последнего членов на их количество. Полусумма равна (n + m)/2, а количество чисел равно n – m + 1. Поэтому сумма равна (n + m)(n – m + 1)/2. Заметим, что в числителе находятся два сомножителя, каждый из которых строго больше 1, и при этом четность их — различна. Выходит, что сумма всех натуральных чисел от m до n включительно делится на нечетное число, большее 1, и потому не может быть степенью двойки. Так что теперь понятно, почему не удалось представить степени двойки в нужном виде.

Осталось убедиться, что не степени двойки представить можно. Что касается нечетных чисел, то с ними мы уже разобрались выше. Возьмем какое-либо четное число, не являющееся степенью двойки. Пусть наибольшая степень двойки, на которую оно делится, это 2^a (a — натуральное). Тогда если число поделить на 2^a, получится уже нечетное число, большее 1, которое мы запишем в знакомом виде — как 2k + 1 (k — тоже натуральное). Значит, в целом наше четное число, не являющееся степенью двойки, равно 2^a (2k + 1). А теперь рассмотрим два варианта:

1. 2^a+1 > 2k + 1. Возьмем сумму 2k + 1 последовательных натуральных чисел, среднее из которых равно 2^a. Легко видеть, что тогда наименьшее из них равно 2^a – k, а наибольшее равно 2^a + k, причем наименьшее (и, значит, все остальные) — положительное, т. е. действительно натуральное. Ну, а сумма, очевидно, составляет как раз 2^a(2k + 1).
2. 2^a+1 < 2k + 1. Возьмем сумму 2^a+1 последовательных натуральных чисел. Здесь нельзя указать среднее число, ибо количество чисел четное, но указать пару средних чисел можно: пусть это числа k и k + 1. Тогда наименьшее из всех чисел равно k + 1 – 2^a (и тоже положительное!), а наибольшее равно k + 2^a. Сумма их тоже равна 2^a(2k + 1).

Вот и всё. Итак, ответ: непредставимые числа — это степени двойки, и только они.

А вот еще одна задача (впервые ее предложил В. Произволов, но в несколько иной формулировке):

Садовый участок окружен сплошным забором из N досок. Согласно приказу тети Полли Том Сойер белит забор, но по собственной системе: продвигаясь всё время по часовой стрелке, сначала белит произвольную доску, затем пропускает одну доску и белит следующую, затем пропускает две доски и белит следующую, затем пропускает три доски и белит следующую, и так далее, каждый раз пропуская на одну доску больше (при этом некоторые доски могут быть побелены несколько раз — Тома это не смущает).

Том считает, что при такой схеме рано или поздно все доски будут побелены, а тетя Полли уверена, что хотя бы одна доска останется непобеленной, сколько бы Том ни работал. При каких N прав Том, а при каких — тетя Полли?

Описанная система побелки представляется довольно хаотичной, поэтому первоначально может показаться, что для любого (или почти любого) N каждой доске когда-нибудь достанется своя доля известки, т. е., в основном, прав Том. Но первое впечатление обманчиво, потому что на самом деле Том прав только для значений N, являющихся степенями двойки. Для остальных N найдется доска, которая так и останется навеки непобеленной. Доказательство этого факта довольно громоздко (хотя, в принципе, несложно). Предлагаем читателю выполнить его самому.

Вот каковы они — степени двойки. С виду — проще простого, а как копнешь… И затронули мы здесь далеко не все удивительные и загадочные свойства этой последовательности, а лишь те, что бросились в глаза. Ну, а читателю предоставляется право самостоятельно продолжить исследования в этой области. Несомненно, они окажутся плодотворными.

Акулич И. Ф.
«Квант» №2, 2012