Отрывок из книги «Невероятные числа профессора Стюарта» заслуженного профессора математики Уорикского университета, известного популяризатора науки Иэна Стюарта, посвященной роли чисел в истории человечества и актуальности их изучения в наше время.

Пифагорова гипотенуза

Пифагоровы треугольники имеют прямой угол и целочисленные стороны. У простейшего из них самая длинная сторона имеет длину 5, остальные — 3 и 4. Всего существует 5 правильных многогранников. Уравнение пятой степени невозможно решить при помощи корней пятой степени — или любых других корней. Решетки на плоскости и в трехмерном пространстве не имеют пятилепестковой симметрии вращения, поэтому такие симметрии отсутствуют и в кристаллах. Однако они могут быть у решеток в четырехмерном пространстве и в занятных структурах, известных как квазикристаллы.

Гипотенуза самой маленькой пифагоровой тройки

Теорема Пифагора гласит, что самая длинная сторона прямоугольного треугольника (пресловутая гипотенуза) соотносится с двумя другими сторонами этого треугольника очень просто и красиво: квадрат гипотенузы равен сумме квадратов двух других сторон.

Традиционно мы называем эту теорему именем Пифагора, но на самом деле история ее достаточно туманна. Глиняные таблички позволяют предположить, что древние вавилоняне знали теорему Пифагора задолго до самого Пифагора; славу первооткрывателя принес ему математический культ пифагорейцев, сторонники которого верили, что Вселенная основана на числовых закономерностях. Древние авторы приписывали пифагорейцам — а значит, и Пифагору — самые разные математические теоремы, но на самом деле мы представления не имеем о том, какой математикой занимался сам Пифагор. Мы даже не знаем, могли ли пифагорейцы доказать теорему Пифагора или просто верили в то, что она верна. Или, что наиболее вероятно, у них были убедительные данные о ее истинности, которых тем не менее не хватило бы на то, что мы считаем доказательством сегодня.

Доказательства Пифагора

Первое известное доказательство теоремы Пифагора мы находим в «Началах» Евклида. Это достаточно сложное доказательство с использованием чертежа, в котором викторианские школьники сразу узнали бы «пифагоровы штаны»; чертеж и правда напоминает сохнущие на веревке подштанники. Известны буквально сотни других доказательств, большинство из которых делает доказываемое утверждение более очевидным.

Рис. 33. Пифагоровы штаны

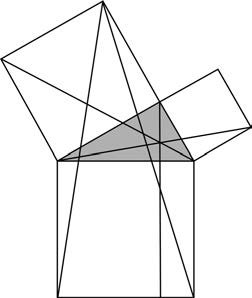
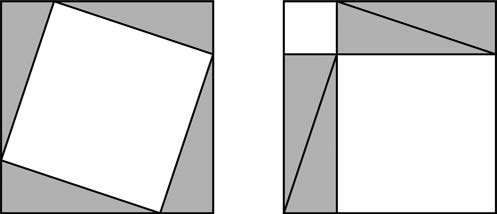
Одно из простейших доказательств — это своего рода математический пазл. Возьмите любой прямоугольный треугольник, сделайте четыре его копии и соберите их внутри квадрата. При одной укладке мы видим квадрат на гипотенузе; при другой — квадраты на двух других сторонах треугольника. При этом ясно, что площади в том и другом случае равны.

Рис. 34. Слева: квадрат на гипотенузе (плюс четыре треугольника). Справа: сумма квадратов на двух других сторонах (плюс те же четыре треугольника). А теперь исключите треугольники

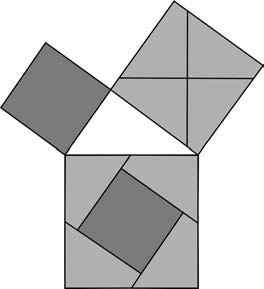
Рассечение Перигаля — еще одно доказательство-пазл.

Рис. 35. Рассечение Перигаля

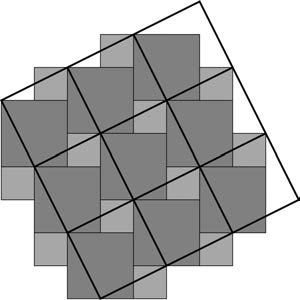
Существует также доказательство теоремы с использованием укладки квадратов на плоскости. Возможно, именно так пифагорейцы или их неизвестные предшественники открыли эту теорему. Если взглянуть на то, как косой квадрат перекрывает два других квадрата, то можно увидеть, как разрезать большой квадрат на куски, а затем сложить из них два меньших квадрата. Можно увидеть также прямоугольные треугольники, стороны которых дают размеры трех задействованных квадратов.

Рис. 36. Доказательство мощением

Есть интересные доказательства с использованием подобных треугольников в тригонометрии. Известно по крайней мере пятьдесят различных доказательств.

Пифагоровы тройки

В теории чисел теорема Пифагора стала источником плодотворной идеи: найти целочисленные решения алгебраических уравнений. Пифагорова тройка — это набор целых чисел a, b и c, таких что

a² + b² = c².

Геометрически такая тройка определяет прямоугольный треугольник с целочисленными сторонами.

Самая маленькая гипотенуза пифагоровой тройки равна 5.

Другие две стороны этого треугольника равны 3 и 4. Здесь

3² + 4² = 9 + 16 = 25 = 5².

Следующая по величине гипотенуза равна 10, потому что

6² + 8² = 36 + 64 = 100 = 10².

Однако это, по существу, тот же треугольник с удвоенными сторонами. Следующая по величине и по-настоящему другая гипотенуза равна 13, для нее

5² + 12² = 25 + 144 = 169 = 13².

Евклид знал, что существует бесконечное число различных вариантов пифагоровых троек, и дал то, что можно назвать формулой для нахождения их всех. Позже Диофант Александрийский предложил простой рецепт, в основном совпадающий с евклидовым.

Возьмите любые два натуральных числа и вычислите:

их удвоенное произведение;

разность их квадратов;

сумму их квадратов.

Три получившихся числа будут сторонами пифагорова треугольника.

Возьмем, к примеру, числа 2 и 1. Вычислим:

удвоенное произведение: 2 × 2 × 1 = 4;

разность квадратов: 2² – 1² = 3;

сумма квадратов: 2² + 1² = 5,

и мы получили знаменитый треугольник 3–4–5. Если взять вместо этого числа 3 и 2, получим:

удвоенное произведение: 2 × 3 × 2 = 12;

разность квадратов: 3² – 2² = 5;

сумму квадратов: 3² + 2² = 13,

и получаем следующий по известности треугольник 5 – 12 – 13. Попробуем взять числа 42 и 23 и получим:

удвоенное произведение: 2 × 42 × 23 = 1932;

разность квадратов: 42² – 23² = 1235;

сумма квадратов: 42² + 23² = 2293,

никто никогда не слышал о треугольнике 1235–1932–2293.

Но эти числа тоже работают:

1235² + 1932² = 1525225 + 3732624 = 5257849 = 2293².

В диофантовом правиле есть еще одна особенность, на которую уже намекали: получив три числа, мы можем взять еще одно произвольное число и все их на него умножить. Таким образом треугольник 3–4–5 можно превратить в треугольник 6–8–10, умножив все стороны на 2, или в треугольник 15–20–25, умножив все на 5.

Если перейти на язык алгебры, правило приобретает следующий вид: пусть u, v и k — натуральные числа. Тогда прямоугольный треугольник со сторонами

2kuv и k (u² – v²) имеет гипотенузу

k (u² + v²).

Существуют и другие способы изложения основной идеи, но все они сводятся к описанному выше. Этот метод позволяет получить все пифагоровы тройки.

Правильные многогранники

Существует ровным счетом пять правильных многогранников. Правильный многогранник (или полиэдр) — это объемная фигура с конечным числом плоских граней. Грани сходятся друг с другом на линиях, именуемых ребрами; ребра встречаются в точках, именуемых вершинами.

Кульминацией евклидовых «Начал» является доказательство того, что может быть только пять правильных многогранников, то есть многогранников, у которых каждая грань представляет собой правильный многоугольник (равные стороны, равные углы), все грани идентичны и все вершины окружены равным числом одинаково расположенных граней. Вот пять правильных многогранников:

тетраэдр с четырьмя треугольными гранями, четырьмя вершинами и шестью ребрами;

куб, или гексаэдр, с 6 квадратными гранями, 8 вершинами и 12 ребрами;

октаэдр с 8 треугольными гранями, 6 вершинами и 12 ребрами;

додекаэдр с 12 пятиугольными гранями, 20 вершинами и 30 ребрами;

икосаэдр с 20 треугольными гранями, 12 вершинами и 30 ребрами.

Рис. 37. Пять правильных многогранников

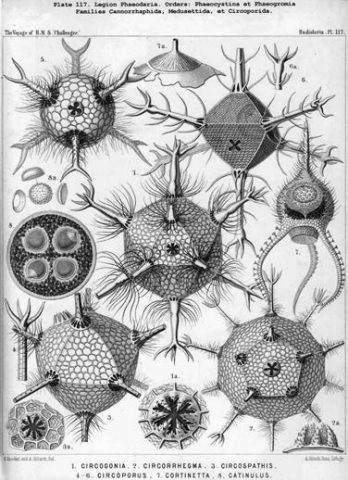
Правильные многогранники можно найти и в природе. В 1904 г. Эрнст Геккель опубликовал рисунки крохотных организмов, известных как радиолярии; многие из них по форме напоминают те самые пять правильных многогранников. Возможно, правда, он немного подправил природу, и рисунки не отражают полностью форму конкретных живых существ. Первые три структуры наблюдаются также в кристаллах. Додекаэдра и икосаэдра в кристаллах вы не найдете, хотя неправильные додекаэдры и икосаэдры там иногда попадаются. Настоящие додекаэдры могут возникать в виде квазикристаллов, которые во всем похожи на кристаллы, за исключением того, что их атомы не образуют периодической решетки.

Рис. 38. Рисунки Геккеля: радиолярии в форме правильных многогранников

Рис. 39. Развертки правильных многогранников

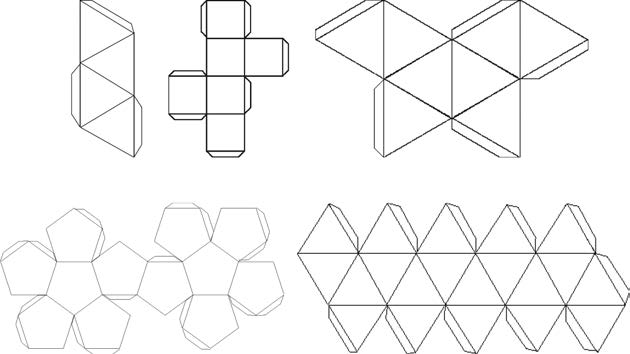
Бывает интересно делать модели правильных многогранников из бумаги, вырезав предварительно набор соединенных между собой граней — это называется разверткой многогранника; развертку складывают по ребрам и склеивают соответствующие ребра между собой. Полезно добавить к одному из ребер каждой такой пары дополнительную площадку для клея, как показано на рис. 39. Если такой площадки нет, можно использовать липкую ленту.

Уравнение пятой степени

Не существует алгебраической формулы для решения уравнений 5-й степени.

В общем виде уравнение пятой степени выглядит так:

ax⁵ + bx⁴ + cx³ + dx² + ex + f = 0.

Проблема в том, чтобы найти формулу для решений такого уравнения (у него может быть до пяти решений). Опыт обращения с квадратными и кубическими уравнениями, а также с уравнениями четвертой степени позволяет предположить, что такая формула должна существовать и для уравнений пятой степени, причем в ней, по идее, должны фигурировать корни пятой, третьей и второй степени. Опять же, можно смело предположить, что такая формула, если она существует, окажется очень и очень сложной.

Это предположение в конечном итоге оказалось ошибочным. В самом деле, никакой такой формулы не существует; по крайней мере не существует формулы, состоящей из коэффициентов a, b, c, d, e и f, составленной с использованием сложения, вычитания, умножения и деления, а также извлечения корней. Таким образом, в числе 5 есть что-то совершенно особенное. Причины такого необычного поведения пятерки весьма глубоки, и потребовалось немало времени, чтобы в них разобраться.

Первым признаком проблемы стало то, что, как бы математики ни старались отыскать такую формулу, какими бы умными они ни были, они неизменно терпели неудачу. Некоторое время все считали, что причины кроются в неимоверной сложности формулы. Считалось, что никто просто не может как следует разобраться в этой алгебре. Однако со временем некоторые математики начали сомневаться в том, что такая формула вообще существует, а в 1823 г. Нильс Хендрик Абель сумел доказать обратное. Такой формулы не существует. Вскоре после этого Эварист Галуа нашел способ определить, решаемо ли уравнение той или иной степени — 5-й, 6-й, 7-й, вообще любой — с использованием такого рода формулы.

Вывод из всего этого прост: число 5 особенное. Можно решать алгебраические уравнения (при помощи корней n-й степени для различных значений n) для степеней 1, 2, 3 и 4, но не для 5-й степени. Здесь очевидная закономерность заканчивается.

Никого не удивляет, что уравнения степеней больше 5 ведут себя еще хуже; в частности, с ними связана такая же трудность: нет общих формул для их решения. Это не означает, что уравнения не имеют решений; это не означает также, что невозможно найти очень точные численные значения этих решений. Все дело в ограниченности традиционных инструментов алгебры. Это напоминает невозможность трисекции угла при помощи линейки и циркуля. Ответ существует, но перечисленные методы недостаточны и не позволяют определить, каков он.

Кристаллографическое ограничение

Кристаллы в двух и трех измерениях не имеют 5-лучевой симметрии вращения.

Атомы в кристалле образуют решетку, то есть структуру, которая периодически повторяется в нескольких независимых направлениях. К примеру, рисунок на обоях повторяется по длине рулона; кроме того, он обычно повторяется и в горизонтальном направлении, иногда со сдвигом от одного куска обоев к следующему. По существу, обои — это двумерный кристалл.

Существует 17 разновидностей обойных рисунков на плоскости (см. главу 17). Они различаются по типам симметрии, то есть по способам сдвинуть жестко рисунок таким образом, чтобы он точно лег сам на себя в первоначальном положении. К типам симметрии относятся, в частности, различные варианты симметрии вращения, где рисунок следует повернуть на определенный угол вокруг определенной точки — центра симметрии.

Порядок симметрии вращения — это то, сколько раз можно повернуть тело до полного круга так, чтобы все детали рисунка вернулись на первоначальные позиции. К примеру, поворот на 90° — это симметрия вращения 4-го порядка*. Список возможных типов симметрии вращения в кристаллической решетке вновь указывает на необычность числа 5: его там нет. Существуют варианты с симметрией вращения 2, 3, 4 и 6-го порядков, но ни один обойный рисунок не имеет симметрии вращения 5-го порядка. Симметрии вращения порядка больше 6 в кристаллах тоже не бывает, но первое нарушение последовательности происходит все же на числе 5.

То же происходит с кристаллографическими системами в трехмерном пространстве. Здесь решетка повторяет себя по трем независимым направлениям. Существует 219 различных типов симметрии, или 230, если считать зеркальное отражение рисунка отдельным его вариантом — притом, что в данном случае нет зеркальной симметрии. Опять же, наблюдаются симметрии вращения порядков 2, 3, 4 и 6, но не 5. Этот факт получил название кристаллографического ограничения.

В четырехмерном пространстве решетки с симметрией 5-го порядка существуют; вообще, для решеток достаточно высокой размерности возможен любой наперед заданный порядок симметрии вращения.

Рис. 40. Кристаллическая решетка поваренной соли. Темные шарики изображают атомы натрия, светлые — атомы хлора

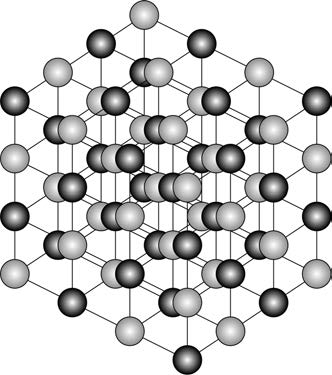
Квазикристаллы

Хотя симметрия вращения 5-го порядка в двумерных и трехмерных решетках невозможна, она может существовать в чуть менее регулярных структурах, известных как квазикристаллы. Воспользовавшись набросками Кеплера, Роджер Пенроуз открыл плоские системы с более общим типом пятикратной симметрии. Они получили название квазикристаллов.

Квазикристаллы существуют в природе. В 1984 г. Даниэль Шехтман открыл, что сплав алюминия и марганца может образовывать квазикристаллы; первоначально кристаллографы встретили его сообщение с некоторым скепсисом, но позже открытие было подтверждено, и в 2011 г. Шехтман был удостоен Нобелевской премии по химии. В 2009 г. команда ученых под руководством Луки Бинди обнаружила квазикристаллы в минерале с российского Корякского нагорья — соединении алюминия, меди и железа. Сегодня этот минерал называется икосаэдрит. Измерив при помощи масс-спектрометра содержание в минерале разных изотопов кислорода, ученые показали, что этот минерал возник не на Земле. Он сформировался около 4,5 млрд лет назад, в то время, когда Солнечная система только зарождалась, и провел большую часть времени в поясе астероидов, обращаясь вокруг Солнца, пока какое-то возмущение не изменило его орбиту и не привело его в конце концов на Землю.

Рис. 41. Слева: одна из двух квазикристаллических решеток с точной пятикратной симметрией. Справа: атомная модель икосаэдрического алюминиево-палладиево-марганцевого квазикристалла