|
||
|
|
||
| Главная ≫ Инфотека ≫ Математика ≫ «Джоконда» как график функции, или Построение функции со всюду плотным графиком // Лейб Штейнгарц |
«Джоконда» как график функции, или Построение функции со всюду плотным графикомЛейб Штейнгарц
В математике давно известны функции с удивительным свойством: их график всюду плотен на плоскости. Такие функции часто называют «странными», «экзотическими», «дикими» и т. п. Они хорошо известны специалистам-математикам, но почти не знакомы «широкой публике», например школьникам. Ведь те построения, которые приводятся в литературе (см., например, список в конце статьи), обычно громоздки и требуют серьезной математической подготовки.
Мне удалось найти совершенно элементарное доказательство существования таких функций, с которым я хочу вас познакомить. Напомню вначале, что множество на плоскости называется всюду плотным,
если в любом круге (даже очень маленьком) обязательно найдется хотя бы
одна точка из этого множества. Например, множество всех точек плоскости,
у которых обе координаты рациональны, — это множество
обозначается Обещанное доказательство довольно абстрактно, и, чтобы оно было более прозрачным для читателей, рассмотрим сначала такую картинку (рис. 1).
Перед нами самая известная картина великого Леонардо да Винчи — «Джоконда». Правда, изображенная при помощи старой вычислительной машины. Такие картинки было очень модно изготавливать в конце прошлого века. Впрочем, и сейчас любая картинка на компьютере примерно так и составляется — из точек.
Портрет Джоконды состоит из громадного количества точек. Сколько этих точек — мы не знаем. Может, миллион. Может, намного больше. Не важно. Главное, что их конечное количество. Рассмотрим множество всех этих точек как некую геометрическую фигуру. Вспомните школьное определение, что геометрическая фигура — это любое множество точек. И зададим следующий вопрос:
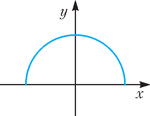
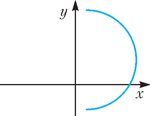
является ли эта фигура графиком некоторой (однозначной) функции? Разумеется, мы предполагаем, что точки тут математические — они не имеют размера (в отличие от компьютерных пикселей, которые имеют хоть и очень маленький, но все же ненулевой размер). Для начала ответьте на другой вопрос (ответ не такой уж тривиальный): является ли полуокружность графиком функции? А это — как посмотреть! Если так, как показано на рисунке 2, то это график функции (почему?). А если так, как изображено на рисунке 3, то нет (опять-таки, почему?). И снова я задаю свой предыдущий вопрос:
является ли «Джоконда» графиком некоторой функции? Отвечаю. Оказывается, можно так подобрать систему координат (т. е. так выбрать оси x и у), что множество всех точек, образующих портрет Джоконды, окажется графиком некоторой функции. Докажем это. Обозначим наше множество буквой G — в честь Джоконды. Будем считать, что оно расположено на некоторой числовой плоскости с числовыми осями x и у. Проведем все прямые, соединяющие попарно все точки нашего множества G. Обозначим множество всех полученных прямых через Каждая прямая из этого множества будет образовывать некоторый угол с осью х
(для определенности, можно брать меньший угол, хотя это и
не принципиально). Таких углов будет тоже конечное множество.
Следовательно, на плоскости непременно найдется некоторая прямая,
которая не будет совпадать ни с одной из прямых Примем эту прямую за новую ось ординат. А любую прямую, ей перпендикулярную, за новую ось абсцисс. Можно сказать и так: посмотрим на портрет Джоконды под другим углом. Но не под каким угодно углом, а так, как было выбрано. Или, что то же самое, просто повернем картинку на нужный угол. Мы увидим примерно то, что изображено на рисунке 4.
При этом на каждой прямой, которая параллельна новой оси ординат, будет лежать не более одной точки из множества G, т. е. не более одной точки из портрета Джоконды. А это и означает, что множество точек, образующих портрет Джоконды, превратилось в график некоторой (однозначной!) функции. Ведь каждому значению х (из соответствующей области определения) соответствует единственное значение у. Это следует из нашего построения. И хотя мы не можем указать, какому числу что именно соответствует, это всё же не мешает тому, что будет получен график функции. Впрочем, при необходимости можно найти формулу даже непрерывной функции, график которой проходит через все точки, принадлежащие портрету Джоконды. Для этого достаточно воспользоваться формулой Лагранжа:
Здесь (x1; у1), (x2; у2), (x3; у3), ... — это и есть точки «Джоконды», занумерованные в каком-то порядке. Несмотря на довольно пугающий вид, понять эту формулу совсем несложно (попробуйте!). Но об этом как-нибудь в другой раз. Тем более что, нарисовав график такой функции, мы уже вряд ли разглядим в нем Джоконду. Слишком много будет «лишних» линий, соединяющих точки Джоконды в непрерывный график. Так что обойдемся лучше без непрерывных функций и двинемся дальше. Я надеюсь, что портрет Джоконды поможет более четко представить построение функции, график которой всюду плотен на плоскости. Ведь при этом работает практически та же идея.
Итак, построим теперь нашу «странную» функцию. Первый способ. Проведем какую-нибудь прямую вида у = mx + n, которая образует с положительным направлением оси абсцисс угол величиной 60°. Тогда m = tg60° = √3. Докажем, что на такой прямой может лежать не более одной точки с рациональными координатами. Действительно, предположим, что этой прямой принадлежат две различные точки с рациональными координатами: A = (x1, у1) и В = (x2, у2). Тогда
Вычитая второе уравнение из первого, получим у1 – у2 = m(x1 – x2). Значит (учитывая, что (x1 ≠ x2),
Но это невозможно, так как √3 — число иррациональное. Поэтому на каждой прямой вида у = x√3 + n лежит не более одной точки с рациональными координатами. А теперь — главная идея (взгляд «с другой стороны»). Оставим множество Если мы хотим, чтобы полученная нами функция была определена для всех действительных чисел, достаточно для остальных точек принять ее значение равным, например, нулю. Таким образом, получим функцию, определенную на всей числовой прямой, график которой, очевидно, всюду плотен на плоскости.
Второй способ. Этот способ еще короче. Но он будет понятен лишь тем, кто знаком с начальными понятиями теории множеств. Он доступен, например, математикам-первокурсникам или ученикам математических классов.
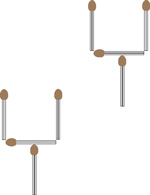
Рассмотрим снова множество В заключение предлагаем решить головоломку, которую я придумал для младших школьников, но которая, как мне кажется, хорошо иллюстрирует главную идею изложенного построения «странной» функции. Головоломка с двумя бокалами. Перед вами два бокала, построенные при помощи спичек (рис. 5). Переставьте две спички так, чтобы у полученной конфигурации была ось симметрии. Найдите два различных способа решения. Литература: Лейб Штейнгарц, доктор педагогики из Иерусалима (Израиль)
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Математика ≫ «Джоконда» как график функции, или Построение функции со всюду плотным графиком // Лейб Штейнгарц |
|
[time: 8 ms; queries: 7]
18 Фев 2026 19:07:21 GMT+3 |







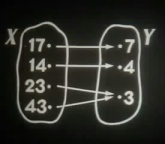 Соответствия между множествами. Определение функции. Способы задания функции. Табличный способ задания функции. Задание функции формулой. График прямой и обратной пропорциональности. Определение линейной функции. График линейной функции. Угловой коэффициент прямой. Графическое решение системы уравнений. Функция квадратичной зависимости (парабола). СССР, Киевнаучфильм, 1975 г.
Соответствия между множествами. Определение функции. Способы задания функции. Табличный способ задания функции. Задание функции формулой. График прямой и обратной пропорциональности. Определение линейной функции. График линейной функции. Угловой коэффициент прямой. Графическое решение системы уравнений. Функция квадратичной зависимости (парабола). СССР, Киевнаучфильм, 1975 г. В школе мы несколько лет подряд прилежно изучаем геометрию. Но не зря ли мы тратим время? Чем может помочь геометрия в жизни? Измерить расстояние от точки до точки, вычислить площадь или объём предмета и только? Нет, конечно. Законы геометрии применимы буквально на каждом шагу. Просто нужно знать, как ими воспользоваться.
В школе мы несколько лет подряд прилежно изучаем геометрию. Но не зря ли мы тратим время? Чем может помочь геометрия в жизни? Измерить расстояние от точки до точки, вычислить площадь или объём предмета и только? Нет, конечно. Законы геометрии применимы буквально на каждом шагу. Просто нужно знать, как ими воспользоваться. Математик Николай Николаевич Андреев рассказывает увлекательные истории о решенных и нерешенных математических задачах на наглядных примерах.
Математик Николай Николаевич Андреев рассказывает увлекательные истории о решенных и нерешенных математических задачах на наглядных примерах. Математика — самый точный и универсальный язык науки, но можно ли с помощью цифр объяснить человеческие чувства? Формулы любви, семена хаоса и романтические дифференциальные уравнения — публикуем главу из книги одного из лучших преподавателей математики в мире — Стивена Строгаца «Удовольствие от Х», выпущенную издательством «Манн, Иванов и Фербер».
Математика — самый точный и универсальный язык науки, но можно ли с помощью цифр объяснить человеческие чувства? Формулы любви, семена хаоса и романтические дифференциальные уравнения — публикуем главу из книги одного из лучших преподавателей математики в мире — Стивена Строгаца «Удовольствие от Х», выпущенную издательством «Манн, Иванов и Фербер». Давайте рассмотрим последовательность чисел, первое из которых равно 1, а каждое последующее вдвое больше: 1, 2, 4, 8, 16, … Называется она вполне ожидаемо: последовательность степеней двойки. Казалось бы, ничего выдающегося в ней нет — последовательность как последовательность, не лучше и не хуже других. Тем не менее, она обладает весьма примечательными свойствами.
Давайте рассмотрим последовательность чисел, первое из которых равно 1, а каждое последующее вдвое больше: 1, 2, 4, 8, 16, … Называется она вполне ожидаемо: последовательность степеней двойки. Казалось бы, ничего выдающегося в ней нет — последовательность как последовательность, не лучше и не хуже других. Тем не менее, она обладает весьма примечательными свойствами. Лекция математика Алексея Владимировича Савватеева в СУНЦ МГУ про великие математические революции и нерешенные задачи, многие из которых уже решены, а некоторые — ждут своих героев. Для старших и "продвинутых" школьников, интересующихся математикой.
Лекция математика Алексея Владимировича Савватеева в СУНЦ МГУ про великие математические революции и нерешенные задачи, многие из которых уже решены, а некоторые — ждут своих героев. Для старших и "продвинутых" школьников, интересующихся математикой.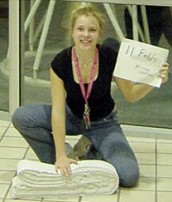 Нам так и не удалось найти первоисточник этого широко распространённого поверья: ни один лист бумаги нельзя сложить вдвое больше семи (по некоторым данным — восьми) раз. Между тем текущий рекорд складывания – 12 раз. И что удивительнее, принадлежит он девушке, математически обосновавшей эту «загадку бумажного листа».
Нам так и не удалось найти первоисточник этого широко распространённого поверья: ни один лист бумаги нельзя сложить вдвое больше семи (по некоторым данным — восьми) раз. Между тем текущий рекорд складывания – 12 раз. И что удивительнее, принадлежит он девушке, математически обосновавшей эту «загадку бумажного листа». Представьте себе, что на стол высыпана кучка совершенно одинаковых по виду монет, но вам сказали, что одна из этих монет — фальшивая. Она отличается от остальных монет по весу, но вам не сообщили, легче она или тяжелее. В вашем распоряжении имеются чашечные весы без гирь. Как нужно действовать, чтобы выделить эту монету и выяснить её тип (то есть узнать, легче она или тяжелее) за минимальное число взвешиваний?
Представьте себе, что на стол высыпана кучка совершенно одинаковых по виду монет, но вам сказали, что одна из этих монет — фальшивая. Она отличается от остальных монет по весу, но вам не сообщили, легче она или тяжелее. В вашем распоряжении имеются чашечные весы без гирь. Как нужно действовать, чтобы выделить эту монету и выяснить её тип (то есть узнать, легче она или тяжелее) за минимальное число взвешиваний? Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определённом отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.
Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определённом отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.