|
||
|
|
||
| Главная ≫ Инфотека ≫ Математика ≫ Математик Николай Андреев: «Мы хотим, чтобы люди обсуждали не сериалы, а математические этюды» |
Математик Николай Андреев: «Мы хотим, чтобы люди обсуждали не сериалы, а математические этюды»
Ученый-популяризатор Николай Андреев создал сайт «Математические этюды», в котором собирает научно-популярные рассказы о современных задачах математики и визуализации математических сюжетов: почему у икосаэдра столько же граней, сколько вершин у додекаэдра, что будет, если зажечь лампочку в фокусе параболы, и какое отношение к квадрату суммы имеет Жан-Жак Руссо. — Зачем вам этот сайт? — В начале прошлого века математик Яков Перельман сделал великую вещь — положил научно-популярную книжку на стол в каждой советской семье. Вот и нам хочется, чтобы люди обсуждали не сериалы, а математические этюды. Наш сайт в интернете посещают порядка 15 тысяч различных людей в день — и это мы пока еще не занимались продвижением в социальных сетях. Одна из возможностей достучаться до молодежи — это переход на мобильные устройства. У человека должна быть возможность получать математические мультфильмы в таком виде, в каком ему удобно. Школьный мультфильм «Теорема Пифагора» у нас, к примеру, для айфонов бесплатный, а для айпадов уже есть минимальная стоимость. Его скачали уже десятки тысяч человек — порядка 60 тысяч — а значит, что у этой аудитории есть потребность в подобном контенте. — А зачем человеку вообще смотреть математические мультфильмы, если школу он закончил лет 10 назад? — Чтобы было интереснее жить. Когда изучаются естественнонаучные задачи, приходит понимание, как решить жизненные проблемы. В голове все встает по местам. Так рождается математика. Вот у меня дочка в третьем классе: садимся, решаем несколько задач, и после этого у нее ум приходит в порядок, она начинает все организованно делать. Прорешали 3–4 задачи, разложили несколько головоломок, потратили немного времени: а мысли просветлели, и вы свои дела начали делать по-другому. Не говоря уже о том, что техника без математики просто не живет. Куда ни ткнешь, всюду есть какая-то математика. — У вас ведь даже есть мультфильм про обычный пакет молока. — Все знают про развертку тетраэдра, но оказывается, что на его примере можно решить современные задачи. Многие, наверное, замечали, что пакеты одной марки сока имеют закругленные углы. Оказывается, если делать такую упаковку с углами не строго прямыми, а закругленными, то при том же внутреннем объеме можно сэкономить на производстве самих пакетов. При гигантских тиражах экономия существенная. — Сколько времени занимает работа над одним таким математическим этюдом? — Набросать основу мультфильма получается довольно быстро. Расчеты делают математики из нашей лаборатории, потом они передаются аниматорам. Больше всего времени уходит на внесение корректив: меньше двух месяцев никогда не бывает, а иногда и по полгода делаем. Бывают мультфильмы, которые мы откладываем и возвращаемся к ним через год. Вот скоро появится мультфильм про радугу. Оказывается, и это тоже математика.
Давно уже сделан фильм про гиперболоиды. Но оказывается, что не осталось никаких чертежей от Шуховской башни. Вот уже 4 месяца наша команда делает качественную модель — на ее примере можно объяснить, какие математические задачи решались по ходу стройки. Если вы посмотрите на записи Шухова, там на каждой странице просто куча формул. Изначально он задумывал создать 350-метровую постройку, но в разрушенной стране не хватило металла, и вышла 150-метровая. Если бы 350-метровая башня была построена, то она была бы выше Эйфелевой — при этом в 4 раза легче и в несколько раз прочнее. — Что вообще такое современная математика? Иногда кажется, что уже доказаны все возможные теоремы. — Когда я начинаю читать лекции, то говорю, что работаю в математическом институте имени Стеклова РАН, где сто взрослых ученых сидят и доказывают теоремы. Все начинают ржать, потому что считают, что во времена Пифагора математика закончилась. На самом деле, постоянно возникает масса нерешенных задач. И одна из целей нашего проекта — показать, что такие задачи есть, и тем самым завлечь. Если не занятием математикой, то хотя бы некоторым уважением к этой науке, ее мощи и красоте. Нормальным людям вообще некая любознательность присуща. Вопрос только — убили в них это качество уже или еще не успели. Одна из проблем наших школ — это то, что зачастую учителя дают ответы на вопросы, которые у учеников еще не возникли. Поэтому на уроках математики они не понимают, зачем нужны косинусы, синусы. И мы, собственно, с помощью мультфильмов стараемся объяснить, показать интересные математические сюжеты. И продемонстрировать, зачем эта математика нужна и что она может делать. — Очень многие школьники учат математику и не понимают, как эти знания могут пригодиться в дальнейшей жизни. Можно ли говорить о том, что школьный курс математики действительно оторван от реальной жизни? — Как-то раз мне звонит знакомый, спрашивает: «Ты читал лекции в школе, которая находится в районе оранжевой ветки?» Говорю: «Читал, а ты откуда знаешь?» Отвечает: «Да вот еду в метро, а тут две девчонки про циклоиды рассуждают». На мой взгляд, это показатель того, что популяризировать математику все-таки стоит. Не бывает человека, который не может понять чего-то. Причина, по которой курс математики чуть сложнее, чем все остальные, — это то, что он непрерывный. Если вы не учили дроби, дальше тяжело. А если вы не прочли Толстого, то Чехова вы можете читать и даже понимать. А у нас на протяжении всего курса обучения нужно поддерживать очень высокий уровень преподавания. — Обратная сторона популяризации — профанация. Не боитесь этого? — Чем выше уровень качества популяризации, тем меньше лженауки. Если поле качественной популяризации не занято учеными, то конечно, всегда приходит профанация. В этом на самом деле беда научной журналистики в России. Невозможно в те сроки, которые ставит редакция, разобраться в качестве. Необходимо некое взаимодействие ученых и журналистов. Здесь очень тонкая грань. Одно из условий — должна быть только правда. Понятно, что всю правду не расскажешь, но все, что доносишь до слушателей, должно быть правдой. Яна Гуменник
T&P
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Математика ≫ Математик Николай Андреев: «Мы хотим, чтобы люди обсуждали не сериалы, а математические этюды» |
|
[time: 11 ms; queries: 8]
22 Фев 2026 05:26:09 GMT+3 |



 Книга известного американского ученого, почетного профессора математики Нью-Йоркского университета, популяризатора науки Мориса Клайна ярко и увлекательно рассказывает о роли математики в сложном многовековом процессе познания человеком окружающего мира, ее места в физических науках. Имя автора давно и хорошо известно советским и российским читателям.
Книга известного американского ученого, почетного профессора математики Нью-Йоркского университета, популяризатора науки Мориса Клайна ярко и увлекательно рассказывает о роли математики в сложном многовековом процессе познания человеком окружающего мира, ее места в физических науках. Имя автора давно и хорошо известно советским и российским читателям.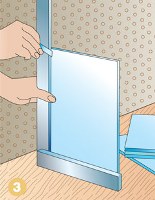 В школе мы несколько лет подряд прилежно изучаем геометрию. Но не зря ли мы тратим время? Чем может помочь геометрия в жизни? Измерить расстояние от точки до точки, вычислить площадь или объём предмета и только? Нет, конечно. Законы геометрии применимы буквально на каждом шагу. Просто нужно знать, как ими воспользоваться.
В школе мы несколько лет подряд прилежно изучаем геометрию. Но не зря ли мы тратим время? Чем может помочь геометрия в жизни? Измерить расстояние от точки до точки, вычислить площадь или объём предмета и только? Нет, конечно. Законы геометрии применимы буквально на каждом шагу. Просто нужно знать, как ими воспользоваться. Давайте рассмотрим последовательность чисел, первое из которых равно 1, а каждое последующее вдвое больше: 1, 2, 4, 8, 16, … Называется она вполне ожидаемо: последовательность степеней двойки. Казалось бы, ничего выдающегося в ней нет — последовательность как последовательность, не лучше и не хуже других. Тем не менее, она обладает весьма примечательными свойствами.
Давайте рассмотрим последовательность чисел, первое из которых равно 1, а каждое последующее вдвое больше: 1, 2, 4, 8, 16, … Называется она вполне ожидаемо: последовательность степеней двойки. Казалось бы, ничего выдающегося в ней нет — последовательность как последовательность, не лучше и не хуже других. Тем не менее, она обладает весьма примечательными свойствами. Математика — самый точный и универсальный язык науки, но можно ли с помощью цифр объяснить человеческие чувства? Формулы любви, семена хаоса и романтические дифференциальные уравнения — публикуем главу из книги одного из лучших преподавателей математики в мире — Стивена Строгаца «Удовольствие от Х», выпущенную издательством «Манн, Иванов и Фербер».
Математика — самый точный и универсальный язык науки, но можно ли с помощью цифр объяснить человеческие чувства? Формулы любви, семена хаоса и романтические дифференциальные уравнения — публикуем главу из книги одного из лучших преподавателей математики в мире — Стивена Строгаца «Удовольствие от Х», выпущенную издательством «Манн, Иванов и Фербер». Математик Николай Николаевич Андреев рассказывает увлекательные истории о решенных и нерешенных математических задачах на наглядных примерах.
Математик Николай Николаевич Андреев рассказывает увлекательные истории о решенных и нерешенных математических задачах на наглядных примерах. Лекция математика Алексея Владимировича Савватеева в СУНЦ МГУ про великие математические революции и нерешенные задачи, многие из которых уже решены, а некоторые — ждут своих героев. Для старших и "продвинутых" школьников, интересующихся математикой.
Лекция математика Алексея Владимировича Савватеева в СУНЦ МГУ про великие математические революции и нерешенные задачи, многие из которых уже решены, а некоторые — ждут своих героев. Для старших и "продвинутых" школьников, интересующихся математикой.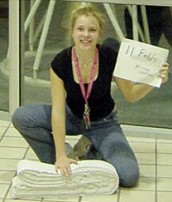 Нам так и не удалось найти первоисточник этого широко распространённого поверья: ни один лист бумаги нельзя сложить вдвое больше семи (по некоторым данным — восьми) раз. Между тем текущий рекорд складывания – 12 раз. И что удивительнее, принадлежит он девушке, математически обосновавшей эту «загадку бумажного листа».
Нам так и не удалось найти первоисточник этого широко распространённого поверья: ни один лист бумаги нельзя сложить вдвое больше семи (по некоторым данным — восьми) раз. Между тем текущий рекорд складывания – 12 раз. И что удивительнее, принадлежит он девушке, математически обосновавшей эту «загадку бумажного листа». Представьте себе, что на стол высыпана кучка совершенно одинаковых по виду монет, но вам сказали, что одна из этих монет — фальшивая. Она отличается от остальных монет по весу, но вам не сообщили, легче она или тяжелее. В вашем распоряжении имеются чашечные весы без гирь. Как нужно действовать, чтобы выделить эту монету и выяснить её тип (то есть узнать, легче она или тяжелее) за минимальное число взвешиваний?
Представьте себе, что на стол высыпана кучка совершенно одинаковых по виду монет, но вам сказали, что одна из этих монет — фальшивая. Она отличается от остальных монет по весу, но вам не сообщили, легче она или тяжелее. В вашем распоряжении имеются чашечные весы без гирь. Как нужно действовать, чтобы выделить эту монету и выяснить её тип (то есть узнать, легче она или тяжелее) за минимальное число взвешиваний? Каустики — это вездесущие оптические поверхности и кривые, возникающие при отражении и преломлении света. Каустики можно описать как линии или поверхности, вдоль которых концентрируются световые лучи.
Каустики — это вездесущие оптические поверхности и кривые, возникающие при отражении и преломлении света. Каустики можно описать как линии или поверхности, вдоль которых концентрируются световые лучи.