10. Парадокс Банаха–Тарского / Парадоксы теории множеств

Иван Ященко

<<< |1|…|7|8|9|10|11|12|13|14|15|…|17| >>>

10. Парадокс Банаха–Тарского

Парадокс был придуман в 1920-х годах двумя замечательными математиками Банахом и Тарским, которые для этого даже не встречались. Они обнаружили, что обычную сферу можно "разрезать" на несколько частей, из которых потом можно сложить две точно такие же сферы. Формально, конечно, речь идет о некотором отображении из множества точек одной сферы в объединение множеств точек двух сфер того же радиуса. Сразу оговорим, какие отображения имеются в виду.

Назовем отображение $f\colon X \to Y$ допустимым, если существует разбиение $X$ на непересекающиеся множества $A_1, A_2,\dots,A_n$ , такие что ограничение $f$ на каждое $A_1$ есть изометрия (или движение) и для каждых $i \ne j$ множества $f(A_i)$ и $f(A_j)$ не пересекаются. В этом случае будем также говорить, что $X$ и $Y$ эквивалентны, или $X \sim Y$ (убедитесь в том, что это действительно отношение эквивалентности). Парадокс Банаха–Тарского заключается в том, что существует допустимое отображение из сферы в объединение двух сфер того же радиуса. Некоторое время этот парадокс считали опровержением аксиомы выбора, используемой при его доказательстве, поскольку в него никто не верил. Потом осознали, что ничего страшного здесь нет. Кроме аксиомы выбора в доказательстве используются построение множества Витали, неизмеримого относительно произвольной "хорошей" меры, сдвиг натурального ряда (если к каждому натуральному числу прибавить 1, то получится тот же самый натуральный ряд и еще одна точка^*17) и еще некоторые ниже сформулированные утверждения. Доказав их, мы перейдем к переклейке сферы на две, а потом и к переклейке шара.

^*17 Ноль или один, в зависимости от идеологических убеждений граждан, то ли они считают, что ноль — натуральное число, то ли нет.

10.1. Две важные теоремы

Итак, первое вспомогательное утверждение.

Теорема. Если $A \subset B \subset C$ и $A \sim C$ , то $A \sim B$ .

Примечательно, что формулировка этой теоремы почти в точности совпадает с формулировкой еще одного известного утверждения, называемого теоремой Кантора–Бернштейна:

Если $A \subset B \subset C$ и $|A| = |C|$ , то $|A| = |B|$ .

Эта теорема является одной из основных в теории множеств. У нее есть другая формулировка, тоже достаточно известная: если $|A| \le |B|$ и $|B| \le |A|$ , то $|A| = |B|$ (мы пишем $|X| \le |Y|$ , или $X \le Y$ , если $X$ равномощно некоторому подмножеству $Y$ , это отношение называется "меньше либо равно по мощности"; таким образом, теорема Кантора–Бернштейна — это всего лишь утверждение, необходимое для доказательства корректности введенного отношения на множествах).

3. Докажите равносильность двух формулировок.

Доказывать теорему 1 и теорему Кантора–Бернштейна мы тоже будем одновременно.

Доказательство. Есть $f\colon C \to A$ . Обозначим $C$ за $C_0$ , $B$ за $B_0$ , $A$ за $C_1$ . Если $f$ применить к $B$ , то получим $B_1$ — подмножество $A$ или $C_1$ . Применяя так дальше $f$ к получаемым множествам, приходим к следующей цепочке:

$C_0 \supset B_0 \supset C_1 \supset B_1 \supset C_2 \supset B_2 \supset \cdots \supset Z$ ,

где $Z$ — пересечение всех $C_i$ или пересечение всех $B_i$ . Заметим, что $B$ и $C$ (т. е. $B_0$ и $C_0$ ) можно разложить в объединение таких интересных множеств:

$%\width{36}\begin{align} C=(C_0 \setminus B_0)\cup (B_0 \setminus C_1)\cup (C_1 \setminus B_1) \cup \cdots \cup Z \tag{1} \\ B=(B_0 \setminus C_1)\cup (C_1 \setminus B_1)\cup (B_1 \setminus C_2) \cup \cdots \cup Z \tag{2} \end{align}%$

Поскольку $C_0 \sim C_1$ и $B_0 \sim B_1$ , то $C_0 \setminus B_0 \sim C_1 \setminus B_1$ , поскольку $B_0 \sim B_1$ и $C_1 \sim C_2$ , то $B_0 \setminus C_1 \sim B_1 \setminus C_2$ , и т. д. Значит, в каждой из цепочек (1) и (2) все четные куски эквивалентны друг другу и все нечетные куски эквивалентны друг другу. В доказательстве теоремы Кантора–Бернштейна здесь можно было бы остановиться: мы уже получили два множества, состоящие каждый из счетного числа множеств одного вида ( $C_0 \setminus B_0$ ), из счетного числа множеств другого вида ( $B_0 \setminus C_1$ ) и множества $Z$ . Но для доказательства теоремы 1 нам нужно отображение, соответствующее разбиению множеств $B$ и $C$ на конечное число частей. Предъявим такое отображение. Пусть отображение $h\colon C \to B$ на всех нечетных множествах из разбиения (1) совпадает с $f$ , а на всех четных и на $Z$ тождественное, т. е.

$h(x) = \begin{cases} f(x), & \text{если}\ x \in \bigcup_{i}(C_i \setminus B_i) \\ x, &\text{если}\ x \in Z \cup \bigcup_{i}(B_i \setminus C_{i+1}) \end{cases}$

Имеется в виду, что все четные множества в объединении образуют первое множество, а все нечетные — второе. Итого всего два множества.

Теперь разрежем сферу на две. Как уже обещалось, будем использовать сдвиг натурального ряда. Сначала покажем, почему сферу в некотором смысле можно считать счетным множеством, а потом объясним, что из этого получается.

10.2. Свободные группы

Рассмотрим два поворота $\varphi$ и $\psi$ в пространстве, причем с разными осями, проходящими через центр сферы, да еще и такие, что один поворот не переводит ось другого в себя. Нужны такие ограничения для того, чтобы всевозможные композиции $\varphi$ и $\psi$ , а также $\varphi^{-1}$ и $\psi^{-1}$ образовывали свободную группу. Объясним, что это значит.

Некоторые, возможно, знают, что группа — это некоторое множество с формально введенной операцией (называемой иногда сложением, иногда умножением, иногда еще как-нибудь), удовлетворяющей нескольким аксиомам. Так вот, это все абстрактные сказки. На самом деле группа — это некоторое множество движений, замкнутое относительно операции композиции, содержащее тождественное и обратное к каждому движение. Для нас будет важен объект под названием свободная группа с двумя образующими. Рассмотрим алфавит из букв $\varphi$ , $\psi$ , $\varphi^{-1}$ и $\psi^{-1}$ . Будем писать конечные слова, состоящие из таких букв. При этом договоримся сокращать буквосочетания $\varphi\varphi^{-1}$ , $\varphi^{-1}\varphi$ , $\psi\psi^{-1}$ и $\psi^{-1}\psi$ . Операцию между этими словами ввести просто: будем приписывать одно слово к другому. Свободной группа называется потому, что она не ограничена никакими соотношениями, т. е. никакое нетривиальное слово не приравнено к пустому. Именно для того, чтобы группа $G = \langle \varphi, \psi \rangle$ (группа, порожденная поворотами $\varphi$ и $\psi$ ) была свободной, нужны различные условия на $\varphi$ и $\psi$ (кроме перечисленных выше есть еще условия, например, $\varphi$ и $\psi$ не могут быть поворотами на угол $q \cdot 2\pi$ , где $q$ — рациональное число; подробно на всех условиях останавливаться не будем).

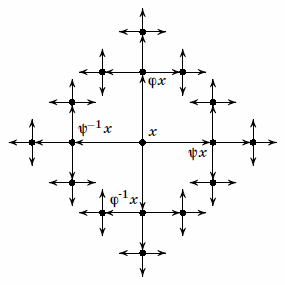
Рис. 7

Вернемся к нашим поворотам. Как только мы зафиксировали повороты $\varphi$ и $\psi$ , у нас тут же появилось действие свободной группы на сфере. Что это значит? Каждому элементу группы $G$ соответствует некоторое отображение $f_g$ сферы на себя. Нужно просто взять в качестве $f_g$ соответствующую композицию поворотов $\varphi$ и $\psi$ . Поскольку группа $G$ — свободная, никакое $f_g$ при $g$ — непустом слове — не является тождественным.

Рассмотрим некоторую точку $x$ на сфере. На этой сфере действует свободная группа с двумя образующими. Различные элементы этой группы действуют на сфере, сдвигая $x$ . Всевозможные образы $x$ при этих сдвигах образуют орбиту точки относительно группы . Схематично она изображена на рис. 7. Несмотря на то, что группа $G$ — свободная, на некоторые точки она все равно действует "плохо", а именно, такие, которые какой-то композицией $\varphi$ , $\psi$ , $\varphi^{-1}$ и $\psi^{-1}$ переводятся на ось поворотов $\varphi$ или $\psi$ . У этих "плохих" точек орбита вырождена, некоторые ветви у нее отсутствуют по сравнению с орбитой "хорошей" точки, у которой из каждой точки выходит по четыре ветви. Заметим, что плохих точек достаточно мало — это точки, содержащиеся в орбитах точек пересечения осей поворотов $\varphi$ и $\psi$ со сферой. Все остальные точки разбиваются на орбиты "хороших" точек, являющихся копиями группы $G$ .

Поняв, как устроена свободная группа и орбиты "хороших" точек под действием этой группы, усложним ее, пытаясь тем самым сразу добиться не очень большого количества частей при разбиении сферы. В качестве образующих поворотов возьмем $\varphi$ и $\psi$ , удовлетворяющие соотношениям $\varphi^2 = 1$ , $\psi^3 = 1$ (т. е. $\varphi$ — поворот на $180^{\circ}$ , $\psi$ — поворот на $120^{\circ}$ ). Нарисуем орбиту точки $x$ на сфере.

Как видно из схемы орбиты точки $x$ (рис. 8), наша новая группа совсем не такая свободная, как была. В ней появились циклы. Как мы помним, это усложнение позволит уменьшить количество частей, на которые мы разбиваем сферу.

Разобьем ее на три равные части $A$ , $B$ и $C$ , так что $A \sim B \cup C$ и $A \sim B \sim C$ . Более того, будут выполняться равенства

$%\width{36}\begin{equation} \left\{ \begin{split} &\varphi(A)=B \cup C,\\ &\psi(A)=B,\\ &\psi^2(A)=C. \end{split} \right. \tag{3} \end{equation} %$

Будем разбивать множества по индукции. Пусть $x$ — некоторая "хорошая" точка, начало своей орбиты. Отправим ее в множество $A$ .

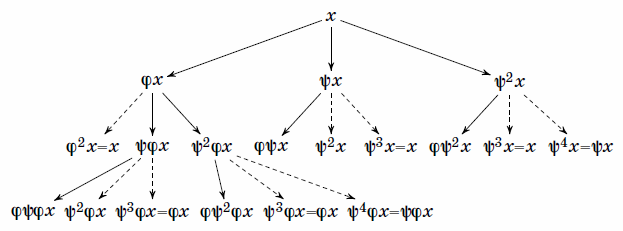
Рис. 8

Точки $\varphi x$ и $\psi x$ отправим в $B$ , а точку $\psi^2 x$ — в $C$ . Далее будем разбивать на множества по индукции с помощью табл. 3.

Таблица 3.

	$\alpha \in A$	$\alpha \in B$	$\alpha \in C$
$\alpha$ начинается на $\psi$	$\varphi\alpha \in B$	$\varphi\alpha \in A$	$\varphi\alpha \in A$
$\alpha$ начинается на $\varphi$	$\psi\alpha \in B$	$\psi\alpha \in C$	$\psi\alpha \in A$
$\alpha$ начинается на $\varphi$	$\psi^2\alpha \in C$	$\psi^2\alpha \in A$	$\psi^2\alpha \in B$

Объясним, как пользоваться этой таблицей. Пусть $\alpha$ принадлежит орбите точки $x$ . Тогда точку $\alpha$ можно формально представить в виде $gx$ , где $g$ — некоторое слово из букв $\varphi$ , $\psi$ и $\psi^2$ . Предположим, что $\alpha$ начинается на букву $\psi$ . Тогда среди следующих образов осмысленно рассматривать только $\varphi\alpha$ , так как остальные получались на предыдущих шагах и уже были отправлены в какие-то множества. Из таблицы видно, куда отправить $\varphi\alpha$ в зависимости от того, где находится сама точка $\alpha$ . Если $\alpha \in A$ , то $\varphi\alpha \in B$ , если $\alpha \in B$ , то $\varphi\alpha \in A$ , если $\alpha \in C$ , то $\varphi\alpha \in A$ . На рис. 9 можно увидеть, в какие множества попадают первые несколько элементов орбиты точки $x$ .

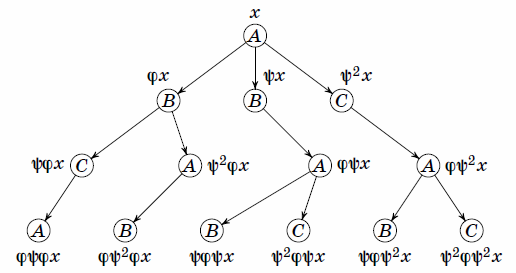
Рис. 9

Предлагаем убедиться самостоятельно, что, во-первых, разложение орбиты точки $x$ на $A$ , $B$ и $C$ в соответствии с представленной таблицей действительно существует, а во-вторых, оно удовлетворяет соотношениям (3).

Итак, мы разбили сферу (обозначим множество ее точек за $S$ ) на четыре множества $A$ , $B$ , $C$ и $Q_1$ (где $Q_1$ — множество "плохих" точек, т. е. точек, лежащих в орбитах точек пересечения осей поворотов $\varphi$ и $\psi$ со сферой), причем $A \sim B \cup C$ и $A \sim B \sim C$ . Заметим, что $Q_1$ — счетное множество. Значит, существует поворот (не равный $\varphi$ и $\psi$ ), переводящий $Q_1$ в такое множество $Q_2$ , что $Q_1 \cap Q_2 = \varnothing$ , т. е. $Q_2 \subset A \cup B \cup C$ (действительно, всего поворотов, переводящих $i$ -ю точку в себя, счетное количество, значит, всего поворотов, переводящих хоть какую-нибудь точку из $Q_1$ в себя, тоже счетное количество, значит, среди континуума поворотов сферы найдется нужный поворот). Поскольку $B \cup C \sim A \sim C$ , можно считать, что $Q_2 \subset C$ . Сфера разбивается в объединение $S = A \cup B \cup C \cup Q_1$ , которое можно записать так:

$S=(A \cup Q_1) \cup (B \cup Q_2) \cup (C \setminus Q_2)$

Далее,

$A \cup Q_1 \sim B \cup C \cup Q_1 \sim A \cup C \cup Q_1 \sim B \cup C \cup A \cup Q_1 \sim S$

аналогично $B \cup Q_2 \sim A \cup Q_1 \sim S$ . Таким образом, из сферы $S$ мы получили две сферы $S$ плюс образ множества $C \setminus Q_2$ . Поэтому по теореме 1 мы можем из одной сферы получить две.

Попробуем теперь из одного шара (обозначим множество его точек за $D$ ) получить два таких же с помощью допустимых преобразований. Шар $D$ естественным образом разбивается на центр (обозначим его за $O$ ) и на объединение сфер с центром в $O$ . Введем на самой большой сфере конструкцию из четырех множеств, которой мы только что пользовались при переклейке сферы. При помощи гомотетии с центром в $O$ продолжим эти множества на все сферы. Ясно, что поскольку мы умеем переклеивать сферу на две, то мы сможем переклеивать шар без центра на два шара без центров, а значит, и на три шара без центров. Значит, шар с центром можно переклеить на три шара, один из которых будет с центром. Возьмем точку из третьего шара и переведем ее в центр второго шара. Значит, из шара мы умеем получать два полноценных шара и еще какие-то точки. Поэтому по теореме 1 мы можем получить из шара два таких же.

Таким образом, мы убедились в возможности разрезать шар на конечное число частей и получить из них два шара того же размера. Немного изменив наши рассуждения, можно доказать, что на самом деле из шара можно получить два шара, но совершенно произвольного размера. Таким образом, в завершение темы мы приходим к одной очень интересной теореме.

Теорема. Если два множества и в пространстве ограничены и имеют внутренние точки, то $A \sim B$ .

Доказательство. Множество $A$ ограничено, т. е. содержится в некотором шаре $C_1$ . Кроме того, $A$ имеет хотя бы одну внутреннюю точку, т. е. содержит в себе некоторый шар $D_1$ . Аналогично определим шары $C_2$ и $D_2$ , так что $C_2 \supset B \supset D_2$ . Согласно сказанному выше, отождествим $C_1$ и $D_1$ . Тогда $C_1 \supset A \supset D_1 \sim C_1$ , следовательно, по теореме 1 получаем, что $A \sim C_1$ . Аналогично $B \sim C_2$ , но $C_1 \sim C_2$ , поэтому $A \sim B$ .

<<< |1|…|7|8|9|10|11|12|13|14|15|…|17| >>>

Содержание

Комментарии: 0

Похожее

Парадоксы теории множеств и их философская интерпретация

Парадоксы являются следствием дихотомии языка и мышления, выражением глубоких диалектических (теорема Гёделя позволила проявить диалектику в процессе познания) и гносеологических трудностей, связанных с понятиями предмета и предметной области в формальной логике, множества (класса) в логике и теории множеств, с употреблением принципа абстракции, позволяющего вводить в рассмотрение новые (абстрактные) объекты (бесконечность), со способами определения абстрактных объектов в науке и т. п. Поэтому не может быть дано универсального способа устранения всех парадоксов.
А нужен ли выбор? (альтернатива аксиоме выбора в теории множеств)

Михаил Раскин

Современная математика в качестве своего основания использует теорию множеств. Традиционно при анализе теоретико-множественных тонкостей используется аксиоматика Цермело-Френкеля с аксиомой выбора, обозначаемая ZFC. На аксиому выбора опираются доказательства наличия базиса в любом векторном пространстве и существования неизмеримого множества в математическом анализе. К сожалению, теория множеств обязана работать и со множествами, которые не описываются достаточно подробно и конкретно, чтобы мы могли себе их представить. В курсе будет рассмотрен один пример, к чему это приводит. Оказывается, ценой ослабления аксиомы выбора можно получить теорию множеств, в которой любая ограниченная функция на отрезке интегрируема по Лебегу. То, что используется аксиома выбора, в каком-то смысле, произошло исторически. Курс основан на статье Р.М. Соловэя о построении теории множеств, в которой все множества вещественных чисел измеримы.
«Мы не можем ждать милостей от природы», или применение метода вынуждения в построении моделей теории множеств

Михаил Раскин

В теории множеств есть несколько известных вопросов о том, следует ли из некоторых аксиом другая аксиома (или гипотеза; аксиома — это просто гипотеза, которой пользуется подавляющее большинство). Как и в других областях математики, недоказуемость можно продемонстрировать с помощью модели, в которой верны предположения, но не верна гипотеза. Для построения одного из самых известных таких примеров, модели теории множеств, в которой есть промежуточная мощность между мощностями натурального ряда и вещественной прямой, Коэн разработал метод вынуждения.
Теория множеств для начинающих

Виктор Викторов

Основные понятия, операции над множествами, тождества, свойства дополнения, правило Де Моргана, свойства симметрической разности; отображение (функция), факторотображение, отношение эквивалентности, парадокс брадобрея; упорядоченные множества, минимальный, наименьший, максимальный и наибольший элементы в упорядоченном множестве, мажоранта и миноранта; аксиома выбора, вполне упорядоченное множество.
Числа и многочлены

Проскуряков И. В.

Целью этой книги является строгое определение чисел, многочленов и алгебраических дробей и обоснование их свойств, уже известных из школы, а не ознакомление читателя с новыми свойствами. Поэтому читатель не найдет здесь новых для него фактов (за исключением, быть может, некоторых свойств, действительных и комплексных чисел), но узнает, как доказываются вещи, хорошо ему известные, начиная с «дважды два — четыре» и кончая правилами действий с многочленами и алгебраическими дробями. Зато читатель познакомится с рядом общих понятий, играющих в алгебре основную роль.
Десять великих идей науки. Как устроен наш мир

Питер Эткинз

Эта книга предназначена для широкого круга читателей, желающих узнать больше об окружающем нас мире и о самих себе. Автор, известный ученый и популяризатор науки, с необычайной ясностью и глубиной объясняет устройство Вселенной, тайны квантового мира и генетики, эволюцию жизни и показывает важность математики для познания всей природы и человеческого разума в частности.
Алиса в Стране Смекалки

Смаллиан Рэймонд

В книге «Алиса в Стране Смекалки» кэрролловская Алиса из Страны Чудес и ее друзья раскрывают перед читателем нескончаемую вереницу задач-головоломок. Они доставят удовольствие всем любителям занимательной математики, а почитателям творчества Льюиса Кэрролла в особенности.
Математическое понимание природы

Владимир Арнольд

Сборник «Задачи для детей от 5 до 15 лет» вызвал много отзывов. И дети, и взрослые читатели часто сожалели, что там были только математические задачи, — ведь и все естествознание заслуживает столь же активного, творческого к себе отношения. Теперь я отвечаю на эти пожелания — следуя скорее Яну Амосу Каменскому, чем современным педагогам, то есть всегда стремясь быть понятным читателю, не имеющему предварительных знаний (но столь же любознательному, как большинство подростков).
Невероятные числа профессора Стюарта

Отрывок из книги «Невероятные числа профессора Стюарта» заслуженного профессора математики Уорикского университета, известного популяризатора науки Иэна Стюарта, посвященной роли чисел в истории человечества и актуальности их изучения в наше время.
Математические чудеса и тайны

Гарднер Мартин

Математические фокусы - очень своеобразная форма демонстрации математических закономерностей. Этой скрытой математичностью и интересна книга Мартина Гарднера - сам автор не формулирует на языке математики закономерностей, лежащих в основе его экспериментов, ограничиваясь описанием действий показывающего, явных и тайных. Но читателю, знакомому с элементами школьной алгебры и геометрии, несомненно, доставит удовольствие самому восстановить по объяснениям автора соответствующую алгебраическую или геометрическую идею. Книга будет интересна многим читателям: юным участникам математических кружков, взрослым любителям математики, а может быть, тот или иной из описанных здесь экспериментов пробудит улыбку и у серьезного ученого в краткий момент отдыха от большой работы.

Далее >>>