|
||
|
|
||
| Главная ≫ Инфотека ≫ Математика ≫ Книги ≫ Приложение 3. Задачи / Парадоксы теории множеств // Иван Ященко |
Приложение 3. Задачи / Парадоксы теории множествИван Ященко
Приложение 3. ЗадачиНабор задач этого раздела взят из листков, предлагавшихся учащимся выпуска 2002 года школы № 57 г. Москвы в 8-м, 10-м и 11-м классах. Операции над множествамиМножества Множество 1. Для каждых двух из следующих множеств указать, является ли одно из них подмножеством другого:
2. Докажите, что множество 3. Докажите, что для произвольных множеств а) Множество называется пустым, если оно не содержит ни одного элемента.
Обозначение: 4. Сколько элементов у каждого из следующих множеств?
5. Сколько подмножеств у множества из трех элементов? 6. Может ли у множества быть ровно а) Объединением множеств Пересечением множеств Разностью множеств 7. Даны множества а) б) в) г) д) е) ж) з) и) к) 8. Пусть 9. Докажите, что для любых множеств а) б) в) г)
10. Верно ли, что для любых множеств а) б) в) г) д) е) ж) Отображения множествЕсли каждому элементу 11. Нарисуйте всевозможные отображения из множества
Пусть 12. Для отображения 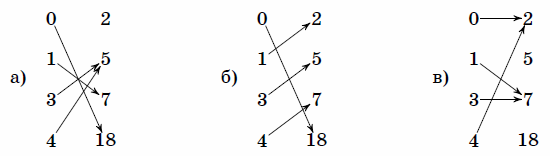
13. Пусть
а) б) в) г) д) е) ж) если з) если Композицией отображений 14. Докажите, что для произвольных отображений 15. Пусть 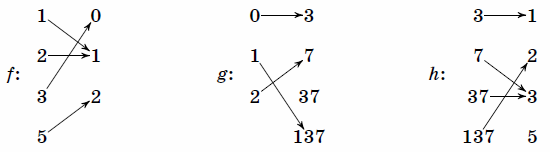
Нарисуйте картинки для следующих отображений: а) б) в) г) Отображение 16. Пусть 17. Пусть 
Нарисуйте картинки для следующих отображений: а) б) в) 18. Про каждые два из следующих множеств выясните, существует ли биекция из первого во второе (надлежит считать, что ноль — натуральное число): а) множество натуральных чисел; б) множество четных натуральных чисел; в) множество натуральных чисел без числа 3. Отображение 19. Каким должно быть отображение, чтобы у него а) не было обратного; б) было ровно одно обратное; в) было более одного обратного. Мощность множествДва множества 20. Докажите, что а) б) в) если 21. Докажите, что следующие множества равномощны: а) любые два отрезка; б) интервал и полуокружность без концов; в) интервал и прямая; г) квадрат и круг; д) действительные числа и неотрицательные действительные числа; е) интервал и отрезок; ж*) отрезок и квадрат. Множество называется счётным, если оно равномощно множеству натуральных чисел. 22. Докажите, что счётны а) конечное объединение счётных множеств; б) счётное объединение счётных множеств; в) произвольное пересечение счётных множеств, не являющееся конечным множеством. 23. Докажите, что следующие множества счётны: а) множество рациональных чисел; б) множество конечных последовательностей нулей и единиц; в) множество непересекающихся кругов на плоскости; г*) множество непересекающихся букв T на плоскости. 24. Докажите, что следующие множества несчётны: а) множество всех подмножеств натуральных чисел; б) множество бесконечных последовательностей нулей и единиц; в) множество всех биекций из множества натуральных чисел в себя; г) все перечисленные множества равномощны. 25*. Множество действительных чисел равномощно множествам из предыдущей задачи. 26. Докажите, что: а) в любом бесконечном множестве найдётся счётное подмножество; б) множество бесконечно тогда и только тогда, когда оно равномощно некоторому своему собственному (отличному от самого себя) подмножеству; в) при объединении бесконечного мнoжества с множеством, которое конечно или счётно, получается множество, равномощное исходному. Метрические пространства и непрерывные отображенияМетрическим пространством называется множетсво 1) 2) 3) 27. Докажите, что следующие пары а) б) в)
г) д)
где Открытым (соответственно, замкнутым) шаром
радиуса Внутренней точкой множества Множество, все точки которого внутренние, называется открытым. Открытое множество, содержащее данную точку, называется окрестностью этой точки. Предельной точкой множества Множество, которое содержит все свои предельные точки, называется замкнутым (сравните это определение с тем, которое было дано в приложении 1). 28. Докажите, что а) множество открыто тогда и только тогда, когда его дополнение замкнуто; б) конечное объединение и счетное пересечение замкнутых множеств замкнуто; в) счетное объединение и конечное пересечение открытых множеств открыто. 29. Докажите, что а) множество предельных точек любого множества является замкнутым множеством; б) объединение множества Отображение 30. Докажите, что это определение согласуется с определением непрерывности функций на прямой. 31. Докажите, что а) расстояние до множества б) множество нулей функции пункта а) совпадает с замыканием Непрерывное взаимно однозначное отображение 33. Для каждой пары из следующих множеств установите, гомеоморфны ли они: а) прямая; б) отрезок; в) окружность; г) буква Т; д) буква Ы; е) круг; ж) плоскость; з) граница квадрата; и) плоскость без начала координат. 34. Для каких пар 35*. Придумайте непрерывное отображение плоскости на тор, которое было бы
локальным гомеоморфизмом (т. е. у каждой точки Полнота. Теорема БэраПусть
36. Докажите, что сходящаяся последовательность фундаментальна. Верно ли обратное утверждение? Метрическое пространство называется полным, если всякая фундаментальная последовательность в нем сходится. 37. Верно ли, что пространство, гомеоморфное полному, полно? 38. Докажите, что замкнутое подпространство полного пространства само полно; полное подпространство произвольного пространства замкнуто в нем. 39. Докажите, что в полном метрическом пространстве последовательность вложенных замкнутых шаров с радиусами, стремящимися к нулю, имеет общий элемент. 40. Можно ли в предыдущей задаче убрать условие полноты пространства или стремления к нулю радиусов шаров? Отображение
41. Докажите, что сжимающее отображение непрерывно. 42. а) Докажите, что сжимающее отображение полного метрического пространства в себя имеет ровно одну неподвижную точку. б) На карту России масштаба 1:5 000 000 положили карту России масштаба 1:20 000 000. Докажите, что найдется точка, изображения которой на обеих картах совпадут. 43*. Существует ли неполное метрическое пространство, в котором верно утверждение задачи 15, а? Подмножество метрического пространства называется всюду плотным, если его замыкание совпадает со всем пространством; нигде не плотным – если его замыкание не имеет непустых открытых подмножеств (сравните это определение с тем, которое было дано в приложениие 2). 44. а) Пусть б) Пусть
нигде не плотно в пространстве всех непрерывных
функций на 45. (Обобщенная теорема Бэра.) Докажите, что полное метрическое пространство нельзя представить в виде объединения счетного числа нигде не плотных множеств. 46. Докажите, что множество непрерывных, не монотонных ни на каком
непустом интервале и нигде не дифференцируемых функций, определенных
на отрезке 47*. Пусть
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Математика ≫ Книги ≫ Приложение 3. Задачи / Парадоксы теории множеств // Иван Ященко |
|
[time: 18 ms; queries: 8]
22 Фев 2026 06:29:10 GMT+3 |


 Парадоксы являются следствием дихотомии языка и мышления, выражением глубоких диалектических (теорема Гёделя позволила проявить диалектику в процессе познания) и гносеологических трудностей, связанных с понятиями предмета и предметной области в формальной логике, множества (класса) в логике и теории множеств, с употреблением принципа абстракции, позволяющего вводить в рассмотрение новые (абстрактные) объекты (бесконечность), со способами определения абстрактных объектов в науке и т. п. Поэтому не может быть дано универсального способа устранения всех парадоксов.
Парадоксы являются следствием дихотомии языка и мышления, выражением глубоких диалектических (теорема Гёделя позволила проявить диалектику в процессе познания) и гносеологических трудностей, связанных с понятиями предмета и предметной области в формальной логике, множества (класса) в логике и теории множеств, с употреблением принципа абстракции, позволяющего вводить в рассмотрение новые (абстрактные) объекты (бесконечность), со способами определения абстрактных объектов в науке и т. п. Поэтому не может быть дано универсального способа устранения всех парадоксов. Целью этой книги является строгое определение чисел, многочленов и алгебраических дробей и обоснование их свойств, уже известных из школы, а не ознакомление читателя с новыми свойствами. Поэтому читатель не найдет здесь новых для него фактов (за исключением, быть может, некоторых свойств, действительных и комплексных чисел), но узнает, как доказываются вещи, хорошо ему известные, начиная с «дважды два — четыре» и кончая правилами действий с многочленами и алгебраическими дробями. Зато читатель познакомится с рядом общих понятий, играющих в алгебре основную роль.
Целью этой книги является строгое определение чисел, многочленов и алгебраических дробей и обоснование их свойств, уже известных из школы, а не ознакомление читателя с новыми свойствами. Поэтому читатель не найдет здесь новых для него фактов (за исключением, быть может, некоторых свойств, действительных и комплексных чисел), но узнает, как доказываются вещи, хорошо ему известные, начиная с «дважды два — четыре» и кончая правилами действий с многочленами и алгебраическими дробями. Зато читатель познакомится с рядом общих понятий, играющих в алгебре основную роль. Эта книга предназначена для широкого круга читателей, желающих узнать больше об окружающем нас мире и о самих себе. Автор, известный ученый и популяризатор науки, с необычайной ясностью и глубиной объясняет устройство Вселенной, тайны квантового мира и генетики, эволюцию жизни и показывает важность математики для познания всей природы и человеческого разума в частности.
Эта книга предназначена для широкого круга читателей, желающих узнать больше об окружающем нас мире и о самих себе. Автор, известный ученый и популяризатор науки, с необычайной ясностью и глубиной объясняет устройство Вселенной, тайны квантового мира и генетики, эволюцию жизни и показывает важность математики для познания всей природы и человеческого разума в частности. В книге «Алиса в Стране Смекалки» кэрролловская Алиса из Страны Чудес и ее друзья раскрывают перед читателем нескончаемую вереницу задач-головоломок. Они доставят удовольствие всем любителям занимательной математики, а почитателям творчества Льюиса Кэрролла в особенности.
В книге «Алиса в Стране Смекалки» кэрролловская Алиса из Страны Чудес и ее друзья раскрывают перед читателем нескончаемую вереницу задач-головоломок. Они доставят удовольствие всем любителям занимательной математики, а почитателям творчества Льюиса Кэрролла в особенности. Сборник «Задачи для детей от 5 до 15 лет» вызвал много отзывов. И дети, и взрослые читатели часто сожалели, что там были только математические задачи, — ведь и все естествознание заслуживает столь же активного, творческого к себе отношения. Теперь я отвечаю на эти пожелания — следуя скорее Яну Амосу Каменскому, чем современным педагогам, то есть всегда стремясь быть понятным читателю, не имеющему предварительных знаний (но столь же любознательному, как большинство подростков).
Сборник «Задачи для детей от 5 до 15 лет» вызвал много отзывов. И дети, и взрослые читатели часто сожалели, что там были только математические задачи, — ведь и все естествознание заслуживает столь же активного, творческого к себе отношения. Теперь я отвечаю на эти пожелания — следуя скорее Яну Амосу Каменскому, чем современным педагогам, то есть всегда стремясь быть понятным читателю, не имеющему предварительных знаний (но столь же любознательному, как большинство подростков). Отрывок из книги «Невероятные числа профессора Стюарта» заслуженного профессора математики Уорикского университета, известного популяризатора науки Иэна Стюарта, посвященной роли чисел в истории человечества и актуальности их изучения в наше время.
Отрывок из книги «Невероятные числа профессора Стюарта» заслуженного профессора математики Уорикского университета, известного популяризатора науки Иэна Стюарта, посвященной роли чисел в истории человечества и актуальности их изучения в наше время. Математические фокусы - очень своеобразная форма демонстрации математических закономерностей. Этой скрытой математичностью и интересна книга Мартина Гарднера - сам автор не формулирует на языке математики закономерностей, лежащих в основе его экспериментов, ограничиваясь описанием действий показывающего, явных и тайных. Но читателю, знакомому с элементами школьной алгебры и геометрии, несомненно, доставит удовольствие самому восстановить по объяснениям автора соответствующую алгебраическую или геометрическую идею. Книга будет интересна многим читателям: юным участникам математических кружков, взрослым любителям математики, а может быть, тот или иной из описанных здесь экспериментов пробудит улыбку и у серьезного ученого в краткий момент отдыха от большой работы.
Математические фокусы - очень своеобразная форма демонстрации математических закономерностей. Этой скрытой математичностью и интересна книга Мартина Гарднера - сам автор не формулирует на языке математики закономерностей, лежащих в основе его экспериментов, ограничиваясь описанием действий показывающего, явных и тайных. Но читателю, знакомому с элементами школьной алгебры и геометрии, несомненно, доставит удовольствие самому восстановить по объяснениям автора соответствующую алгебраическую или геометрическую идею. Книга будет интересна многим читателям: юным участникам математических кружков, взрослым любителям математики, а может быть, тот или иной из описанных здесь экспериментов пробудит улыбку и у серьезного ученого в краткий момент отдыха от большой работы.