|
||
|
|
||
| Главная ≫ Инфотека ≫ Математика ≫ Книги ≫ Глава 4. Ученый игрок / Истина и красота. Всемирная история симметрии // Иэн Стюарт |
Глава 4. Ученый игрок / Истина и красота. Всемирная история симметрииИэн Стюарт
Глава 4. Ученый игрок«Клянусь святым Евангелием Господа нашего и как истинный человек чести не только никогда не публиковать ваши открытия, если вы мне доверите их, но да будет моя вера истинного христианина вам порукой, что я зашифрую их так, чтобы после моей смерти никто не смог их понять». Этот торжественный обет был, как говорят, дан в 1539 году. Италия эпохи Возрождения была колыбелью нового, и математика не составляла исключения. В иконоборческом духе того времени математики Ренессанса задались целью преодолеть ограничения древней математики. Один из них разрешил загадку кубического уравнения и теперь обвинял другого в воровстве своего секрета. Гневающегося математика звали Никколо Фонтана по прозвищу Тарталья — Заика. В воровстве интеллектуальной собственности обвинялся математик, врач, неисправимый плут и закоренелый азартный игрок по имени Джироламо Кардано, также известный как Жером Кардан. Около 1520 года Джироламо, как истинный блудный сын, успешно растратил наследство, оставленное ему отцом. Разорившись, он обратился к азартным играм как к источнику дохода, найдя эффективное примененное своих математических способностей для оценки шансов на выигрыш. Он водился с сомнительной компанией; как-то раз, заподозрив другого игрока в нечестной игре, он полоснул его ножом по лицу. То были суровые времена, и Джироламо был суровым человеком. А кроме того — на редкость оригинальным мыслителем и автором одного из наиболее знаменитых и влиятельных текстов по алгебре во всей истории. О Джироламо нам известно много, потому что в 1575 году он сам рассказал нам о себе в «Книге моей жизни». Начинается она так: Эту Книгу Моей Жизни я намереваюсь написать, следуя примеру Антонина Философа [Марка Аврелия, римского императора с 161 по 180 г. (Примеч. перев.)], прославленного как мудрейший и достойнейший из людей, хорошо понимая, что ни одно деяние смертных не совершенно, а еще менее того — свободно от злословия; однако сознавая при этом и то, что из всего, что человеку дано достичь, ничто другое не доставляет больше радости и не ценится сильнее, чем познание истины. Ни единого слова, спешу заверить, не было добавлено в угоду тщеславию, и ни единого для пустого приукрашивания; вместо того, насколько возможно, здесь собрано только пережитое, события, о которых мои ученики… были осведомлены или в коих они принимали участие. Эти краткие эпизоды моей истории в свою очередь записаны были мною в повествовательной форме, дабы стать частью этой книги. Как и многие математики того времени, Джироламо занимался астрологией, так что он отмечает астрологические обстоятельства, сопутствовавшие его рождению: Хотя, как я слышал, напрасно пытались применить различные абортивные средства, я нормально родился в 24-й день сентября года 1500, когда первый час ночи истек уже более чем наполовину, но менее чем на две трети… Марс угрожал обоим главным светилам из-за неблагоприятного их расположения и потому, что он был в четвертном аспекте с Луною… Я легко мог родиться уродом, если бы не тот факт, что положение предыдущего соединения приходилось на 29° в Деве, где господствует Меркурий. И так как его положение не совпадало ни с местом Луны, ни с местом асцендента и он не находился в аспекте с предпоследним делением Девы, я непременно должен был бы родиться уродом, и даже легко могло случиться, что я выйду из утробы разорванным, чего едва и не произошло. Так был я рожден, или, скорее, исторгнут мощными силами из чрева матери; я был почти мертв. Волосы мои были темны и завиты. Меня вернули к жизни ванной из теплого вина, которая могла бы оказаться гибельной для любого другого ребенка. Моя мать провела в тяготах три полных дня, и однако же я выжил [Не без некоторых потерь: «…и Солнце, и обе зловещие планеты — Венера и Меркурий — находились в человеческих знаках, вследствие чего у меня и не обнаружилось отклонений от человеческого образа; а так как в асценденте был Юпитер и во всем гороскопе господствовала Венера, у меня обнаружились неправильности только в половых органах: случилось так, что в возрасте от 21 до 31 года я оказался не способен к совокуплению с женщинами и часто горько оплакивал свою участь, завидуя судьбе других людей». (Примеч. перев.)]. Одна глава в «Книге моей жизни» перечисляет написанные Джироламо книги, и первой в списке идет «Великое искусство» [Лат.: Ars Magna. (Примеч. перев.)] — один из трех упоминаемых им «трактатов по математике». Он также писал об астрономии, физике, вопросах морали, драгоценных камнях, воде, медицине, предсказаниях и теологии. Однако для нашего рассказа важно только «Великое искусство». Подзаголовок этой книги — «Правила алгебры» — объясняет почему. В этой книге Джироламо не только собрал методы решения квадратных уравнений, известные вавилонянам, но и открыл новые решения кубических уравнений и уравнений четвертой степени. В отличие от решений Хайяма, которые опирались на геометрию конических сечений, решения в «Великом искусстве» были чисто алгебраическими. Я уже упоминал о двух типах математических обозначений, которые оба видны в таких выражениях, как x3 для куба неизвестного. Обозначение первого типа состоит в использовании букв (в нашем случае — x) для чисел — или неизвестных, или известных, но произвольных. Обозначение второго типа — это использование приподнятых над строкой чисел для указания степени, так что верхняя 3 в данном случае обозначает куб числа x, то есть x×x×x. Теперь мы подошли к обозначениям третьего типа — последним из тех, что нам понадобятся. Обозначение третьего типа очень милое и выглядит так: √. Этот символ означает квадратный корень. Например, √9 — квадратный корень из девяти — обозначает число, которое, будучи умножено на само себя, дает 9. Поскольку 3×3 = 9, мы видим, что √9 = 3. Однако не всегда все обстоит так просто. Наиболее печально известный квадратный корень, который, согласно не слишком правдоподобной легенде, оказался причиной того, что математика, привлекшего к нему внимание, — Гиппаса из Метапонта — выбросили с корабля за борт, — это квадратный корень из двух: √2. Его точное выражение в виде десятичной дроби требует неограниченного продолжения. Начинается оно так: 1,4142135623730950488…, но не может на этом прекратиться, поскольку квадрат приведенного числа на самом деле равен 1,99999999999999999999522356663907438144, что, очевидно, есть не вполне то же самое, что 2. На этот раз известно, откуда взялось такое обозначение. Это искаженная буква «r», обозначающая «radix» — латинское слово «корень». Математики понимают его таким образом и читают выражение √2 как «корень из двух». Кубические корни, корни четвертой, пятой и так далее степеней обозначаются помещением маленького приподнятого числа перед знаком «корень» — таким образом: 3√, 4√, 5√. Кубический корень из данного числа — это такое число, куб которого дает исходное, и аналогично для других корней. Таким образом, кубический корень из 8 есть 2, поскольку 23 = 8. Кубический же корень из 2 можно выразить в виде десятичной дроби только приближенно. Он начинается таким образом: 1,2599210498948731648… и продолжается, если вы запасетесь достаточным терпением, бесконечно. Именно это число появляется в античной задаче об удвоении куба. Примерно к 400 г. греческая математика утратила свое место на переднем крае этой науки. Место действия переместилось на Восток — в Аравию, Индию и Китай. Европа погрузилась в «темные века», и хотя они были не такими уж темными, какими их нередко изображают, но все же темными в достаточной мере. Распространение христианства возымело тот плачевный побочный эффект, что знание и ученость сконцентрировались в церквях и монастырях. Многие монахи переписывали работы великих математиков, таких как Эвклид, но лишь очень немногие из них понимали, что они переписывают. Древние греки были в состоянии с двух сторон прорыть туннель через гору так, чтобы обеспечить встречу посередине; способ же, которым ранние англосаксы проводили землемерные работы, состоял в том, чтобы разложить в поле план в масштабе 1:1. Даже понятие изображения, сделанного в определенном масштабе, было утеряно. Если бы англосаксы пожелали создать точное изображение Англии, им пришлось бы сделать его размером с Англию. Их карты обычного размера были крайне неточными. К концу пятнадцатого столетия фокус математической активности снова сдвинулся в сторону Европы. На Среднем и Дальнем Востоке подошел к концу заряд креативности, а Европа включила второе дыхание, освобождаясь от объятий Римской церкви и ее страха перед всем новым. По иронии судьбы новым центром интеллектуальной активности становится Италия — по мере того как Рим ослаблял хватку в своем собственном тылу. Это тектоническое изменение в европейской науке и математике началось с публикации в 1202 году книги под названием Liber Abbaci, написанной Леонардо Пизанским, который много позднее получил прозвище Фибоначчи, сына Боначчио, под которым теперь и известен, несмотря на то что имя это придумали в девятнадцатом столетии. Отец Леонардо — Гильельмо — служил на таможне в Буджии (ныне в Алжире) и в своей работе неминуемо сталкивался с людьми самых разных культур. Он обучил своего сына новомодным знакам для чисел, изобретенным индусами и арабами, — предшественникам наших десятичных обозначений от 0 до 9. Леонардо позднее писал, что «мне так нравилось обучение, что я продолжал изучать математику во время поездок по работе в Египет, Сирию, Грецию, Сицилию и Прованс и получал особое удовольствие от дебатов с учеными из тех мест». На первый взгляд заглавие книги Леонардо говорит о том, что это книга — об абаке, т.е. механическом вычислительном приспособлении, состоящем из бусинок, скользящих по проволочкам, или же из галечных камешков, передвигаемых в песчаном желобе. Но как латинское слово calculus, относящееся к этой гальке, позднее приобрело другое, более техническое значение [По-английски «calculus» означает «исчисление», наиболее часто — в значении «дифференциальное и интегральное исчисление». По-русски этот же предмет называется математическим анализом или, когда контекст ясен, просто анализом (откуда производится и прилагательное «аналитический»). (Примеч. перев.)], так и слово abbaco — рамка для счета — стало обозначать искусство вычисления. Liber Abbaci была первым арифметическим текстом, в котором индоарабские символика и методы были принесены в Европу. Значительная часть книги отведена новым применениям арифметики к практическим предметам, подобным обмену валют. Одна задача — об идеализированной модели роста популяции кроликов — привела к замечательной числовой последовательности 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и так далее, где каждое следующее число, начиная с 2, равно сумме двух предыдущих. Эта «последовательность Фибоначчи» более всего прославила Леонардо — не применительно к размножению кроликов, где следствия из нее нулевые, а за то, что она представляет собой замечательный пример математической закономерности и играет ключевую роль в теории иррациональных чисел. Леонардо и представить себе не мог, что этот маленький jeu d'esprit [Игра ума. (Примеч. перев.)] затмит в глазах потомков все остальное, что он сделал в своей жизни. Леонардо написал еще несколько книг, и его Practica Qeometriae, появившаяся в 1220 году, содержала значительную часть «Начал» Эвклида, а также кое-что из греческой тригонометрии. В Книге X «Начал» Эвклида обсуждаются иррациональные числа, построенные как вложенные друг в друга квадратные корни, типа В 1494 году Лука Пачоли свел вместе значительную часть существовавшего тогда математического знания в книге по арифметике, геометрии и пропорции. Она также включала индо-арабские числа, коммерческую арифметику, выжимки из Эвклида и тригонометрию Птолемея. Сквозной темой был элемент замысла в природе, воплощенный в пропорциях — пропорциях человеческого тела, перспективы в живописи, теории цвета. Пачоли продолжил традицию «риторической» алгебры, используя слова, а не символы. Неизвестное было «штукой» — итальянское слово cosa, и в течение определенного периода практикующие алгебраисты были известны под именем cossist'ов. Он также использовал ряд стандартных сокращений, продолжая (но не сумев улучшить) подход, впервые намеченный Диофантом. Моррис Клайн в своем монументальном «Математическом мышлении от Античности до современности» констатирует: «Серьезное замечание по поводу математического развития арифметики и алгебры между 1200 и 1500 годами состоит в том, что книга Пачоли едва ли содержит что-либо, выходящее за рамки Liber Abbaci Леонардо Пизанского. В действительности арифметика и алгебра… основывались на книге Леонардо». В конце своей книги Пачоли замечает, что относительно решения кубического уравнения понимания ничуть не больше, чем относительно квадратуры круга. Но такому положению дел скоро предстояло измениться. Первое по-настоящему существенное продвижение произошло в городе Болонья примерно в конце первой трети шестнадцатого столетия. Внимания на это событие поначалу не обратили. Джироламо Кардано был побочным сыном миланского юриста Фацио Кардано и молодой вдовы по имени Кьяра Микериа, у которой было еще трое детей от первого брака. Он родился в 1501 году в Павии — городе, входившем в герцогство Миланское. Когда к Милану подобралась чума, беременную Кьяру убедили уехать в деревню, где и родился Джироламо. Все трое ее старших детей, оставшиеся в городе, умерли от чумы. Согласно автобиографии Джироламо, «отец мой носил багряную накидку — одеяние, нетипичное для нашего сообщества; его никогда не видели без маленькой черной шапочки… К пятидесяти пяти годам он лишился всех зубов. Он был хорошо знаком с работами Эвклида; надо сказать, что плечи его были сгорблены от усердных занятий… Мать мою легко было вывести из себя; она была скора на память и сообразительность и была тучной и набожной женщиной. Скоропалительность отличала обоих моих родителей». Хотя Фацио и был юристом по профессии, он был достаточно искушен в математике, чтобы консультировать по геометрии Леонардо да Винчи. Он преподавал геометрию в университете в Павии и в благотворительном учреждении Пьятти в Милане. И еще он учил математике и астрологии своего незаконного сына Джироламо: В раннем детстве отец обучил меня основам арифметики, и примерно тогда же он приобщил меня к таинствам; откуда он приобрел эти познания, мне неизвестно. Вскоре он обучил меня началам арабской астрологии… А когда мне исполнилось двенадцать, он преподал мне первые шесть книг Эвклида. У ребенка наблюдались проблемы со здоровьем; попытка вовлечь его в семейное дело успеха не принесла. Джироламо сумел убедить находившегося в сомнениях отца позволить ему изучать медицину в университете Павии, но отец предпочитал право. В 1494 году Карл VIII Французский вторгся в Италию, и последовавшая война продолжалась, утихая и вновь разгораясь, пятьдесят лет. Обострение военных действий привело к закрытию университета в Павии, и Джироламо перебрался в Падую, чтобы продолжать занятия. Судя по всему, он был одним из лучших студентов, и когда Фацио умер, Джироламо начал кампанию с целью стать ректором университета. Хотя многие не любили его за склонность высказываться без обиняков, он был избран с перевесом в один голос. Тогда-то он и растратил по мелочам полученное им наследство и обратился к азартным играм, которые превратились в пагубную привычку на всю оставшуюся часть его неспокойной жизни. И не только это: В очень ранний период моей жизни я начал серьезно посвящать себя занятиям фехтованием всякого рода и путем упорных упражнений достиг некоторых успехов даже среди наиболее дерзких… По ночам, даже в нарушение распоряжений герцога, я вооружался и отправлялся рыскать по городу, в котором жил… Лицо мое скрывал капюшон из черной шерсти, а еще я надевал туфли из овчины… Я часто бродил всю ночь, пока не брезжил рассвет, с меня же капал пот от напряжения, с которым я исполнял серенады на своих музыкальных инструментах. Даже подумать страшно. В 1525 году, после присуждения ему медицинской степени, Джироламо попытался вступить в Коллегию врачей в Милане, но его не приняли — формально из-за незаконного происхождения, но на самом деле главным образом из-за печальной известности, которую он приобрел в качестве человека, лишенного такта. Так что вместо того, чтобы стать членом престижной коллегии, Джироламо устроился врачом в соседнюю деревушку Сакко. Это обеспечивало ему небольшой доход, но дело шло вяло. Он женился на Лучии Бандарини — дочери капитана милиции — и перебрался ближе к Милану в надежде увеличить свой доход, чтобы содержать семью, однако Коллегия снова его отвергла. Не в силах следовать по пути законной карьеры врача, он обратился к азартным играм, но даже его математические познания не помогли восстановить свое состояние: Вероятно, ни в каком отношении не достоин я похвалы; ибо насколько сильно меня привлекали излишества шахматной доски и игорного стола, настолько же я знаю, что в глазах людей я заслуживаю самого сурового порицания. Я играл и в то и в другое многие годы — в шахматы более сорока лет, а в кости — около двадцати пяти; и не только каждый год, но — сознаюсь со стыдом — каждый день, теряя при этом все — мысль, состояние и время. Семейство поселилось в бедном доме. Мебель и драгоценности Лучии давно уже были заложены. «Я вступил на путь долгой и почетной карьеры. Но долой почести и приобретения вместе с пустым тщеславием и неумеренными наслаждениями! Мне конец! Я погиб!» На свет появился их первый ребенок. После двух выкидышей и рождения двух мертвых младенцев мужского пола, доношенных лишь до четырех месяцев, так что я… временами уже подозревал какое-то зловредное влияние, моя жена разродилась первым сыном… Он был глух на правое ухо… Два пальца на левой ноге у него… соединялись перепонкой. Сзади он был слегка горбат, но не до степени уродства. Мальчик мирно жил до своего двадцатитрехлетия. После того он влюбился… и женился на женщине без приданого Брандонии ди Серони. В тот момент покойный уже отец Джироламо пришел ему на выручку, пусть и не совсем прямым образом. Кафедра, которую некогда занимал Фацио в университете, оставалась вакантной, и Джироламо ее получил. Кроме того, он немного врачевал на стороне, несмотря на отсутствие официального разрешения. Несколько чудесных исцелений — судя по всему, счастливых случайностей, если учесть состояние медицины в то время, — создали ему репутацию. Даже некоторые из членов коллегии обращались к нему по поводу случаев из своей практики, и в течение некоторого времени казалось, что для него наконец откроются двери этой уважаемой организации. Но снова, в который раз, склонность Джироламо высказывать вслух то, что у него на уме, свела все на нет; он опубликовал ядовитые нападки на компетенцию и характер членов коллегии. Джироламо осознавал, что ему недостает деликатности, но, судя по всему, не считал это недостатком: «При чтении лекций и в публичных спорах я был намного более искренним и аккуратным, чем в выказывании осмотрительности». В 1537 году это отсутствие осмотрительности привело к тому, что его прошение было снова отклонено. Однако в конце концов его репутация укрепилась настолько, что у Коллегии просто не осталось выбора, и по прошествии двух лет он стал ее членом. Жизнь стала налаживаться — особенно после опубликования двух книг о математике. Карьера Джироламо развивалась сразу на нескольких фронтах. Примерно в то же время Тарталья добился значительного успеха — ему удалось решить широкий класс кубических уравнений. Неохотно поддавшись на уговоры, он рассказал Кардано о своем эпическом открытии. Не приходится удивляться, что, получив шесть лет спустя экземпляр текста Кардано по алгебре под названием «Великое искусство, или О правилах алгебры» и найдя там полное изложение своего секрета, Тарталья был разъярен. Кардано не приписывал себе его авторство, поскольку сослался на Тарталью: «В наши дни Шипионе [В традиционной транслитерации — Сципион. (Примеч. перев.)]-дель Ферро из Болоньи решил случай куба и первой степени, равных постоянной, — очень изящное и достойное восхищения достижение… Состязаясь с ним, мой друг Никколо Тарталья из Брешии… решил тот же случай, когда участвовал в поединке с его [дель Ферро] учеником Антонио Марио Фиором, и, подвигнутый к тому многократными мольбами, передал решение мне». Тем не менее Тарталья был страшно раздосадован тем, что его бесценный секрет разглашен по всему свету, а еще более его уязвлял тот факт, что многие люди будут помнить автора книги, а не истинного открывателя этого секрета. Так, по крайней мере, видел события Тарталья, и этот взгляд практически целиком лег в основу всех известных свидетельств. Как указывает Ричард Уитмер в своем переводе «Великого искусства», «Мы почти полностью зависим от печатного изложения позиции Тартальи, которую ни при каком усилии воображения нельзя считать объективной». Один из слуг Кардано по имени Лодовико Феррари позднее утверждал, что присутствовал на встрече, и говорил, что там не было решено держать метод в тайне. Феррари позднее стал учеником Кардано и решил — или помог решить — уравнение четвертой степени, так что и его нельзя рассматривать как свидетеля более объективного, чем Тарталья. Положение бедного Тартальи усугублялось тем, что дело было не просто в отказе признать его авторство. В Европе эпохи Возрождения математические секреты могли стоить немалых денег. Для этого не обязательно было играть в азартные игры — способ, который предпочитал Кардано, — а можно было участвовать в публичных состязаниях. Часто говорят, что математика — это не спорт, где есть зрители, но в 1500-х годах дело обстояло по-другому. Математики вполне могли обеспечивать себе дополнительный заработок, вызывая друг друга на публичные поединки, в которых каждый предлагал своему оппоненту ряд задач и победителем объявлялся тот, кто получит наибольшее число правильных ответов. Эти представления захватывали меньше, чем кулачный бой или фехтовальные поединки, но зрители могли биться об заклад по поводу того, кто выиграет, даже если сами они не имели ни малейшего представления о том, что для этого требуется. Кроме призовых денег победители привлекали к себе и учеников, готовых платить за обучение, так что публичные состязания были прибыльны вдвойне. Тарталья был не первым, кто нашел алгебраическое решение кубического уравнения. Болонский профессор Шипионе дель Ферро открыл свое решение некоторых типов кубических уравнений где-то около 1515 года. Он умер в 1526-м, после чего и его бумаги, и его профессорскую должность унаследовал зять Аннибале дель Наве. В этом можно быть уверенным, поскольку около 1970 года благодаря усилиям Э. Бартолотти сами бумаги обнаружились в библиотеке Болонского университета. Согласно Бартолотти, дель Ферро, скорее всего, знал, как решать три типа кубических уравнений, но передал метод решения только одного из них: куб плюс вещь равно числу. Знание об этом решении сохранил ученик дель Наве и дель Ферро по имени Антонио Марио Фиор. И именно Фиор, выбравший своей целью зарабатывать на жизнь преподаванием математики, выступил с эффектным маркетинговым ходом. В 1535 году он вызвал Тарталью на публичный поединок по решению кубических уравнений. Ходили слухи, что метод решения кубических уравнений найден, а ничто не воодушевляет математика сильнее, чем знание, что задача имеет решение. Риск зря потратить время на неразрешимую задачу исключен; основная опасность состоит лишь в том, что можно оказаться недостаточно умным, чтобы найти ответ, факт существования которого не подлежит сомнению. Все, что требуется, — это значительная доля уверенности в себе (которой у математиков обычно в достатке — даже если она оказывается самонадеянностью). Тарталья заново открыл метод дель Ферро, но он подозревал, что Фиору известно, как решать другие типы кубических уравнений и за счет этого он получит преимущество. Тарталья не скрывал, сколь беспокоила его такая перспектива, и в конце концов, незадолго до состязания, сумел решить остальные случаи. Теперь преимущество было у Тартальи, и он не мешкая стер в порошок несчастного Фиора. Информация об этом поражении стала распространяться; Кардано услышал о нем в Милане. В то время он работал над своей книгой по алгебре. Как и всякий настоящий автор, Кардано вознамерился включить в книгу самые последние открытия — без них его труд устареет еще до публикации. Поэтому Кардано обратился к Тарталье, надеясь ласковым обхождением и лестью выманить у него секрет и включить его в «Великое искусство». Тарталья отказался, говоря, что сам имеет планы написать книгу. В конце концов, однако, настойчивость Кардано была вознаграждена, и Тарталья открыл ему секрет. Действительно ли он заставил Кардано поклясться, что тот будет хранить тайну, зная, что книга, которую тот пишет, уже почти готова? Или же он поддался на вкрадчивые уговоры со стороны Кардано, а потом жалел об этом? Нет сомнения, что он был предельно зол, когда «Великое искусство» увидело свет. В течение года после этого он опубликовал книгу «Проблемы и различные изобретения», в которой обрушился на Кардано в более чем определенных выражениях. Он включил туда всю переписку между ними, утверждая, что она воспроизведена точно. В 1547 году Феррари пришел на помощь своему патрону, послав Тарталье картель — вызов на ученый диспут на любую тему по выбору противника. Он даже предложил награду в 200 скудо для победителя. И выразился предельно ясно: «Я сделал это, дабы стало известно, что ты написал вещи, которые ложно и недостойно клевещут… на синьора Джироламо, по сравнению с которым ты вообще не заслуживаешь упоминания». Феррари отправил экземпляры картеля многочисленным итальянским ученым и общественным лицам. Через девять дней Тарталья ответил, представив свое изложение фактов, после чего эти два математика обменялись двенадцатью картелями за полтора года. Диспут, как представляется, должен был проходить по стандартным правилам настоящей дуэли. За Тартальей, который был оскорбленной стороной, оставался выбор оружия, т.е. темы дебатов. Но он стремился вызвать не своего обидчика Феррари, а самого Кардано. Феррари сохранял хладнокровие и заявлял, что в любом случае начать надо с того, что решил кубическое уравнение не Тарталья, а дель Ферро. Коль скоро дель Ферро не проявлял никакой озабоченности по поводу неоправданных утверждений Тартальи об авторстве, что же тогда мешало Тарталье вести себя аналогичным образом? Это был сильный ход, и Тарталье, возможно, пришлось это признать, потому что он подумывал отказаться от участия в состязании. Однако он не стал этого делать, по всей вероятности, из-за отцов своего родного города Брешиа. Тарталья добивался там кафедры, и его местные покровители могли пожелать посмотреть, как он себя покажет. Как бы то ни было, Тарталья согласился на участие в дебатах, которые состоялись в августе 1548 года перед большим скоплением народа в Миланской церкви. Не сохранилось никаких отчетов о происшедшем, за исключением нескольких указаний у Тартальи, который пишет, что встреча прервалась, когда приближался решающий раунд. Это может служить намеком на то, что диспут оказался не слишком захватывающим. Кажется, однако, что Феррари умело одержал победу, потому что после этого ему предложили несколько заманчивых должностей, из которых он выбрал пост руководителя налогового управления при правителе Милана и вскоре стал очень богат. Тарталья, напротив, никогда не утверждал, что выиграл дебаты, не получил работу в Брешии, и на его долю достались лишь горькие упреки и обвинения. Тарталья не мог знать, что Кардано и Феррари заранее продумали совершенно иную линию защиты, для чего отправились в Болонью и изучили там бумаги дель Ферро. Там содержалось первое настоящее решение кубического уравнения, и в последующие годы оба они утверждали, что источником материала, включенного в «Великое искусство», послужил не секрет, доверенный Кардано Тартальей, а исходные записи дель Ферро. Ссылка на Тарталью включалась только для пояснения того, как именно сам Кардано узнал о работе дель Ферро. У этой истории имеется и последний поворот сюжета. Вскоре после выхода второго издания «Великого искусства», в 1570 году, инквизиция заключила Кардано в тюрьму. Причина ареста могла быть связана с обстоятельством, ранее казавшимся совершенно невинным, — не с содержанием книги, а с ее посвящением. Кардано в свое время решил посвятить ее относительно малоизвестному интеллектуалу Андреасу Осиандеру — второстепенному деятелю Реформации, на которого, однако, пало сильное подозрение в авторстве анонимного предисловия к книге «О вращении небесных сфер» Николая Коперника — первой книге, где говорилось, что планеты движутся не вокруг Земли, а вокруг Солнца. Церковь считала эти взгляды еретическими и в 1600 году сожгла Джордано Бруно за то, что тот продолжал их отстаивать, подвесив его раздетого догола и с кляпом во рту вниз головой на столбе на рыночной площади в Риме. В 1616 году, а потом еще раз, в 1633-м, по сходным причинам она доставила немало неприятностей Галилею, однако на сей раз инквизиция удовлетворилась помещением ученого под домашний арест. Чтобы оценить, чего же достигли Джироламо и его соотечественники, нам надо вернуться к вавилонским табличкам, которые объясняют, как решать квадратные уравнения. Если следовать их предписанию, но выразить все шаги вычисления в современных обозначениях, мы увидим, что вавилонский писец на самом деле сообщал нам, что решение квадратного уравнения x2 − ax = b есть
Эта формула эквивалентна той, которую наизусть знает каждый школьник и которая в наши дни присутствует во всех справочниках. Решение кубического уравнения, данное во времена Возрождения, выглядит похоже, но посложнее. В современных обозначениях оно имеет следующий вид. Пусть x3 + ax = b. Тогда
Коль скоро речь зашла о формулах, то эта среди них — относительно простая (поверьте!), однако для того, чтобы стало возможным записать ее в таком виде, потребовалось развитие большого числа алгебраических идей. Это заведомо самая сложная формула из тех, что нам встретятся в этой книге, и в ней использованы все три типа обозначений, которые я ввел: буквы, приподнятые числа и знак, причем корни здесь как квадратные, так и кубические. Понимания этой формулы от вас не требуется и определенно не требуется производить с ней никаких вычислений. Но важно понять ее общее устройство. Начнем с некоторой терминологии, которая будет нам полезна по мере продвижения вперед. Алгебраическое выражение вида 2x4 − 7x3 − 4x2 + 9 называется полиномиальным выражением или, иначе говоря, многочленом. Такие выражения образованы путем сложения друг с другом различных степеней неизвестного. Числа 2, −7, −4 и 9, на которые умножаются эти степени, называются коэффициентами. Старшая степень, в которой неизвестное входит в многочлен, называется степенью этого многочлена, так что приведенный выше многочлен имеет степень 4. Имеются специальные названия для многочленов младших степеней (от 1 до 3 включительно): линейный, квадратичный и кубический [В английском оригинале имена даются также многочленам степеней 4, 5 и 6: они произведены от соответствующих слов «квартика», «квинтика» и «секстика», которые мы также будем иногда употреблять, называя уравнения четвертой и пятой степени соответственно квартикой и квинтикой (а третьей степени заодно — кубикой). (Примеч. перев.)]. Решения соответствующего уравнения 2x4 − 7x3 − 4x2 + 9 = 0 называются корнями многочлена. Теперь можно разобрать формулу Кардано на части. Она построена из коэффициентов a и b с использованием сложения, вычитания, умножения и деления (но только на определенные целые числа — 2, 4 и 27). Эзотерические аспекты двояки. Имеется квадратный корень — в действительности один и тот же квадратный корень встречается дважды, но один раз он прибавляется, а другой раз вычитается. Наконец, имеются два кубических корня, причем это кубические корни из величин, в которые входят квадратные корни. Так что помимо безобидных алгебраических операций (под которыми я понимаю те, что попросту перемешивают члены) «скелет» решения можно выразить так: «Берем квадратный корень, затем кубический корень; делаем это еще раз; складываем результаты». Это все, что нам понадобится. Но без этого, я полагаю, нам не обойтись. Чего математикам эпохи Возрождения сначала никак не удавалось ухватить, пока последующие поколения этого не поняли, так это того факта, что данная формула есть не просто решение одного типа кубических уравнений. Это — полное решение всех типов кубических уравнений, с точностью до простых алгебраических преобразований. Для начала, если кубический член есть, скажем, 5x3, а не x3, то можно просто разделить все уравнение на 5; с этим-то математики эпохи Возрождения неплохо разобрались. Более тонкая идея, которая потребовала тихой революции во взглядах на числа, состоит в том, что если разрешить коэффициентам а и b быть при необходимости отрицательными, то можно избежать бесплодных разграничений между различными случаями. Наконец, имеется чисто алгебраический фокус: если в уравнение входит квадрат неизвестного, от него всегда можно избавиться — надо заменить x на x плюс специальным образом подобранная постоянная, и если все сделать правильно, то слагаемое с квадратом замечательным образом исчезает. Здесь опять же будет легче, если перестать беспокоиться о том, являются ли числа положительными или отрицательными. Наконец, математики Возрождения тревожились по поводу слагаемых, которые полностью отсутствовали в уравнении, в то время как, на наш современный взгляд, средство от их тревоги очевидно: такие слагаемые не столько отсутствуют, сколько имеют перед собой коэффициент, равный нулю. Тогда одна и та же формула применима во всех случаях. Задача решена? Не совсем. Я вас обманул. Обман вот где: я сказал, что формула Кардано решает все кубики (то есть кубические уравнения). В некотором смысле это утверждение неверно, и этот факт оказался важным. С другой стороны, обман был не очень серьезным, поскольку все зависит от того, что понимать под словом «решает». Сам Кардано заметил эту сложность — и этот факт красноречиво свидетельствует о его внимании к мелочам. Кубическое уравнение, как правило, имеет или три решения (меньше, если исключить отрицательные числа), или одно. Кардано заметил, что когда имеются три решения — скажем, 1, 2 и 3, — то их никаким разумным образом не удается получить из формулы для решений. Вместо этого появляются квадратные корни из отрицательных чисел. А именно, Кардано заметил, что кубическое уравнение x3 = 15x + 4 имеет очевидное решение x = 4. Но, применив формулу Тартальи, он получил «ответ»
казавшийся бессмысленным. Немногие среди европейских математиков тех дней были настолько отчаянными, чтобы согласиться принять отрицательные числа. Их коллеги на Востоке пришли к пониманию отрицательных величин намного раньше. В Индии последователи джайнизма развили зачатки понятия отрицательных величин уже в 400 году, а в 1200-м в китайской системе «счетных палочек» использовались красные палочки для положительных чисел и черные для отрицательных — хотя и только в определенном, ограниченном контексте. Если уже отрицательные числа вызывали затруднение, то квадратные корни из них представляли собой затруднение куда большее. Сложность состоит в том, что квадрат как положительного, так и отрицательного числа всегда положителен — я не буду объяснять почему, но это единственный способ заставить все законы алгебры работать непротиворечивым образом. Так что, даже если вы не против использования отрицательных чисел, вам вроде бы придется признать, что разумным способом изрекать квадратные корни из них нельзя. А поэтому всякое алгебраическое выражение, содержащее квадратный корень из отрицательной величины, должно быть бессмыслицей. И тем не менее формула Тартальи привела Кардано именно к таким выражениям. В особенности тревожил его тот факт, что в случаях, когда было известно решение, полученное каким-то другим способом, формула как будто отказывалась его воспроизводить. В 1539 году обеспокоенный Кардано решил обсудить вопрос с Тартальей: «Я обратился с вопросом о решении различных проблем, на которые вы не дали мне ответа; одна из них — задача о кубе, равном неизвестному плюс число. Я, без сомнения, уловил правило, но когда куб одной трети коэффициента при неизвестном превосходит квадрат половины числа, тогда, как кажется, я не могу с помощью этого правила удовлетворить мое уравнение». Здесь Кардано в точности описывает условие, когда квадратный корень оказывается корнем из отрицательного числа. Ясно, что он превосходно ухватил всю суть вопроса и обнаружил подводный камень. Менее ясно, достиг ли Тарталья того же уровня понимания своей собственной формулы, потому что ответ его сводился к следующему: «Вы не владеете настоящим способом решения задач этого типа…. Ваши методы целиком неправильны». Возможно, Тарталья намеренно отказывал Кардано в помощи. А может быть, он просто не понимал, о чем тот говорит. Как бы то ни было, Кардано смог разглядеть трудный вопрос, которому предстояло занимать умы математиков всего мира в течение последующих 250 лет. Даже во времена Возрождения проскальзывали намеки, что здесь происходит нечто важное. Тот же вопрос возник в другой задаче, обсуждавшейся в «Великом искусстве», — найти два числа, сумма которых равна 10, а произведение равно 40. Получалось «решение» 5 + √−15 и 5 − √−15. Кардано заметил, что если не обращать внимания на вопрос о том, что же означает квадратный корень из минус пятнадцати, а просто делать вид, что перед нами обычный квадратный корень, то удается проверить, что эти «числа» действительно удовлетворяют требуемому уравнению. При их сложении друг с другом квадратные корни сокращаются, а две остающиеся пятерки складываются в число 10, как того и требовало условие задачи. При умножении же получается 25 − (√−15)2, что равно 25 + 15, т.е. 40. Кардано не знал, как понять эти странные вычисления. «Таковы, — писал он, — пути арифметической изысканности, приводящей в конце концов к вещам столь же изощренным, сколь и бесполезным». В своей «Алгебре» 1572 года Рафаэле Бомбелли — сын болонского торговца шерстью — заметил, что подобные же вычисления, в которых с «мнимыми» корнями обращаются так, как если бы они были настоящими числами, позволяют преобразовать таинственную формулу для решения озадачившего Кардано кубического уравнения в правильный ответ x = 4. Книгу он написал, чтобы занять свободное время, образовавшееся у него, пока он руководил осушением болот для Апостольской палаты — папского юридического и финансового ведомства. Бомбелли заметил, что (2 + √−1)3 = 2 + √−121 и (2 − √−1)3 = 2 − √−121, так что сумма двух странных кубических корней принимает вид (2 + √−1) + (2 − √−1), что равно 4. Бессмысленный корень каким-то образом оказался осмысленным и привел к правильному ответу. Бомбелли, возможно, был первым математиком, кто понял, что можно выполнять алгебраические действия с квадратными корнями из отрицательных чисел и получать при этом осмысленные ответы. Это недвусмысленно намекало, что таким числам можно дать разумную интерпретацию, но у Бомбелли не было указаний на то, какую именно. Математической вершиной книги Кардано была не кубика, а квартика. Его ученик Феррари сумел перенести методы Тартальи и дель Ферро на уравнения, содержащие четвертую степень неизвестного. Формула Феррари включает только квадратные и кубические корни — корни четвертой степени не нужны, поскольку такой корень есть просто квадратный корень квадратного корня. «Великое искусство» не содержит решения квинтики — уравнения, в котором неизвестное появляется в пятой степени. Но ведь по мере возрастания степени уравнения метод его решения в свою очередь усложнялся, так что мало кто сомневался, что, применив достаточную изобретательность, можно будет решить и уравнение пятой степени — скорее всего, потребуется использовать корни пятой степени, так что соответствующая формула окажется весьма громоздкой. Кардано не стал тратить время на поиски такого решения. После 1539 года он вернулся к другим своим многочисленным занятиям, в особенности к медицине. В это время его семейная жизнь начала рушиться самым ужасающим образом: «Мой [младший] сын между днем своей женитьбы и днем своего рокового конца был арестован по обвинению в попытке отравления собственной жены, пока она еще оправлялась после родов. В 17-й день февраля он был задержан, а пятьдесят три дня спустя, 13 апреля, обезглавлен в тюрьме». Кардано пытался примириться с этой трагедией, но беда не приходит одна. «Наш дом — мой дом — на протяжении нескольких дней стал свидетелем трех похорон: моего сына, маленькой внучки Диареджины и кормилицы; мой новорожденный внук также был недалек от смерти». При всем этом в силу своей природы Кардано был неисправимым оптимистом: «Тем не менее во мне еще так много благодати, что, если бы она принадлежала кому-то другому, тот бы считал себя счастливчиком».
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Математика ≫ Книги ≫ Глава 4. Ученый игрок / Истина и красота. Всемирная история симметрии // Иэн Стюарт |
|
[time: 9 ms; queries: 7]
21 Фев 2026 07:01:44 GMT+3 |


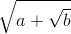 . Леонардо доказал, что эти иррациональные числа не подходят для решения кубических уравнений. Отсюда не следует, что корни кубического уравнения нельзя построить при помощи циркуля и линейки, поскольку другие комбинации квадратных корней могут в принципе приводить к решению. Но это был намек на то, что, если пользоваться лишь предлагаемыми Эвклидом инструментами, кубическое уравнение может оказаться неразрешимым.
. Леонардо доказал, что эти иррациональные числа не подходят для решения кубических уравнений. Отсюда не следует, что корни кубического уравнения нельзя построить при помощи циркуля и линейки, поскольку другие комбинации квадратных корней могут в принципе приводить к решению. Но это был намек на то, что, если пользоваться лишь предлагаемыми Эвклидом инструментами, кубическое уравнение может оказаться неразрешимым.
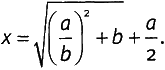

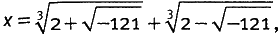
 Немецкий математик Леопольд Кронекер писал: «Бог создал целые числа, всё остальное — дело рук человека». Число — основное понятие математики, используемое для количественной характеристики, сравнения, нумерации объектов и их частей. Возникнув ещё в первобытном обществе из потребностей счёта, понятие числа с развитием науки значительно расширилось.
Немецкий математик Леопольд Кронекер писал: «Бог создал целые числа, всё остальное — дело рук человека». Число — основное понятие математики, используемое для количественной характеристики, сравнения, нумерации объектов и их частей. Возникнув ещё в первобытном обществе из потребностей счёта, понятие числа с развитием науки значительно расширилось. Отрывок из книги нобелевского лауреата Фрэнка Вильчека об идеях красоты и симметрии, лежащих в основе физических концепций.
Отрывок из книги нобелевского лауреата Фрэнка Вильчека об идеях красоты и симметрии, лежащих в основе физических концепций.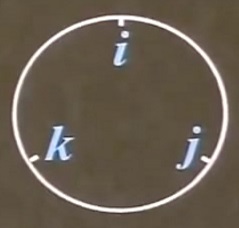 В середине XIX века были сделаны открытия, которые в корне изменили алгебру и привели к ее окончательному отделению от арифметики. История открытия алгебры кватернионов и булевой алгебры.
В середине XIX века были сделаны открытия, которые в корне изменили алгебру и привели к ее окончательному отделению от арифметики. История открытия алгебры кватернионов и булевой алгебры. Математик, профессор Маркус дю Сатель рассказывает в этом фильме о том, как законы математики пронизывают своей строгой красотой все формы нашего мира.
Математик, профессор Маркус дю Сатель рассказывает в этом фильме о том, как законы математики пронизывают своей строгой красотой все формы нашего мира. Документальный фильм «Измерения» – это два часа математики, постепенно выводящие вас в четвёртое измерение.
Документальный фильм «Измерения» – это два часа математики, постепенно выводящие вас в четвёртое измерение. Математик Илья Щуров о десятичных дробях, трансцендентности и иррациональности числа Пи.
Математик Илья Щуров о десятичных дробях, трансцендентности и иррациональности числа Пи.