|
||
|
|
||
| Главная ≫ Инфотека ≫ Математика ≫ Что такое число? |
Что такое число?
«Бог создал целые числа, всё остальное — дело рук человека.» (Леопольд Кронекер)  Число — основное понятие математики, используемое для количественной характеристики, сравнения, нумерации объектов и их частей. Письменными знаками для обозначения чисел служат цифры, а также символы математических операций. Возникнув ещё в первобытном обществе из потребностей счёта, понятие числа с развитием науки значительно расширилось. Число — основное понятие математики, используемое для количественной характеристики, сравнения, нумерации объектов и их частей. Письменными знаками для обозначения чисел служат цифры, а также символы математических операций. Возникнув ещё в первобытном обществе из потребностей счёта, понятие числа с развитием науки значительно расширилось.История развития понятия Понятие числа возникло в глубокой древности из практической потребности людей и усложнялось в процессе развития человечества. Область человеческой деятельности расширялась и соответственно, возрастала потребность в количественном описании и исследовании. Сначала понятие числа определялось теми потребностями счёта и измерения, которые возникали в практической деятельности человека, всё более усложняясь. Позже число становится основным понятием математики, и потребности этой науки определяют дальнейшее развитие этого понятия. Доисторические времена Считать предметы человек умел ещё в глубокой древности, тогда и возникло понятие натурального числа. На первых ступенях развития понятие отвлечённого числа отсутствовало. В те времена человек мог оценивать количества однородных предметов, называемых одним словом, например "три человека", "три топора". При этом использовались разные слова "один" "два", "три" для понятий "один человек", "два человека", "три человека" и "один топор", "два топора", "три топора". Это показывает анализ языков первобытных народностей. Такие именованные числовые ряды были очень короткими и завершались неиндивидуализированным понятием "много". Разные слова для большого количества предметов разного рода существуют и сейчас, такие, как "толпа", "стадо", "куча". Примитивный счёт предметов заключался "в сопоставлении предметов данной конкретной совокупности с предметами некоторой определённой совокупности, играющей как бы роль эталона", которым у большинства народов являлись пальцы ("счёт на пальцах"). Это подтверждается лингвистическим анализом названий первых чисел. На этой ступени понятие числа становится не зависящим от качества считаемых объектов. Появление письменности Возможности воспроизведения чисел значительно увеличились с появлением письменности. Первое время числа обозначались чёрточками на материале, служащем для записи, например папирус, глиняные таблички, позже стали применяться специальные знаки для некоторых чисел (сохранившиеся до наших дней "римские цифры") и знаки для больших чисел. О последних свидетельствуют вавилонские клинописные обозначения или знаки для записи чисел в кириллической системе счисления. Когда в Индии появилась позиционная система счисления, позволяющая записать любое натуральное число при помощи десяти знаков (цифр), это стало большим достижением человека. Осознание бесконечности натурального ряда явилось следующим важным шагом в развитии понятия натурального числа. Об этом есть упоминания в трудах Евклида и Архимеда и других памятниках античной математики 3 века до н. э. В "Началах" Евклид устанавливает безграничную продолжаемость ряда простых чисел. Здесь же Евклид определяет число, как «множество, составленное из единиц». Архимед в книге "Псаммит" описывает принципы для обозначения сколь угодно больших чисел. Появление арифметики Со временем начинают применяться действия над числами, сначала сложение и вычитание, позже умножение и деление. В результате длительного развития сложилось представление об отвлечённом характере этих действий, о независимости количественного результата действия от рассматриваемых предметов, о том, что, например, два предмета и три предмета составляют пять предметов независимо от характера этих предметов. Когда стали разрабатывать правила действий, изучать их свойства и создавать методы решения задач, тогда начинает развиться арифметика — наука о числах. Потребность в изучении свойств чисел как таковых проявляется в самом процессе развития арифметики, становятся понятными сложные закономерности и их взаимосвязи, обусловленные наличием действий, выделяются классы чётных и нечётных чисел, простых и составных чисел и так далее. Тогда появляется раздел математики, который сейчас называется теория чисел. Когда было замечено, что натуральные числа могут характеризовать не только количество предметов, но и ещё могут характеризовать порядок предметов, расположенных в ряд, возникает понятие порядкового числа. Вопрос об обосновании понятия натурального числа, столь привычного и простого, долгое время в науке не ставился. Только к середине 19 века под влиянием развития математического анализа и аксиоматического метода в математике, назрела необходимость обоснования понятия количественного натурального числа. Введение дробных (рациональных) чисел Понятие дроби возникло несколько тысяч лет назад, когда, сталкиваясь с необходимостью измерять некоторые вещи (длину, вес, площадь и т. п.), люди поняли, что не удаётся обойтись целыми числами и необходимо ввести понятие доли: половины, трети и т. п. Дробями и операциями над ними пользовались, например, шумеры, древние египтяне и греки. Введение в употребление дробных чисел стало исторически первым расширением понятия числа. Введение отрицательных чисел В Средние века были введены отрицательные числа, с помощью которых стало легче учитывать долг или убыток. Необходимость введения отрицательных чисел была связана с развитием алгебры как науки, дающей общие способы решения арифметических задач, независимо от их конкретного содержания и исходных числовых данных. Необходимость введения в алгебру отрицательного числа возникает уже при решении задач, сводящихся к линейным уравнениям с одним неизвестным. Отрицательные числа систематически применялись при решении задач ещё в 6—11 веках в Индии и истолковывались примерно так же, как это делается в настоящее время. После того, как Декарт разработал аналитическую геометрию, позволившую рассматривать корни уравнения как координаты точек пересечения некоторой кривой с осью абсцисс, что окончательно стёрло принципиальное различие между положительными и отрицательными корнями уравнения, отрицательные числа окончательно вошли в употребление в европейской науке. Введение действительных чисел Ещё в Древней Греции в геометрии было совершено принципиально важное открытие: не всякие точно заданные отрезки соизмеримы, другими словами, не у каждого отрезка длина может быть выражена рациональным числом, например сторона квадрата и его диагональ. В "Началах" Евклида была изложена теория отношений отрезков, учитывающая возможность их несоизмеримости. В Древней Греции умели сравнивать такие отношения по величине, производить над ними арифметические действия в геометрической форме. Хотя греки обращались с такими отношениями, как с числами, они не осознали, что отношение длин несоизмеримых отрезков может рассматриваться как число. Это было сделано в период зарождения современной математики в 17 веке при разработке методов изучения непрерывных процессов и методов приближённых вычислений. И. Ньютон во "Всеобщей арифметике" даёт определение понятия действительного числа: "Под числом мы понимаем не столько множество единиц, сколько отвлечённое отношение какой-нибудь величины к другой величине того же рода, принятой нами за единицу". Позже, в 70 годах 19 века, понятие действительного числа было уточнено на основе анализа понятия непрерывности Р. Дедекиндом, Г. Кантором и К. Вейерштрассом. Введение комплексных чисел С развитием алгебры возникла необходимость введения комплексных чисел, хотя недоверие к закономерности пользования ими долго сохранялось и отразилось в сохранившемся до сих пор термине "мнимое". Уже у итальянских математиков 16 века (Дж. Кардано, Р. Бомбелли), в связи с открытием алгебраического решения уравнений третьей и четвёртой степеней, возникла идея комплексного числа. Дело в том, что даже решение квадратного уравнения, в том случае, если уравнение не имеет действительных корней, приводит к действию извлечения квадратного корня из отрицательного числа. Казалось, что задача, приводящаяся к решению такого квадратного уравнения, не имеет решения. С открытием алгебраического решения уравнений третьей степени обнаружилось, что в том случае, когда все три корня уравнения являются действительными, по ходу вычисления оказывается необходимо выполнить действие извлечения квадратного корня из отрицательных чисел. После установления в конце XVIII века геометрического истолкования комплексных чисел в виде точек на плоскости и установления несомненной пользы от введения комплексных чисел в теории алгебраических уравнений, в особенности после знаменитых работ Л. Эйлера и К. Гаусса, комплексные числа были признаны математиками и начали играть существенную роль не только в алгебре, но и в математическом анализе. Значение комплексных чисел особенно возросло в 19 веке в связи с развитием теории функций комплексного переменного. Современная иерархия чисел Натуральные числа — числа, возникающие естественным образом при счёте. Существуют два подхода к определению натуральных чисел — это числа, возникающие при:
Можно сказать, что первый подход вводит порядковые числа (ординалы), а второй количественные числа (кардинальные числа). В первом случае ряд натуральных чисел начинается с единицы, во втором — с нуля. Не существует единого для большинства математиков мнения о предпочтительности первого или второго подхода (то есть считать ли ноль натуральным числом или нет). В подавляющем большинстве российских источников традиционно принят первый подход. Второй подход, например, применяется в трудах Бурбаки, где натуральные числа определяются как мощности конечных множеств. Множество натуральных чисел обозначается или, если к множеству натуральных чисел также относят ноль, то Натуральные числа замкнуты относительно сложения и умножения (но не вычитания или деления). Сложение и умножение натуральных чисел коммутативны и ассоциативны, а умножение натуральных чисел дистрибутивно относительно сложения и вычитания. Интуитивное представление о натуральном ряде впервые было формализовано в XIX веке в итальянским математиком Джузеппе Пеано. Необходимость формализации арифметики не принималась всерьёз до появления работы Германа Грассмана, который показал в 1860-х, что многие факты в арифметике могут быть установлены из более элементарных фактов о функции следования и математической индукции. В 1881 году Чарльз Сандерс Пирс опубликовал свою аксиоматизацию арифметики натуральных чисел. Формальное определение натуральных чисел в 1889 году сформулировал Джузеппе Пеано, основываясь на более ранних построениях Грассмана, в своей книге "Основания арифметики, изложенные новым способом" (лат. Arithmetices principia, nova methodo exposita). В 1888 году (за год до Пеано) практически в точности подобную аксиоматическую систему опубликовал Дедекинд. Аксиомы Пеано позволили формализовать арифметику, доказать многие свойства натуральных и целых чисел, а также использовать целые числа для построения формальных теорий рациональных и вещественных чисел. В сокращённом виде аксиомы Пеано использовались в ряде метаматематических разработок, включая решение фундаментальных вопросов о непротиворечивости и полноте теории чисел. Изначально Пеано постулировал девять аксиом. Первая утверждает существование по меньшей мере одного элемента множества чисел. Следующие четыре — общие утверждения о равенстве, отражающие внутреннюю логику аксиоматики и исключённые из современного состава аксиом, как очевидные. Следующие три — аксиомы на языке логики первого порядка о выражении натуральных чисел через фундаментальное свойство функции следования. Девятая и последняя аксиома на языке логики второго порядка — о принципе математической индукции над рядом натуральных чисел. Арифметика Пеано — система, получаемая заменой аксиомы индукции системой аксиом на языке логики первого порядка и добавлением символов операций сложения и умножения. Словесная формулировка:
Математическая формулировка использует функцию следования
Последнее утверждение может быть сформулировано так: если некоторое высказывание Примечательно, что единственность единицы Формализация арифметики включает в себя аксиомы Пеано, а также вводит число
Принципиальным фактом является то, что эти аксиомы по сути однозначно определяют натуральные числа (категоричность системы аксиом Пеано). А именно, можно доказать, что если Поэтому, достаточно зафиксировать в качестве Непротиворечивость арифметики Пеано была доказана в 1936 году Генценом с помощью трансфинитной индукции до ординала Также есть теоретико-множественное определение натуральных чисел (определение Фреге — Рассела) Согласно теории множеств, единственным объектом конструирования любых математических систем является множество. Таким образом, и натуральные числа вводятся, исходя из понятия множества, по двум правилам:
Числа, заданные таким образом, называются ординальными. Опишем несколько первых ординальных чисел и соответствующих им натуральных чисел:
Отношение порядка Вычитание натуральных чисел определяется как операция обратная к сложению. Целые числа, получаемые объединением натуральных чисел с множеством чисел противоположных натуральным и нулём, обозначаются Кольцо целых чисел является минимальным кольцом, содержащим (с согласованием операций) натуральные числа. Кольцо целых чисел может быть формально определено как множество классов эквивалентности множества пар натуральных чисел которые стандартным образом переносятся на классы эквиалентности. Расположение кольца Кольцо
Расположение порождает порядок в Говорят, что на множестве
Рациональные числа — числа, представимые в виде дроби Можно доказать, что поле рациональных чисел является минимальным полем, содержащим (с согласованием операций) кольцо целых чисел. Поле рациональных чисел может быть формально определено как поле отношений целостного кольца Вещественные (действительные) числа представляют собой расширение множества рациональных чисел, замкнутое относительно некоторых (важных для математического анализа) операций предельного перехода. Множество вещественных чисел обозначается В Исторически первыми строгими определениями вещественного числа были конструктивные определения. В 1872 году были опубликованы одновременно три работы: теория фундаментальных последовательностей Кантора, теория Вейерштрасса (в современном варианте — теория бесконечных десятичных дробей) и теория сечений в области рациональных чисел Дедекинда. В подходе Кантора вещественное число рассматривается как предел последовательности рациональных чисел. Чтобы последовательность рациональных чисел сходилась, на неё накладывается условие Коши: Смысл этого условия заключается в том, что члены последовательности, начиная с некоторого номера будут лежать сколь угодно близко друг от друга. Последовательности, удовлетворяющие условию Коши, называются фундаментальными. Вещественное число, определяемое фундаментальной последовательностью рациональных чисел Два вещественных числа Если даны два вещественных числа Отношение порядка на множестве вещественных чисел устанавливается посредством соглашения, в соответствии с которым число Способ построения множества вещественных чисел с помощью фундаментальных последовательностей рациональных чисел является частным случаем конструкции пополнения произвольного метрического пространства. Как и в общем случае, полученное в результате пополнения множество вещественных чисел само уже является полным, то есть содержит пределы всех фундаментальных последовательностей своих элементов. В подходе Дедекинда вещественные числа определяются с помощью сечений в множестве рациональных чисел. Сечением в множестве рациональных чисел Если существует число Если же в нижнем классе сечения нет максимального элемента, а в верхнем — минимального, то не существует никакого рационального числа, которое разделяло бы множества Объединение всех рациональных и всех иррациональных чисел называют множеством вещественных чисел, а его элементы — вещественными числами. Арифметические операции над вещественными числами определяются как непрерывное продолжение соответствующих операций над рациональными числами. Например, суммой вещественных чисел Подобным образом определяется и произведение вещественных чисел. Комплексные числа При любом из способов определения арифметические операции для комплексных чисел имеют те же свойства, что и аналогичные операции с вещественными числами. Исключением являются только свойства, связанные с отношением порядка (больше-меньше), потому что невозможно расширить порядок одиночных чисел, включив в него такие упорядоченные пары чисел, чтобы операции отношения порядка по-прежнему были согласованы. Стандартная модель строится с помощью процедуры удвоения алгебры (процедуры Кэли — Диксона) Комплексное число Введём операции сложения и умножения таких пар следующим образом:
Вещественные числа являются в этой модели подмножеством множества комплексных чисел и представлены парами вида Квадрат числа Гиперкомплексные числа Дальнейшие обобщения чисел происходят также с помощью процедуры удвоения (процедуры Кэли — Диксона) — это итеративная процедура построения алгебр над полем (или над кольцом), с удвоением размерности на каждом шаге. Названа в честь Артура Кэли и Леонарда Диксона. Эта процедура позволяет построить из действительных чисел комплексные числа, кватернионы, октонионы, седенионы и т.д. Процедура Кэли — Диксона (процедура удвоения алгебры) Если для некоторых чисел
Если исходная алгебра имеет единицу Кватернионы (от лат. quaterni, по четыре) — система гиперкомплексных чисел, образующая векторное пространство размерностью четыре над полем вещественных чисел. Обычно обозначаются символом Анри Пуанкаре писал о кватернионах: «Их появление дало мощный толчок развитию алгебры; исходя от них, наука пошла по пути обобщения понятия числа, придя к концепциям матрицы и линейного оператора, пронизывающим современную математику. Это была революция в арифметике, подобная той, которую сделал Лобачевский в геометрии». Кватернионы можно определить как формальную сумму Например, Произвольный кватернион или эквивалентно где Существуют разные способы определения регулярных функций кватернионного переменного. Самый явный — рассмотрение кватернионно дифференцируемых функций, при этом можно рассматривать праводифференцируемые и леводифференцируемые функции, не совпадающие в силу некоммутативности умножения кватернионов. Очевидно, что их теория полностью аналогична. Определим кватернионно леводифференцируемую функцию Оказывается, что все такие функции имеют в некоторой окрестности точки где Кватернионы удобны для описания изометрий трёх- и четырёхмерного евклидовых пространств, и поэтому получили широкое распространение в механике. Также их используют в вычислительной математике, например, при создании трёхмерной графики. Теорема Фробениуса утверждает, что перечисленные расширения поля вещественных чисел Теорема Фробениуса Пусть
Другими словами, Тогда тело
Октонионы (или алгебра Кэли) — система гиперкомплексных чисел, 8-мерная алгебра над полем вещественных чисел. Обычно обозначается Октинион — это линейная комбинация элементов с вещественными коэффициентами Подобно кватернионам в отношении комплексных чисел, каждый октинион Октонионы, являющиеся расширением алгебры кватернионов с помощью процедуры удвоения, уже теряют свойство ассоциативности. Из теоремы Фробениуса следует, что алгебра Кэли является единственной 8-мерной вещественной альтернативной алгеброй без делителей нуля. Октонионы находят применение в физике: например, в СТО и теории струн. Седенионы — элементы 16-мерной алгебры над полем вещественных чисел. Каждый седенион — это линейная комбинация элементов которая формирует базис векторного пространства седенионов. Каждый сединион Как и в случае октонионов, умножение седенионов не является ни коммутативным, ни ассоциативным. В отличие от октонионов, седенионы не обладают свойством альтернативности. Альтернативная операция — это бинарная операция, обладающая альтернативностью (лат. alternare): для любых элементов
Если операция является ассоциативной, то она также является альтернативной. Обратное в общем случае неверно: например, умножение октонионов альтернативно, но не ассоциативно. То есть альтернативность — это некоторое ослабление условия ассоциативности. Тем не менее седенионы обладают свойством степенной ассоциативности. Степенная ассоциативность — ослабленная форма ассоциативности, используемая в общей алгебре. Алгебраическая структура с заданным умножением (например, магма, квазигруппа, почтикольцо, алгебра над кольцом) называется степенно-ассоциативной, если её подсистема, порождаемая любым элементом, ассоциативна. Это значит, что если элемент х умножается на себя несколько раз, то не важно, в какой последовательности производится умножение, например, В множестве седионов есть единичный элемент, есть обратные элементы, но нет алгебры деления. Это происходит из-за того, что есть делители нуля, то есть два ненулевых элемента могут быть перемножены и получится нулевой результат. Множество седенионов обозначается как Таким образом, гиперкомплексные числа выстраиваются в следующую цепочку по включению: p-адические числа Помимо расширения и обобщения числовых структур с помощью удвоения алгебры, есть обобщения, основанные на иных принципах. Любое рациональное число Поле Норма Если при всех в целых Кардиналы и ординалы (порядковые числа) Натуральные числа (к которым в данном случае относится и Мощность множества, кардинальное число множества (лат. cardinalis — главное обстоятельство, стержень, сердцевина) — характеристика множеств (в том числе бесконечных), обобщающая понятие количества (числа) элементов конечного множества. До построения теории мощности множеств, множества различались по признакам: пустое/непустое и конечное/бесконечное, также конечные множества различались по количеству элементов. Бесконечные же множества нельзя было сравнить. Мощность множеств позволяет сравнивать бесконечные множества. Например, счётные множества являются самыми "маленькими" бесконечными множествами. Говорят, что множества Мощность множества натуральных чисел Про множества, равномощные множеству всех вещественных чисел, говорят, что они имеют мощность континуума, и мощность таких множеств обозначается символом c Для мощностей, как и в случае конечных множеств, имеются понятия: "равенство", "больше", "меньше". То есть для любых множеств
Ситуация, в которой Ситуация, в которой В то время как понятие кардинального числа, связанного с множеством, не требует задания на нем какой-либо структуры, ординалы тесно связаны с особой разновидностью множеств, которые называются вполне упорядоченными (в сущности эти понятия настолько близки, что некоторые математики не делают между ними никаких различий). Данный термин обозначает линейно упорядоченное множество (то есть множество с некоторым единообразным способом выбора наименьшего и наибольшего значения для произвольной пары элементов), в котором нет бесконечно убывающих последовательностей (хотя могут существовать бесконечно возрастающие), или — в эквивалентной формулировке — множество, в котором любое непустое подмножество содержит наименьший элемент. Порядковые числа можно использовать как для обозначения элементов любого заданного вполне упорядоченного множества (наименьший элемент получает метку Порядковым числом, или ординалом (лат. ordinalis — порядковый) называется порядковый тип вполне упорядоченного множества. Ординалы представляют собой одно из расширений натуральных чисел, отличающееся как от целых, так и от кардинальных чисел. Как и другие разновидности чисел, их можно складывать, перемножать и возводить в степень. Бесконечные порядковые числа называют трансфинитными (лат. trans — за, через + finitio — край, предел). Ординалы играют ключевую роль в доказательстве многих теорем теории множеств — в частности, благодаря связанному с ними принципу трансфинитной индукции. Предположим, что на множествах Порядковые числа были введены Георгом Кантором в 1883 году как способ описания бесконечных последовательностей, а также классификации множеств, обладающих определенной упорядоченной структурой. Он случайно открыл порядковые числа, работая над задачей, связанной с тригонометрическими рядами. Любое порядковое число определяется множеством предшествующих ординалов: фактически наиболее распространенное определение порядкового числа отождествляет его со множеством предшествующих ординалов. Так, ординал Наименьшим среди бесконечных ординалов является порядковый тип натуральных чисел (конечных ординалов) Вероятно, более интуитивное представление о порядковых числах можно получить, рассмотрев несколько их первых представителей: как уже упоминалось выше, множество ординалов начинается с натуральных чисел Сложение и умножение ординалов уже не обладают свойством коммутативности: так напрммер, Множество всех счетных ординалов образует первое несчетное порядковое число Вполне упорядоченные кардинальные числа отождествляются с их начальными ординалами, то есть минимальными ординалами соответствующей мощности. Мощность порядкового числа задает между классами порядковых и кардинальных чисел соответствие по типу "многие к одному". Число в философии Философское понимание числа заложили пифагорейцы. Аристотель свидетельствует, что пифагорейцы считали числа "причиной и началом" вещей, а отношения чисел — основой всех отношений в мире. Числа придают миру упорядоченность и делают его космосом. Такое отношение к числу было принято Платоном, а позже неоплатониками. Платон при помощи чисел различает подлинное бытие (то, что существует и мыслится само по себе), и неподлинное бытие, (то, что существует лишь благодаря другому и познаётся только в отношении). Срединное положение между ними занимает число. Оно придаёт меру и определённость вещам и делает их причастными бытию. Благодаря числу вещи могут быть подвергнуты пересчёту и поэтому они могут быть мыслимы, а не только ощущаемы. Неоплатоники, особенно Ямвлих и Прокл, почитали числа столь высоко, что даже не считали их сущими — устроение мира исходит от числа, хотя и не непосредственно. Числа сверхсущны, пребывают выше Ума, и недоступны знанию. Неоплатоники различают божественные числа (прямую эманацию Единого) и математические числа (составленные из единиц). Последние являются несовершенными подобиями первых. Аристотель, наоборот, приводит целый ряд аргументов, показывающих, что утверждение о самостоятельном существовании чисел приводит к нелепостям. Арифметика выделяет в этих реально сущих вещах только один аспект и рассматривает их с точки зрения их количества. Числа и их свойства являются результатом такого рассмотрения. Кант считал, что явление познано тогда, когда оно сконструировано в соответствии с априорными понятиями — формальными условиями опыта. Число — одно из таких условий. Число задаёт конкретный принцип или схему конструирования. Любой объект является исчислимым и измеряемым, потому что он сконструирован по схеме числа (или величины). Поэтому всякое явление может рассматриваться математикой. Разум воспринимает природу подчинённой числовым закономерностям именно потому, что сам строит её в соответствии с числовыми закономерностями. Так объясняется возможность применения математики в изучении природы. Математические определения, разработанные в XIX веке, были серьёзно пересмотрены в начале XX века. Это было вызвано не столько математическими, сколько философскими проблемами. Определения, которые были даны Пеано, Дедекиндом или Кантором, и которые используются в математике и в настоящее время, нужно было обосновать с помощью фундаментальных принципов, коренящихся в самой природе знания. Различают три таких философско-математических подхода: логицизм, интуиционизм и формализм. Философскую базу логицизма разработал Рассел. Он полагал, что истинность математических аксиом неочевидна. Истинность обнаруживается сведением к наиболее простым фактам. Отражением таких фактов Рассел считал аксиомы логики, которые он положил в основу определения числа. Важнейшим понятием у него является понятие класса. Натуральное число Интуицист Брауэр имел противоположную точку зрения: логику он считал лишь абстракцией от математики, рассматривал натуральный ряд чисел как базовую интуицию, лежащую в основании всякой мыслительной деятельности. Гильберт, главный представитель формальной школы, видел обоснование математики в построении непротиворечивой аксиоматической базы, в пределах которой можно бы было формально обосновать любое математическое понятие. В разработанной им аксиоматической теории действительных чисел представление о числе лишается всякой глубины и сводится лишь к графическому символу, подставляемому по определённым правилам в формулы теории.
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Математика ≫ Что такое число? |
|
[time: 36 ms; queries: 8]
19 Фев 2026 04:51:21 GMT+3 |


 Целью этой книги является строгое определение чисел, многочленов и алгебраических дробей и обоснование их свойств, уже известных из школы, а не ознакомление читателя с новыми свойствами. Поэтому читатель не найдет здесь новых для него фактов (за исключением, быть может, некоторых свойств, действительных и комплексных чисел), но узнает, как доказываются вещи, хорошо ему известные, начиная с «дважды два — четыре» и кончая правилами действий с многочленами и алгебраическими дробями. Зато читатель познакомится с рядом общих понятий, играющих в алгебре основную роль.
Целью этой книги является строгое определение чисел, многочленов и алгебраических дробей и обоснование их свойств, уже известных из школы, а не ознакомление читателя с новыми свойствами. Поэтому читатель не найдет здесь новых для него фактов (за исключением, быть может, некоторых свойств, действительных и комплексных чисел), но узнает, как доказываются вещи, хорошо ему известные, начиная с «дважды два — четыре» и кончая правилами действий с многочленами и алгебраическими дробями. Зато читатель познакомится с рядом общих понятий, играющих в алгебре основную роль. На протяжении многих веков симметрия оставалась ключевым понятием для художников, архитекторов и музыкантов, однако в XX веке ее глубинный смысл оценили также физики и математики. Именно симметрия сегодня лежит в основе таких фундаментальных физических и космологических теорий, как теория относительности, квантовая механика и теория струн. Начиная с древнего Вавилона и заканчивая самыми передовыми рубежами современной науки Иэн Стюарт, британский математик с мировым именем, прослеживает пути изучения симметрии и открытия ее основополагающих законов.
На протяжении многих веков симметрия оставалась ключевым понятием для художников, архитекторов и музыкантов, однако в XX веке ее глубинный смысл оценили также физики и математики. Именно симметрия сегодня лежит в основе таких фундаментальных физических и космологических теорий, как теория относительности, квантовая механика и теория струн. Начиная с древнего Вавилона и заканчивая самыми передовыми рубежами современной науки Иэн Стюарт, британский математик с мировым именем, прослеживает пути изучения симметрии и открытия ее основополагающих законов.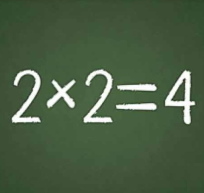 Наверное, каждый хотя бы раз в жизни слышал это выражение. Действительно, что может быть проще? Однако я знавал преподавателя математического анализа, который, услыхав подобное, ехидно улыбался в усы и предлагал доказать этот факт. После этого у говорившего обычно случался когнитивный диссонанс. И действительно, как же доказать, что 2 × 2 = 4?
Наверное, каждый хотя бы раз в жизни слышал это выражение. Действительно, что может быть проще? Однако я знавал преподавателя математического анализа, который, услыхав подобное, ехидно улыбался в усы и предлагал доказать этот факт. После этого у говорившего обычно случался когнитивный диссонанс. И действительно, как же доказать, что 2 × 2 = 4? В середине XIX века были сделаны открытия, которые в корне изменили алгебру и привели к ее окончательному отделению от арифметики. История открытия алгебры кватернионов и булевой алгебры.
В середине XIX века были сделаны открытия, которые в корне изменили алгебру и привели к ее окончательному отделению от арифметики. История открытия алгебры кватернионов и булевой алгебры. Парадоксы являются следствием дихотомии языка и мышления, выражением глубоких диалектических (теорема Гёделя позволила проявить диалектику в процессе познания) и гносеологических трудностей, связанных с понятиями предмета и предметной области в формальной логике, множества (класса) в логике и теории множеств, с употреблением принципа абстракции, позволяющего вводить в рассмотрение новые (абстрактные) объекты (бесконечность), со способами определения абстрактных объектов в науке и т. п. Поэтому не может быть дано универсального способа устранения всех парадоксов.
Парадоксы являются следствием дихотомии языка и мышления, выражением глубоких диалектических (теорема Гёделя позволила проявить диалектику в процессе познания) и гносеологических трудностей, связанных с понятиями предмета и предметной области в формальной логике, множества (класса) в логике и теории множеств, с употреблением принципа абстракции, позволяющего вводить в рассмотрение новые (абстрактные) объекты (бесконечность), со способами определения абстрактных объектов в науке и т. п. Поэтому не может быть дано универсального способа устранения всех парадоксов. Существует ли единый «Код Природы»? Может ли число порождать свет, а свет — материю? В чем суть основных принципов «неопифагорейского» подхода к построению физических теорий? О «реке времени» и частицах как точках «сгущения» первичных световых потоков — кандидат физико-математических наук, доцент кафедры общей физики Российского университета дружбы народов (РУДН) Владимир Всеволодович Кассандров.
Существует ли единый «Код Природы»? Может ли число порождать свет, а свет — материю? В чем суть основных принципов «неопифагорейского» подхода к построению физических теорий? О «реке времени» и частицах как точках «сгущения» первичных световых потоков — кандидат физико-математических наук, доцент кафедры общей физики Российского университета дружбы народов (РУДН) Владимир Всеволодович Кассандров.