Квантовая механика, не говоря уже о квантовой теории поля, имеет репутацию странной, пугающей и контринтуитивной науки. В научном сообществе есть те, кто по сей день ее не признает. Однако же квантовая теория поля — единственная подтвержденная экспериментом теория, способная объяснить взаимодействие микрочастиц при низких энергиях. Почему это важно? Андрей Ковтун, студент МФТИ и сотрудник кафедры фундаментальных взаимодействий, рассказывает, как с помощью этой теории добраться до главных законов природы или придумать их самим.

Со времен возникновения письменности и до середины XX века криптография была искусством. Сейчас это не только проработанная область науки на стыке математики и информатики, но и то, чем мы пользуемся ежедневно. К чему может привести незнание криптографии и любовь к халяве, как прочитать вашу переписку, почему шифрование на открытых ключах безопаснее и что значит cLhmGccA4aSaRslIsnA, рассказывает кандидат физико-математических наук, лектор по защите информации в МФТИ Сергей Владимиров.

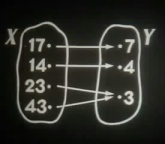
Соответствия между множествами. Определение функции. Способы задания функции. Табличный способ задания функции. Задание функции формулой. График прямой и обратной пропорциональности. Определение линейной функции. График линейной функции. Угловой коэффициент прямой. Графическое решение системы уравнений. Функция квадратичной зависимости (парабола). СССР, Киевнаучфильм, 1975 г.

Корректно ответить на этот вопрос нельзя, поскольку числовой ряд не имеет верхнего предела. Так, к любому числу достаточно всего лишь прибавить единицу, чтобы получить число ещё большее. Хотя сами числа бесконечны, собственных названий у них не так уж и много, так как большинство из них довольствуются именами, составленными из чисел меньших. Понятно, что в конечном наборе чисел, которых человечество наградило собственным именем, должно быть какое-то наибольшее число. Но как оно называется и чему оно равно? Давайте же, попробуем в этом разобраться и заодно узнать, насколько большие числа придумали математики.

Немецкий математик Леопольд Кронекер писал: «Бог создал целые числа, всё остальное — дело рук человека». Число — основное понятие математики, используемое для количественной характеристики, сравнения, нумерации объектов и их частей. Возникнув ещё в первобытном обществе из потребностей счёта, понятие числа с развитием науки значительно расширилось.

Парадоксы являются следствием дихотомии языка и мышления, выражением глубоких диалектических (теорема Гёделя позволила проявить диалектику в процессе познания) и гносеологических трудностей, связанных с понятиями предмета и предметной области в формальной логике, множества (класса) в логике и теории множеств, с употреблением принципа абстракции, позволяющего вводить в рассмотрение новые (абстрактные) объекты (бесконечность), со способами определения абстрактных объектов в науке и т. п. Поэтому не может быть дано универсального способа устранения всех парадоксов.

Математик Илья Щуров о десятичных дробях, трансцендентности и иррациональности числа Пи.

Математик Владимир Побережный об экспонентах, источниках дифференциальных уравнений и векторном пространстве функций.

Что умеют благодаря компьютерной лингвистике компьютеры? Они умеют понимать, что за слово перед ними. Это не такой простой вопрос, потому что, казалось бы, слово и слово, но в русском языке слова умеют склоняться и в разных падежах выглядят немного по-разному. Как объяснить компьютеру, что это одно и то же слово, а не разные? Филолог Борис Орехов о семантическом анализе, машинном переводе и автоматической морфологии.

В своей лекции я сначала вкратце расскажу об истории, об эволюции искусственного интеллекта, что под ним понимается, в каком состоянии он сегодня. Затем попытаюсь кратко проанализировать текущее состояние и, возможно, предложить что-то для будущего искусственного интеллекта. Эта лекция будет в основном посвящена тому, как делать искусственный интеллект и что он из себя представляет, но в основной части я не буду затрагивать вопрос, нужен ли он, и к каким последствиям создание искусственного интеллекта может привести. В нескольких словах этого вопроса я коснусь в самом конце лекции. И потом постараюсь ответить на все ваши вопросы.

Как устроен процесс обучения? Что представляет собой нейрональная культура? Как можно объяснить активность нейронов в нейрональной культуре? Об электрической активности нейронов, следах памяти в нейрональных культурах и теории функциональных систем рассказывает кандидат физико-математических наук Михаил Бурцев.

Кого считают "отцом" искусственной жизни? Какова структура клеточных автоматов Джона фон Неймана? В чем состоит проблема цифровой стерильности? Как развивается это направление сегодня? О концепции клеточных автоматов, проблеме цифровой стерильности и эволюции программ рассказывает кандидат физико-математических наук Михаил Бурцев.

Почему в процессе эволюции появляется кооперативное поведение? Как объясняют возникновение кооперации различные теории? И как исследование данного вопроса может отразиться на представлениях о морали человека? Об условиях возникновения кооперации, истоках человеческой морали и теории родственного отбора рассказывает специалист по эволюционной кибернетике Михаил Бурцев.

Какие подходы к изучению мозга существуют в современной нейробиологии? Как можно увидеть работу отдельной клетки мозга? Когда стали появляться нейрогибридные системы? О механизме обучения мозга, экспериментах с нейрогибридными системами и рисующем роботе рассказывает кандидат физико-математических наук Михаил Бурцев.

Недавно на сайте Geektimes вышла статья «Искусственные нейронные сети простыми словами». Мы побеседовали с ее автором о развитии искусственного интеллекта и нейронных сетей. Юрий работает сейчас в небольшой фирме РСПК, изучает чат-ботов.

Эссе Пола Локхарда «Плач математика» о преподавании математики в средней школе. Хотя в сочинении говорится об американской современной средней школе, многие проблемы, идентифицируемые Локхардом, относятся к любой стране мира, за исключением, возможно, Эльдорадо, которой нет. Еще менее привязаны к американской реальности размышления автора о том, что такое математика и как она должна преподаваться. Даже если вы не математик и не имеете отношения к преподаванию, думаю, вы найдете это эссе интересным, а возможно, и сделаете для себя несколько небольших открытий и сломаете кое-какие стереотипы. В конце концов, вы ведь учили математику в школе!

Когда я заводил разговор о нейронных сетях — люди обычно начинали боязливо на меня смотреть, грустнели, иногда у них начинал дёргаться глаз, а в крайних случаях они залезали под стол. Но, на самом деле, эти сети просты и интуитивны. Да-да, именно так! И, позвольте, я вам это докажу!

Основные понятия, операции над множествами, тождества, свойства дополнения, правило Де Моргана, свойства симметрической разности; отображение (функция), факторотображение, отношение эквивалентности, парадокс брадобрея; упорядоченные множества, минимальный, наименьший, максимальный и наибольший элементы в упорядоченном множестве, мажоранта и миноранта; аксиома выбора, вполне упорядоченное множество.

При развитии теории множеств, на которой базируется вся современная математика, возникали парадоксы. Например, парадокс брадобрея, формулируемый следующим образом: «Бреет ли себя брадобрей, если он бреет тех и только тех, кто сам себя не бреет?» В брошюре рассказывается о том, как теория множеств обходится с подобными ситуациями, а также о других парадоксах, в том числе возникающих при рассмотрении аксиомы выбора. В частности, вы узнаете, как из одного апельсина сделать два. Приведены задачи, самостоятельное решение которых поможет читателю более полно разобраться в материале. Брошюра рассчитана на широкий круг читателей, интересующихся математикой: школьников старших классов, студентов младших курсов, учителей.

От всемирной известности до греховных глубин — все это познал на своей шкуре Джон Форбс Нэш-младший. Математический гений, он на заре своей карьеры сделал титаническую работу в области теории игр, которая практически перевернула этот раздел математики и принесла ему международную известность. Однако буквально в то же время заносчивый и пользующийся успехом у женщин Нэш получает удар, который переворачивает уже его собственную жизнь — врачи ставят ему диагноз «параноидная шизофрения». Лишь после долгих лет борьбы ему удается победить свой недуг и наконец получить заслуженную Нобелевскую премию.