|
||
|
|
||
| Главная ≫ Инфотека ≫ Физика ≫ Наша реальность состоит из полей, а мы лишь элементарные возбуждения этих полей |
Наша реальность состоит из полей, а мы лишь элементарные возбуждения этих полей
Как известно, все естественные науки подчиняются определенной иерархии. Например, биология и химия имеют физические основания. И если смотреть на мир через лупу и каждый раз увеличивать ее силу, проводя таким образом редукцию знания, мы потихоньку придем к квантовой теории поля. Это наука, которая описывает свойства и взаимодействия самых маленьких крупиц матери, из которых мы состоим, — частиц, которые принято называть элементарными. Некоторые из них — такие, как, например, электрон — существуют сами по себе, другие же объединяются и образуют составные частицы. Всем известные протоны и нейтроны как раз являются таковыми — они состоят из кварков. А вот сами по себе кварки уже элементарны. Так вот задача физиков — понять и вывести все свойства этих частиц и ответить на вопрос, есть ли еще что-то, что лежит глубже в иерархии фундаментальных физических законов. Наша реальность — полевая, она состоит из полей, а мы лишь элементарные возбуждения этих полей Для радикальных ученых конечная цель — полная редукция знаний о мире, для менее радикальных — более глубинное проникновение в тонкости микромира или сверхмикромира. Но как это возможно, если мы имеем дело лишь с частицами? Ответ очень прост. Мы просто берем и сталкиваем их, в прямом смысле разбиваем друг о друга — как дети, которые, желая посмотреть устройство какой-нибудь занятной вещицы, просто бросают ее на пол, а потом изучают осколки. Также и мы сталкиваем частицы, а потом смотрим, какие новые частицы получаются при столкновении, а какие распадаются после продолжительного путешествия в гордом одиночестве. Все эти процессы в квантовой теории описываются так называемыми вероятностями распада и рассеяния. Расчетами этих величин и занимается квантовая теория поля. Но не только ими. Векторы вместо координат и скоростей Основное отличие квантовой механики — в том, что мы больше не будем описывать физические тела с помощью координат и скоростей. Основное понятие в квантовой механике — это вектор состояния. Это шкатулка с квантово-механической информацией о физической системе, которую мы изучаем. Причем я использую слово «система», потому что вектор состояния — это штука, которая может описывать состояние как электрона, так и бабушки, лузгающей семечки на скамейке. То есть это понятие имеет очень широкий круг охвата. И мы хотим найти все векторы состояния, которые содержали бы в себе всю необходимую нам информацию об изучаемом объекте. Далее естественно задаться вопросом «А как же нам эти векторы найти, а потом извлечь из них то, что хочется?». Здесь нам на помощь приходит следующее важное понятие квантовой механики — оператор. Это правило, по которому одному вектору состояния ставится в соответствие другой. Операторы должны обладать определенными свойствами, и некоторые из них (но не все) извлекают информацию из векторов состояния о нужных нам физических величинах. Такие операторы называются операторами физических величин. Измерить то, что трудно измерить Квантовая механика последовательно решает две задачи — стационарную и эволюционную, причем по очереди. Суть стационарной задачи состоит в том, чтобы определить все возможные векторы состояния, которые могут описывать физическую систему в данный момент времени. Такие векторы являются так называемыми собственными векторами операторов физических величин. Определив их в начальный момент, интересно проследить, как они будут эволюционировать, то есть меняться со временем.
Пусть мы также решаем задачу о переходе физической системы из состояния-1 в состояние-2. Допустим, у вас есть шарик. Он хочет попасть из точки A в точку B, и существует множество мыслимых путей, по которым он мог бы совершить это путешествие. Но повседневный опыт показывает, что если вы кидаете шарик под определенным углом и с определенной скоростью, то у него есть только один реальный путь. Квантовая же механика утверждает другое. Она говорит, что шарик путешествует одновременно по всем этим траекториям. Каждая из траекторий вносит свой (больший или меньший) вклад в вероятность перехода из одной точки в другую. Поля Квантовая теория поля называется так потому, что она описывает не частицы сами по себе, а некоторые более общие сущности, которые называются полями. Частицы же в квантовой теории поля являются элементарными переносчиками полей. Представьте воды мирового океана. Пусть наш океан спокоен, на его поверхности ничего не бурлит, нет волн, пены и так далее. Наш океан есть поле. А теперь представьте уединенную волну — только один гребень волны в форме горки, родившийся в результате какого-то возбуждения (например, удара по воде), который теперь путешествует по бескрайним просторам океана. Это частица. Эта аналогия иллюстрирует главную идею: частицы есть элементарные возбуждения полей. Таким образом, наша реальность — полевая, а мы состоим лишь из элементарных возбуждений этих полей. Будучи рожденными этими самыми полями, их кванты содержат в себе все свойства своих прародителей. Такова роль частиц в мире, в котором одновременно существует множество океанов, именуемых полями. С классической точки зрения поля сами по себе — это обычные числовые функции. Они могут состоять только из одной функции (скалярные поля), а могут — из множества (векторные, тензорные и спинорные поля). Действие Вот теперь пришло время снова вспомнить о том, что каждая траектория, по которой физическая система переходит из состояния-1 в состояние-2, формируется некоторой амплитудой вероятности. В своих работах американский физик Ричард Фейнман предположил, что вклады всех траекторий равны по величине, но отличаются на фазу. По-простому, если у вас волна (в данном случае — квантовая волна вероятности) путешествует из одной точки в другую, фаза (деленная на множитель 2π) показывает, сколько колебаний укладывается на этом пути. Эта фаза есть число, которое вычисляется с помощью некоторого правила. А число это называется действием. В основе мироздания, по сути, лежит понятие красоты, которое получило отражение в термине «симметрия» С действием связан основной принцип, на котором сейчас строятся все разумные модели, описывающие физику. Это принцип наименьшего действия, и, коротко говоря, суть его состоит в следующем. Пусть у нас есть физическая система — это может быть как точка, так и шарик, который хочет переместиться из одного места в другое, или это может быть какая-то конфигурация поля, которая хочет измениться и стать другой конфигурацией. Они могут сделать это множеством способов. Например, частичка пытается в поле тяготения Земли попасть из одной точки в другую, и мы видим, что, в общем-то, путей, по которым она может это сделать, бесконечно много. Но жизнь подсказывает, что в действительности при заданных начальных условиях траектория, которая позволит ей попасть из одной точки в другую, только одна. Теперь — к сути принципа наименьшего действия. Мы каждой траектории по определенному правилу приписываем число, называемое действием. Потом сравниваем все эти числа и выбираем только те траектории, для которых действие будет минимальным (в некоторых случаях — максимальным). Используя такой способ выбора путей наименьшего действия, можно получать законы Ньютона для классической механики или уравнения, описывающие электричество и магнетизм! Остается осадок оттого, что не очень понятно, что это за число такое — действие? Если сильно не приглядываться, то это некоторая абстрактная математическая величина, которая, на первый взгляд, не имеет никакого отношения к физике — кроме того, что она случайным образом выплевывает известный нам результат. На самом деле все намного интереснее. Принцип наименьшего действия в самом начале был получен как следствие законов Ньютона. Потом на его основе сформулировали законы распространения света. Также его можно получить из уравнений, описывающих законы электричества и магнетизма, а потом в обратную сторону — из принципа наименьшего действия прийти к этим же законам.
Замечательно, что разные, на первый взгляд, теории обретают одинаковую математическую формулировку. И это наталкивает нас на следующее предположение: не можем ли мы сами придумывать какие-нибудь законы природы с помощью принципа наименьшего действия, а потом искать их в эксперименте? Можем и делаем! В этом и состоит значение этого неестественного и сложного для понимания принципа. Но он работает, что заставляет задуматься о нем именно как о некоторой физической характеристике системы, а не как об абстрактной математической формулировке современной теоретической науки. Важно также отметить, что мы не можем писать любые действия, которые подскажет нам наше воображение. Пытаясь придумать, как должно выглядеть действие очередной физической теории поля, мы используем симметрии, которыми обладает физическая природа, и наряду с фундаментальными свойствами пространства-времени мы можем использовать множество других интересных симметрий, которые подсказывает нам теория групп (раздел общей алгебры, изучающий алгебраические структуры, называемые группами, и их свойства. — Прим. ред.). О красоте симметрии Замечательно, что мы получили не просто сводку законов, описывающую какие-то природные явления, а именно способ теоретически получать законы типа ньютоновских или уравнений Максвелла. И хотя квантовая теория поля описывает элементарные частицы лишь на уровне низких энергий, она уже сослужила хорошую службу физикам во всем мире и пока является единственной теорией, здраво описывающей свойства самых мелких кирпичиков, составляющих наш мир. То, чего, собственно, хотят ученые, — это написать такое вот действие, только квантовое, которое содержало бы в себе сразу все возможные законы природы. Хотя даже если бы это удалось, то не разрешило бы всех интересных нам вопросов. В основе глубинного понимания законов природы лежат некоторые сущности, которые имеют чисто математическую природу. И сейчас, чтобы попытаться проникнуть в глубины мироздания, приходится отказываться от качественных, интуитивно понятных аргументов. Рассказывая о квантовой механике и квантовой теории поля, очень тяжело найти понятные и наглядные аналогии, но самое главное, что я хотел бы донести, — это то, что в основе мироздания лежит, по сути, понятие красоты, которое получило отражение в термине «симметрия». Симметрия поневоле ассоциируется с красотой, как это было, например, у древних греков. И именно симметрии наряду с законами квантовой механики лежат в основе устройства самых маленьких кирпичиков мира, до которых к настоящему моменту удалось добраться физикам.
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Физика ≫ Наша реальность состоит из полей, а мы лишь элементарные возбуждения этих полей |
|
[time: 12 ms; queries: 7]
22 Фев 2026 07:05:23 GMT+3 |



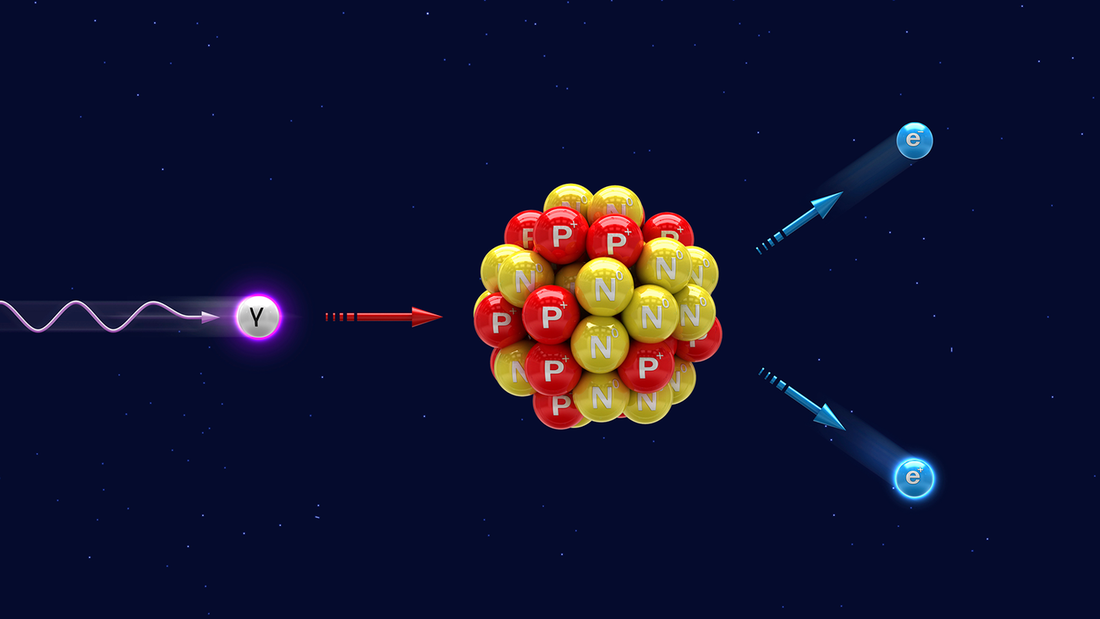
 Как человек становится математиком? Наверное, существует множество разных путей и способов. Позвольте рассказать, как это произошло со мной. Вы, наверное, удивитесь, но в школе я ненавидел математику. Хотя нет, «ненавидел», пожалуй, слишком сильное слово. Скажем просто, я не очень-то ее любил. Мне казалось, что математика скучная. Я усердно выполнял все задания, но не понимал, зачем мне это. Материал, который мы разбирали в классе, казался мне бессмысленным и бесполезным.
Как человек становится математиком? Наверное, существует множество разных путей и способов. Позвольте рассказать, как это произошло со мной. Вы, наверное, удивитесь, но в школе я ненавидел математику. Хотя нет, «ненавидел», пожалуй, слишком сильное слово. Скажем просто, я не очень-то ее любил. Мне казалось, что математика скучная. Я усердно выполнял все задания, но не понимал, зачем мне это. Материал, который мы разбирали в классе, казался мне бессмысленным и бесполезным. Отрывок из книги нобелевского лауреата Фрэнка Вильчека об идеях красоты и симметрии, лежащих в основе физических концепций.
Отрывок из книги нобелевского лауреата Фрэнка Вильчека об идеях красоты и симметрии, лежащих в основе физических концепций. Представьте себе электрические и магнитные поля. Что вы для этого сделали? Знаете ли вы, как это нужно сделать? И как я сам представляю себе электрическое и магнитное поля? Что я на самом деле при этом вижу? Что требуется от научного воображения? Отличается ли оно чем-то от попытки представить себе комнату, полную невидимых ангелов? Нет, это не похоже на такую попытку.
Представьте себе электрические и магнитные поля. Что вы для этого сделали? Знаете ли вы, как это нужно сделать? И как я сам представляю себе электрическое и магнитное поля? Что я на самом деле при этом вижу? Что требуется от научного воображения? Отличается ли оно чем-то от попытки представить себе комнату, полную невидимых ангелов? Нет, это не похоже на такую попытку. В этих двух лекциях мы хотим рассказать вам о дифференциальных формах, расслоениях и связностях. Эти понятия сейчас активно используются в разных областях математики и физики, и нам хотелось бы хотя бы немного вас с ними познакомить. Для того чтобы наш рассказ не был излишне абстрактным, мы привязаться к такому физическому объекту, как электромагнитное поле, и показать вам как при попытке описания этого поля естественным путем возникают все перечисленные понятия.
В этих двух лекциях мы хотим рассказать вам о дифференциальных формах, расслоениях и связностях. Эти понятия сейчас активно используются в разных областях математики и физики, и нам хотелось бы хотя бы немного вас с ними познакомить. Для того чтобы наш рассказ не был излишне абстрактным, мы привязаться к такому физическому объекту, как электромагнитное поле, и показать вам как при попытке описания этого поля естественным путем возникают все перечисленные понятия. Что общего между формами галактики и атмосферного циклона, расположением листьев на стебле и семян в подсолнухе? Все эти закономерности сводятся к так называемой золотой спирали, к удивительной последовательности Фибоначчи — числам, открытым гениальным итальянским математиком XIII века.
Что общего между формами галактики и атмосферного циклона, расположением листьев на стебле и семян в подсолнухе? Все эти закономерности сводятся к так называемой золотой спирали, к удивительной последовательности Фибоначчи — числам, открытым гениальным итальянским математиком XIII века. О современной математике рассказывает Михаил Цфасман, доктор физико-математических наук, ведущий научный сотрудник Института проблем передачи информации РАН и Национального центра научных исследований (Франция), проректор по научной работе и профессор Независимого московского университета.
О современной математике рассказывает Михаил Цфасман, доктор физико-математических наук, ведущий научный сотрудник Института проблем передачи информации РАН и Национального центра научных исследований (Франция), проректор по научной работе и профессор Независимого московского университета. Пусть на плоскости (или на прямой) задано векторное поле: в каждой точке нарисован вектор. Этому полю можно сопоставить дифференциальное уравнение: точка x(t) движется «по стрелочкам» – так, что dx/dt=v(x(t)) при всех t. Типичный вопрос теории динамических систем – описать качественное поведение решений при t→+∞. Скажем, решения могут стремиться к устойчивому положению равновесия, «наматываться» на периодическую траекторию («предельный цикл»), и так далее. Следующий вопрос – а что будет, если система зависит от параметра, и мы начинаем этот параметр менять? Как будет изменяться качественное поведение системы?
Пусть на плоскости (или на прямой) задано векторное поле: в каждой точке нарисован вектор. Этому полю можно сопоставить дифференциальное уравнение: точка x(t) движется «по стрелочкам» – так, что dx/dt=v(x(t)) при всех t. Типичный вопрос теории динамических систем – описать качественное поведение решений при t→+∞. Скажем, решения могут стремиться к устойчивому положению равновесия, «наматываться» на периодическую траекторию («предельный цикл»), и так далее. Следующий вопрос – а что будет, если система зависит от параметра, и мы начинаем этот параметр менять? Как будет изменяться качественное поведение системы?