Бифуркации векторных полей на плоскости

Юлий Ильяшенко

Часть 1

Часть 2

Пусть на плоскости (или на прямой) задано векторное поле: в каждой точке нарисован вектор. Этому полю можно сопоставить дифференциальное уравнение: точка $x(t)$ движется «по стрелочкам» – так, что

$\frac{dx}{dt}=v(x(t))$ при всех $t$ .

Типичный вопрос теории динамических систем – описать качественное поведение решений при 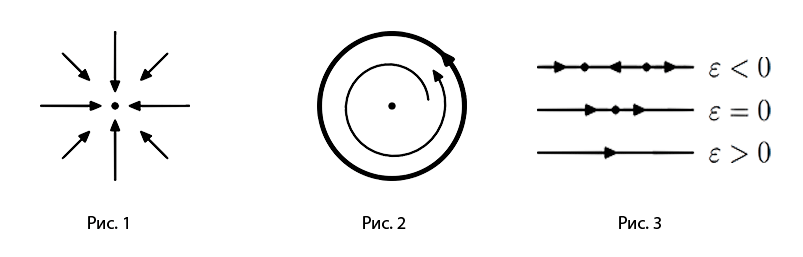$t\to+\infty$ . Скажем, решения могут стремиться к устойчивому положению равновесия (см. рис. 1), «наматываться» на периодическую траекторию («предельный цикл», см. рис. 2), и так далее.

Следующий вопрос – а что будет, если система зависит от параметра, и мы начинаем этот параметр менять? Как будет изменяться качественное поведение системы?

Достаточно часто при изменении параметра в каком-то интервале качественное поведение не изменяется, пока параметр не достигает некоторого критического («бифуркационного») значения, при котором поведение резко изменяется. Простейший пример такой картины (для динамики на прямой) изображен на рис. 3: у уравнения

$\frac{dx}{dt}=x^2+\varepsilon$

при $\varepsilon<0$ два положения равновесия, $x_{\pm}=\pm\sqrt{\varepsilon}$ , из которых одно устойчивое, а одно неустойчивое. В момент $\varepsilon=0$ происходит бифуркация: эти положения равновесия сливаются в одно полуустойчивое. Наконец, при сколь угодно малом положительном εε это положение равновесия исчезает, и точки проходят из минус бесконечности в плюс бесконечность, «нигде не задерживаясь». Этот сценарий называют бифуркацией седлоузла.

Типичные однопараметрические бифуркации векторных полей на прямой и на плоскости полностью изучены. На прямой такая бифуркация всего одна – это описанная выше бифуркация седлоузла. Список типичных бифуркаций в однопараметрических семействах оказался счетным (а не конечным, как ранее ожидалось).

«Картографирование» двупараметрических бифуркаций представляет собой интересную, объемную, и почти еще не тронутую задачу. Однако, удивительным образом, когда параметров становится три – список бифуркаций становится континуальным: у некоторой группы сценариев появляется числовой инвариант.

В курсе мы построим «руками» явный пример («плачущее сердце») такого инварианта, придуманный меньше двух лет назад в совместной работе лектора, Ю. Кудряшова и И. Щурова.

Ильяшенко Юлий Сергеевич, доктор физико-математических наук, профессор.

Летняя школа «Современная математика», г. Дубна
24–25 июля 2016 г.

Комментарии: 0

Похожее

Динамические системы и их аттракторы (история динамических систем в картинках)

Юлий Ильяшенко

Как менялись наши представления об аттракторах? Чего мы ожидаем от аттракторов? Предполагается, что слушатели знают определение и свойства компактных множеств в евклидовом пространстве, а также знакомы с определениями и примерами гомеоморфизмов и диффеоморфизмов. Последние определения будут даны в курсе, но лучше знать их заранее.
Эволюционные процессы и философия общности положения

Юлий Ильяшенко

Эволюционные процессы происходят повсюду вокруг нас — от движения атомов до движения планет. Ньютон понял, что эти процессы описываются дифференциальными уравнениями, и что эти уравнения полезно решать. В последующие полтора столетия стало ясно, что большинство дифференциальных уравнений решить нельзя. Пуанкаре создал новую ветвь математики — качественную или геометрическую теорию дифференциальных уравнений, которая изучает свойства решений непосредственно по уравнению, минуя попытки это уравнение решить. Оказалось, что даже на качественном уровне поведение решений может быть очень сложным. Ситуация резко упрощается, если «все» уравнения заменить на «типичные». С физической точки зрения интересны именно типичные дифференциальные уравнения. В лекциях будет рассказано об эволюции этих концепций и сформулированы некоторые нерешенные проблемы.
Три взгляда на векторные поля

Дмитрий Аносов

Лекции читает Аносов Дмитрий Викторович, доктор физико-математических наук, профессор, академик РАН. Летняя школа «Современная математика», г. Дубна. 2001 г.
Уравнения Максвелла, внешние дифференциальные формы и расслоения

Андрей Болибрух

В этих двух лекциях мы хотим рассказать вам о дифференциальных формах, расслоениях и связностях. Эти понятия сейчас активно используются в разных областях математики и физики, и нам хотелось бы хотя бы немного вас с ними познакомить. Для того чтобы наш рассказ не был излишне абстрактным, мы привязаться к такому физическому объекту, как электромагнитное поле, и показать вам как при попытке описания этого поля естественным путем возникают все перечисленные понятия.
Дифференциальные уравнения

Валерий Опойцев

Тематику дифференциальных уравнений, безусловно, надо расширять, иначе «молодые побеги» — хаос, аттракторы, солитоны — будут расти сквозь асфальт. С другой стороны, базовые курсы нуждаются в резком сокращении, поскольку для самих дифуров не так много места остается в этой жизни. Из-за информационного переполнения. При этом стандартных мер недостает. Единственное средство — тривиализация дисциплины. Математика, как и человек, — иногда надувает щеки, наряжается и творит мифы. Поэтому в дифурах немало лишнего, вычурного, случайного — и одно лишь наведение порядка высвобождает массу свободного места. Данный мини-курс адресован «всем», поскольку преподносит некую общую часть. Не простую и не сложную, но дающую представление об основах и позволяющую при необходимости быстро войти в предмет и двигаться дальше.
Эффект бабочки

Владимир Буданов, Аркадий Липкин, Алексей Семихатов

На грани безумия

Путешественник в прошлое случайно раздавил бабочку. Незначительная оплошность. Однако она повлекла катастрофические изменения в далеком будущем. Насекомое из рассказа Рэя Бредбери "И грянул гром" породило термин "эффект бабочки", широко известный в естественных науках. Сюжет писателя-фантаста стал предисловием к дискуссии экспертов о свойстве хаотических систем. В чем секреты и закономерности хаотичных явлений?
Теория КАМ для начинающих

Юлий Ильяшенко

Теория Колмогорова–Арнольда–Мозера отвечает на вопросы типа «Могут ли планеты упасть на Солнце? Если да, то с какой вероятностью? И через какое время?» Математическая постановка задачи: предположим, что массы столь малы, что их притяжением друг к другу можно пренебречь. Тогда траектории движения планет можно посчитать; это сделал ещё Ньютон. Если перейти к реальному случаю, когда взаимное притяжение планет влияет на их орбиты, получится малое возмущение интегрируемой, т.е. точно решаемой, системы. Исследование малых возмущений интегрируемых систем классической механики Пуанкаре считал основной задачей теории дифференциальных уравнений. В лекциях будет рассказано, на уровне, доступном старшим школьникам, об основных идеях теории КАМ. Мы не поднимемся до задачи n тел и классической механики, но обсудим диффеоморфизмы окружности и основной шаг индукционного процесса, предложенного Колмогоровым для задач небесной механики.
Динамические системы и бифуркации

Виктор Клепцын

Лекцию читает Клепцын Виктор Алексеевич. Летняя школа «Современная математика», г. Дубна. 29 июля 2017 г.
Порядок Шарковского

Дмитрий Аносов

Теорема Шарковского, доказанная в 1960-х гг., даёт ответ на вопрос: как для непрерывного отображения отрезка в себя связано наличие периодических точек различных периодов? Эта теорема была первым общим результатом о динамических системах, получающихся при итерировании отображений отрезка в себя. Хотя эта «одномерная динамика» кажется чем-то весьма специальным, подобные отображения возникают в некоторых вопросах естествознания и техники, а также играют важную вспомогательную роль при чисто теоретических исследованиях более сложных динамических систем.
Дифференциальные уравнения: не решаем, а рисуем

Дмитрий Аносов

Как геометрические соображения помогают понять свойства решений дифференциальных уравнений. С этим и связаны слова «то решаем, то рисуем» в названии лекции. Рассмотрено несколько физических примеров. На максимально упрощённом уровне рассказано о некоторых достижениях XX века, включая понимание механизма возникновения «хаоса» в поведении детерминированных объектов.

Далее >>>

∀ x, y, z

Бифуркации векторных полей на плоскости

Юлий Ильяшенко

Теги

Похожее