|
||
|
|
||
| Главная ≫ Инфотека ≫ Математика ≫ Видео ≫ Откуда берутся дифференциальные уравнения? // Владимир Побережный |
Откуда берутся дифференциальные уравнения?Владимир Побережный
Математик Владимир Побережный об экспонентах, источниках дифференциальных уравнений и векторном пространстве функций. Что такое дифференциальные уравнения? Это уравнения на какую-то неизвестную функцию или соотношения, которым должна удовлетворять эта функция и какие-то ее производные (если функция одной переменной, то просто производные, если функция многих переменных, то частные производные). Это обобщение наших обычных уравнений, например алгебраических. Мы сначала учим в школе линейные уравнения, их графики дают прямые на плоскости — бывают квадратичные, кубические и так далее. Это все алгебраические уравнения. Можно брать более сложные функции и более сложные уравнения, они дают какие-то более сложные графики. Объекты, которые они описывают, становятся более сложными, то есть линейные уравнения рисуют прямые, квадратичные — параболы, это все какие-то графики на плоскости или в более общем случае в большой размерности, какие-то поверхности в пространстве той или другой размерности. Поверхности или более сложные объекты, сделанные из поверхностей, — так называемые многообразия и так далее. Дифференциальные уравнения — это следующий шаг. Уравнения, которые мы сейчас перечислили, задают в пространстве какие-то точки, подмножества точек. Уравнение Возникает нужда в анализе: как это все устроено и почему мы вообще на это так смотрим? Такой взгляд действительно имеет вполне разумное содержание и смысл. Если мы рассматриваем линейные дифференциальные уравнения, то у нас возникает аналогия с обычными линейными уравнениями. Например, мы знаем, что линейные уравнения на плоскости — это прямая, в пространстве — какая-то гиперплоскость. То есть это какой-то плоский объект. Оказывается, что множество функций, удовлетворяющих линейному дифференциальному уравнению, устроено примерно так же, это в каком-то смысле плоскость, или прямая, или плоскость какой-то размерности, но уже в бесконечномерном пространстве функций (официально это называется векторным пространством). Множество решений линейного дифференциального уравнения образует векторное пространство во множестве всех функций. Откуда берутся дифференциальные уравнения? Конечно, основной поставщик дифференциальных уравнений (это мы тоже со школы знаем) — это физика и механика. Законы Ньютона, например, ускорение материальной точки Физика не единственный источник этих уравнений. Практически любая околоестественная наука является таким источником. Например, в химии происходят какие-то реакции, скорость реакций зависит от количества и пропорций компонентов. Два вещества смешиваются и как-то превращаются в третье с какой-то скоростью, пропорциональной чему-то. Это дифференциальные уравнения. В биологии тоже есть дифференциальные уравнения. Конечно, это не биология, а какой-то детский пример. Есть стандартная задача о размножении кроликов. У вас есть парочка кроликов, они с какой-то периодичностью рожают еще пару. У вас была пара кроликов, она родила — стало две пары. Каждая пара еще родила — стало четыре и так далее. Как устроен закон? Видно, что число растет очень быстро, это экспоненциальный рост. Здесь возникает очень интересный, но уже не совсем математический вопрос моделестроительства или адекватного построения модели. Вот мы хотим описать размножение кроликов. Если мы его описываем таким образом, то легко подсчитать, что если уравнение устроено так, что Эта модель, очевидно, не дает нам правильного приближения к жизни, на маленьких порядках немножко дает. С другой стороны, если бы все было в жизни устроено так, то кролики очень быстро бы захватили всю землю во много слоев, некуда было бы между ними наступить. Значит, надо как-то менять наше уравнение, подстраивать свойства модели под картинку, которую мы наблюдаем в жизни, и то, чему хотим быть адекватными. Например, чем больше кроликов, чем чаще они встречаются, тем больше вероятность, что у них возникнет какая-нибудь болезнь, которая будет заразной и будет передаваться от одного к другому, то есть надо вычесть какое-то слагаемое, пропорциональное частоте встреч. А как устроена частота встреч? Если кролики живут в каком-то лесу, каждый кролик занимает какое-то место, надо поделить площадь леса на площадь кроликов и так далее. Стандартное, вполне обозримое и разумное приближение. Например, добавление в модель волков. У нас есть волки, есть кролики. Кролики как-то размножаются, и волки как-то размножаются. Кроликам для размножения нужен только лес и другие кролики, а волкам нужно что-то есть, им нужны, собственно, кролики. Поэтому скорость роста кроликов ( Даже в классической механике мы знаем, что если бросаем камень, то вблизи Земли у него ускорение постоянно Можно строить разные модели, как-то их усложнять, исследовать те интересные вопросы, которые возникают почти в любом приложении, где как-то используется математика. Но математика ради математики здесь тоже имеется: дифференциальные уравнения — это очень большой отдельный разнообразный раздел со множеством вариаций. Он настолько большой, что даже практически не бывает конференций по дифференциальным уравнениям, потому что нужно более тонкое деление: качественная теория, асимптотические методы, интегрируемые системы, уравнения в частных производных и так далее. Это вполне большая развитая наука, продолжающая развиваться. Какие основные свойства и характеристики есть у дифференциальных уравнений? Что можно о них сказать? Во-первых, краеугольный камень для обыкновенных дифференциальных уравнений для одной переменной (неважно, вещественной или комплексной, комплексной даже лучше, как всегда это устроено в анализе) — это теорема существования и единственности. Если у вас есть дифференциальное уравнение с достаточно разумными коэффициентами (эти слова формализуются разными способами, например гладкие) и есть начальные данные, то всегда есть локальное решение. Например, вы знаете, что ваш камень как-то падает, знаете, где он был в начальный момент времени и какая у него была в начальный момент времени скорость. После этого у него траектория считается по крайней мере локально, в окрестности этого положения. Это очень сильный результат, опять-таки похожий на то, что у нас было с обычными уравнениями: мы знаем, что алгебраическое уравнение Это специфика обыкновенных уравнений от одной переменной, но при этом все-таки уравнение локально решается, то есть мы знаем, что решение существует, а вот найти его мы в явном виде можем не всегда. Мы можем использовать какие-то приближенные методы, как-то бороться, но гарантий, что мы напишем какое-то конечное выражение и оно будет решать наше уравнение, нет. Это была деятельность XIX века, когда люди активно занимались этой областью и изучали уравнения математической физики, из этого возникла целая наука про классические многочленные специальные функции Лежандра, Лагерра, Чебышева. Это была попытка как-то решать уравнения, которые возникали при тогдашнем развитии науки. В явном и конечном виде решения не выписывались, но это совершенно не мешало заниматься их анализом: исследовать свойства, связи, асимптотики. Современная наука занимается более сложными уравнениями. Сейчас, например, вполне популярная деятельность — исследование уравнений Пенлеве. Это такие новые специальные функции — решения уравнений Пенлеве, сейчас занимаются их исследованиями, асимптотикой, связями, геометрическим смыслом, содержанием и так далее по аналогии с физикой XIX века. Владимир Побережный, кандидат физико-математических наук, научный сотрудник международной лаборатории теории представлений и математической физики, доцент факультета математики НИУ ВШЭ
ПостНаука
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Математика ≫ Видео ≫ Откуда берутся дифференциальные уравнения? // Владимир Побережный |
|
[time: 12 ms; queries: 7]
19 Фев 2026 13:47:29 GMT+3 |


 Математик Владимир Побережный об уравнениях Шлезингера, интегрируемости и полиномиальных функциях.
Математик Владимир Побережный об уравнениях Шлезингера, интегрируемости и полиномиальных функциях. Математик Владимир Побережный о том, из чего состоят комплексные дифференциальные уравнения, об обратных задачах монодромии, понятии горизонтальности и топологическом характере препятствий.
Математик Владимир Побережный о том, из чего состоят комплексные дифференциальные уравнения, об обратных задачах монодромии, понятии горизонтальности и топологическом характере препятствий. Что такое монодромия? Как продолжаются функции в комплексном мире? Каково пространство решений в комплексной плоскости? Как построить линейное дифференциальное уравнение? На эти и другие вопросы ответил кандидат физико-математических наук Владимир Побережный.
Что такое монодромия? Как продолжаются функции в комплексном мире? Каково пространство решений в комплексной плоскости? Как построить линейное дифференциальное уравнение? На эти и другие вопросы ответил кандидат физико-математических наук Владимир Побережный.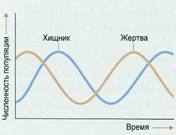 Иногда простая математическая модель хорошо описывает сложную биологическую систему. Примером этого служат долговременные отношения между видами хищника и жертвы в какой-либо экосистеме. Математические расчеты роста популяции отдельно взятого вида показывают, что пределы плотности популяции можно описать простыми уравнениями, которые на выходе дают характерную S-образную кривую. Это — кривая численности популяции, которая растет экспоненциально, пока она небольшая, а затем выравнивается, когда она достигает пределов возможности экосистемы поддерживать ее. Простое продолжение этой концепции позволяет нам понять экосистему, в которой взаимодействуют два вида — хищник и жертва.
Иногда простая математическая модель хорошо описывает сложную биологическую систему. Примером этого служат долговременные отношения между видами хищника и жертвы в какой-либо экосистеме. Математические расчеты роста популяции отдельно взятого вида показывают, что пределы плотности популяции можно описать простыми уравнениями, которые на выходе дают характерную S-образную кривую. Это — кривая численности популяции, которая растет экспоненциально, пока она небольшая, а затем выравнивается, когда она достигает пределов возможности экосистемы поддерживать ее. Простое продолжение этой концепции позволяет нам понять экосистему, в которой взаимодействуют два вида — хищник и жертва.