|
||
|
|
||
| Главная ≫ Инфотека ≫ Математика ≫ Видео ≫ О стратегии Петровского–Ландиса, амплитуде колебаний маятника и движении по предельному циклу // Илья Щуров |
О стратегии Петровского–Ландиса, амплитуде колебаний маятника и движении по предельному циклуИлья Щуров
Представим себе маятник – любимый предмет и объект исследования математиков, которые занимаются дифференциальными уравнениями. Математический маятник – это пример вечного движения. Если вы его отклонили на какое-то расстояние и отпустили, то дальше он будет колебаться с постоянной амплитудой, ровно с той амплитудой, на какое расстояние вы его отклонили. На самом деле, мы с вами знаем, что реальные маятники, которые нам приходится наблюдать в жизни, так себя не ведут. Из-за трения, если вы маятник отклоните и отпустите, он со временем покачается-покачается и остановится в том состоянии, что у математиков называется состоянием равновесия, то есть просто остановится. Тем не менее, мы знаем, что в часах, возможно, вы помните, что когда-то были часы с маятниками, а не только электронные, так вот в этих часах есть маятник, который тоже движется практически неограниченное время, по крайней мере, до тех пор, пока есть завод. Однако, у этого маятника есть такое свойство, что он движется все время с одинаковой амплитудой и одинаковой частотой, это как раз позволяет использовать маятник в качестве элемента часов. Давайте разберемся с тем, как такой маятник устроен с математической точки зрения. Представим себе заведенные часы, в которых маятник находится в положении равновесия. Возможно, вы знаете, что для того, чтобы такие часы запустить, маятник нужно немного качнуть в сторону. Но после того, как вы его качнете, вы можете его качнуть совсем слабенько или вы можете его качнуть достаточно сильно, вне зависимости от того, как сильно вы это сделаете, маятник достаточно быстро начнет колебаться с той частотой и с той амплитудой, с которой он должен это делать. Именно это позволяет ему аккуратно отмерять время. С точки зрения математика, маятник переходит в режим, который называется движением по предельному циклу. Что это означает? Почему предельному? Это как раз означает, что более-менее вне зависимости от начального положения, со временем поведение маятника приближается к какому-то конкретному периодическому движению. Слово «цикл» здесь указывает на тот факт, что движение именно периодическое. Что мы постоянно проходим одни и те же этапы. Вот маятник в часах является простейшей системой, которая обладает предельными циклами, конкретно одним предельным циклом, как раз тем самым, который нам нужен для того, чтобы часы правильно шли. Предельным циклом обладают всякие разные другие системы. В экономике известны деловые циклы, которые можно наблюдать, как циклическое изменение каких-то параметров, например, курсов или стоимости чего-нибудь. Предельные циклы также встречаются в экологии: известна система, которую называют моделью «хищник – жертва», когда у вас есть две популяции двух разных видов, один вид – хищники, другой вид – жертвы, например, можно думать о кроликах и лисах, и периодически один из этих видов начинает активно размножаться, например, кролики начинают активно размножаться, это увеличивает количество еды для лис. После этого лисы тоже начинают активно размножаться. Через какое-то время лис становится очень много, и они съедают всех кроликов. После этого кроликов становится мало, лисам становится нечего есть, лисы начинают тоже потихоньку вымирать, лис становится мало, у кроликов становится хорошая жизнь, кроликов становится много и так далее. Дальше этот процесс циклически повторяется. Это тоже пример циклического поведения, и в системах «хищник – жертва» могут тоже появляться такие предельные циклы. Сами по себе предельные циклы важны для изучения, потому что это именно то самое устоявшееся движение, к которому система может стремиться. Оказывается, что даже очень простые системы, которые можно описать какими-то простыми формулами, могут обладать несколькими предельными циклами. И задача по определению того, сколько именно предельных циклов есть в конкретной системе, оказывается очень сложной. В частности, для определенного класса систем, описываемых полиномиальными уравнениями. Полиномиальное уравнение – это уравнение, в котором нет правой части, это просто многочлен, выражение, содержащее переменные x, y, их степени, четыре арифметических действия. Даже вот такие простые системы, про то, сколько в них предельных циклов, мы зачастую не знаем. Этому посвящена 16-я проблема Гильберта, в которой спрашивается, что мы можем сказать о числе и расположении предельных циклов в дифференциальном уравнении на плоскости. В настоящий момент эта проблема является открытой, она не решена, люди не знают ответ на этот вопрос. Стоит отметить, что предельные циклы – это сравнительно простой тип поведения. Если у вас есть простая система, в частности система, у которой есть всего два параметра, например, у маятника есть два числа, которые описывают его состояние, это то, насколько сильно он отклонён от положения равновесия, и то с какой скоростью он движется в данный момент, вот для таких простых систем предельные циклы, наряду с положением равновесия, являются единственными вариантами для вообще предельного поведения. Это теорема Андронова – Понтрягина. Оказывается, что, если система становится чуть-чуть более сложной, например, для систем, у которых есть три параметра и больше, это уже не правда. Такие системы могут испытывать уже не только такие регулярные периодические колебания, но и гораздо более сложную динамику, которая не описывается предельными циклами, и которая относится к так называемой хаотической динамике. Но если мы говорим именно про плоскость, про системы с двумя параметрами, то там типичным образом могут возникать только предельные циклы и ничего сложнее, чем периодическое движение, не бывает. Однако даже в этом случае мы многого не знаем. В частности, мы не знаем ответа на 16-ю проблему Гильберта. 16-я проблема Гильберта, а точнее, ее вторая часть, которая как раз спрашивает про предельные циклы, оказалась довольно коварной. В середине 20-го века была предпринята очень мощная попытка ее решить: российские математики Петровский и Ландис представили свое решение, использующее методы комплексного анализа, и это решение некоторое время считалось правильным. Однако в нем была обнаружена ошибка, и эту ошибку не удалось исправить. И более того, по всей видимости ее невозможно исправить, и тот путь, который был предложен Петровским и Ландисом, оказался неправильным. Однако этот путь привел к открытию многих интересных явлений, связанных именно с дифференциальными уравнениями в комплексной области. Стратегия Петровского – Ландиса была связана с использованием комплексных чисел. Для большинства людей комплексные числа являются чем-то загадочным, в них используется число, которое называется квадратный корень из -1. Мы со школы знаем, что нельзя вычислить квадратный корень из отрицательного числа, нет такого числа, которое при возведении в квадрат дает -1. Однако математики придумали такие числа, и оказалось, что с этими числами многие проблемы решаются гораздо проще, чем без них. Петровский и Ландис пытались применить комплексные числа к 16-й проблеме Гильберта, но оказалось, что таким путем эта проблема не решается. 16-я проблема Гильберта до сих пор вызывает интерес со стороны математиков. Например, совсем недавно было опубликовано еще одно, по всей видимости, тоже неверное решение этой проблемы. Неизвестно, будет ли решена 16-я проблема Гильберта в ближайшее время. Возможно, что и не будет. Тем не менее, подходы и методы, которые были и, возможно, еще будут разработаны при попытках ее решения, внесут свой вклад в развитие математики и других наук. Илья Щуров
кандидат физико-математических наук, доцент кафедры высшей математики НИУ ВШЭ «ПостНаука»
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Математика ≫ Видео ≫ О стратегии Петровского–Ландиса, амплитуде колебаний маятника и движении по предельному циклу // Илья Щуров |
|
[time: 10 ms; queries: 7]
11 Мар 2026 21:19:48 GMT+3 |


 8 августа 1900 года Давид Гильберт сделал на Втором Математическом конгрессе доклад, представив слушателям ставший с тех пор знаменитым список проблем столетия. За прошедшие сто с лишним лет большая их часть была решена – и, что важнее, в ходе их решения появились новые сюжеты и новое понимание. Я собираюсь затронуть несколько из них и обсудить, в каком контексте они формулировались и куда продвинулось наше понимание за эти сто лет. Этот курс предполагается обзорным и адресованным школьникам (в частности, он не предполагает предварительных сведений).
8 августа 1900 года Давид Гильберт сделал на Втором Математическом конгрессе доклад, представив слушателям ставший с тех пор знаменитым список проблем столетия. За прошедшие сто с лишним лет большая их часть была решена – и, что важнее, в ходе их решения появились новые сюжеты и новое понимание. Я собираюсь затронуть несколько из них и обсудить, в каком контексте они формулировались и куда продвинулось наше понимание за эти сто лет. Этот курс предполагается обзорным и адресованным школьникам (в частности, он не предполагает предварительных сведений). Математик Владимир Побережный об уравнениях Шлезингера, интегрируемости и полиномиальных функциях.
Математик Владимир Побережный об уравнениях Шлезингера, интегрируемости и полиномиальных функциях. Математик Владимир Побережный о том, из чего состоят комплексные дифференциальные уравнения, об обратных задачах монодромии, понятии горизонтальности и топологическом характере препятствий.
Математик Владимир Побережный о том, из чего состоят комплексные дифференциальные уравнения, об обратных задачах монодромии, понятии горизонтальности и топологическом характере препятствий.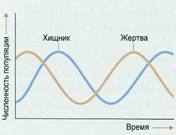 Иногда простая математическая модель хорошо описывает сложную биологическую систему. Примером этого служат долговременные отношения между видами хищника и жертвы в какой-либо экосистеме. Математические расчеты роста популяции отдельно взятого вида показывают, что пределы плотности популяции можно описать простыми уравнениями, которые на выходе дают характерную S-образную кривую. Это — кривая численности популяции, которая растет экспоненциально, пока она небольшая, а затем выравнивается, когда она достигает пределов возможности экосистемы поддерживать ее. Простое продолжение этой концепции позволяет нам понять экосистему, в которой взаимодействуют два вида — хищник и жертва.
Иногда простая математическая модель хорошо описывает сложную биологическую систему. Примером этого служат долговременные отношения между видами хищника и жертвы в какой-либо экосистеме. Математические расчеты роста популяции отдельно взятого вида показывают, что пределы плотности популяции можно описать простыми уравнениями, которые на выходе дают характерную S-образную кривую. Это — кривая численности популяции, которая растет экспоненциально, пока она небольшая, а затем выравнивается, когда она достигает пределов возможности экосистемы поддерживать ее. Простое продолжение этой концепции позволяет нам понять экосистему, в которой взаимодействуют два вида — хищник и жертва. Что такое монодромия? Как продолжаются функции в комплексном мире? Каково пространство решений в комплексной плоскости? Как построить линейное дифференциальное уравнение? На эти и другие вопросы ответил кандидат физико-математических наук Владимир Побережный.
Что такое монодромия? Как продолжаются функции в комплексном мире? Каково пространство решений в комплексной плоскости? Как построить линейное дифференциальное уравнение? На эти и другие вопросы ответил кандидат физико-математических наук Владимир Побережный.