4. Равномощность множеств / Парадоксы теории множеств

Иван Ященко

4. Равномощность множеств

Рассмотрим два множества $A$ и $B$ .

Отображение $f$ из $A$ в $B$ (обозначается $f\colon A \to B$ ) — это правило, которое каждому элементу множества $A$ ставит в соответствие элемент множества $B$ , причем ровно один. (При этом не запрещается двум элементам множества $A$ ставить в соответствие один и тот же элемент множества $B$ , рис. 1,а.)

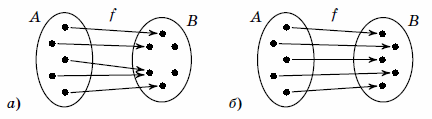
Рис. 1

Отображение $f$ называется взаимно однозначным, если каждый элемент множества $B$ поставлен в соответствие ровно одному элементу множества $A$ (рис. 1,б).

Множества $A$ и $B$ называются равномощными , если существует взаимно однозначное отображение $f\colon A \to B$ . Понимать это можно так: множества равномощны, если в них одинаковое количество элементов.

Например, множества $\{0,1,2\}$ и $\{$ лошадь, корова, телевизор $\}$ равномощны, а множества $\{0,1,2\}$ и $\{$ лошадь, корова $\}$ неравномощны^*7. А равномощны ли множества $\varnothing$ и $\{\varnothing\}$ ? Неравномощны: в множестве $\varnothing$ нет ни одного элемента, а в множестве $\{\varnothing\}$ есть один элемент — пустое множество (множество $\{\varnothing\}$ — это коробка, в которой лежит пустое множество, а пустое множество — это коробка, в которой ничего не лежит).

^*7 Телевизор был по делу…

Таблица 1.


$\varnothing$	$\{\varnothing\}$
$\{1\}$	$\{\varnothing, \{1\}\}$
$\{1,2\}$	$\{\varnothing, \{1\}, \{2\}, \{1,2\}\}$

Таблица 2.


	1	2	3	4	5	6	7	8
1	+	+	+	–	–	–	+	–
2	+	+	–	+	–	+	–	–
3	+	–	+	+	+	–	–	–

Множества $\mathbb{N}$ (множество всех натуральных чисел) и $\mathbb{N} \setminus \{1\}$ (множество всех натуральных чисел без единицы) равномощны: легко видеть, что отображение $f \colon \mathbb{N} \to \mathbb{N} \setminus \{1\}$ , $f \colon n \mapsto n + 1$ , является взаимно однозначным. Множества $\mathbb{N}$ и $\mathbb{Z}$ (множество всех целых чисел) также равномощны (достаточно рассмотреть отображение, которое переводит четные натуральные числа в целые неотрицательные, а нечетные — в отрицательные).

Обозначим через $P(A)$ множество всех подмножеств множества $A$ . Примеры $P(A)$ для некоторых множеств $A$ приведены в табл. 1. (Eстественно, подмножествами множества $A$ являются и пустое множество, и само множество $A$ .)

Подмножества множества $A = \{1,2,3\}$ не будем выписывать в строчку (так недолго запутаться), а перечислим при помощи таблицы: если элемент $i$ входит в подмножество с номером $j$ , то на пересечении $i$ -й строки и $j$ -го столбца ставится плюс, если не входит — минус (табл. 2). Например, первый столбец, в котором стоит три плюса, соответствует подмножеству $\{1,2,3\}$ .

Если составить такую же таблицу для множества из $n$ элементов, каждое подмножество будет определяться столбцом из $n$ символов (по числу элементов), и каждый символ можно выбрать двумя способами — либо " + ", либо " – ". Поэтому всего получится $2^n$ различных столбцов. Итак, если в множестве $A$ содержится $n$ элементов, то в множестве $P(A)$ содержится $2^n$ элементов — существенно больше, чем в множестве $A$ .

Но если подмножества конечного множества мы можем просто сосчитать, то как же быть с бесконечными? Например, подмножеств множества натуральных чисел бесконечно много, и самих натуральных чисел бесконечно много. Оказывается, что в множестве $P(\mathbb{N})$ "бесконечно больше" элементов, чем в множестве $\mathbb{N}$ .

Теорема. Каково бы ни было множество , множество его подмножеств неравномощно самому множеству .

Это один из важнейших фактов теории множеств.

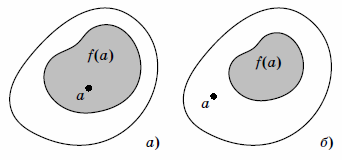
Рис. 2

Доказательство. Доказывать будем методом от противного^*8. Предположим, что $A$ равномощно $P(A)$ , т. е. существует взаимно однозначное отображение

$f\colon A \to P(A)$ ,

которое каждому элементу $a$ множества $A$ ставит в соответствие $f(a)$ — подмножество множества $A$ .

^*8 Вообще, все, что можно доказать, можно доказать от противного. Поэтому на всякий случай будем доказывать от противного.

Вспоминая рефлексивные прилагательные, которые сами обладают тем свойством, которое определяют, мы назовем элемент $a$ хорошим, если $a \in f(a)$ (рис. 2,а), и плохим, если $a \notin f(a)$ (рис. 2,б). Пусть $\Pi \subset A$ — множество всех плохих элементов (возможно, пустое). Поскольку отображение $f$ взаимно однозначно, существует элемент $x \in A$ , такой что $f(x) = \Pi$ . Вопрос: элемент $x$ — хороший или плохой? Предположим, элемент $x$ — хороший. Но тогда $x \in f(x)$ , а $f(x) = \Pi$ — множество плохих элементов, и значит, элемент $x$ — плохой. Противоречие. Если же элемент $x$ — плохой, то $x \notin f(x) = \Pi$ , а раз $x$ не принадлежит множеству плохих элементов, то $x$ — хороший. Снова противоречие. Получается, что элемент $x$ , с одной стороны, должен принадлежать $\Pi$ , а с другой стороны, не должен.

Но сейчас, в отличие от парадокса с прилагательным "нерефлексивный", у нас есть лазейка. Мы получили противоречие, предположив, что $A$ равномощно $P(A)$ . Значит, наше предположение неверно, т. е. $A$ и $P(A)$ неравномощны. Теорема доказана.

<<< |1|2|3|4|5|6|7|8|9|…|17| >>>

Содержание

Комментарии: 0

Похожее

Парадоксы теории множеств и их философская интерпретация

Парадоксы являются следствием дихотомии языка и мышления, выражением глубоких диалектических (теорема Гёделя позволила проявить диалектику в процессе познания) и гносеологических трудностей, связанных с понятиями предмета и предметной области в формальной логике, множества (класса) в логике и теории множеств, с употреблением принципа абстракции, позволяющего вводить в рассмотрение новые (абстрактные) объекты (бесконечность), со способами определения абстрактных объектов в науке и т. п. Поэтому не может быть дано универсального способа устранения всех парадоксов.
А нужен ли выбор? (альтернатива аксиоме выбора в теории множеств)

Михаил Раскин

Современная математика в качестве своего основания использует теорию множеств. Традиционно при анализе теоретико-множественных тонкостей используется аксиоматика Цермело-Френкеля с аксиомой выбора, обозначаемая ZFC. На аксиому выбора опираются доказательства наличия базиса в любом векторном пространстве и существования неизмеримого множества в математическом анализе. К сожалению, теория множеств обязана работать и со множествами, которые не описываются достаточно подробно и конкретно, чтобы мы могли себе их представить. В курсе будет рассмотрен один пример, к чему это приводит. Оказывается, ценой ослабления аксиомы выбора можно получить теорию множеств, в которой любая ограниченная функция на отрезке интегрируема по Лебегу. То, что используется аксиома выбора, в каком-то смысле, произошло исторически. Курс основан на статье Р.М. Соловэя о построении теории множеств, в которой все множества вещественных чисел измеримы.
«Мы не можем ждать милостей от природы», или применение метода вынуждения в построении моделей теории множеств

Михаил Раскин

В теории множеств есть несколько известных вопросов о том, следует ли из некоторых аксиом другая аксиома (или гипотеза; аксиома — это просто гипотеза, которой пользуется подавляющее большинство). Как и в других областях математики, недоказуемость можно продемонстрировать с помощью модели, в которой верны предположения, но не верна гипотеза. Для построения одного из самых известных таких примеров, модели теории множеств, в которой есть промежуточная мощность между мощностями натурального ряда и вещественной прямой, Коэн разработал метод вынуждения.
Теория множеств для начинающих

Виктор Викторов

Основные понятия, операции над множествами, тождества, свойства дополнения, правило Де Моргана, свойства симметрической разности; отображение (функция), факторотображение, отношение эквивалентности, парадокс брадобрея; упорядоченные множества, минимальный, наименьший, максимальный и наибольший элементы в упорядоченном множестве, мажоранта и миноранта; аксиома выбора, вполне упорядоченное множество.
Числа и многочлены

Проскуряков И. В.

Целью этой книги является строгое определение чисел, многочленов и алгебраических дробей и обоснование их свойств, уже известных из школы, а не ознакомление читателя с новыми свойствами. Поэтому читатель не найдет здесь новых для него фактов (за исключением, быть может, некоторых свойств, действительных и комплексных чисел), но узнает, как доказываются вещи, хорошо ему известные, начиная с «дважды два — четыре» и кончая правилами действий с многочленами и алгебраическими дробями. Зато читатель познакомится с рядом общих понятий, играющих в алгебре основную роль.
Десять великих идей науки. Как устроен наш мир

Питер Эткинз

Эта книга предназначена для широкого круга читателей, желающих узнать больше об окружающем нас мире и о самих себе. Автор, известный ученый и популяризатор науки, с необычайной ясностью и глубиной объясняет устройство Вселенной, тайны квантового мира и генетики, эволюцию жизни и показывает важность математики для познания всей природы и человеческого разума в частности.
Алиса в Стране Смекалки

Смаллиан Рэймонд

В книге «Алиса в Стране Смекалки» кэрролловская Алиса из Страны Чудес и ее друзья раскрывают перед читателем нескончаемую вереницу задач-головоломок. Они доставят удовольствие всем любителям занимательной математики, а почитателям творчества Льюиса Кэрролла в особенности.
Математическое понимание природы

Владимир Арнольд

Сборник «Задачи для детей от 5 до 15 лет» вызвал много отзывов. И дети, и взрослые читатели часто сожалели, что там были только математические задачи, — ведь и все естествознание заслуживает столь же активного, творческого к себе отношения. Теперь я отвечаю на эти пожелания — следуя скорее Яну Амосу Каменскому, чем современным педагогам, то есть всегда стремясь быть понятным читателю, не имеющему предварительных знаний (но столь же любознательному, как большинство подростков).
Невероятные числа профессора Стюарта

Отрывок из книги «Невероятные числа профессора Стюарта» заслуженного профессора математики Уорикского университета, известного популяризатора науки Иэна Стюарта, посвященной роли чисел в истории человечества и актуальности их изучения в наше время.
Математические чудеса и тайны

Гарднер Мартин

Математические фокусы - очень своеобразная форма демонстрации математических закономерностей. Этой скрытой математичностью и интересна книга Мартина Гарднера - сам автор не формулирует на языке математики закономерностей, лежащих в основе его экспериментов, ограничиваясь описанием действий показывающего, явных и тайных. Но читателю, знакомому с элементами школьной алгебры и геометрии, несомненно, доставит удовольствие самому восстановить по объяснениям автора соответствующую алгебраическую или геометрическую идею. Книга будет интересна многим читателям: юным участникам математических кружков, взрослым любителям математики, а может быть, тот или иной из описанных здесь экспериментов пробудит улыбку и у серьезного ученого в краткий момент отдыха от большой работы.

Далее >>>

∀ x, y, z

4. Равномощность множеств / Парадоксы теории множеств

Иван Ященко

4. Равномощность множеств

Теги

Похожее