Пифагорейцы утверждали, что числа правят миром, а Александр Суворов называл математику «гимнастикой ума». Сейчас интерес к этой науке постепенно возрождается. T&P поговорили с пятью известными математиками, чтобы разобраться, зачем формулы и уравнения нужны в повседневной жизни, почему математика — интересный и творческий предмет, и что теряет гуманитарий, отмахиваясь от этой науки.

После монгольского нашествия (XIII век) научное развитие России затормозилось. Конфликты с католическими соседями вызвали изоляцию русских княжеств от западной культуры, а связь с единоверной Византией была затруднена. Грамотность даже среди духовенства, где она требовалась по уставу, была удручающе низкой. Все научные книги, изданные на Западе (где как раз с XII века начался научный подъём), были запрещены. Сохранилось поучение тех лет, гласящее: «Богомерзостен перед Богом всякий, кто любит геометрию; а се душевные грехи учиться астрономии и эллинским книгам; по своему разуму верующий легко впадает в различные заблуждения»

Мир вокруг нас полон математических объектов — чисел, функций, геометрических фигур. Вся современная цивилизация есть продукт развития технологий, немыслимых без точных математических расчетов. Но математика не просто помогает нам совладать с миром. Она проникает в самую суть этого мира. Это удивительное обстоятельство впервые было отмечено Пифагором, одним из наиболее влиятельных мыслителей в истории человечества. Своим девизом «Все есть число» он на тысячи лет предвосхитил как будущую роль математики, так и представления о природе ее объектов. Способом своего существования они кардинально отличаются от предметов, знакомых нам посредством органов чувств. Как многие считают, эта особенность делает математику главным источником веры в существование мира, «населенного» вневременными и сверхчувственными объектами.

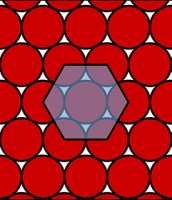
Математики установили, что максимально плотная упаковка любых других центрально-симметричных выпуклых тел не может оставлять больше свободного пространства, чем упаковка шаров. Хотя это утверждение интуитивно очевидно, верным оно оказывается только в трёх измерениях.

Арифметико-геометрическая прогрессия — последовательность чисел u_{n}, задаваемая рекуррентным соотношеним: u_{1}=a_{1}, u_{n+1}=qu_{n}+d, где q и d — постоянные числа. Частными случаями арифметико-геометрической прогрессии являются арифметическая прогрессия (при q=1) и геометрическая прогрессия (при d=0).

Нам так и не удалось найти первоисточник этого широко распространённого поверья: ни один лист бумаги нельзя сложить вдвое больше семи (по некоторым данным — восьми) раз. Между тем текущий рекорд складывания – 12 раз. И что удивительнее, принадлежит он девушке, математически обосновавшей эту «загадку бумажного листа».

Каустики — это вездесущие оптические поверхности и кривые, возникающие при отражении и преломлении света. Каустики можно описать как линии или поверхности, вдоль которых концентрируются световые лучи.

Ключевая проблема в теории суперструн — выяснить, конечно или бесконечно число «вселенных», которые она может описать. В недавно вышедшей статье делается попытка доказать, что это число конечно.

Берём любое натуральное число n. Если оно чётное, то делим его на 2, а если нечётное, то умножаем на 3 и прибавляем 1 (получаем 3n+1). Над полученным числом выполняем те же самые действия, и так далее. Гипотеза Коллатца заключается в том, что какое бы начальное число мы ни взяли, рано или поздно мы получим единицу.

Действительно ли в математике всё определяется и доказывается? Можно ли определить понятие натурального числа? Можно ли определить Натуральный Ряд (с прописной буквы)? Можно ли аксиоматически определить понятие натурального ряда (со строчной буквы)? Можно ли доказать, что Великую теорему Ферма нельзя ни доказать, ни опровергнуть? Что такое доказательство? Можно ли математику сделать понятной?

Парадокс Монти Холла — одна из известных задач теории вероятностей, решение которой, на первый взгляд, противоречит здравому смыслу.

На протяжении большей части XX столетия в «чистой» математике царило замечательное единодушие относительно того, как нужно представлять результаты. Весь предмет сводился к комплексу теорем, каждая из которых, в конечном счете, выводилась из фиксированного набора аксиом путем так называемого строгого логического доказательства. В отдельных разделах математики, таких, например, как арифметика Пеано, справедливость аксиоматики выглядела самоочевидной, однако во многих случаях аксиомы попросту очерчивали рассматриваемую область вопросов. Для математиков, если только они не выходили за рамки математики, выступая в роли философов-любителей, принципиального различия между изобретением и открытием новых концепций не было.

На протяжении тысячелетий считалось, что математика открывает неопровержимые вечные истины. Множество замечательных математических утверждений, таких как теоремы евклидовой геометрии, верны в наши дни, точно так же, как и две тысячи лет назад. И тем не менее в XX веке математика пережила три глубоких кризиса, которые существенно меняют статус математического исследования.

В школе мы несколько лет подряд прилежно изучаем геометрию. Но не зря ли мы тратим время? Чем может помочь геометрия в жизни? Измерить расстояние от точки до точки, вычислить площадь или объём предмета и только? Нет, конечно. Законы геометрии применимы буквально на каждом шагу. Просто нужно знать, как ими воспользоваться.

Из идей сложности и случайности, впервые высказанных Готфридом Лейбницем в его «Рассуждении о метафизике» (1686), и их подтверждения в современной теории информации следует, что невозможно создать «самую общую теорию всего» в математике.

Стенограмма и видеозапись лекции доктора физико-математических наук, ведущего научного сотрудника Математического института имени Стеклова, ведущего научного сотрудника ИППИ РАН, профессора факультета математики Высшей школы экономики, директора исследований Национального центра научных исследований во Франции (CNRS) Александра Буфетова, прочитанной в рамках цикла «Публичные лекции "Полит.ру"» 6 февраля 2014 г.

Со времён изобретения Джеймсом Уаттом паровой машины стояла задача построения шарнирного механизма, переводящего движение по окружности в прямолинейное движение. Великий русский математик Пафнутий Львович Чебышев не смог точно решить изначальную задачу, однако, исследуя её, разработал теорию приближения функций и теорию синтеза механизмов. Используя последнюю, он подобрал размеры лямбда-механизма так, чтобы…

В математике давно известны функции с удивительным свойством: их график всюду плотен на плоскости. Такие функции часто называют «странными», «экзотическими», «дикими» и т. п. Они хорошо известны специалистам-математикам, но почти не знакомы «широкой публике», например школьникам. Ведь те построения, которые приводятся в литературе, обычно громоздки и требуют серьезной математической подготовки. Но автору удалось найти совершенно элементарное доказательство существования таких функций.

Представьте себе электрические и магнитные поля. Что вы для этого сделали? Знаете ли вы, как это нужно сделать? И как я сам представляю себе электрическое и магнитное поля? Что я на самом деле при этом вижу? Что требуется от научного воображения? Отличается ли оно чем-то от попытки представить себе комнату, полную невидимых ангелов? Нет, это не похоже на такую попытку.

Провернувшись несколько кругов с колесом, куда полетит камень, когда выскочит из протектора? Против направления движения мотоцикла или по направлению? Как известно, свободное движение тела начинается по касательной к той траектории, по которой оно двигалось. Касательная к циклоиде всегда направлена по направлению движения и проходит через верхнюю точку производящей окружности. По направлению движения полетит и наш камушек. Помните, как Вы катались в детстве по лужам на велосипеде без заднего крыла? Мокрая полоска на вашей спине является житейским подтверждением только что полученного результата.