|
||
|
|
||
| Главная ≫ Инфотека ≫ Математика ≫ Математика случая. История теории вероятностей // Александр Буфетов |
Математика случая. История теории вероятностейАлександр Буфетов
Лекция доктора физико-математических наук, ведущего научного сотрудника Математического института имени Стеклова, ведущего научного сотрудника ИППИ РАН, профессора факультета математики Высшей школы экономики, директора исследований Национального центра научных исследований во Франции (CNRS) Александра Буфетова, прочитанная в рамках цикла «Публичные лекции "Полит.ру"» 6 февраля 2014 г. Стенограмма лекцииБорис Долгин: Добрый вечер, уважаемые коллеги. Мы начинаем очередную лекцию из цикла «Публичные лекции «Полит.ру»». У нас получился такой подцикл лекций с Институтом проблем передачи информации. Наш сегодняшний гость – Александр Игоревич Буфетов, доктор физ.-мат. наук, ведущий научный сотрудник ИППИ РАН имени Харкевича, профессор факультета математики НИУ-ВШЭ, директор исследований Национального центра научных исследований во Франции (CNRS). Сегодня мы говорим о теории вероятностей, тема звучит: «Математика случая. История теория вероятностей».
Надо сказать, что это та часть математики, которая, хотя известна и не всем гуманитариям, но может оказаться одной из самых полезных для них. Если они только возьмутся в ней разобраться. Регламент традиционный: сначала лекционная часть, затем можно будет задавать вопросы, высказывать комментарии, но только в микрофон, представляясь, для стенограммы, не таясь от читателей. Пожалуйста, Александр. Александр Буфетов: Спасибо большое. Для меня большая честь выступать в рамках проекта «Полит.ру». Мы начнем рассмотрение математики случая, и даже, в первую очередь, того, как исследование случая стало математикой. Как мы увидим, это очень долгий, очень драматичный процесс, занявший много веков. И, собственно, то, что теория вероятностей стало областью математики – это событие XX века. Как раз об истории этого события я и хочу поговорить. Мы сначала обратимся к самому понятию случая. Кстати, прежде чем приступать к делу, скажу, что я старался, чтобы лекция была доступной совсем не математикам. Но очень может быть, что я где-то ошибся в своих предположениях, тогда, пожалуйста, спрашивайте. Итак, мы обратимся сперва к философской категории случая. Существует ли случай, что такое случайное – этот вопрос обсуждали греки. Я буду держаться в рамках европейской традиции. Есть интереснейшие исследования про, скажем, индийских или среднеазиатских философов, но от этого я полностью, по незнанию своему, уйду. Итак, мы обратимся к Левкиппу, учителю Демокрита, который пишет совершенно недвусмысленно, что случая не бывает, а все происходит по необходимости. Это стандартное выражение идеи детерминизма, с которым мы столкнемся еще много раз, и вплоть до XX века.
Итак, Левкипп говорит, что случая нет. Мы, к сожалению, не располагаем точными цитатами, которые позволили бы сказать, что по этому поводу думает Демокрит. А позднейшие комментаторы утверждают вещи прямо противоположные. Одни говорят, что Демокрит считал, что случай как раз есть, что явления природы подразделяются на случайные и необходимые, другие утверждают, что Демокрит считал, что случая никакого нет. Ясности в комментариях на этот счет тоже нет. Поэтому мы сразу обратимся к Аристотелю, который утверждает в «Метафизике», что случай как раз есть. И вот он пишет совершенно четко: возможно, что для какого-то события нет определенной причины, и это – случайность. Вот это самое греческое слово Τύχη «Тюхэ», обозначающее случай. Именно неопределенная причина, тут дословный перевод греческого слова Аoriston. Аристотель приводит характерный пример: если путешественник ехал не в Эгину, но в результате морской бури или из-за того, что был пойман пиратами, оказался в Эгине, то вот это как раз проявление случая. Кроме того, Аристотель подробно пишет об этом и в своей «Физике», и, разбирая различные причины явлений, он пишет совершенно ясно, что случай Τύχη «Тюхэ» нужно воспринимать среди причин. Я привожу здесь краткую цитату, но в «Физике Аристотеля» этот вопрос разбирается достаточно подробно. Для Аристотеля случайное вполне существует. И никого из нас не удивит, что вся эта тематика изначально увязывается со свободой воли человека. Здесь мы обратимся к Эпикуру, который пишет, вступая в противоречие с Левкиппом, что некоторые вещи происходят по необходимости (некоторые, но не все), а другие, напротив, волей случая. И наконец, еще другие – по нашей собственной воле. И, – пишет Эпикур, – разумеется, если все происходит по необходимости, то и нет свободы воли (в несколько вольном пересказе). Так что сразу греки смотрят на все те вопросы, над которыми и философы науки XX века, скажем, Пуанкаре, тоже ломали голову. И мы несколько спекулятивно можем спросить себя, а почему греки не занимались математической теорией вероятностей? Казалось бы, чтобы выписать все комбинации при бросании трех костей (а в кости греки даже очень играли, и об азартных играх мы будем говорить подробнее в течение сегодняшней лекции), потому что в игре всегда использовалось несколько костей, казалось бы, не нужно ничего особенного. Но греки совершенно этого не сделали. И тут можно спекулировать, почему не сделали. Я от таких спекуляций воздержусь, а замечу только, что правильно такие комбинации были выписаны очень-очень поздно, и было много неправильных попыток и неправильных ответов, как мы увидим в течение лекции. Расставаясь с классиками, я позволю себе небольшое отступление, и приведу любопытную цитату из Лукреция Кара, которая показывает, что броуновское движение совершенно напрасно называется броуновским движением, а надо было бы называть его движением Лукреция: Кроме того, обратить тебе надо вниманье На суматоху в телах, мелькающих в солнечном свете, Что из нее познаешь ты материи также движенье, Происходящее в ней потаенно и скрыто от взора. Ибо увидишь ты там, как много пылинок меняют Путь свой от скрытых толчков, и опять отлетают обратно, Всюду туда и сюда разбегаясь во всех направленьях. Знай же, идет от начал всеобщее это блужданье. Первоначала вещей сначала движутся сами, Следом за ними тела из малейшего их сочетанья, Близки, как бы сказать, по силам к началам первичным, Скрыто от них получают толчки, начинают стремиться Сами к движенью затем понуждая тела покрупнее. Так, исходя от начал, движение мало-помалу Наших касается чувств, и становится видимым также Нам и в пылинках оно, что движутся в солнечном свете, Хоть незаметны толчки, от которых оно происходит. Ну, просто, ни дать, ни взять, цитата из современного учебника физики, описывающего Броуновское движение. Мне нужно сказать о моих источниках, я активно черпал из двух книг Л.Е. Майстрова «Развитие теории вероятностей» и «Исторический очерк по теории вероятностей», это были основные мои источники для этой лекции, но, впрочем, были некоторые другие второстепенные, о которых я скажу позже. Мы расстаемся с греками, делаем большой скачок и обращаемся сразу к Rinascimento, к Итальянскому Возрождению, и наш следующий герой – это Лука Пачоли, мы видим его портрет из галереи Каподимонте в Неаполе.
Лука Пачоли написал фундаментальный труд, имевший огромное влияние на современников, и мы это увидим и подробнее, об арифметике, о пропорциях, о пропорциональности. В частности, он приводит такую задачу в главе «Необычные задачи». Я сейчас ее процитирую полностью, и мы, кстати сказать, попробуем с этим разобраться. Я приведу сперва задачу Пачоли, а потом мы рассмотрим задачу все-таки немножко более простую. Итак, Пачоли пишет: компания играет в мяч до шестидесяти очков и делает ставку в двадцать два дуката, имеется ввиду – до того, как будет забито шестьдесят мячей. По непонятным обстоятельствам, игра не может быть закончена, ну мало ли, дождь пошел, или обедать позвали. Причем одна сторона имеет пятьдесят мячей, а другая тридцать. В какой пропорции следует разделить ставку? Давайте возьмем какой-нибудь более простой пример, пример, который потом будут рассматривать Паскаль и Ферма. Два игрока поставили на кон по десять золотых дукатов. Игра идет до трех побед. Игра, скажем, в кости или в орлянку, выбрасывается орел или решетка, и соответственно, один из игроков побеждает в одном случае, другой – в другом. Игра идет до трех побед, победитель забирает все. Игра по какой-то причине остановилась, если у одного игрока две победы, а у другого одна. Тут есть еще одно решение – чтобы игроки сыграли еще один кон, это подсказка, тем не менее, вот мой вопрос к публике, при этом я прошу профессиональных математиков воздержаться от отвечания. Вопрос к публике: в каком соотношении следует разделить ставки? Игра идет до трех побед, у одного игрока две победы, ясно, что его шансы больше. У другого игрока одна победа, его шансы меньше, но в каком соотношении следует разделить ставки, какие будут предложения? Я сразу скажу, что предлагает по этому поводу Пачоли, он предлагает в задаче про мячи, но в сущности, это задача того же свойства, разделить ставки в соотношении по числу побед. То есть в случае, у него там было пятьдесят и тридцать мячей, в этом случае он предлагает два к одному. Какие будут другие предложения? Зритель: Предложение поровну разделить, потому что они играют примерно одинаково. Александр Буфетов: Да, речь идет о том, разумеется, что в этом случае, что просто бросаются кости, и соответственно, одинаковы шансы выпадения и того, и другого. Зритель: Мы вообще не можем разделить, пока не закончена изначальная игра. Александр Буфетов: Нет, ну и все же. Задача практическая. Ситуация практическая, что делать? Вопрос же совершенно практический: вот они играют, им надо разойтись. Как-то им всё равно надо разойтись? Может быть, я непонятно объяснил. Еще раз: бросается монетка, если она выпадает орлом, то победа засчитывает первому игроку, если она выпадает решеткой, то победа засчитывается второму игроку, больше никаких ходов нет. То есть бросается монетка, предполагается, что она честная, так что шансы выпадения одинаковые. До трех орлов. Вот выпало три орла прежде решетки, и соответственно все себе забирает первый игрок. Если выпало три решетки, прежде, чем три орла, все себе забирает второй игрок. А вот тут получилось, что выпало два орла и одна решетка, и там, надо спешить на лекцию в «Полит.ру», и продолжать игру нет возможности. Зритель: Нужно два разделить на три, получается…. Александр Буфетов: Нет, ответ, ответ, в каком соотношении? Как разделить? Зритель: Один к трем. Александр Буфетов: Один к трем, почему? Зритель: Три к одному. Александр Буфетов: Значит, зал «Полит.ру» предлагает три к одному. Так, как бы нам с этим разобраться. Зритель: Поровну. Александр Буфетов: Поровну, простите, да, поровну. Вы совершенно правы, да, поровну. Зритель: А можно все разделить в одну сторону? Александр Буфетов: Все отдать первому игроку? Зритель: Просто у него шансов больше. Александр Буфетов: Все отдать первому игроку, можно. Зритель: Еще тот, кто играет 2:0, тот получает приз. Александр Буфетов: Тут давайте не будем уклоняться от условий задачи. Зритель: Тут два варианта есть: или выиграет один, или будет ничья. И тогда будет равный счет. Александр Буфетов: Совершенно справедливо. В том, что вы сказали, в этом и состоит решение Паскаля. Его решение состоит в следующем: игра в любом случае закончится через два кона. Если в следующем коне выпадет орел, то первый игрок уже выиграл. Если же выпадет решетка, то получается «вилка», то есть во втором туре шансы одинаковы. Поэтому Паскаль излагает решение примерно так: вот из этих двадцати дукатов, десять дукатов первый игрок забирает в любом случае, как бы ни повернулось. А дальше есть уже неопределенность. И соответственно в соотношении три к одному предлагается разделить, потому что такова вероятность. Можно еще так это увидеть, какие есть варианты: представьте себе два кона, если выиграл первый, то второй можно уже не рассматривать, то есть эти варианты идут в зачет первому игроку. А, соответственно, если в первом случае выиграл второй, то в этом случае есть два варианта. В одном случае опять выигрывает первый, а в этом случае, и только в этом случае выигрывает второй, соответственно у первого игрока есть три шанса, а у второго только один, и отсюда получается решение три к одному. Я хочу заметить сейчас только то, что на это рассуждение, на вот такое решение потребовалось очень много лет. Переписка Паскаля и Ферма – это середина XVII века, а задача, как видите, встречается уже в работе Пачоли 1492-го года. То есть на то, чтобы правильно решить эту задачу, потребовалось несколько веков. Так или иначе, замечу, что критику предложения Пачоли делить пропорционально числу побед дал итальянский математик Тарталья. Он сказал: пусть второй игрок вообще ничего не выиграл, то есть два раза выиграл первый игрок, и ни одного раза не выиграл второй. Что ж, ему вообще ничего не нужно дать? Но ведь какой-то шанс на победу у него все-таки есть, и это было бы нечестно. Так или иначе, то, что решение Пачоли неверное, это Тарталья понял. А вот дать правильное решение у Тартальи не получилось, он дает ответ неправильный. Мы видим ситуацию в Италии эпохи Возрождения - задачи ставятся, а ответов на них нет. И более того, вот этот самый подсчет комбинаций оказывается чрезвычайно затруднен, и это можно увидеть из следующего фрагмента, несколько предшествующего работе Пачоли. Значит, еще раз, мой тезис состоит в том, что правильно выписать комбинации, возникающие, скажем, при бросании костей, оказалось сложной задачей. И мы, чтобы проиллюстрировать этот тезис, уходим немножечко назад, мы обращаемся к Данте, который описывает игру в кости в шестой главе «Чистилища»: Когда кончается игра в три кости, Перевод Лозинского. Для нас тут важно не только то, что описывается игра в кости, а то, что Данте комментировался. Точно также, как греки комментировали Гомера. Даже сейчас 80% папирусов, которые мы находим, это папирусы, содержащие тексты Гомера. Точно также в Италии Возрождения комментировали Данте. Было великое множество комментариев, но нас интересуют комментарии венецианца Бенедетто д'Имола, который как раз объясняет для читателя, как проходит игра в три кости и, в частности, выписывает всевозможные комбинации. Только выписывает он их неправильно. Он считает, что за одну комбинацию, скажем, может на одной кости выпасть единичка, на другой шестерка, а может на другой кости выпасть шестерка, а может единичка. Вот эту комбинацию он считает за одну, то есть допускает ошибку при выписывании комбинаций. Говорю я это только для того, чтобы подчеркнуть, насколько сложна эта задача комбинаторного анализа. Первый математик, который переводит эту дискуссию на совершенно новый уровень, это Джеролано Кардано, который пишет замечательный труд «Об игре случая» или «О случайных играх». Речь, разумеется, идет об азартных играх. Азартные игры известны с глубокой древности. Играли в древности костями, костями животных, использовалась кость, которая называется «астрагал». Астрагал – это кость парнокопытного животного, находящаяся как раз над копытом, она замечательна тем, что у нее есть несколько граней, ее удобно держать в руке, она сама полируется от того, что ее держишь.
Астрагалы находят в очень древних захоронениях, гораздо раньше греков, но мы не имеем точных сведений, что они использовались для игры. Это остается только гипотезой. Напротив того, Геродот пишет, что игру в кости придумали лидийцы, потому что в Лидии был голод, и так как есть было нечего, то жители развлекали себя игрой в кости. Так игра в кости и возникла. Другая версия, что игра в кости была придумана во время троянской войны, потому что опять-таки осада Трои затянулась, делать было нечего, и играли в кости. Так или иначе, игра в кости, конечно, была чрезвычайно популярна в Греции, а также в Риме. Император Август был страстным игроком в кости, что следует из переписки. Светоний пишет, что император Клавдий даже написал книгу об игре в кости (книга, к сожалению, до нас не дошла). Во всяком случае, игра в кости была чрезвычайно популярной, и опытный греческий игрок хорошо представлял себе варианты выпадения различных комбинаций. Точно также, как сегодня опытный игрок в покер примерно представляет, даже если он никогда не занимался теорией вероятностей, какие варианты более-менее вероятны. Точно также. Интересно здесь то, что приз, который назначался за выпадение той или иной комбинации, совсем не точно связан с вероятностью. Например, одной из самых прибыльных комбинаций была такая, в которой на четырех разных костях выпадали четыре разных символа. Это называлось «Венера». Но «Венера» - это не самая маловероятная комбинация. Надо заметить, что астрагал не совсем симметричен, не совсем кубик, поэтому разные грани выпадают с разной вероятностью. Это видно, если взять в руки астрагал. И, кстати, Кардано этого не знает, откуда историки делают вывод, что он, наверное, с астрагалами не играл. Так или иначе, в греческой игре призы не были увязаны с вероятностными соображениями. Сочинений о том, как выиграть в кости, была тьма, хотя мы обычно вспоминаем Достоевского. Это было очень популярное занятие, и вот мы обращаемся к тому сочинению, которое представляет собой очень важный этап в развитии теории вероятностей. Сперва я хочу совсем коротко поговорить о Кардано, и я попробую (тоже попросив профессиональных математиков воздержаться от комментариев), попробую спросить у публики, что сделал Кардано в математике? Помимо азартных игр. Какие достижения Кардано в математике? Зритель: Уравнения Кардано. Александр Буфетов: Совершенно верно, уравнения. Уравнения, с которыми связана драматичная история, о которой как раз я говорить не буду. О самом же Кардано скажу буквально несколько слов. Отец Кардано был знакомым Леонардо да Винчи, он был врачом и адвокатом, а кроме того, в свободное от работы время, читал лекции в университете итальянского города Павия, основанном Карлом Великим. Мальчик Джероламо был незаконнорожденным. Замечу, немного забегая вперед, что Колмогоров тоже был незаконнорожденным. Но в Италии конца XVI века, в отличие от Российской Империи, как показывает пример Фета, всю жизнь страдавшего от своего незаконного рождения, в Италии незаконное рождение не ставило серьезных препятствий в развитии карьеры. Он учится в Университете Павии, потом в Милане и Падуе, становится доктором медицины, женится, и начинает работать как медик (Кардано, между прочим, был известнейший медик). Ему в ученики каким-то чудеснейшим образом попадает Людовико Феррари, который решил как раз уравнение четвертой степени. Формула решения называется «Формула Феррари». Но решил он это уравнение, находясь как раз в доме Кардано. Начинает писать о математике только в 1539 году, я не взял годы жизни на слайд, я напишу их здесь. Входит в острый конфликт с Николо Тарталья по поводу решения уравнений 3-ей степени, публикует свою книгу «Книга о великом искусстве» - учебник алгебры, оказавшийся одним из самых влиятельных трудов по алгебре на много столетий вперед. Та самая книга, где он решил уравнение третьей степени, украв, как считает Тарталья, у него. Феррари, например, защищает своего учителя. Любовь и преданность к своему учителю очень видна из переписки Феррари и из переписки с Тартальей.
В 1552-м году Кардано лечит архиепископа шотландского. Его из Италии, из Милана, через всю Европу везут, чтобы он вылечил шотландского архиепископа. Лечение оказалось удачным. Интересно, что рекомендации Кардано сохранились и сводятся к тому, чтобы нужно вести здоровый образ жизни. Кроме того, Кардано советует архиепископу, который страдал от астмы, не спать на перьях, а спать на шелке. То есть некое понятие об аллергиях у Кардано было. Кардано – поляризующая фигура в истории науки. Я посмотрел несколько историй его биографий, и сразу видно, что оценка, которую биограф дает Кардано, больше говорит о том, что сам биограф думает о человеке-Кардано. Оценки полярные, даже и в сочинениях XX века. Я процитирую Лейбница: «Кардано был великий человек со всеми своими недостатками. Если бы этих недостатков у него не было, был бы человек несравненный». Так или иначе, тут на Кардано обрушивается удар судьбы. Его старший сын неудачно женился, да так неудачно, что, в конце концов, отравил свою жену мышьяком, и чуть ли все семейство не отравил. Преступление было раскрыто, и мальчика казнили. Кардано, чрезвычайно влиятельный врач с европейской славой, которого в Лондоне принимал король, напряг все каналы своего влияния, чтобы вытащить сына из тюрьмы, но ничего не помогло, его судили и пытали, отрубили левую руку, а потом казнили. И это был страшный удар для Кардано. В 1562 году он берет отставку в Университете Павии и перебирается в Болонью к Феррари. Но Феррари тут отравила жена, и в Болонье обстоятельства для Кардано складываются не очень благоприятно. По некоторым сведениям то, что он очень любил принимать мальчиков у себя в доме, не нравилось властям. Впрочем, в Италии к этому относились совершенно спокойно, и возможно, причины были совершенно другие. Так или иначе, в 1570 году он попадает под домашний арест, и обвиняется в ереси. Дело в том, что он составил гороскоп Иисуса Христа. А это, конечно, ересь - составлять гороскоп Иисуса Христа. Составил он его за 30 лет до того, как его арестовали. Но у инквизиции око недреманное, и Кардано отправляется в тюрьму. Из тюрьмы ему, впрочем, удается выйти, и с другим своим учеником, Рудольфо Сильвестро, Кардано отправляется в Россию. Кардано был счастлив в учениках. Он в людях возбуждал противоположные чувства. Из его современников некоторые его ненавидели, другие любили. Он воспитал гениального математика Людовико Феррари, и он воспитал замечательного врача Рудольфо Сильвестро, с которым он едет в Рим, где на удивление, несмотря на обвинения в ереси, к Кардано относятся очень тепло, и он под присмотром Сильвестро кончает свои дни. 20-го сентября 1576 года он умирает в Риме. Кардано – автор 131 книги, 111 манускриптов, которые будут изданы собранием сочинений в 10 фолиантов через 100 лет в Леоне. И 170 манускриптов, как пишет сам Кардано, которые он сжег, считая их недостойными опубликования. Хотя сочинения Кардано, в известной степени, компилятивны. Например, его первая работа по математике, – это как раз обработка Пачоли. Он учил своего ученика Людовико Феррари, естественно, по учебникам Пачоли, как и вся Италия в это время. И заодно переписал его, достаточно изменив и дополнив. Он обладал удивительной жаждой познания, и кроме того, удивительным желанием поделиться знаниями и размышлениями со своими читателями. В частности, он написал автобиографию «О моей жизни», которая много раз переводилась и издавалась (я сам не читал), про которую комментаторы говорят, что «Исповедь» Жан Жака Руссо просто детский лепт по сравнению с автобиографией Кардано. Что откровенность, которой достигает Кардано в описании своей жизни, своих недостатков, разных событий, совершенно не имеет аналогов ни в средневековой литературе, ни в литературе Нового Времени. Кардано был страстным игроком, и, так как доходы у него были очень значительные, а при этом семья все время была без денег, по-видимому, он проигрывал больше, чем выигрывал. Несмотря на то, что утверждает обратное в своих книгах. Так или иначе, вот он написал труд, интересующий нас «Об азартных играх или об игре случая». Естественно, он подробнейшим образом разбирает игры, правила, всевозможные варианты; как играть, как понять, что ваш партнер недобросовестен и т.п. То есть это, в первую очередь, практическое руководство для играющего. Но при этом Кардано делает несколько фундаментальной важности наблюдений для развития исчисления вероятностей. Как я уже сказал, фигура Кардано вызывает полярные оценки, соответственно, и оценка его вклада в теорию вероятностей, сильно зависит от того, находится биограф под обаянием Кардано или нет. Самые восторженные комментаторы говорят, что Кардано уже предвосхитил закон больших чисел Бернулли. Комментаторы, которым не нравится Кардано, категорически это отвергают. В чем нет сомнений – это в том, что Кардано уже владеет исчислением комбинаций, что уже у него есть идея вероятностного пространства, пространства всевозможных исходов равновероятных. Что надо разделить все возможности, зависящие от случая, в равновероятные исходы, и тогда вероятность будет пониматься как число благоприятных комбинаций к общему числу комбинаций. И Кардано уже очень близко подходит, а в сущности, пишет формулу для умножения вероятностей. Учитывая, что вероятность – это пропорция благоприятных исходов, то формула для сложения вероятностей уже как-то была ясна. А вот формула умножения вероятностей – открытие Кардано. Здесь мы расстаемся с этим замечательным исследователем, и я перехожу к уже известным творцам теории вероятностей, о которых можно прочесть в самых разных руководствах по истории теории вероятностей, поэтому я пройду их более бегло. Конечно, тут надо сказать про задачу шевалье де Мере, тоже идущую от игры в кости, и о переписке Паскаля и Ферма, где они как раз дали правильное решение задачи разделения ставки, во всяком случае, согласующееся с теорией вероятностей.
Говоря о задаче разделения ставки и правильном ее решении, я хотел бы сделать замечание, важное для дальнейшего. Вот кто-то говорил: давайте разделим всё поровну, или давайте первый всё заберет. Ясно, что, как разделить ставку, это вопрос психологический, – как хотят, пусть так и разделят. Тут есть элемент субъективного. И вот эта серия вопросов, которая в большей степени относится к философии, чем к математике, случай существует объективно, или, как пишет Пуанкаре, «мера нашего незнания»? Что такое эта субъективная случайность? Мы увидим, что все эти вопросы всплывут при попытках построения аксиоматической теории вероятностей. Но это все впереди. Итак, я сказал про переписку Паскаля и Ферма, ей посвящено много исследований, поэтому я не буду останавливаться на ней подробно.
Удивительно, как практика науки в XVII веке отличалась от нашей, не говоря уже о XVI веке. И в этом смысле Кардано, который все всегда публиковал, ведет себя, как современный исследователь. А вот, например, Паскаль и Ферма писали друг другу письма, публика знала, что эти письма существуют, и знала, о чем эти письма, знала, какая задача решается в письмах, знала, какой ответ – что делить три к одному. Но сами письма известны не были, они были изданы гораздо позже. И Гюйгенс свое сочинение, фундаментальный труд о теории вероятностей как раз начинает с доказательства результатов, о которых он знал, что они содержатся в переписке Паскаля и Ферма, но саму переписку он не видел. Поэтому он и говорит, что он переоткрывает результаты Паскаля и Ферма, приоритета он себе приписать не может, но он эти результаты получил самостоятельно. Мы же обращаемся к новой эпохе в развитии теории вероятностей, к сочинению «Искусство предположения» Якова Бернулли, профессора в Базеле, члена Парижской Академии Наук. И вот факсимиле его главного труда Аrs Сonjectandi.
Тут надо сказать, что по-гречески это будет «Стохэстикэ Технэ», отсюда и происходит слово «стохастика». Что такое «стохас» – это цель, мишень. Стохастика – это искусство предположения, искусство попадания в цель. Труд Бернулли – в четырех частях. В этом труде теория вероятностей выходит на совершенно новый уровень. Первая часть сочинения Бернулли – это комментарии к работе Гюйгенса. Сейчас в школьный учебник включены элементы теории вероятностей. Вычисление комбинаций школьники в России проходят, кажется, в 9-м классе. Я помню, когда я учился в школе, на меня произвело неизгладимое впечатление, что школьный учебник доводит школьника до конца XVII века. Я думал, а когда же можно выучить все, что сделано за последние 300 лет? Во всяком случае, в начале XVIII века уже есть математический анализ, какие-то начала дифференциальных уравнений, и геометрию эти мастера знают, может быть, и гораздо лучше, чем современные работающие математики. Геометрию Евклида, я имею в виду. А вот это искусство правильного исчисления комбинаций, в котором именно Бернулли ставит точку, оказалось чрезвычайно трудным. Первая часть – это комментарии к книге Гюйгенса; вторая часть – комбинаторика. Именно комбинаторика, вычисление всевозможных комбинаций, биномиальный коэффициент, то, что мы сейчас называем распределением Бернулли, какова вероятность при n играх в орлянку, что успех будет достигнут десять, например, раз. Все это вторая часть труда. Третья часть – двадцать четыре задачи с решениями. И главная для нас четвертая часть, которая называется очень интересным образом «Применение предыдущего учения к гражданским, моральным и экономическим вопросам». Четвертая часть – это неоконченная часть сочинения. Экономические вопросы, это, в первую очередь, вопросы демографии. Как вы знаете, и Спаситель наш (Ред. – Иисус Христос) был включен в перепись населения при Императоре Августе. Именно в Риме начали переписывать население, и уж конечно это было и в итальянских республиках, и были там, скажем, контракты на страхование судна. Такие контракты, может быть, и у греков были, но тут ясности меньше. Известно, что из 10-ти судов, отправляющихся в Африку, несколько, конечно же, не вернутся. Вот эти самые контракты о страховании: какую нужно назначать сумму? Вот об этой всей проблематике и идет речь, когда говорят об экономических вопросах. И, разумеется, вопросы демографии, скажем, вопросы продолжительности жизни, сколько рождается мальчиков и девочек. Например, вычислить население Лондона трудно, но известно, например, сколько рождается, во всяком случае, сколько, например, крестят в данном приходе, так как это фиксируется в записях. И соответственно, проводя вычисления, можно оценить по общему числу рождений общее население Лондона. И т.д. Это все я оставляю за кадром. Четвертая часть сочинения Бернулли – это именно закон больших чисел, который Бернулли, важно подчеркнуть, доказывает абсолютно математически достоверно и четко. Доказательство Бернулли, в некотором частном случае, – это то доказательство, которое сейчас написано в школьном учебнике. Вот такое удивительное свойство математики, математическое доказательство, как и стихи, не стареет. В сегодняшнем учебнике дается доказательство Евклида про бесконечные количества простых чисел, то самое доказательство, которое вы изучали в школе. Его придумал Евклид, и оно вот так без изменений пришло в сегодняшний учебник. Аналогичным образом доказательство закона больших чисел Бернулли – абсолютно безупречное доказательство. Интересует нас здесь, в первую очередь, детерминизм, как Бернулли относится к самому понятию случая. Мы увидим, что Бернулли вместе с Левкиппом, и против Аристотеля. Итак, Бернулли рассуждает о случайных событиях. Он приводит характерный пример –затмения исчисляются достаточно точно, уже это вполне умели делать еще и греки, а вот прогнозировать погоду мы и сейчас не умеем, и тем меньше умели современники Бернулли. «Однако, – пишет Бернулли, – только затмения причисляются к явлениям необходимым, падение же кости и будущая погода – к случайным. Причина этому исключительно та, что предполагаемое данным для определения данных последующих действий, на самом деле, в природе нам недостаточно известны. И если бы даже и были известны, то недостаточно развиты математические и физические знания, чтобы исходя из данных причин подвергнуть такие явления вычислениям». Иначе говоря, тезис, который будет потом повторяться, что случай – это только мера нашего незнания. То есть на самом деле все известно. Этот тезис переходит из сочинения в сочинение. Гоббс пишет, что мы не знаем, как выглядит кость, но если б мы точно знали, каким образом ее бросила рука игрока, и под каким углом она упала, то мы бы точно знали, как она выпадет, поэтому на самом деле, ничего случайного нет. Бернулли, так или иначе, стоит на позициях детерминизма, несмотря на вероятностные свои достижения, и считает, что случай – это только мера нашего незнания. Немного забегая вперед - Пуанкаре приводит прекрасный пример на этот счет, он говорит: если вы придете в агентство по страхованию жизни, вам зададут соответствующие вопросы, и назначат плату. При этом, разумеется, агентство не знает деталей вашей медицинской истории, и все равно существует и извлекает прибыль. Теперь представьте себе, говорит Пуанкаре, что болтливый врач пришел к страховщику с медицинскими картами своих клиентов. Теперь страховщик точно знает, у кого печень, у кого сердце и т.п. Но он извлекать прибыль от этого не перестает. Его знания стали точнее, но прибыль он извлекать не перестает. Так и, говорит Пуанкаре, наши вероятностные заключения связаны с несовершенством наших знаний, мы не знаем, но от этого они становятся менее точными, потому что они связаны с усредненными рассмотрениями. Говоря о детерминизме XVIII века, я хочу еще привести цитату из Лапласа, цитату прославленную и оказавшую большое влияние на развитие науки в целом, а не только теории вероятностей. Лаплас пишет: «Ум, которому были бы известны для какого-либо данного момента все силы, одушевляющие природу, и относительное положение всех её составных частей, если бы вдобавок он оказался достаточно обширным, чтобы подчинить эти данные анализу, обнял бы в одной формуле движение величайших тел вселенной наравне с движениями легчайших атомов; не осталось бы ничего, что было бы для него недостоверно, и будущее, так же, как и прошедшее, предстало бы пред его взором». Таким образом, позиция Лапласа, давшего фундаментальные результаты в теории вероятностей, состоит в том, что в действительности, если бы мы только знали начальное положение и начальную скорость, то мы бы знали все прошлое, все будущее и никакого случая никогда и ни за что не было бы. Я бегло прохожу здесь следующие этапы развития теории вероятностей. Так, Эйлер пришел к решению вероятностной задачи, потому что король Пруссии поручил ему организовать лотерею.
Прусский бюджет был истощен войной, его требовалось пополнить, и было принято решение организовать лотерею, а лотерею организовывал Эйлер, она успешно прошла. Муавр и Лаплас дают центральную предельную теорему теории вероятностей, то, что мы сейчас называем «Гауссов закон ошибок». Те, кто еще помнят немецкие марки, помнят, что, кажется, на десятимарочной банкноте был этот самый нормальный закон ошибок изображен вместе с портретом Гаусса. Во всяком случае, уже Муавр и Лаплас дают эту центральную предельную теорему, но не дают для нее, впрочем, строгого предельного доказательства, это очень важно.
Пуассон занимается вероятностными рассмотрениями тоже без строгих доказательств. Я хочу подчеркнуть, что теория вероятностей воспринимается в Европе как область не математики, и это вплоть до середины XX века. Вероятностные рассуждения носят какой-то такой нематематический характер. Никто не считает, что вероятность – область чистой математики. В частности, Муавр и Лаплас не дают математических доказательств своих верных результатов, в отличие от Эйлера. Теперь мы обращаемся к теории вероятности в России, постепенно идем к математике Колмогорова. И первая фигура, к которой мы обращаемся, это Пафнутий Львович Чебышев. Это замечательная фигура в истории математики и науки, пожалуй, недостаточно оцененная. Тут я вновь могу спросить публику, что сделал Чебышев, каковы его достижения? Зритель: полиномы. Александр Буфетов: А что такое полиномы? В чем их особенность? Зритель: Они определяются кривыми. Александр Буфетов: Любой полином определяется кривой. Но, действительно, полиномы Чебышева, которые от нуля уклоняются меньше всего. Чтобы не усложнять свой рассказ, я только скажу, что Чебышев первым начал рассмотрение ортогональных полиномов как отдельного предмета исследования. Отдельные полиномы рассматривали Лежандр, Якоби и другие исследователи, но вот саму теорию создал Чебышев. Чебышев интересен для нас своими сочинениями по теории вероятности. Замечу, что теория вероятности была одной из любимых дисциплин Пафнутия Львовича, а теория вероятности изучалась в университетах Российской Империи. Любимыми предметами Чебышева были теория чисел и теория вероятностей, к которым он обращался 31 раз. 31 раз он прочел курсы по теории чисел и теории вероятностей. Он написал 4 работы по теории вероятностей, магистерскую диссертацию, доказательство закона Пуассона, доказательство закона больших чисел в более общем ключе, чем у Бернулли, и, в сущности, в той общности, в которой он встречается в сегодняшнем учебнике. И главная работа Чебышева, дело всей жизни, это – доказательство центральной предельной теоремы Муавра и Лапласа. К сожалению, он не смог дать абсолютно безупречного доказательства, И тут нужно четко сказать, что Чебышев уже стоит на позициях, это очень важно, и совершенно не имеет аналогов в Западной Европе, что теория вероятностей – это математика, что ее теоремы надо доказывать. Вы можете спросить, как же так, аксиоматика Колмогорова, а теорема Чебышева. Очень просто. Утверждения, относящиеся к теории вероятностей, переформулируются из чистого анализа, это можно сделать, и они уже доказываются. Утверждения доказываются строго (например, утверждения из чистого анализа, о сходимости каких-то рядов), а вот связь их с теорией вероятностей остается в области фантазии.
То есть само понятие случайной величины не может быть в математической работе, потому что это не математика для математиков XIX века. Колмогоров пишет о Чебышеве: «Вывел русскую теорию вероятностей на первое место в мире П.Л. Чебышев. С методологической стороны основной переворот, совершенный Чебышевым, заключается не в том, что впервые с полной настойчивостью он выдвинул требования абсолютной строгости доказательства теорем. Выводы Муавра-Лапласа и Пуассона были с формально-логической стороны совсем не безупречны, в отличие от Бернулли, который свою предельную теорему доказал с исчерпывающей строгостью. Но главным образом и в том, что Чебышев всюду стремится получать точные оценки». Для нас тут важно, что для Чебышева теория вероятностей – это математика. Хотя эти сочинения для него ветвь анализа, а вероятностные связи остаются полностью в стороне. Обратимся совсем коротко к двум его замечательным ученикам – Александру Михайловичу Ляпунову, который продолжал исследования Чебышева, и, в частности, дал ту формулировку центральной предельной теоремы, которая есть сейчас в экзаменационных билетах. А главное, к замечательному академику – Андрею Андреевичу Маркову, о котором я скажу несколько слов, хотя он, конечно, заслуживает совершенно отдельной лекции. Марков, как я и говорил в интервью «Полит.ру» перед лекцией, прославился, среди прочего, и тем, что когда праздновали 300-летие Дома Романовых, то он организовал как бы в пику празднование 200-летия больших чисел. И, кстати, Академия Наук недавно отпраздновала 300-летие больших чисел наряду с празднованием 400-летия Дома Романовых в прошлом году. Марков написал в Синод письмо с просьбой отлучить его от церкви – отлучили же графа Льва Толстого, а «я придерживаюсь тех же взглядов, что и Лев Толстой, отлучайте меня». Это был, конечно же, большой скандал. Академик Марков, член Императорской Академии. Марков особенно знаменит своим главным открытием, так называемыми, цепями Маркова. Марков взял роман «Евгений Онегин», и заинтересовался таким вопросом. Все хорошо знают, что в русском языке гласные в целом чередуются с согласными, хотя возможны комбинации нескольких гласных и нескольких согласных. Марков заинтересовался таким вопросом: с какой частотой идет гласная после согласной? И с какой частотой согласная после гласных? Он нашел такие величины: гласная после согласной в романе «Евгений Онегин» идет с вероятностью 0,663. Гласная после гласной – всего-навсего 0,128. Эти вероятности не должны складываться к единице, напротив, они позволяют найти вероятность согласной после согласной, гласной после гласной. Такие он нашел вероятности, и этим нашел новую страницу в литературоведении, такой статистический анализ текста. Потом этим будет заниматься Колмогоров, но не символами «Евгения Онегина», а ритмами стиха, и даст удивительные результаты в этой области. Главное, что Марков, отталкиваясь от этого примера, открыл свои собственные цепи Маркова. Давайте представим себе два события, гласные и согласные. Разумеется, нельзя сравнить появление гласной или согласной с бросанием монетки, потому что, как видно здесь, гласная после согласной появляется гораздо вероятнее, чем после гласной. Две гласные это не так часто бывает в русском языке, как сочетание согласной и гласной. Наоборот, представим себе, говорит Марков, что все прошлое слово «мой дядя», когда в этом слове «дядя» комбинация «д»-«я» появления вот этой гласной «я», оно зависит от предыдущего «д», а больше ни от чего прошлого не зависит. Иначе говоря, будущее зависит от настоящего, но если зафиксировать настоящее, то будущее и прошлое независимы. Будущее независимо от прошлого, если зафиксировано настоящее. Будущий символ гласной и согласной зависит от того, какой символ этой гласной или согласной, но не зависит от предыдущего текста. Это, конечно, упрощение, разумеется, на самом деле, зависит, но упрощение, которое оказалось чрезвычайно плодотворным, и цепи Маркова один из таких абсолютно фундаментальных объектов в современной математике, важные для вычисления цен на бирже, котировок; давшее математическое объяснение броуновского движения. Здесь очень важную роль сыграл французский математик Башелье, чьи работы при его жизни не получили должного признания. Такие вот замечательные ученики Чебышева – академик Ляпунов и, особенно, А.А.Марков.
Мы вплотную подходим к аксиоматизации теории вероятностей. Обратите внимание, уже накоплен огромный пласт результатов по теории вероятностей. По ней пишутся всевозможные учебники. Вот замечательный учебник Пуанкаре по теории вероятностей, использовавшийся во французских учебных заведениях довольно долго. Но при этом сами теоремы формулируются как теоремы из анализа, а понятия случайных величин остаются полностью за кадром. Я приведу здесь один пример, недостаточно широко известный даже для математиков. Мы тут скакнем на тридцать лет вперед, прежде чем потом сделать обратный прыжок. И обратимся на секунду к Алану Тьюрингу, замечательному английскому математику со страшной судьбой. Алан Тьюринг начинал в теории вероятностей. Давайте быстро посмотрим на работы, а потом вернемся к Тьюрингу. Я следую тут работе «Алан Тьюринг и центральная предельная теорема» Забелла. Тьюринг передоказал центральную предельную теорему. Это был фактически его диплом, если перевести на русский язык. Он не знал о работе Линдеберга, но передоказал именно в такой форме, и в действительности, работа никогда не была опубликована, что там в точности произошло не совсем ясно, но признания эта работа не получила. Хотя он смог остаться, получить fellowship, и защищал его Джон Мейнард Кейнс. Так или иначе, когда Тьюринг в 1934-м году написал свою работу по теории вероятностей, работа Колмогорова уже была, но она еще не была усвоена. И вот видно, что Тьюринг свою теорему формулирует как теорему из анализа, оставляя вероятностную терминологию полностью в стороне. А потом полностью уходит из теории вероятностей. Тут нам, с одной стороны, интересно, что Тьюринг начинал в теории вероятностей, прежде чем переключиться на логику, а с другой стороны это характерный пример, что в Кембридже 1930-х годов, а на самом деле гораздо позже, теория вероятностей – это была не математика. Джентльмен может заниматься теорией чисел, а теорией вероятностей нет. Вот что показывает нам случай Тьюринга.
Мы приходим к попыткам аксиоматизации теории вероятностей. И тут, прежде чем переходить к их описанию, я хочу привести пример из книги Эмиля Бореля «Случай», которым я хочу проиллюстрировать следующий тезис, что границы применения теории вероятностей, что на этот счет раньше высказывали суждения, которые сегодня мы можем воспринимать только с некоторым юмором. Борель пишет: «Самое возвышенное правило морали, когда-либо предлагавшееся людям, казалось бы, заключается в евангельской заповеди «Люби ближнего как самого себя». Наиболее практической иллюстрацией этого может служить жизнеописание св. Мартина, делящего свой плащ. Если позволительно применять к такому предмету научную критику, рискуя услышать обвинения в чрезмерной сухости сердца, то мы вынуждены признать, что если ближние это все люди, то буквальное исполнение евангельских заповедей приводит к нелепым выводам. Сам св. Мартин не мог бы разделить свой плащ на тысячу кусков, если бы встретил тысячу несчастных. Таким образом, единственное разумное толкование, которое можно дать евангельскому изречению такое: рассматривай каждого своего ближнего как величину, эквивалентную, во всяком случае, не тебе самому, а какой-нибудь части тебя, заключающейся между нулем и единицей. Не думаю, что такую формулировку можно было назвать эгоистической. Различные степени проявления альтруизма и эгоизма определяются при определении коэффициентов. Скольким лицам каждый из нас припишет коэффициент «1», скольким коэффициент «0,9», скольким «0,5»? Я не стану входить в компетенцию этих величин, которые входят в компетенцию практической морали. Пусть меня поправят, в математике морали нет на сегодняшний день. Приписывать вероятностные коэффициенты, любить ближнего с вероятностью «0,75», это не входит в современную теорию вероятностей. А говорю я это совсем не для того, чтобы посмеяться над Борелем. Борель оказал несомненное влияние, в т.ч., и на Колмогорова. А просто, чтобы показать две вещи: это все было очень трудно, понять, как поставить теорию вероятностей на твердые математические начала, с другой стороны, показать субъективный характер вероятности. Вероятность это то, что существует в природе вещей, или это все же то, что существует в нашем уме? И мы увидим этот конфликт в самих попытках аксиоматизации.
Первая попытка аксиоматизации принадлежит Сергею Натановичу Бернштейну, замечательному русскому математикую. Он дает 3 аксиомы: аксиому сравнения, аксиому совместимости, аксиому совмещения. И потом из этих аксиом выводится само понятие вероятности. Прошу обратить внимание, понятие вероятности является вторичным. Вспомним, из курса геометрии, что точки, прямые, треугольник или угол, градусная мера угла это понятие уже вторичное, оно выводится из аксиом. И вот для Бернштейна понятие вероятности вторичное. Бернштейн его выводит. Это очень интересная попытка, 1917-й год, первая в мире, но не имевшая продолжения. Аксиоматика есть, но проку от нее нет. Очень интересна попытка Рихарда фон Мизеса. Он интересуется таким вопросом, тоже очень важным. С теорией вероятности связан такой парадокс. Когда мы говорим, что вероятность выпадения монетки ½, что это значит? Что если мы долго будем играть в орлянку, то орлов и решеток будет примерно поровну. Что это значит? Ведь может так случиться, что мы играем в орлянку, 10 раз бросили, и выпали одни орлы, это же возможные события, маловероятное, но возможное. Или играли 100 раз, и орлов оказалось 60%, это крайне маловероятное событие, но, тем не менее, возможное. Как это нужно понимать?
Классическое понимание такое. Одна игра в орлянку вероятность ½. Это значит, что если 100 раз сыграть в орлянку, то, скорее всего, орлов будет примерно половина. Это значит, что если взять 100 ансамблей по 100 игр в орлянку, то среди них тех, где орлов будет гораздо больше половины, будет очень мало. Что это значит, в свою очередь? Это такой парадокс, само понятие вероятности само в себе заключает противоречие. И фон Мизес, пытаясь разрешить это противоречие, пытается разъяснить, что такое одна случайная последовательность. Он пытается определить, в первую очередь, что такое индивидуальная случайная последовательность. Ну, ясно, например, что орлов и решеток должно быть примерно поровну. Ну, например, возьмем последовательность 0,1,0,1,0,1,0,1, ... По четным дням всегда выпадает орел, по нечетным – всегда решетка. Ясно, что эту последовательность нельзя считать случайной. Тогда Мизес говорит про подпоследовательности: «Хорошо, если мы играем в орлянку, то не может быть, чтобы, скажем, по понедельникам, выигрывали только вы, а по средам только я. Это не совместимо с правилом случая. По понедельникам тоже должна быть случайная последовательность». Но тогда можно сказать, давайте возьмем подпоследовательность по тем дням, когда выигрываю только я. Получится последовательность из одних единиц, опять парадокс. Фон Мизес не дает разрешение этого парадокса. Его рассмотрение чрезвычайно важное для истории науки, очень интересное. Шестая проблема Гильберта и состоит в том, чтобы дать аксиоматику теории вероятностей и статистической механики. Фон Мизеса интересовали более практические вопросы, что такое случайная последовательность. Аксиоматику фон Мизес не построил. Чрезвычайно интересная попытка аксиоматизации теории вероятностей была предпринята Бруно де Финетти, замечательным итальянским математиком, потом взаимодействовавшим с Колмогоровым. Он предлагает определить вероятность как сумму, которую вы готовы заплатить в случае такого-то исхода. Вы знаете, как там проходила какая-то игра, какую сумму вы готовы заплатить, или наоборот, какую сумму проиграть. Какое пари вы готовы заключить? С чем связана такая попытка аксиоматизации? Очень просто – конечно, с петербургским парадоксом. Что это такое? Представьте себе, вы идете на лекцию «Полит.ру» по улице Сретенка, там стоит павильон, в павильоне предлагается играть в такую игру: бросается монетка. Если выпадает орел, вам платят рубль. Монетка бросается еще раз. Если выпадает 2 орла, вам платят 2 рубля. Если 3 орла, 4 рубля. Если 4 орла, 8 рублей. Если 8, то 16 и т.д. Если 10 орлов, то 1000 рублей. Если 20 орлов, то миллион рублей. Сколько вы готовы заплатить за вход в такой павильон? Тут парадокс связан с тем, что автоматическое ожидание вашего выигрыша бесконечно. Вы в принципе можете выиграть сумму, сколь угодно большую. Может быть, 100 раз выпадет монетка орлом, и вам миллиард дадут, какую-то баснословную сумму, столько денег, сколько в банке нет. А сколько вы готовы заплатить? Если так подумать про себя, то 10000 рублей не захочется платить. Хотя, казалось бы, есть шанс выиграть миллиарды, но шанс настолько ничтожный, что крупную сумму за это не хочется платить. Можно иначе: или я вам сразу даю миллион, или я с вами играю в орлянку. При этом если выпадает орел, я вам ничего не даю. А если выпадает решетка, я вам даю три миллиона. Что вы предпочтете, получить верный миллион или сыграть в орлянку на три миллиона? Достаточно ясно, во всяком случае, в некоторых случаях, синица в руках дороже, чем журавль в небе, и вот эти вычисления среднего совершенно не отвечают психологической реальности. Это, кстати, и в экономической теории хорошо известное явление, что потребитель не любит идти на риск, даже с большими дивидендами в случае выигрыша. Об этом писал еще петербургский академик Даниэль Бернулли. Де Финетти и пытается построить эту субъективную теорию. Джон Мейнард Кейнс тоже пытался определить вероятность как меру правдоподобия. Субъективная трактовка вероятности. Это замечательная работа, она привела к появлению замечательных результатов. Сама теорема де Финетти о перестановочных событиях отсюда и возникает, как бы идея в том, что вы совершаете решения только на основе частот предыдущих событий, а не на основе порядка предыдущих событий.
И отсюда и возникает теорема де Финетти о перестановочных событиях. То есть де Финетти создал прекрасную теорию вероятностей, но аксиоматики на этом пути совершенно не получается. И постфактум можно сказать, почему ничего у них не получалось, потому что они пытались дать определение теории вероятностей. И Бернштейна и де Финетти интересовал вопрос не сколько математического, сколько философского характера, что такое вероятность. Мы обращаемся к главному герою нашей лекции, Андрею Николаевичу Колмогорову. Вот его фотография времен, когда он уже написал несколько блестящих вероятностных работ и, наверное, уже думал и над аксиоматическим основанием теории вероятностей.
Колмогоров - автор фундаментального труда, изданного по-немецки - «Основные понятия теории вероятностей». И Колмогоров дает правильную аксиоматику теории вероятностей. Не вдаваясь в математические детали, скажу, что она основана на теории меры Лебега, теории интеграла. Потому что именно Лебег дал удовлетворительное объяснение того, что такое интеграл. Колмогоров и говорит, что вероятность – это есть мера. Давайте посмотрим коротко на аксиомы Колмогорова, хотя это не так и важно.
Важно нам здесь то, что вероятность для Колмогорова является совершенно неопределяемым понятием. Это написано в любом учебнике, тут никакого секрета нет. Колмогоров говорит, пусть есть вероятность, тогда там есть такие-то свойства. И, в сущности, Колмогоров увязывает теорию вероятностей с теорией меры и интеграла Лебега. Колмогоров в предисловии к своей работе пишет: «после исследования Лебега стала ясна аналогия между мерой множества и вероятностью события. Эта аналогия допускает и дальнейшее продолжение. Попытки построения основ теории вероятностей, исходящей из этой общей точки зрения, уже имеются, и весь круг идей, излагаемых здесь, уже успел приобрести известную популярность в узком кругу специалистов». – В частности, Борель находился под влиянием таких идей. – «Однако отсутствовало полное и свободное от излишних усложнений изложение всей системы». Опять-таки эта идея, вот Майстров приводит польское исследование, кажется, Ломоницкого, если я не ошибся с фамилией, который тоже предлагал подобную идею. Идея, что это правильный путь, уже была. Но именно заслугу Колмогорова можно сравнить с открытиями Лобачевского. Идеи, связанные с неевклидовой геометрией, все были до Лобачевского. Но именно Лобачевский твердо встал на эту точку: вот она - новая геометрия. И, соответственно, именно Колмогоров ввел теорию вероятностей в математику. Теория вероятностей – это ветвь математики. Вот что такое случайная величина. Вот что такое мера. В этом смысле гигантское психологическое значение для нашего понимания науки и места теории вероятностей в математике, в естествознании играет аксиоматика Колмогорова. Аксиоматика Колмогорова, надо сказать, подвергалась критике, вот почему: Колмогоров рассматривает теорию вероятностей как теорию меры, а теория меры – на пространстве всевозможных событий. То есть вот, например, всевозможных последовательностей русских символов. Это пространство содержит все романы, в том числе ненаписанные. Завтра Пелевин напишет роман, а он уже в этом пространстве есть. Такое пространство – совершенно идеалистично. То есть, например, функция распределения случайной величины – это то, что вычисляется прибором, что видит инженер или астроном, который проводит измерения. А вот пространство вероятностных событий – это платоновский идеальный объект, это что-то, чего инженер совершенно не видит. Так критиковали Колмогорова. Критиковать можно, но альтернативы никакой нет и по сей день. Напротив того, колмогоровская аксиоматика есть, и именно она дала такой мощнейший толчок развитию теории вероятностей, ввела теорию вероятностей в математику. Дала толчок чрезвычайно бурному развитию теории вероятностей во всей первой половине XX столетия вплоть, скажем, до 1960-70-х годов. С чисто математической точки зрения, значение работ Колмогорова состоит в том, что он, в частности, дал основы для объяснения случайностей непрерывных, например, броуновского движения. Случайности в бесконечном числе измерений, случайной траектории. Вы бросили монетку, и это понятно. А что значит случайная траектория? Траектория молекулы воздуха в этой комнате. Ведь она может идти в любом направлении, тут бесконечное множество выборов, как вот это объяснить. То есть молекула в каждый момент времени бросает новую монетку, и пускается в новом направлении. И вот строгую теорию процесса бесконечных вероятностных пространств как раз и построил Колмогоров в своей фундаментальной работе. И в этом ее математическое значение. Потому что еще раз подчеркну, что идеи, связанные с теорией меры, они уже были, а это построение теории бесконечных вероятностных пространств – это то, чем сейчас открывается курс случайных процессов, и эта теорема сформулирована и доказана в этой работе. В заключение скажу о том, что Колмогоров возвращался к построению теории вероятностей за свою жизнь. И если эта книга - это шедевр молодого Колмогорова, то ответ на этот вопрос, это, может быть, последний математический шедевр Колмогорова, это его определение, которое называется колмогоровская сложность. О ней, кажется, уже были лекции «Полит.ру». Мне кажется, у вас была лекция Александра Ханиевича Шеня, а если не было, то очень стоит, чтоб была (Ред. – идея была быстро реализована, лекция Шеня состоялась 6 марта 2014 года). А я скажу совсем кратко, что идея Колмогорова состоит вот в чем: почему эта последовательность случайна, а эта не случайна? Потому что эту последовательность можно очень коротко описать, последовательность из одних нулей. Это очень короткое описание. Причем заметьте, если бы это было семь нулей, сто двадцать семь нулей – все равно это последовательность из одних нулей. Это очень короткое описание. Для описания этой последовательности уже понадобится очень много сил: на втором и третьих местах единицы, и на пятом месте единица. Вам надо написать компьютерную программу, которая выдает эту последовательность. Для этой последовательности можно дать очень короткую последовательную программу, а для этой понадобится компьютерная программа довольно длинная. Вы можете сказать, что компьютерная программа зависит от языка программирования; если писать на одном одно, на другом будет другое. Но на самом деле, на любом языке программирования можно запрограммировать любой другой, то это все при рассмотрении достаточно длинных последовательностей, не имеет никакого значения. Это называется колмогоровская сложность. Он дает объяснение того, почему это случайное, а это нет, почему оно
именно такое. Потому что эта последовательность задается простой
закономерностью. А эта последовательность такой простой закономерности
не допускает. И вот именно мера сложности закономерности, которая дает
последовательность, это абсолютная четкая математическая закономерность.
Длина компьютерной программы или математическая длина алгоритма,
выдающая нам последовательность, называется колмогоровской сложностью.
Последние годы работы Колмогорова по теории сложности связаны с работами
его молодости по аксиоматике теории вероятностей. Большое спасибо. ДискуссияБорис Долгин: Спасибо большое, Александр. Я бы начал с вопроса о том, что же все-таки такое полином? А дальше уже приступим к другим вопросам. Александр Буфетов: Хорошо. Полином – это функция от одной до нескольких переменных, в нашем примере одной, которая получается выполнением операции сложения и умножения. Борис Долгин: Теперь несколько вопросов о вас. Насколько то, о чем вы сегодня рассказывали, близко к роду ваших занятий? В чем здесь ваш интерес? Как вы соотноситесь с теорией вероятностей? Как вы пришли в математику? Александр Буфетов: Ну, это несколько разных вопросов. В математику я пришел, придя в Независимый Университет, как я думаю, и все математики, присутствующие в этой комнате.
Борис Долгин: Но в Независимый Университет приходят также не с нуля, это совершенно неочевидное место, куда приходят. Наверное, вы пришли с интересом к математике в этот Университет? Александр Буфетов: Да, в этом смысле, я – продукт советской системы, советского миросозерцания моих родителей, состоявшего в том, что математические школы самые лучшие в городе, и вот меня за руку взяли и отвели во 2-ую математическую школу. С этого все и началось. Собственно, Независимый Университет тогда и занимался во 2-ой школе, так что мне даже не надо было выходить из здания, чтобы пойти на занятия. Я занимаюсь эргодической теорией динамических систем, и это область близкая к теории вероятностей. Как я уже говорил в интервью Наталии Деминой, Джозеф Дуб (Doob Joseph Leo) начал свое выступление со слов «математика – это часть теории вероятностей». Во всей математике используется теория вероятностей, и то, что она используется в эргодической теории динамических систем, кстати, это понял еще Пуанкаре. И, конечно, я постоянно цитирую работы Колмогорова. Борис Долгин: Спасибо. И последнее, дальше уже дам возможность задавать вопросы коллегам. Что бы вы посоветовали почитать по теории вероятностей? Александр Буфетов: Вы имеете ввиду с математической или с исторической точки зрения? Борис Долгин: Представьте себе человека, который имеет некоторый интерес к математике, но не является математиком, и даже не является физиком. И элементы истории, и введение в историю теории вероятностей, все, что угодно. Александр Буфетов: Этот вопрос ставит меня в тупик. По истории есть замечательная книжка Феллера, но всё же она написана для студента-математика, и даже если не для него, то для студента математика, физика или биолога. Сами книги Майстрова мне очень понравились, я взял их для подготовки этой лекции, но они связаны, первая – с историей теории вероятностей, а вторая – с философскими проблемами. И таких книг очень много, есть кембриджская книга фон Плато. Вообще, философия теории вероятностей, философские вопросы, с которых я начал, сегодня не могут быть решены, поэтому они обсуждаются по сей день, и таких книг много. Но вы, кажется, спросили не об этом. А если говорить о каком-то изложении теории вероятностей, скажем, как физика Ландберга, то я, пожалуй, затрудняюсь с ответом, может быть, по незнанию моему. Борис Долгин: Да, если кто-то может помочь, пожалуйста. Владимир Потапов: Я бы рекомендовал книгу братьев Ягломов «Вероятность и информация». Александр Буфетов: Да, это очень правильно. Я когда-то очень давно держал в руках эту книгу и недолго, ее довольно трудно было достать во время моего детства. Я думаю, что это очень правильно. Константин Иванович: Спасибо за лекцию. У меня вопрос такой: В свое время Лобачевского признали в России и не посадили в сумасшедший дом, только потому, что его признал Гаусс. Александр Буфетов: Про сумасшедший дом, мне кажется, это все-таки преувеличение. Константин Иванович: А почему Колмогорову пришлось писать свою работу на немецком языке, публиковать в немецком журнале? Александр Буфетов: Нет, в немецком издательстве. Константин Иванович: И кто из немцев признал, потому что среди наших специалистов таких, наверное, было мало. Александр Буфетов: Во-первых, давайте начнем с Лобачевского. Лобачевский – трагическая фигура в истории науки. Он, несмотря на многие свои годы ректорства, так и не смог составить состояние, после его смерти его вдова оказалась в очень стесненных обстоятельствах, есть письма на этот счет. Его дети плохо кончили. Лобачевский подвергался страшной травле академиком Остроградским. Тот вписал себя в историю науки как такой Герострат. Зритель: У Колмогорова тоже трагедия. Александр Буфетов: Давайте по порядку, я об этом тоже скажу. Но все-таки сумасшедший дом – это риторическое преувеличение, мне кажется, так вопрос никогда не стоял. И поддержка Гауссом работ Лобачевского высказывалась, если я не ошибаюсь, только частным образом, а не официально, и поэтому Лобачевскому никакого прока от этого не было. Что до публикации работ Колмогорова по-немецки, то я думаю, что таким образом можно было достичь большего охвата. Все-таки языки математики в 30-е годы – это немецкий и французский, и все же еще не совсем английский, и уж во всяком случае, не русский. Это потом, тут я имею личный опыт, американские логики и американские вероятностники с большой вероятностью говорят по-русски. Я знаю несколько специалистов, которые говорят по-русски очень хорошо, и вот причину мы видим на доске. Но это было потом. Первая публикация была по-немецки – возможно, чтобы застолбить приоритет, по каким-то совершенно практическим соображениям. Тут я могу рассказать две истории, поэтому спасибо большое за ваш вопрос. Колмогоров пошел очень не туда в 40-м году, когда подверг критике академика Лысенко. Это потрясающая история, которая описана и переописана, но я напомню. Давайте обратимся к работе Лысенко. Аспирантка академика Лысенко написала опровержение законов Менделя из теории вероятностей. Дело в том, что законы Менделя предсказывают соотношение три к одному, аспирантка провела исследование, и получилось не три к одному, а некоторые другие числа. И академик Колмогоров написал письмо в «Доклады Академии наук», в которых указал, что работа аспирантки, кажется, Ермолаевой, подтверждает законы Менделя, потому что в любых измерениях есть ошибка, и ошибка, получающаяся у аспирантки, прекрасно ложится в законы Менделя. И вообще эта работа является подтверждением, а не опровержением. За что он получил вот такой подарок, что «работы Колмогорова никакого отношения к биологической науке не имеют. Нас, биологов, не интересуют математические выкладки» и т.д. Опять-таки, я не жил в 1940-м году, но учитывая высокое положение академика Лысенко и общий характер научной полемики в сталинском СССР, принято говорить, что всё это пахло ГУЛАГом. Что вот это был уже почти билет в ГУЛАГ. Если Вавилов кончил в ГУЛАГе, то чем Колмогоров лучше? Но Колмогоров в ГУЛАГ не попал. Как известно, в нашей истории никогда не знаешь, что произойдет завтра, и я не уверен, что эта тема исчерпывающе разобрана. Я слышал от Шеня, но не знаю, где здесь грань между анекдотами из кухни 60-х и правдой. Я слышал, что критиковали теорию вероятностей, потому что она противоречит теории марксизма. С одной стороны, наука – враг случайного, с другой стороны – теория вероятностей говорит о независимых событиях, а как вы понимаете, в природе все взаимосвязано, учат нас Маркс и Энгельс, и соответственно теория вероятностей – это лжеучение как кибернетика, генетика и т.д. Будто бы удалось отбить эту атаку Александру Яковлевичу Хинчину, может быть, и самому Колмогорову. Еще раз говорю, не знаю, насколько достоверны эти свидетельства. Удалось ответить на атаку, ответив вопросом на вопрос «Считают ли, что если после того, как помолились о дожде, идет дождь, – это события независимые или взаимосвязанные?» И будто бы так атаку на теорию вероятностей удалось отбить. Во всяком случае, Колмогоров тут как-то вышел сухим из воды, в ГУЛАГ не попал, и атаку удалось отбить. Что не спасло Колмогорова от мученического венца. Колмогорова, конечно, травили, и по-видимому, затравили, но совсем в другом контексте. Колмогоров был, как известно, очень здоровый человек. Хорошо известно, что он в очень преклонном возрасте обратился за консультациями к высокопоставленному советскому врачу, академику. Тот спрашивает его, на что вы жалуетесь, и вот пожилой, скажем, 70-летний Колмогоров говорит: «Вы знаете, я в последнее время чувствую себя неуверенно, когда плаваю на спине». А вот в 1978-м году, когда он достигает 75-летнего возраста, его здоровье начинает стремительно ухудшаться, очень быстро. И последние годы Колмогорова были очень мучительны, и он очень тяжело болел. И конечно это связано с той травлей, которой он был подвергнут академиком Понтрягиным. По поводу его школьных учебников, и особенно, в сегодняшнем контексте, переоценка теории Колмогорова, об этом обязательно нужно говорить, и нужно найти правильное место реформе Колмогорова в истории русского образования. Я очень хорошо помню, что как-то я под влиянием Владимира Игоревича Арнольда, не скрывавшего своего чрезвычайно критического отношения к реформе образования Колмогорова, спросил Николая Николаевича Константинова: «Как вы думаете, почему реформа Колмогорова оказалась неудачной?» И Константинов резко спросил: «А почему вы считаете, что она была неудачной?» И стал объяснять мне, что реформа Колмогорова был чрезвычайно удачной, что он много сделал для средней школы, что он, например, ввел в программу начала математического анализа. Можно говорить до полуночи о реформе Колмогорова, это сюжет, еще не закрытый и вызывающий сильные эмоции. Материалы, кстати, можно найти на сайте Независимого Университета. Была статья Понтрягина в журнал «Коммунист», была травля Колмогорова, и было голосование на Отделении математических наук, куда входили и ученики Андрея Николаевича. Оно проголосовало за то, чтобы официально осудить реформу Колмогорова. Кто-то один воздержался. Может быть, это был сам Колмогоров, подробности неизвестны. А может, Колмогоров в голосовании не участвовал, и воздержался кто-то другой. Факт в том, что после 1978-го года, после такого публичного унижения, публичной травли в прессе, инициированной академиком Понтрягиным и поддержанной учениками Андрея Николаевича, здоровье Колмогорова стремительно деградирует, и последние годы жизни Колмогорова чрезвычайно мучительны. Константин Иванович: Колмогоров написал на доске какую-то последовательность цифр 15926535 8979323846 … и спросил аудиторию: «Что это за цифры?» Никто не мог сказать. Оказалось, что это число Пи без первых цифр. Александр Буфетов: Это очень интересная история, я никогда не слышал! Это очень похоже на Колмогорова. Вам надо обязательно ее записать и положить в Интернет. Зритель: Колмогоров поставил точку на аксиоматике? После него уже никаких аксиоматик не предвидится? Борис Долгин: А что бывает вообще в науке, когда точка поставлена? Александр Буфетов: С аксиоматикой да, бывает. Борис Долгин: Разве не может быть создана другая аксиоматика? Это научный подход? Александр Буфетов: Во всяком случае, сейчас аксиоматика Колмогорова совершенно стандартна, и даже если вы откроете учебник по финансовой математике… Борис Долгин: Я не говорю о ее недостатках возможных. Я говорю о том, что любая аксиоматика предполагает возможность другой аксиоматики. Александр Буфетов: Это выводит нас в плоскость методологической дискуссии, в которой я не чувствую себя на высоте уважаемого оппонента. Аксиоматика Колмогорова свои задачи полностью выполняет, и даже в серьезном учебнике по финансовой математике, вы увидите на первой странице аксиоматику Колмогорова. Действительно, была критика аксиоматики Колмогорова, но альтернативы, которые реально бы использовались, мне неизвестны. Борис Долгин: То есть на настоящий момент, это, в общем-то, последнее слово науки. Александр Буфетов: Последнее слово – это не совсем правильная фраза. Это такая же последняя вещь, как аксиоматика геометрии Гильберта. Аксиомы Колмогорова теории вероятностей – такая же стандартная вещь, как аксиома натуральных чисел Пеано. Мне очень трудно себе представить, чтобы аксиоматика натуральных чисел Пеано подверглась пересмотру. И точно также мне очень трудно себе представить, чтобы подверглась пересмотру аксиоматика Колмогорова. Кстати Колмогоров занимался, например, турбулентностью, и очень подробно обрабатывал данные эксперимента, что привело к появлению Колмогоровской теории турбулентности. А чуть ли не первой любовью Колмогорова была биология. В школе он больше всего любил биологию. Я знал про его биологические работы, связанные с предельными циклами, с системой Лотка-Вольтерра «хищник-жертва», на которой Колмогоров построил некоторую общую теорию. Жизнь слишком коротка для того, чтобы изучить все работы Колмогорова. Эргодическая теория – это область, в которую фундаментальный вклад внес Колмогоров, связанная с обоснованием теории Больцано в статистической механике. Получена конкатенацией двух греческих слов – «эргос» и «одос», работа и путь. То есть эргодическая теория – это как бы путь энергии. Эргодическая теория – это изучение систем, возникших из статистической физики. Алексей Барабанов: Вопрос связан с квантовой механикой. Я занимаюсь ею, слушаю вас, и как-то в учебниках сплошная вероятность. Я не замечал, чтобы кто-то вот так специально интересовался вопросами вероятности. Есть ли какие-то люди, которые занимаются квантовой механикой и теорией вероятностей? Александр Буфетов: Конечно, такие исследования ведутся, я очень далек от этого, но, в конце концов, и знаменитый интеграл Фейнмана – на него можно смотреть, как на попытку написать интеграл, аналогичный тому интегралу, который пишется для броуновского движения. Кажется, на этом пути нет строгой математической теории, но я не специалист. Математическими аспектами квантовой механики занимаются очень многие математики, но не я. Александр Печень: Есть такая область науки – квантовая вероятность, получена неким обобщением колмогоровской теории вероятностей. Наталия Демина: Это было уточнение от лауреата премии Правительства Москвы молодым ученым Александра Печеня из Стекловки. Сегодня была церемония награждения этой премией Александр Буфетов: Давайте его поздравим! (аплодисменты). Борис Долгин: Такой вопрос. Вы, говоря об истории развития теории вероятностей, говорили о стадии, когда она не воспринималась как математика. А воспринималась как что? Как наука? Александр Буфетов: На этот счет были споры. Именно это я и пытался передать, что как такая сомнительная наука. Борис Долгин: Нечто на грани науки? Александр Буфетов: Нет, понимаете, от теории вероятностей нельзя отмахнуться. Понимаете, невозможно в одной лекции рассказать обо всей истории теории вероятностей, и тут не ставил я себе такой задачи. Я сконцентрировался на вопросах формального обоснования. Но еще Галилей интересовался вопросом, вы проводите астрономические измерения (их проводили чрезвычайно точно во времена Галилея), но естественно, какие-то ошибки есть. Вот нанесены результаты десяти измерений, как найти правильно среднее значение? Гаусс этой задачей занимался. То, что теория вероятности дает правильные ответы на нужные вопросы, в этом ни у кого сомнений нет. Прикладное значение теории вероятностей никогда не подвергалось сомнению (страхование, азартные игры), это с древнейших времен. А вот наука это или нет, и какова роль субъективного (была же попытка де Финетти), здесь мы уходим в область философии науки, это совсем уже другое. Я не знаю, ясно ли я ответил. Борис Долгин: Вполне ясно. По крайней мере, во многих случаях, из лекции, в которой нам рассказывали по поводу некоторых лекарств: эффект их до какого-то момента понятен, но механизм их обоснования не был научен, но факт использования. Видимо, это довольно близкая аналогия. Виктор Табаков (НИУ-ВШЭ): У вас в лекции связаны такие, на первый взгляд, никак не связанные вещи, как математический анализ, который занимается функциями, и теория вероятностей. Можете объяснить почему? Александр Буфетов: Да, конечно могу. Это как раз очень легко сделать, потому что вместо случайной величины рассматривается ее распределение. Это функция на прямой. Например, независимым случайным величинам отвечает произведение плотностей или свертка функций распределения. Тут неважно знать, что такое свертка, это некое понятие из математического анализа, оно есть в учебниках математического анализа, тут не нужно знать вероятность. И можно сформулировать теорему о свертках функций, и где-то в уме понимать на самом деле, что речь идет о независимых случайных величинах. Тьюринг так и делает. Англичане так плохо поступили с Тьюрингом при жизни, что стараются всеми силами загладить это после его смерти, и в электронный архив Тьюринга выложена эта работа, вы можете посмотреть сами. Тьюринг доказывает теоремы про свертку функций. Сам Тьюринг заинтересовался этими вопросами, потому что он слушал в Кембридже лекции по астрономии, где естественно обсуждалась статистика ошибок измерений, это фундаментальный вопрос в астрономии, как распределены ошибки в измерениях. И он захотел это обосновать, доказать. Но все это переформулируется в терминах теории функций. Я понятно сказал? Борис Долгин: Да. Спасибо большое за лекцию! (Аплодисменты)
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Математика ≫ Математика случая. История теории вероятностей // Александр Буфетов |
|
[time: 7 ms; queries: 7]
7 Мар 2026 10:49:48 GMT+3 |





















 Лекция прочитана 29 июня 2009 г. в поселке Московский на V Конференции лауреатов конкурса учителей физики и математики фонда Дмитрия Зимина «Династия».
Лекция прочитана 29 июня 2009 г. в поселке Московский на V Конференции лауреатов конкурса учителей физики и математики фонда Дмитрия Зимина «Династия». Теория вероятностей — один из важнейших разделов математики, занимающийся изучением случайных явлений и выявлением их закономерностей. Эта теория возникла ещё в средние века, благодаря выдающимся учёным: Блезу Паскалю и Пьеру Ферма, которые провели математический анализ азартных игр. Едва появившись, она во мгновение ока вызвала к себе неподдельный интерес учёных и быстро проникла в научный мир, став его неотъемлемой частью. Какие законы управляют случаем?
Теория вероятностей — один из важнейших разделов математики, занимающийся изучением случайных явлений и выявлением их закономерностей. Эта теория возникла ещё в средние века, благодаря выдающимся учёным: Блезу Паскалю и Пьеру Ферма, которые провели математический анализ азартных игр. Едва появившись, она во мгновение ока вызвала к себе неподдельный интерес учёных и быстро проникла в научный мир, став его неотъемлемой частью. Какие законы управляют случаем? Природа статистических законов вызывала споры с самого рождения теории вероятностей и продолжает их вызывать. Эти философские споры привели к рождению интересной математической теории: алгоритмической теории вероятностей и информации, которая — в отличие от классической — пытается дать определение индивидуального случайного объекта. Мы обсудим основные понятия этой теории и их связь с основаниями и парадоксами теории вероятностей. Об этом в публичной лекции математика Александра Шеня, кандидата физико-математических наук, старшего научный сотрудник Лаборатории теории передачи информации и управления ИППИ РАН.
Природа статистических законов вызывала споры с самого рождения теории вероятностей и продолжает их вызывать. Эти философские споры привели к рождению интересной математической теории: алгоритмической теории вероятностей и информации, которая — в отличие от классической — пытается дать определение индивидуального случайного объекта. Мы обсудим основные понятия этой теории и их связь с основаниями и парадоксами теории вероятностей. Об этом в публичной лекции математика Александра Шеня, кандидата физико-математических наук, старшего научный сотрудник Лаборатории теории передачи информации и управления ИППИ РАН.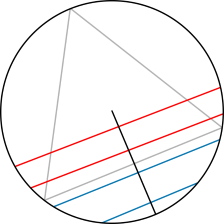 Парадокс Бертрана заключается в следующем: рассмотрим равносторонний треугольник, вписанный в окружность. Наудачу выбирается хорда окружности. Какова вероятность того, что выбранная хорда длиннее стороны треугольника. Бертран предложил три решения, дающие различный результат.
Парадокс Бертрана заключается в следующем: рассмотрим равносторонний треугольник, вписанный в окружность. Наудачу выбирается хорда окружности. Какова вероятность того, что выбранная хорда длиннее стороны треугольника. Бертран предложил три решения, дающие различный результат.