Природа статистических законов вызывала споры с самого рождения теории вероятностей и продолжает их вызывать. Эти философские споры привели к рождению интересной математической теории: алгоритмической теории вероятностей и информации, которая — в отличие от классической — пытается дать определение индивидуального случайного объекта. Мы обсудим основные понятия этой теории и их связь с основаниями и парадоксами теории вероятностей. Об этом в публичной лекции математика Александра Шеня, кандидата физико-математических наук, старшего научный сотрудник Лаборатории теории передачи информации и управления ИППИ РАН, научный сотрудник LIRMM CNRS (Франция, Монпелье). Лекция состоялась 6 марта 2014 года в рамках цикла «Публичные лекции «Полит.ру».

Стенограмма лекции

Я начну с двух «дисклеймеров». Во-первых, не очень понятно, правильное ли время выбрано для этой лекции — тут происходит аншлюc, а мы собираемся говорить о теории вероятностей. Но лекция была назначена уже давно. Второе. Я вообще не очень понимаю, есть ли смысл в таких научно-популярных лекциях. Можно ли рассказать, чем занимается современная наука, за пять минут или за два часа?

Я постарался сделать всё, что смог, подготовил разные слайды и фотографии. Для начала я хочу показать кусочек фильма, — возможно, вы его видели, — «Розенкранц и Гильденстерн мертвы». Фильм совершенно не про теорию вероятностей, а по пьесе Стоппарда по мотивам Шекспира. Я покажу кусочек, который касается теории вероятностей, может быть, люди соберутся за это время.

Что такое наука, в терминах философов? Она что-то такое предсказывает, и потом эти предсказания подтверждаются. Так, небесная механика предсказывает, где какая планета будет, и почти никто не сомневается, что через 20 лет они будут на тех самых местах, даже если на них некому будет уже смотреть. С другой стороны, когда мы в реальном мире бросаем монету или пытаемся узнать, когда распадется атом, то наука этого предсказать не может, по крайней мере, это до сих пор не удавалось. И если рассуждать философски, можно спросить, почему так: мы не умеем предсказывать или этого в принципе предсказать нельзя?

Это вопросы философские и поэтому довольно бессмысленные. Но если в одной фразе попытаться сказать, что такое теория вероятностей, то получится такое определение: это некая попытка сделать позитивные выводы из невозможности предсказаний. Я попытаюсь объяснить, что здесь имеется в виду.

Здесь представлен кусочек из письма Достоевского жене, как он в городе Баден-Баден решил сходить в казино. Это на самом деле не одно письмо, он написал много душераздирающих писем, как он проигрывал, а она ему присылала деньги, он их опять проигрывал, она еще присылала деньги, уже последние — очень грустно читать.

Достоевскому казалось, что можно выиграть, просто надо знать, как играть — он говорит, что «играть надо много времени, много дней, довольствуясь малым, если не везет, и не бросаясь на шанс». Дальше приводится позитивный пример (в стандартном издании тут прочерк, но в интернете можно найти вариант, где он заполнен): «есть тут один [жид], он играет уже несколько дней с ужасным хладнокровием и расчетом, нечеловеческим, его начинает бояться банк, он каждый день уносит выигрыш». То есть идея, что выиграть в казино в принципе нельзя, никакая система не поможет, на самом деле не очевидна — по крайней мере, Достоевскому она не была понятна.

Я не знаю, кто и что слышал про теорию вероятностей, поэтому — если совсем по-простому: что, собственно, мы имеем в виду, когда говорим, что вероятность выпадения орла у «честной» монеты 50%? Что, собственно, нарушалось в этом самом фильме? Ответ очень простой: если мы будем бросать монету много раз, то доля единиц будет примерно равна доле нулей. Конечно, не в точности будет половина, а примерно. Если мы бросаем монету миллион раз, то я бы взялся поспорить, что отклонение будет не больше 5%. (На самом деле, скорее всего, даже меньше — это надо вычислять, но я думаю, что уж точно можно поставить сто против одного, что не больше 5%.)

Более того — это важно в случае с Достоевским и вообще с игрой, – доля единиц останется примерно равной доле нулей, даже если мы будем выбирать бросания по какому-то правилу. Скажем, в казино можно пропустить ход. На самом деле, казино устроено так: там есть красное и черное, одинаковое количество секторов на рулетке, и есть еще сектор, который ни то, ни другое — если он выпадает, то ставки уходят в пользу казино. В остальных случаях часть людей ставит на красное, часть — на черное, какая-то из этих групп угадывает, и все ставки делятся между угадавшими. Если бы игрок мог как-то предвидеть, будет единица или ноль, то можно было бы выигрывать. Но вроде бы предвидеть этого нельзя. Если бы нули и единицы (красное и чёрное) чередовались, то можно было бы выбрать каждое второе бросание и тогда среди выбранных членов доли единиц и нулей были бы неравными.

К сожалению, все картинки — сжатые, я прошу прощения у изображенных товарищей. Это Рихард фон Мизес, у него был более известный брат-экономист (основатель так называемой «австрийской школы», у его последователей есть разные оригинальные идеи про экономику). А сам он занимался аэродинамикой и математикой, — в частности, ему принадлежит идея, что случайность означает устойчивость частот и невозможность уклонения от этой устойчивости никакими правилами выбора.

Если мы знаем, что выпадало до этого момента (какие были последние бросания), помогает ли это нам предвидеть, какое будет следующее? Например, пусть мы бросаем монету и почему-то выпало пять орлов подряд. Это редко, но бывает (теоретически 1/32 всех случаев). Как вы думаете, в следующий раз скорее выпадет решка или орел?

(обращаясь к слушателю) Вы отрицательно качаете головой, это что означает?

Слушатель: Одинаково.

Александр Шень: Одинаково. Это стандартная точка зрения теории вероятностей, которая и состоит в отсутствии правил выигрыша — если б мы знали, например, что чаще выпадает решка (или орел), то это бы позволило нам успешно играть.

Тут надо сделать оговорку. Скажем, если мы бросаем монету, которую я принес и при вас бросаю, но вы ее сами не видели, и пять раз подряд выпал орел, то можно заподозрить, что там с обеих сторон орёл. (Странно, между прочим, что в этом фильме они не стали внимательно проверять обе стороны — ведь не так сложно изготовить такую монету.)

Теория вероятностей — наука, о которой очень часто разные люди пишут какую-то ерунду. Достоевский — это, скорее, трагический случай, а следующая история — наоборот, забавная. Есть такой рассказ Эдгара По «Тайна Мари Роже» (The Mystery of Marie Rogêt). «Ничто не может быть более трудным, чем объяснить применительно к понятиям нижних чинов, что если шестерки уже выпали подряд дважды, то есть основания ожидать, что на третий раз они уже не выпадут. Обычно это предположение отвергается нашим сознанием. Кажется, что два случившихся бросания уже в прошлом и не могут иметь никакого влияния на третье. И шанс выбросить шестёрки кажется таким же, как всегда — и попытка возразить вызывает улыбку, а не желание разобраться».

И дальше По пишет про эту (якобы) ошибку: «я не могу ее объяснить в пределах этого рассказа, а для философски мыслящих она не требует объяснения, достаточно сказать, что это одна из бесконечной серии ошибок, которые возникают на пути сознания» (не знаю, как в конце перевести «склонность к поиску деталей»).

Обычно, когда философы говорят возвышенно, это какая-то банальная путаница — и у Эдгара По тоже. Или, может быть, он разыгрывал читателей, чего не знаю, того не знаю, но вот такая странная вещь написана (и в русских переводах). То ли он действительно этого не понимал, то ли он хотел поставить опыт над читателями.

Так или иначе, теория вероятностей говорит нам, что любые комбинации одинаково вероятны. Возникает некоторый парадокс, и именно его я хочу сегодня обсудить.

Как вообще устроена наука? Обычно говорят примерно так: есть гипотеза, например, о законах движения планет. Проводится эксперимент, проверяющий предсказания, даваемые этой гипотезой. В этом эксперименте она подтверждается или не подтверждается. Если не подтверждается, то строится новая гипотеза, более точная, делается новый эксперимент — получается такой цикл научного познания.

Теперь возникает вопрос: допустим, у нас появляется гипотеза, что монета честная, и мы хотим проверить эту гипотезу. Чтобы ее проверять, нужно монету бросать. Допустим, мы бросили ее много раз, и получились чередующиеся нули и единицы. Наверно, мы отвергнем гипотезу честной монеты — ведь странно, почему это нули и единицы вдруг чередуются.

Можно объяснять так, почему мы отвергаем гипотезу случайной монеты: «последовательность 010101010… чередующихся нулей и единиц имеет очень малую вероятность, если монета падает случайным образом, и поэтому монета не случайна». Но проблема с этим объяснением состоит в том, что ведь любая другая последовательность имеет ту же самую малую вероятность. Собственно, в том и состоит гипотеза честной монеты, что все последовательности одинаково маловероятны.

Возникает парадокс.

Я еще раз написал его на слайде. Если мы говорим, что монета честная, это значит, что все последовательности одинаково вероятны. Мы бросили монету, получили какую-то последовательность. Если мы с самого начала говорили, что падения монеты одинаково вероятны, то как же мы можем по этому результату отвергнуть эту гипотезу? Казалось бы, какая разница, если они все одинаковые.

С другой стороны, если мы не можем отвергнуть эту гипотезу, то как сказали бы философы, какой же в ней смысл, если ей ничего не противоречит (как, в свое время, марксизму-ленинизму)? Есть ли в ней тогда вообще какой-то смысл? И это, действительно, философский вопрос, который на самом деле возник не в XX веке, он волновал и Лапласа (1749-1827), и Паскаля (1623-1662). Вопрос совершенно практический и не такой простой; я хочу привести еще несколько ситуаций, в которых он возникает.

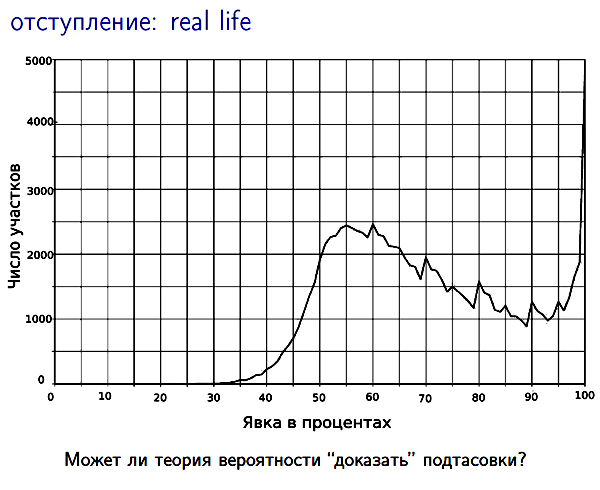
Это фрагмент из книги, изданной примерно в 1950-м году, она называется «Таблица случайных чисел». Не знаю, видно или нет, там левый ряд чисел — это, конечно, не случайные числа, а номера строк (50, 51, 52 и т. д.). А дальше приведены, как утверждается, случайные числа, полученные в результате некоторого физического опыта (не знаю, монету ли бросали или что-то еще). Опыт сделали симметричным, качественным, записали то, что получилось, и опубликовали — для статистических выборок и пр.

Так или иначе, такая книга с таблицей случайных чисел опубликована. Возникает тот же самый вопрос. Представим, что вы купили такую книгу, а в ней одни нули. Наверное, вы будете недовольны, и захотите вернуть книгу обратно. Вас спросят: «А чем вы недовольны, чем плоха книга?» Вы скажете: «Ну как, в ней одни нули. Они имеют малую вероятность, это невозможно, чтобы при случайном бросании выпала целая книга одних нулей». «Ну, хорошо, — ответят вам, — у нас есть другая книга, вот такая, как на слайде, она вас устроит?». И вроде да, такая книга должна устроить, но в чем же разница? Вероятность появления такой последовательности, как в этой книге — такая же маленькая, как появление одних нулей. В этом есть некоторый парадокс.

Другой парадокс. Я в свое время прочел в книжке Лотмана (то ли в комментариях к «Евгению Онегину», то ли просто в «Беседах о русской культуре») — оказывается, в XIX веке играли так: колода подавалась запечатанной, и ее прямо на месте игроки распечатывали (может, после этого снимали, не знаю, будем считать, что нет) и с ее помощью играли. А потом эти карты бросали на пол, и дальше играли слуги в своего «дурака» или во что-то ещё — серьезные люди второй раз карты не использовали.

Представим себе (тогда, конечно это было не так), что это происходит сейчас — тогда на фабрике, где делают колоды, их тасует какая-то машина. Потом хорошо бы как-то проверять качество тасования — перед тем, как запечатывать, надо посмотреть и понять, хорошо ли перетасована эта колода или плохо. И вот опять возникает вопрос: что значит «хорошо перетасована», если все варианты расположения одинаково вероятны?

Если мы какие-то варианты отвергаем и говорим, что «карты плохо перетасованы», а другие допускаем, потому что «карты хорошо перетасованы», то это противоречит самой идее хорошего тасования. А если мы допускаем все варианты, то, спрашивается, что же мы проверяем?

Или практический вопрос. Допустим, в поезде вас обыграли шулеры, и вы даже решили судиться с ними, доказать, что тот расклад, который случился, является результатом сговора, а при честной игре такого быть не может.

Я помню, что еще в советское время читал в газете, как осудили шулеров за то, что они в поезде обыграли какого-то бедного (богатого?) человека. И даже помню, какие были доказательства. Во-первых, были запрошены математики, и они сообщили, что вероятность такого расклада очень мала. А во-вторых, был поставлен эксперимент, милиционеры два дня подряд играли в карты, и такого расклада ни разу не случилось. Кажется, обвиняемые к тому же признались.

На практике это может быть убедительно — иногда достаточно только посмотреть, и сразу можно заподозрить. Но ясно, что вероятность любого конкретного расклада очень мала. И пусть даже милиционеры играли два дня подряд, крайне маловероятно, что то же самое получится еще раз. Так что с точки зрения науки эти доказательства какие-то странные.

Синим цветом на слайде сформулирован философский вопрос, к которому все сказанное раньше было иллюстрацией. Можно ли говорить о случайности индивидуального объекта?

Борис Долгин: Вопрос на уточнение.

Слушатель: Вы тут ввели индивидуальные объекты, и почему-то последовательность записываете не в индивидуальный объект, откуда это взялось?

Александр Шень: В каком смысле индивидуальный объект? Нет, я ничего научного не хочу сказать, одна конкретная последовательность.

Слушатель: Последовательность в целом, а не из отдельных событий.

Александр Шень: Нет, вопрос такой, допустим, у нас есть книжка, имеет ли смысл вообще спрашивать, а случайны ли числа в этой книжке?

Борис Долгин: На самом деле, вопрос заключался в том, что такое индивидуальный объект? Перед тем, как оперировать этой категорией, надо ее ввести.

Слушатель: Нет, автор дал ответ, что эта таблица и есть конкретный в данном случае индивидуальный объект.

Борис Долгин: Стоп. Это не определение.

Александр Шень: Хорошо. Можно ли говорить, когда какое-то событие уже произошло и какие-то экспериментальные данные уже есть, — можно ли по этим данным судить, подтверждается или нет та или иная статистическая гипотеза? Именно этот вопрос я пытался проиллюстрировать на разных примерах.

В качестве отступления о доказательствах с помощью теории вероятностей приведу еще один пример. Наверное, эту картинку многие из вас видели, это известная картиночка с красивыми пиками про голосование какого-то года — 2007-го или 2011-го.

Что там сделано? Там для всех участков, которые были в России, отмечено, сколько процентов избирателей туда явилось, и нарисован такой график. Чем выше кривая, тем больше число участков, на которые пришло столько-то процентов избирателей. По-видимому, это с шагом в один процент сделано, я сейчас не помню точно. Видно, скажем, что в интервале от 65-ти до 66-ти процентов было две тысячи с чем-то участков. Вот такая картинка.

Что стали говорить люди? «Смотрите, вот тут на каждом целом десятке имеется острый пик, а на пятерках имеется менее острый, но тоже пик. Вероятность такого события при любой разумной гипотезе очень мала». С чего бы это на кратных 5 получается вдруг больше, чем в других местах? И можно даже пытаться как-то оценить вероятность и понять, что она очень маленькая. Но является ли это доказательством чего бы то ни было? Этот вопрос к теории вероятностей многие обсуждали.

* * *

Теперь, сказав про вопрос, хочу немного сказать про возможный ответ. Он был давно интуитивно ясен многим, но окончательно сформулирован в середине 1960-х годов несколькими людьми.

Я постарался найти фотографии этих людей. Это Андрей Николаевич Колмогоров в конце 1960-х годов — начале 1970-х, он что-то такое обсуждает со школьниками колмогоровского интерната, видимо, на природе. В 1965-м году он написал свою знаменитую статью на эту тему.

А это другой человек, который, как видите, гораздо моложе, эта фотография сравнительно недавняя, может быть, лет десять назад. Это Грегори Чейтин (Gregory John Chaitin), который тоже в середине 1960-х годов этим заинтересовался, при этом он был еще школьником. С ним была интересная история. Он придумал совершенно независимо ту же самую идею, что и Колмогоров, и послал статью, еще будучи школьником, в известный научный журнал (Journal of the ACM). Но там ее долго рецензировали, потом печатали по частям (в начале там была менее интересная часть), в конце концов, ее напечатали уже после того, как статья Колмогорова стала известной. Зато Чейтин достиг необычайных успехов в области рекламы. На слайде обложка журнала, на которой написано «The Omega man». Не знаю, можете вы прочесть или нет, там замечательная по бессмысленности фраза: «он знает число, которое разрушит всю определенность». Это, конечно, полный вздор (хотя я даже понимаю, откуда это происходит), зато очень красиво, — и видно по обложке, что явно он разрушит что-нибудь.

Тоже поучительная и по жизни интересная история про третьего человека. Это Рэй Соломонов (Ray Solomonoff), он недавно, к сожалению, умер.

Американский ученый, его жизнь тоже необычна. Он математике не учился, не работал ни в каком университете, организовал компанию из одного человека, которая почему-то называлась «Затор» (не знаю, было ли это связано с его русскими корнями) — и даже иногда получал гранты, публиковал статьи. Его статьи вышла даже раньше, чем статья Колмогорова, в 1964 г.. в хорошем журнале "Information and Control". Написаны они были — с точки зрения математиков — очень забавно, я даже специально выписал фрагмент из статьи Соломонова.

«Автору кажется, что уравнение (1) скорее всего правильное, ну или почти правильное, но что методы работы с задачами разделов 4.1–4.3 скорее будут правильными, чем уравнение (1). И что если уравнение (1) окажется бессмысленным, противоречивым или даст какие-то результаты, которые интуитивно неразумны, то его надо модифицировать так, чтобы не разрушить методы, использованные в разделах 4.1–4.3».

Это его главная публикация в серьезном журнале. Естественно, люди к этому относились скептически, пока Колмогоров не сослался на него — до Колмогорова никто на Соломонова не обращал серьёзного внимания. Но Колмогоров тоже про работы Соломонова не знал, пока ему кто-то не сказал.

Какой же ответ предлагают эти три уважаемых товарища? Идея такая, что случайность индивидуального объекта, последовательности нулей и единиц, означает то, что в ней нет закономерностей. Ну а закономерности — это то, что можно использовать, чтобы задать последовательность короче. Скажем, в компьютерных терминах, если вы можете написать программу, которая порождает (печатает) эту последовательность, и программа короче, чем сама эта последовательность, то, значит, в последовательности есть закономерность. Если же самый простой способ описать последовательность состоит в том, что просто написать все ее биты, то, значит, закономерности в ней нет. Это некоторое неформальное описание сложности по Колмогорову (или по Соломонову, или по Чейтину, но обычно говорят «колмогоровская сложность», так как все читали Колмогорова).

Сложность конечной последовательности нулей и единиц — это минимальная длина программы, которая порождает эту последовательность. А случайность означает, что сложность равняется длине самой последовательности, что никакое сокращение тут невозможно.

Здесь показана рукопись Колмогорова — это не самая его первая статья на эту тему, а обзорная статья, которая была написана к 1970-му году к докладу на конгрессе в Ницце. Каждые четыре года происходит всемирный математический конгресс, туда приглашаются наиболее уважаемые люди, чтобы сделать доклад. Колмогоров должен был делать доклад об этой своей теории. Потом была выпущена книжка докладов советских участников этой конференции.

Но там, как это было типично для советского времени, произошел скандал. Это –- те же самые конгрессы, где вручаются Филдсовские премии. И Сергея Петровича Новикова, лауреата этой премии 1970 года, на этот конгресс в Ницце не пустили. Колмогоров пытался чего-то добиться, в конце концов, кончилось тем, что из сборника текстов советских участников его статья была исключена. И была она напечатана только в 1983-м году.

Тогда уже Колмогоров был очень болен, и у него все время кто-то должен был дежурить. И я был одним из дежурных. И вот как раз на период моего дежурства пришелся момент, когда ее перепечатывали для «Успехов математических наук» (за тринадцать лет скандал как-то забылся, ее решили напечатать, был юбилей Колмогорова, семидесятилетие). Оригинальную рукопись выбросили в мусорную корзинку, я не выдержал и тихо ее вынул из этой мусорной корзинки и сохранил. Увы, музея Колмогорова нет и отдать ее некуда, но, тем не менее, она сохранилась.

Там сверху написана основная формула: cложность K(x) –- это минимальная длина l(p) программы p, для которой результат работы S(p) равен номеру n(x) последовательности x. Считается, что все последовательности пронумерованы (технические детали), но речь идет о той же самой идее: сложность объекта (последовательности) — это минимальная длина программы, которая его (ее) порождает.

Итак, случайная последовательность -– эта та, у которой сложность близка к длине (т.е. которую нельзя описать короче). Возникает интересный психологический вопрос. Допустим, кто-нибудь хочет привести пример случайной последовательности. Может ли он «из головы» (не бросая монеты реально) написать, скажем, последовательность из тысячи нулей и единиц так, чтобы ее потом нельзя было отличить от случайной? (Можно, конечно, сжульничать и взять пример из книжки с таблицами случайных чисел –- там не нули и единицы, а цифры, но это несущественно.)

Это совсем не просто, по крайней мере, без специальной тренировки. Я проводил такой конкурс для студентов в Лионе: им предлагалось написать случайную последовательность, и потом к написанным ими последовательностям были добавлены последовательности из таблиц случайных чисел, и дальше предлагалось определить, какие из них написаны человеком, а какие нет. Это более-менее можно сделать, и как раз из-за того самого эффекта: последовательности, которые пишет человек, обычно можно сжать. То есть, как вы ни старайтесь написать что-то такое произвольное и несжимаемое, это у вас вряд ли получится.

Для конечных последовательностей все-таки нельзя сказать, что вот эта случайна, а эта нет — нельзя провести четкую границу. Потому что мы можем постепенно заменять единицы на нули, начав с самой настоящей случайной последовательности, а в конце получить явно не случайную последовательность из одних нулей. Трудно себе представить, что при этом в какой-то конкретный момент произошло качественное изменение — было случайно, а стало неслучайно. То есть для конечных последовательностей бессмысленно пытаться провести четкую границу.

Это можно сделать для бесконечных последовательностей. Первое удовлетворительное определение такого рода предложил шведский математик Пер Мартин-Лёф.

Поскольку меня учили, что должно быть человеческое измерение — надо рассказывать байки. Одна перекликается с современным моментом. Мартин-Лёфа призвали в шведскую армию. Швеция, как известно, нейтральная страна (потому, может быть, и нейтральная, что они там тренируются). Когда я был в Швеции, как раз при мне писали от факультета письмо королю, что аспирант такой-то очень ценный, и не надо его призывать на месяц тренироваться в армии, а вот пусть он у нас тут лучше будет на факультете. Кажется, король с одобрением отнесся к этому прошению.

Так вот, в армии Мартин-Лёф в качестве военной службы изучал русский язык. После этого он решил, что раз русский язык он изучил, надо это использовать в каких-то мирных целях. Он по специальности был статистиком, и решил, что надо бы поехать в Москву к Колмогорову, и это ему удалось. (Он говорит по-русски не то, чтобы совсем свободно, но неплохо.)

И вот он ходил на семинары, и Колмогоров ему дал какую-то задачу по статистике, но она его не очень увлекла. Зато ученик Колмогорова, Леонид Бассалыго, который работает сейчас в ИППИ, ему рассказал, что у Колмогорова есть идеи о случайности. И он, вместо того, чтобы решать задачу, которую Колмогоров ему выдал, изучал эти идеи, и придумал определение случайной последовательности, и рассказал Колмогорову. Тому это очень понравилось, и Мартин-Лёф стал известен в первую очередь этими своими работами.

А потом он стал философом. Владимир Андреевич Успенский, мой научный руководитель, однажды его спросил — раз он философ — как так получается, что философов совершенно невозможно понять? И Мартин-Лёф сказал: «Ну, вы знаете, философы, действительно, очень трудны для понимания. Вот представьте себе, что вы — математик, решаете задачу, пишете статью, и в этой статье вы пишете все, что вам приходит в голову, все ваши мысли подряд — и то, от чего вы потом отказались. Можно это потом будет прочесть или нельзя?». Это объяснение произвело на Успенского большое впечатление. Ещё Мартин-Лёф, кстати, рекомендовал читать Хайдеггера как наиболее доступного простым людям философа. Может быть, это и понятно простому человеку, не знаю. Возможно, у Мартин-Лёфа были высокие представления о «простом человеке». Потом Мартин-Лёф занялся интуиционистской теорией типов, и это стало математической основой для системы проверки доказательств под названием Coq, в которой разные доказательства пишутся и автоматически проверяются.

Так или иначе, Мартин-Лёф придумал определение «случайной последовательности» в середине 1960-х годов, следуя идеям Колмогорова. И после этого удалось доказать, что это определение случайности действительно связано со сложностью.

Доказали это два человека.

Это Клаус Петер Шнор (Claus-Peter Schnorr), немецкий математик, который потом занимался криптографией.

И бывший наш соотечественник Леонид Анатольевич Левин, который родился примерно тогда же, когда Чейтин. Левин тоже в середине 1960-х был школьником, учился в киевском физико-математическом интернате, а потом переехал в Москву и поступил в колмогоровский интернат. Как он рассказывал, у него возникла идея, что можно определить понятие сложности логически. Он рассказал про это Алексею Брониславовичу Сосинскому, который тогда работал в интернате. А Сосинский хорошо знал Колмогорова и сказал, что «да-да, Колмогоров недавно этим занимался», и рассказал, в чем состоят работы Колмогорова, и это произвело на Левина большое впечатление.

Левин рассказывал, что, будучи школьником, он знал, что Колмогоров — академик, и вообще-то понимал, конечно, что академики больше знают. Но что они еще и лучше соображают, этого он никак себе представить не мог, и это произвело на него неизгладимое впечатление, и с тех пор он с исключительным уважением отзывается о Колмогорове (не только поэтому, конечно). Левин написал диссертацию о колмогоровской сложности, где впервые было введено понятие так называемой «префиксной сложности», и сделал множество других интересных работ.

В Москве его даже до защиты не допустили, потому что он «развалил комсомольскую работу» или что-то в этом роде. И даже потом, кажется, следующий секретарь комитета ВЛКСМ, который его выгнал, сказал, что «нам нужен ленинский комсомол, а не левинский». Он подал диссертацию к защите в Новосибирске, но КГБ это тоже проследил, и совет в Новосибирске под председательством ныне здравствующего академика Юрия Леонидовича Ершова эту работу отверг. Но Левин, кстати, говорил, что по справедливости он бы должен часть своей американской зарплаты жертвовать Ершову, потому что, если бы не Ершов, он бы не уехал — не собирался. В Америке Левин работал в MIT, сейчас он — профессор Бостонского университета (США), так что с материальной точки зрения (по крайней мере) он очень выиграл и должен быть благодарен Юрию Леонидовичу. (Кажется, они даже один раз встречались, но я не видел, чтобы Левин осуществил свой план.)

Так вот, Шнорр и Левин установили связь между случайностью по Мартин-Лёфу и сложностью.

Еще немного о том, что такое сложность, и как ее можно себе представлять. Наверное, все пользовались компьютерами, многие, может быть, даже пользовались командной строкой и знают, что бывают команды zip, unzip, gunzip, bzip2, которые сжимают файлы. Идея состоит в том, что если есть, скажем, какой-то текст в виде файла, то на самом деле он хранится неэкономно. Если его предварительно обработать, то можно получить сжатую версию этого файла, из которой можно восстановить исходный, и эту сжатую версию удобнее хранить (больше поместится на дискету, и пр.)

Если файл удалось сжать, то это означает, что его колмогоровская сложность мала. Размер после сжатия можно в первом приближении считать сложностью файла — точнее, некоторой верхней оценкой колмогоровской сложности. Почему верхней оценкой? Потому что, возможно, что архиватор просто не понял, какие в файле есть закономерности, и не использовал их полностью, или вообще не использовал. Если нам не удалось сжать файл, то, может быть, он сжимаемый, а может быть и нет, это неизвестно. Если удалось, то у него маленькая колмогоровская сложность.

Можно проделать такой эксперимент. Бросим монету 80 тысяч раз (8 битов = 1 байт, то есть, скажем, чтобы получить 10 килобайтов, надо бросать 80 тысяч раз), и полученный файл в 10 килобайтов попытаемся сжать. И — такой экспериментальный факт — сжать не удастся. С точки зрения математика, есть теорема, состоящая в том, что подавляющее большинство последовательностей не сжимается (или, может быть, чуть-чуть сжимается). Сильно сжать можно только небольшую долю последовательностей — просто потому, что сжатых файлов мало.

Теперь философы могут рассуждать о возникающем законе природы. Если мы поставим опыт, состоящий в том, что мы бросаем монету, а потом пытаемся сжать результат бросаний, то это не получается. Это — новый закон физики или это следствие других законов? На эту тему можно долго разговаривать.

Еще один великий человек, так или иначе связанный с колмогоровской сложностью. Его основные работы были сделаны задолго до колмогоровской сложности, хотя умер он позже — последние годы жизни он был не так активен. Наверное, все слышали о «теоремах Геделя». Есть четыре знаменитых теоремы. Первая называется «теорема о полноте», вторая — «о неполноте», что сбивает с толку; третья («вторая теорема о неполноте») – про недоказуемость непротиворечивости формальных теорий, четвертая — про совместность аксиомы выбора и континуум-гипотезы с аксиомами теории множеств (это 1940-е годы).

Про каждую из них можно долго говорить, и у него есть еще и другие результаты; он участвовал в формировании идеи вычислимости функций. Это, по-видимому, самый великий логик, если смотреть на всю историю науки. В частности, одна из вещей, благодаря которой он заслуженно прославился, состоит в том, что он придумал пример недоказуемого истинного утверждения.

Вторая из перечисленных теорем — «о неполноте» — говорит о том, что есть истинные утверждения, которые нельзя доказать. Вот пример такого утверждения, который предложил уже не сам Гёдель, а Чейтин: надо бросить монету, скажем, два миллиона раз, и получить последовательность нулей и единиц. И дальше сформулировать такую теорему: «сложность этой последовательности не меньше миллиона» (ее можно сжать не более чем вполовину). Практически наверняка это будет истинно для случайно выбранной последовательности — сжимаема очень небольшая часть всех последовательностей. Так что большинство таких утверждений истинно, но ни одно из них не доказуемо. Получаем пример истинного, но недоказуемого утверждения. В существовании таких утверждений и состоит теорема о неполноте.

Идею доказательства тоже можно пытаться интуитивно объяснить в одной фразе. Есть такой парадокс, который Бертран Рассел приписал библиотекарю своего колледжа по фамилии Берри (он ничем вроде больше не известен, я не смог найти его фотографию). А именно, «рассмотрим минимальное число, которое нельзя описать семью словами». (Имеются в виду натуральные числа.) Ясно, что семью словами можно описать конечное количество натуральных чисел, и потому есть какое-то минимальное, которое нельзя описать. Рассмотрим его. Мы замечаем, что его нельзя описать, а, с другой стороны, мы написали семь слов, которые его описывают. Возникает противоречие. Этот «парадокс Берри» лежит в основе доказательства Чейтина теоремы Геделя.

Последнее, что я хотел сказать. Меня много спрашивали, есть ли какая-то практическая польза в колмогоровской сложности. Сам этот вопрос, по-моему, неправильно поставлен.

Я уже многим это рассказывал, может быть, кто-то уже слышал эту мою болтовню о том, какая польза от науки. Пользу от науки можно объяснить примерно так же, как пользу от кефирного грибка. В советское время была такая распространенная вещь, как кефирный грибок (поднимите руки, кто вообще его видел). Это что-то типа цветной капусты, такая довольно склизкая штука, там маленькие чешуйки. Ее можно было положить в молоко, и это молоко прокисало, образовывалась закваска. Сам по себе грибок несъедобен, и его даже мыть было противно. Закваска тоже была несъедобна, но если эту закваску развести с молоком и поставить на день, то получался вкусный кефир.

Такая же примерно и польза от науки. На факультет математики в университет поступают сотни людей каждый год, из них математиками становятся, скажем, десять. Это число зависит от того, где провести границу, но, в общем, профессионально занимается наукой очень небольшая часть. И эта часть как раз бесполезная. От них никакой пользы в жизни нет. Но зато от тех, кто не стал заниматься наукой, может произойти большая польза — они могут придумать что-нибудь интересное. Или, наоборот, сделать что-нибудь вредное, типа атомной бомбы — то есть они могут оказать влияние на жизнь.

Да и те, кто математику не бросит, могут, скажем, стать профессорами математики — и будут преподавать большому количеству людей, из которых лишь небольшая часть станет заниматься наукой или станет преподавать. В общем, те люди, которые занимаются наукой, они как кефирный грибок. Они и на вид какие-то неприятные, и пользы от них как бы никакой. Но, с другой стороны, без грибка закваски бы тоже не было.

Примерно то же самое можно сказать и про колмогоровскую сложность. Это не так, чтобы «утром в газете, вечером в куплете», чтобы сегодня математик что-то доказал, а завтра инженер это прочел и применил. Конечно, нет. Но, тем не менее, бывают идеи, которые возникают при изучении математических вопросов о колмогоровской сложности, и которые впоследствии оказываются полезными. Может быть, кто-то из присутствующих видел текст, отсканированный и сжатый в формате djvu. Авторы этого формата, когда они его разрабатывали, отчасти вдохновлялись идеями Колмогорова (точнее, идеями алгоритмической статистики, использующей понятие колмогоровской сложности) — что понять структуру объекта означает, в сущности, его сжать, и сравнивать разные методы его структурирования это, по существу, сравнивать способы сжатия.

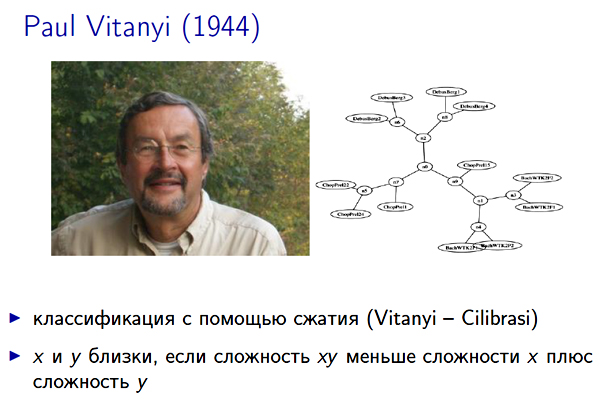
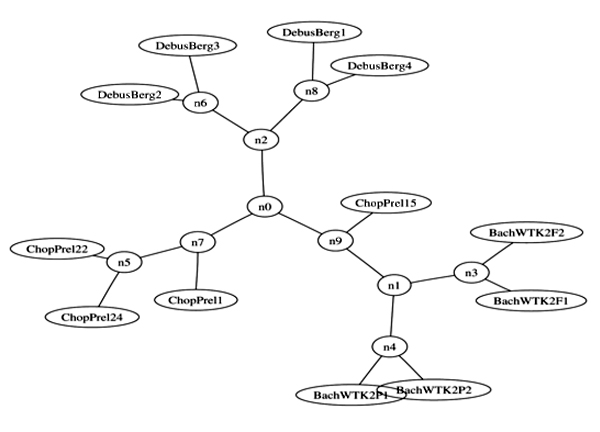
Совсем знаменитый пример на эту тему связан с именем Пола Витаньи (Paul Vitanyi). Он живет в Голландии; в свое время он написал большую книжку о колмогоровской сложности, благодаря которой многие заинтересовались и которая сыграла большую роль в возрождении интереса к этой области исследований (после Колмогорова и его учеников был некоторый спад). Он и его коллега Руди Силибраси (Rudi Cilibrasi) проделали забавный опыт. Они решили классифицировать разные файлы с помощью идеи, которая изначально была связана со сложностью — с помощью сжатия.

Идея очень проста. Что значит, что файлы X и Y близки? Это значит, что если мы их соединим, напишем подряд и сожмем, то получится короче, чем если мы отдельно сожмем X и отдельно сожмем Y. Соответственно, то, насколько тут возникает сокращение, как бы измеряет расстояние между файлами.

На слайде рядом с фотографией картинка из одной из статей про эти эксперименты. На этой картинке классифицированы музыкальные midi-файлы (условно говоря, нотные записи произведений). И они расположены в виде дерева — рядом те, которые близки (похожи).

Если посмотреть внимательно, в одном таком кусте две прелюдии из «Хорошо темперированного клавира» Баха. Рядом две другие прелюдии, тоже из «Хорошо темперированного клавира».

С другой стороны наоборот - три прелюдии Шопена, а выше Дебюсси. Так что эта классификация более-менее согласована с нашей интуицией. Такие опыты делались не только на музыкальных примерах — как раз в то время открыли вирус то ли птичьего гриппа, то ли свиного гриппа, и его расшифровали, получив генетический код. И сразу после этого Витаньи с коллегами этот код (последовательность нуклеотидов) расклассифицировали вместе с известными вирусами, и выяснили, на что этот вирус похож, в какой группе вирусов она оказывается.

И потом, когда независимо биологи посмотрели на этот вирус и тоже сказали, в какой он группе — вирус оказался в той же самой группе, что и при машинной классификации. Это не то чтобы большое достижение, наверно, но всё же показано, что такой совершенно грубый, банальный способ классификации с помощью сжатия оказывается совсем не бессмысленным. При большом воображении это можно объявить практическим приложением идеи колмогоровской сложности.

Ну и совсем последнее — на картинке есть та самая музыка, которую вы слушали в начале. Это прелюдия Шопена ре бемоль мажор (часто называется «Капли дождя», Rain drops). Если знать музыку Шопена, то можно заметить, что она действительно довольно нетипична среди его произведений. И вот она попала ближе к группе с Бахом, несмотря на то, что на самом деле её написал Шопен. И всё это просто результат анализа сжатия midi-последовательностей. На конференции, где про это был доклад, скептики спрашивали, не забыли ли они удалить из файла имя композитора – нет, не забыли.

Обсуждение лекции

Борис Долгин: Как вы ко всему этому пришли? Для начала, к математике, а затем и к этой тематике.

Александр Шень: Я не очень уверен, что это интересно, но в детстве я ходил в музыкальную школу. Еще меня отвели в кружок начального технического моделирования во Дворце пионеров. Самолеты надо было делать, они все очень плохо летали. Потом там открылся математический кружок, который набрал ныне уже довольно пожилой человек, известный православный философ Виктор Николаевич Тростников. Тогда же он просто вел хороший математический кружок. Я туда ходил и несколько моих приятелей туда ходили, мы все ему очень признательны и благодарны. Мы недавно с ним встречались.

А потом мне сказали, что есть «Вторая школа», я туда пришел, меня поспрашивали и сказали, что, так уж и быть, вас примем. А к этому моменту меня очень достала необходимость постоянно заниматься на рояле, и я решил, что математика будет гораздо проще. Ничего не требуют, а главное, невозможно ничего проверить; моя бабушка не сможет сказать, что я не занимаюсь. А в музыке этого не скроешь.

Постепенно я перешел в эту школу. Но и в музыкальной школе нас учили геометрии. Я помню, что у нас был такой замечательный человек, тогда он мне казался глубоким стариком, я не знаю, сколько ему было лет, он был с бородой, прямо как Евклид. Еще он был главным судьей московского клуба канареечного пения (поэтому когда были канареечные олимпиады, уроки геометрии отменялись).

Естественно, что школьники не интересовались геометрией, и всегда на родительских собраниях обсуждалось, зачем она нужна. Родители были очень недовольны, что геометрией отвлекают маленьких музыкантов от занятий. Но он преподавал очень интересно, поэтому во «Второй школе» учиться было не сложно, и проблем с тем, что надо было все время что-то делать, было меньше, чем в музыкальной.

Я ездил на физические олимпиады, пытался и на математические, но там невозможно было что-то сложное решить. А на физических олимпиадах было гораздо проще. Я ездил и на Всесоюзную физическую олимпиаду, это было тогда в Горьком. Я даже думал, что надо поступать на физический факультет МГУ, но потом стало ясно, что туда поступить нельзя. Я помню, что я и двое моих знакомых были в команде Москвы на Всесоюзной олимпиаде, и вроде нас должны были пригласить на какие-то сборы для подготовки к международной олимпиаде. Но ни одного из нас не пригласили. И мудрые люди сказали, что это намек, что лучше не надо пытаться поступать на физфак, добром это не кончится. А на механико-математический (мехмат), может быть, и можно.

Поскольку у меня не было четкого понимания, чего я хочу, физика была немного проще, но математика тоже интересна, я поступил на мехмат МГУ. Я ходил, еще будучи школьником, на лекции Владимира Андреевича Успенского, которого, может быть, кто-то из присутствующих знает. Он рассказывал про вычислимые функции, с тех пор я заинтересовался теорией алгоритмов. Когда я был аспирантом, Колмогоров был уже очень болен, последний семинар в его жизни, который он организовал, был по сложности определений и сложности вычислений. Он открыл этот семинар и сделал свой доклад, и с тех пор семинар по традиции собирается (по понедельникам). Последние ученики Колмогорова были на этом семинаре — Евгений Асарин, Владимир Вовк, теперь они во Франции и в Англии. Конечно, семинар уже не тот, но все-таки он до сих пор продолжает работу.

Борис Долгин: Как произошла встреча с Владимиром Андреевичем Успенским?

Александр Шень: Меня с ним познакомил Виктор Николаевич Тростников, он сказал, вот есть такой спецкурс по вычислимым функциям на мехмате, и что можно туда попробовать сходить. Тогда это было проще, были какие-то бабушки, которые не очень хотели пускать, но милиционеров не было, и можно было пройти. Мы ходили с моим знакомым, который учился потом на мехмате, ходили и слушали спецкурс, это было очень интересно.

Слушатель: То есть, получается, колмогоровская сложность — это совершенно неконструктивное понятие, потому что минимальная длина программы уже строго формализовалась в математические единицы? Потому что, если мы знаем колмогоровскую сложность, то мы можем предсказать минимальный объем сжатого файла, такое сделано?

Александр Шень: Да. Ответ такой, что колмогоровская сложность — это строгое математическое понятие. С другой стороны, она зависит от того, какой язык программирования мы используем. Она зависит, но зависит не сильно. Если есть два языка программирования, то разница в колмогоровской сложности [определённой в терминах этих языков] будет ограничена некоторой константой. Ну и последнее, наиболее критическое замечание, которое вы правильно отмечаете и которое нельзя опровергнуть, состоит в том, что она невычислима. То есть, никакого алгоритма нет.

Можно формально спросить, какова колмогоровская сложность «Войны и мира», и даже фиксировав какой-то конкретный язык программирования, можно исследовать этот вопрос совершенно точно и он имеет смысл, но нет никакой надежды, что кто-нибудь когда-нибудь на него ответит. Потому что ответ, скорее всего, будет недоказуем.

Слушатель: Кто-нибудь пытался с этой точки зрения рассмотреть ДНК-последовательности, поддаются ли они сжатию?

Александр Шень: Конечно, некоторому сжатию они, безусловно, поддаются. Вопрос очень естественный, и, конечно, люди этим занимались, более или менее поиск закономерностей в этих последовательностях и есть поиск эффективных способов сжатия. Но, насколько я понимаю, радикально они не научились их сжимать. То есть внутренней структуры в них, которая позволила бы сжать их в десятки раз, не обнаружено. До сжатия UAGC — это 2 бита на каждую букву. Надо спросить у каких-то знающих биологов, но я думаю навскидку, что вдвое их сжать можно. Сжать в двадцать раз — вряд ли.

Слушатель: Остались ли «белые пятна» в теории сложности Колмогорова, и, в целом, в этом вопросе? Второй вопрос: все ли теории, над которыми вы работаете, вы понимаете? Есть ли теории, которых не понимаете?

Борис Долгин: Простите, что такое «понимать»?

Александр Шень: Во-первых, про «белые пятна» — это всегда вопрос философский. Можно спрашивать, получены ли ответы на основные вопросы, которые в первую очередь приходят в голову? В этом смысле, ситуация лучше, чем с теорией сложности вычислений, так как основной вопрос там, "P=NP?", остаётся широко открытым. С ним до сих пор никто не знает, что делать, и поэтому, вместо того, чтобы отвечать на этот вопрос, они себе изобретают какие-то другие вопросы, и на них пытаются ответить.

В колмогоровской сложности нет такого главного открытого базового вопроса, над которым все бы думали. С другой стороны, если начать заниматься более технически, то там много интересных открытых вопросов – я могу даже некоторые из них сформулировать. Как математическая наука, конечно, она не закончена. Если речь о том, есть ли какой-то центральный вопрос, имеющий философский смысл, и без ответа на который мы не можем двигаться, такого, пожалуй, нет.

Борис Долгин: А что вы сами пытаетесь делать?

Александр Шень: Я пытаюсь найти какой-то вопрос, на который можно подумать и ответить, — с переменным успехом, но пытаюсь. Понимаю ли я вопрос? Я бы сказал, что все-таки трудно работать над вопросом, не понимая его. Не то, что я все понимаю, просто я не работаю над теми вопросами, которые я не могу понять.

Слушатель: Очень часто у вас звучал такой момент, что «трудно поверить», «невозможно себе представить, что такое случается», такое повторение. То есть всегда ли соотнесение с присутствием наблюдателя, что это не просто последовательность, фиксированная числами, которая измеряется каким-то математическим алгоритмом. Но всегда присутствует некоторое человеческое восприятие. У меня, в связи с этим, такой вопрос: здесь на лекции когда-то говорили, что сложность информационных соединений в мозге человека превышает количество атомов во Вселенной. Не является ли то, что мы интуитивно чувствуем, что что-то неслучайно, это то, что наш этот аппарат предполагает, что где-то нарушается последовательность.

Борис Долгин: Кто предполагает, прошу прощения?

Слушатель: Интуитивный аппарат. Вы говорите, можно последовательность составить одну из миллиона чисел, но возможности же мозга значительно больше, чем миллион последовательностей. Может быть, мы останавливаемся на миллионе, но продолжаем просчитывать? Насколько математика, математические алгоритмы соотносится с тем, что здесь участвует наблюдатель, автор, ученый, который вносит в эту теорию вероятностей что-то такое непознанное из нашего человеческого интеллекта, что пока еще математическим алгоритмом нельзя вычислить.

Александр Шень: Давайте, я отвечу по порядку. Во-первых, про субъективный момент. Естественно, если мы обсуждаем основания теории вероятностей, то есть обсуждаем, как люди приходят к заключениям, и как они проверяют те или иные гипотезы, то естественно, что мы говорим о том, в каком случае люди отвергают эту гипотезу. То есть неизбежно люди участвуют, но это — история науки или философия науки.

Сложность человеческого мозга трудно определить формально, что бы это значило. Если мы говорим про число комбинаций возможных состояний нейронов, оно, конечно, больше числа атомов во Вселенной, потому что это примерно два в степени их количества. Естественно, что число самих нейронов не больше числа атомов Вселенной, а значительно меньше, и число парных соединений между ними тоже, потому что они осуществляются некоторыми физическими соединениями. Но есть разные экстравагантные теории. Мой коллега по ИППИ Ефим Арсентьевич Либерман объяснял, что в мозгу есть квантовый компьютер, нейроны это просто так, внешние устройства — хотя не берусь пересказать точно, что он говорил.

Борис Долгин: Это было всерьез?

Александр Шень: Он к этому относился совершенно серьезно. Если бы это была шутка, то, как минимум, очень затянувшаяся. Он приходил в лабораторию, мы с ним много разговаривали, пили чай. Насколько я могу судить, он был в этом глубоко убежден. Вряд ли это был розыгрыш.

Возвращаясь к вопросу о том, как математическая теория сложности могла бы в принципе пытаться учесть субъективные факторы: можно рассматривать сложность с ограниченными ресурсами, то есть можно рассматривать не просто кратчайшую программу, а программу, которая восстанавливает последовательность за небольшое (ограниченное чем-то) время. И такая программа может быть гораздо длиннее, чем по-настоящему кратчайшая. То есть бывают последовательности, которые можно коротко записать, но чтобы эту короткую запись развернуть, нужно потратить большое время.

Слушатель: Кто-нибудь исследовал связь колмогоровской сложности и динамических систем? Можно предположить, что если мы возьмем динамическую систему, то она динамически стремится к состоянию, описание которой является приближением к колмогоровской сложности.

Александр Шень: Можно сказать следующее. Пусть у нас имеется динамическая система с некоторой энтропией в смысле динамических систем. Тогда, если мы рассмотрим начальные условия и рассмотрим колмогоровскую сложность траектории, то для почти всех траекторий удельная колмогоровская сложность в расчете на одну итерацию с ростом длины будет стремиться к энтропии. Есть такая теорема, когда-то этим занимался Брудно. Это сложностная переформулировка теоремы из эргодической теории — так что такая связь, действительно, есть.

Слушатель: Я, к сожалению, остался на уровне тех персонажей, которых вы вначале показывали. Если я начинаю собирать какую-то информацию о вероятности, вероятность меняется или все равно я выберу ту же вероятность? Будет ли мой выбор осознанный или нет?

Александр Шень: Слово «вероятность» часто употребляется в очень странном смысле. «Какова вероятность того, что Наполеон не существовал?» Или «Какова вероятность того, что город Самара был арабским городом Арамас?» С точки зрения теории вероятностей эти вопросы никакого смысла не имеют. Можно говорить о математической теории, когда мы исходим из того, что что-то равновероятно, и считаем какие-то вероятности. Можно говорить, что какие-то модели подтверждаются экспериментом или не подтверждаются, как сегодня мы обсуждали. Можно говорить о субъективной вероятности. К сожалению, часто понятие вероятности употребляется очень некритически. (Есть такая компания, которая выпускает учебники по теории вероятностей — Ященко, Тюрин, Макаров и Высоцкий. И вот они недавно выпустили новую книжку, она еще ужаснее, чем прежняя. И там просто, как назло, масса всяких ошибок. В частности, они очень некритически отнеслись к задачам такого рода.)

Есть и другое, «экономическое» толкование вероятности. Представьте себе, что я принес конверт и говорю, что я забыл — я либо положил туда 100 рублей, либо не положил. Какова вероятность того, что они там есть? Это можно измерить таким способом, что я готов продать этот конверт — какова его «справедливая цена»?. Вряд ли кто-нибудь, разве что только уж совсем доброжелательный человек, захочет купить его за сто рублей. Но разные люди, исходя из разных представлений о том, зачем я это спрашиваю, могут предложить какие-то суммы.

Если говорить о рынке: когда есть много продавцов и покупателей, на рынке складывается равновесие. Соответственно возникает рыночный уровень цен на подобные предложения. Этот уровень можно считать субъективной вероятностью, с которой люди считают, что нечто случится. Но это чисто психологическое явление, и это другой смысл слова «вероятность». Так что слово «вероятность» надо употреблять с осторожностью и не писать в книгах неправильно, и не приплетать математику повсюду, где надо и где не надо.

Я могу рассказать историю в качестве разрядки. Прихожу я как-то в 1990-е в ИППИ, и там замдиректора Иосиф Абрамович Овсеевич говорит, чтобы я к нему зашел. (Он был важным человеком, но мы были знакомы.) Он серьезно сказал, что «у нас намечается международное сотрудничество, что мы хотим организовать международную лабораторию по изучению каббалы». Я опешил, а он сказал, что «есть какие-то богатые евреи, которые готовы это финансировать. Будет такая лаборатория, не хотите ли вы быть заместителем заведующего?».

Я еще более опешил и решил как-то уклониться. И сказал, что «я знаю, что это такое уважаемое дело, и что были великие математики, которые нашли какие-то закономерности в тексте библии. Но я думаю, что для изучения этого необходимо уж если не быть верующим, то хотя бы знать иврит, или, как минимум, отличать одни буквы от других. Я не умею этого». Овсеевич сказал: «Ладно». На этом разговор с ним кончился.

Борис Долгин: Прошу прощения, кто предполагался в должности заведующего лабораторией?

Александр Шень: Этого он мне не сказал. Возможно, я забыл. Потом я прохожу через неделю мимо его кабинета, и вижу, что дверь его открыта, он сидит за своим столом, где и обычно, но почему-то в кипе. Я обалдел — но впрочем, это было зимой и там дуло, может быть, это была такая вязаная шапочка. Так или иначе, с этой лабораторией по изучению каббалы в ИППИ ничего не вышло, и тем самым проблема возникновения жизни, и можно ли найти в Библии генетический код (кстати, Либерман тоже очень интересовался этим: может быть, там прямо так все и написано, только нужно правильно раскодировать) — эта проблема осталась неизученной, поскольку я саботировал эту научную программу, не стал в ней участвовать.

Слушатель: У меня вопрос касательно истории с этой монетой, что можно вообще называть случайностью? Может быть, есть человек, который подбрасывает монету пальцами с такой точной силой, что она переворачивается определенное количество раз и всегда падает на орла. То есть в любом событии, которое мы называем случайностью, только из-за того, что мы не можем его понять, присутствует случайность? Можно прийти к тому, что случайности вообще не бывает.

Борис Долгин: Это глубокий философский вопрос. Бывает ли случайность?

Александр Шень: Тут много разных вопросов. Во-первых, конечно, конкретно с монетой. Недавно какие-то люди, занимающиеся компьютерным зрением, сделали такую машину, которая, если невысоко бросить монету, сфотографирует, как она крутится, и за некоторое время до того, как монета падает, уже знает, упадет ли она орлом или решкой. Наверно, можно и так бросать, чтобы падало только орлом. То есть в этом смысле монета, конечно, является лишь метафорой случайного процесса. С другой стороны, скажем, в ситуациях типа радиоактивного распада в современной физике принято считать, что предсказать это в принципе нельзя.

Но, так или иначе, возникает формальный вопрос. Посмотрим на эксперимент, связанный с белым шумом или радиоактивным распадом, и получим последовательность нулей и единиц. Какова ее сложность? Может быть, она, на самом деле очень мала, просто мы не знаем закона, позволяющего ее предсказывать?

Если такой закон обнаружится, окажется, что правы были те люди, которые это предполагали. Если не обнаружится, то так и останется неизвестным, правы они или неправы. Есть целая теория, которая математически исследует эту проблему, к колмогоровской сложности она не имеет отношения, но есть важные работы Блюма, Микели и Яо о «псевдослучайных генераторах». Это некоторые простые алгоритмические преобразования, которые из сравнительно короткой последовательности, например, из тысячи битов делают миллион, но так, что на вид этот миллион ничем не отличается от миллиона настоящих случайных битов. Это отдельная теория, о которой можно долго рассказывать, но это другая теория.

Слушатель: Что относится к сфере ваших творческих интересов сейчас?

Александр Шень: За последнее время мы с Н.К.Верещагиным и В.А.Успенским написали книгу о колмогоровской сложности Верещагин Н.К., Шень В.А. Колмогоровская сложность и алгоритмическая случайность. — МЦНМО, 2013, она есть в интернете. Ну и пытаемся чем-то подобным заниматься в этой области.

Слушатель: Можно ли построить алгебру?

Александр Шень: В смысле, структуру с умножением? Это вряд ли. Но, скажем, можно рассматривать некую естественную полурешетку последовательностей слов с отношением порядка «одна последовательность проста относительно другой». Про это Андрей Ромащенко доказал, что бывают два элемента, у которых нет нижней грани (верхняя грань всегда есть). Так что какие-то алгебраические структуры бывают, но чтобы получилась алгебра в том же смысле, что и, скажем, алгебра кватернионов, про это я ничего такого не слышал.

Слушатель: Вы определили колмогоровскую сложность как сложность алгоритма порождающего последовательность.

Александр Шень: Как длину алгоритма, порождающего эту последовательность.

Слушатель: Пытались ли распознавать колмогоровскую сложность?

Александр Шень: В смысле — распознаватель должен эту последовательность одобрить, а эту последовательность не одобрить?

Слушатель: Да, если я ее распознал.

Александр Шень: То есть на этой последовательности распознаватель должен говорить «да», а на всех остальных «нет», и нас интересует длина такого алгоритма-распознавателя? Тогда, если нет ограничений на время работы (мы требуем, чтобы оно было конечно, но не пытаемся его ограничить), то это, более или менее, то же самое. Если мы можем породить, то мы можем распознать. Если мы можем распознать, то мы можем пробовать все последовательности, пока одна из них не будет одобрена. Но если нас интересует вариант с ограниченными ресурсами, то это уже другая сложность, она изучалась под названием distinguishing complexity. Про нее есть разные интересные результаты, но это другая тема, не связанная с общей теорией вычислимости и сложности.

Слушатель: За счет чего происходит сжатие файла?

Александр Шень: Например, файл у нас такой: "01010101…01" (пятьсот нулей и пятьсот единиц чередуются). Мы пишем программу: «для i от 1 до 500: написать "0", написать "1"». Сама программа занимает две строчки, а получается последовательность из тысячи нулей и единиц, аналогично и для миллиона нулей и единиц. Соответственно, программа оказывается короче, чем та последовательность, которую она порождает. Поэтому сложность указанной последовательности меньше ее длины. Или, скажем, миллион знаков числа «пи», это будет целая книга. Но программа, которая вычисляет этот миллион знаков, совсем не такая длинная программа, она на нескольких страничках поместится. То есть сам по себе тот факт, что программа короче, чем результат ее работы – в этом вроде ничего противоестественного нет.

Слушатель: Дилетантский вопрос о последовательности. Есть таблица Менделеева, она, наверное, была непонятно устроена до того, как Менделеев не показал эту закономерность. Вот если сейчас ее описывать языками программирования, она будет короче?

Александр Шень: Во-первых, не очень понятно, какая тут последовательность. Последовательность свойств каких-то элементов, наверно, то есть это еще надо как-то закодировать. У элементов свойств много, поэтому не очень понятно, что именно мы кодируем. Но, действительно, если мы пытаемся отметить, скажем, какие элементы щелочные, какие металлы, а какие не металлы, то обнаруживаем, что Менделеев обнаружил некие закономерности, которые в принципе позволяют что-то описать короче. Но таблица Менделеева не такая длинная, элементов не так много, и закономерности Менделеева тоже не так просты. Для таких коротких последовательностей трудно говорить.

Слушатель: То есть его открытие имеет меньшую сложность?

Александр Шень: В математическом смысле трудно измерить что-то количественно в этой области, слишком короткая последовательность. В философском смысле, он обнаружил некоторые закономерности в последовательности. Если бы этих атомов было не 90, а миллион, и они подчинялись бы каким-то закономерностям, то, конечно, открытие этих закономерностей упростило бы описание свойств всех атомов.

Слушатель: Может ли быть так, что сложность XY существенно больше, чем сумма сложностей X и Y?

Александр Шень: Нет, потому что всегда можно написать программу, которая сначала напечатает Х, а потом дальше написать ту программу, которая печатает Y. Поэтому сложность ХУ не больше суммы сложностей X и Y. Вопрос только в том, меньше она или примерно такая же.

Слушатель: То есть нельзя составить что-то сложное из многих простых кусочков?

Александр Шень: Конечно, можно составить что-то сложное из простых кусочков, из нуля и единицы можно составить любую последовательность. Но если мы берем только два простых кусочка, вместе из них тоже будет что-то не очень сложное.

Слушатель: А можно ли разграничить последовательности? Например, в метеорологии, там влажность, давление, влажность, температура.

Александр Шень: Это возможно и даже не требует никаких специальных усилий. Тут два вопроса, что можно рассматривать программу, которая печатает не нули и единицы, а нули, единицы и двойки. И сложность также определяется, как минимальная длина программы, которая эту последовательность печатает.

Слушатель: Если три параметра, то к двоичному языку она не сведется?

Александр Шень: Нет, сама программа может быть написана и в двоичной системе, тут другой вопрос. Если мы записываем последовательность в троичной системе, то этих цифр понадобится меньше. Бывают биты, а бывают байты. Если мы используем байты, то их нужно в восемь раз меньше, чем битов. Никакой принципиальной сложности нет.

Борис Долгин: Спасибо большое.