|
||
|
|
||
| Главная ≫ Инфотека ≫ Математика ≫ Семь размышлений на темы философии математики // Владимир Успенский |
Семь размышлений на темы философии математикиВладимир Успенский
ПредисловиеС 26 по 29 сентября 1985 г. в городе Обнинске проходил Всесоюзный симпозиум «Закономерности и современные тенденции развития математики». Автор принял участие в этом мероприятии по приглашению Владимира Ивановича Купцова, которому симпозиум в немалой степени обязан царившей на нем непринужденной, творческой и деловой атмосферой. Доклады сопровождались интенсивными обсуждениями, продолжавшимися на так называемых «круглых столах». Автор, не заявивший какого-либо специального доклада, неоднократно выступал в ходе этих обсуждений. Высказанные им соображения показались достойными опубликования Михаилу Ивановичу Панову, который и предложил оформить их в виде статьи для составляемого им сборника. Так появились настоящие «Семь размышлений». Вот их темы: 1. Действительно ли в математике всё определяется и доказывается? 2. Можно ли определить понятие натурального числа? 3. Можно ли определить Натуральный Ряд (с прописной буквы)? 4. Можно ли аксиоматически определить понятие натурального ряда (со строчной буквы)? 5. Можно ли доказать, что Великую теорему Ферма нельзя ни доказать, ни опровергнуть? 1. Действительно ли в математике все определяется и доказывается?Математики, как правило, очень гордятся тем, что они математики. Источник гордости они видят в своей науке — причем не столько в той пользе, которую приносит математика, сколько в том, что это такая уникальная, ни на какую другую не похожая область знаний. И с этой исключительностью согласны и нематематики (так что величие математиков, к их удовольствию, осознается не только ими самими, но и окружающими). В самом деле, считается общепризнанным, что математика имеет по крайней мере следующие три присущие только ей черты. Во-первых, в математике, в отличие от других наук, все понятия строго определяются. Во-вторых, в математике — опять-таки в отличие от других наук — все строго доказывается из аксиом. В-третьих, математика непонятна в такой вызывающей уважительный трепет степени, какая недоступна ни одной другой пауке. Репетиторов по математике едва ли не больше, чем по всем другим школьным предметам, вместе взятым, а уж о современной «высшей» математике и говорить нечего: достаточно раскрыть любую монографию, а тем более журнальную статью. (Заметим, что обычно не задумываются, что третья из перечисленных черт вступает в известное противоречие с первыми двумя.) Когда что-то слишком общеизвестно, закрадывается подозрение, не является ли это «что-то» мифом (ведь общественное мнение обладает автономным механизмом самоподдержания). Постараемся непредвзятым, по возможности, образом критически рассмотреть три только что названные общеизвестные черты математики. Тогда, во-первых, обнаруживаем, что определить все математические понятия невозможно. Одно определяется через другое, другое через третье и т. д.; где-то мы должны остановиться. («Портной учился у другого, другой у третьего, да первый-то портной у кого же учился?» — справедливо замечает г-жа Простакова.) Рассказывают, что известный одесский математик С. И. Шатуновский, приводя определение все новых и новых понятий, в ответ на повторные вопросы «А что такое то-то и то-то» наконец не выдерживал и сам спрашивал: «А что такое "что такое?"» Давайте задумаемся об устройстве толкового словаря какого-либо языка — русского, английского и т. д. В нем одни слова определяются через другие, другие через третьи и т. п. Но поскольку слов в языке конечное число, то неизбежно возникает круг (т. е. ситуация, в которой слово определяется в конечном счете через само себя 1). Избежать такого круга можно лишь одним способом: оставить некоторые слова без объяснений. В некоторых словарях так и делают 2. Так же, разумеется, обстоит дело и с понятиями математики. А именно, если только не допускать порочного круга, некоторые понятия должны остаться без определения. Спрашивается, как же могут быть усвоены эти понятия. Ответ: из непосредственного наблюдения, из опыта, из интуиции. Нет нужды напоминать, что формирование общих, абстрактных понятий в мозгу человека — сложный процесс, принадлежащий более психологии, нежели логике. Эти понятия, усваиваемые не из словесного определения, а из непосредственного личного опыта, естественно называть первичными понятиями, или категориями, математики. К числу таких категорий относятся, например, понятия точки, прямой, множества, натурального числа и т. д. При составлении перечня (вряд ли могущего быть вполне отчетливым) категорий (первичных понятий) математики следует соблюдать известную осторожность. Иначе число первичных понятий будет неоправданно велико в нарушение принципа «бритвы Оккама». В самом деле, возьмем, например, такое понятие, как шар. Шар, как известно, есть геометрическое место точек пространства, равноудаленных от одной определенной точки — центра шара. Однако вряд ли кто-нибудь впервые узнает, что такое шар, из этого определения. Надо полагать, что человек усваивает понятие шара в детстве — на примере мяча, глобуса, шарика из подшипника и бильярдного шара. Приведенное выше определение он узнает лишь на уроках в школе. При этом отнюдь не всегда удосуживаются объяснить учащемуся, что тот шар, который он знает с раннего детства, и тот шар, которому его обучили в школе, — это один и тот же шар. В результате и возникает представление, что «у них в физике и математике все наоборот. Может быть, у них и шар пойдет вверх» 3. Но следует ли на основании того, что понятие шара узнается из опыта, а не из словесной формулировки, считать понятие шара неопределяемым понятием, одной из категорий математики? Казалось бы, дело обстоит яснее с более сложными и дальше отстоящими от опыта понятиями математики, такими, например, как понятие группы — уж понятие-то группы никак не отнесешь к числу первичных. Однако образование понятия группы в умах профессионалов-математиков, возможно, не слишком отличается от образования понятия шара в умах людей вообще (как математиков, так и нематематиков): как понятие шара возникает в результате многочисленного рассмотрения различных шаров, так и понятие группы возникло в результате рассмотрения конкретных групп — а уж потом это понятие закрепляется в словесной формулировке (здесь, разумеется, речь идет о возникновении понятия группы в коллективном опыте математиков, а не в опыте отдельного математика). Поэтому характерным признаком первичности (категориальности) понятия надлежит считать не способ его возникновения, а способ передачи сведений о нем при передаче системы знаний. Для разъяснения сказанного представим себе, что носитель некоторой системы знаний — в нашем случае знаний о математике — должен передать свои знания другому. Тогда он может сообщить другому, что такое шар или что такое группа, пользуясь словесным определением соответствующего понятия. И потому эти понятия — не категориальные. Если же нужно сообщить, что такое множество, что такое прямая или что такое натуральное число, то это делается по-другому. Говорится примерно так: все стулья в этой комнате составляют множество, и все страусы за Полярным кругом 4 составляют множество, и все иррациональные числа отрезка [0,1] составляют множество; и далее, после приведения достаточного числа примеров, говорится: «все это множества» — и так возникает общее понятие множества. Аналогично: ноль 5, один, два, три, четыре, пять и т. д.— всё это натуральные числа, и так возникает общее понятие натурального числа. (Мы видим, что при объяснении понятия натурального числа явно или неявно присутствует слово «и т. д.» — и это иначе и не может быть для первичных понятий: указывается достаточное количество примеров, а дальше — «и т. д.».) Итак, первый из мифов о математике — «в математике все определено» — оказывается разрушенным. Перейдем ко второму: «В математике все доказывается из аксиом». Чтобы убедиться, что это не так и, таким образом, разрушить и этот миф, достаточно открыть классический школьный учебник геометрии А. П. Киселева, или какой-нибудь втузовский учебник математического анализа, или университетский учебник теории чисел. Мы встречаем в этих учебниках доказываемые теоремы, но вряд ли (за исключением аксиомы о параллельных — она же пятый постулат Евклида) найдем какие-либо аксиомы. Дело обстоит несколько загадочным образом. В самом деле, если нет аксиом, то на основе чего происходят доказательства, скажем теорем теории чисел? По-видимому, на основе здравого смысла и неких представлений об основных свойствах натуральных чисел, каковые представления, хотя и одинаковые у всех людей, не сформулированы явно в виде списка аксиом. (Насколько их можно сформулировать — тема следующего размышления.) Необходима честная констатация того наблюдения, что в реальной математике сплошь и рядом встречаются теоремы, доказываемые без опоры на какие бы то ни было аксиомы. Сложнее дело обстоит с третьей отмеченной нами чертой математики — ее непонятностью. Проще всего сказать, что это миф, по если относительно первых двух черт достаточно было спросить самое математику — спросить и получить отрицательный ответ,— то здесь, конечно, обращение к математике с вопросом, понятна ли она, неуместно. А опрос общественного мнения, безусловно, выставит математику на призовое место по уровню непонятности. Выяснение причин этого явления — которое следует признать настолько объективным, насколько вообще могут быть объективными явления социальной психологии — тема отдельного большого исследования, на которое мы не замахиваемся. Некоторым комментариям на эту тему будет посвящено наше последнее размышление. ^2. Можно ли определить понятие натурального числа?Конечно, можно сказать, что натуральное число — это количество предметов в конечной совокупности. Эта формулировка, по-видимому, будет отвечать как значению (точнее, одному из значений) слова «определить», предложенному «Толковым словарем русского языка» под редакцией Д. Н. Ушакова [5] («дать научную, логическую характеристику, формулировку какого-либо понятия, раскрыть его содержание (научн.)»), так и формулировке Философской энциклопедии [11] («Определение» объекта, результаты изучения которого отображаются в соответствующих понятиях, «можно рассматривать как формулирование (в явной и сжатой форме) содержания этих понятий»). Подойдем, однако, к понятиям «определить», «определение» с позиций математика. А именно потребуем, чтобы определение содержало в себе исчерпывающую информацию об определяемом понятии — настолько исчерпывающую, что человек, ничего ранее не знавший об этом понятии, мог бы составить правильное представление о нем исключительно из предложенного определения. Можно ли в таком случае предположить, что человек, вовсе не знающий, что такое натуральное число (не термин, а именно понятие), может усвоить это понятие из первой фразы этого абзаца? Весьма сомнительно: вряд ли, искренне не зная, что такое число, он понимает, что количество предметов не означает, скажем, их суммарный вес, да и само понятие конечной совокупности предметов расплывается при переходе к очень большим совокупностям. Вероятно, все согласны, что триллион в триллионной степени — это натуральное число; но, однако, это число больше числа атомов во Вселенной. Неясно, насколько уместно говорить о конечной совокупности, состоящей из триллиона в триллионной степени количества предметов [16]. Итак, будем придирчиво требовать от определения исчерпывающей полноты, т. е. будем требовать, чтобы определяемое понятие выражалось с помощью общепринятых синтаксических конструкций через другие понятия, отправные для рассматриваемого определения. С учетом сказанного попробуем предложить такую формулировку: натуральное число — это мощность конечного множества. В этом определении участвуют три основных понятия: 1) множество, 2) мощность, 3) конечное. В рамках тех теорий, в которых эти понятия уже как-то разъяснены (в частности, объявлены неразъясняемыми или первичными), приведенная только что формулировка действительно является определением натурального числа. Именно такое определение — в идейном смысле такое, с точностью до несущественных деталей — принято, например, в трактате Николая Бурбаки «Начала математики» 6. (Напомним в этой связи, что полное имя единицы в теории Бурбаки требует для своей записи десятки тысяч знаков [6, с. 188].) Однако здравый смысл отказывается признать понятия множества, мощности, конечного более простыми, чем понятия натурального числа. Здесь типичный пример определения простого через сложное. Сказанное не следует воспринимать как критику в адрес Н. Бурбаки и других авторов, предлагающих аналогичные формулировки. Разумеется, они, как и все люди, имеют априорное представление о натуральном числе (априорное, разумеется, по отношению к предлагаемому определению, но не к опыту). Они не ставят себе цель дать объясняющее определение понятия натурального числа (т. е. определение, посредством которого можно было бы обучить новичка). Их цель более скромная и более техничная: дать определение этому понятию в рамках излагаемой аксиоматической теории множеств. Можно определить понятие функции через понятие пары, а можно понятие пары через понятие функции. Ясно, что эти умственные построения имеют мало общего с объяснением непосвященному, что такое пара и что такое функция; Все предыдущие рассуждения имеют целью подвести к следующей почти очевидной мысли. Оставим в стороне математическую и логическую "проблематику, связанную с поисками определения (а правильнее было бы сказать,— поисками отражения, моделирования) понятия натурального числа в рамках тон или иной аксиоматической теории. Займемся попытками дать «наивное» объяснение понятия натурального числа, позволяющее незнающему узнать, что это такое. Довольно скоро мы убеждаемся, что такие попытки бесплодны. Натуральное число следует признать первичным, неопределяемым понятием, одной из категорий математики. ^3. Можно ли определить Натуральный Ряд (с прописной буквы)?Потерпев неудачу в попытках определить, что такое натуральное число (или, напротив, обретя удачу в отнесении этого понятия к категории неопределяемых), обратимся к понятию Натурального Ряда. Натуральный Ряд — с большой, или прописной, буквы — это совокупность всех натуральных чисел. Если мы знаем, что такое натуральное число и понимаем слова «совокупность всех», то мы знаем и что такое Натуральный Ряд. Обратно, зная Натуральный Ряд, мы легко определим натуральное число как его элемент. Поэтому понятие Натурального Ряда столь же неопределимо, как и понятие натурального числа. (Впрочем, можно считать фразу «Натуральный Ряд есть множество всех натуральных чисел» законным определением понятия Натурального Ряда через первичные неопределимые понятия «натуральное число» и «множество всех».) «Как же так? — воскликнет читатель. — А аксиомы Пеано? Разве они не определяют Натуральный Ряд?» Конечно нет, да они на это и не претендуют, если понимать Натуральный Ряд так, как мы его понимаем — т. е. как единственную (!) совокупность некоторых однозначно понимаемых сущностей, называемых натуральными числами. В самом деле, посмотрим, как выглядят аксиомы Пеано. Они гласят: «Ноль есть натуральное число, и ноль не следует ни за каким натуральным числом, и т. д.». Таким образом, они опираются па понятие «ноль» и «следовать за» (имеется в виду непосредственное следование). Но они не разъясняют, да и не могут разъяснить, что означают эти понятия (т. е. что такое «ноль» и что такое «следовать за»), а лишь указывают связи между ними. Причем аксиомы сформулированы таким образом, что если ноль этих аксиом — это обычный Ноль 7 Натурального Ряда, а «следование за» означает непосредственное следование одного числа за другим в Натуральном Ряду (так что за Нолем следует Единица, за Единицей — Двойка и т. д.), то все эти связи будут выполнены в Натуральном Ряду. Иными словами, аксиомы Пеано оказываются верными, истинными утверждениями при естественной их интерпретации на Натуральном Ряду. Но они, разумеется, будут верны не только на Натуральном Ряду, но и на всякой структуре, изоморфной 8 Натуральному Ряду. Например, если интерпретировать встречающийся в аксиомах Пеано термин «ноль» как наименьшее простое число, а термин «следовать за» — как переход от одного простого числа к ближайшему за ним следующему, то при такой интерпретации все аксиомы Пеано окажутся верными. Выходит, они, эти аксиомы, не дают даже возможности отличить Натуральный Ряд от совокупности всех простых чисел. Повторяю, они на это и не претендуют. Они претендуют на то, чтобы, как говорят, «определить Натуральный Ряд с точностью до изоморфизма». Более точно это означает, что аксиомы Пеано определяют не одну, а сразу много математических структур, причем все они изоморфны Натуральному Ряду и, следовательно, изоморфны между собой. Еще более точно, аксиомы Пеано определяют весь класс таких структур. Любую такую структуру будем называть натуральным рядом (с маленькой, или строчной, буквы!). Таким образом, Натуральный Ряд есть один из натуральных рядов. Говоря коротко, изоморфизм двух математических структур — это
взаимно-однозначное соответствие между совокупностями элементов первой
структуры и второй структуры, сохраняющее определенные на этих структурах
операции и отношения. В нашем примере изоморфизм между структурой
Операция «следовать за» при этом соответствии действительно
сохраняется: 6 следует за 5, и одновременно 17 следует за 13, и вообще у следует за х в верхнем ряду тогда и только тогда, когда соответствующие им
члены нижнего ряда ру и рх (именно в этом порядке!) следуют
один за другим (следуют в смысле, определенном для Иногда говорят, что Натуральный Ряд — это есть ряд ноль, один, два, три, …, сто двадцать шесть, … (его членами являются выражения, составленные из русских букв и пробелов между словами); или ряд 0, 1, 2, 3, …, 126, … (его членами являются выражения, составленные из арабских цифр); или ряд
(его членами являются выражения, составленные из римских цифр с
добавлением придуманного нами символа Разумеется, любой из этих рядов не есть Натуральный Ряд, (который состоит из абстрактных количественных категорий и не может быть изображен), а есть всего лишь ряд имен, обозначений для его членов, т. е. для натуральных чисел. Вместе с тем каждый из этих рядов имен может рассматриваться как один из натуральных рядов с маленькой буквы. Ситуация с Натуральным Рядом имеет универсальный характер. Аналогичным образом обстоит, например, дело с тем трехмерным евклидовым пространством, в котором мы живем. Отвлечемся от того, что мы, скорее всего, живем в неевклидовом пространстве, да и вообще живем в пространстве не математическом, а физическом 10, а это разные вещи. Вообразим, отвлекаясь от реальности, что мы живем в совершенно конкретном трехмерном Евклидовом Пространстве (мы опять употребляем прописные буквы, чтобы подчеркнуть уникальность этого пространства). Конечно, его нельзя определить никаким числом аксиом, а только — «указав пальцем». С другой стороны, существуют многочисленные системы аксиом (наиболее известная из них принадлежит Гильберту [3]), определяющих это пространство «с точностью до изоморфизма». Взятый в кавычки фразеологизм означает, что система аксиом определяет целый класс изоморфных между собой пространств, а наше «реальное» Евклидово Пространство — одно из них. Вообще, никакая система математических аксиом никогда не определяет какую-либо структуру однозначным образом, а в лучшем случае — с точностью до изоморфизма. (Мы говорим «в лучшем случае», поскольку бывают и весьма важны системы аксиом, определяющие класс неизоморфных структур. Например, аксиомы теории групп определяют математические структуры, называемые группами, но не все они изоморфны между собой.) Подведем итоги. Определить аксиоматически Натуральный Ряд невозможно. Можно попытаться определить аксиоматически понятие натурального ряда — т. е. понятие произвольной структуры, изоморфной Натуральному Ряду. Обсуждению этих попыток мы посвящаем наше следующее размышление. ^4. Можно ли аксиоматически определить понятие натурального ряда (со строчной буквы)?Итак, приступим к попыткам определить аксиоматически понятие натурального ряда — структуры, изоморфной Натуральному Ряду. Как только произносится слово «изоморфизм», уже тем самым предполагается, что указано, какие отношения и операции должны сохраняться при этом изоморфизме. Следовательно, мы должны прежде всего точно указать, какие отношения и операции мы желаем рассматривать на Натуральном Ряду и изоморфных ему натуральных рядах. В число этих операций могут быть включены нольместные операции (т. е. индивидные константы; например, индивидную константу «ноль» можно рассматривать как нольместную операцию) и одноместные отношения (т. е. свойства). Указание этих выделенных операций и отношений в значительной мере произвольно. Например, можно рассматривать Натуральный Ряд (и тем самым любой изоморфный ему натуральный ряд): 1) как структуру лишь с отношением порядка «<», или 2) как структуру с выделенным элементом «ноль» и операцией «переход к следующему», или 3) как структуру, в которой, помимо уже названных отношений и операций, выделены еще операции сложения и умножения. Для наших целей нагляднее всего не задавать никаких операций, а задать лишь отношение порядка «<». Итак, мы рассматриваем каждый натуральный ряд как множество, на котором определено бинарное отношение порядка «<». Именно свойства такой математической структуры мы и будем исследовать. Перейдем к перечислению этих свойств. Каждое свойство отношения «<» в произвольном натуральном ряду должно (в силу наличия изоморфизма) иметь место и в обычном Натуральном Ряду, когда отношение «<» понимается как обычное отношение порядка между натуральными числами. После этого замечания сформулируем несколько таких свойств. 1. Отношение «<» транзитивно. В символах:
2. Отношение «<» антирефлексивно. В символах:
3. Отношение «<» связно. В символах:
Эти три свойства в своей совокупности утверждают просто-напросто, что «<» есть отношение строго линейного порядка. Прежде чем двигаться дальше, остановимся и задумаемся: а зачем, собственно, мы перечисляем эти свойства? А вот зачем. Мы надеемся, что, перечислив некоторое число свойств, мы сумеем дать аксиоматическое определение натурального ряда. Более подробно наш план таков. Сперва мы выписываем некоторое число характерных для Натурального Ряда свойств. Затем мы объявляем эти свойства аксиомами и определяем натуральный ряд как произвольную математическую структуру, удовлетворяющую выписанным аксиомам. Мы не претендуем на то, что ровно одно определенное множество с заданным на нем бинарным отношением «<» будет удовлетворять нашим аксиомам (такая претензия была бы совершенно нереальна), но претендуем на то, что все такие множества (с заданным на них отношением) окажутся изоморфными между собой. А поскольку наши аксиомы будут выполняться на Натуральном Ряду (так мы будем выбирать аксиомы), то Натуральный Ряд будет одной из попарно изоморфных структур, удовлетворяющих аксиомам, и значит, все эти изоморфные между собой структуры будут изоморфны и Натуральному Ряду. Если нам удастся достичь изложенной только что цели, мы и будем считать, что мы сумели аксиоматически определить натуральный ряд. Можем ли мы, имея в виду поставленную цель, довольствоваться тремя
выписанными свойствами — аксиомами? Разумеется, нет. Этим аксиомам
удовлетворяют все линейно упорядоченные множества, среди которых много
неизоморфных и, следовательно, заведомо неизоморфных Натуральному Ряду 4. В
5. В

Эти пять аксиом уже значительно сужают круг удовлетворяющих им линейно упорядоченных множеств. Этим аксиомам удовлетворяет Натуральный Ряд, а также, например, такое множество действительных чисел (рассматриваемое с обычным порядком)
Наличие этой, отличной от
Графический образ этой порядковой структуры приведен на рис. 2. В этой структуре у двух элементов (у 0 и у 10) нет непосредственных предшественников. Запретим эту ситуацию следующей аксиомой 6. 6. Если у двух элементов x1 и x2 нет непосредственных предшественников, то они равны. В символах:
Аксиома 6 исключает структуру (**), но не исключает такую структуру:

Структура (***), очевидно, не изоморфна натуральному ряду. Наша цель подобно горизонту отодвигается все дальше и дальше… Оказывается, она вообще недостижима. Оказывается, имеет место следующий замечательный факт: сколько бы мы ни выписывали аксиом, использующих логические знаки, знак отношения «<» и переменные, пробегающие по элементам определяемой структуры, — у совокупности выписанных аксиом всегда будет модель, неизоморфная натуральному ряду. Ввиду фундаментальной важности этого факта (означающего невозможность аксиоматического определения натурального ряда с использованием указанных средств) изложим его подробнее. Будем записывать аксиомы на формализованном символическом языке, в алфавит которого входят следующие знаки; 1) знаки препинания: левая скобка «(»и правая скобка «)», 2) логические знаки «¬», «∧», «∨», «⇒», «∀», «∃», «=», 3) индивидные переменные х, у, z, u, v, w, х1, у1, z1, u1, v1, w1,… 4) знак «<». С помощью этих букв по естественным, но легко формулируемым синтаксическим правилам составляются формулы. Простейшие примеры формул:
Возьмем теперь какое-либо множество с каким-либо определенным на нем бинарным отношением (не обязательно отношением строгого порядка), обозначаемым через «<». Всякое такое множество с отношением «<» будем называть структурой сигнатуры <. Таким образом, структура сигнатуры < состоит из множества (называемого носителем структуры) и отношения «<». Назначим для каждой индивидной переменной носитель структуры в качестве области изменения этой переменной. Тогда каждая формула становится либо высказыванием, как вторая, третья и пятая формула из приведенного только что списка, либо высказывательной формой, как первая и четвертая формулы. Формулы, превращающиеся в высказывания, называются закрытыми 11, только их мы и будем впредь рассматривать. Про (закрытую) формулу, становящуюся — при рассмотрении на данной структуре — истинным высказыванием, говорят, что она истинна на данной структуре или выполняется на данной структуре, а про структуру — что она удовлетворяет данной формуле. Среди структур сигнатуры < выделена структура Получается, таким образом, что натуральный ряд нельзя
определить аксиоматически: ведь определить «Позвольте, — снова возразит читатель, — но аксиомы Пеано ведь определяют Натуральный Ряд как раз с точностью до изоморфизма. Система аксиом Пеано категорична, а это как раз и означает, что все их модели 12 изоморфны». Немножко терпения, разберемся и с аксиомами Пеано. А сейчас обсудим вот какой вопрос. На Натуральном Ряде определено не
только отношение порядка «<», но и бесчисленное множество других отношений и
операций. Среди них двуместное (или бинарное) отношение делимости двух чисел;
трехместное (или тернарное) отношение «х + у = z»; одноместное (или
сингулярное) 13
отношение «быть простым числом» (напомним, что свойства мы трактуем как
одноместные отношения); двуместная
операция сложения; двуместная операция умножения; двуместная операция возведения в степень (причем 00
= 1); одноместная операция непосредственного следования (мы будем, как это
часто делается, обозначать ее штрихом, так что, например, 0′ = 1; 13′ = 14);
константы 0, 1, 2, 3, 4, … (напомним, что константы мы трактуем как
нульместные операции); четырехместная операция [logu+1(z + yx-z+u)] (здесь, как
обычно, через [a]
обозначается целая часть числа a); и многие другие. Мы привели лишь несколько примеров, а
всего на Выделенные на множестве операции и отношения называют в контексте
наших рассмотрении — сигнатурными, а список таких операций и отношений —
сигнатурой. Точнее, сигнатурой называют список не самих операций и
отношений, а список их имен, но для наших целей это различие (само по себе очень
важное) не слишком существенно, и нам проще его не замечать. Множество, с
выделенными операциями и отношениями, образующими список
Может быть, причина нашего неуспеха в попытке определить аксиоматически натуральный ряд вызвана именно бедностью сигнатуры? Давайте расширять сигнатуру и наблюдать, что при этом будет происходить. Сперва добавим к «<» константу «0» (для обозначения наименьшего,
относительно порядка «<», элемента) и штрих «′» для обозначения
операции непосредственного следования. На Натуральном Ряде 7. 8. Всякий натуральный ряд с сигнатурой {0, ′, <} изоморфен, по определению, натуральному ряду 0 < 0′ < 0′′ < 0′′′ < … Замечание. Следует отдавать себе отчет, что в каждом
натуральном ряду свой 0, свой ′ и свое <, т. е. свой элемент,
обозначенный через «0», своя операция, обозначенная через «′», и свое
отношение, обозначенное через «<». Строго
говоря, для каждого натурального ряда мы должны были бы придумать свое
обозначение для этих объектов — например, если мы рассматриваем натуральный ряд

Посмотрим теперь, как выглядит произвольная структура сигнатуры {0, ′, <}, подчиняющаяся
аксиомам 1 — 8
(аксиомы 4 и 5 следуют из аксиом 7 и 8, но в этом нет большой беды). Она,
очевидно, представляет собой линейно упорядоченное множество, в котором 0 есть
наименьший элемент, 0′ — непосредственно следующий за 0 элемент (так что
между 0 и 0′ ничего нет). 0′′
— непосредственно следующий за 0′ элемент и т. д. Все эти элементы 0, 0′,
0′′, 0′′′ образуют начальный отрезок нашей структуры. Этот
начальный отрезок называется стандартной частью структуры, а оставшаяся
часть (она может быть и пустой) — нестандартной. Стандартная часть
изоморфна Натуральному Ряду Более того, оказывается, что никакие аксиомы не могут задать натуральный ряд сигнатуры {0, ′, <}, поскольку структура рис. 3 всегда будет моделью для таких аксиом. Может быть, дело все еще в бедности сигнатуры? Что будет, если
добавить сложение и умножение и рассматривать натуральный ряд не сигнатуры
{0, ′, <}, а сигнатуры {0, ′, +, •}? Можно ли для такой более
богатой сигнатуры составить список аксиом, определяющих понятие натурального
ряда этой сигнатуры, — т.е. выделить из всех структур этой сигнатуры те
структуры, которые относительно 0, ′, <, +, • изоморфны Более того, какую бы мы ни взяли сигнатуру и какую
бы ни взяли для этой сигнатуры систему аксиом, всегда будет существовать модель этой системы аксиом, не
изоморфная натуральному ряду 
Если в число аксиом входят аксиомы 1 — 8 или какие-нибудь
им равносильные, то в любой модели можно выделить стандартную часть 0, 0′, 0′′,…;
нестандартность модели означает в этом случае непустоту нестандартной части.
Эта нестандартная часть может оказаться устроенной более сложно, чем на
рис. 3. На рис. 3 нестандартная часть подобна, с точки зрения
порядка, множеству Итак, предъявить систему аксиом, определяющую понятие
натурального ряда (какой угодно сигнатуры), невозможно. Более
подробная расшифровка этого утверждения, как мы знаем, такова: какие ни
выбрать определенные на Вот теперь и ответим на вопрос: «А как же аксиомы Пеано?» Классические аксиомы Пеано с несущественными изменениями устроены так. Рассматривается сигнатура {0, ′}. Формулируются три аксиомы: I. II. III. Аксиома индукции. Третью аксиому, аксиому индукции, мы пока только назвали, но не выписали. Теперь выпишем ее: III. Приглядимся к аксиоме индукции. Мы замечаем, что в ней наряду с обычной индивидной переменной встречается еще переменная Р. Разъясним смысл этой переменной. Прежде всего напомним, что семантика формулы (т. е. придание этой формуле смысла) возникает лишь после того, как предъявляется математическая структура соответствующей сигнатуры. В частности, чтобы обрели смысл аксиомы Пеано (формулы I — III), надо предъявить какую-либо структуру сигнатуры {0, ′}, т. е. множество с выделенным элементом, обозначенным через «0» и выделенной одноместной операцией, обозначенной через «′». Тогда сразу определяется область изменения переменной х (как и всякой индивидной переменной) — это есть множество всех элементов рассматриваемой структуры. Какова же область изменения переменной Р? Переменная P — особая, не встречавшегося еще в нашем изложении типа. Ее область изменения состоит из всевозможных свойств (= одноместных отношений), определенных на рассматриваемой структуре, т. е. свойств элементов этой структуры. Понятие свойства относится к первичным и постигается из примеров. На натуральных числах определено свойство четности — каждое число может быть либо четным, либо нечетным. Здесь несущественно, что бывают как четные, так и нечетные числа, нас устроила бы ситуация, когда все числа — четные; важно, что про каждое число осмысленно спросить, четное оно или нечетное. А вот свойство зелености не определено на натуральном ряду; для числа «быть зеленым» бессмысленно. Выше мы сформулировали свойства, которыми, как целое, обладает Натуральный Ряд. Свойствами могут обладать и отношения: так, среди отношений выделяются, например, транзитивные. Но в данный момент нас интересуют лишь свойства элементов рассматриваемой структуры (для которой выполняются аксиомы Пеано). Именно эти свойства могут выступать в качестве значений переменной P. Тот факт, что элемент а обладает свойством Q, записывается как Q(а). Если на элементах какого-то множества М определено свойство Q, то можно ввести в рассмотрение подмножество К этого множества, состоящее из тех и только тех элементов М, которые обладают свойством Q
Обратно, для каждого подмножества К можно ввести свойство Q: «быть элементом К», и опять-таки будет выполнено соотношение (+). Таким образом, свойство — это почти то же самое, что подмножество: «язык свойств» и «язык подмножеств» тривиально переводимы один в другой. На языке подмножеств, например, аксиома индукции записывалась бы так:
Итак, область изменения Р в аксиоме индукции — совокупность
всех свойств, определенных на рассматриваемой структуре. Посмотрим, как эта
аксиома используется для того, чтобы установить, что удовлетворяющая аксиомам
Пеано структура изоморфна
Заключенная в квадратные скобки посылка, очевидно, истинна (0 принадлежит
стандартной части и если х принадлежит стандартной части, то принадлежит
и x′); поэтому ∀x P0 (x), т. е. все х (все элементы структуры!) принадлежат
стандартной части. Стандартная часть, как уже было замечено, изоморфна Таким образом, всякая структура, удовлетворяющая аксиомам Пеано,
изоморфна Однако противоречия нет, и вот почему. Ранее речь шла лишь о свойствах Натурального Ряда, способных быть выраженными определенными языковыми средствами — иными словами, об аксиомах, записанных на определенном языке. В этом языке был лишь один вид переменных — индивидные переменные x, y, z, …. Сущность этих индивидных переменных заключается в том, что при интерпретации на какой-либо структуре каждая из этих переменных получает в качестве области изменения одно и то же множество — множество всех элементов рассматриваемой структуры. В аксиоме же индукции участвует переменная другого вида — переменная Р. Ее значениями являются не элементы рассматриваемой структуры, а свойство этих элементов (иначе — определенные на этих элементах одноместные предикаты, отчего сама переменная Р называется предикатной, точнее — предикатной переменной валентности 1). Таким образом, аксиома индукции — это формула другого, расширенного языка, более широкого, нежели рассматривавшийся до сих пор узкий язык. (Узкий потому, что в нем бывают только индивидные переменные). А когда мы говорили, что систем аксиом, полностью характеризующих натуральный ряд, не бывает, мы имели в виду этот прежний, узкий язык. Разъяснение, конечно, дано, но вряд ли оно кого-нибудь удовлетворит. Что с того, что на каком-то языке нельзя написать систему аксиом натурального ряда — это, как говорится, «факт не биографии натурального ряда, а биографии этого языка». Просто-напросто узкий язык плохой, а вот теперь мы нашли хороший, расширенный язык, на котором как раз и возможно выписать адекватные аксиомы натурального ряда. Однако все не так просто. Грубо говоря, дело обстоит как раз наоборот: узкий язык «хороший», а расширенный — «плохой». Попробуем разъяснить ситуацию.. Начнем с терминологии. Формулы, в которых все переменные индивидные, называются элементарными
формулами, а язык, в котором допускаются только элементарные формулы — элементарным
языком. Синонимом для термина «элементарный» в данном контексте является термин
«1-го порядка» или «первопорядковый». Все рассматриваемые выше аксиомы, кроме
аксиомы индукции (т. е. аксиомы 1 — 8
и I — II) были элементарными
аксиомами, т. е. элементарными формулами. Не существует никакой (ни конечной,
ни бесконечной, и притом любой сигнатуры) системы элементарных аксиом, которой
удовлетворял бы Натуральный Ряд Бывают и неэлементарные формулы, но они принадлежат неэлементарному языку. В этом языке допускаются переменные более сложной природы — предикатные переменные валентности 1, значением которых служат свойства (= одноместные отношения), предикатные переменные валентности 2, значениями которых служат бинарные (= двуместные) отношения и т. п., а также функциональные переменные (значением функциональной переменной валентности 1 может быть любая одноместная операция, такая, как, скажем, «следование за», а значением функциональной переменной валентности 2 может быть любая двуместная операция, такая, как скажем, сложение). Аксиома индукции служит примером неэлементарной формулы. Более точно неэлементарный язык с описанными только что возможностями называется языком 2-го порядка: это значит, что в нем допускаются переменные, пробегающие по отношениям и операциям (каковые отношения и операции должны быть определены на элементах структуры), но не рассматриваются более сложные переменные, значениями которых могут служить, скажем, свойства операций или операций над отношениями (или свойства отношений — такие, как «транзитивность»). Аксиома индукции служит примером неэлементарной формулы языка 2-го порядка (или просто примером формулы 2-го порядка). Язык второго порядка — простейший из неэлементарных языков. Казалось бы — и наличие аксиом Пеано это как бы подтверждает — возможна система неэлемеитарных аксиом 2-го порядка (т. е. аксиом, записанных в виде формул этого неэлементарного языка), определяющая понятие натурального ряда в следующем точном смысле: 1) 2) всякая модель этой системы изоморфна Как известно, количество элементов какого-либо множества называется кардинальным
числом, или мощностью, этого множества. Понятие кардинального числа,
или мощности, является обобщением понятия натурального числа, поскольку
натуральные числа — это мощности конечных множеств. Среди бесконечных мощностей
выделяются следующие две: мощность множества всех натуральных чисел и мощность
множества всех действительных чисел. Первая обозначается
Знаменитая континуум-гипотеза состоит в том, что такой мощности нет. Известно (в силу результатов К. Гёделя и П. Коэна), что ни доказать, ни опровергнуть континуум — гипотезу невозможно. Говоря «доказать» и «опровергнуть», мы имеем в виду все мыслимые средства, допускаемые современной математикой. Тем самым повисает в воздухе вопрос о самом смысле континуум-гипотезы. В самом деле, воспринимается как туманный смысл такого утверждения, истинность или ложность которого заведомо нельзя установить никакими средствами. Эта чрезвычайная ситуация радикально отличается от такой часто встречающейся ситуации, когда мы просто чего-то не знаем (но хотя бы ясно понимаем сам вопрос 15). Оказывается, что можно выписать формулу 2-го порядка, которая тогда и только тогда имеет модель (т.е. такую структуру, для которой она становится верной), когда континуум-гипотеза справедлива. Можно выписать и такую формулу 2-го порядка, наличие у которой модели равносильно, напротив, наличию промежуточной мощности, т. е. справедливости отрицания континуум-гипотезы 16. Таким образом, для формул 2-го порядка вопрос о наличии у них модели может оказаться столь же туманным, как сама континуум-гипотеза. Кажется сомнительным, чтобы язык со столь неясной семантикой мог служить удовлетворительным средством для аксиоматического определения чего-нибудь — в частности, натурального ряда. И действительно, если мы проанализируем использование аксиомы
индукции в процессе доказательства того, что любая модель аксиом
I — III изоморфна 5. Можно ли доказать, что великую теорему Ферма нельзя ни доказать, ни опровергнуть?Проблема континуума, упомянутая в конце нашего предыдущего размышления, относится к числу главных проблем, волновавших умы математиков. В знаменитом докладе «Математические проблемы», с которым великий Гильберт выступил в 1900 г. на Международном конгрессе в Париже, она была названа первой. Как было отмечено, проблема континуума оказалась неразрешимой: континуум-гипотезу невозможно ни доказать, ни опровергнуть. Перечисляя 23 основные проблемы математики, Гильберт не упомянул проблему доказательства (или опровержения) Великой теоремы Ферма. По-видимому, Гильберт не считал эту проблему достаточно важной. Тем не менее нет сомнения, что это самая знаменитая из нерешенных математических проблем. И притом единственная из нерешенных проблем, известных, к сожалению, широкой массе нематематиков. Мы написали «к сожалению», ибо ощутимый процент времени математиков-профессионалов тратится на изучение и опровержение сочинений ферматистов — так называются люди, не имеющие должной математической подготовки, но считающие, что именно они доказали теорему Ферма. Строго говоря, теорему Ферма нельзя назвать теоремой. «Математическая энциклопедия» [22] определяет теорему как «математическое утверждение, истинность которого устанавливается путем доказательства». А ведь доказательство для «теоремы» Ферма пока еще не найдено 17. Тем не менее та же «Математическая энциклопедия» в том же 5-м томе дает статью «Ферма теорема», и мы будем пользоваться этим же общепринятым, хотя и неточным термином — признавая, что правильнее было бы говорить о гипотезе Ферма. Много факторов способствовало популярности теоремы Ферма в среде непрофессионалов. Среди них: 1) авторитетность автора: ее высказал один из создателей теории чисел — французский математик Пьер де Ферма; 2) почтенность возраста: она была высказана около 1630 г.; 3) романтические обстоятельства, при которых она была сформулирована: Ферма записал ее на полях «Арифметики» Диофанта издания 1621 г. Восьмая задача второй книги «Арифметики» Диофанта гласит: «Заданный квадрат разложить на два квадрата». Ферма сделал к этой задаче следующее замечание: «Наоборот, невозможно разложить ни куб на два куба, ни биквадрат на два биквадрата, и вообще никакую степень большую квадрата, на две степени с тем же показателем. Я открыл этому поистине чудесное доказательство, но эти поля для него слишком узки». В бумагах Ферма доказательства найдено не было; 4) учреждение в 1908 г. премии Вольфскеля в сто тысяч германских марок за доказательство теоремы Ферма («приятный» факт учреждения большой премии, естественно, получил гораздо большую известность, чем «неприятный» факт ее полного обесценивания вследствие наступившей после первой мировой войны инфляции); 5) простота формулировки. Конечно, первые четыре фактора не смогли бы сработать, не будь теорема Ферма столь общедоступна по своей формулировке. Вот в чем она состоит: Каково бы ни было целое число n, большее, чем 2, уравнение xn + yn = zn не имеет целых положительных решений. Как видим, участвующее в формулировке теоремы Ферма уравнение рассматривают как уравнение с тремя неизвестными — x, y, z. Поскольку n может принимать значения 3, 4, 5, 6 и т. д., то на самом деле здесь бесконечная серия уравнений, и утверждается, что ни одно из них не имеет решения в таких целых x, y, z, что x > 0, y > 0, z > 0. С логической точки зрения более естественно рассматривать уравнение xn + yn = zn как одно уравнение с четырьмя неизвестными n, x, y, z. Теорема Ферма, стало быть, утверждает, что это уравнение не имеет целых решений, таких, что n > 2, x > 0, y > 0, z > 0. Поиски доказательств теоремы Ферма продолжаются. Теоретически говоря, могли бы происходить и поиски ее опровержения, но они не происходят. Ситуация с гипотезой, называемой «теоремой Ферма», значительно отличается от той, которая имеет место для континуум-гипотезы: ведь для континуум-гипотезы, как мы знаем, доказано, что ее нельзя ни доказать, ни опровергнуть (более точно Гёдель в 1939 г. показал, что ее нельзя опровергнуть, а Коэн в 1963 г. — что ее нельзя доказать). Для гипотезы (теоремы) Ферма такое доказательство — доказательство невозможности ее ни доказать, ни опровергнуть — отсутствует. Спрашивается: это доказательство пока отсутствует (с надеждой его получить в будущем) или оно в принципе невозможно? Если бы это доказательство удалось получить, это несомненно принесло бы математике большую пользу, поскольку раз навсегда закрыло бы шлюз для потока безграмотных попыток доказать теорему Ферма. К сожалению, такое доказательство невозможно. И мы сейчас разъясним, почему невозможно. Правда, остается теоретическая возможность того, что удастся доказать, что теорему Ферма нельзя доказать. Появление такого доказательства также перекрыло бы вышеназванный шлюз — но тогда, вероятно, возник бы поток попыток опровергнуть теорему Ферма (например, путем предъявления в косвенной форме четверок астрономически больших чисел n, x, y, z, для которых нужное равенство было бы практически непроверяемым). Итак предположим, что (а) существует доказательство того, что теорему Ферма нельзя доказать; (б) существует доказательство того, что теорему Ферма нельзя опровергнуть. Наша цель теперь — показать, что (а) и (б) несовместимы, т. е. не может быть, чтобы оба эти утверждения были истинны одновременно. На самом же деле мы обнаружим, что (б) несовместимо даже с более слабым, чем (а), утверждением (а1): «теорему Ферма нельзя доказать». Именно, мы покажем, что из (б) следует наличие у теоремы ферма доказательства и тем самым отрицание (а1). Сперва — некоторые предварительные комментарии. Всякую четверку натуральных чисел n, х, у, z, такую, что n > 2, x > 0, y > 0, z > 0 и xn + yn = zn, условимся называть четверкой Ферма. Теорема Ферма гласит, что четверок Ферма не существует в природе. Опровергнуть какую-либо теорему 18 — это значит доказать ее отрицание. Опровергнуть теорему Ферма — это значит доказать, что четверки Ферма существуют. Лемма 1. Если нельзя доказать, что четверки Ферма существуют, то их не существует. Замечание. Пусть А — какое-либо утверждение. Нет никаких причин считать, что если нельзя доказать, что А, то А неверно. Однако — и в этом содержание леммы — это так, коль скоро А есть утверждение «четверки Ферма существуют». Доказательство леммы 1 ведем от противного. В самом деле, предположим, что четверки Ферма существуют. Выпишем какую-либо из них. Это будет четверка натуральных чисел a, b, c, d. Проверим, что это действительно четверка Ферма, т. е. проверим выполнение неравенства a>2, b>0, c>0, d>0 и равенства ba + ca = da. Предъявление четверки a, b, c, d вкупе с указанной проверкой образует доказательство существования четверки Ферма. Лемма 2. Если нельзя опровергнуть теорему Ферма, то теорема Ферма верна. Замечание. Не видно причин, почему это должно быть верно для любой теоремы. Доказательство леммы 2. Лемма 2 есть просто переформулировка леммы 1. Ведь «опровергнуть теорему Ферма» значит «доказать, что четверки Ферма существуют», а «теорема Ферма верна» значит «четверки Ферма не существуют». Лемма 2, которую мы доказали, имеет строение «если P, то Q». Поэтому если P имеет доказательство, то и Q имеет доказательство (доказательство Q состоит в сочетании доказательства леммы с доказательством Р). Поэтому имеем такое Следствие леммы 2. Если существует доказательство того, что нельзя опровергнуть теорему Ферма, то существует и доказательство того, что теорема Ферма верна, т. е. попросту, доказательство теоремы Ферма. Ввиду важности этого следствия еще раз сформулируем его: если существует доказательство того, что теорему Ферма нельзя опровергнуть, то теорему Ферма можно доказать. Итак, если (б), то теорему Ферма можно доказать, что и представляет собою обещанное отрицание утверждения (а1). Полученное противоречие и завершает наше рассуждение о том, что (а1) и (б), а тем более (а) и (б) несовместимы. Возникает следующий естественный вопрос: а почему проведенное
рассуждение нельзя повторить для континуум-гипотезы? В самом деле, гипотеза
(теорема) Ферма утверждает, что нет четверок Ферма, а континуум-гипотеза — что
нет множеств мощности, промежуточной между Обсуждаемая тема имеет самое тесное отношение к знаменитой теореме Гёделя о неполноте. Теорема эта утверждает, что какое ни предложить понятие формального доказательства, имеется такое утверждение о натуральных числах, что ни оно само, ни его отрицание не обладает формальным доказательством в рамках предложенного понятия. Мы исходим из очевидности того, что возможны различные определения формального доказательства. Эти определения отличаются друг от друга набором допускаемых аксиом и правил вывода. Могут быть такие представления о формальном доказательстве, в котором вообще не используются ни аксиомы, ни правила вывода. Короче говоря, подходы к понятию формального доказательства могут быть весьма различны. Но все эти подходы имеют и фундаментальную общность, выражаемую в следующих принципах: 1) каждое формальное доказательство есть текст — т. е. конечная цепочка знаков, выбранных из некоторого алфавита; 2) по каждому тексту, составленному из букв рассматриваемого алфавита, можно алгоритмически распознать, является ли оно формальным доказательством или нет, и если да, то какого именно утверждения; 3) только истинные утверждения могут обладать формальными доказательствами. В силу третьего принципа предъявление формального доказательства кого-либо утверждения гарантирует его истинность и, следовательно, может считаться его доказательством. Обратное, конечно, не предполагается: не предполагается, что каждое истинное или даже содержательно доказуемое утверждение имеет — при заранее заданном понятии формального доказательства — формальное доказательство. Анализ теоремы Гёделя о неполноте показывает, что утверждение, о
котором в ней идет речь, всегда имеет вид ∃x Ужесточим наши требования к представлениям о формальном
доказательстве. Именно, потребуем, чтобы,
коль скоро для какого-то алгоритмически проверяемого свойства Наше требование вытекает, в частности, из следующих двух еще более естественных требований: 1) если для числа с справедливо (алгоритмически) проверяемое
свойство 2) для какого угодно свойства Теперь рассуждениями, аналогичными тем, которые применялись в связи
с теоремой Ферма, приходим к следующему выводу: если ни утверждение ∃x В самом деле, если бы было верно ∃x Давайте еще раз оценим парадоксальность ситуации: из одного только факта, что ни А, ни не-А не обладают формальным доказательством, можно заключить, которое из этих двух высказываний истинно на самом деле. ^6. Что такое доказательство?
Если мы читаем книгу,
написанную пятьдесят лет назад, то рассуждения, которые мы в ней находим,
кажутся нам большей частью лишенными логической строгости.
Анри Пуанкаре, 1908г.
(Наука и метод, кн. II, гл. 2, п. 4; [2, с. 356]). В предыдущем размышлении встречались как термин «доказательство», так и термин «формальное доказательство». Иногда считают, что формальное доказательство — это такое доказательство, которое формально. Мы предпочитаем смотреть на эти понятия иначе. Формальное доказательство — это математический объект, подобный, скажем, матрице или треугольнику. Это конечная цепочка знаков некоторого заранее фиксированного алфавита, т. е., как говорят в математике, слово в этом алфавите. Говоря «знак», мы не имеем в виду — в данном случае — какую-либо смысловую, содержательную сторону, но только внешнюю, графическую. Чтобы подчеркнуть это обстоятельство, в математике, когда имеют в виду внешнюю, графическую сторону, говорят не «знак», а «буква». К числу букв относят обычно буквы алфавитов реальных языков (русского, латинского и т. д.), цифры, знаки препинания. Разумно отнести к числу букв и пробел между словами (словами в обычном, не математическом смысле), изобретая для его обозначения какой-либо специальный символ, например #. Это дает возможность текст, т. е. последовательность слов, также рассматривать как слово (в уточненном выше математическом смысле). Итак, формальное доказательство — это прежде всего слово в некотором алфавите — алфавите формальных доказательств. Разумеется, этим ни в малейшей степени не исчерпывается понятие формального доказательства: мы просто хотели подчеркнуть, что понятие формального доказательства относится к разряду слов — так же как понятие треугольника к разряду геометрических фигур. Какие именно слова следует считать формальными доказательствами — это тема особого разговора, выходящего за круг сюжетов, которые мы хотели бы здесь обсудить. Подчеркнем, что возможны различные определения понятия формального доказательства, каждое из которых приводит к своему множеству формальных доказательств. Некоторые общие положения, которым должно подчиняться любое разумное определение, были: изложены в предыдущем размышлении. Заметим, впрочем, что иногда делают еще один шаг в сторону общности и не требуют заранее, чтобы формальными доказательствами обладали только истинные утверждения, полностью отделяя понятие формального доказательства от понятия истины. А затем это отброшенное требование вводят в виде дополнительного свойства (которым формальное доказательство, вообще говоря, может и не обладать): именно, множество формальных доказательств называют семантически непротиворечивым, если всякое утверждение, обладающее формальным доказательством, истинно. Более точно общие представления о формальных доказательствах излагаются с помощью понятия дедуктики (см., например, [21]). Подчеркнем еще, что формальными доказательствами могут обладать (или не обладать) не сами содержательно понимаемые утверждения, а лишь их записи (т. е. опять-таки слова) в каком-либо точно заданном логико-математическом языке. Определение понятия формального доказательства — быть может, лучше сказать: определение множеств формальных доказательств — в широких пределах (обусловленных указанными выше общими ограничительными свойствами множества формальных доказательств) произвольно. Здесь имеется в виду тот «юридический» произвол, который отличает математические определения вообще. Мы имеем «юридическое» право, например, произвольно определить класс функций и назвать, «как хотим», например — непрерывными. Другое дело, что всякое разумное математическое определение обычно претендует на то, чтобы соответствовать некоторым интуитивным представлениям, отражать их. Законность определения еще не означает его разумности. Так, математическое понятие непрерывной кривой отражает (с той или иной точностью) наши интуитивные, содержательные представления о траектории движущейся точки. Аналогично понятие формального доказательства отражает интуитивные представления о содержательном доказательстве. Можно сказать, что понятие формального доказательства является математической моделью понятия доказательства — в том же смысле, в каком понятие непрерывной кривой является математической моделью понятия траектории. Остается выяснить, что же такое доказательство. Хотя, как мы отмечаем в самом начале настоящего очерка, неправильно полагать, что в математике все доказывается, нет сомнений, что понятие доказательства играет в математике центральную роль. «Со времен греков говорить "математика" — значит говорить "доказательство"» — так начинает свои «Начала математики» Николай Бурбаки [6, с. 23]. Вместе с тем мы отмечали, что понятие доказательства не принадлежит математике (математике принадлежит лишь его математическая модель — формальное доказательство). Оно принадлежит логике, лингвистике и больше всего — психологии. Итак, термин «доказательство» — один из самых главных в математике — не имеет точного определения. А приблизительное его определение таково: доказательство — это убедительное рассуждение, убеждающее нас настолько, что с его помощью мы способны убеждать других [12]. Восприняв доказательство, мы делаемся в известной степени агрессивными, приобретая готовность убеждать других с помощью этого воспринятого нами рассуждения. Если же мы не приобретаем такой готовности, это значит, что мы еще не восприняли предъявленное нам рассуждение как доказательство и если даже признали его доказательством, то просто, чтобы отмахнуться. Заметим, что понятия, присутствующие в нашем определении доказательства — либо логико-лингвистические («рассуждение»), либо психологические («убеждающая сила», «готовность»). Это полностью отвечает сути дела: само представление о доказательстве неразрывно связано с языковыми средствами и с социальной психологией человеческого общества. И то и другое изменяется с ходом истории. Меняется языковое оформление доказательств. Меняется и представление об убедительности. Представление об убедительности зависит не только от эпохи, но и от социальной среды. К сожалению, я не могу сейчас вспомнить, где я читал пассаж на следующую тему. Кардиналы, современники Галилея, были неглупые люди, некоторые из них могли воочию наблюдать горы на Луне в Галилеев телескоп, а также с пониманием следить за логикой рассуждений Галилея. Однако для них их собственные взгляды, основанные на априорной догме, были убедительнее любого эксперимента и любой логики. (Интересный анализ того, как априорно суженное представление о способах показывания препятствует признанию некоторых фактов, приведен в статье С. П. Божича [13].) Представление об убедительности того или иного рассуждения зависит от многих факторов. Выявление этих факторов представляется важной задачей логики и психологии. В число таких факторов входит, например, разделение понятий (а точнее, терминов) на осмысленные и бессмысленные. Понятия флогистона и теплорода, считавшиеся осмысленными в XVIII в., признаются сейчас бессмысленными. Эйнштейн открыл, что бессмысленным является и понятие одновременности двух событий — как объективное понятие, не зависящее от наблюдателя (более точно, он открыл, что одновременность не двуместное отношение между двумя событиями, а трехместное отношение, членами которого являются 1-е событие, 2-е событие и наблюдатель). С другой стороны, такое «очевидно бессмысленное понятие», как бесконечно малое число, наполняется сейчас точным смыслом в рамках новой ветви математики — так называемого нестандартного анализа. С изменением представлений об осмысленности или бессмысленности понятий меняется и представление и о самой сущности научной истины. Меняется представление об очевидности. Как в свое время все знали, что гроза вызывается высшими силами, так теперь все знают, что причина грозы — в атмосферном электричестве. Наличие у инертных газов свойства не вступать в химическое соединение было настолько очевидным, что это свойство было закреплено в самом названии «инертные»; когда же в 1962 г. были получены первые соединения с участием этих газов, химики, по-видимому, не испытали никакого стыда, а лишь с удовольствием констатировали, что «для объяснения строения этих соединений не потребовалось принципиально новых представлений о природе химической связи» (Большая Советская Энциклопедия, изд. 3-е, статья «Инертные газы»). То, что человеческое знание меняется с ходом истории — разумеется, общее место. Здесь хотелось бы подчеркнуть, что в состав знания входят не только сами факты, но и исходные предпосылки, презумпции, на основе которых тот или иной факт делается членом системы знаний: представления об осмысленности и бессмысленности, об очевидности и неочевидности, о возможном и невозможном, о частном и общем, об убедительности и неубедительности, о доказанном и недоказанном, о достоверном и недостоверном. Все эти представления, хотя, возможно, и меняющиеся более медленно, чем простые представления о фактах, в сущности так же исторически относительны, как и последние. Математика иногда воспринимается как скала, неподвижно возвышающаяся над волнами переменчивых представлений, относящихся к другим наукам. Конечно, основания для такого взгляда на математику имеются. Тем не менее представление о некоей абсолютности математики, видимо, преувеличено. Если математика и абсолютна, то только на уровне повседневного опыта — точно так же, как абсолютна ньютоновская физика в применении к явлениям «средних размеров» (а в очень малом и в очень большом действует уже иная, эйнштейновская физика) 21. В частности, социально-историческая обусловленность представлений о доказательствах вообще распространяется и на математические доказательства. Для иллюстрации сказанного автор сейчас попытается изложить вкратце свои представления о понятии доказательства в Древнем Египте, в Древней Греции и в Индии. У нас не так много достоверных сведений о том, как излагались и воспринимались математические доказательства в древности. Дошедшие до нас тексты во многих случаях весьма отрывочны: к тому же встречающиеся в них термины имеют зачастую спорную интерпретацию 22. Многое приходится домысливать. Каждый домысливает в желательную для себя сторону, и автор этих строк, надо думать, не исключение. С учетом этих оговорок можно составить следующую схему. В основе предлагаемой схемы лежит убеждение, что представление о доказательстве есть продукт социальной истории общества. Мы отдаем себе отчет в упрощенности наших исторических экскурсов, приписывая Древнему Египту централизованную государственность, хотя и там были периоды раздробленности, а Древней Греции — демократию, хотя и там случались тиранические или олигархические правления. Но любая схема предполагает упрощения. Итак, Древний Египет. Централизованное теократическое государство с необычайно сильной дисциплиной. В качестве действенного инструмента поддержания централизации, дисциплины, порядка выступает постоянное строительство пирамиды, требующее колоссальных людских и материальных ресурсов и объединяющее усилия всей страны. Авторитет фараона и жрецов непререкаем. Непререкаем и авторитет написанного слова. Если что-то сказал или написал жрец, писец, учитель — значит, это так и есть. Если что-то написано на папирусе — значит, это так и есть. Убедительность основывается на авторитетности источника. Математические тексты Древнего Египта содержат готовые рецепты без какого бы то ни было их обоснования. Говоря об отсутствии обоснования, мы имеем здесь в виду современное понимание слова «обоснование». С точки зрения современника рецепт на папирусе был полностью обоснован тем, что он исходил из авторитетного источника и был оформлен в авторитетной форме записи на папирусе. Факт записанности на папирусе и был сам по себе доказательством. Действительно, этот факт был достаточен для того, чтобы с его помощью убеждать других. Ряд рецептов для вычисления площадей треугольников и четырехугольников не получил в наши дни однозначного толкования; идут споры, как надо понимать входящие в них термины [4, гл. IV, § 2, а]. В зависимости от толкования эти формулы должны восприниматься либо как точные, либо как приближенные, либо как вообще неверные. Говоря о неверной формуле, мы имеем в виду выражение площади треугольника через полупроизведение основания на боковую сторону 23. Многие исследователи считают, впрочем, что соответствующий древнеегипетский термин надо трактовать не как боковую сторону, а как высоту (и тогда формула из папируса оказывается верной). Однако, даже если бы этот термин означал в действительности не высоту, а боковую сторону, соответствующую (неверную с нашей современной точки зрения) формулу следует считать доказанной в древнеегипетском понимании слова «доказана»: ведь эта формула убедительно обоснована тем, что она (конечно, не в виде формулы, а в виде словесного рецепта) содержится в авторитетном документе. Иначе обстояло дело в Древней Греции. Сравнительно (с Египтом) небольшие государственные образования с народными собраниями. В народных собраниях выступают ораторы, не являющиеся носителями априорного авторитета. Они должны убедить слушателей посредством рассуждения. Формирование правильных рассуждений становится повседневной и актуальной потребностью. Отсюда — зарождение логики у Сократа и окончательное оформление ее в виде науки у Аристотеля. Отсюда же — приближающиеся к современным представления о доказательстве, начало дедуктивного метода в математике. Основой математической убедительности становится рассуждение. Возникает понятие об основах правильных рассуждений — аксиомах и постулатах. Убедительно (и следовательно, доказуемо) то, что может быть получено «законным рассуждением» из отправных утверждений, признаваемых справедливыми. Наконец, Индия. Хотя те геометрические иллюстрации, на которые мы собираемся ссылаться, относятся к средневековой Индии, не исключено, что они появились уже в Индии древней. Вообще, датировка индийских математических представлений вызывает значительные трудности, поскольку одни тексты могут представлять собою изложение более ранних. С другой стороны, это и не так существенно: в то время как средневековый Египет и средневековая Греция не имели ничего общего с Древним Египтом и Древней Грецией, средневековая Индия оставалась хранителем духовного наследия древней Индии. Существенной чертой этого наследия являлось и является придание статуса высшей достоверности внутреннему озарению. Непосредственное внутреннее озарение представляет собой основной источник знания и обладает неоспоримой убедительностью. То, что познано таким образом, считается доказанным. Чтобы убедить в этом другого, надо привести его в такое состояние, чтобы и он мог испытать внутреннее озарение. Поэтому геометрические доказательства выглядели так: чертеж, а под ним подпись: «Смотри!» Примеры таких чертежей с подписями «Смотри!», относящиеся к XII и XVI вв., приведены, например, в [9] на с. 76 и 154. Один из этих чертежей (он воспроизведен также на стр. 75 в [15]), на наш взгляд, достоин того, чтобы излагаться в сегодняшней средней школе: он нагляднее современных доказательств показывает, что площадь круга равна площади прямоугольника, стороны которого суть полуокружность и полудиаметр круга. Поэтому мы приводим этот чертеж здесь — см. рис. 5. 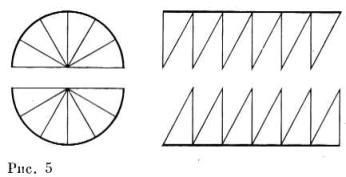
Автор отдает себе отчет, что его мнение по поводу индийских доказательств расходится с мнением такого авторитета в области истории математики, как А. П. Юшкевич, который пишет (см. [9, с. 155]): «Лаконичность выводов в индийских сочинениях по математике или наличие в последних чертежей с одной лишь припиской «Смотри»! не следует рассматривать как проявление особого подхода к проблеме доказательства или особого хода мышления». На наш взгляд, как раз следует. Почему же в противном случае такого рода «Смотри!» мы не встречаем нигде, кроме Индии? Ценные соображения об эволюции понятия математического доказательства высказывает в [15] С. С. Демидов, который, в частности, указывает, «что доказательность математических рассуждений также в конечном итоге есть их убедительность. То, что нам казалось убедительным вчера, уже не кажется таким сегодня». Определение доказательств как убеждающего текста делает понятие доказательства довольно-таки субъективным (для кого текст убеждающий, а для кого нет). Нам не представляется это недостатком определения. Такова суть вещей. Употребленное выше слово «делает», пожалуй, неудачно. Наше определение не столько делает понятие доказательства субъективным, сколько отражает субъективный характер этого понятия. Тем интереснее задача (от решения которой мы весьма далеки), почему же все-таки понятие доказательства носит характер общекультурный в том смысле, что в пределах одной и той же культуры споры о том, доказано или нет то или иное утверждение, хотя и бывают, но сравнительно редки. Говоря о таких спорах, мы не имеет в виду несогласия между представителями разных логических направлений в математике, например, между представителями обычной, классической математики и представителями интуиционистской (конструктивистской) математики. Последние не признают доказанными (а, напротив, считают неверными) многие утверждения обычной математики. Можно считать, что интуиционисты и конструктивисты принадлежат к разным математическим культурам и даже самые привычные слова (такие, как, скажем, «существует») наполняют другим смыслом (разумеется, интуиционисты и конструктивисты считают, что это представители традиционной математики наполняют слова другим смыслом, а они, интуиционисты, как раз и употребляют эти слова в единственно правильном смысле). Поэтому интуиционисты считают неверными многие доказательства традиционной математики. Мы говорим здесь о другом — не об изменении семантики терминов, ведущем к изменению истинностной оценки утверждений, а о том, что доказательство может оказаться непонятным и потому неубедительным (а раз неубедительным — значит, вообще не доказательством). Современная математика имеет сложное строение, которое почти перестает быть обозримым. Доказательства некоторых теорем оказываются столь громоздкими, что надо иметь чрезвычайно большое желание, терпение и время, чтобы их проверить. О том, что надо иметь специальные знания, нечего и говорить — для ряда теорем не только изобретение их доказательств, но и проверка этих доказательств оказывается доступной лишь узкому кругу изощренных специалистов. Иногда интересуются объемом доказательства той или иной теоремы. При этом обычно имеют в виду, что в доказательстве разрешается использовать в виде готовых формулировок, уже не требующих доказательств, теоремы, установленные ранее. Будет ли такое рассуждение доказательством — т. е. убеждающим текстом — для того, кто не знаком с доказательствами этих «установленных ранее» теорем? Мы не беремся дать однозначный ответ на этот вопрос. Заметим еще, что само слово «ранее» вносит дополнительный субъективный «релятивистский» момент (две почти одновременно доказанные теоремы могут по-разному хронологически упорядочиваться разными наблюдателями). Если же запретить ссылаться в доказательстве на какие бы то ни было ранее доказанные теоремы и восходить непосредственно к определениям и первичным, неопределяемым понятиям (о которых мы рассуждали в нашем первом размышлении), то такое полное доказательство может в ряде случаев простираться на тысячи страниц математического текста (и быть затруднительным для восприятия даже еще более, чем доказательство, опирающееся хотя бы и на неизвестные читателю, но ясно сформулированные факты). Изучение трудных математических доказательств можно сравнить с альпинистским восхождением на вершину. Уровень моря соответствует начальным понятиям. Восхождение от уровня моря может занимать месяцы, а его математический аналог (понимание доказательства) — годы. В обоих случаях — много промежуточных остановок. Сперва добираются до общего высокогорного лагеря, в котором собираются альпинисты, направляющиеся на различные окрестные вершины. Этому этапу соответствует получение серьезной математической подготовки, достаточной для владения более специальными темами. Затем начинается движение к избранной вершине, опять-таки с промежуточными лагерями и остановками. Для математика роль этих лагерей и остановок играют, соответственно, теории и теоремы. Как альпинист может совершить за свою жизнь ограниченное число восхождений, так и математик — узнать ограниченное число доказательств. Следующая общая для альпинизма и математики черта является существенной — известная условность в выборе точки отсчета. Собственно восхождение начинается не с уровня моря, а с точки, куда профессиональные альпинисты могут добраться как бы без труда, хотя для обычных людей попадание в эту точку может представить весьма большие трудности. Собственно доказательство начинается с аналогичной точки: эта точка расположена на некоем общекультурном (имеется в виду математическая культура) уровне. Впрочем, при современном состоянии математики общность приставки «обще-» непрерывно снижается, и ныне многие доказательства начинаются с точки, доступной лишь узким специалистам. Вторая общая черта — расчлененность на этапы, наличие достаточного числа промежуточных остановок. Откуда же в математике берется убеждение, что доказанные теоремы, доказательства которых он так никогда и не узнает, действительно являются доказанными, т. е. располагают доказательствами? Видимо, такое убеждение основано не на чем ином, как на доверии. Это положение внешне не должно казаться слишком странным. В самом деле, многие ли читатели этих строк видели остров Пасхи? Ведь для тех, кто его не видел, убеждение в том, что этот остров существует, также основано в конечном счете на доверии. Но если современное доказательство основано на доверии к авторитету, то в чем же его принципиальное отличие от древнеегипетского? Ответ на этот непростой вопрос заключается, возможно, в том, что доказательства постепенно переходят из разряда явлений индивидуального опыта в разряд явлений опыта коллективного. Тенденция к выдвижению на первый план коллективного вообще характерна для истории цивилизации. Хорошо известно (и много обсуждено), что с развитием человеческого общества возникает и неуклонно усиливается разделение и кооперация труда. Лишь в глубокой древности человек мог сам, лично производить все необходимое для себя: сейчас каждый вынужден пользоваться результатами труда других. Известно (хотя и в меньшей степени обсуждено), что одновременно происходит разделение и кооперация научных знаний. Трудно сказать, когда — по-видимому, в средние века — еще находились отдельные ученые, способные охватить всю доступную их современникам сумму знаний. Сейчас каждый вынужден так или иначе использовать знания других. Аналогично обстоит дело и с доказательствами: деятельность в сфере производства и потребления доказательств стала в такой же степени объектом разделения и кооперации, как и деятельность в сфере производства и потребления знаний. Само понятие убедительности начинает терять свой индивидуализированный оттенок и все больше приобретает характер «коллективной убедительности». По-видимому, следует постепенно приучаться говорить об убедительности не для отдельного индивидуума, а для некоторого научного коллектива. При этом коллективная убедительность отнюдь не означает равную «непосредственную убедительность» для каждого в отдельности члена коллектива. Коллектив выступает не как простая сумма членов, а как единое целое. Смысл коллективной убедительности в том, что для каждой составной части доказательства найдется свой «отвечающий за нее» член коллектива, для которого непосредственно убедительна именно эта часть (а другие члены коллектива полагаются в данном вопросе на этого члена). Век информатики вносит свои коррективы и в представления о доказательствах. Возникают, например, случаи, когда доказательство требует перебора столь большого числа вариантов, что этот перебор делается недоступным человеку — а машине доступен. Допустим, машина перебрала все требуемые варианты, и перебор привел к нужным результатам. Можем ли мы считать, что получили доказательство? А что если машина дала так называемый «сбой»? (Но ведь и человек может ошибаться!) Кроме того, необходима гарантия, что сама программа (работы машины) составлена правильно; правильность программы требует специального доказательства, и теория таких доказательств образует специальный раздел теоретического программирования. Реально компьютер был привлечен для решения проблемы четырех красок. По простоте формулировки эта проблема 24, состоящая в доказательстве гипотезы четырех красок, мало уступает проблеме Ферма (состоящей в доказательстве гипотезы Ферма), а по естественности постановки (и прикладному значению) ее превосходит. В 1976 г. Аппелем и Хакеном было анонсировано [17], а в 1977 г. изложено в [18] и [19] решение этой проблемы, основанное на сведении решения к большому числу частных случаев, рассмотрение которых можно поручить машине. Машина все проверила, и тем самым было получено доказательство того, что всякую карту можно раскрасить четырьмя красками так, как нужно. Сами Аппель и Хакен высказывают такие мысли по поводу своего доказательства [20]: «При доказательстве было осуществлено беспрецедентное применение компьютеров. Дело в том, что используемые в доказательстве вычисления делают его более длинным, чем традиционно считается допустимым. На самом деле, правильность предложенного доказательства вообще не может быть проверена без помощи компьютера. Более того, некоторые из решающих идей доказательства материализовались посредством компьютерных экспериментов. Не исключено, конечно, что в один прекрасный день появится короткое доказательство теоремы о четырех красках… Вместе с тем не исключено, что такое короткое доказательство вообще невозможно. В этом последнем случае возникает новый и интересный тип теорем, для которых не существует доказательств традиционного типа». В последнее время, однако, правильность доказательства Аппеля и Хакена стала подвергаться сомнению — причем как раз не машинная часть, а домашинная, теоретическая, та, в которой устанавливается, что к рассмотрению частных случаев действительно все сводится. Комментарий. Скажем о ситуации с доказательством Аппеля и Хакена чуть подробнее. Основная идея этих авторов связана со следующими представлениями. Прежде всего авторы переходят от раскраски областей карты к раскраске вершин плоского графа, причем такого, который представляет собою триангуляцию. Далее, они называют конфигурацией любой подграф, образованный циклом и внутренностью этого цикла. Конфигурация называется сводимой, если некоторыми стандартными методами можно доказать, что она не может быть погружена в минимальный контрпример к гипотезе четырех красок. Множество конфигураций называется неизбежным, если каждая плоская триангуляция содержит как подграф одну из конфигураций множества. Из определений немедленно следует, что для решения (положительного) проблемы четырех красок достаточно предъявить неизбежное множество сводимых конфигураций. В [19] на с. 505—567 авторы предъявляют в явном виде 1834 сводимые конфигурации, образующие неизбежное множество. Длина цикла в каждой из этих конфигураций — 14 или менее того. И для поиска неизбежного множества, и для доказательства сводимости его членов использовался компьютер. Однако если в первом случае (построение множества) привлечение компьютера носило вспомогательный характер, поскольку само доказательство неизбежности найденного (теперь уже неважно, каким способом) множества не опирается на машинные вычисления, то во втором случае (проверка сводимости) использование компьютера является существенным компонентом доказательства, и на каждую конфигурацию идет примерно 10 минут машинного времени такой проверки. Оценивая доказательство Аппеля и Хакена, авторы обзора [23] указывают, что авторам доказательства понадобилось для его построения четыре года и 1200 часов машинного времени и что текст доказательства занимает 139 страниц, в том числе 99 страниц рисунков с более чем 30 рисунками в среднем на страницу. Они отмечают также, что «существенно переборный характер доказательства затрудняет его проверку (по оценке Аппеля проверка всех деталей требует 300 часов машинного времени)». Названные 300 часов относятся, по-видимому, к проверке сводимости. Однако, как мы уже отмечали, сомнения вызывает как раз немашинная часть — проверка неизбежности предъявленного множества конфигураций. Дело в том, что непосредственно в тексте [18] и [19] эта проверка исчерпывающим образом не проводится. На с. 460 текста сделано подстрочное примечание, в котором сообщено, что детали доказательства неизбежности предъявленного множества (более точно, детали доказательства лежащей в основе этой неизбежности так называемой теоремы о разряжении) содержатся на микрофишах, образующих специальное приложение к журналу. Автору этих строк, однако, не довелось увидеть это приложение. Создается впечатление, что с развитием математики (и появлением все более и более сложных и длинных доказательств) доказательства теряют свое главное свойство — свойство убедительности. Делается непонятным, что же тогда остается от доказательства: ведь убедительность как бы входит в их определение. Кроме того, с усложнением доказательства возрастает его элемент субъективности. Конечно, формальное доказательство объективно. Но, во-первых, формальными доказательствами обладают не сами суждения, а их выражения, записи в формализованных языках. Во-вторых, проверка утверждения, что данный текст является формальным доказательством, хотя и осуществляется алгоритмически, может, при объемистом тексте, вызвать значительные практические трудности. Большие доказательства начинают жить по каким-то своим, макроскопическим законам. При чрезмерном возрастании объема доказательства расплывается само представление о доказательстве — подобно тому как в «большом» расплывается понятие о натуральном числе (еще раз отсылаем читателя к статье П. К. Рашевского [16]). Получается, что хотя все доказательства должны, по определению, быть убедительными, одни доказательства убедительнее других, т. е. как бы в большей степени являются доказательствами, чем другие. Возникает нечто вроде градации доказательств по степени доказательности — идея, которая, конечно, в корне противоречит первоначальным представлениям об одинаковой непреложности всех доказательств. Но ведь и математические истины допускают нечто вроде такой градации. Каждое из следующих трех утверждений: «2•2 = 4», «1714 > 3111», «300! > 100300» истинно. Однако мы говорим: «Верно, как 2•2 = 4», но не говорим «Верно, как 1714 > 3111» или «Верно, как 300! > 100300». ^7. Можно ли математику сделать понятной?В чем причины того, что математика непонятна столь многим? Эта проблема волновала великого Пуанкаре: «Чем объяснить, что многие умы отказываются понимать математику? Не парадоксально ли это? В самом деле… здесь имеется проблема, которая не легко решается, но которая должна занимать всех, желающих посвятить себя делу преподавания» [2, с. 353]. Скорее всего, «виноваты» обе стороны. Виноваты нематематики, приученные дурным воспитанием к непониманию и даже неприязненному отношению к математике (как указывает Пуанкаре, «зачастую ум людей, нуждающийся в руководящей нити, слишком ленив для поисков ее» [2, с. 354]). Виноваты математики, не желающие тратить свои усилия на то, чтобы разъяснить свою математику непосвященным (а сколько людей удивляется, что в математике еще осталось, что открывать!). Конечно, в математике всегда останутся многочисленные детали, недоступные непрофессионалу (и даже профессионалу, но в другой области математики). Но ведь так обстоит дело всюду — в шахматах, например, многие ходы Карпова и Каспарова в их сражениях друг с другом были непонятны даже гроссмейстерам. В то же время гораздо больше из математики, чем думают обычно, могло бы быть объяснено широким кругам доброжелательных слушателей и читателей — не в деталях, конечно, а на уровне общей сути. Разумеется это требует от математиков целенаправленной деятельности в новом для них направлении. Возможно, что в этом и состоит их нравственный долг перед человечеством. «Но, чтобы помочь непонимающим, мы должны сначала хорошо узнать то,
что их останавливает» [2, с. 354]. Во многих случаях, по-видимому, препятствием
является сложное логическое строение математических определений и утверждений —
строение, в котором логические связки и кванторы существования и общности
чередуются друг с другом. Всякий преподававший математический анализ знает
трудности, возникающие на пути параллельного усвоения понятия предельной точки
последовательности, определение которой имеет структуру По-видимому, все же математические понятия, как и всякие разумные понятия, существуют в виде представлений, не обязательно связанных с текстами. Определяющие же эти понятия словесные тексты следует признать важным, но не единственным способом их усвоения. Думается, что уже сегодня мы располагаем более совершенными способами внедрения в сознание обучающегося понятия предела и предельной точки последовательности (обучающегося, не имеющего специальных «математических способностей», которые — при современном понимании этого взятого в кавычки словосочетания — предполагают высокое умение воспринимать именно словесные формулировки). Представим себе экран, на котором рисуется траектория движения точки, неограниченно приближающейся к некоторой неподвижной точке, которая и есть предел. Этот сюжет многократно повторяется с изменением как положения предела (чтобы не создавалось ложного впечатления, что у всех последовательностей один и тот же предел), так и способа приближения движущейся точки к пределу (чтобы не создавалось, в частности, ложного впечатления, что расстояние между движущейся точкой и ее пределом изменяется монотонно). Можно представить и аналогичную наглядную иллюстрацию понятия предельной точки, когда траектория хотя и неограниченно приближается временами к той точке, но вместе с тем опять-таки временами отдаляется от нее на определенное расстояние. Кажется правдоподобным, что у любого наблюдающего такие картинки возникнет правильное представление и о пределе, и о предельной точке. Можно быть уверенным, что с внедрением компьютеров преподавание пойдет по пути визуализации понятий, традиционно считавшихся совершенно абстрактными. Если бы излагаемая тема имела только педагогическое значение, мы бы не останавливались на ней так подробно в сочинении философского характера. Однако тема выходит за рамки педагогики, смыкаясь с вопросом об онтологической природе математических сущностей. Вопрос же этот, как и всякий разумный теоретический вопрос, имеет прикладное значение — в данном случае, в порядке обратной связи, педагогическое. В самом деле, если математическое понятие имеет сущность, отдельную от воплощения в словесном определении или формуле, то можно надеяться на лучшее понимание этой сущности путем демонстрации различных ее проявлений (а не только формулировки). Чтобы не быть голословными, приведем свежий пример. На с. 71—72 недавно вышедшего учебного пособия [24] приведена формула, определяющая некое математическое понятие — так называемый конус Кларка. Сформулировав определение, авторы пишут: «Однако с первого взгляда невозможно понять ни свойств конуса Кларка, ни сам смысл его формального определения». И дальше они сперва приводят эвристические соображения, позволяющие уяснить конус Кларка, а затем переводят эти соображения на язык нестандартного анализа. Здесь можно уловить мысль, что понятие конуса Кларка существует как бы само по себе; определение же в виде формулы — лишь один из способов (и не наиболее удобный) постижения этого понятия, а для лучшего постижения полезны описания вроде «результаты разглядывания множества в микроскоп» [24, с. 86]. Независимо от того, так ли это на самом деле, представляется плодотворной следующая рабочая гипотеза: подлинно глубокое математическое понятие или математическое утверждение должно быть в своей сути просто. А тогда есть надежда, что оно окажется понятным, (или, лучше сказать, понятым): ведь к простому легче привыкнуть, а мы не знаем иного толкования для «понять», чем «привыкнуть». Литература1. Маркс К., Энгельс Ф. Соч. 2-е изд. Т. 20. 2. Пуанкаре А. О науке. М., 19ЯЗ. 3. Гильберт Д. Основания геометрии. М.: Л., 1948. 4. Нейгебауэр О. Лекции по истории античных математических наук. Т. 1. Догреческая математика. М.; Л., 1937. 5. Толковый словарь русского языка. М., 1938. Т. 2. 6. Бурбаки Н. Теория множеств. М., 1965. 7. Черч А. Введение в математическую логику. М., 1960. 8. Hornby A. S., Parnwell E. C. An English-reader′s dictionary. L.; Oxford, 1959. 9. Юшкевич А. П. История математики в средние века. М., 1961. 10. Потоцкий М. В. О педагогических основах обучения математике. М., 1963. 11. Горский Д.. Определение // Филос. энциклопедия. М., 1967. Т. 4. С. 150-152. 12. Успенский В. А. Предисловие // Математика в современном мире. М., 1967. 13. Божич С. П. О способах истинностной оценки естественнонаучного высказывания // Логика и эмпирическое познание. М., 1982. 14. Изоморфизм // БСЭ. 3-е изд. М., 1972. Т. 10. 15. Демидов С. С. К истории аксиоматического метода II История и методология естественных наук; Математика. Механика. М., 1973. Вып. 14. 16. Рашевский II. К. О догмате натурального ряда // Успехи мат. наук. 1973. Т. 28. Вып. 4 (172). 17. Appel K., Haken W. Every planar map is four colorable // Bull. Amer. Math. Soc. 1976. Vol. 82, N 5. 18. Appel K., Haken W. Every planar map is four colorable. Pt I: Discharging // III. J. Math. 1977. Vol. 21, N 3. 19. Appel K., Haken W., Koch J. Every planar map is four colorable. Pt II: Reducibility II Ibid. 20. Appel K., Haken W. The solution of the Four-Color-Map problem // Scientific American 1977. Vol.237, N 4. 21. Успенский В. А. Теорема Гёделя о неполноте. М., 1982. 22. Плиско В. Е. Теорема // Мат. энциклопедия. М., 1985. Т. 5. 23. Козырев В. П., Юшманов С. В. Теория графов: (Алгоритм., алгебраич. и метр. пробл.) // Теория вероятности: Мат. статистика. Теорет. кибернетика. М., 1985. Т. 23. 24. Кусраев А. Г., Нутателадзе С. С. Субдифференциалы и их применения: Учеб. пособие. Новосибирск, 1985. 25. Уроки открывает беседа с математиком Л. Понтрягиным: Интервью акад. Л. С. Понтрягина «Учит. газ.» // Учит. газ. 1985, 23 мая. Примечания1. Полезно представить себе граф, в котором в вершинах размещены слова, а стрелка идет от вершины Х в вершину Y в том случае если в словарной статье, толкующей слово X, встречается слово Y 2. Например, в толковом словаре английского языка Хорнби и Парнуэлла |8] оставлены без объяснений такие слова, как «thing» (в основном значении) и «all». К сожалению, для русского языка подобный словарь еще не создан. 3. Цитированные слова произнес «неглупый ученик» в оправдание сделанному на уроке заявлению, что шар, положенный на наклонную плоскость, покатится вверх. Этот замечательный эпизод описан в [10]. 4. Пример акад. П. С. Александрова. 5. Давно пора покончить с анахронизмом, начинающим натуральный ряд с единицы. В пенале всегда какое-то натуральное число карандашей — может быть нуль. Натуральное число — это мощность (число элементов) конечного множества, в частности — пустого. 6. Автор пользуется случаем выразить свой протест против получившего, к сожалению, распространение русского перевода названия трактата Бурбаки как «Элементы математики» (в подлиннике «Elements de mathematique»). Французские издания «Начал Евклида» также озаглавлены «Elements». Параллель замыслов, Евклида и Бурбаки бросается в глаза. (Несколько менее очевидное сходство заключается в загадочности личностей обоих авторов и скудности биографических сведении о них. Ведь само существование Евклида как отдельного человека иногда также подвергается сомнению.) Перевод «Elements» как «Элементы» (в применении к сочинению Бурбаки) представляется чистым недоразумением. 7. Члены Натурального Ряда — Ноль, Один (Единица), Два (Двойка) и т. д. — мы пишем с большой буквы, чтобы подчеркнуть их уникальность, т. е. абсолютную единственность. Слова «Ноль», «Один» (или «Единица»), «Два» (или «Двойка») и т. д. — собственные имена в абсолютном смысле (такие, как слона «Солнце», «Луна», «Земля»), у каждого из них единственное значение — количество элементов пустого, одноэлементного, двухэлементного и т. д. множества. А «ноль» аксиом Пеано является именем собственным лишь относительно, в пределах данного контекста, а точнее — в контексте той структуры, которая описывается этими аксиомами. Таких структур много, и в каждой из них свой ноль. 8. По поводу понятий «изоморфизм», «изоморфный» мы отсылаем читателя ко второй из двух статей «Изоморфизм» в 3-м издании Большой Советской Энциклопедии [14]. 9. Не отсутствием ли "римского ноля" в традиционном наборе символов объясняется упорное исключение ноля из натурального ряда? Короче говоря, не находимся ли мы в этом вопросе в плену у латыни? 10. Заметим в этой связи, что «физический» Натуральный Ряд, скорее всего, отличается от своей математической модели — «математического» Натурального Ряда. См. по этому поводу глубокую и недостаточно оцененную статью П. К. Рашевского [16]. 11. Нетрудно заметить, что свойство формулы «быть закрытой» не зависит от того, в применении к какой структуре мы рассматриваем эту формулу; это свойство может быть определено чисто синтаксически по внешнему виду формулы. (Все переменные должны быть связаны кванторами; в этом и состоит закрытость.) 12. Моделью системы, или списка аксиом, называется всякая структура, удовлетворяющая каждой из аксиом системы. 13. «Вслед за У. В. Куайном мы принимаем этот этимологически более правильный термин вместо распространенного в настоящее время термина "unary"» ([7], примечание 29). 14. Когда мы говорим об аксиомах, мы имеем в виду символический язык, подобный описанному выше для сигнатуры {<}; только теперь в алфавит его знаков вместе с «<» входят «0», «′», «+», «•». 15. А залог ясности понимания вопроса состоит в ясности понимания возможных ответов. 16. Примечание для специалистов. Известные автору примеры подобных формул содержат предикатные символы валентности 2. Однако и аксиома индукции, если заменить в ней функциональный символ штрих на предикатный, будет содержать предикатный символ валентности 2. 17. Впрочем, не все придерживаются этой точки зрения. Так, Виктолий Иванович Судкин па стр. 45 своей книги «Методика познания "истины". Доказательство Великой теоремы Ферма» (Ярославль: Верх.-Волж. кн. изд-во, 1975. 48 с.) указывает: «Итак, сменилось 13 поколений людей, а Великая теорема Ферма осталась еще не доказанной. Только в настоящей работе впервые приводится полное доказательство теоремы в общем виде». 18. Мы по-прежнему пользуемся неточной терминологией и отождествляем слово «теорема» со словом «утверждение», а не со словосочетанием «доказанное утверждение». 19.
Это значит, что существует алгоритм, который для любого c проверяет, верно ли 20. Слова «истинно» и «верно» — синонимы. Слово «доказуемо» имеет другой смысл (и даже другие смыслы). 21. По поводу «расплывания в большом» представлении о натуральном числе см. уже упоминавшуюся статью П. К. Рашевского [16]. 22. См., например, относящееся к толкованию древнеегипетских текстов примечание переводчика на с. 139 в [4]. 23. Вот что говорит по этому поводу академик Л. С. Понтрягин: «Первая известная нам математическая рукопись — это рукопись Ахмеса, составленная за две тысячи лет до нашей эры. В ней содержатся некоторые алгебраические и геометрические правила — например, вычисление площади треугольника… Однако в папирусе Ахмеса была допущена ошибка. Согласно ему, площадь равнобедренного треугольника равна произведению основания на половину боковой стороны — а каждый сегодняшний школьник знает, что это неверно» [25]. 24. См. ее формулировку в Большой Советской Энциклопедии, изд. 3-е, в статье «Четырех красок задача». 25. Эти умственные построения вряд ли могут быть осуществлены человеческим умом, если они не опираются на общечеловеческую логику, а следовательно, на реальность, из оперирования с которой эта логика происходит. Текст приводится по публикации в сборнике «Закономерности развития современной математики». М. Наука, 1987. с. 106 – 155. с учетом поправок, внесенных автором. Владимир Андреевич Успенский — доктор физико-математических наук, профессор, заведующий кафедрой математической логики и теории алгоритмов механико-математического факультета МГУ им. М. В. Ломоносова.
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Математика ≫ Семь размышлений на темы философии математики // Владимир Успенский |
|
[time: 8 ms; queries: 7]
22 Фев 2026 05:23:54 GMT+3 |



 (Натуральный Ряд с операцией «следовать за») и структурой
(Натуральный Ряд с операцией «следовать за») и структурой  (простые числа
с операцией «следовать за») задает бесконечная таблица
(простые числа
с операцией «следовать за») задает бесконечная таблица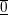 , I, II, III, …, CXXVI, …
, I, II, III, …, CXXVI, …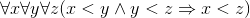 .
.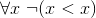 .
.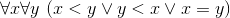 .
.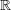 всех действительных чисел с обычным отношением порядка будет
удовлетворять выписанным трем аксиомам. Наблюдая совместно
всех действительных чисел с обычным отношением порядка будет
удовлетворять выписанным трем аксиомам. Наблюдая совместно 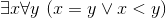 .
.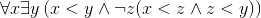 .
.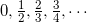 (*)
(*)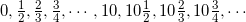 (**)
(**)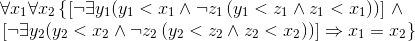
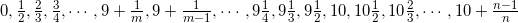 (***)
(***)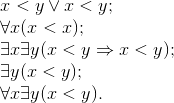
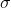 , называется (математической) структурой сигнатуры
, называется (математической) структурой сигнатуры 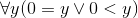 .
.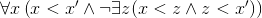 .
.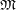 , то нужно прибавлять эту букву «
, то нужно прибавлять эту букву «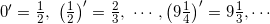 и т. д.
удовлетворяет аксиомам 1 — 8, но не изоморфна
и т. д.
удовлетворяет аксиомам 1 — 8, но не изоморфна 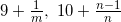 ).
).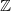 всех целых чисел. При
естественных же аксиомах для сигнатуры, включающей операцию сложения,
нестандартная часть всякой счетной (т. е. насчитывающей счетное число элементов) структуры,
удовлетворяющей этим аксиомам, имеет вид, который мы (не очень удачно) пытались
изобразить на рис. 4. На этом рисунке мы пытались как-то выразить
следующую идею: берется очень много (бесконечное счетное число) экземпляров
множеств целых чисел
всех целых чисел. При
естественных же аксиомах для сигнатуры, включающей операцию сложения,
нестандартная часть всякой счетной (т. е. насчитывающей счетное число элементов) структуры,
удовлетворяющей этим аксиомам, имеет вид, который мы (не очень удачно) пытались
изобразить на рис. 4. На этом рисунке мы пытались как-то выразить
следующую идею: берется очень много (бесконечное счетное число) экземпляров
множеств целых чисел 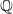 .
.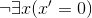
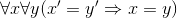
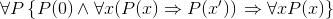
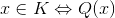 (+)
(+)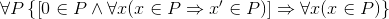
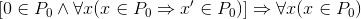
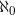 (читается
«алеф-ноль») и называется счетно-бесконечной (или бесконечной счетной)
мощностью; вторая обозначается c
(строчное готическое «це») и называется континуальной мощностью. Очевидно,
(читается
«алеф-ноль») и называется счетно-бесконечной (или бесконечной счетной)
мощностью; вторая обозначается c
(строчное готическое «це») и называется континуальной мощностью. Очевидно, 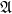 (x), где
(x), где 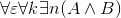 и понятие предела
последовательности, определение которого имеет структуру
и понятие предела
последовательности, определение которого имеет структуру  . Однако являются ли возникающие при усвоении этих
понятий учащимися психологические трудности трудностями сути дела или
трудностями словесного выражения? Автор не знает окончательного ответа на этот
вопрос, который связан с еще более глубоким вопросом: можно ли отделить
математику от словесных формулировок? Иначе говоря, пребывает ли математика
исключительно в математических текстах или же математика имеет некоторую
отличительную от текстов сущность, а тексты служат лишь тем или иным (и потому,
может быть, не всегда удачным) способом выражения этой сущности. По-видимому
этот вопрос, который мы назвали более «глубоким», применим не только к
математике, но и к любой другой науке. Математика же выделяется среди других
наук тем, что она есть, по формулировке Энгельса, «абстрактная наука,
занимающаяся умственными построениями»
. Однако являются ли возникающие при усвоении этих
понятий учащимися психологические трудности трудностями сути дела или
трудностями словесного выражения? Автор не знает окончательного ответа на этот
вопрос, который связан с еще более глубоким вопросом: можно ли отделить
математику от словесных формулировок? Иначе говоря, пребывает ли математика
исключительно в математических текстах или же математика имеет некоторую
отличительную от текстов сущность, а тексты служат лишь тем или иным (и потому,
может быть, не всегда удачным) способом выражения этой сущности. По-видимому
этот вопрос, который мы назвали более «глубоким», применим не только к
математике, но и к любой другой науке. Математика же выделяется среди других
наук тем, что она есть, по формулировке Энгельса, «абстрактная наука,
занимающаяся умственными построениями»  В отличие от метрической теории алгоритмов, дескриптивная теория не занимается измерением ресурсов (таких как время, объём памяти), затрачиваемых при применении алгоритма к его возможным исходным данным (в другой терминологии — к его входам). Её интересует лишь, возможен алгоритм для решения данной задачи или нет. Начальные понятия дескриптивной теории алгоритмов суть: конструктивный обьект, алгоритм, число шагов алгоритма, вычислимая функция, перечислимое множество, разрешимое множество, сводимость нумераций, главная вычислимая нумерация, вычислимая операция.
В отличие от метрической теории алгоритмов, дескриптивная теория не занимается измерением ресурсов (таких как время, объём памяти), затрачиваемых при применении алгоритма к его возможным исходным данным (в другой терминологии — к его входам). Её интересует лишь, возможен алгоритм для решения данной задачи или нет. Начальные понятия дескриптивной теории алгоритмов суть: конструктивный обьект, алгоритм, число шагов алгоритма, вычислимая функция, перечислимое множество, разрешимое множество, сводимость нумераций, главная вычислимая нумерация, вычислимая операция. Всякая надежда на создание единой математической теории, амбициозного проекта, который был предложен математиком Давидом Гильбертом в 19 веке и продолжил существовать, поддерживаемый многими, в 20 столетии, рухнула. Основы математики были далеко не столь надежными, как того хотел бы Гильберт. А Гëдель своими теоремами ясно продемонстрировал, что любая система аксиом, какой бы обширной она ни была, уязвима для возникновения невосполнимых пробелов. Попытки же восполнить их созданием более полной системы породили бы только бóльшее количество утверждений без доказательств — так что и тут возникнет необходимость в усовершенствовании системы, и так далее до бесконечности. И случилось нечто странное: математики решили не обращать на это внимания. Они посчитали, что неполнота систем не имеет непосредственного влияния на их работу.
Всякая надежда на создание единой математической теории, амбициозного проекта, который был предложен математиком Давидом Гильбертом в 19 веке и продолжил существовать, поддерживаемый многими, в 20 столетии, рухнула. Основы математики были далеко не столь надежными, как того хотел бы Гильберт. А Гëдель своими теоремами ясно продемонстрировал, что любая система аксиом, какой бы обширной она ни была, уязвима для возникновения невосполнимых пробелов. Попытки же восполнить их созданием более полной системы породили бы только бóльшее количество утверждений без доказательств — так что и тут возникнет необходимость в усовершенствовании системы, и так далее до бесконечности. И случилось нечто странное: математики решили не обращать на это внимания. Они посчитали, что неполнота систем не имеет непосредственного влияния на их работу. Наверное, каждый хотя бы раз в жизни слышал это выражение. Действительно, что может быть проще? Однако я знавал преподавателя математического анализа, который, услыхав подобное, ехидно улыбался в усы и предлагал доказать этот факт. После этого у говорившего обычно случался когнитивный диссонанс. И действительно, как же доказать, что 2 × 2 = 4?
Наверное, каждый хотя бы раз в жизни слышал это выражение. Действительно, что может быть проще? Однако я знавал преподавателя математического анализа, который, услыхав подобное, ехидно улыбался в усы и предлагал доказать этот факт. После этого у говорившего обычно случался когнитивный диссонанс. И действительно, как же доказать, что 2 × 2 = 4? Целью этой книги является строгое определение чисел, многочленов и алгебраических дробей и обоснование их свойств, уже известных из школы, а не ознакомление читателя с новыми свойствами. Поэтому читатель не найдет здесь новых для него фактов (за исключением, быть может, некоторых свойств, действительных и комплексных чисел), но узнает, как доказываются вещи, хорошо ему известные, начиная с «дважды два — четыре» и кончая правилами действий с многочленами и алгебраическими дробями. Зато читатель познакомится с рядом общих понятий, играющих в алгебре основную роль.
Целью этой книги является строгое определение чисел, многочленов и алгебраических дробей и обоснование их свойств, уже известных из школы, а не ознакомление читателя с новыми свойствами. Поэтому читатель не найдет здесь новых для него фактов (за исключением, быть может, некоторых свойств, действительных и комплексных чисел), но узнает, как доказываются вещи, хорошо ему известные, начиная с «дважды два — четыре» и кончая правилами действий с многочленами и алгебраическими дробями. Зато читатель познакомится с рядом общих понятий, играющих в алгебре основную роль. Если в качестве значений переменных разрешается брать только элементы носителя, язык называют элементарным языком, или языком первого порядка. Если же в качестве значений переменных разрешается брать также функции и отношения, язык называют языком второго порядка. Выразительные возможности языков первого порядка довольно ограничены. Например, на языке первого порядка можно сообщить, что носитель содержит ровно 17 элементов, но невозможно выразить его конечность. На языке второго порядка выразить конечность носителя возможно. Возникает совершенно естественное недоумение: а зачем тогда пользоваться языками первого порядка с их бедными выразительными средствами, не лучше ли пользоваться языками второго порядка?
Если в качестве значений переменных разрешается брать только элементы носителя, язык называют элементарным языком, или языком первого порядка. Если же в качестве значений переменных разрешается брать также функции и отношения, язык называют языком второго порядка. Выразительные возможности языков первого порядка довольно ограничены. Например, на языке первого порядка можно сообщить, что носитель содержит ровно 17 элементов, но невозможно выразить его конечность. На языке второго порядка выразить конечность носителя возможно. Возникает совершенно естественное недоумение: а зачем тогда пользоваться языками первого порядка с их бедными выразительными средствами, не лучше ли пользоваться языками второго порядка? Знаменитая Теорема Гёделя о неполноте имеет две версии — синтаксическую (объявленную и доказанную самим Гёделем) и семантическую (чаще всего фигурирующую в популярных рассуждениях о великой Теореме). Семантическая версия утверждает, что какую бы систему формальных доказательств ни придумать, в языке найдутся истинные утверждения, не доказуемые в рамках предложенной системы. Таким образом, семантическая версия исходит из того, что некоторые выражения языка выражают осмысленные утверждения, являющиеся истинными или ложными. Синтаксическая версия не опирается на то, что какие бы то ни было выражения языка имеют какой-то смысл, она смотрит на выражения как на синтаксические конструкции, то есть как на цепочки символов, организованные по определённым правилам.
Знаменитая Теорема Гёделя о неполноте имеет две версии — синтаксическую (объявленную и доказанную самим Гёделем) и семантическую (чаще всего фигурирующую в популярных рассуждениях о великой Теореме). Семантическая версия утверждает, что какую бы систему формальных доказательств ни придумать, в языке найдутся истинные утверждения, не доказуемые в рамках предложенной системы. Таким образом, семантическая версия исходит из того, что некоторые выражения языка выражают осмысленные утверждения, являющиеся истинными или ложными. Синтаксическая версия не опирается на то, что какие бы то ни было выражения языка имеют какой-то смысл, она смотрит на выражения как на синтаксические конструкции, то есть как на цепочки символов, организованные по определённым правилам.