|
||
|
|
||
| Главная ≫ Инфотека ≫ Математика ≫ Гипотеза Коллатца и сиракузская последовательность |
Гипотеза Коллатца и сиракузская последовательность
Гипотеза Коллатца (также сиракузская проблема или проблема 3n + 1) — одна из нерешённых проблем математики, названная по имени немецкого математика Лотара Коллатца, предложившего её в 1937 году. Для объяснения сути гипотезы рассмотрим следующую последовательность чисел, называемую сиракузской последовательностью. Берём любое натуральное число n. Если оно чётное, то делим его на 2, а если нечётное, то умножаем на 3 и прибавляем 1 (получаем 3n + 1). Над полученным числом выполняем те же самые действия, и так далее.
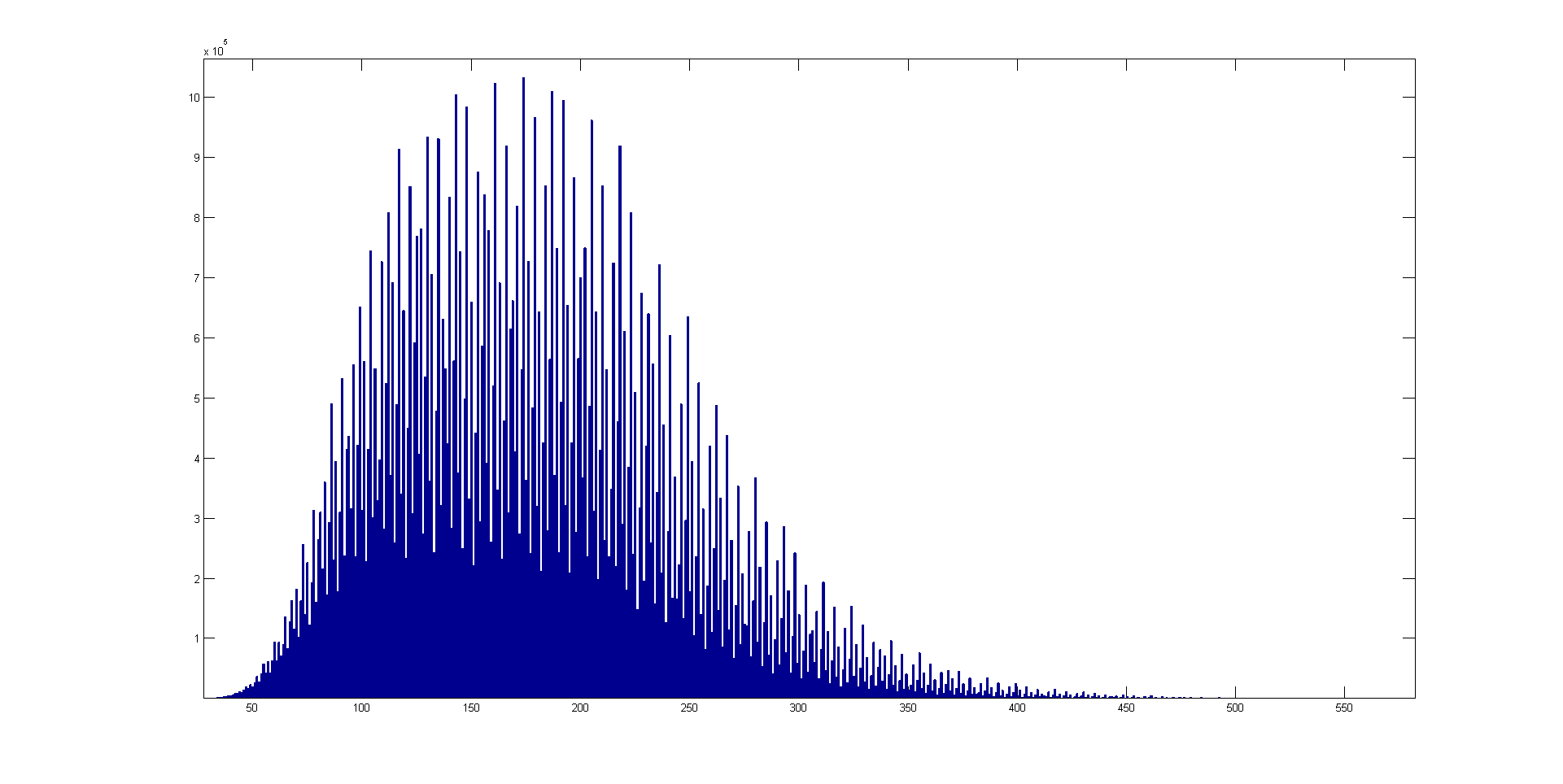
Например, для числа 3 получаем: 3 — нечётное, 3×3 + 1 = 10 10 — чётное, 10:2 = 5 5 — нечётное, 5×3 + 1 = 16 16 — чётное, 16:2 = 8 8 — чётное, 8:2 = 4 4 — чётное, 4:2 = 2 2 — чётное, 2:2 = 1 1 — нечётное, 1×3 + 1 = 4 Очевидно, что, начиная с 1, начинают циклически повторяться числа 1, 4, 2. Для числа 27 получаем: 27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1, … Последовательность пришла к единице только через 111 шагов, достигнув в пи́ке значения 9232. Гипотеза Коллатца заключается в том, что какое бы начальное число мы ни взяли, рано или поздно мы получим единицу.
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Математика ≫ Гипотеза Коллатца и сиракузская последовательность |
|
[time: 11 ms; queries: 8]
19 Фев 2026 03:14:52 GMT+3 |


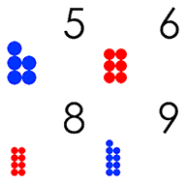 Простые числа — это целые числа больше единицы, которые не могут быть представлены как произведение двух меньших чисел. Если у вас есть несколько монет, но вы не можете расположить их все в форме прямоугольника, а можете только выстроить их в прямую линию, ваше число монет — это простое число. Математик Джеймс Мэйнард о теореме Евклида, гипотезе Римана и современных исследованиях тайн простых чисел.
Простые числа — это целые числа больше единицы, которые не могут быть представлены как произведение двух меньших чисел. Если у вас есть несколько монет, но вы не можете расположить их все в форме прямоугольника, а можете только выстроить их в прямую линию, ваше число монет — это простое число. Математик Джеймс Мэйнард о теореме Евклида, гипотезе Римана и современных исследованиях тайн простых чисел. Продолжительность циклов большинства цикад не случайна, а представляет собой интервалы из простых чисел (чисел, делимых без остатка только на себя — 3, 5, 7, 11, 13, 17 и т. д.), являясь наиболее действенной стратегией выживания и размножения.
Продолжительность циклов большинства цикад не случайна, а представляет собой интервалы из простых чисел (чисел, делимых без остатка только на себя — 3, 5, 7, 11, 13, 17 и т. д.), являясь наиболее действенной стратегией выживания и размножения. Давайте рассмотрим последовательность чисел, первое из которых равно 1, а каждое последующее вдвое больше: 1, 2, 4, 8, 16, … Называется она вполне ожидаемо: последовательность степеней двойки. Казалось бы, ничего выдающегося в ней нет — последовательность как последовательность, не лучше и не хуже других. Тем не менее, она обладает весьма примечательными свойствами.
Давайте рассмотрим последовательность чисел, первое из которых равно 1, а каждое последующее вдвое больше: 1, 2, 4, 8, 16, … Называется она вполне ожидаемо: последовательность степеней двойки. Казалось бы, ничего выдающегося в ней нет — последовательность как последовательность, не лучше и не хуже других. Тем не менее, она обладает весьма примечательными свойствами. Некоторое время назад на сайте препринтов arXiv.org появилось сразу две работы, посвященные задаче о плотнейшей упаковке шаров в пространствах размерности 8 и 24. До настоящего момента аналогичные результаты были известны только для размерностей 1, 2 и 3 (причем тут не все так просто, но об этом ниже). Прорыв — а речь идет про настоящий революционный прорыв — стал возможен благодаря работам Марины Вязовской, математика украинского происхождения, которая сейчас работает в Германии. Мы расскажем историю этого достижения в десяти коротких сюжетах.
Некоторое время назад на сайте препринтов arXiv.org появилось сразу две работы, посвященные задаче о плотнейшей упаковке шаров в пространствах размерности 8 и 24. До настоящего момента аналогичные результаты были известны только для размерностей 1, 2 и 3 (причем тут не все так просто, но об этом ниже). Прорыв — а речь идет про настоящий революционный прорыв — стал возможен благодаря работам Марины Вязовской, математика украинского происхождения, которая сейчас работает в Германии. Мы расскажем историю этого достижения в десяти коротких сюжетах.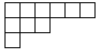 Диаграммы Юнга дают естественный способ параметризовать разбиение натурального числа в сумму невозрастающих слагаемых. Вопросом о количестве диаграмм Юнга с данным числом клеток занимался еще Эйлер.
Диаграммы Юнга дают естественный способ параметризовать разбиение натурального числа в сумму невозрастающих слагаемых. Вопросом о количестве диаграмм Юнга с данным числом клеток занимался еще Эйлер.