Математик Джеймс Мэйнард о теореме Евклида, гипотезе Римана и современных исследованиях тайн простых чисел.

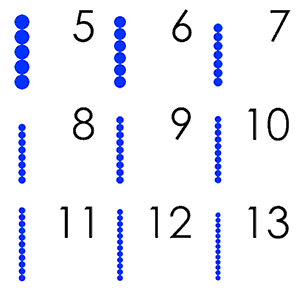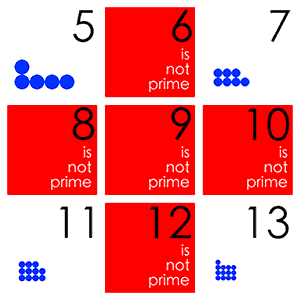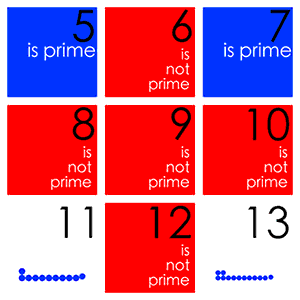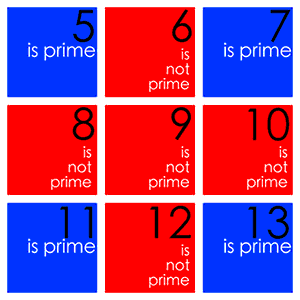Простые числа — это целые числа больше единицы, которые не могут быть представлены как произведение двух меньших чисел. Таким образом, 6 — это не простое число, так как оно может быть представлено как произведение 2×3, а 5 — это простое число, потому что единственный способ представить его как произведение двух чисел — это 1×5 или 5×1. Если у вас есть несколько монет, но вы не можете расположить их все в форме прямоугольника, а можете только выстроить их в прямую линию, ваше число монет — это простое число.


Некоторые считают, что простые числа не стоят глубокого изучения, но они имеют фундаментальное значение для математики. Каждое число может быть представлено уникальным способом в виде простых чисел, умноженных друг на друга. Это значит, что простые числа — это «атомы умножения», маленькие частички, из которых может быть построено что-то большое.

Так как простые числа — это строительные элементы целых чисел, которые получаются с помощью умножения, многие проблемы целых чисел могут быть сведены к проблемам простых чисел. Подобным образом некоторые задачи в химии могут быть решены с помощью атомного состава химических элементов, вовлеченных в систему. Таким образом, если бы существовало конечное число простых чисел, можно было бы просто проверить одно за другим на компьютере. Однако оказывается, что существует бесконечное множество простых чисел, которые на данный момент плохо понимают математики.

Греческий математик Евклид доказал, что существует бесконечное множество простых чисел. Если у вас есть определенное количество простых чисел, например , вы можете рассмотреть число , которое на единицу больше, чем все простые числа, умноженные друг на друга. Это число не может быть произведением любых чисел из вашего списка, но оно точно больше, чем . Так что все простые множители должны быть простыми числами, которых нет в вашем списке. Добавляя новые простые числа в ваш список и повторяя те же действия, вы всегда можете найти по крайней мере одно новое простое число. Поэтому должно существовать бесконечное множество простых чисел.


Никто точно не знает, в каком обществе стали впервые рассматривать простые числа. Их изучают так давно, что у ученых нет записей тех времен. Есть предположения, что некоторые ранние цивилизации имели какое-то понимание простых чисел, но первым реальным доказательством этого являются египетские записи на папирусах, сделанные более 3500 лет назад.

Древние греки, скорее всего, были первыми, кто изучал простые числа как предмет научного интереса, и они считали, что простые числа важны для чисто абстрактной математики. Теорему Евклида по-прежнему изучают в школах, несмотря на то что ей уже больше 2000 лет.

После греков серьезное внимание простым числам снова уделили в XVII веке. С тех пор многие известные математики внесли важный вклад в наше понимание простых чисел. Пьер де Ферма совершил множество открытий и известен благодаря Великой теореме Ферма, 350-летней проблеме, связанной с простыми числами и решенной Эндрю Уайлсом в 1994 году. Леонард Эйлер доказал много теорем в XVIII веке, а в XIX веке большой прорыв был сделан благодаря Карлу Фридриху Гауссу, Пафнутию Чебышёву и Бернхарду Риману, особенно в отношении распределения простых чисел. Кульминацией всего этого стала до сих пор не решенная гипотеза Римана, которую часто называют важнейшей нерешенной задачей всей математики. Гипотеза Римана позволяет очень точно предсказать появление простых чисел, а также отчасти объясняет, почему они так трудно даются математикам.


У простых чисел существует огромное количество применений как в области математики, так и за ее пределами. Простые числа в наши дни используются практически ежедневно, хотя чаще всего люди об этом не подозревают. Простые числа представляют такое значение для ученых, поскольку они являются атомами умножения. Множество абстрактных проблем, касающихся умножения, можно было бы решить, если бы люди знали больше о простых числах. Математики часто разбивают одну проблему на несколько маленьких, и простые числа могли бы помочь в этом, если бы понимали их лучше.

Вне математики основные способы применения простых чисел связаны с компьютерами. Компьютеры хранят все данные в виде последовательности нулей и единиц, которая может быть выражена целым числом. Многие компьютерные программы перемножают числа, привязанные к данным. Это означает, что под самой поверхностью лежат простые числа. Когда человек совершает любые онлайн-покупки, он пользуется тем, что есть способы умножения чисел, которые сложно расшифровать хакеру, но легко покупателю. Это работает за счет того, что простые числа не имеют особенных характеристик — в противном случае злоумышленник мог бы получить данные банковской карты.


Один из способов нахождения простых чисел — это компьютерный поиск. Путем многократной проверки того, является ли число множителем 2, 3, 4 и так далее, можно легко определить, простое ли оно. Если оно не является множителем любого меньшего числа, оно простое. В действительности это очень трудоемкий способ выяснения того, является ли число простым. Однако существуют более эффективные пути это определить. Эффективность этих алгоритмов для каждого числа является результатом теоретического прорыва 2002 года.

Простых чисел достаточно много, поэтому если взять большое число и прибавить к нему единицу, то можно наткнуться на простое число. В действительности многие компьютерные программы полагаются на то, что простые числа не слишком трудно найти. Это значит, что, если вы наугад выберете число из 100 знаков, ваш компьютер найдет большее простое число за несколько секунд. Поскольку 100-значных простых чисел больше, чем атомов во Вселенной, то вполне вероятно, что никто не будет знать наверняка, что это число простое.

Как правило, математики не ищут отдельных простых чисел на компьютере, однако они очень заинтересованы в простых числах с особыми свойствами. Есть две известные проблемы: существует ли бесконечное количество простых чисел, которые на один больше, чем квадрат (например, это имеет значение в теории групп), и существует ли бесконечное количество пар простых чисел, отличающихся друг от друга на 2.


Несмотря на то, что простые числа изучаются уже более трех тысячелетий и имеют простое описание, о простых числах до сих пор известно на удивление мало. Например, математики знают, что единственной парой простых чисел, отличающихся на единицу, являются 2 и 3. Однако неизвестно, существует ли бесконечное количество пар простых чисел, отличающихся на 2. Предполагается, что существует, но это пока не доказано. Это проблема, которую можно объяснить ребенку школьного возраста, однако величайшие математические умы ломают над ней голову уже более 100 лет.

Многие из наиболее интересных вопросов о простых числах как с практической, так и с теоретической точки зрения заключаются в том, какое количество простых чисел имеет то или иное свойство. Ответ на самый простой вопрос — сколько есть простых чисел определенного размера — теоретически можно получить, решив гипотезу Римана. Дополнительный стимул доказать гипотезу Римана — приз размером в один миллион долларов, предложенный математическим институтом Клэя, равно как и почетное место среди самых выдающихся математиков всех времен.

Сейчас существуют неплохие способы предположить, каким будет правильный ответ на многие из этих вопросов. На данный момент догадки математиков проходят все численные эксперименты, и есть теоретические основания, чтобы на них полагаться. Однако для чистой математики и работы компьютерных алгоритмов чрезвычайно важно, чтобы эти догадки действительно были верными. Математики могут быть полностью удовлетворены, только имея неоспоримое доказательство.

Самым серьезным вызовом для практического применения является сложность нахождения всех простых множителей числа. Если взять число 15, можно быстро определить, что 15=5х3. Но если взять 1000-значное число, вычисление всех его простых множителей займет больше миллиарда лет даже у самого мощного суперкомпьютера в мире. Интернет-безопасность во многом зависит от сложности таких вычислений, потому для безопасности коммуникации важно знать, что кто-то не может просто взять и придумать быстрый способ найти простые множители.


Несмотря на то, что эта тема стара и затрагивала многих известных математиков на протяжении всей истории, она по-прежнему актуальна. Ученые не знают, существует ли бесконечное количество пар таких простых чисел, как 3 и 5, отличающихся на 2. Это известная нерешенная проблема. Математик Итан Чжан сделал большой прорыв в отношении этой проблемы. В начале 2013 года ученые не знали, существует ли бесконечное количество пар простых чисел в пределах 1 квинтиллиона друг от друга или для любого числа, помимо 1 квинтиллиона, независимо от его величины. Благодаря теоретическим наработкам, основанным на работе Чжана, математики знают, что существует бесконечное количество простых чисел, отличающихся друг от друга не больше чем на 246. Число 246 гораздо больше двух, однако оно заметно меньше бесконечности.

Вместо того чтобы искать простые числа, находящиеся рядом, можно искать те из них, что находятся далеко друг от друга на числовой оси. Заметный теоретический прорыв в этой проблеме был сделан впервые за более чем 75 лет в начале 2014 года, когда исследователи из Математического института Оксфорда решили одну из проблем Эрдёша. Другие два интересных решения проблем Эрдёша, связанных с простыми числами, были сделаны Бобом Хафом и Теренсом Тао, чья работа была основана на еще одном прорыве, сделанном Каисой Матомаки и Максимом Раджвиллом в 2014 году. Харальд Гельфготт с Дэвидом Платтом наконец доказали слабую гипотезу Гольдбаха, доведя до кульминации сто лет различных находок. Математики привыкли к тому, что нужно ждать десять лет до достижения серьезного результата в области простых чисел, однако на этот раз получили полдюжины таких результатов за последние три года.


Сейчас невозможно сказать, как простые числа будут использоваться в будущем. Чистая математика (например, изучение простых чисел) неоднократно находила способы применения, которые могли показаться совершенно невероятными, когда теория впервые разрабатывалась. Снова и снова идеи, воспринимавшиеся как чудной академический интерес, непригодный в реальном мире, оказывались на удивление полезными для науки и техники. Годфри Харольд Харди, известный математик начала XX столетия, утверждал, что простые числа не имеют реального применения. Сорок лет спустя был открыт потенциал простых чисел для компьютерной коммуникации, и сейчас они жизненно необходимы для повседневного использования интернета.

Поскольку простые числа лежат в основе проблем, касающихся целых чисел, а целые числа постоянно встречаются в реальной жизни, простым числам найдется повсеместное применение в мире будущего. Это особенно актуально, учитывая, как интернет проникает в жизнь, а технологии и компьютеры играют большую роль, чем когда-либо раньше.

Существует мнение, что определенные аспекты теории чисел и простых чисел выходят далеко за рамки науки и компьютеров. В музыке простые числа объясняют, почему некоторые сложные ритмические рисунки долго повторяются. Это порой используется в современной классической музыке для достижения специфического звукового эффекта. Последовательность Фибоначчи постоянно встречается в природе, и есть гипотеза о том, что цикады эволюционировали таким образом, чтобы находиться в спячке в течение простого числа лет для получения эволюционного преимущества. Также предполагается, что передача простых чисел по радиоволнам была бы лучшим способом для попытки установления связи с инопланетными формами жизни, поскольку простые числа абсолютно независимы от любого представления о языке, но при этом достаточно сложны, чтобы их нельзя было спутать с результатом некоего в чистом виде физического природного процесса.