Двое учёных из Принстонского университета и Кентского университета штата (оба — США) показали, что шары дают наихудшее решение задачи о плотной упаковке выпуклых тел. Иными словами, математики установили, что максимально плотная упаковка любых других центрально-симметричных выпуклых тел не может оставлять больше свободного пространства, чем упаковка шаров. Хотя это утверждение, доказательство которого было представлено на недавно завершившемся Международном семинаре по проблемам упаковки в Дублине (Ирландия), интуитивно очевидно, верным оно оказывается только в трёх измерениях.


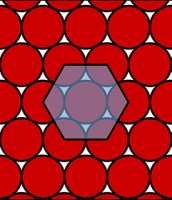
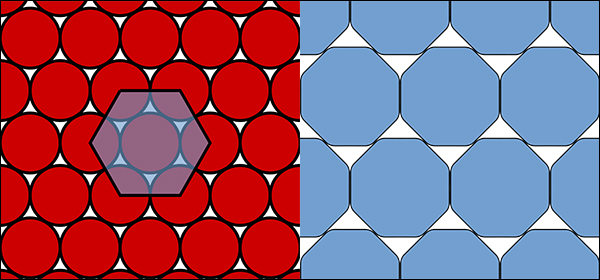
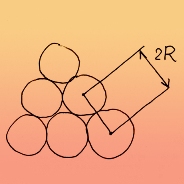
Если мы будем рассматривать двумерный вариант задачи, то есть заменим объёмное пространство на плоскость, а шары — на круги, то максимальная возможная плотность упаковки последних составит ≈0,9069. Это значение действительно невелико, но известна и более низкая величина, рассчитанная для так называемых сглаженных правильных восьмиугольников — фигур, углы которых «сглаживаются» дугами гипербол. Плотность их упаковки может подниматься лишь до ≈0,9024.

В пространствах более высокой размерности, чем привычное для нас трёхмерное, сферы продолжают своё существование как особые математические объекты. Их предельно плотная упаковка также, вероятно, не должна быть наименее эффективной, на что указала проведённая авторами проверка для случаев 4, 5, 6, 7, 8 и 24 измерений.

Подготовлено по материалам NewScientist.