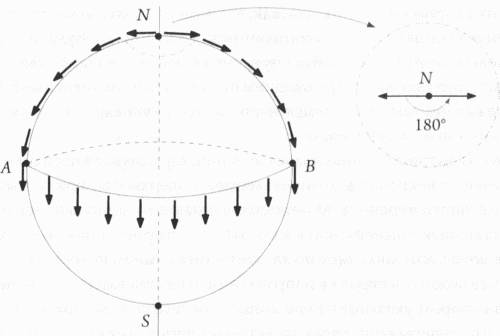
Глава 6. ДНК теории струн

При поиске алмазов, если вам повезет, вы также можете найти и другие драгоценные камни. Когда я заявил о своем доказательстве гипотезы Калаби в 1977 году в своей двухстраничной статье, за которой последовало само доказательство на семидесяти трех страницах в 1978-м, я также объявил о доказательстве еще пяти теорем, относящихся к данной гипотезе. Такая плодотворность во многом стала следствием тех необычных обстоятельств, в которых завязывались мои отношения с гипотезой Калаби, — начав с попыток доказать ее ошибочность, я затем резко сдал назад и стал доказывать ее истинность. К счастью, оказалось, что мои усилия не были потрачены даром — все мои ошибочные шаги, все те безвыходные положения, в которые я попадал, впоследствии были мной использованы. Придуманные мной контрпримеры — следствия, логически вытекающие из гипотезы Калаби, которые, как я полагал, должны были оказаться ложными, — также оказались истинными. Эти неудавшиеся контрпримеры на самом деле были настоящими примерами и вскоре были представлены мной в виде нескольких небезынтересных математических теорем.

Важнейшая из этих теорем вела к доказательству гипотезы Севери (комплексного варианта гипотезы Пуанкаре), задачи, которая оставалась нерешенной на протяжении двух десятилетий. Но прежде чем дойти до этого, я доказал одно важное неравенство, напрямую связанное с вопросом классификации поверхностей на основе их топологии, которым я заинтересовался, отчасти благодаря моему разговору с гарвардским математиком Дэвидом Мамфордом, проезжавшим в то время через Калифорнию. Задача, о которой идет речь, впервые была выдвинута Антониусом ван де Веном из Лейденского университета и относилась к вопросу о неравенстве между классами Черна для кэлеровых многообразий. Ван де Вен доказал, что для любого многообразия второй класс Черна, умноженный на восемь, должен быть больше или равен квадрату первого класса Черна того же многообразия. Притом многие полагали, что этому неравенству можно придать более сильную форму, заменив восьмерку на тройку. Действительно, тройку можно было бы считать оптимальным значением. Вопрос, поставленный Мамфордом, состоял в возможности доказательства этого более сильного утверждения. Смысл выражения «более сильное утверждение» заключается в том, что, согласно предположению Мамфорда, некая величина, а именно второй класс Черна, будет больше, чем некая другая, не только при умножении на восемь, но и при умножении на меньшее число — три.

Мамфорд поднял этот вопрос во время своей лекции в Калифорнийском университете в Ирвине в сентябре 1976 года; я также присутствовал на ней, как раз незадолго до этого закончив работу над доказательством гипотезы Калаби. Во время доклада Мамфорда мне стало понятно, что я уже сталкивался с этой задачей раньше. Поэтому в процессе дискуссии, возникшей по окончании лекции, я сказал Мамфорду, что смогу доказать этот более сложный случай. Придя домой, я проверил свои расчеты и обнаружил, что, как я и подозревал, этот тип неравенства я пытался использовать в 1973 году для опровержения гипотезы Калаби; теперь же я мог использовать теорему Калаби-Яу для доказательства этого неравенства. Более того, доказав упомянутое выше утверждение, я теперь мог воспользоваться его частным случаем, а именно случаем равенства (второй класс Черна, умноженный на три, равен квадрату первого класса Черна) для доказательства гипотезы Севери.

Эти две теоремы, открывшие путь к доказательству гипотезы Севери и более общего неравенства, иногда называемого неравенством Богомолова-Мияока-Яу (я привожу полное название, чтобы выразить признательность двум другим математикам, внесшим вклад в решение этой задачи), стали первыми побочными результатами доказательства гипотезы Калаби, за которыми последовали многие другие. Гипотеза Калаби, по сути, оказалась намного обширнее, чем я считал до этого. Она применима не только к случаю нулевой кривизны Риччи, но и к случаям постоянной отрицательной и постоянной положительной кривизны. Никто до сих пор не исследовал случай положительной кривизны в наиболее общем виде, для которого гипотеза Калаби заведомо ложна. Я сформулировал новую гипотезу, определяющую условия, при которых метрика с положительной кривизной Риччи может существовать. На протяжении последних двух десятилетий многие математики, в том числе и Дональдсон, внесли значительный вклад в доказательство этой гипотезы, но окончательного доказательства до сих пор нет. При этом мне удалось исследовать случай отрицательной кривизны как часть общего доказательства гипотезы Калаби, независимо от меня этот же результат был получен французским математиком Тьерри Обеном. Решение, найденное для случая отрицательной кривизны, позволило показать существование широкого класса объектов, называемых многообразиями Кэлера-Эйнштейна, создав тем самым новые области геометрии, оказавшиеся необычайно плодотворными.

Справедливости ради стоит сказать, что я плодотворно провел время, посвященное поиску непосредственных применений гипотезы Калаби, — я доказал порядка полудюжины теорем. Оказалось, что одно лишь знание того, что определенная метрика существует, уже приводит к огромному числу следствий. Это знание можно было использовать для дедуктивного рассуждения и получить топологию многообразия, даже не зная точного значения метрики. И напротив, зная свойства многообразия, можно предсказать некоторые его уникальные особенности — подобно тому как, не зная всех деталей, можно сделать определенные выводы и о колоде карт, например об общем числе карт и маркировке каждой из них, или даже о строении Галактики. Как мне кажется, подобные возможности, предоставляемые математикой, представляют собой нечто сверхъестественное и говорят даже больше о ее силе, чем в тех ситуациях, когда каждая из деталей нам известна.

Мне было весьма приятно пожинать плоды своих трудов и наблюдать, как другие вслед за мной прокладывают пути в те места, которые самому мне оказались недоступны. И все же, несмотря на все успехи, кое-что по-прежнему не давало мне покоя. В глубине души я был уверен, что эта работа должна иметь не только математические, но и физические приложения, хотя и не мог точно сказать, какие. В некоторой степени моя уверенность объяснялась тем, что дифференциальные уравнения, задействованные в гипотезе Калаби — в случае нулевой кривизны Риччи, — представляли собой уравнения Эйнштейна для пустого пространства, соответствующие Вселенной без дополнительной вакуумной энергии, космологическая постоянная для которой была бы равна нулю. В настоящее время космологическую постоянную принято считать положительной и связанной с темной энергией, заставляющей Вселенную расширяться. Кроме того, многообразия Калаби-Яу представляли собой решения дифференциальных уравнений Эйнштейна, также как, например, единичная окружность представляет собой решение уравнения x²+y²=0.

Конечно, для описания пространств Калаби-Яу необходимо намного больше уравнений, чем для описания окружности, и сложность этих уравнений гораздо выше, но основная идея остается той же. Многообразия Калаби-Яу не только удовлетворяют уравнениям Эйнштейна, они удовлетворяют им чрезвычайно элегантным образом, что я, в частности, нахожу поразительным. Все это давало мне основание надеяться на их применимость в физике. Я только не знал, где именно.

Мне не оставалось ничего иного, кроме как пытаться объяснить моим друзьям и постдокам физикам те причины, по которым я считаю гипотезу Калаби и возникшую из нее так называемую теорему Яу столь важными для квантовой гравитации. Основная проблема состояла в том, что в то время мое понимание теории квантовой гравитации было явно недостаточным, чтобы я мог всецело положиться на собственную интуицию. Я время от времени возвращался к этой идее, но в основном сидел сложа руки и ждал, что из этого выйдет.

Шли годы, и в то время, пока я и другие математики продолжали работать над гипотезой Калаби, пытаясь воплотить в жизнь обширные планы по ее применению в области геометрического анализа, в мире физики также началось некое закулисное движение, о котором я не догадывался. Этот процесс начался в 1984 году, который оказался поворотным для теории струн, начавшей в тот год стремительное восхождение от умозрительной идеи к полновесной теории.

Прежде чем приступить к описанию этих захватывающих событий, следует рассказать подробнее о самой теории струн, которая дерзко попыталась преодолеть разрыв между общей теорией относительности и квантовой механикой. В ее основе лежит предположение, что мельчайшие частицы материи и энергии представляют собой не точечные частицы, а крошечные, колеблющиеся участки струн, либо замкнутые в петли, либо открытые. Подобно струнам гитары, способным воспроизводить различные ноты, эти фундаментальные струны также способны колебаться огромным количеством способов. Теория струн предполагает, что струны, колебания которых различны, соответствуют разным частицам и силам, встречающимся в природе. Если эта теория справедлива, то проблема объединения сил решается следующим образом: все силы и частицы связаны между собой, поскольку все они являются проявлениями возбуждений одной и той же основной струны. Можно сказать, что это именно то, из чего состоит Вселенная: спустившись на наиболее элементарный уровень мироздания, вы обнаружите, что все состоит из струн.

Теория струн заимствует у теории Калуцы-Клейна общую идею, что осуществление великого синтеза физических сил требует наличия дополнительных измерений. Доказательство отчасти основано на тех же постулатах: всем четырем существующим в природе взаимодействиям — гравитационному, электромагнитному, слабому и сильному — в четырехмерной теории просто не хватает места. Если воспользоваться подходом Калуцы и Клейна и задаться вопросом, сколько измерений необходимо, чтобы соединить все четыре силы в рамках единой теории, то с учетом пяти измерений, необходимых для гравитации и электромагнетизма, пары измерений для слабого взаимодействия и еще нескольких для сильного, окажется, что минимальное число измерений равно одиннадцати. Впрочем, это не совсем так — что в числе прочего было показано физиком Эдвардом Виттеном.

К счастью, теория струн не основана на столь произвольном обращении с физическими понятиями, каким является выбор случайного числа измерений и пропорциональное ему расширение матрицы или метрического тензора Римана с последующей оценкой, сколько и каких сил поместится в этот тензор. Напротив, теория точно предсказывает число необходимых измерений, и это число равно десяти — четыре «обычных» пространственно-временных измерения, исследуемых при помощи телескопов, плюс шесть дополнительных.

Причина, по которой теория струн требует наличия именно десяти измерений, весьма сложна и основана на необходимости сохранения симметрии — важнейшем условии построения любой фундаментальной теории, — а также на необходимости достижения совместимости с квантовой механикой, являющейся, несомненно, одним из ключевых ингредиентов любой современной теории. Но по сути объяснение сводится к следующему: чем больше число измерений системы, тем больше в ней число возможных колебаний. Чтобы воспроизвести весь диапазон возможностей для нашей Вселенной, число допустимых типов колебаний, согласно теории струн, должно быть не просто очень велико, а еще и четко определено — и это число можно получить только в десятимерном пространстве. Несколько позже мы обсудим еще один вариант, или «обобщение» теории струн, носящее название М-теории и требующее одиннадцати измерений, но в настоящий момент мы не будем его касаться.

Струна, колебания которой ограничены одним измерением, может колебаться только в продольном направлении — путем сжатия и растяжения. В случае двух измерений колебания струны возникнут как в продольном, так и в перпендикулярном к нему поперечном направлении. Для трех и более измерений число независимых колебаний будет продолжать расти до тех пор, пока размерность не станет равной десяти (девять пространственных измерений и одно временное) — именно тот случай, в котором удовлетворяются математические требования теории струн. Вот почему теория струн требует как минимум десяти измерений. Строго говоря, причина, по которой теория струн требует ровно десять измерений, а не больше и не меньше, относится к понятию о сокращении аномалий, которое возвращает нас в 1984 год, к тому месту, на котором я прервал повествование.

Большинство струнных теорий, разработанных на тот момент, страдали наличием аномалий или несовместимостей, делающих все их предсказания бессмысленными. Эти теории, к примеру, приводили к возникновению неверного типа лево-правой симметрии — несовместимой с квантовой теорией. Ключевой прорыв был сделан Майклом Грином, в то время работавшим в Колледже Королевы Марии в Лондоне, и Джоном Шварцем из Калифорнийского технологического института. Основная проблема, которую удалось преодолеть Грину и Шварцу, относилась к так называемому нарушению четности — идее о том, что фундаментальные законы природы несимметричны в отношении зеркального отражения. Грин и Шварц обнаружили способ формулирования теории струн в таком виде, который подразумевал, что нарушение четности в системе действительно имеет место. Квантовые эффекты, из-за которых в теории струн возникали всевозможные несоответствия, в десятимерном пространстве удивительным образом взаимно уничтожились, породив тем самым надежды на то, что именно эта теория и является истинной. Успех Грина и Шварца обозначил начало того, что впоследствии было названо первой струнной революцией. То, что им удалось обойтись без аномалий, позволило говорить о способности данной теории привести к объяснению вполне реальных физических эффектов.

Отчасти задача исследователя состоит в том, чтобы убедиться в способности теории струн дать ответ на вопрос: почему Вселенная именно такова, какова она есть? Этот ответ должен объяснить и причину, по которой пространство-время, в котором мы живем, выглядит четырехмерным, в то время как теория настаивает на его десятимерности. В теории струн это кажущееся несоответствие объясняется компактификацией. Это понятие не является совершенно новым, поскольку Калуца и Клейн (особенно Клейн) уже предполагали, что дополнительное измерение в их пятимерной теории на самом деле компактифицировано — сжато до столь малых размеров, что увидеть его было попросту невозможно. В аналогичной ситуации оказались и струнные теоретики — только они имели в своем распоряжении не одно, а шесть «лишних» измерений.

Слово «лишние» вводит в заблуждение, поскольку мы на самом деле не пытаемся избавиться от каких-либо измерений. Задача состоит в том, чтобы неким замысловатым образом свернуть эти измерения — придать им строго определенную геометрическую форму, которая позволила бы произвести магический акт компактификации, составляющий одну из основных задач теории струн. При этом количество возможных геометрий, ведущих к различным способам компактификации, чрезвычайно велико.

Вся идея, по словам гарвардского физика Кумруна Вафы, может быть представлена в виде простого уравнения, понятного каждому: 4+6=10.^[54] Этим можно ограничиться, хотя вы, возможно, захотите переформулировать его в виде: 10-6=4, означающем, что, скрыв (или вычтя) шесть измерений, мы получим десятимерную Вселенную, кажущуюся нам четырехмерной. Компактификацию с тем же успехом можно рассматривать как своеобразную разновидность умножения, известную как декартово, или прямое, произведение — произведение, в котором количества измерений складываются, а не умножаются. Соответствующее уравнение, описывающее результирующее многообразие, в котором четыре измерения объединяются с шестью (4×6=10), предполагает, что наше десятимерное пространство-время имеет подструктуру, являющуюся прямым произведением четырех- и шестимерного пространства-времени, точно так же как плоскость представляет собой прямое произведение двух линий, а цилиндр — прямое произведение линии и окружности. Цилиндр, как уже говорилось, представляет собой наглядную и часто используемую иллюстрацию идеи Калуцы и Клейна. Если вы представите наше четырехмерное пространство-время в виде линии, имеющей бесконечную протяженность в обоих направлениях, а затем мысленно разрежете ее и рассмотрите один из концов в микроскоп, то сможете увидеть, что на самом деле эта линия имеет некую толщину, и правильнее было бы говорить о ней не как о линии, а как о цилиндре, хотя и очень маленького радиуса. Именно внутри этой окружности крошечного радиуса и спрятано пятое измерение теории Калуцы-Клейна. Теория струн продвигает эту идею на несколько шагов дальше, утверждая, что, посмотрев на сечение этого тонкого цилиндра при помощи еще более мощного микроскопа, можно обнаружить не одно, а целых шесть скрытых внутри него измерений. Независимо от того, где вы находитесь — в четырехмерном пространстве-времени или на поверхности бесконечно длинного цилиндра, — к каждой точке прикреплено крошечное шестимерное пространство. И независимо от того, где вы находитесь в этом бесконечном пространстве, можете быть уверены, что компактное шестимерное пространство, спрятанное «по соседству», будет точно таким же.

Эта картина, конечно, является весьма грубой и схематичной и ничего не говорит нам о подлинной геометрии этого компактифицированного шестимерного мира. Возьмем, к примеру, обычную сферу, представляющую собой двухмерную поверхность, и мысленно сожмем ее в точку, то есть превратим ее в нульмерный объект. Таким образом, мы компактифицировали два измерения, превратив их в ничто. Можно попытаться таким же образом свести десять измерений к четырем, сжимая теперь уже шестимерную сферу a²+b²+c²+d²+e²+f²=1, но в качестве геометрии дополнительных измерений этот вариант не пройдет; уравнения теории струн требуют строго определенной структуры шестимерного пространства, и обычная сфера этим требованиям не соответствует.

Было ясно, что требовалась более сложная форма, и после успеха Грина и Шварца с нарушением четности задача нахождения этой формы вышла на первый план. Как только физикам стал бы известен точный вид многообразия, в которое сворачиваются дополнительные шесть измерений, они, наконец, смогли бы перейти от слов к делу.

Следующий шаг был предпринят в 1984 году, когда Грин, Шварц и Питер Вест из Кингс-Колледжа заинтересовались K3-поверхностями — широким классом комплексных многообразий, который изучался математиками уже более столетия, хотя внимание именно физиков K3 привлекли, когда мои доказательства гипотезы Калаби показали, что эти поверхности могут поддерживать риччи-плоскую метрику. «Я понял, что компактное пространство должно быть риччи-плоским, для того чтобы космологическая постоянная пространства более низкой размерности, в котором мы живем, не была положительной — как и требовали все теории того времени», — вспоминает Шварц.^[55] В свете последующего открытия темной энергии, предполагающей наличие чрезвычайно малой, но все же положительной космологической постоянной, пришлось разработать более сложные варианты теории, предполагающей возникновение очень малой космологической постоянной в нашем четырехмерном мире из компактных риччи-плоских пространств, — об этом пойдет речь в десятой главе.

Поверхность K3, обязанная своим названием горе K2 и трем математикам, исследовавшим геометрию подобных пространств, — Эрнсту Куммеру, упоминавшемуся ранее Эриху Кэлеру и Кунихико Кодайра, — была выбрана для предварительной проверки несмотря на наличие у нее только четырех вещественных (или двух комплексных) измерений вместо требуемых шести, во многом благодаря тому, что коллеги убедили Грина, Шварца и Веста в отсутствии аналогов этих многообразий более высокой размерности. Однако, как говорит Грин: «Я совершенно уверен в том, что мы нашли бы способ расставить все по местам… даже если бы в то время и не получили этой информации [о существовании шестимерных аналогов риччи-плоских K3 поверхностей]».^[56] «То, что исследование было начато с испытанных K3 поверхностей, — добавляет Шварц, — было обусловлено совсем не желанием найти подлинный вид компактификации. Мы просто хотели поиграть, посмотреть, что мы получим в результате и как это связано с сокращением аномалий».^[57] С тех пор поверхности K3 имеют неоценимое значение для струнных теоретиков, исполняя роль «игрушечных моделей» для компактификации. Они также незаменимы при исследовании двойственностей в теории струн, о которых пойдет речь в следующей главе.

Примерно в то же время, в 1984 году, физик Эндрю Строминджер, сейчас работающий в Гарварде, а тогда — в Институте перспективных исследований (ИПИ) в Принстоне, объединил свои усилия с физиком-теоретиком Филиппом Канделасом, сейчас работающим в Оксфорде, а тогда — в Техасском университете, для того чтобы определить класс шестимерных пространств, удовлетворяющий строгим условиям теории струн. Им было известно, что внутренние пространства этих шестимерных многообразий должны быть компактными, чтобы иметь возможность перейти от десяти к четырем измерениям, а кривизна должна удовлетворять как уравнениям теории гравитации Эйнштейна, так и требованиям симметрии, налагаемым теорией струн. Эти исследования в конце концов привели их и еще двоих их коллег — Гари Горовица из Калифорнийского университета и Виттена — к тем пространствам, существование которых я установил, доказав гипотезу Калаби, хотя Виттен пришел к этим многообразиям собственным путем. «Одной из важнейших особенностей открытий в современной науке является то, что физики и математики по совершенно разным причинам зачастую приходят к одним и тем же структурам, — делится своим наблюдением Строминджер. — Порой физики обгоняют математиков, порой математики обгоняют физиков. В данном случае математики оказались впереди. Им удалось понять важность этих пространств раньше нас».^[58]

То, что говорит Строминджер, несомненно является правдой, но так же верно и то, что математики, и в их числе я сам, изначально не имели ни малейшего представления о связи пространств Калаби-Яу с физикой. Причина, по которой я занялся исследованием этих пространств, состояла в том, что я находил их чрезвычайно красивыми; именно их необычайная красота зародила во мне подозрение, что физики обязательно должны взглянуть на них повнимательнее, что эти пространства содержат в себе множество загадок, достойных того, чтобы быть открытыми. В конечном итоге, именно физикам предстояло создать эту связь, построив мост между геометрией и физикой и положив тем самым начало долгому и продуктивному сотрудничеству между двумя областями знаний — сотрудничеству, которое процветает и по сей день.

История установления этой связи интересна сама по себе. Строминджер подытожил ее следующим образом: «Суперсимметрия позволила перебросить мост к голономии, а голономия стала мостом к пространствам Калаби-Яу».^[59]

Как вы помните, мы кратко обсудили суперсимметрию в четвертой главе, в контексте вопроса об одной из разновидностей внутренней — ограниченной симметрии — в отличие от более радикальной, глобальной, симметрии такого объекта, как, например, сфера, — которую должны были демонстрировать многообразия Калаби-Яу будучи классом кэлеровых многообразий. Эта внутренняя симметрия представляет собой часть того, что мы подразумеваем под термином «суперсимметрия», но прежде чем мы попытаемся нарисовать ясную картину, скажем несколько слов о голономии.

Грубо говоря, голономия является мерой, характеризующей поведение касательных векторов для определенной поверхности при попытке их параллельного переноса по петле, охватывающей данную поверхность. Представьте, к примеру, что вы стоите на Северном полюсе и держите в руке копье, направленное по касательной к земной поверхности. Сначала вы движетесь строго в направлении экватора вдоль того направления, в котором указывает ваше копье. Достигнув экватора, вы обнаружите, что теперь ваше копье направлено перпендикулярно экватору в сторону Южного полюса. После этого, двигаясь по экватору, вы обходите половину земной окружности, держа копье направленным на юг. Пройдя это расстояние, вы вновь держите путь на Северный полюс, не меняя направления копья. Оказавшись на Северном полюсе, вы неожиданно обнаружите, что, несмотря на все ваши старания, копье, которое вы держали в руках, оказалось повернутым на 180 градусов относительно первоначального направления.

Мы могли бы повторить этот процесс любое число раз, совершая более длинные или более короткие путешествия вдоль экватора, каждый раз обнаруживая, что копье повернулось на некоторый угол, иногда меньше 180 градусов, иногда больше — в зависимости от длины нашего пути по экватору. Для того чтобы определить голономию нашей планеты, которую в первом приближении можно считать двухмерной сферой, рассмотрим все возможные пути — или все возможные петли, — которые можно проложить на ее поверхности. Оказывается, на поверхности сферы можно получить любой наперед заданный угол поворота от 0 до 360 градусов, делая соответствующую петлю больше или меньше. Можно даже получить угол больше 360 градусов, пройдя один и тот же путь два или более раз. Принято говорить, что двумерная сфера относится к группе голономии SO(2) или к специальной ортогональной группе 2, содержащей в себе все возможные углы. Сферы более высоких размерностей относятся к группам SО(n), содержащим все возможные вращения, сохраняющие ориентацию, а n относится к числу измерений.

Рис. 6.1. Одним из способов классификации пространства или поверхности является его классификация при помощи голономии, показывающей, что происходит с касательным вектором при параллельном переносе в таком пространстве — то есть перемещении, при котором мы стремимся сохранить направление вектора, несмотря на искривленность траектории. В данном примере, взяв на северном полюсе касательный вектор, направленный в точку А, мы начинаем движение в сторону экватора. По достижении экватора оказывается, что вектор теперь направлен на юг. Сохраняя это направление, мы перемещаемся вдоль экватора из точки А в точку В, проходя при этом половину земной окружности. После этого мы опять движемся на северный полюс, вновь сохраняя направление вектора неизменным. Оказавшись на северном полюсе, мы неожиданно обнаруживаем, что вектор оказался повернутым на 180 градусов относительно первоначального направления, несмотря на все наши попытки сохранить его направление неизменным

Многообразия Калаби-Яу, с другой стороны, относятся к более ограниченной группе голономии SU(n), что означает специальную унитарную группу, имеющую n комплексных измерений. Те из многообразий Калаби-Яу, к которым проявляет особый интерес теория струн, имеют три комплексных измерения, что позволяет поместить их в группу голономии SU(3). Конечно, пространства Калаби-Яу намного сложнее сфер, и голономия SU(3) намного сложнее предыдущего примера с вектором, который поворачивается при движении по поверхности сферы, несмотря на все наши усилия сохранять его направление неизменным. Более того, поскольку в многообразиях Калаби-Яу, в отличие от сферы, отсутствует глобальная симметрия, не существует осей, при повороте вокруг которых эти многообразия совпали бы сами с собой. Впрочем, они имеют более ограниченный тип симметрии, который, как мы уже говорили, относится к голономии и суперсимметрии. Для многообразия обладание суперсимметрией равнозначно обладанию так называемым ковариантно-постоянным спинором. Спиноры, хотя их весьма тяжело описать, во многом аналогичны касательным векторам. Для кэлерова многообразия существует единственный спинор, который остается неизменным при параллельном переносе вдоль любой замкнутой петли. В многообразиях Калаби-Яу — как и во всей группе SU(3), к которой они принадлежат, помимо этого спинора существует еще один, который также не изменяется при параллельном переносе по любой замкнутой петле, принадлежащей многообразию.

Наличие этих спиноров помогает убедиться в наличии суперсимметрии для соответствующих многообразий, и именно требование суперсимметрии определенного типа было предъявлено Строминджером и Канделасом к группе SU(3) в первую очередь. Группа SU(3), в свою очередь, является группой голономии, связанной с компактными кэлеровыми многообразиями с обращающимся в нуль первым классом Черна и нулевой кривизной Риччи. Иными словами, голономия SU(3) неявно подразумевает многообразия Калаби-Яу. Или, что эквивалентно, если нужно найти такое решение, которое удовлетворяло бы как уравнениям Эйнштейна, так и уравнениям суперсимметрии — и если при этом нужно оставить дополнительные измерения скрытыми и сохранить суперсимметрию в наблюдаемом мире, — единственным решением будут многообразия Калаби-Яу. Как сказал физик из Университета Джона Хопкинса Раман Сандрам: «Они представляют собой прекрасный математический ответ».^[60]

«Я едва ли хорошо разбирался в математике в то время, но мне удалось установить связь с многообразиями Калаби-Яу благодаря группе голономии, их характеризующей, — говорит Строминджер. — Я обнаружил статью Яу в библиотеке и мало что из нее понял, но из того немногого, что мне удалось понять, я сделал однозначный вывод о том, что эти многообразия — это как раз то, что доктор прописал».^[61] Хотя чтение моих статей далеко не для всех становится незабываемым жизненным опытом, Строминджер действительно говорил (почти через двадцать лет после того, как это произошло) о том возбуждении, которое он испытал, впервые наткнувшись на мое доказательство гипотезы Калаби.^[62] Однако прежде чем полностью предаться своим чувствам, Строминджер позвонил мне, чтобы убедиться в том, что он действительно правильно понял мою статью. Я подтвердил его ожидания. В тот момент я осознал, что после восьми лет поисков физика наконец обнаружила многообразия Калаби-Яу.

Итак, в этот укромный уголок математики физиков привела суперсимметрия, — впрочем, я еще не объяснил, по какой именно причине принято рассматривать суперсимметрию как нечто сверхъестественно важное, если не считать таковым общего утверждения о значимости симметрии в понимании любого типа многообразий. Как поясняет принстонский физик Хуан Малдасена: «Суперсимметрия не только делает расчеты проще, она делает их возможными. Почему? Потому что проще описать движение сферы, катящейся с идеального холма, чем движение футбольного мяча по реальному склону, траектория которого будет в значительной степени случайна».^[63]

Наличие симметрии делает все проблемы более простыми для разрешения. Предположим, что нам необходимо найти все решения уравнения xy=4. Это займет много времени, поскольку число решений этого уравнения бесконечно. Если, однако, ввести условие симметрии, x=y, то решений будет только два: 2 и -2. Аналогично, если известно, что необходимые нам точки плоскости x-y симметричны относительно начала координат, то есть находятся на окружности, то вместо двух переменных — x и y — для описания этой окружности вам будет достаточно только одной — ее радиуса. Подобным образом и суперсимметрия сокращает число переменных, значительно упрощая тем самым решаемые задачи, накладывая ограничения на те геометрические формы, которые могут принимать скрытые шесть измерений. По словам математика из Техасского университета Дэна Фрида, «это ограничение и дает вам Калаби-Яу».^[64]

Конечно, мы не имеем права настаивать на существовании суперсимметрии в нашей Вселенной только ради того, чтобы сделать наши расчеты проще. Должна существовать более веская причина, чем простое удобство. И она существует. Одним из преимуществ теории суперсимметрии является то, что она автоматически обеспечивает устойчивое состояние вакуума — основного состояния в общей теории относительности, благодаря чему наша Вселенная может избежать постоянного падения во все более и более глубокие энергетические ямы. Эта идея относится к гипотезе о положительности массы, о которой уже шла речь в третьей главе. На самом деле суперсимметрия была одним из инструментов Эдварда Виттена в доказательстве его гипотезы, основанной на физических представлениях, однако в более нелинейном математическом подходе, разработанном Ричардом Шоном и мной, ей места не нашлось.

Но большинство физиков заинтересованы в идее суперсимметрии по иной причине, которая, собственно, и привела к возникновению этого понятия. Для физиков наиболее важным аспектом является концепция симметрии, связывающей элементарные частицы материи, иначе называемые фермионами, к которым относятся, например, кварки или электроны, и частицы, отвечающие за взаимодействия, иначе называемые бозонами, — такие как фотоны и глюоны. Суперсимметрия приводит к возникновению подобия, своего рода математической эквивалентности, между силами и материальными объектами, то есть между этими двумя классами частиц. Теория утверждает, что каждый фермион связан с определенным бозоном — его суперпартнером, и то же самое верно для любого бозона. Таким образом, теория предсказывает существование целого класса элементарных частиц с забавными названиями, такими как скварки, сэлектроны, фотино и глюино, — более тяжелыми по сравнению со своими известными аналогами и со спином, отличающимся от спина своих партнеров на 1/2. До настоящего времени эти суперпартнеры в природе не наблюдались, хотя исследователи продолжают их поиск при помощи мощнейших ускорителей (см. двенадцатую главу).

Мир, в котором мы живем, называемый физиками «миром низких энергий», несомненно, суперсимметричным не является. В то же время принято считать, что суперсимметрия доминирует в области высоких энергий, и в этой области элементарные частицы и их суперпартнеры идентичны. Но как только энергия становится ниже некого определенного значения, суперсимметрия «разрушается», и тот мир, в котором мы живем, является миром нарушенной суперсимметрии, где элементарные частицы и их суперпартнеры различны как по массе, так и по другим свойствам. Разрушившись, суперсимметрия не исчезает полностью, но переходит в скрытую фазу. По словам физика Тристана Хабша из Университета Говарда, моего бывшего постдока, можно понять существование различия в массах, мысленно заменив суперсимметрию на вращательную симметрию некого объекта, например вертикально расположенного гибкого стержня. Представьте, что вы закрепили концы стержня и изгибаете его в двух направлениях, перпендикулярных стержню. Вне зависимости от того, под каким углом вы на него нажимаете, объясняет Хабш, пока вы будете делать это в направлении, перпендикулярном направлению стержня, каждое из этих возмущений будет требовать одно и то же количество энергии. «И поскольку эти малые перемещения связаны друг с другом посредством вращательной симметрии, можно свободно заменять одно из них на другое».

Предположим, что мы ударили по стержню, возбудив в нем поперечные колебания. Эти колебания будут обладать вращательной симметрией и будут эквивалентны двум различным элементарным частицам, а энергия колебаний будет определять массу частиц. Наличие вращательной симметрии (или суперсимметрии, в случае теории струн) позволяет двум элементарным частицам иметь одинаковую массу и оставаться неразличимыми во всех прочих отношениях.

Вращательную симметрию — в данном случае служащую заменой суперсимметрии — можно разрушить, согнув стержень наподобие лука. Чем сильнее мы сведем его концы, тем больше будет изгиб и тем сильнее нарушится симметрия. «После того как симметрия нарушена, по-прежнему существуют два вида колебаний, но они уже не связаны друг с другом вращательной симметрией», — говорит Хабш. Чтобы возбудить колебания в плоскости изгиба, как и раньше, требуется энергия, и чем больше величина изгиба, тем эта энергия больше. Но если толкнуть стержень в направлении, перпендикулярном плоскости изгиба, стержень придет во вращательное движение, не требующее для своего поддержания никаких затрат энергии (конечно, при условии, что затратами энергии на преодоление силы трения между концами стержня и их креплениями можно пренебречь). Иными словами, между этими двумя движениями существует разница в энергиях, или энергетическая щель, — одно из них требует затрат энергии, а второе — нет, что соответствует энергетической разнице (или разнице в массах) между безмассовой элементарной частицей и ее суперпартнером, обладающим массой, в случае разрушенной суперсимметрии.^[65] Физики пытаются обнаружить признаки существования подобной энергетической щели и таким образом доказать существование обладающих массой суперсимметричных партнеров привычных нам частиц в высокоэнергетических экспериментах, приводящихся в настоящее время на Большом адронном коллайдере.

Если с точки зрения математика способ объединения сил и материи при помощи суперсимметрии прекрасен сам по себе, то физики-теоретики интересуются симметрией по другой причине, выходящей за пределы ее эстетически привлекательных аспектов. Без суперсимметрии теория струн становится малоосмысленной. Она начинает предсказывать немыслимые частицы типа тахионов, движущихся быстрее света и имеющих отрицательное значение квадрата массы — то есть их масса содержит в себе комплексную единицу i. Большинство физических теорий отвергают возможность существования столь странных объектов. Суперсимметрия, возможно, не нуждается в теории струн — хотя она обязана своим развитием именно этой теории — но теория струн, несомненно, очень многое приобретает за счет суперсимметрии. Суперсимметрия же, как уже говорилось выше, была именно тем понятием, которое привело физиков на порог двери, за которой скрывались многообразия Калаби-Яу.

Когда Строминджер и Канделас получили в свои руки многообразие Калаби-Яу, у них тут же возникло страстное желание сделать следующий шаг — проверить, действительно ли это то многообразие, которое они искали, то самое, которое обусловливает всю физику, с которой мы имеем дело. Они приехали в Санта-Барбару в 1984 году, горя желанием приступить к этому проекту, и вскоре сошлись с Горовицем, который годом раньше перешел в Санта-Барбару из ИПИ. Помимо всего прочего, они были в курсе, что Горовиц являлся моим постдоком и в результате этого сотрудничества знал больше о гипотезе Калаби, чем ему нужно было для его непосредственной работы. Когда Горовиц понял, чем занимаются Строминджер и Канделас, а именно пытаются определить математические требования к внутреннему пространству теории струн, — он подтвердил, что многообразия Калаби-Яу полностью им соответствуют. Имея более близкие отношения с этой областью математики, чем кто-либо другой, Горовиц стал весьма ценным членом команды.

Вскоре после этого Строминджер посетил Виттена в Принстоне и посвятил его в те результаты, которые им удалось получить. Оказалось, что Виттен независимо от них добрался практически до того же места, хотя и попал туда несколько иным путем. Канделас и Строминджер начинали с утверждения о существовании в теории струн десяти измерений, которые должны были быть компактифицированы в некое шестимерное многообразие. Затем физики попытались выяснить, какая из разновидностей шестимерных пространств (помимо прочих требований) дает правильный тип суперсимметрии. С другой стороны, Виттен подошел к проблеме с точки зрения замкнутой струны, движущейся в пространстве-времени и заметающей при этом поверхность с одним комплексным и двумя вещественными измерениями, известную также как риманова поверхность. Подобно обычной поверхности в дифференциальной геометрии, риманова поверхность оснащена метрикой, позволяющей определять расстояние между любыми двумя точками поверхности, и «механизмом» измерения углов. От всех остальных поверхностей римановы поверхности отличает возможность обладания (за некоторыми незначительными исключениями) уникальной метрикой с отрицательной (-1) кривизной во всех точках.

Расчеты Виттена в рамках двухмерной разновидности квантовой теории, называемой конформной теорией поля, заметно отличались от расчетов его коллег, поскольку он сделал намного меньше предположений относительно лежащего в ее основе пространства-времени. Впрочем, он пришел к тому же заключению, что и другие, а именно что геометрия внутренних пространств должна принадлежать к типу Калаби-Яу. Ничто другое не подходило. «Тот факт, что результат был получен двумя независимыми путями, укреплял уверенность в его истинности, — говорит Горовиц. — Более того, это свидетельствовало в пользу того, что это наиболее естественный путь проведения компактификации, поскольку к одним и тем же условиям мы пришли с двух совершенно разных стартовых позиций».^[66]

Четверка закончила свою работу в 1984 году и моментально поделилась своими открытиями с коллегами, выпустив несколько препринтов, хотя их статья вышла только через год. Эта статья ввела в оборот термин «пространства Калаби-Яу», впервые познакомив физиков со странным шестимерным миром.

До публикации в 1985 году статьи Калаби «не ожидал, что наша работа может иметь какое-либо физическое значение. Это была чистая геометрия», — по его же собственным словам. Вышедшая статья, однако, изменила все, введя многообразия Калаби-Яу в самое сердце теоретической физики. «Она также привлекла неожиданное внимание к двум математикам, причастным к открытию этих пространств, — вспоминает Калаби, — поместив нас на передовицы газет. Подобные вещи всегда льстят, это относится и к той известности, которая пришла к нам с началом разговоров о пространствах Калаби-Яу, хотя на самом деле наша заслуга была не столь велика».^[67]

Наша работа, по крайней мере, на некоторое время стала последним писком моды в физике, перекинувшись с «газетных передовиц» и на другие области. Многообразия Калаби-Яу стали названием экспериментальной театральной постановки «Калаби-Яу», заглавием альбома в жанре электро/синтпоп группы DopplerEffekt — «Пространства Калаби-Яу», названием картины «Мона Лиза Калаби-Яу» итальянского художника Франческо Мартино и мишенью шутки в рассказе Вуди Аллена из «Нью Йоркера»: «Мой милый, — сказала она, кокетливо улыбаясь и свернувшись в форме поверхности Калаби-Яу».^[68] Известность, которую приобрела эта столь трудная для понимания идея, была весьма неожиданной, учитывая то, что многообразия данного типа непросто даже описать словами, не то что представить. Пространство, обладающее шестью измерениями, по замечанию одного физика, имеет «на три измерения больше, чем то, которое я способен вообразить». Картина осложняется и присутствием скрученностей, многомерных дыр, которых может быть как небольшое количество, так и свыше пятисот, словно в элитном сорте швейцарского сыра.

Рис. 6.2. Наглядное изображение двухмерного «поперечного сечения» шестимерного многообразия Калаби-Яу (Эндрю Хэнсон, Университет Индианы)

Возможно, наиболее простой особенностью пространств Калаби-Яу является их компактность. Многообразия Калаби-Яу похожи на бесконечный лист бумаги, но не ровный и простирающийся неограниченно во всех направлениях, а скомканный и покрытый складками, но скомканный строго определенным образом. Компактное пространство не содержит областей с бесконечной длиной или шириной, так что при наличии достаточно большого чемодана пространство легко уместится внутри него. Можно выразиться по-другому: по словам Лайама Макаллистера из Корнеллского университета, компактное пространство «можно накрыть одеялом из конечного числа лоскутов» — при этом каждый лоскут, разумеется, должен быть конечного размера.^[69] Оказавшись на поверхности подобного пространства и начав прогулку по «большому кругу», можно вернуться в ту же точку, из которой вы вышли. Впрочем, даже если вы не вернетесь именно в ту точку, вы все же никогда не уйдете бесконечно далеко от точки, из которой вы вышли, вне зависимости от продолжительности вашей прогулки. Назвать пространство Калаби-Яу компактным никоим образом не будет преувеличением. Хотя вопрос о точном размере подобного многообразия по-прежнему остается открытым, очевидно, что оно должно быть чрезвычайно мало и иметь диаметр порядка 10^-30 сантиметров, что в двести восемьдесят квадриллионов раз меньше классического радиуса электрона. Обитатели четырехмерного пространства, подобные нам, не в силах даже увидеть это шестимерное пространство, но оно все же всегда на месте, будучи прикреплено к каждой точке нашего пространства. Мы просто слишком велики, чтобы зайти внутрь и осмотреться.

Рис. 6.3. Калаби-Яу собственной персоной: Эудженио Калаби (слева) и Шинтан Яу (фотография Калаби публикуется с разрешения Э. Калаби, фотография Яу сделана Сьюзан Таун Гильберт)

Это, впрочем, совсем не значит, что мы не взаимодействуем с этими невидимыми измерениями. Прогуливаясь или двигая рукой, мы каждую секунду пронизываем скрытые измерения, даже не замечая этого, — эти движения в каком-то смысле компенсируют друг друга. Представим себе стадо северных оленей в сто тысяч голов, движущееся в одном направлении — например, с прибрежной равнины Аляски на хребет Брукса, где их ждет прекрасная долина, в которой они смогут провести зиму. «Каждое животное, — объясняет Алан Адамс из Массачусетского технологического института, — пройдет эти 800 миль по своей собственной траектории, но в целом отклонения от среднего компенсируют друг друга, и можно считать все стадо движущимся по одному общему пути».^[70] Наши краткие вторжения в пространства Калаби-Яу взаимно компенсируют друг друга аналогичным образом, что делает их несущественными по сравнению с более длинными путями, которые мы проходим в четырехмерном пространстве.

Рис. 6.4. Если теория струн верна, то в любой точке четырехмерного пространства-времени присутствует скрытое шестимерное пространство Калаби-Яу (изображения многообразий Калаби-Яу сделаны Эндрю Хэнсоном, Университет Индианы)

Можно объяснить и по-другому: мы живем в бесконечном пространстве, и наши горизонты чрезвычайно широки, даже если та часть пространства, которую мы успели посетить, чрезвычайно мала. Однако куда бы мы ни шли в этом большом и широком мире, везде «на расстоянии вытянутой руки» нас будет сопровождать крошечное пространство, полный доступ к которому мы никогда не получим. Представим себе необычную систему координат, в которой ось x представляет собой наше бесконечное четырехмерное пространство, а ось y — внутреннее пространство Калаби-Яу. Каждой точке на оси x соответствует скрытая шестимерная область. Напротив, каждой точке на оси у соответствует четырехмерное пространство или направление, также доступное для исследований.

Пожалуй, наиболее удивительным является то, что эта скрытая, внутренняя часть Вселенной — область, которую невозможно увидеть, ощупать, понюхать или ощутить иным образом, — может оказывать большее влияние на физические процессы, чем привычный нам мир из кирпича и камня, машин и ракет, а также миллиардов и миллиардов галактик. По крайней мере, именно это утверждает теория струн. «Все физические величины, которые можно измерить, — все фундаментальные понятия, такие как масса кварков и электронов, — определяются геометрией многообразий Калаби-Яу, — объясняет физик Джозеф Полчинский из Калифорнийского университета. — Зная форму, мы, по сути, знаем все».^[71]Или, как выразился Брайан Грин: «Код Вселенной можно успешно записать языком геометрии пространств Калаби-Яу».^[72] Если общая теория относительности Эйнштейна сводит гравитацию к геометрии, то струнные теоретики надеются развить это утверждение дальше, доказав, что геометрия в виде многообразий Калаби-Яу лежит в основе не только гравитации, но и всей физики в целом.

Я, конечно, не собираюсь ставить под сомнение эти фундаментальные утверждения. Но разумный человек может задаться вопросом: если гипотеза Калаби слишком хороша для того, чтобы быть истинной, то как относиться к вышеуказанному утверждению? И каким образом можно объяснить все вышесказанное? Я опасаюсь, что настоящее объяснение покажется кому-то неудовлетворительным и даже представляющим собой подобие порочного круга — способность многообразий Калаби-Яу к столь чудесным свершениям объясняется тем, что это их свойство с самого начала было встроено в механизм работы теории струн. Впрочем, даже если и так, то все же возможно дать некое общее представление о том, как этот «механизм» — с десятимерными многообразиями на входе и четырехмерной физикой на выходе — работает на самом деле. Попробуем представить максимально упрощенную картину способа получения элементарных частиц и их масс из заданного многообразия Калаби-Яу при учете того, что соответствующее многообразие является неодносвязным. Неодносвязное многообразие подобно тору с одной или большим числом дырок, часть петель которого, находящихся на его поверхности, не могут быть стянуты в точку, в противоположность сфере — односвязной поверхности, на которой любая петля может быть стянута в точку подобно тому как натянутая на глобус упругая резиновая лента соскальзывает с экватора на один из полюсов. Начав со сложного шестимерного многообразия с определенным числом дырок, рассчитаем все возможные пути, которыми можно пропустить струны через многообразие, проходя через различные дырки один или более раз. Это нелегкая задача, поскольку путей пропускания струн через многообразие существует огромное множество, а петли могут иметь разные размеры, зависящие, в свою очередь, от размеров дырок. Из всех этих возможностей вы можете составить список потенциальных частиц. Массы частиц можно определить, умножая длины струн на их натяжение, эквивалентное линейной плотности энергии струны, входящей в кинетическую энергию колебания. Объекты, получаемые таким образом, могут иметь любое число измерений между нулем и шестью. Некоторые из них разрешены, некоторые — нет. Взяв все разрешенные объекты и все разрешенные движения, вы и получите окончательный список частиц и их масс.

Рассматривая этот вопрос с другой стороны, можно отметить, что, согласно представлениям, царящим в квантовой физике, в силу концепции так называемого корпускулярно-волнового дуализма, каждую частицу можно представить в виде волны и каждую волну в виде частицы. Различные частицы в теории струн, как уже говорилось ранее, соответствуют различным модам колебаний струны, тогда как струна, колеблющаяся определенным, заранее заданным образом, также подобна волне. Вопрос в том, чтобы понять, как геометрия этих пространств будет влиять на возникающие волны.

Представим, что пространство, о котором идет речь, это Тихий океан, и мы находимся в его середине, за тысячи миль от ближайшего континента и намного выше его дна. Можно представить себе, что в волны, возникающие возле нас на поверхности океана, практически не будут зависеть от формы или топографии океанического дна, находящегося под нами на расстоянии многих миль. Но в ограниченном пространстве, например в мелкой и узкой бухте, в которой даже небольшое сотрясение дна может привести к возникновению цунами или, если брать менее экстремальный пример, для которой рифы и скалы под поверхностью воды имеют огромное влияние на формирование и разрушение волн, картина будет совсем иная. В этом примере открытый океан играет роль некомпактного или протяженного пространства, тогда как прибрежные воды больше похожи на небольшие, компактные измерения теории струн, где геометрия определяет форму возникающих волн и, следовательно, тип возможных частиц.

В качестве еще одного примера компактного пространства можно привести струнные музыкальные инструменты, например скрипку, которые при помощи определенных колебаний, или волн, порождают не частицы, а звуки. Звук, производимый струной, зависит не только от ее длины и толщины, но и от формы внутренней части инструмента — акустической камеры, — где волны определенных частот входят в резонанс, достигая максимальной амплитуды. Струны музыкальных инструментов получили названия по их основным частотам, для большинства скрипок это G, D, A и E (соль, ре, ля, ми). Физики, подобно скрипичным мастерам, подбирающим формы, соответствующие тем звукам, которые они собираются получить, охотятся на многообразия Калаби-Яу с соответствующей геометрией, способной привести к возникновению тех волн и частиц, с которыми мы постоянно сталкиваемся в окружающем нас мире.

Путь, который физики обычно выбирают для атаки на задачи такого рода, состоит в нахождении решений волнового уравнения, более известного как уравнение Дирака. Решениями волнового уравнения, что неудивительно, являются волны — и соответствующие им частицы. Но это очень сложное для решения уравнение, и мы обычно не в состоянии решить его для всех элементарных частиц, существующих в природе. Это возможно только для так называемых безмассовых частиц, соответствующих нижним, или фундаментальным, частотам определенной струны. К безмассовым принято относить все частицы, которые мы видим или интуитивно чувствуем в окружающем мире, включая те, которые лишь на считанные мгновения возникают внутри ускорителей. Некоторые из этих частиц — например, электроны, мюоны и нейтрино — на самом деле имеют массу, хотя и называются безмассовыми. Но механизм обретения ими массы совершенно не похож на механизм обретения массы так называемыми массивными частицами, формирование которых ожидается при более высоких энергиях на «струнной шкале». Масса обычных частиц (например, электронов) намного меньше массы частиц, называемых массивными, — в квадриллион раз или даже больше, — поэтому определение обычных частиц как безмассовых представляет собой достаточно хорошую аппроксимацию.

Даже если ограничить себя только безмассовыми частицами, получив тем самым возможность найти решения уравнения Дирака, задача по-прежнему останется весьма непростой. К счастью, многообразия Калаби-Яу обладают определенными характеристиками, которые помогают в этом вопросе. Первой из них является суперсимметрия, уменьшающая число переменных, превращая тем самым дифференциальное уравнение второго порядка (уравнение, в котором некоторые из производных взяты дважды) в дифференциальное уравнение первого порядка (уравнение, в котором все производные взяты только единожды). Еще одним вкладом суперсимметрии в решение уравнения является то, что она сопоставляет каждому фермиону свой собственный бозон. Найдя все фермионы, вы автоматически найдете и все бозоны, и наоборот. Итак, достаточно разобраться только с одним из классов частиц, поэтому можно выбрать тот из них, для которого уравнения решать проще.

Еще одной особенностью многообразий Калаби-Яу и, в частности, их геометрии, является то, что для них решения уравнения Дирака — в этом случае соответствующие безмассовым частицам — совпадают с решениями другого уравнения, известного как уравнение Лапласа, работать с которым намного проще. Наибольшее преимущество в данном случае заключается в том, что решения уравнения Лапласа можно получить — и, следовательно, распознать безмассовые частицы, — в принципе, и не решая каких-либо дифференциальных уравнений. Нет необходимости знать точную геометрию или метрику многообразий Калаби-Яу. Вместо этого все необходимое можно получить из топологических «данных» о многообразии Калаби-Яу, содержащихся в матрице 4×4, называемой ромбом Ходжа. О ромбах Ходжа речь пойдет в следующей главе, поэтому сейчас я скажу только то, что эта топологическая уловка позволяет нам весьма успешно собрать воедино все безмассовые частицы.

Впрочем, нахождение частиц является только началом. В конце концов, физика — это нечто большее, чем простой набор частиц. Кроме этого существуют еще и силы или взаимодействия между частицами. В теории струн струнные петли, движущиеся через пространство, могут либо соединяться, либо расщепляться, и их склонность к одному или другому процессу зависит от струнной константы связи, выступающей мерой взаимодействия между струнами.

Расчет сил взаимодействия между частицами является весьма кропотливой задачей, требующей для своего решения использования почти всего арсенала инструментов теории струн, так что работа над одной моделью на практике занимает не меньше года. И вновь суперсимметрия делает наши вычисления менее накладными. Также может помочь и математика, поскольку этот тип проблем уже давно знаком геометрам, в результате чего у них появилось множество инструментов, которыми можно воспользоваться. Петля, свободно движущаяся и колеблющаяся в пространстве Калаби-Яу, может самопроизвольно превратиться в восьмерку и затем расщепиться на две отдельные петли. И напротив, две отдельные петли могут объединиться в восьмерку. При прохождении через пространство-время эти петли заметают риманову поверхность, точно определяющую картину взаимодействий между струнами, хотя до появления на сцене теории струн математикам не приходило в голову каким-то образом связать ее с физикой.

Насколько же близко могут подойти ученые в своих предсказаниях к свойствам реального мира, получив в руки все эти инструменты? Этой теме будет посвящена девятая глава, а сейчас мы рассмотрим статью Канделаса, Горовица, Строминджера и Виттена, вышедшую в 1985 году и представляющую собой первую серьезную попытку показать способность теории струн при помощи компактификаций Калаби-Яу описывать реальный мир.^[73] Уже тогда физики были способны получать хорошее соответствие теории с практикой. В частности, их модель предсказала оптимальную для случая четырех измерений суперсимметрию, обозначаемую как N=1, что означает инвариантность пространства относительно четырех симметричных преобразований, которые можно рассматривать как четыре различных вида вращений. Это само по себе уже являлось большим успехом, так как в случае получения ими максимального значения суперсимметрии N = 8, что соответствовало бы наиболее сложной ситуации — инвариантности относительно двадцати двух различных симметричных операций, — это наложило бы на физику столь сильные ограничения, что единственным допустимым вариантом Вселенной стало бы плоское пространство без какой-либо кривизны, в существовании которой, конечно, сомнений быть не может, или любых других неоднородностей типа черных дыр, делающих жизнь, по крайней мере, физиков-теоретиков, столь интересной. В случае, если бы Канделас и его коллеги потерпели неудачу на этом фронте и было бы получено доказательство, что данные шестимерные пространства не способны обладать необходимой суперсимметрией, компактификация в теории струн, по крайней мере, для данного примера, потерпела бы неудачу.

Эта статья стала огромным шагом вперед и в настоящее время рассматривается как этап первой струнной революции, хотя в некоторых вопросах, например в предсказании количества поколений элементарных частиц, она промазала мимо цели. В стандартной модели, принятой в физике элементарных частиц, — модели, на протяжении уже нескольких десятилетий задающей тон в этой области физики и включающей в себя электромагнитное, слабое и сильное взаимодействия, — все элементарные частицы, из которых состоит вещество, разделены на три поколения. Каждое из поколений состоит из двух кварков, электрона или одного из его аналогов (мюона или таона) и нейтрино, которое также бывает трех видов — электронное, мюонное и таонное. Частицы, принадлежащие к первому поколению, наиболее привычны для нашего мира, являясь одновременно наиболее стабильными и наименее массивными. Частицы из третьего поколения обладают наименьшей стабильностью и наибольшей массой, тогда как члены второго поколения находятся примерно посередине. К глубокому сожалению для Канделаса и компании, многообразия Калаби-Яу, с которыми они работали, дали на выходе четыре поколения элементарных частиц. Они ошиблись лишь на единицу, но в этом случае разница между тремя и четырьмя была огромной.

В 1984 году Строминджер и Виттен начали активно работать над решением задачи о числе поколений и в конце концов обратились ко мне с вопросом о существовании многообразий Калаби-Яу, которые приводили бы не к четырем, а к трем поколениям элементарных частиц. Горовиц в общении со мной также подчеркнул важность этого момента. Итак, существовала необходимость в многообразии с эйлеровой характеристикой, равной 6 или -6, поскольку, как показал Виттен за несколько лет до этого, для определенного класса многообразий Калаби-Яу, обладающих, помимо всего прочего, нетривиальной фундаментальной группой или нестягиваемой петлей, число поколений равно модулю эйлеровой характеристики, деленному на два. Один из вариантов этой формулы фигурировал в часто цитируемой статье, выпущенной «четверкой» в 1985 году.

Мне удалось выкроить немного времени на то, чтобы заняться этой проблемой, в том же году во время перелета из Сан-Диего в Чикаго по пути в Аргоннскую национальную лабораторию, проводившую одну из первых крупных конференций по теории струн. Мне предстояло выступить с докладом, и время, проведенное на борту самолета, я планировал посвятить подготовке к своему выступлению. Мне пришло в голову, что я, возможно, смогу прояснить вопрос о трех поколениях, который мои друзья-физики считают столь важным. Я оказался прав и по окончанию полета смог представить искомое решение — многообразие Калаби-Яу с эйлеровой характеристикой, равной -6, что сделало это многообразие первым, приводящим к трем поколениям элементарных частиц, как и требовалось в рамках стандартной модели. Хотя это и не было огромным прыжком вперед, тем не менее стало своеобразным «маленьким шагом» — как представил его Виттен.^[74]

Я сконструировал это многообразие при помощи скорее формального, хотя впоследствии и доказавшего свою действенность, метода. Для начала я взял декартово произведение двух кубических гиперповерхностей. Гиперповерхность является подмногообразием, то есть поверхностью, размерность которой на единицу меньше размерности пространства, в котором она находится, подобно диску, входящему в шар, или отрезку прямой, являющемуся частью диска. Таким образом, гиперповерхность кубической поверхности с тремя комплексными измерениями имеет два комплексных измерения. Произведение двух таких гиперповерхностей имеет 2×2=4 комплексных измерения. Это на одно измерение больше, чем нужно, и я укоротил многообразие до трех комплексных измерений (или шести вещественных), необходимых для теории струн, найдя его поперечное сечение.

К сожалению, многообразие, полученное в результате этой процедуры, являлось не совсем тем, которое нам было нужно, поскольку оно порождало не три поколения частиц, а девять. Однако это многообразие характеризуется симметрией третьего порядка, что позволило мне создать так называемое фактор-многообразие, в котором каждая точка соответствовала трем точкам в исходном многообразии. Нахождение фактор-многообразия в этом случае было подобно делению исходного многообразия на три равных части. Таким образом, число точек уменьшилось в три раза, так же как и число поколений.

Насколько мне известно, это фактор-многообразие было первым — и долгое время единственным — многообразием Калаби-Яу, имеющим эйлерову характеристику 6 или -6, что открывало возможность его использования для создания трех поколений элементарных частиц. И действительно, я не слышал ни о чем подобном вплоть до конца 2009 года, когда Канделасу с двумя его коллегами — Фолькером Брауном из Дублинского института перспективных исследований и Рисом Дэвисом из Оксфорда — удалось проделать что-то подобное, создав многообразие Калаби-Яу с эйлеровой характеристикой, равной -72, и фактор-многообразие с эйлеровой характеристикой, равной -6. По иронии судьбы, в конце 1980-х Канделасу с двумя его коллегами удалось создать и исходное (или «родительское») многообразие Калаби-Яу — одно из восьми тысяч многообразий, созданных на то время, — но его потенциальную применимость он осознал только более чем через двадцать лет.^[75]

Рис. 6.5. Геометрия позволяет нам уменьшить число измерений объекта, разрезав его и рассматривая только полученное поперечное сечение. К примеру, разрезав трехмерное яблоко, вы обнаружите двухмерную поверхность — одну из множества поверхностей, которые можно получить, в зависимости от того, где и как вы разрезали. Следующий разрез позволит получить одномерную линию на поверхности. Разрезая эту линию, вы получите отдельную (нульмерную) точку. Таким образом, каждый успешный разрез, вплоть до получения точки, уменьшает размерность объекта на единицу

Я затронул этот вопрос, поскольку в далеком 1986 году, когда Брайан Грин только начинал свои попытки извлечь подлинную физику из многообразий Калаби-Яу, возможных вариантов многообразий существовало не так уж много. Для того чтобы получить правильное число поколений, он принял на вооружение то многообразие, которое я создал в 1984 году по пути в Аргонскую национальную лабораторию. Работая над этой проблемой сначала в качестве аспиранта Оксфордского университета, а затем моего постдока в Гарварде, Грин совместно с Келли Кирклином, Полом Мироном и своим бывшим руководителем по Оксфорду Грэхемом Россом подошел еще ближе к Стандартной модели, чем Канделас, Горовиц, Строминджер и Виттен за год до этого. Модель Грина содержала гораздо больше информации — буквально пошаговое руководство по извлечению физических характеристик из многообразий Калаби-Яу. Он и его коллеги получили правильную суперсимметрию, верное число поколений, массивные нейтрино (с чрезвычайно малой массой) и почти все, что только можно было желать, за исключением нескольких дополнительных частиц, существование которых в данном случае и не предполагалось. Итак, это многообразие Калаби-Яу оказалось близко к желаемому — ближе, чем какое-либо другое до этого, — но все же не совсем тем, которое требовалось для решения данного вопроса. Это, конечно, не стоит воспринимать как критику их работы, так как почти четверть века спустя полностью разобраться в этом «вопросе» так никому и не удалось.

В те далекие дни физики надеялись, что существует только одно многообразие Калаби-Яу, которым им придется заниматься, — уникальное решение, из которого можно рассчитать все остальное, — или, по крайней мере, что количество их столь невелико, что не составит труда быстро отбросить наименее подходящие и выбрать из оставшихся то, которое нужно. Когда Строминджер и Виттен впервые спросили меня о количестве известных и уже сконструированных многообразий Калаби-Яу, я смог привести с определенностью только два примера. Одна из этих поверхностей, трехмерная поверхность пятого порядка, по-видимому, является простейшим возможным многообразием Калаби-Яу. Это поверхность пятого порядка, поскольку ее можно описать при помощи полиномиального уравнения пятого порядка, имеющего общий вид

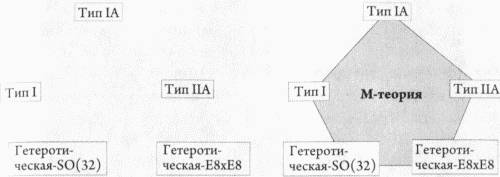
Трехмерной она называется потому, что имеет три комплексных измерения. Второе многообразие Калаби-Яу можно было получить путем объединения (или нахождения прямого произведения) трех комплексных одномерных тороидов и модифицирования полученного результата.

Примерно в это время Строминджер спросил меня об общем количестве возможных многообразий Калаби-Яу. Я сказал, что, вероятно, речь может идти о десятках тысяч многообразий, каждое из которых обладает своей собственной топологией и является определенным решением уравнений теории струн. В рамках каждого из этих топологически различных семейств, кроме того, лежало бесконечное разнообразие возможных форм. Именно это я и заявил перед огромной толпой физиков, собравшихся на мою лекцию в Аргоннской национальной лаборатории в 1984 году, и многие из них испытали потрясение, когда я сказал о цифре десять тысяч, — что впоследствии оказалось достаточно точной оценкой.

Нужно сказать, что тогда физики еще не были способны самостоятельно конструировать многообразия Калаби-Яу, поскольку эта математика была им малознакома, что означало их зависимость от людей, подобных мне, в вопросах о структуре данных объектов. Впрочем, знакомство с соответствующей литературой позволило им быстро вырваться вперед и самостоятельно создать множество примеров, работая независимо от математиков. Вскоре после моей лекции Канделас и его студенты взяли на вооружение тот же общий подход, который использовал я, конструируя первое многообразие, порождавшее три поколения элементарных частиц, и, создав на основе этого метода компьютерную программу, дали начало тысячам многообразий Калаби-Яу. Только несколько из них было разработано непосредственно мной, в расчетах же на компьютере я никогда не был особо силен. Но в свете достижений Канделаса и результатов, полученных при помощи его компьютера, утверждение об огромном количестве многообразий перестало быть чистой абстракцией или грубой оценкой предвзятого математика. Оно превратилось в строго установленный факт, и если вас одолевают какие-либо сомнения в этом вопросе, то все, что вам нужно, — это заглянуть в базу данных Канделаса.

Все это привело к тому, что теория струн стала выглядеть намного более сложной, чем планировалось первоначально. Проблема уже состояла не в нашей способности, взяв многообразие Калаби-Яу, извлечь из него всю заложенную в нем физику. Прежде чем приступить к работе, нужно было сначала ответить на вопрос: какое, собственно, из многообразий нам брать? И, как будет показано в десятой главе, проблема, порожденная избытком многообразий Калаби-Яу, год от года скорее усложнялась, нежели упрощалась. Эта проблема вышла на первый план уже в 1984 году, когда, по словам Строминджера, «единственность теории струн была поставлена под сомнение».^[76]

И если со всем этим еще можно было смириться, то существовали и другие проблемы, преследовавшие теорию струн на ее начальном этапе, и одной из них был вопрос о количестве струнных теорий самих по себе. Единой теории струн попросту не существовало. Вместо этого имелись пять отдельных теорий — типа I, типа IIA, типа IIB, гетеротическая SO(32) и гетеротическая Е8×Е8, — отличавшиеся, к примеру, тем, что в одних струны могли существовать только в виде замкнутых петель, другие же допускали существование незамкнутых струн. Каждая из этих теорий предполагала наличие различных групп симметрии и каждая из них содержала уникальный набор допущений о таких понятиях, как, например, хиральность (зеркальная неразличимость) фермионов и т. д. Началась дискуссия о том, какая же из этих пяти возможных теорий в конце концов одержит верх и станет подлинной Теорией Всего. В то время мы находились в парадоксальной — если не сказать неловкой — ситуации, когда параллельно существовали целых пять «единых» теории природы.

В 1995 году, проявив немалую силу интеллекта, Виттен показал, что все пять струнных теорий представляют собой взгляд под разными углами на одну и ту же всеохватывающую теорию, которую он назвал М-теорией. Виттен никогда не объяснял, что значит в этом контексте буква «М», породив тем самым массу догадок: мастерская, магическая, могущественная, мистическая, материнская, матричная или мембранная.

Последнее слово в этом списке имеет особое значение, поскольку к фундаментальным составляющим М-теории теперь относились не только струны. На смену им пришли более общие объекты, называемые мембранами, или бранами, которые могли иметь от нуля до девяти измерений. Одномерный вариант (1-брана) аналогичен обычной струне, тогда как 2-брана близка нашему представлению о мембране, а 3-брана подобна трехмерному пространству. Эти многомерные браны получили название p-бран, тогда как разновидность этих объектов, называемая D-бранами, представляет собой подповерхности в пределах пространств большей размерности, к которым прикреплены открытые (в противоположность замкнутым петлям) струны. Появление бран сделало теорию струн более богатой и более приспособленной для объяснения широкого спектра явлений, о чем пойдет речь в дальнейших главах. Более того, установленная фундаментальная связь между пятью струнными теориями открыла возможность для ученого выбирать тот из вариантов теории, который упрощает решение именно его проблемы.

М-теория имеет еще одну важную особенность, отличающую ее от теории струн. Эта теория существует не в десяти, а в одиннадцати измерениях. «Физики утверждают, что у них есть красивая и последовательная теория квантовой гравитации, однако им не удается договориться о количестве измерений, — замечает Малдасена. — Некоторые говорят, что измерений десять, некоторые — что одиннадцать. На самом деле наша Вселенная может иметь как десять, так и одиннадцать измерений».^[77]

Рис. 6.6. Вначале пять различных струнных теорий рассматривались как конкурирующие, они исследовались раздельно и считались отличными между собой. Эдвард Виттен и другие архитекторы «второй струнной революции» показали, что эти теории взаимосвязаны — соединены в общую структуру, носящую название М-теории (хотя, по-видимому, никто не знает, что означает М)

Строминджер утверждает, что «понятие размерности не является абсолютным». Он сравнивает теорию струн и М-теорию с различными фазовыми состояниями воды. «Охладив ее ниже температуры замерзания, вы получите лед, выше нуля — жидкость, над точкой кипения — пар, — говорит он. — В зависимости от фазового состояния, в котором она находится, вода может иметь совершенно различный внешний вид. Но в какой из этих фаз на самом деле живем мы — нам неизвестно».^[78]

Даже главный создатель М-теории, Виттен, признает, что десяти- и одиннадцатимерное описания Вселенной «могут быть истинными одновременно. Я не считаю одно из них более фундаментальным, чем другое, но, по крайней мере, для некоторых целей, одно может быть более полезным, чем другое».^[79]

Подходя с практической точки зрения, можно сказать, что физики больше преуспели в объяснении физических явлений нашего четырехмерного мира, рассматривая его с десяти-, а не одиннадцатимерной перспективы. Исследователи делают попытки перейти от одиннадцати измерений непосредственно к четырем путем компактификации дополнительных измерений в семимерное, так называемое G2-многообразие, — первый компактный вариант которого был предложен в 1994 году Домиником Джойсом, математиком, работающим в настоящее время в Оксфорде. Если бы это удалось, то большая часть того, о чем мы говорили до сих пор, — например, получение четырехмерного физического мира из десятимерной Вселенной при помощи шестимерных многообразий Калаби-Яу (4+6=10), — могло бы мгновенно устареть благодаря открытиям Виттена. К счастью, по крайней мере, в контексте нашей дискуссии, это не так.

Рис. 6.7. Эдвард Виттен в Институте перспективных исследований (фотография Клиффа Мура)

Одним из недостатков G2-подхода, поясняет физик из Беркли Петр Хорава, сотрудник Виттена и человек, внесший ключевой вклад в М-теорию, состоит в том, что мы не можем восстановить четырехмерную физику путем компактификации на «гладком» семимерном многообразии. Еще одной проблемой является то, что семимерные многообразия, в отличие от многообразий Калаби-Яу, не могут быть комплексными, поскольку комплексные многообразия должны иметь четное число измерений. Это, возможно, важнейшее отличие, добавляет Хорава, «поскольку комплексные многообразия намного лучше ведут себя, их намного проще понять и с ними гораздо легче обращаться».^[80]

Более того, о существовании, уникальности и других математических характеристиках семимерных G2-многообразий еще очень многое предстоит узнать. Не существует даже систематического пути поиска этих многообразий или общего набора правил их нахождения, как в случае многообразий Калаби-Яу. Мы с Виттеном пытались разработать нечто подобное гипотезе Калаби для G2-многообразий, но до сих пор ни я, ни он, ни кто-либо другой пока не смогли ничего обнаружить. Впрочем, одной из возможных причин, по которым М-теория на сегодня развита не так сильно, как теория струн, является то, что ее математика намного сложнее и изучена далеко не столь подробно.

По причине затруднений с G2-многообразиями основные усилия в М-теории следовали непрямыми путями компактификации одиннадцати измерений в четыре. Во-первых, одиннадцатимерное пространство-время рассматривается как произведение десятимерного пространства-времени и одномерной окружности. Окружность можно компактифицировать, сделав ее радиус крошечным, что оставляет нам только десять измерений. После этого десять оставшихся измерений обычным путем компактифицируют при помощи многообразия Калаби-Яу, получая тем самым четыре измерения нашего мира. «Итак, даже в М-теории многообразия Калаби-Яу по-прежнему находятся в центре событий», — говорит Хорава.^[81] Этот подход, инициированный Виттеном, Хоравой, Бартом Оврутом и другими, носит название гетеротической М-теории. Она сыграла важную роль при создании концепции бранных вселенных, считающей, что наша Вселенная находится на бране, а также породила альтернативные теории ранней Вселенной.

Итак, по крайней мере, на текущий момент, оказалось, что все дороги проходят через многообразия Калаби-Яу. Извлечь подлинную физику и космологию из теории струн и М-теории невозможно без знания геометрии этих пространств, содержащих в себе «генетический код Вселенной» — генеральный план строительства мира. Именно по этой причине стэнфордский физик Леонард Сасскинд, один из основателей теории струн, утверждает, что многообразия Калаби-Яу представляют собой нечто большее, чем просто вспомогательную структуру или строительные леса теории. «Они — это ДНК теории струн», — говорит он.

54. Cumrun Vafa (Harvard University), interview with author, January 19,2007.

55. John Schwarz (California Institute of Technology), interview with author, August 13, 2008.

56. Michael Green (University of Cambridge), e-mail letter to author, August 15, 2008.

57. John Schwarz, interview with author, August 13, 2008.

58. Andrew Strominger (Harvard University), interview with author, February 7, 2007.

59. Andrew Strominger, interview with author, November 1, 2007.

60. Raman Sundrum (Johns Hopkins University), interview with author, January 25,2007.

61. Andrew Strominger, interview with author, February 7, 2007.

62. Dennis Overbye, “One Cosmic Question, Too Many Answers,” New York Times, September 2, 2003.

63. Juan Maldacena (Princeton University), interview with author, September 9, 2007.

64. Dan Freed (University of Texas), interview with author, June 24, 2008.

65. Tristan Hubsch (Howard University), interview with author, August 30, 2008.

66. Gary Horowitz (University of California, Santa Barbara), interview with author, February 15, 2007.

67. Eugenio Calabi (University of Pennsylvania), interview with author, October 18, 2007.

68. Woody Allen, “Strung Out,” New Yorker, July 28, 2003.

69. Liam McAllister (Cornell University), e-mail letter to author, April 24, 2009.

70. Allan Adams (MIT), interview with author, August 10, 2007.

71. Joe Polchinski (University of California, Santa Barbara), interview with author, January 29, 2007.

72. Brian Greene, The Fabric of the Cosmos (New York: Alfred A. Knopf, 2004), p. 372.

73. P. Candelas, G. Horowitz, A. Strominger, and E. Witten, “Vacuum Configurations for Superstrings,” Nuclear Physics В 258 (1985): 46–74.

74. Edward Witten (IAS), e-mail letter to author, July 24, 2008.

75. Volker Braun, Philip Candelas, and Rhys Davies, “A Three-Generation Calabi-Yau Manifold with Small Hodge Numbers,” October 28, 2009, http://arxiv.org/PS_cache/arxiv/pdf/0910/0910.5464vl.pdf.

76. Dennis Overbye, “One Cosmic Question, Too Many Answers,” New York Times, September 2, 2003.

77. Dale Glabach and Juan Maldacena, “Who’s Counting?” Astronomy, May 2006, p. 72.

78. Andrew Strominger, “String Theory, Black Holes, and the Fundamental Laws of Nature,” lecture, Harvard University, Cambridge, Mass., April 4, 2007.

79. Edward Witten (IAS), e-mail letter to author, July 21, 2008.

80. Petr Horava (University of California, Berkeley), interview with author, July 6, 2007.

81. То же.