|
||
|
|
||
| Главная ≫ Инфотека ≫ Математика ≫ Книги ≫ Глава 3. Новая разновидность молотка / Теория струн и скрытые измерения Вселенной // Шинтан Яу, Стив Надис |
Глава 3. Новая разновидность молотка / Теория струн и скрытые измерения ВселеннойШинтан Яу, Стив Надис
Глава 3. Новая разновидность молоткаГеометрия, несмотря на весьма насыщенную историю и впечатляющие достижения, которыми она может похвастаться на сегодняшний день, не является завершенным произведением, она по-прежнему развивается, постоянно открывая заново саму себя. Одним из последних нововведений в геометрии, внесшим определенный вклад в теорию струн, стало создание геометрического анализа — подхода, который ярко проявил себя только в последние десятилетия. Основной идеей этого подхода является использование мощных методов математического анализа (частью которого является дифференциальное исчисление) для интерпретации геометрических понятий и, напротив, использование геометрической интуиции для интерпретации понятий анализа. Едва ли это новшество станет последним в геометрии — как не стали последними в истории геометрии те нововведения, о которых мы уже говорили. Тем не менее геометрический анализ уже достиг весьма значительных успехов. К работе в этой области я приступил в 1969 году, учась на первом курсе аспирантуры в Беркли. Для меня лично все началось с необходимости найти книгу для чтения во время рождественских каникул. Не проявив интереса к четырем наиболее продаваемым книгам того года — «Случай портного», «Крестный отец», «Машина любви» и «Штамм “Андромеда”», я остановился на книге, название которой было куда менее популярным — «Теория Морса» американского математика Джона Милнора. Меня особенно заинтересовала глава этой книги, посвященная топологии и кривизне, в которой разбиралось утверждение, что локальная кривизна заметно влияет на геометрию и топологию. С тех пор я постоянно возвращаюсь к этому утверждению, поскольку локальная кривизна поверхности определяется путем взятия производных по этой поверхности. Иными словами, определение кривизны требует использования методов анализа. Исследование влияния кривизны на геометрию, таким образом, составляет самую сущность геометрического анализа. Не имея рабочего кабинета, в те дни я практически жил в математической библиотеке Беркли. Ходят слухи, будто первой моей целью по прибытию в Соединенные Штаты стало посещение этой библиотеки, а не, скажем, осмотр достопримечательностей Сан-Франциско, на чем, возможно, остановили бы свой выбор другие. И хотя я и не могу вспомнить точно, чем я занимался сорок лет назад, у меня нет оснований сомневаться в достоверности этих слухов. Я имел привычку постоянно прохаживаться по библиотеке, читая каждый журнал, который попадал мне в руки. Однажды, во время упомянутых рождественских каникул, просматривая каталог, я наткнулся на статью Милнора 1968 года, книгу которого я как раз читал в то время. В этой статье, в свою очередь, упоминалась теорема Александре Прайсмана, которая привлекла мое внимание. И поскольку у меня не было каких-либо других занятий (в то время большинство моих коллег разъехались на каникулы), я решил посмотреть, не смогу ли я доказать что-либо, относящееся к теореме Прайсмана. В своей теореме Прайсман рассмотрел две нетривиальные петли, А и В, на заданной поверхности. Петлей в топологии называется кривая, начинающаяся в определенной точке поверхности и неким образом охватывающая эту поверхность, возвращаясь в конце концов в ту же точку. Нетривиальная означает в данном контексте, что эту петлю нельзя стянуть в точку, не отрывая ее от поверхности. Иными словами, существует некая преграда, не дающая петле стянуться в точку: так, например, петлю, продетую через дырку бублика, можно стянуть в точку, только разрезав этот бублик (после этого петля уже не будет находиться на поверхности, а бублик, с точки зрения топологии, перестанет быть бубликом). Если проследовать вдоль петли А, а затем вдоль петли В, то результирующий путь будет представлять собой новую петлю В×А. Напротив, если сначала обойти вокруг петли В, а потом вокруг петли А, возникнет петля А×В. Прайсман доказал, что в пространстве, кривизна которого всюду отрицательна — подобно внутренней поверхности седла, — петли В×А и А×В можно непрерывно преобразовать одну в другую путем изгиба, растяжения и сжатия только в одном особом случае: а именно, если петлю, кратную петле А (такую петлю можно получить, обойдя вокруг петли А один или целое число раз), можно плавно преобразовать в петлю, кратную петле В. В этом частном случае петли А и В носят название коммутирующих, точно так же, коммутирующими являются операции сложения и умножения (2 + 3 = 3 + 2 и 2 × 3 = 3 × 2), тогда как вычитание и деление некоммутативны (2 – 3 ≠ 3 – 2 и 2/3 ≠ 3/2). Моя теорема имела несколько более общую форму, чем теорема Прайсмана. Данная теорема была применима к любому пространству неположительной кривизны (то есть либо отрицательной, либо — в отдельных местах — равной нулю). Для доказательства более общего случая мне пришлось прибегнуть к разделу математики, который никогда до этого не использовался в топологии или дифференциальной геометрии, — к теории групп. Группой в математике называется набор элементов, для которых выполняется определенный набор правил, таких как обязательное присутствие в группе нейтрального (например, единицы) и обратного (например, 1/x для каждого x) элементов. Группа является замкнутой, то есть, проведя определенную операцию над двумя элементами группы (такую, как сложение или умножение), мы получим еще один ее элемент. Помимо этого, в группе должен выполняться ассоциативный закон — а именно a × (b × c) = (a × b) × c. Элементами той группы, которую рассматривал я (так называемой фундаментальной группы), были петли, которые можно изобразить на поверхности, такие как упоминавшиеся уже петли А и В. В том случае, если в пространстве есть нетривиальные петли, говорят, что пространство имеет нетривиальную фундаментальную группу. И напротив, если каждую петлю в пространстве можно стянуть в точку, то соответствующая фундаментальная группа будет тривиальной. Я доказал, что в том случае, если две петли коммутируют (то есть А × В = В × А), должна существовать «подповерхность» более низкой размерности — а именно имеющая форму тора, — находящаяся где-то внутри данной поверхности. В двухмерном случае тор можно представить как «произведение» двух окружностей. Рассмотрим сначала одну окружность — она будет проходить вокруг дырки бублика, и представим, что все ее точки являются центрами одинаковых окружностей. Соединив вместе эти окружности, мы и получим тор. Мы как бы нанизываем колечки на нитку и связываем концы нитки вместе. Именно это и подразумевалось под утверждением, что тор — это произведение двух окружностей. В моей теореме (основанной, в свою очередь, на статье Прайсмана) в роли таких окружностей выступали петли А и В. Конечно, наши с Прайсманом рассуждения носили скорее формальный характер и могут показаться вам малопонятными. Принципиально важным здесь является то, что наши доказательства показали, как глобальная топология поверхности влияет не только на ее локальную геометрию, но и на ее геометрию в целом. Петли в этом случае определяют фундаментальную группу, что является скорее глобальной, чем локальной особенностью пространства. Чтобы показать, что одну петлю можно непрерывно преобразовать в другую, необходимо рассмотреть поверхность в целом, обращаясь к глобальным свойствам данного пространства. По сути дела, вопрос о том, какие глобальные геометрические структуры соответствуют заданной топологии, является одним из основных вопросов современной геометрии. Так, если геометрическая поверхность топологически эквивалентна сфере, то ее кривизна всегда неотрицательна. Математики имеют на руках весьма длинный список подобных утверждений. Поскольку мое доказательство показалось мне убедительным, по окончании зимних каникул я показал его одному из своих наставников, молодому преподавателю университета Блейну Лоусону. Лоусон согласился с ним и, используя некоторые идеи из той же статьи, мы совместными усилиями попытались доказать еще одну теорему, затрагивающую вопрос связи кривизны и топологии. Несомненно, я был доволен тем, что мне удалось внести определенный вклад в корпус математических знаний, хотя и не полагал, что сделал нечто особо примечательное. Я все еще искал тот путь, на котором мог бы оставить свой след. Мне неожиданно пришло в голову, что ответ на вопрос, который меня интересовал, я смогу найти в курсе лекций по нелинейным дифференциальным уравнениям в частных производных, который я слушал в то время. Преподаватель, читавший нам эти лекции, профессор Чарльз Морри, производил на меня огромное впечатление. Его курс по предмету, который не пользовался большой популярностью, требовал огромных усилий для понимания, будучи основан на чрезвычайно тяжелой для чтения книге самого Морри. Вскоре после начала занятий на его лекциях не осталось других студентов, кроме меня, что во многом было обусловлено начавшимися в то время студенческими демонстрациями против бомбардировок Камбоджи. Впрочем, Морри не прекращал своих лекций, уделяя, по-видимому, достаточно большое внимание их подготовке несмотря на то, что посещал их теперь всего один студент.
Морри был специалистом в области дифференциальных уравнений в частных производных, и методы их решения, разработанные им, отличались большой глубиной. Отдавая ему должное, могу сказать, что именно лекции Морри стали основой всей моей дальнейшей научной карьеры. Дифференциальные уравнения используются везде, где встречаются бесконечно малые изменения переменных, в том числе и в физических законах. Одним из наиболее важных и сложных классов этих уравнений являются так называемые дифференциальные уравнения в частных производных, описывающие изменение некоей функции при изменении сразу нескольких переменных. При помощи дифференциальных уравнений в частных производных можно предсказать поведение данной, функции не только, например, во времени, но и при изменении других переменных, например при перемещении в пространстве вдоль осей x, y или z. Подобные уравнения дают возможность заглянуть в будущее и увидеть возможную эволюцию системы; без них физика была бы лишена своей предсказательной силы. Геометрия тоже не может обойтись без дифференциальных уравнений. Мы используем их, чтобы определить кривизну объекта и вычислить ее изменение при переходе от точки к точке. Именно это делает геометрию необходимой для физических приложений. Приведем простой пример: ответ на вопрос, будет ли катящийся мяч двигаться с ускорением, то есть будет ли его скорость изменяться во времени, напрямую зависит от кривизны траектории мяча. Это только один пример тесной связи кривизны с физическими понятиями. По этой причине и геометрия — «наука о пространстве», включающая в себя все, что связано с кривизной, — играет важную роль во многих областях физики. Фундаментальные законы физики являются локальными в том смысле, что они всегда описывают поведение той или иной физической величины не во всем пространстве, а в отдельных, локальных, областях. Это справедливо даже для общей теории относительности, стремящейся описать кривизну всего пространственно-временного континуума в целом. В конце концов, и производные, фигурирующие в дифференциальных уравнениях, тоже берутся именно в отдельных точках. Все это создает проблему для физиков. Как сказал математик UCLA Роберт Грин: «Итак, исходя из локальной информации, такой как кривизна, необходимо узнать строение объекта как целого. Вопрос состоит в том, как это сделать»[25]. Рассмотрим для начала кривизну поверхности Земли. Поскольку провести измерения всего земного шара сразу крайне сложно, Грин предложил рассмотреть вместо этого следующую картину. Представим себе собаку, сидящую на прикрепленной к столбу цепи во дворе. Если у собаки есть возможность перемещаться хотя бы в небольших пределах, она сможет узнать, какую кривизну имеет тот участок земли, который ограничен длиной цепи. В данном случае предполагается, что эта кривизна положительна. Представим теперь, что в каждом дворе мира живет подобная собака, привязанная к столбу, и каждый из участков земли вокруг этих столбов имеет положительную кривизну. Сведя воедино все эти данные о локальной кривизне, можно сделать вывод, что топологически данная планета должна иметь сферическую форму.
Конечно, существуют и более строгие методы определения кривизны участка поверхности, не основанные на субъективных ощущениях привязанной на нем собаки. К примеру, если цепь имеет длину r и собака движется вокруг столба так, что ее цепь все время натянута, то в случае плоского пространства (плоской Земли) длина описываемой собакой окружности будет равна точно 2πr. На поверхности сферы, обладающей положительной кривизной, длина окружности будет несколько меньше, чем 2πr, из-за того что сферическая поверхность как бы «наклоняется вниз» при движении в любом из возможных направлений; в том же случае, когда столб находится на горном перевале или в седловой точке, обладающей отрицательной кривизной, имеющей наклон вниз в одних направлениях и наклон вверх в других, длина окружности будет несколько больше, чем 2πr. Таким образом, наша задача сводится к тому, чтобы определить кривизну каждого конкретного участка, измерив расстояния, проходимые по кругу каждой из собак, — и затем свести эти результаты воедино. Именно этим и занимается дифференциальная геометрия. Кривизна в дифференциальной геометрии определяется локально, то есть в отдельных точках, однако полученная таким образом информация применяется для того, чтобы сделать выводы о пространстве в целом. «Кривизна управляет топологией» — наш основной девиз. А нашим основным инструментом являются дифференциальные уравнения. Геометрический анализ — сравнительно новая область математики, к обсуждению которой мы сейчас приступим, — развивает эту идею дальше. Следует отметить, что общий подход, предусматривающий использование дифференциальных уравнений в геометрии, развивался в течение нескольких столетий, зародившись практически одновременно с дифференциальным исчислением. Одним из первых исследователей в этой области стал великий швейцарский математик XVIII столетия Леонард Эйлер. Помимо всего прочего, он первым применил дифференциальные уравнения в частных производных для систематического исследования трехмерных поверхностей. Через два с лишним столетия после Эйлера мы продолжаем идти по его стопам. По сути, Эйлер был одним из первых, кто обратил внимание на нелинейные уравнения, лежащие сегодня в основе геометрического анализа. Нелинейные уравнения, как правило, весьма сложны для решения, отчасти потому, что описываемые ими модели носят более запутанный характер. Так, нелинейные системы по своей природе менее предсказуемы, чем линейные, — хорошим примером здесь может служить погода — даже небольшие изменения в начальных условиях могут привести к совершенно другим результатам. Возможно, наиболее известной формулировкой того же утверждения является так называемый эффект бабочки в теории хаоса, парадоксальным образом предсказывающий возможность того, что взмах крыла бабочки в одной части мира может стать причиной возникновения торнадо в другой. Линейные системы, напротив, содержат в себе гораздо меньше подводных камней и, следовательно, гораздо более просты для понимания. Линейные зависимости — это зависимости типа y = 2x, названные так, поскольку их графиками являются прямые линии. Каждому значению аргумента здесь соответствует единственное значение функции. Двоение x автоматически приведет к удвоению y и наоборот. Изменение одной переменной всегда пропорционально изменению другой; невозможно получить огромный скачок в значении одной из переменных, лишь слегка изменив другую. Если бы законы природы описывались исключительно линейными зависимостями, наш мир был бы намного проще для понимания — хотя и значительно менее интересным. Но это не так — и именно поэтому приходится иметь дело с нелинейными уравнениями. Впрочем, существуют некоторые методы, упрощающие работу с нелинейными уравнениями. К примеру, сталкиваясь с нелинейной задачей, можно прибегнуть к соответствующему линейному приближению и использовать его до тех пор, пока оно не перестанет быть применимым. Так, проанализировать волнистую (нелинейную) кривую можно путем нахождения производных соответствующей функции, что дает возможность представить кривую в виде совокупности касательных или, другими словами, линейных элементов (прямых линий) в любых необходимых нам точках кривой. Аппроксимация нелинейного мира линейными зависимостями является для ученых обычной практикой, что, конечно, никоим образом не изменяет сам факт принципиальной нелинейности Вселенной. Для того чтобы получить возможность работать с нелинейными системами непосредственно, необходимо использовать математические приемы, лежащие на границе между геометрией и нелинейными дифференциальными уравнениями. Именно это было осуществлено в рамках геометрического анализа, математического подхода, оказавшегося весьма полезным как для теории струн, так и для всей современной математики в целом. Я не хотел бы, чтобы у вас возникло впечатление, будто бы начало геометрического анализа было заложено только в первой половине 1970-х годов, когда я остановил свой выбор на этой области математики. Как я уже говорил, в математике никто не может заявить о том, что он начал что-либо с чистого листа. Так и идея геометрического анализа восходит еще к XIX столетию — а именно к работам французского математика Анри Пуанкаре, который, в свою очередь, основывался на трудах Римана и других его предшественников.
Вклад, внесенный многими из моих непосредственных предшественников в математику, был весьма значителен, таким образом, к моменту моего выхода на сцену в области нелинейного анализа уже имелось множество детально разработанных теорий. К подобным теориям относится разработанная Морри, Алексеем Погореловым и другими теория нелинейных дифференциальных уравнений в частных производных для случая двухмерного пространства, которые называют эллиптическими уравнениями и которые будут обсуждаться в пятой главе. В 1950-х годах Эннио де Джорджи и Джон Нэш разработали методы исследования подобных уравнений для случая большего числа измерений и более того — для любого числа измерений. Вскоре после этого теории, созданные для большого числа измерений, были развиты такими учеными, как Морри и Луис Ниренберг, что говорит о том, что я выбрал отличное время для начала работы в данной области и применения разработанных ими методов к геометрическим задачам. Несмотря на то что подход, который я и мои коллеги взяли на вооружение в начале 1970-х, не был чем-то совершенно новым, мы попытались взглянуть на него с совершенно иной точки зрения. Так, для Морри дифференциальные уравнения в частных производных имели фундаментальное значение сами по себе и представляли скорее подлежащее изучению прекрасное творение разума, нежели средство для достижения какой-либо цели. Интересуясь также и геометрией, он рассматривал ее в основном как источник интересных дифференциальных уравнений, точно так же он смотрел и на многие области физики. И хотя мы оба восхищались этими уравнениями, наши цели были практически противоположны — вместо того, чтобы пытаться искать новые нелинейные уравнения в геометрических задачах, я собирался использовать эти уравнения для решения геометрических задач, до этого считавшихся неразрешимыми. Вплоть до 1970-х годов геометры всячески избегали нелинейных уравнений, впрочем, я и мои современники не испытывали перед ними сильного страха. Мы поставили себе целью узнать, как следует обращаться с подобными уравнениями, чтобы затем использовать их в своей повседневной работе. Рискуя показаться нескромным, я все же скажу, что эта стратегия не только оправдала себя, но и вышла далеко за рамки первоначальных задач. На протяжении многих лет, используя методы геометрического анализа, мы занимались решением важнейших задач, не разрешенных до этого каким-либо другим способом. «Смесь геометрии с теорией [дифференциальных уравнений в частных производных], — отметил математик Имперского колледжа Лондона Саймон Дональдсон, — задает тон во всей обширной области, касающейся данного предмета, на протяжении последней четверти столетия».[26] Итак, чем же занимается геометрический анализ? Рассмотрим сначала простейший пример. Предположим, что вы нарисовали окружность и сравнили ее с произвольной петлей или замкнутой кривой, которая имеет несколько меньшую длину, — в роли подобной петли может выступать обычная резинка, небрежно брошенная на письменный стол. Эти две кривые выглядят совершенно различными и, естественно, имеют разную форму. Однако можно представить, как резинка деформируется (или растягивается) и превращается в окружность — такую же, как та, что нарисована на бумаге. Существует много способов сделать это. Вопрос в том, какой из них лучше? Иными словами, существует ли такой способ, который будет безотказно работать во всех возможных случаях и никогда не приведет к возникновению узлов или перекручиваний? Можно ли найти этот универсальный способ, не прибегая к методу проб и ошибок? Узнать все это можно в рамках геометрического анализа, который позволяет, исходя из геометрии произвольной кривой (в нашем случае резинки), сделать выводы о способах ее преобразования в окружность. Этот процесс не должен быть произвольным. Строго определенный или — еще лучше — канонический путь превращения нашей кривой в окружность однозначно определяется ее геометрией. Для математиков слово канонический является синонимом слова «единственно верный», что, впрочем, иногда звучит излишне строго. Представим себе, что мы хотели бы попасть с Северного полюса на Южный. Существует бесконечно много меридианов, соединяющих эти точки. Каждый из меридианов будет кратчайшим путем, но ни один из них не будет единственно верным; вместо этого мы называем такие пути каноническими. Те же вопросы остаются актуальными и в случае более высоких размерностей. Вместо окружности и резинки теперь можно сравнить сферу или полностью надутый баскетбольный мяч со сдутым баскетбольным мячом с разнообразными углублениями и выступами. Задача состоит в том, чтобы превратить сдутый баскетбольный мяч в идеальную сферу. Конечно, для этого лучше всего использовать насос, но можно и математику. Математическим аналогом насоса в геометрическом анализе является дифференциальное уравнение, служащее движущим механизмом процесса преобразования формы путем крошечных непрерывных изменений. Стоит только определиться с начальной ситуацией (геометрией сдутого мяча) и найти подходящее дифференциальное уравнение — и задача будет решена. Самым тяжелым во всем этом является нахождение подходящего для данного случая дифференциального уравнения, равно как и выяснение, существует ли в принципе уравнение, подходящее для данной задачи. К счастью, Морри и другие математики создали немало инструментов для анализа дифференциальных уравнений, при помощи которых можно узнать, имеет ли решение задача, с которой мы столкнулись, и, если да, то является ли это решение единственным. Описанный выше тип задач принадлежит к категории задач, известных как геометрический поток. Подобные задачи в последнее время привлекли достаточно большое внимание по причине их использования в доказательстве сформулированной сто лет назад гипотезы Пуанкаре, о которой еще пойдет речь в этой главе. При этом, однако, необходимо отметить, что задачи данного типа составляют лишь часть круга исследований геометрического анализа, который охватывает гораздо большую область возможных применений. Говорят, что, для того кто держит в руке молоток, любая проблема кажется гвоздем. Загвоздка лишь в том, как правильно определить направление «удара», необходимое для того, чтобы разрешить ту или иную задачу. Так, одним из важных классов задач, для решения которых используется геометрический анализ, является исследование минимальных поверхностей. Для таких гвоздей геометрический анализ порой является идеальным молотком.
Любой человек неоднократно сталкивался с минимальными поверхностями. При погружении пластмассового кольца из набора для пускания пузырей в сосуд с мыльной водой действие поверхностного натяжения приводит к тому, что образующаяся мыльная пленка принимает совершенно плоскую форму, стремясь иметь минимальную возможную площадь. Выражаясь математическим языком, минимальная поверхность является наименьшей по площади из всех поверхностей, которые можно натянуть на заданный замкнутый контур. Задачи на нахождения минимума уже на протяжении сотен лет играют одну из ведущих ролей в геометрии и физике. Так, в XVII столетии французский математик Пьер Ферма показал, что свет, проходя через различные среды, всегда следует по тому пути, который требует наименьшего времени, что впоследствии привело к открытию так называемого «принципа наименьшего действия», ставшему одним из первых фундаментальных физических принципов, основанных на понятии нахождения минимума. По словам стэнфордского математика Леона Симона, «мы постоянно сталкиваемся с подобным явлением в природе, поскольку из всех возможных конфигураций всегда реализуются только те, которые имеют наименьшую энергию»[27]. Поверхность, обладающая наименьшей возможной площадью, соответствует состоянию с минимальной энергией, которое, при прочих равных условиях, всегда будет предпочтительным. Поверхность с наименьшей площадью будет иметь нулевую нормальную составляющую поверхностного натяжения, иными словами, средняя кривизна этой поверхности также будет равна нулю. По этой причине поверхность жидкости имеет плоскую форму (с нулевой кривизной) и точно такую же форму имеют мыльные пленки. В области исследований минимальных поверхностей присутствует некоторая путаница, берущая свое начало в терминологии, не изменявшейся на протяжении столетий, несмотря на постепенное усложнение математических понятий. Дело в том, что существует еще один класс поверхностей, которые также иногда называют минимальными, хотя они и не обязательно имеют минимальную площадь. Этот класс включает поверхности, площадь которых меньше, чем площадь других поверхностей, ограниченных тем же контуром, — это могут быть как истинно минимальные поверхности или «основные состояния» так и поверхности, носящие название стационарных, которые имеют минимальную возможную площадь на отдельных участках (локально), но не в целом (глобально). Поверхности этого типа, имеющие нулевую нормальную составляющую поверхностного натяжения и нулевую среднюю кривизну, весьма интересны как математикам, так и инженерам. Мы привыкли думать о минимальных поверхностях как о членах одного семейства, весьма похожих между собой. И поскольку каждая из этих поверхностей по-своему интересна, все их можно считать уникальными. Нахождение кратчайшего пути является одномерным вариантом более сложной задачи нахождения минимальной поверхности для большего числа измерений. Кратчайший путь между двумя точками — будь то прямая линия, плоскость или дуга окружности, соединяющая две точки на земном шаре, — иногда называют геодезической линией, хотя это понятие, также вызывая путаницу, включает в себя и те пути, которые не обязательно являются кратчайшими, что, впрочем, не мешает им иметь большое значение для геометров и физиков. Если на дуге большого круга взять две точки, не лежащие на противоположных полюсах, то возникнет сразу два возможных пути из одной точки в другую — короткий и длинный. Оба пути представляют собой геодезические линии, но лишь один из них соответствует кратчайшему расстоянию между точками. Более длинный путь также имеет минимально возможную длину, однако только локально, среди всех возможных путей, проходящих вблизи данной геодезической линии. При рассмотрении всех возможных вариантов этот путь уже не будет кратчайшим — более кратким будет противоположный ему путь. Ситуация становится еще более запутанной в случае эллипсоида — поверхности, имеющей форму сплюснутой сферы, которую можно получить, вращая эллипс вокруг одной из его осей, — на эллипсоиде существует много геодезических линий, не являющихся кратчайшими путями из всех возможных. Для нахождения упомянутых выше минимальных путей необходимо использовать дифференциальные уравнения. Чтобы найти минимальные значения, необходимо обратить внимание на точки, в которых производная равна нулю. Поверхность с наименьшей площадью должна удовлетворять определенному дифференциальному уравнению, а именно такому уравнению, которое выражает факт равенства нулю средней кривизны во всех возможных точках поверхности. Как только вы нашли требуемое дифференциальное уравнение в частных производных — вы сразу же получаете огромное количество информации о вашей задаче, поскольку за годы работы мы узнали многое об этих уравнениях.
«Впрочем, это совсем не означает, что мы занимаемся разграблением хорошо разработанной области и просто подбираем все, что плохо лежит. Наше сотрудничество — это скорее улица с двухсторонним движением, поскольку большой объем информации о поведении дифференциальных уравнений в частных производных был получен именно благодаря геометрии», — говорит Роберт Грин.[28] Чтобы увидеть то, что может получиться из соединения геометрического анализа с теорией минимальных поверхностей, давайте продолжим наш разговор о мыльных пленках. В XIX столетии бельгийский физик Жозеф Плато провел в этой области серию классических экспериментов, состоявших в погружении изогнутых различными способами кусков проволоки в сосуды с мыльной водой. Плато сделал вывод, что мыльные пленки, которые образовывались в ходе эксперимента, всегда имели минимальную поверхность. Более того, он предположил, что для любой замкнутой кривой всегда можно найти минимальную поверхность, контуром которой служила бы данная кривая. В большинстве случаях будет существовать только одна минимальная поверхность — и тогда задача будет иметь единственное решение. Но в некоторых случаях существует больше чем одна поверхность с минимальной площадью, и мы не знаем, сколько их будет всего. Гипотеза Плато оставалась недоказанной вплоть до 1930 года, когда Джесси Дуглас и Тибор Радо независимо друг от друга нашли решение этой проблемы. За свою работу в этой области Дуглас получил в 1936 году медаль Филдса, став первым обладателем этой награды.
Не всякая минимальная поверхность столь же проста, как мыльная пленка. Некоторые минимальные поверхности, над которыми ломают головы математики, намного сложнее и характеризуются многочисленными изгибами и складками, называемыми особенностями, или сингулярностями, — впрочем, многие из них встречаются в природе. Через несколько десятилетий после того, как Дуглас и Радо опубликовали свои работы, их разработки были продолжены стэнфордским математиком Робертом Оссерманом, автором блестящей книги по геометрии под названием «Поэзия Вселенной», который показал, что минимальные поверхности, фигурирующие в экспериментах, подобных экспериментам Плато, могут иметь только один тип особенностей, выглядящих как диски или плоскости, пересекающиеся по прямым линиям. Следующий шаг был совершен мной и Уильямом Миксом, профессором Массачусетского университета, с которым мы вместе учились в Беркли.
Мы рассмотрели ситуацию, в которой в роли минимальных поверхностей выступали так называемые вложенные диски, представляющие собой поверхности, которые на всем своем протяжении ни разу не изгибаются настолько, чтобы пересечь сами себя. Локально подобное пересечение выглядело бы как пересечение двух или нескольких плоскостей. В частности, нас заинтересовали выпуклые тела, то есть такие объекты, для которых отрезок прямой (или геодезическая линия), соединяющий любые две точки, всегда будет лежать на поверхности или внутри данного объекта. Таким образом, куб и сфера являются выпуклыми объектами, а седло — нет. Любые полые тела, обладающие выступами или имеющие форму полумесяца, не считаются выпуклыми, поскольку отрезки, соединяющие некоторые точки, обязательно будут выходить за пределы тела. Нами было доказано, что для любой замкнутой кривой, которую можно нарисовать на поверхности выпуклого тела, минимальная поверхность, опирающаяся на данную кривую, всегда будет вложенной, то есть не будет иметь тех складок или пересечений, которые упоминал Оссерман. Иными словами, в выпуклых пространствах все идет гладко и красиво. Таким образом мы разрешили важнейший вопрос геометрии, являвшийся предметом дискуссий на протяжении десятилетий. Впрочем, на этом история не закончилась. Для доказательства данной версии теоремы Плато мы с Миксом использовали некую лемму, называемую леммой Дена. (Леммой в геометрии называется вспомогательное утверждение, доказанное исключительно с целью доказательства в дальнейшем более общего положения.) Долгое время считалось, что эта лемма была доказана в 1910 году немецким математиком Максом Деном, однако по прошествии десяти лет в его доказательстве была обнаружена ошибка. Ден утверждал, что для случая трехмерного пространства диск, имеющий особенность, то есть самопересечение под углом или крест-накрест, можно заменить на другой диск, не имеющий каких-либо особенностей и опирающийся на тот же контур. В случае своей истинности это утверждение было бы весьма полезно, поскольку оно изрядно упростило бы работу геометров и топологов, предоставив им возможность заменять самопересекающиеся поверхности поверхностями, не имеющими подобных пересечений. Окончательное доказательство леммы Дена было найдено в 1956 году греческим математиком Христосом Папакирьякопулосом. Это событие было запечатлено в шуточном стишке Джона Мильнора:
Вероломнейшая лемма Дена
Пред топологом ставила стену. Но явился Христос Папакирьякопулос, Доказав эту лемму мгновенно. Мы с Миксом применили основанный на топологии подход Папакирьякопулоса к геометрической проблеме, затронутой в работах Плато. Затем мы пошли в обратном направлении и при помощи геометрии доказали более строгие варианты (по сравнению с теми, которые можно было получить исходя исключительно из топологии) как леммы Дена, так и относящейся к ней теоремы о петле. Прежде всего, мы показали возможность существования диска с наименьшей площадью во вложенном (и, следовательно, несамопересекающемся) пространстве. Однако в этом частном случае (называемом эквивариантным) необходимо было рассматривать не один диск, а множество симметричных пар — нечто подобное многочисленным отражениям в кривом зеркале. Случай, рассмотренный нами, предполагал конечное, хотя и произвольно большое число зеркальных отражений — или симметричных пар. Мы доказали, что диск минимальной площади ни при каких условиях не пересекается ни с самим собой, ни с дисками из его группы симметрии. Можно сказать, что диски, принадлежащие одной группе, «параллельны» друг другу за одним только исключением: в тех случаях, когда диски все же пересекаются, они должны полностью совпадать. Данная задача важна и сама по себе, однако еще большую важность она приобретает в связи со знаменитой топологической задачей, сформулированной в 1930 году и известной как гипотеза Смита. Эта гипотеза основана на размышлениях американского тополога Пола Смита о возможности вращения обычного трехмерного пространства вокруг бесконечно длинной вертикальной оси. Смиту было известно, что в том случае, когда ось является прямой линией, осуществить вращение вокруг нее трехмерного пространства довольно просто. Его гипотеза состояла в том, что подобное вращение становится невозможным при наличии на оси хотя бы одного узла. Вас, конечно, может удивить, что кого-то заинтересовал подобный вопрос, но это именно тот тип задач, которыми и занимаются топологи и геометры. Как заметил Кэмерон Гордон из Техасского университета по этому поводу: «Наша интуиция подсказывает нам, что это утверждение самоочевидно, поскольку возможно ли представить вращение пространства вокруг завязанной в узел линии?» Наше с Миксом доказательство леммы Дена и теоремы о петле стали двумя последними фрагментами, необходимыми для того, чтобы подтвердить гипотезу Смита. Окончательное подтверждение его гипотезы было получено путем объединения наших результатов с результатами Уильяма Тёрстона и Хаймана Басса. Упоминавшийся ранее Кэмерон Гордон свел воедино разрозненные фрагменты и получил безупречное доказательство, подтвердившее предположение Смита о невозможности вращения трехмерного пространства вокруг завязанной в узел оси. При этом, правда, оказалось, что — как бы смешно это ни прозвучало — это утверждение неверно для пространств более высокой размерности, и для них подобные вращения все-таки возможны.[29] Это доказательство представляет собой прекрасный пример совместной работы геометров и топологов над проблемой, которая потребовала бы от них много больше времени в том случае, если бы они пытались решить ее поодиночке. Кроме того, работая над упомянутой задачей, я впервые осознал, что рассуждения о минимальных поверхностях применимы к вопросам топологии. Наконец, доказательство гипотезы Смита подтвердило идею о возможности использования геометрии для решения проблем в области топологии и физики. Впрочем, пока мы говорили только о топологии и практически не затрагивали физику, оставив открытым вопрос о возможном использовании в ней геометрического анализа. На международной конференции по геометрии, проходившей в Стэнфорде в 1973 году, мое внимание впервые привлекла одна задача из области общей теории относительности, которой всего через несколько лет после этого суждено было стать подтверждением действенности методов геометрического анализа в физике. Я узнал об этой задаче от физика Чикагского университета Роберта Героха, затронувшего в своем докладе неподтвержденную на то время гипотезу о положительности массы или энергии. Согласно этой гипотезе, в изолированной физической системе общая масса и общая энергия должны быть положительны. В данном случае понятия массы и энергии эквивалентны, как было показано Эйнштейном в его знаменитом уравнении E = mc2. Поскольку Вселенную можно рассматривать как изолированную систему, гипотеза должна быть применима также и к Вселенной в целом. Вопрос о правомерности этого утверждения был столь важен, что на протяжении многих лет на всех основных конференциях по общей теории относительности ему отводили отдельную сессию. Причиной этого являлось непосредственное отношение гипотезы о положительности массы к вопросу о стабильности пространственно-временного континуума и, следовательно, непротиворечивости теории Эйнштейна самой по себе. Говоря простыми словами, пространственно-временной континуум может быть стабилен только в том случае, если его общая масса положительна. На Стэнфордской конференции Герох бросил вызов геометрам, призвав их заняться задачей, которую физики на тот момент собственными усилиями решить не могли. Его надежда на помощь основывалась не только на фундаментальной связи между геометрией и гравитацией, но также и на том факте, что утверждения о положительности плотности материи и о положительности средней кривизны в каждой точке пространства по сути эквивалентны. Герох был крайне заинтересован в окончательном разрешении этого вопроса. «Трудно было поверить, что эта гипотеза может быть ошибочной, но не менее трудно было доказать ее истинность», — заметил он впоследствии. Нельзя полагаться на интуицию, когда речь идет о подобных вещах, поскольку, добавил он, «она далеко не всегда ведет нас в правильном направлении».[30] Призыв Героха прочно засел у меня в голове, и через несколько лет после этого, занимаясь совершенно иным вопросом, мы с моим бывшим аспирантом Ричардом Шоном (теперь стэнфордским профессором) обратили внимание на то, что некоторые из разработанных нами в последнее время методов геометрического анализа могут быть использованы для доказательства гипотезы о положительности массы. Тогда, применив стратегию, обычную для решения крупных задач, мы попытались разбить задачу на небольшие фрагменты, с которыми можно было бы работать поодиночке. Перед тем как приступить к доказательству гипотезы в целом (которую для геометра тяжело даже осознать, не то что пытаться доказывать), мы сосредоточили наше внимание на нескольких частных случаях. Кроме того, мы не были до конца уверены, что эта гипотеза верна с чисто геометрической точки зрения, поскольку ее утверждения казались нам чересчур строгими. В своих попытках мы были не одиноки. Так, Михаил Громов, известный геометр, работающий в Нью-Йоркском университете и в Институте высших научных исследований (Франция), поделился с нами своим мнением о том, что, согласно его геометрической интуиции, общий случай этой гипотезы ошибочен, с чем были согласны и многие из его коллег. С другой стороны, большинство физиков были твердо уверены в истинности гипотезы, что они постоянно демонстрировали, год за годом поднимая вопрос о ней на всевозможных научных конференциях. Все это побудило нас более пристально взглянуть на эту идею, чтобы понять, что мы сможем сделать в этой области. Подход, который мы задействовали, был тесно связан с понятием о минимальных поверхностях. К доказательству гипотезы о положительности массы этот метод был применен впервые, поскольку никакой очевидной связи между этой задачей и минимальными поверхностями не существовало. Впрочем, Шон и я чувствовали, что мы выбрали правильный путь. В геометрии, как и в инженерии, для того чтобы решить задачу, необходимо прежде всего правильно подобрать инструменты для ее решения, хотя, после того как доказательство уже завершено, мы порой обнаруживаем и другие пути для его нахождения. Если бы локальная плотность материи оказалась положительной, как постулировалось в общей теории относительности, то геометрии пришлось бы считаться с этим фактом. Шон и я предположили, что именно минимальные поверхности являются наиболее подходящим инструментом для определения влияния локальной плотности материи на глобальную кривизну и топологию. Доказательство, найденное нами, сложно объяснить «на пальцах», Поскольку уравнения поля Эйнштейна, на которых основывается переход от физики к геометрическим построениям, имеют сложную нелинейную форму, которая трудна для интуитивного восприятия. По сути, свое доказательство мы начали от противного, предположив существование такого пространства, для которого масса не является положительной. Затем мы показали, что в пространстве, средняя кривизна которого неотрицательна, можно представить себе поверхность с минимальной площадью. Иными словами, можно представить себе такую поверхность, средняя кривизна которой равна нулю. Это было бы невозможно, если бы в роли пространства, в котором находится данная поверхность, выступала наша Вселенная, в которой плотность наблюдаемой материи положительна. Если считать общую теорию относительности истинной, то из положительности плотности материи будет следовать положительность кривизны. Хотя может показаться, что это рассуждение представляет собой подобие замкнутого круга, на самом деле это не так. В определенном пространстве, таком как наша Вселенная, плотность вещества может быть положительной даже при условии неположительности общей массы. Это обусловлено тем, что свой вклад в общую массу дает как вещество, так и гравитация. Даже если вклад вещества в общую массу будет положителен, как мы предположили в нашем доказательстве, общая масса может иметь отрицательное значение благодаря отрицательному вкладу со стороны гравитации.
Иными словами, представив себе пространство с неположительной общей массой, мы доказали необходимость существования в нем «мыльной пленки» с минимально возможной площадью, в то время как в пространстве, подобном нашей Вселенной, такая пленка невозможна, поскольку ее средняя кривизна всюду будет отлична от нуля. Итак, предположение о неположительности общей массы привело нас к противоречию, показав тем самым, что верно обратное — то есть и масса, и энергия положительны. Мы доказали это утверждение в 1979 году, поставив финальную точку в вопросе, на разрешение которого так уповал Герох. Это открытие стало только первой частью нашей работы, которую Шон и я разделили, на две части, поскольку проблема, предложенная Герохом, на самом деле представляла собой частный случай, который специалисты называют симметричным по отношению к обращению времени. Мы с Шоном рассмотрели этот случай в первую очередь, и утверждение, приведшее нас к противоречию, было основано на том же предположении. Для доказательства более общего случая нам необходимо было решить уравнение, предложенное студентом Героха П. С. Янгом. Янг не пытался решить это уравнение самостоятельно, поскольку полагал, что оно не имеет общего решения. Строго говоря, это действительно было так, но мы с Шоном обнаружили, что уравнение все же разрешимо при введении определенного допущения, обращающего его решение на границе черной дыры в бесконечность. При помощи этого упрощения мы получили возможность свести общий случай к уже доказанному нами частному. Важную роль в нашей работе сыграло руководство и мотивация со стороны физического сообщества. Несмотря на то что наше доказательство было основано на чистой математике — и прежде всего на нелинейных понятиях, с которыми едва ли близко знакомы большинство физиков, — именно их интуиция давала нам надежду на правильность нашего доказательства или, по крайней мере, на то, что затраченное нами время не прошло напрасно. Наша же с Шоном геометрическая интуиция позволила нам преуспеть в том, что не удалось сделать физикам. Однако доминирование геометров в этой области продолжалось недолго. Спустя два года физик Эдвард Виттен, из Института перспективных исследований в Принстоне, доказал гипотезу о положительности массы совершенно иным способом, основанным на линейных (в отличие от нелинейных, использованных нами) уравнениях, благодаря чему доказательство этой гипотезы стало намного понятнее для физиков. Оба доказательства подтвердили стабильность пространственно-временного континуума, что, фигурально выражаясь, позволило ученым вздохнуть с облегчением. «Если бы гипотеза о положительности массы оказалась ошибочной, это привело бы к драматическим последствиям для всей теоретической физики, поскольку означало бы то, что в общей теории относительности пространственно-временной континуум является нестабильным образованием», — объяснил нам Виттен.[31] Несмотря на то что вряд ли кто-то из обычных граждан лишился бы сна из-за этой проблемы, следствия, вытекающие из нее, относятся отнюдь не только к области теоретической физики, они затрагивают основы существования Вселенной как единого целого. Причиной этому является факт, что любая система стремится перейти на самый низкий из доступных энергетических уровней. Если энергия может принимать только положительные значения, то роль «пола», ниже которого не может упасть энергия системы, будет играть уровень с нулевой энергией. Однако если бы общая полная энергия могла быть отрицательной, то никакого энергетического «дна» в принципе бы не существовало. Вакуум, являющийся основным состоянием в общей теории относительности, бесконечно падал бы на все более и более низкие энергетические уровни. При этом пространственно-временной континуум непрерывно деградировал бы и распадался до тех пор, пока Вселенная как целое не прекратила бы свое существование. К нашему с вами счастью, это не так. Вселенная по-прежнему радует наш глаз, чем доказывает стабильность пространственно-временного континуума — по крайней мере, в настоящее время. О его возможном распаде я расскажу чуть позже. Несмотря на столь серьезные следствия, все же может возникнуть впечатление, что в этих двух доказательствах гипотезы о положительности массы не было особой необходимости. В конце концов, многие физики использовали предположение о том, что общая масса положительна, и ранее, когда гипотеза еще не была окончательно доказана. Можно ли считать, что появление доказательств что-то изменило? Что касается моего мнения по этому поводу, то я считаю, что между понятиями «знать что-то» и «предполагать что-то» существует огромная разница. В какой-то степени это разница между знанием и верой. В данном случае невозможно было с уверенностью говорить об истинности гипотезы до тех пор, пока не было получено строгое доказательство. Как сказал Виттен в своей статье 1981 года, представляя это доказательство, «то, что общая энергия всегда положительна, совсем не является очевидным фактом».[32] Помимо общефилософских выводов, следующих из доказательства гипотезы о положительности массы, эта — теперь уже — теорема дает некоторые подсказки по поводу природы массы как таковой, представляющей собой весьма эфемерное и на удивление неуловимое понятие в общей теории относительности. Частично эти сложности проистекают из нелинейности самой теории. Эта нелинейность означает то, что гравитация также является нелинейной. Благодаря этому гравитация может взаимодействовать сама с собой и в процессе взаимодействия порождать массу — тот ее вид, с которым особенно сложно иметь дело. В общей теории относительности масса может быть определена только как глобальное понятие. Иными словами, мы привыкли оперировать понятием массы системы как целого, представляя эту систему заключенной в гипотетический ящик, так, как если бы мы посмотрели на нее из очень сильно удаленной точки — по сути, из бесконечности. Что касается «локальной» массы — например, массы данного тела, — то, хотя это понятие и покажется проще для непрофессионала в нашей области, на сегодняшний день четкого определения оно не имеет. Понятие плотности в общей теории относительности также определено весьма нечетко. Вопрос о том, откуда берется масса и как дать ей определение, волновал меня на протяжении десятилетий и, когда позволяло время, я возвращался к нему совместно с коллегами, такими как Мелисса Лю и Мутао Ванг из Колумбии. Как мне сейчас кажется, нам удалось в конце концов конкретизировать понятие локальной массы, используя при этом идеи различных физиков и геометров, и, возможно даже, мы были недалеки от окончательного решения проблемы. Но мы не смогли бы даже начать думать над этой проблемой, если бы не имели в основе прочного фундамента в виде положительности общей массы. К тому же гипотеза о положительности массы привела нас с Шоном к доказательству другого утверждения из области общей теории относительности, касающегося так называемых черных дыр. Большинство людей, размышляя о столь причудливых астрофизических объектах, как черные дыры, едва ли как-то связывают их с геометрическими понятиями. Тем не менее геометрия достаточно многое может сказать о черных дырах, и по сути именно ей мы обязаны самой возможностью предсказания существования таких объектов до их обнаружения астрономическими методами. Это предсказание стало триумфом применения геометрического подхода к общей теории относительности. В 1960-х годах Стивен Хокинг и Роджер Пенроуз при помощи геометрических методов, точнее, той особой разновидности геометрии, которая рассматривается в нашей книге, и законов общей теории относительности доказали, что любая ловушечная поверхность, то есть чрезвычайно искривленная поверхность, которую не может покинуть даже свет, обязана в конце концов эволюционировать в сингулярность того типа, который, как полагают, находится в центре черной дыры — в том месте, где кривизна пространства-времени стремится к бесконечности. Оказавшись в черной дыре, можно обнаружить, что при движении к центру кривизна будет неуклонно возрастать. Предела этому возрастанию попросту не существует — кривизна будет возрастать вплоть до самого центра, где ее величина станет равной бесконечности. С кривизной вообще связано много удивительных вещей. Прогуливаясь по поверхности Земли, имеющей огромный (порядка шести тысяч километров), по сравнению с нашим ростом (как правило, не большим двух метров), радиус, мы не ощущаем ее кривизны. Однако если бы мы решили совершить прогулку по планете с радиусом 5-10 метров, такой как планета Маленького Принца у Антуана де Сент-Экзюпери, то пренебречь ее кривизной мы бы уже не смогли.
Поскольку кривизна сферы обратно пропорциональна квадрату радиуса, возрастание радиуса до бесконечности приводит к уменьшению кривизны до нуля. И напротив, при стремлении радиуса к нулю кривизна неуклонно возрастает и стремится к бесконечности. Представим себе вспышку света, произошедшую одновременно во всех точках поверхности обычной двухмерной сферы в трехмерном пространстве. Свет будет двигаться вдоль радиуса в двух направлениях — внутрь и наружу. Для лучей света, направленных к центру сферы, совокупность точек, до которых доходит свет в определенный момент времени, будет представлять собой поверхность, площадь которой быстро уменьшается и в пределе стремится к нулю, тогда как площадь подобной поверхности для лучей, распространяющихся вовне, со временем будет неуклонно возрастать. Ловушечная поверхность отличается от обычной сферы тем, что описанная выше площадь уменьшается вне зависимости от направления движения.[33] Какое направление ни выберешь — из ловушки не выбраться. Иными словами, пути наружу в данном случае нет. Как такое может быть возможно? Отчасти это обусловлено тем, что ловушечная поверхность по определению должна обладать такими свойствами. Но объяснение также кроется и в том, что для ловушечных поверхностей так называемая средняя положительная кривизна имеет экстремум. Под действием столь заметной кривизны даже идущие наружу лучи света будут вынуждены изменить свое направление на противоположное, как если бы крыша и стены начали надвигаться на них, и в результате сойтись в центре. «Если площадь поверхности изначально уменьшается, то она будет продолжать уменьшаться, поскольку здесь работает эффект фокусировки, — объяснил это явление мой коллега Шон. — Можно представить себе расходящиеся круги на глобусе с центром на Северном полюсе, которые, благодаря положительности кривизны сферы, сходятся в точку на Южном полюсе. Подобный эффект фокусировки дает положительная кривизна».[34] Пенроуз и Хокинг доказали, что, однажды возникнув, ловушечные поверхности обязательно вырождаются в объекты, которые свет не может покинуть, — так называемые черные дыры. Но как возникают ловушечные поверхности? До того как мы с Шоном начали свою работу над этим вопросом, было принято считать, что единственным условием для формирования черной дыры является достаточно высокая плотность материи в некоторой области пространства, — впрочем, аргументы были весьма расплывчаты и показывали скорее нежелание вникать в суть проблемы. Никому до нас не удавалось сформулировать утверждение о природе ловушечных поверхностей в ясном и строгом виде. Именно эту проблему мы с Шоном избрали своей целью, и снова в дело пошел метод минимальных поверхностей, столь детально разработанный нами во время доказательства теоремы о положительности массы. Нам были интересны точные условия, при которых может возникнуть ловушечная поверхность, и в 1979 году мы доказали, что для достижения кривизны пространства, достаточной для ее формирования, плотность материи в данной области должна в два раза превышать плотность нейтронных звезд, которая, в свою очередь, в 100 триллионов раз превышает плотность воды. Наше доказательство совместно с исследованиями Хокинга и Пенроуза позволили понять те обстоятельства, при которых должны возникать черные дыры. Более конкретно, мы показали, что небесный объект, имеющий плотность материи больше, чем нейтронная звезда, должен коллапсировать непосредственно в черную дыру, а не в какое-либо иное промежуточное состояние. Это открытие было основано на чистой математике и относилось к объектам, существование которых еще предстояло установить в будущем. Несколько лет назад Деметриос Христодулу из Швейцарской высшей технической школы Цюриха открыл иной механизм формирования ловушечных поверхностей путем гравитационного коллапса.[35] Недавно Феликс Финстер, Ники Камран, Джоэль Смоллер и я рассмотрели вопрос о стабильности вращающихся черных дыр по отношению к внешним возмущениям. Иными словами, можно ли ожидать, что от какого-либо «удара» по вращающейся черной дыре она развалится на две, начнет беспорядочно вращаться или поломается еще каким-нибудь образом? Несмотря на все наши труды, на сегодняшний день эту работу нельзя считать законченной, и мы пока ничего не можем сказать по поводу всех возможных разновидностей «ударов», способных дестабилизировать систему. Два года спустя Финстер, Камран, Смоллер и я представили на всеобщее обозрение то, что, по нашему мнению, представляло собой первое строгое математическое доказательство давней проблемы, сформулированной Роджером Пенроузом. В 1969 году Пенроуз предложил механизм высвобождения энергии из вращающейся черной дыры при уменьшении ее момента импульса. Этот сценарий предусматривал распад падающего в черную дыру тела на два фрагмента, один из которых пересекает горизонт событий и затягивается в черную дыру, а второй отбрасывается прочь от дыры с энергией, большей, чем энергия первоначального тела. Вместо того чтобы рассматривать материальную частицу, мы с коллегами сосредоточили внимание на ее аналоге — а именно на волне, распространяющейся по направлению к черной дыре, доказав, что со стороны математики против так называемого процесса Пенроуза возражений нет. При обсуждении нашего доказательства на Гарвардской конференции по геометрическому анализу, проходившей в 2008 году, Смоллер пошутил, что однажды при помощи этого механизма можно будет навсегда разрешить проблему мирового энергетического кризиса. Впрочем, несмотря на вклад геометров в разрешение загадок черных дыр, изучение этих объектов в настоящее время находится в большей степени в руках астрофизиков, наблюдающих явления, происходящие вблизи самого края горизонта событий — границы, за пределами которой никакие наблюдения невозможны, поскольку ничто, включая свет, не способно вернуться «с той стороны». Тем не менее если бы не работы теоретиков, таких как Хокинг, Пенроуз, Джон Уиллер, Кип Торн и другие, вряд ли астрономы сосредоточили бы свое внимание на поисках именно этих объектов. Описанные мной достижения имеют огромное значение, но я не хочу, чтобы у вас возникло впечатление, что возможности геометрического анализа на этом исчерпываются. Я сознательно ограничился только теми результатами, которые мне известны лучше всего, в получении которых я принимал непосредственное участие. В то же время данная область математики является намного более обширной, представляя собой плод усилий более чем сотни первоклассных ученых всего мира, и описанные мной задачи представляют лишь небольшой фрагмент общей картины. Кроме этого на протяжении большей части этой главы, темой которой является геометрический анализ, мы ни разу не упомянули некоторые из крупнейших достижений нашей дисциплины. Объять необъятное я не в состоянии; один лишь перечень успехов геометрического анализа, который я составил в 2006 году, занимает семьдесят пять страниц плотного текста, поэтому мы рассмотрим только те три из них, которые я считаю наиболее важными. Первое из этих ключевых достижений лежит в области четырехмерной топологии. Основная задача тополога не сильно отличается от основной задачи таксономиста: классифицировать все возможные типы пространств или многообразий, допустимых для данной размерности. Многообразием называется пространство или поверхность любой размерности, поэтому мы можем использовать эти термины как синонимы. В следующей главе мы рассмотрим многообразия более подробно. Топологи пытаются свалить в одну кучу различные объекты, имеющие одинаковую базовую структуру, даже если те совершенно не похожи внешне и даже различаются в отдельных деталях. Так, двухмерные поверхности — при условии их компактности, то есть замкнутости и ограниченности, и ориентируемости (наличии внешней и внутренней стороны) — можно классифицировать по количеству имеющихся дырок: тороидальные поверхности имеют по крайней мере одну дырку, тогда как топологическими сферами называются поверхности, которые дырок не имеют вовсе. Если число дырок для двух подобных поверхностей одинаково, то для тополога они эквивалентны, несмотря на всю разницу в их внешнем виде. Так, и чашка кофе и сушка, которую в нее обмакнули, являются торами первого рода. Тем же, кто предпочитает сушки с молоком, интересно будет узнать, что стакан, из которого они пьют, топологически эквивалентен сфере — его можно получить, протолкнув северный полюс в направлении южного и чуть подкорректировав форму полученного объекта. Если двухмерный случай был досконально изучен более столетия назад, то ситуация для более высоких размерностей выглядела намного сложнее. «Удивительно, что классификация поверхностей становится проще для пяти измерений и выше, — заметил математик Уорикского университета Джон Д. С. Джонс. — Сложнее всего работать с тремя и четырьмя измерениями».[36] К несчастью, именно случай трех и четырех измерений является важнейшим в физике. Уильям Тёрстон в 1982 году разработал схему классификации трехмерных поверхностей, разделив их на восемь основных типов геометрии. Его гипотеза, известная как гипотеза геометризации Тёрстона, была доказана два десятилетия спустя, о чем вкратце будет рассказано далее. Атака на четвертое измерение началась примерно в то же время, когда Тёрстон высказал свое смелое предположение. Четырехмерные пространства тяжело не только представлять, но и описывать математически. Чтобы наглядно представить себе четырехмерный объект, вообразите трехмерный объект, форма которого изменяется со временем, например пульсирующий баскетбольный мяч, который периодически сжимается и вновь восстанавливает прежнюю форму. Детальная геометрия таких объектов весьма запутанна, если не сказать больше, однако она является ключом к пониманию того четырехмерного пространства-времени, в котором мы живем. Некоторые из ключей к разгадке геометрии четырехмерных объектов были найдены в 1982 году, когда Саймон Дональдсон, в то время аспирант Оксфордского университета второго года обучения, опубликовал первую из нескольких статей, посвященных структуре четырехмерного пространства. Чтобы открыть окно в четвертое измерение, Дональдсон воспользовался нелинейными уравнениями в частных производных, разработанными в 1950 году физиками Чжэньнином Янгом и Робертом Миллсом. Уравнения Янга-Миллса, объединяющие сильное взаимодействие, ответственное за поведение кварков и глюонов в атомном ядре, со слабым, связанным с радиоактивным распадом, и электромагнитным — взаимодействием между заряженными частицами — работают именно в четырехмерном пространстве. Вместо того чтобы решать эти уравнения «в лоб», для чего необходимо было бы вначале установить геометрические и топологические особенности соответствующего пространства, Дональдсон подошел к проблеме с другой стороны: он рассудил, что решения уравнений должны содержать в себе информацию о том четырехмерном пространстве, в котором они работают. Точнее, данные решения должны привести к установлению некоторых ключевых величин, характеризующих соответствующие им пространства, — математики называют эти величины инвариантами, — которые впоследствии используются для определения тождественности или различности этих пространств. Работа Дональдсона не только пролила свет на разыскиваемые им инварианты, но также позволила обнаружить весьма неожиданный и загадочный факт, а именно существование неизвестного прежде класса «экзотических» пространств, возможных только в четырех измерениях. Чтобы объяснить, что в данном контексте значит слово экзотический, необходимо вначале затронуть вопрос о том, какие две поверхности или многообразия можно считать идентичными. У математиков существуют различные методы сравнения многообразий. Первый из них связан с представлением о топологической эквивалентности. Проиллюстрировать этот метод можно при помощи примера со сдутым и накачанным мячом. Два объекта называют топологически идентичными, или гомеоморфными, если один из них можно преобразовать в другой исключительно путем изгиба, сжатия или растяжения, не прибегая к разрезам. Подобный переход от одного многообразия к другому носит название непрерывного отображения. Это отображение является взаимно-однозначным, то есть каждая точка одной поверхности соответствует строго определенной точке другой поверхности. Более того, точки, находившиеся в непосредственной близости друг от друга на первой поверхности, после подобного отображения по-прежнему останутся рядом. Второй метод сравнения многообразий характеризуется несколько большей утонченностью и строгостью. В этом случае вопрос состоит в том, возможно ли перейти от одного многообразия к другому, не нарушая его гладкости, то есть не вводя так называемые сингулярности, например острые углы или пики на поверхности. Многообразия, эквивалентные в этом смысле, носят название диффеоморфных. Чтобы два многообразия можно было считать диффеоморфными, функция, преобразующая одно многообразие в другое — или, иными словами, переводящая набор координат одного пространства в набор координат второго, — должна быть гладкой — дифференцируемой, то есть иметь производную во всех точках пространства в любой момент времени. График такой функции также должен быть гладким — не иметь никаких «зазубрин» во всех смыслах этого слова — наличие на нем обрывов, участков скачкообразного роста или падения привело бы к тому, что в определенных точках само понятие производной потеряло бы смысл. В качестве примера рассмотрим сферу, помещенную внутрь эллипсоида — поверхности, имеющей форму дыни, — так, что их центры совпадают. Лучи, проведенные из их общего центра во всех возможных направлениях, соединят точки на сфере с точками на эллипсоиде. Подобная операция может быть проделана для любой точки эллипсоида или сферы. Отображение в данном случае не только является непрерывным и однозначным, но оно также не нарушает гладкости отображаемой поверхности. Функция, связывающая две эти поверхности, также не имеет никаких особенностей — это просто прямая линия без зигзагов, резких поворотов и вообще чего-либо необычного. Таким образом, два рассматриваемых объекта — сферу и эллипсоид — можно назвать как гомеоморфными, так и диффеоморфными.
Противоположным примером является так называемая экзотическая сфера. Экзотической сферой называется гладкое во всех точках семимерное многообразие, которое, тем не менее, невозможно без нарушения гладкости преобразовать в обычную круглую семимерную сферу даже при соблюдении условия непрерывности преобразования. Таким образом, подобные поверхности являются гомеоморфными, но не диффеоморфными. Джон Мильнор, уже упоминавшийся в данной главе, получил медаль Филдса во многом благодаря установлению им факта существования экзотических пространств. До открытия Мильнора многие сомневались в существовании таких пространств, поэтому их и назвали экзотическими. Плоское евклидово пространство для случая двух измерений является простейшим из всех пространств, которые можно себе представить, — это плоская поверхность, подобная крышке стола, которая простирается бесконечно во всех возможных направлениях. На вопрос, будет ли двухмерный диск, множество точек которого является подмножеством точек плоскости, гомеоморфным и диффеоморфным данной плоскости, можно ответить — да, будет. Можно представить себе толпу людей, стоящих на плоскости, каждый из которых берет в руку краешек диска и идет с ним в направлении от центра диска. Как только они достигнут бесконечности, диск точно, непрерывно и однозначно совпадет с плоскостью. Таким образом, эти объекты идентичны с точки зрения тополога. Очевидно и то, что подобный процесс растягивания диска в радиальном направлении можно проделать без нарушения его гладкости. Все вышесказанное сохраняет свою силу для трех и любого другого числа измерений за исключением случая четырех. В четырехмерном пространстве многообразия могут быть гомеоморфны плоскости или плоскому евклидовому пространству, не будучи при этом диффеоморфны ему. По сути, существует бесконечное множество четырехмерных многообразий, гомеоморфных, но не диффеоморфных четырехмерному евклидовому пространству, носящих общее название ℝ4 (ℝ — от «real» — означает, что элементами пространства являются действительные числа, в противоположность комплексному четырехмерному пространству). Четырехмерное пространство преподносит нам множество особенностей и загадок. Так, к примеру, в пространственно-временном континууме, содержащем 3+1 измерение (три пространственных и одно временное), по словам Дональдсона, «электрическое и магнитное поля будут идентичны». «Но для другого числа измерений с геометрической точки зрения это будут два совершенно разных объекта. Одно из них представляет собой тензор и описывается при помощи матрицы, тогда как другое — вектор, и сравнивать их невозможно. Только в четырех измерениях и то и другое поле будет описываться векторами. Симметрия, имеющая место в данном случае, для иного числа измерений будет отсутствовать».[37] Дональдсона, по его словам, восхищает тот факт, что с фундаментальной точки зрения невозможно точно указать, что именно выделяет случай четырех измерений среди всех остальных. До того как вышла его работа, о «гладкой эквивалентности» (диффеоморфизме) не было известно практически ничего, хотя благодаря математику Майклу Фриману (ранее работавшему в Калифорнийском университете, Сан-Диего) уже существовали определенные наработки в области топологической эквивалентности (гомеоморфизма). В свою очередь Фриман классифицировал четырехмерные многообразия с топологической точки зрения, основываясь на более ранней работе Эндрю Кассона, в настоящее время работающего в Йельском университете. Дональдсон привнес в топологию целый ряд свежих идей, использование которых на практике позволило решить сложнейшую задачу классификации гладких (диффеоморфных) четырехмерных многообразий, открыв, фигурально выражаясь, закрытую прежде дверь. До него подобные многообразия были темным лесом. И хотя четырехмерные многообразия еще содержат в себе много загадок, по крайней мере, вопрос, с чего начинать их исследование, уже не стоит. При этом, однако, метод Дональдсона оказался чрезвычайно труден для практического применения. «Мы работали как лошади, пытаясь этим путем извлечь хоть какую-то информацию!» — рассказал гарвардский геометр Клиффорд Таубс.[38] В 1994 году Эдвард Виттен и его коллега — физик Натан Зайберг обнаружили намного более простой метод исследования геометрии четырехмерных пространств, несмотря на то что их подход основывался не собственно на геометрии, как метод Дональдсона, а на одной из теорий из области физики элементарных частиц — так называемой теории суперсимметрии. «В новом уравнении содержится вся информация, которая содержалась и в старом, — прокомментировал это открытие Таубс. — Разница лишь в том, что извлечь эту информацию из нового уравнения в тысячу раз проще».[39] Таубс, как и многие другие, использовал подход Зайберга-Виттена для расширения наших знаний о геометрических структурах в четырехмерном пространстве, понимание которых на сегодняшний день остается весьма условным, но тем не менее очень важным для ответа на вопрос о природе пространства-времени в общей теории относительности. Виттен показал, что для большей части четырехмерных многообразий число решений уравнения Зайберга-Виттена определяется исключительно топологией соответствующего многообразия. После этого Таубс доказал теорему, согласно которой количество решений этих уравнений, предопределенное топологией многообразия, совпадает с числом подпространств или кривых определенного типа (семейства), которые можно поместить в данном многообразии. Определив количество кривых конкретного типа, соответствующих данному многообразию, можно как определить его геометрию, так и получить о нем много другой важной информации. Таким образом, справедливым будет заметить, что теорема Таубса позволила значительно продвинуться в области исследования подобных пространств. Взглянув на историю исследований четырехмерных пространств, начиная с работ физиков Янга и Миллса в 1950-х, можно обнаружить, что в своем развитии эта теория проходила этапы, на которых физика оказывала влияние на математику, плавно переходящие в этапы, на которых математика влияла на физику. Несмотря на свое физическое происхождение, теория Янга-Миллса возникла не без участия геометрии, которая помогла лучше понять природу сил, объединяющих элементарные частицы в единое целое. Подойдя к данной проблеме с другой стороны, геометр Дональдсон использовал теорию Янга-Миллса для того, чтобы понять топологию и геометрию четырехмерных пространств. Тот же взаимовыгодный обмен между математикой и физикой был продолжен в работе физиков Зайберга и Виттена и в последовавших за ними работах. Таубс так подвел итог этой бурной истории: «Однажды на Землю прилетел марсианин, дал нам уравнения Янга-Миллса и улетел. Мы изучали их, и в конце концов возникла теория Дональдсона. Много лет спустя марсианин прилетел вновь и дал нам уравнения Зайберга-Виттена»[40]. Хотя я и не могу поручиться за достоверность истории Таубса, пожалуй, из всех объяснений, которые я когда-либо слышал, это — наиболее правдоподобное… Второе важнейшее достижение геометрического анализа — и многие поставили бы именно его на первое место по важности — относится к доказательству знаменитой гипотезы, сформулированной в 1904 году Анри Пуанкаре и на протяжении более столетия остававшейся важнейшей проблемой трехмерной топологии. Основной причиной, по которой я считаю эту гипотезу выдающейся, является возможность сформулировать ее в виде одного простого утверждения, которое, тем не менее, держало в напряжении все математическое сообщество на протяжении сотни лет. В двух словах, эта гипотеза утверждает, что компактное трехмерное пространство топологически эквивалентно сфере, если любая петля, которую можно построить в данном пространстве, может быть стянута в точку без нарушения при этом целостности петли или пространства. Как уже было сказано ранее в данной главе, пространство, удовлетворяющее этому условию, содержит тривиальную фундаментальную группу. Гипотеза Пуанкаре звучит весьма просто, но на самом деле она далеко не очевидна. Рассмотрим двухмерный аналог этой задачи, не обращая внимания на то, что в действительности проблема сформулирована для трех измерений (и решить ее в этом случае намного сложнее). Представим себе сферу, например глобус, по экватору которого проходит резинка. Теперь легонько подтолкнем эту ленту в направлении северного полюса так, чтобы при этом она не переставала касаться поверхности. Если резиновая лента достаточно эластична, то, достигнув полюса, она фактически стянется в одну точку. В случае тора ситуация будет иная. Представим себе, что резиновая лента проходит через дырку тора и выходит с противоположной стороны. В данном случае стянуть резиновую ленту в одну точку, не разрезая при этом тор, невозможно. Резиновую ленту, идущую вокруг внешней поверхности тора, можно переместить в его верхнюю часть и оттуда уже спустить на внутреннюю поверхность. Однако пока лента находится на поверхности тора, стянуть ее в точку не удастся. По этой причине для тополога сфера имеет фундаментальное отличие от тора или любого другого многообразия, имеющего одну или несколько дырок. Гипотеза Пуанкаре, по сути, представляет собой вопрос, чем в действительности является топологическая сфера. Прежде чем перейти к доказательству, я хотел бы вернуться на несколько десятилетий назад, в 1979 год, когда я еще работал в Институте перспективных исследований. В тот год я пригласил в Принстон более дюжины исследователей со всего мира, работающих в области геометрического анализа, чтобы вместе с ними попытаться заложить основы этой новой дисциплины. Мною было отобрано 120 важнейших геометрических вопросов, почти половина из которых в настоящее время полностью решена. Гипотеза Пуанкаре в этот список не входила. Причиной тому, с одной стороны, было отсутствие необходимости привлекать внимание к задаче, которая и без того являлась одной из известнейших в математике. С другой стороны, я искал задачи, имеющие более узкую формулировку, — такие, на которые можно найти однозначный ответ, — причем, по возможности, в обозримое время. И хотя нам порой приходилось бороться за то, чтобы узнать что-то новое, мы достигли заметного прогресса именно на пути решения подобных задач; это как раз то, что стимулирует математиков к работе сильнее, чем что-либо другое. В то время, однако, никто не знал, что делать с гипотезой Пуанкаре. Одним из тех, кто не принимал участия в наших дискуссиях, был математик Ричард Гамильтон, работавший тогда в Корнеллском университете и впоследствии осевший на математическом факультете Колумбийского университета. В то время он как раз приступал к выполнению амбициозного проекта, посвященного поиску методов преобразования сложной и не обладающей гладкостью метрики в более гладкую. Несмотря на все упования Гамильтона, эти разработки не принесли столь быстрого успеха, на который он рассчитывал. Его интересовала чрезвычайно сложная система уравнений, относящаяся к вопросу о потоке Риччи — одном из видов геометрического потока, которые уже упоминались ранее. По сути дела, геометрический поток представляет собой метод, позволяющий разгладить выпуклости и прочие неровности на неоднородной поверхности, придавая таким образом поверхностям более однородную кривизну и выявляя фундаментальные формы, лежащие в их основе. Идеи Гамильтона не вошли в мой список из 120 основных задач хотя бы потому, что в то время он еще ничего не опубликовал по этой теме. Он скорее забавлялся ими, чем пытался найти решение. Возможность познакомиться с его достижениями на 1979 год я получил, выступая с докладом в Корнеллском университете. Гамильтон тогда не считал свои уравнения применимыми к доказательству гипотезы Пуанкаре — он рассматривал их просто как задачу, небезынтересную для исследователя. Впервые столкнувшись с подобными уравнениями, я также занял весьма скептическую позицию по поводу их применимости… Уравнения выглядели слишком сложными, чтобы их можно было использовать на практике. Однако работа, проделанная Гамильтоном после этого, позволила ему опубликовать в 1983 году статью, посвященную решению уравнений, которые сейчас носят название гамильтоновых. В этой статье Гамильтон доказал особый случай гипотезы Пуанкаре, а именно тот случай, при котором кривизна Риччи положительна. О кривизне Риччи, тесно связанной с физикой, более подробно будет рассказано в следующей главе. Мой изначальный скептицизм побудил меня досконально исследовать статью Гамильтона, вчитываясь буквально в каждую строку, прежде чем я окончательно согласился с ней. При этом доказательство Гамильтона столь захватило меня, что по прочтении я немедленно поручил трем моим аспирантам из Принстона начать работу над его уравнениями. Тогда же я посоветовал Гамильтону попытаться воспользоваться своим подходом для доказательства гипотезы геометризации Тёрстона, относящейся к классификации трехмерных многообразий по восьми типам геометрий, расширенная форма которой включает в себя и общее доказательство гипотезы Пуанкаре. К сожалению, в то время я был мало осведомлен о каких-либо других методах, которые бы пригодились для дальнейшей работы над этим вопросом. Как ни удивительно, Гамильтон взялся за эту задачу с огромной энергией, постепенно продвигаясь в области исследований потока Риччи на протяжении следующих двадцати лет, работая в основном самостоятельно, хотя и находясь в тесном контакте со мной и моими студентами. Контакты между нами заметно оживились в 1984 году, когда мы с Гамильтоном вместе поступили на работу в Калифорнийский университет в Сан-Диего, где заняли смежные офисы. Посещение его семинаров по потокам Риччи было обязательным для всех моих студентов. Сотрудничество с Гамильтоном позволило нам узнать много нового, впрочем, я надеюсь, что он также перенял кое-что и от меня. Переехав в Гарвард в 1987 году, я больше всего жалел об утраченной возможности работать в тесном контакте с Гамильтоном. Не обращая внимания на окружающих, Гамильтон с неколебимой решительностью занимался решением своей задачи. Помимо прочего им было опубликовано полдюжины важнейших статей — порядка девяноста страниц каждая, — и в конце концов, ни один из его аргументов не оказался бесполезным. Все они пригодились при восхождении на гору Пуанкаре. Так, например, Гамильтон показал, что все без исключения геометрические объекты, имеющие округлую форму, могут быть преобразованы в сферы при помощи потока Риччи — в полном соответствии с идеями Пуанкаре. Однако, как им было установлено, при деформации более сложных объектов будут неминуемо возникать выступы, складки и прочие сингулярности. Возможности обойти эти сингулярности не было, поэтому столь важным являлся вопрос, с какими именно сингулярностями можно столкнуться в данном процессе. Полный список всевозможных особенностей, которые могут возникнуть при деформации, был сформулирован Гамильтоном на основании моей совместной работы с Питером Ли, к которой я привлек его внимание за несколько лет до этого, — впрочем, Гамильтон весьма впечатляюще обобщил наши результаты. Мой личный вклад в описываемые исследования восходит к 1973 году, когда я приступил к использованию нового метода, разработанного мной для гармонического анализа — области математики, насчитывающей несколько сотен лет и используемой для описания равновесных ситуаций. Созданный мной метод был основан на так называемом принципе максимума, который предполагает рассмотрение худшего из всех возможных сценариев. Представим, к примеру, что нам требуется доказать неравенство А < 0. Для этого нужно сформулировать вопрос так: «Какое максимальное значение может принимать А?» Если рассмотреть наихудший случай, то есть взять наибольшее из возможных значений А и его величина все равно останется меньше нуля, то этим мы и подтвердим истинность исходного утверждения. На этом работу по доказательству можно считать законченной и насладиться заслуженным отдыхом. Я, иногда работая сам, иногда — совместно с Ш. Ю. Ченгом, моим бывшим однокурсником из Китайского университета Гонконга, применил этот принцип к огромному количеству нелинейных проблем. Работа включала в себя исследование уравнений, повсеместно возникающих в геометрии и физике и носящих в математике название эллиптических. Хотя подобные задачи, как правило, чрезвычайно сложны, в них отсутствует зависимость от времени, и поэтому их можно рассматривать как стационарные, что заметно упрощает решение. В 1978 году мы с Питером Ли рассмотрели более сложную, зависящую от времени — динамическую ситуацию. В частности, мы исследовали уравнения, описывающие процессы распространения тепла через тело или многообразие. Мы рассмотрели случай, в котором одна из переменных, например энтропия — величина, характеризующая беспорядок системы, — изменяется во времени. Наиболее известным нашим вкладом в эту область стало неравенство Ли-Яу, описывающее с математической точки зрения процесс изменения теплового потока или другой аналогичной ему переменной во времени. Гамильтон и Перельман, в свою очередь, рассмотрели изменение во времени не теплового потока, как мы, а именно энтропии, отвечающей за беспорядок в системе. Соотношение Ли-Яу называется «неравенством», поскольку значение некой величины — в данном случае значение теплового потока или энтропии — в конкретной точке в определенный момент времени больше или меньше значения теплового потока или энтропии в той же точке в другой момент времени. Наш подход дал в руки ученым количественный метод исследования процессов развития сингулярностей в нелинейных системах путем отслеживания расстояния между двумя точками с течением времени. Когда две точки сближаются настолько, что расстояние между ними становится равным нулю, вы получаете сингулярность. И сингулярность, и понимание этих сингулярностей является ключевым моментом для исследования процессов распространения тепла в целом. В частности, наш метод позволил подобраться к сингулярности настолько близко, насколько только это возможно, показывая, что происходило непосредственно перед столкновением — например, какова была скорость сближения точек. Это напоминает попытку реконструкции событий, предшествовавших автомобильной аварии. Для того чтобы увидеть сингулярность крупным планом — или разрешить ее, как принято говорить в математике, — нами был изобретен особый вид «увеличительного стекла». Этот прибор мы используем для того, чтобы получше рассмотреть ту область, в которой пространство сходится в особую точку. Затем мы увеличиваем выбранную область, сглаживая при этом все складки и неровности. Этот процесс повторяется не один или два, но бесконечное число раз. Чтобы увидеть полную картину, мы растягиваем не только пространство, но и время — то есть замедляем его. На следующем этапе происходит сравнение полученного описания точки сингулярности, соответствующее бесконечно большому числу увеличений, с описанием системы до столкновения точек. Неравенство Ли-Яу позволяет непосредственно сопоставить то, что было до столкновения, с тем, что стало после. Гамильтон воспользовался нашим подходом, чтобы более пристально взглянуть на поток Риччи, исследуя структуру сингулярностей, которые могут возникать в процессе преобразования. Введение неравенства Ли-Яу в модель потока Риччи оказалось сложной задачей, на которую Гамильтону потребовалось почти пять лет, поскольку те уравнения, с которыми он имел дело, характеризовались куда большей нелинейностью — и, следовательно, куда большей сложностью, чем наши. Один из подходов Гамильтона заключался в исследовании особого класса решений, являющихся стационарными в определенной системе координат. Выбор подходящей системы координат позволяет упростить многие задачи — например, при рассмотрении движения людей, находящихся на вращающейся карусели, оптимальным будет выбор системы координат, вращающейся с той же скоростью, что и карусель. Путем отбора стационарных решений, являющихся более простыми для понимания, Гамильтон разработал оптимальный метод введения методов оценки Ли-Яу в свои уравнения. Это, в свою очередь, позволило ему уяснить динамику потока Риччи — то есть процессов движения и развития объектов. В частности, Гамильтон был очень заинтересован исследованием процесса порождения сингулярностей в результате сложного движения в пространственно-временном континууме. В конечном итоге ему удалось описать структуру всех возможных сингулярностей, которые могли бы возникнуть в процессе преобразования, хотя он и не мог доказать, что все эти сингулярности обязательно возникнут. Из тех сингулярностей, которые удалось идентифицировать Гамильтону, все, кроме одной, были устранимы — удалить их можно было при помощи методов топологической «хирургии», методики, разработанной и широко применяемой в четырехмерном пространстве. «Хирургические» процедуры весьма сложны, но при удачной реализации дают возможность убедиться в эквивалентности исследуемого пространства сфере, что и требовал Пуанкаре. Однако существовал еще один тип сингулярностей, представляющих собой сигарообразные выступы, от которого Гамильтон подобным образом избавиться не сумел. Если бы он смог показать, что «сигары» в процессе трансформации многообразий не возникают, проблема сингулярностей стала бы намного яснее, что позволило бы сделать огромный шаг в направлении доказательства гипотез Пуанкаре и Тёрстона. Ключевым моментом, согласно идее Гамильтона, стало применение оценок Ли-Яу в случае любой, не обязательно положительной, кривизны многообразия. Он немедленно привлек меня к решению этой задачи, оказавшейся на удивление трудной. Однако нам все же удалось достичь некоторых результатов, и окончание всей работы казалось только вопросом времени. Мы были весьма удивлены, когда в ноябре 2002 года в Интернете появилась первая из трех статей под авторством санкт-петербургского математика Григория Перельмана, посвященная геометрическим применениям методов потока Риччи. Менее чем через год на том же сайте были выложены вторая и третья статьи. В этих статьях Перельман задался целью «прояснить некоторые детали программы Гамильтона» и «дать краткий набросок доказательства гипотезы геометризации».[41] Он, так же как и Гамильтон, использовал неравенства Ли-Яу для контроля над поведением сингулярностей, хотя и ввел их несколько иным образом, добавив помимо этого много собственных нововведений. В определенном смысле статьи Перельмана появились буквально из ниоткуда. Никто не знал, что Перельман когда-либо занимался проблемами, связанными с потоком Риччи, поскольку он был известен благодаря своим успехам в совершенно иной области математики — так называемой метрической геометрии, где он доказал знаменитую гипотезу, предложенную геометрами Джефом Чигером и Детлефом Громоллом. Но за несколько лет до появления в Интернете его статей Перельман надолго пропал из виду. Иногда другие математики получали от него электронные письма, в которых он интересовался литературой по вопросам потока Риччи. Однако никто не догадывался, что Перельман серьезно работает над использованием потока Риччи для доказательства гипотезы Пуанкаре, поскольку он практически никому не сообщал об этом. По сути дела его деятельность была столь незаметна, что многие из его бывших коллег сомневались в том, что он все еще вообще занимается математикой. Сами по себе статьи были не менее поразительны — всего шестьдесят восемь страниц текста, — что привело к тому, что другим ученым пришлось потратить немало времени на то, чтобы понять их содержание и извлечь из них ключевые аргументы, кратко набросанные Перельманом. На сегодняшний день является общепризнанным, что программа исследований, начатая Гамильтоном и продолженная Перельманом, в конце концов привела к разрешению как давней гипотезы Пуанкаре, так и более свежей проблемы Тёрстона. Если это единодушное признание действительно имеет под собой основу, то совместные успехи Гамильтона и Перельмана представляют собой важнейшее достижение геометрического анализа. Согласно моим расчетам, почти половина теорем, лемм и прочих вспомогательных утверждений, полученных в этой области на протяжении последних тридцати лет, были использованы в работах Гамильтона и Перельмана, что и привело в конце концов к доказательству гипотезы Пуанкаре. Итак, вы увидели некоторые из тех гвоздей, которые по самые шляпки загнал в дерево молоток геометрического анализа. Однако вы, наверное, помните, что я обещал описать три важнейших достижения геометрического анализа. Успехи в области четырехмерной топологии и доказательство гипотезы Пуанкаре вместе с методами потока Риччи, понадобившимися для ее доказательства, представляют собой только два из них. Остается еще и третье достижение — то, в котором я принял непосредственное участие и о котором пойдет речь далее. 25. Robert Greene (UCLA), interview with author, March 13, 2008. 26. Lizhen Ji and Kefeng Liu, “Shing-Tung Yau: A Manifold Man of Mathematics,” Proceedings of Geometric Analysis: Present and Future Conference, Harvard University, August 27-September 1, 2008. 27. Leon Simon (Stanford University), interview with author, February 6, 2008. 28. Greene, interview with author, March 13, 2008. 29. Cameron Gordon (University of Texas), interview with author, March 14, 2008. 30. Robert Geroch (University of Chicago), interview with author, February 28, 2008. 31. Edward Witten (Institute for Advanced Study), interview with author, March 31, 2008. 32. Edward Witten, “A New Proof of the Positive Energy Theorem,” Communications in Mathematical Physics 80 (1981): 381–402. 33. Roger Penrose, “Gravitational Collapse: The Role of General Relativity,” 1969, reprinted in Mathematical Intelligencer 30 (2008): 27–36. 34. Richard Schoen (Stanford University), interview with author, January 31, 2008. 35. Demetrios Christodoulou, The Formation of Black Holes in General Relativity (Zurich: European Mathematical Society, 2009). 36. John D. S. Jones, “Mysteries of Four Dimensions,” Nature 332 (April 7, 1998): 488–489. 37. Simon Donaldson (Imperial College), interview with author, April 3, 2008. 38. Faye Flam, “Getting Comfortable in Four Dimensions,” Science 266 (December 9, 1994): 1640. 39. То же. 40. Mathematical Institute at the University of Oxford, “Chart the Realm of the 4th Dimension,” http://www2.maths.ox.ac.uk/~dusautoy/2soft/4D.htm. 41. Grisha Perelman, “The Entropy Formula for the Ricci Flow and Its Geometric Applications,” November 11, 2002, http://arxiv.org/abs/math/0211159vl.
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Математика ≫ Книги ≫ Глава 3. Новая разновидность молотка / Теория струн и скрытые измерения Вселенной // Шинтан Яу, Стив Надис |
|
[time: 8 ms; queries: 7]
15 Дек 2025 11:03:48 GMT+3 |



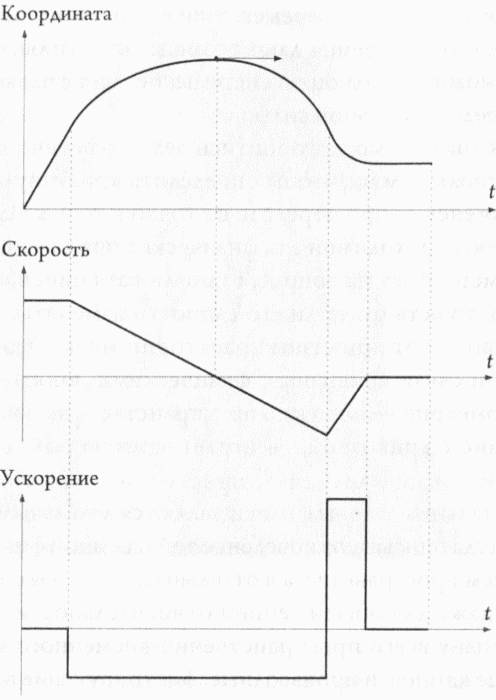
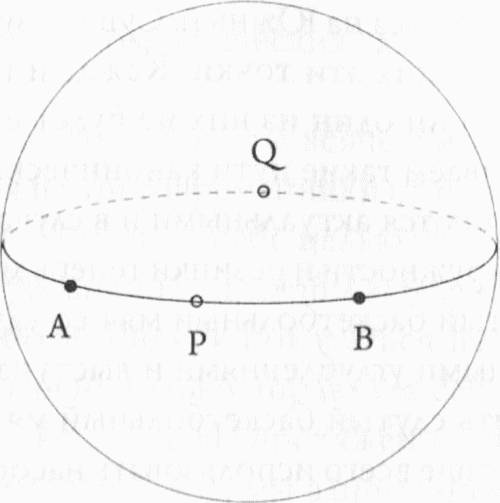
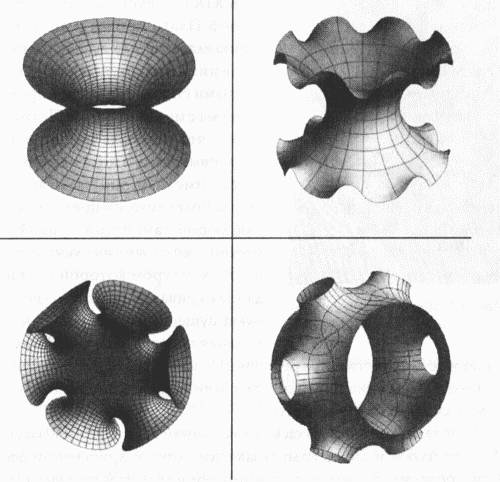

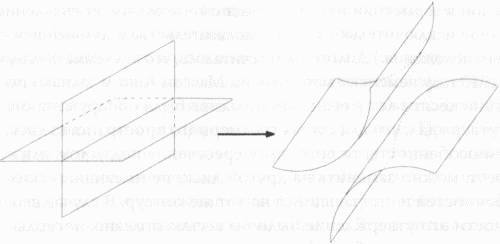


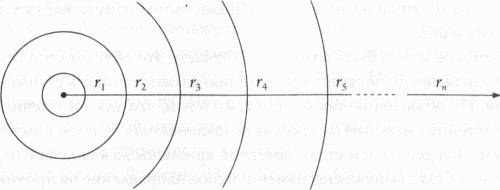

 Эта книга предназначена для широкого круга читателей, желающих узнать больше об окружающем нас мире и о самих себе. Автор, известный ученый и популяризатор науки, с необычайной ясностью и глубиной объясняет устройство Вселенной, тайны квантового мира и генетики, эволюцию жизни и показывает важность математики для познания всей природы и человеческого разума в частности.
Эта книга предназначена для широкого круга читателей, желающих узнать больше об окружающем нас мире и о самих себе. Автор, известный ученый и популяризатор науки, с необычайной ясностью и глубиной объясняет устройство Вселенной, тайны квантового мира и генетики, эволюцию жизни и показывает важность математики для познания всей природы и человеческого разума в частности. В последнее время учёным удаётся всё лучше и подробнее изучить, как выглядит микромир. Микроскопы позволили увеличить объекты в сто раз, в тысячу, в десять тысяч раз. Наконец, удалось построить электронные микроскопы, способные показать отдельные атомы. Но учёным интересно увидеть не только атомы, но и заглянуть внутрь атомов. Ядро атома — в сто тысяч раз меньше самого атома. Для изучения материи на этом масштабе нужны ускорители частиц. Всё более мощные и более изощрённые. И, наконец, дойдя до самого глубокого уровня, куда невозможно заглянуть даже при помощи самых мощных ускорителей, учёным приходится браться за неожиданный инструмент — за телескоп. Фильм рассказывает о том, какими методами ведется изучение структуры нашей вселенной в различных микромасштабах.
В последнее время учёным удаётся всё лучше и подробнее изучить, как выглядит микромир. Микроскопы позволили увеличить объекты в сто раз, в тысячу, в десять тысяч раз. Наконец, удалось построить электронные микроскопы, способные показать отдельные атомы. Но учёным интересно увидеть не только атомы, но и заглянуть внутрь атомов. Ядро атома — в сто тысяч раз меньше самого атома. Для изучения материи на этом масштабе нужны ускорители частиц. Всё более мощные и более изощрённые. И, наконец, дойдя до самого глубокого уровня, куда невозможно заглянуть даже при помощи самых мощных ускорителей, учёным приходится браться за неожиданный инструмент — за телескоп. Фильм рассказывает о том, какими методами ведется изучение структуры нашей вселенной в различных микромасштабах. Андрей Дмитриевич Линде рассказывает о теории инфляционной Вселенной или теории Мультивселенной (Мультиверса). Термин «Multi-verse», заменяющий слово «Universe», означает, что вместо одной Вселенной — много вселенных сразу в одной.
Андрей Дмитриевич Линде рассказывает о теории инфляционной Вселенной или теории Мультивселенной (Мультиверса). Термин «Multi-verse», заменяющий слово «Universe», означает, что вместо одной Вселенной — много вселенных сразу в одной. Нобелевскую премию поделили канадец Артур Макдональд и японец Такааки Кадзита, экспериментально доказавшие взаимное превращение разных видов нейтрино, что означает наличие у них массы.
Нобелевскую премию поделили канадец Артур Макдональд и японец Такааки Кадзита, экспериментально доказавшие взаимное превращение разных видов нейтрино, что означает наличие у них массы.