Глава 2. Место геометрии в мироздании

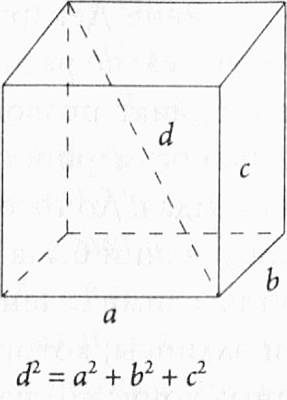
Так что же такое геометрия? Многие полагают, что геометрия — это только предмет, который они изучали в средней школе, — совокупность технических приемов, необходимых для измерения углов между прямыми, вычисления площадей треугольников, кругов и прямоугольников и, возможно, для установления некоторой меры эквивалентности между различными геометрическими объектами. Даже если пользоваться столь ограниченным определением, не возникает сомнений, что геометрия является весьма полезным инструментом — к примеру, для архитекторов, ежедневно использующих ее в своей работе. Да, несомненно, геометрия включает в себя все вышеперечисленное, но также и многое другое, поскольку она имеет отношение к архитектуре в самом широком смысле этого слова, начиная от мельчайших масштабов и заканчивая огромнейшими. А для некоторых людей вроде меня, одержимых идеей определения размера, формы, кривизны и структуры космического пространства, геометрия — основной инструмент.

Слово геометрия, произошедшее от слов гео (земля) и метрео (измеряю) изначально значило «измерение земли». Но сейчас это слово используется в гораздо более общем значении — «измерение пространства», хотя пространство само по себе и не является достаточно строго определяемым понятием. Как сказал однажды Георг Фридрих Бернхард Риман: «Геометрия предполагает заданными заранее как понятие пространства, так и первые основные понятия, которые нужны для выполнения пространственных построений, давая таким образом лишь номинальные определения понятий».^[14]

Как бы странно это ни прозвучало, но мы предпочитаем сохранять понятие пространства весьма расплывчатым по той причине, что оно подразумевает многое, для чего мы не имеем других обозначений. Таким образом, эта неопределенность в каком-то плане удобна. К примеру, когда мы рассматриваем вопрос о размерности пространства или размышляем о его форме как единого целого, мы могли бы отнести эти рассуждения и ко всей Вселенной. В более узком значении понятие пространства может относиться как к весьма простой геометрической конструкции, такой как точка, линия, плоскость, сфера или тор — все те типы геометрических фигур, которые способен нарисовать студент, так и к гораздо более сложным и неизмеримо более трудноизображаемым объектам.

Представим, к примеру, что у нас имеется некая совокупность точек, расположенных совершенно случайным образом, и что при этом абсолютно невозможно ввести определение расстояния между ними. С точки зрения математики это пространство не будет иметь геометрии; это будет просто случайный набор точек. Однако стоит лишь ввести некую измерительную функцию, дающую возможность рассчитывать расстояния между любыми двумя точками, называемую метрикой, как пространство неожиданно приобретает упорядоченность. Теперь оно характеризуется определенной геометрией. Иными словами, метрика предоставляет всю информацию, необходимую для того, чтобы сделать вывод о форме пространства, на котором она задана. Вооружившись способом измерять форму пространства, можно с большой точностью определить, является ли пространство плоским, и установить степень его отклонения от плоскости, или, иными словами, вычислить кривизну пространства, что я лично нахожу наиболее интересным.

Таким образом, геометрия представляет собой нечто большее, чем просто набор методов для измерения расстояний — что, разумеется, не принижает измерительную функцию геометрии, которой я также восхищаюсь, — геометрия является одним из основных доступных нам способов исследования Вселенной. Физика и космология уже по одному своему названию играют главные роли в понимании Вселенной. Роль геометрии, хотя и менее заметна, но так же важна. Я даже рискну сказать, что геометрия не только заслуживает места за одним столом с физикой и космологией, но во многих отношениях она и является этим столом.

Это действительно так, поскольку вся вселенская драма — сложнейший танец частиц, атомов, звезд и других объектов, постоянно изменяющихся, движущихся, взаимодействующих, — разыгрывается на подмостках, называемых «пространством», и ее никогда не понять без понимания существенных особенностей самого пространства. Пространство представляет собой нечто гораздо большее, чем просто театральный задник, по сути оно обусловливает важнейшие физические свойства тех объектов, которые в нем находятся. Действительно, как принято считать в настоящее время, материя или частицы, покоящиеся или движущиеся в пространстве, на самом деле являются частями этого пространства, или, точнее, пространственно-временного континуума. Геометрия в свою очередь может накладывать ограничения на поведение пространственно-временного континуума и физических систем в целом — ограничения, которые можно обнаружить исходя исключительно из принципов математики и логики.

Рассмотрим, например, климат Земли. Хотя это и не очевидно, геометрия оказывает существенное влияние на климат — в этом случае основную роль играет форма нашей планеты. Если бы мы жили не на поверхности сферы, а на поверхности тора или бублика, то наша жизнь — так же, как и климат нашей планеты, — была бы совершенно другой.

На сфере все ветры не могут дуть одновременно в одном и том же направлении (например, восточном), так же как не могут иметь одно и то же направление одновременно все океанические течения (как было показано в предыдущей главе). Неизбежно будут существовать точки, такие как Северный и Южный полюсы, где ветры или течения больше не будут иметь восточного направления, в таких точках исчезает само понятие «восточное направление». Иная ситуация складывается на тороидальной поверхности, где подобных препятствий нет, и ветры или течения могут перемещаться в одном и том же направлении по всей поверхности без каких-либо помех. Топологические различия, несомненно, влияют на глобальные процессы циркуляции, однако, если вас интересуют более конкретные климатические последствия, такие как различие сезонных изменений на поверхности сферы и тора, — вам лучше спросить об этом метеоролога.

Область исследований геометрии на самом деле еще шире. Использование геометрии совместно с общей теорией относительности Эйнштейна показало, что масса и энергия Вселенной являются положительными величинами, и, следовательно, четырехмерное пространство-время, в котором мы живем, стабильно. Помимо этого, согласно геометрическим принципам, где-то во Вселенной должны существовать странные места, называемые сингулярностями, расположенные, к примеру, в центрах черных дыр, где плотность вещества стремится к бесконечности и известные нам законы физики перестают работать. В качестве еще одного примера — на этот раз из теории струн — можно привести геометрию загадочных шестимерных пространств, называемых многообразиями Калаби-Яу, в которых предположительно и происходит большая часть важнейших физических процессов. Эта геометрия способна объяснить разнообразие существующих элементарных частиц, предсказывая не только их массу, но и характер сил взаимодействия между ними. Помимо прочего, исследование подобных многомерных пространств позволило выявить возможные причины слабости гравитации по сравнению с другими фундаментальными взаимодействиями, а также дало ключи к открытию механизмов, лежащих в основе инфляционного расширения ранней Вселенной и существования темной энергии, управляющей расширением космического пространства.

Как видите, мои слова о том, что геометрия наряду с физикой и космологией является бесценным орудием для раскрытия секретов Вселенной, не были пустым хвастовством. Более того, если принять во внимание последние успехи математики, которые будут описаны в этой книге, прогресс в области наблюдательной космологии и возникновение теории струн, пытающейся осуществить никому не удавшийся до сих пор великий синтез, складывается впечатление, что эти три направления исследований должны сойтись в одной точке. Следовательно, человеческое познание сейчас стоит на пороге выдающихся открытий и готово сделать огромный шаг вперед, причем геометрия во всех смыслах командует парадом.

Следует помнить, что, куда бы мы ни двигались в области геометрии и что бы мы ни делали, мы не начинаем наш путь с чистого листа. Мы всегда ссылаемся на то, что было установлено до нас: гипотезы, доказательства, теоремы или аксиомы, используя фундамент, который в большинстве случаев был возведен за тысячи лет до этого. В этом смысле геометрию, как и другие науки, можно считать тщательно продуманным строительным проектом. В первую очередь закладывается фундамент, и если он заложен удачно, так сказать, положен на твердую поверхность, то устоит и само здание и надстройки на его крыше, если, конечно, они также сделаны с соблюдением разумных принципов.

В этом, по сути, и состоит красота и сила моего призвания. Если речь идет о математике, от нее всегда ожидают абсолютно точных утверждений. Математическая теорема — это точное утверждение, остающееся непреложной истиной вне зависимости от пространства, времени, мнения людей и авторитетов. Эта особенность математики резко отличает ее от эмпирических наук, в которых основным методом исследования является постановка экспериментов, по результатам которых и принимается или не принимается то или иное утверждение (конечно, после достаточно большого испытательного срока). В этом случае при последующей проверке результаты могут быть пересмотрены, и нельзя быть уверенными на сто процентов, что установленный вами факт — истина в последней инстанции.

Конечно, часто удается найти более общий и совершенный вариант известной математической теоремы, что, впрочем, не упраздняет ее истинности. Продолжая аналогию со строительством, можно сказать, что здание при этом остается столь же крепким; производится всего лишь небольшое расширение или перепланировка, не затрагивающая фундамента. Иногда косметического ремонта оказывается недостаточно, и тогда приходится даже разрушать «интерьер» здания и создавать новый. Несмотря на то что старые теоремы все так же справедливы, порой возникает потребность в новых разработках или свежем наборе данных, чтобы создать более полную картину.

Наиболее важные теоремы обычно проверяют и перепроверяют много раз и многими способами, не оставляя ни единого шанса на ошибку. Разумеется, доказательства менее очевидных теорем, которые не подверглись столь тщательной проверке, могут содержать ошибки. Если ошибка обнаружена, комнату в здании или даже целое крыло приходится разрушать и выстраивать заново. И все же остальное здание — прочное сооружение, прошедшее проверку временем, — остается нетронутым.

Одним из величайших архитекторов геометрии стал Пифагор, которому приписывают открытие формулы, представляющей собой одно из самых прочных сооружений из когда-либо возведенных в математике. Теорема Пифагора (именно такое название она носит) утверждает, что в прямоугольном треугольнике, то есть в треугольнике, один из углов которого равен 90°, квадрат длины наибольшей из сторон (гипотенузы) равен сумме квадратов двух более коротких (катетов). Бывшие и нынешние школьники легко вспомнят соответствующую формулу: a² + b² = c². Это весьма простое, но невероятно мощное утверждение столь же важно сегодня, как и 2500 лет назад, когда оно было сформулировано. Применение данной теоремы не ограничивается школьной математикой. Эта теорема настолько важна и всеобъемлюща, что я, например, использую ее почти каждый день, практически не замечая этого.

На мой взгляд, теорема Пифагора — важнейшее утверждение в геометрии, одинаково важное как для современной математики высоких размерностей, например для нахождения расстояний в пространствах Калаби-Яу и решения эйнштейновских уравнений движения, так и для расчетов на двухмерной плоскости, такой как лист бумаги с домашним заданием, или в трехмерной классной комнате начальной школы. Значимость этой теоремы обусловлена тем, что ее можно использовать для расчета расстояний между двумя точками в пространстве любой размерности. Как я уже сказал в начале этой главы, геометрия постоянно использует понятие расстояния, по причине чего эта формула является основой практически всех расчетов.

Более того, я нахожу эту теорему также чрезвычайно красивой, хотя о вкусах, как известно, не спорят. Нам, как правило, нравятся те вещи, которые хорошо нам знакомы, — вещи, которые стали для нас настолько привычными, настолько естественными, что мы считаем их само собой разумеющимися, подобно восходу и заходу солнца. Кроме того, теорема Пифагора очень лаконична — три простые переменные, возведенные во вторую степень, a² + b² = c², — ее запись почти столь же кратка, как и запись других известных законов, таких как F = ma или E = mc². Красота для меня заключается в элегантности столь простого утверждения, находящегося в настолько полном согласии с природой.

Помимо ценности теоремы Пифагора самой по себе, без сомнения являющейся краеугольным камнем геометрии, не менее важным представляется и тот факт, что ее истинность была доказана, и это доказательство стало первым зафиксированным доказательством в математике. Египетские и вавилонские математики использовали отношение между катетами и гипотенузой прямоугольного треугольника задолго до рождения Пифагора. Но ни египтяне, ни вавилоняне не только никогда не пытались доказать эту теорему, но, по-видимому, и само понятие доказательства им было незнакомо. По словам математика Э. Т. Белла, именно доказательство теоремы и стало наибольшим вкладом Пифагора в геометрию:

Вполне возможно, что именно Пифагор впервые доказал эту теорему, хотя вы должны были обратить внимание на мои слова о том, что ему лишь «приписывается» ее доказательство, будто бы существуют некоторые сомнения по поводу авторства. Так оно и есть. Пифагор был культовой фигурой, и многие из открытий его помешанных на математике последователей были приписаны Пифагору задним числом. Таким образом, вполне возможно, что доказательство теоремы Пифагора было получено одним из продолжателей его дела через одно или два поколения после Пифагора. Правды мы уже никогда не узнаем: Пифагор жил в VI столетии до нашей эры и практически не оставил после себя никаких записей.

К нашему счастью, сказанное выше не относится к наследию Евклида, одного из наиболее известных геометров всех времен и народов, превратившего геометрию в точную, строгую дисциплину. В отличие от Пифагора, Евклид оставил после себя огромное количество сочинений, наиболее выдающимся из которых являются «Начала», увидевшие свет примерно в 300 году до нашей эры — трактат в тринадцати томах, восемь из которых посвящены геометрии в двух и трех измерениях. «Начала» называют одной из наиболее влиятельных книг из когда-либо написанных, «прекрасным трудом, значение которого сравнимо разве что со значением Библии».^[16]

Рис. 2.1. Теорему Пифагора чаще всего иллюстрируют для случая двух измерений, изображая прямоугольный треугольник, в котором сумма квадратов катетов равна квадрату гипотенузы: a2 + b2 = c2. Однако, как показано на приведенном рисунке, эта теорема так же верна и для случая трех и большего числа измерений a2 + b2 + c2 = d2

В своем знаменитом сочинении Евклид заложил основы не только геометрии, но и всей математики, которая неразрывно связана с тем принципом аргументации, который сейчас называют Евклидовым: любое доказательство начинается с четкого определения понятий и набора однозначно установленных аксиом или постулатов (эти два слова являются синонимами) и осуществляется при помощи строгих логических умозаключений; доказанная теорема, в свою очередь, может быть положена в основу доказательства дальнейших утверждений. Евклид, пользуясь исключительно этим методом, доказал в общей сложности больше четырехсот теорем, сведя таким образом воедино все геометрические знания своего времени.

Стэнфордский математик Роберт Оссерман объяснил столь безапелляционное приятие метода Евклида следующим образом: «В основе всего лежало чувство уверенности, что в мире абсурдных суеверий и сомнительных догадок утверждения, приведенные в “Началах”, являются твердо установленной истиной без малейшей тени сомнения». Эдна Сент-Винсент Миллей выразила аналогичное восхищение в своем стихотворении «Евклид один лишь видел обнаженной красоту».^[17]

Следующим человеком, внесшим решающий вклад в предмет нашего рассказа, — впрочем, без какого-либо пренебрежения к заслугам других достойных математиков, о достижениях которых мы не упомянули — можно считать Рене Декарта. Как уже говорилось в предыдущей главе, Декарт значительно расширил сферу исследований геометрии, введя систему координат, позволившую математикам рассуждать о пространствах любых размерностей и использовать алгебру при решении геометрических задач. До того как Декарт преобразовал геометрию, ее область исследований была ограничена прямыми линиями, окружностями и коническими сечениями — такими кривыми, как параболы, гиперболы и эллипсы, которые можно получить, рассекая плоскостью бесконечный конус под разными углами. Появление системы координат дало возможность описывать при помощи уравнений очень сложные фигуры, которые невозможно вообразить каким-либо другим способом. Рассмотрим, к примеру, уравнение xⁿ + yⁿ = 1. При помощи декартовых координат решить это уравнение и нарисовать соответствующую кривую не составит труда. Однако до появления системы координат было непонятно, как ее изобразить. В местах, которые ранее считались непроходимыми, Декарт указал путь, по которому двигаться дальше.

Этот путь стал еще четче, когда через пятьдесят лет после Декарта Исаак Ньютон и Готфрид Лейбниц, разделяющие идеи Декарта в области аналитической геометрии, создали дифференциальное и интегральное исчисление. На протяжении десятилетий и столетий новые инструменты дифференциального и интегрального исчисления внедрялись в геометрию такими математиками, как Леонард Эйлер, Жозеф Лагранж, Гаспар Монж и, в первую очередь, Карл Фридрих Гаусс, под чьим руководством в 1820-х достигла своего совершеннолетия так называемая дифференциальная геометрия. Дифференциальная геометрия предполагает использование декартовой системы координат для описания поверхностей, которые затем могут быть детально проанализированы с помощью методов дифференциального исчисления; дифференцирование — это метод нахождения угла наклона любой гладкой кривой.

Создание дифференциальной геометрии, которая продолжила свое развитие и после Гаусса, стало величайшим достижением. С помощью инструментов дифференциального исчисления геометры описывали свойства кривых и поверхностей с намного большей точностью, чем это было возможно ранее. Подобные сведения можно получить путем дифференцирования или, что эквивалентно, путем нахождения производных, показывающих, как изменяется функция в ответ на изменение аргумента. Функцию можно рассматривать как алгоритм или формулу, в которой каждому числу, поданному на вход (значению аргумента), ставится в соответствие некоторое число на выходе (значение функции). Например, в функции y = x² значение аргумента x подается на вход, а на выходе получается значение функции y. Функция однозначна: если вы будете подставлять в нее одно и то же значение x, то всегда получите одно и то же значение y, так, в нашем примере, подставляя x = 2, вы всегда получите y = 4. Производная характеризует отношение приращения значения функции к заданному приращению аргумента; величина производной отражает чувствительность функции к незначительным изменениям аргумента.

Производная — это не только абстрактное понятие; это реальное число, которое можно вычислить и которое сообщает нам о наклоне кривой или поверхности в данной точке. Например, в приведенном выше примере можно найти производную функции (которая в данном случае оказывается параболой) в точке x = 2. Что произойдет со значением функции y, если немного сместиться из этой точки, например, в точку x = 2,001? В этом случае значение y станет равным 4,004 (с точностью до трех знаков после запятой). Производная в этой точке будет равна отношению приращения значения функции (0,004) к приращению значения аргумента (0,001), то есть 4. Именно это число и будет производной функции при x = 2 или, другими словами, наклоном кривой (параболы) в этой точке.

Расчеты, конечно, могут оказаться гораздо более трудоемкими при переходе к более сложным функциям и более высоким размерностям. Но вернемся на время к нашему примеру. Мы получили производную функции y = x² из отношения приращения y к приращению x, поскольку производная функции говорит нам о наклоне (или крутизне) в данной точке — тогда как наклон служит непосредственной мерой приращения y по отношению к приращению x.

Проиллюстрируем это другим способом: рассмотрим мяч, лежащий на некоей поверхности. Если мы слегка толкнем мяч в какую-либо сторону, как это отразится на его вертикальной координате? Если поверхность более или менее плоская, то высота, на которой находится мяч, практически не изменится. Но если мяч находился на крутом склоне, изменение высоты будет более существенным. Таким образом, производные характеризуют наклон поверхности в непосредственной близости от мяча.

Рис. 2.2. Площадь фигуры, ограниченной кривой, можно вычислить при помощи интегрального исчисления, разделив область под кривой на бесконечно узкие прямоугольники и затем сложив их площади. По мере того как прямоугольники становятся все уже и уже, это приближение становится все точнее и точнее. Если перейти к пределу, при котором ширина прямоугольников стремится к нулю, результат станет точным

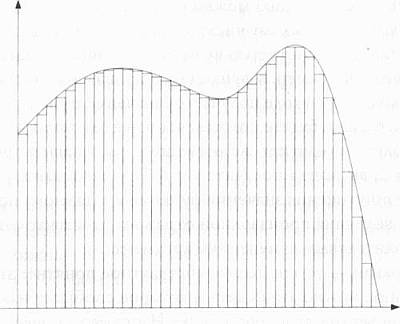
Конечно, нет причин ограничиваться только одной точкой на поверхности. Путем вычисления производных, показывающих изменение геометрии (или формы) для различных точек поверхности, можно точно рассчитать кривизну объекта в целом. Хотя наклон в каждой данной точке дает только локальную информацию, относящуюся к «окрестностям» указанной точки, значения, полученные для различных точек, можно объединить и вывести функцию, описывающую наклон объекта в любой точке. Затем при помощи интегрирования — грубо говоря, путем сложения и усреднения — можно получить функцию, описывающую объект как единое целое. Таким образом, мы получим представление о структуре всего объекта, что и является центральной идеей всей дифференциальной геометрии — возможность создать общую картину для всей поверхности или многообразия на основе локальной информации, полученной из производных, отражающих геометрию (или метрику) в каждой точке.

Помимо достижений в области дифференциальной геометрии, Гаусс внес существенный вклад и в другие области математики и физики. Пожалуй, наибольшее значение для нас имеет его поразительное предположение, что не только объекты, находящиеся в пространстве, но и пространство само по себе также может быть искривлено. Открытие Гаусса бросило вызов евклидовой концепции плоского пространства — представлению, относившемуся не только к интуитивно понятной двухмерной плоскости, но и к трехмерному пространству, называя которое плоским подразумевают, что параллельные линии в таком пространстве не пересекаются, а сумма углов треугольника всегда составляет ровно 180°.

θ1 + θ2 + θ3> 180° Положительная кривизна θ1 + θ2 + θ3= 180° Нулевая кривизна θ1 + θ2 + θ3< 180° Отрицательная кривизна Рис. 2.3. На поверхности с положительной кривизной (такой, как сфера) сумма углов треугольника больше 180°, и линии, кажущиеся параллельными (такие, как меридианы) могут пересечься, например, на Северном и Южном полюсах. На плоской поверхности (поверхности с нулевой кривизной), которая является основой евклидовой геометрии, сумма углов треугольника равна 180°, и параллельные линии не пересекаются. На поверхности с отрицательной кривизной, например имеющей форму седла, сумма углов треугольника меньше 180°, а линии, кажущиеся параллельными, на самом деле расходятся

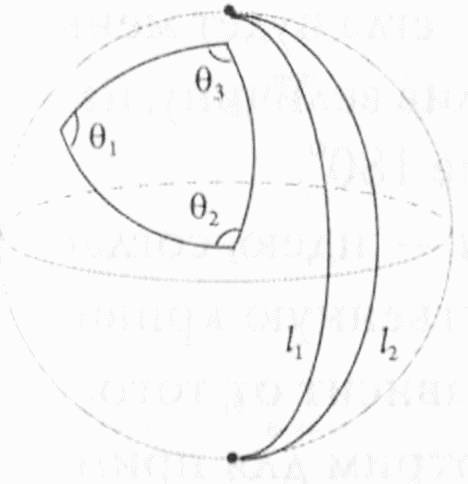
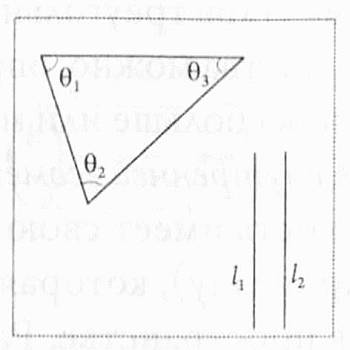
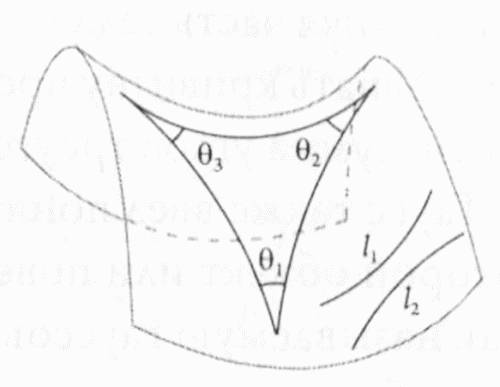
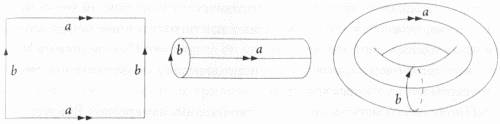
Эти принципы, являющиеся ключевыми для евклидовой геометрии, не выполняются в искривленных пространствах. Рассмотрим сферическое пространство, подобное поверхности глобуса. Если смотреть на глобус со стороны экватора, линии меридианов кажутся параллельными, поскольку все они перпендикулярны экватору. Но если вы проследуете по ним в одном из двух направлений, то увидите, что они в конце концов сходятся на Северном и Южном полюсах. Этого не произойдет в плоском евклидовом пространстве, таком как карта в проекции Меркатора, на которой две линии, перпендикулярные третьей, являются действительно параллельными и никогда не пересекаются.

В неевклидовом пространстве сумма углов треугольника может быть или больше, или меньше, чем 180°, в зависимости от того, как искривлено пространство. Если пространство, подобно сфере, имеет положительную кривизну, сумма углов треугольника всегда будет больше 180°. И напротив, если пространство имеет отрицательную кривизну, как внутренняя часть седла, сумма углов треугольника всегда будет меньше 180°. Узнать кривизну пространства можно, определив величину, на которую сумма углов треугольника больше или меньше 180°.

Гаусс также ввел понятие внутренней геометрии — идею, согласно которой объект или поверхность имеет свою собственную кривизну (так называемую гауссову кривизну), которая не зависит от того, как этот объект располагается в пространстве. Рассмотрим для примера лист бумаги. Можно ожидать, что его кривизна равна нулю, и так оно и есть. Теперь свернем этот лист бумаги в цилиндр. Двухмерная поверхность цилиндра, согласно Гауссу, имеет две главные кривизны, проходящие в направлениях, перпендикулярных друг другу: первая кривизна относится к окружности и имеет величину 1/r, где r — это радиус основания цилиндра. Если r = 1, то эта кривизна также равна единице. Вторая кривизна проходит вдоль образующей цилиндра, которая представляет собой прямую линию. Кривизна прямой линии, очевидно, равна нулю, поскольку прямая — она и есть прямая. Гауссова кривизна цилиндра, как любого другого двухмерного объекта, равна произведению одной кривизны на вторую, которое в нашем случае равно 1×0 = 0. Таким образом, в понятиях собственной кривизны цилиндр представляет собой то же самое, что и лист бумаги, из которого он свернут, — он совершенно плоский. Нулевая собственная кривизна цилиндра обусловлена тем, что цилиндр можно сделать из листа бумаги, не растягивая и не деформируя его. Иными словами, измерения расстояний между любыми двумя точками на поверхности листа — вне зависимости от того, разложен ли лист на столе или свернут в трубочку, — дадут одинаковые результаты. Это значит, что геометрия и, следовательно, собственная кривизна листа бумаги остаются неизменными вне зависимости от того, плоский этот лист или свернутый.

Аналогично, если бы удалось сделать из цилиндра тор, соединив его концы вместе — также без растяжений и деформаций, — то внутренняя кривизна полученного тора все равно осталась бы равной внутренней кривизне цилиндра, то есть нулю. На практике, однако, сделать так называемый плоский тор — по крайней мере в двух измерениях — невозможно по причинам, которые будут обсуждаться далее (в четвертой главе). Но теоретически подобный объект (называемый абстрактной поверхностью) изготовить можно, и он столь же важен для математики, как и те объекты, которые мы называем реальными.

Рис. 2.4. Тороидальная (имеющая форму бублика) поверхность может быть совершенно «плоской» (имеющей нулевую гауссову кривизну), поскольку ее можно изготовить, сворачивая лист бумаги в трубку или цилиндр и затем соединяя концы полученного цилиндра

С другой стороны, сфера довольно существенно отличается от цилиндра или плоского тора. Рассмотрим, к примеру, кривизну сферы радиуса r. В этом случае кривизна одинакова по всей поверхности сферы, и ее можно определить как 1/r². Мы видим, что на поверхности сферы все направления эквивалентны, что явно неверно в случае цилиндра или бублика. Именно по этой причине не важно, как ориентирована сфера в трехмерном пространстве; маленький жучок, живущий на ее поверхности, скорее всего, не замечает пространственной ориентации сферы и все, что его беспокоит и дается ему в ощущениях, — это геометрия его локального двухмерного мира.

Наряду с Николаем Лобачевским и Яношем Бойяи Гаусс внес большой вклад в наше понимание абстрактного пространства, в частности для двухмерного случая, хотя он сам признавал наличие определенной путаницы в этой области. И все же, в конечном итоге, ни Гаусс, ни его коллеги не сумели полностью освободить наши представления о пространстве от евклидовых рамок. Гаусс выразил свое замешательство в письме, написанном им в 1817 году астроному Генриху Вильгельму Маттеусу Ольберсу: «Я все больше убеждаюсь, что необходимость нашей геометрии не может быть доказана, по крайней мере, человеческим рассудком и для человеческого рассудка. Может быть, в следующей жизни мы придем к взглядам на природу пространства, которые нам сейчас недоступны».^[18]

Некоторые ответы были получены не в «следующей жизни», как написал Гаусс, а в следующем поколении благодаря усилиям и прекрасным способностям его студента Георга Фридриха Бернхарда Римана. Риман отличался слабым здоровьем и умер молодым, но за сорок лет своей жизни он смог перевернуть существовавшие представления о геометрии, а вместе с ними и представления о Вселенной. Риман ввел особую разновидность поля — набор чисел, соответствующий каждой точке пространства, пользуясь которым можно найти расстояние между двумя точками вдоль любой линии, которая их соединяет. Полученная информация, в свою очередь, может быть использована для определения степени искривленности пространства.

Проще всего мерить пространство в одном измерении. Все, что необходимо для измерения, например, прямой линии, — это линейка. Для двухмерного пространства, такого как пол большого танцевального зала, мы обычно берем две перпендикулярные линейки — одна из которых сопоставляется оси x, а вторая — оси y — и находим расстояние между двумя точками путем построения прямоугольного треугольника и применения теоремы Пифагора. В свою очередь, в трех измерениях нам необходимы три перпендикулярные линейки, соответствующие осям x, y и z.

В искривленных, неевклидовых пространствах все становится сложнее и интереснее, поскольку точно откалиброванные перпендикулярные линейки для измерения искривленного пространства уже не пригодны. Однако в этом случае для расчета расстояний мы можем использовать риманову геометрию. Подход, который мы применяем для расчета длины кривой, лежащей на искривленном многообразии, вам уже знаком: кривую представляют в виде ломаной, состоящей из касательных бесконечно малой длины, и затем берут интеграл вдоль всей линии, чтобы получить полную длину.

Сложность этого подхода обусловлена тем, что в искривленном пространстве длина каждого отрезка ломаной может изменяться при перемещении от одной точки многообразия к другой. Для того чтобы преодолеть эту трудность, Риман создал инструмент, известный как метрический тензор, дающий алгоритм для расчета длины отрезка касательной в каждой точке. В двух измерениях метрический тензор представляет собой матрицу 2×2, в n измерениях — матрицу n×n. Следует отметить, что этот новый подход к измерению, несмотря на всю важность нововведений Римана, по-прежнему основан на теореме Пифагора, только переформулированной для неевклидового пространства.

Пространство, наделенное римановой метрикой, носит название риманова многообразия. Вооружившись метрикой, мы можем измерить длину любой кривой, принадлежащей многообразию произвольной размерности. Впрочем, мы не ограничены возможностью измерения длин кривых — таким же способом мы можем измерять и площади поверхностей в подобных пространствах, причем понятие «поверхность» в этом случае не ограничено привычными нам двумя измерениями.

Изобретя понятие метрики, Риман показал, что пространству, имевшему до этого весьма неясное определение, можно строго приписать определенную геометрию, кривизну же лучше представлять не в виде расплывчатого понятия, а в виде точных чисел, соответствующих различным точкам пространства. И этот подход, как показал Риман, применим к пространствам любой размерности.

До Римана искривленный объект мог быть изучен только «снаружи», подобно тому, как издалека проводят геодезическую съемку горного хребта или смотрят на Землю с борта космического корабля. Вблизи же все кажется плоским. Риман указал способ установить, что мы живем в искривленном пространстве, даже не имея под рукой ничего, с чем его можно сравнить.^[19] Это открытие поставило перед физиками и астрономами важнейший вопрос: если Риман прав и пространство, в котором мы живем, действительно искривлено, не означает ли это необходимости нового пересмотра наших представлений практически обо всем? Но значит ли это, что в больших масштабах Вселенная не ограничена рамками евклидовой геометрии, а пространство способно сдвигаться, искривляться и вообще — делать что угодно? Именно по этой причине астрономы и космологи проводят в настоящее время тщательные измерения в надежде установить, искривлено наше пространство или нет. Благодаря Риману теперь известно, что для проведения этих измерений совсем не нужно покидать нашу Вселенную (что было бы весьма затруднительно сделать). Напротив, узнать, искривлена ли наша Вселенная, можно, буквально не сходя с того места, на котором сидим, — что весьма комфортно как для космологов, так и для обывателей.

Такими были некоторые из новых витающих в воздухе идей в области геометрии в то время, когда Эйнштейн приступил к упорядочению своих размышлений относительно гравитации. В начале XX столетия Эйнштейн на протяжении почти десяти лет пытался объединить специальную теорию относительности с законами гравитации Ньютона. Он подозревал, что ответ может лежать где-то в области геометрии, и обратился за помощью к своему другу, геометру Марселю Гроссману. Гроссман, ранее помогавший Эйнштейну закончить университетскую курсовую работу, которую сам Эйнштейн находил скучной, познакомил своего друга с римановой геометрией, которая была неизвестна физике того времени, — хотя и сделал это с предостережением, назвав риманову геометрию «ужасной смесью, с которой физикам лучше не связываться».^[20]

Риманова геометрия стала ключом к решению головоломки, над которой Эйнштейн бился много лет. Как уже говорилось в предыдущей главе, Эйнштейн отстаивал идею искривленного четырехмерного пространства-времени (иначе известного как наша Вселенная), не являющегося частью большего пространства. К счастью для него, Риман уже создал каркас теории, определив пространство нужным образом. По словам Брайана Грина: «Гениальность Эйнштейна состояла в способности распознать, что этот математический аппарат идеально подходит для реализации его идей относительно гравитации. Он четко показал, что математические понятия римановой геометрии прекрасно подходят для физического описания гравитации».^[21]

Эйнштейн не только догадался, что пространственно-временной континуум можно описать при помощи римановой геометрии, но показал, что геометрия пространства-времени неразрывно связана с его физическими характеристиками. Тогда как специальная теория относительности уже объединила пространство и время путем введения понятия единого пространства-времени, последовавшая за ней общая теория относительности объединила пространство и время с материей и гравитацией. Это стало настоящим прорывом в научных представлениях. Ньютоновская физика рассматривала пространство как пассивную сцену, а не как активного участника происходящих на ней событий. Прорыв был тем более впечатляющим, что в то время еще не существовало никаких экспериментальных предпосылок для этой теории. Эта теория в буквальном смысле слова возникла в голове одного человека (что, конечно, не означает, что она могла возникнуть в любой голове).

Физик Ч. Янг назвал формулировку Эйнштейном общей теории относительности актом «чистого творения», который был «уникальным в человеческой истории… Эйнштейн не пытался воспользоваться благоприятным случаем, который ему подвернулся. Он сам создал этот случай. И он сумел реализовать свою идею, благодаря глубокой проницательности и грандиозности замысла».^[22]

Общая теория относительности стала поразительным достижением, которое удивило, возможно, даже самого Эйнштейна, не подозревавшего, что основы физики и математики могут быть столь тесно переплетены друг с другом. Много лет спустя он сделает вывод, что «в основе принципов творения лежит математика. Поэтому я считаю в определенном смысле истинным, что чистая мысль может ухватить реальность, как мечтали древние».^[23] Теория гравитации Эйнштейна была создана при помощи именно такого процесса чистого мышления — исключительно из математических предпосылок, без каких-либо подсказок из внешнего мира.

Используя метрический тензор Римана, Эйнштейн получил форму и другие характеристики (иными словами, геометрию) по-новому осознанного им пространственно-временного континуума. Синтез геометрии и физики, завершившийся созданием знаменитых эйнштейновских уравнений поля, продемонстрировал, что гравитацию — силу, формирующую наш мир в космических масштабах, — можно рассматривать как иллюзию, вызываемую искривлением пространства-времени. В новой теории Эйнштейна метрический тензор римановой геометрии описывает не только кривизну пространственно-временного континуума, но и гравитационное поле. Массивное тело, подобное Солнцу, деформирует ткань пространства-времени точно так же, как под толстяком прогибается сетка батута. И подобно тому, как маленький шарик, брошенный на батут, будет двигаться по спирали вокруг тяжелого человека и, в конце концов, скатится ему под ноги, геометрия деформированного пространства-времени заставляет Землю двигаться по орбите вокруг Солнца. Иными словами, гравитация — это геометрия. Физик Джон Уилер однажды пояснил нарисованную Эйнштейном картину гравитации следующим образом: «Материя говорит пространству, как ему искривляться; пространство говорит материи, как ей двигаться».^[24]

Вот еще один пример, помогающий понять эту точку зрения: представим себе, что два человека начинают движение с одной и той же скоростью из разных точек на экваторе и движутся в направлении Северного полюса вдоль меридианов. С течением времени они становятся все ближе друг к другу. Возможно, они полагают, что находятся под действием некой невидимой силы, постепенно сближающей их. Но с другой стороны, предполагаемая сила — на самом деле всего лишь иллюзия, вызванная геометрией Земли, и в действительности никакой силы не существует; вот в двух словах суть идеи о тождественности гравитации и геометрии.

Наглядность приведенного примера произвела на меня огромное впечатление, когда я учился на первом курсе магистратуры и впервые услышал об общей теории относительности. Ни для кого не секрет, что гравитация определяет форму нашей Вселенной и является, по сути, ее главным архитектором в космических масштабах. В области же малых масштабов, изучению которой посвящена большая часть современной физики, гравитация пренебрежительно слаба по сравнению с другими взаимодействиями: электромагнитным, сильным и слабым. Но в общей схеме мироздания гравитация охватывает почти все сущее: именно она ответственна за создание структуры Вселенной, начиная от отдельных звезд и галактик вплоть до огромнейших сверхскоплений протяженностью в миллиарды световых лет. И если Эйнштейн был прав и гравитация сводится к геометрии, то геометрия также представляет собой силу, с которой необходимо считаться.

Я сидел в аудитории, пытаясь сделать выводы из услышанного, и тут меня захлестнул поток мыслей. Я интересовался кривизной начиная с колледжа и чувствовал, как в свете открытий Эйнштейна кривизна может играть ключевую роль для понимания Вселенной и что именно в эту область исследований я могу однажды внести свой собственный вклад. Дифференциальная геометрия предоставляет средства для описания движения массы в искривленном пространстве-времени, не вскрывая при этом причины этого искривления. Эйнштейн, в свою очередь, при помощи тех же средств попытался объяснить, откуда берется искривление. Форма пространства как результат действия гравитации и форма пространства как следствие его кривизны, рассматривавшиеся ранее как две разные задачи, слились в единую проблему.

Затем я задался следующим вопросом: поскольку известно, что причиной возникновения гравитации является масса, задающая кривизну пространства, что можно сказать о форме пространства, называемого вакуумом, в котором какое-либо вещество полностью отсутствует? Что определяет кривизну пространства в этом случае? Говоря иными словами, имеют ли эйнштейновские уравнения гравитационного поля какое-либо еще решение в вакууме, кроме плоского, которое нас менее всего интересует: с пространственно-временным континуумом, в котором нет ни материи, ни гравитации, ни взаимодействий и совершенно ничего не происходит? Существует ли такое «нетривиальное» пространство, в котором отсутствует материя, но существует кривизна и силы гравитации?

Тогда я был еще не в состоянии ответить на эти вопросы. Не знал я и того, что ученый по имени Эудженио Калаби рассмотрел частный случай этой же проблемы более чем за пятнадцать лет до того, впрочем, исходя из чисто математических предпосылок и не касаясь ни гравитации, ни идей Эйнштейна. Единственное, что я тогда мог сделать, — это удивиться и задать вопрос: «А что, если бы?»

Рис. 2.5. Геометр Ч. Ш. Черн (фотография Джорджа М. Бергмана)

Это был весьма неожиданный для меня вопрос по многим причинам — особенно если учесть, с чего я начинал свой жизненный путь: следуя по пути, который должен был привести меня к торговле домашней птицей, в конце концов я пришел к геометрии, общей теории относительности и теории струн.

Я родился в 1949 году в континентальном Китае, через год после моего рождения семья переехала в Гонконг. Отец был университетским профессором, имеющим весьма скромное жалованье и жену с восемью детьми, которых нужно было как-то прокормить. Несмотря на то что ему приходилось преподавать сразу в трех университетах, его заработок был столь скуден, что нам едва хватало на еду. Мы росли в бедности, без электричества и водопроводной воды; ванной нам служила ближайшая река. Однако наше богатство состояло в другом. Будучи философом, отец побуждал меня воспринимать мир с более отвлеченной точки зрения. Помню, как маленьким ребенком, подслушивая беседы, которые он вел со студентами и коллегами, я чувствовал волнение, хотя не понимал точного значения многих слов.

Отец всегда поощрял мои занятия математикой, хотя их и нельзя было назвать многообещающими. В возрасте пяти лет я сдавал вступительный экзамен в престижную городскую школу, но провалился именно на математике, поскольку вместо числа 75 я написал 57, а вместо числа 96 — 69 — ошибка, которую, как я сейчас полагаю, проще допустить в китайском, чем в английском. В результате мне пришлось учиться в посредственной сельской школе вместе с кучей хулиганистых ребятишек, которых едва ли заботило их образование. Чтобы выжить, мне тоже приходилось быть хулиганистым, настолько хулиганистым, что подростком я на время оставил школу и возглавил шайку юнцов, которые, так же как и я, привыкли слоняться по улицам в поисках неприятностей, и чаще всего их находили. Трагическое событие все изменило в моей жизни. Когда мне было четырнадцать, неожиданно умер отец, оставив нашу семью не только убитой горем, но и без средств к существованию, с кучей долгов и отсутствием какого-либо дохода. Поскольку теперь мне приходилось зарабатывать деньги для поддержания семьи, дядя посоветовал мне бросить школу и заняться разведением уток. Но у меня была другая идея: я решил преподавать математику другим ученикам. Учитывая наши финансовые обстоятельства, я понимал, что у меня есть только один шанс на успех, и сделал ставку на математику — все или ничего. Если бы я не справился с этим, моя судьба была бы предрешена, и второго шанса (кроме разведения домашней птицы) у меня не было. В подобных ситуациях, как мне кажется, люди стараются трудиться с удвоенным упорством. И хотя у меня, возможно, есть свои недостатки, никто и никогда не мог обвинить меня в лени.

Я не был лучшим учеником в средней школе, но старался наверстать упущенное в колледже. В первый же год я зарекомендовал себя как весьма неплохой студент, хотя и не добился каких-либо исключительных успехов. Все стало гораздо лучше во второй год, когда в наш Китайский университет Гонконга пришел преподавать юный геометр из Беркли, Стивен Салафф. Благодаря Салаффу я впервые почувствовал вкус настоящей математики. Мы вместе читали курс по обыкновенным дифференциальным уравнениям и позже совместно написали книгу по этому предмету. Салафф представил меня Дональду Сарасону, выдающемуся математику из Беркли, который проложил для меня дорогу поступления в аспирантуру после окончания всего трех курсов бакалавриата. Никакие проблемы, с которыми мне приходилось сталкиваться в математике, не могут сравниться с теми бюрократическими преградами, которые нам пришлось преодолеть при помощи Ч. Ш. Черна, великого китайского геометра, также работающего в Беркли, — чтобы добиться разрешения на мое досрочное поступление.

Попав в Калифорнию в двадцать лет и видя все многообразие математических дисциплин, открывающееся передо мной, я плохо представлял, в каком направлении мне двигаться. Сначала я склонился к операторной алгебре, одной из наиболее абстрактных областей математики, поскольку у меня было смутное чувство, что качество теории определяется степенью ее абстрактности.

Хотя в Беркли процветало множество математических дисциплин, в то время он был прежде всего одним из мировых центров — если не единственным мировым центром — развития геометрии, и присутствие в нем многих блестящих ученых, таких как Черн, начало оказывать на меня неумолимое влияние. Все это вместе с растущим пониманием того, что геометрия представляет собой огромную и богатую область, изобилующую многими возможностями, постепенно привело меня в их сообщество.

При этом я продолжал изучать столько разных предметов, сколько мог, посещая сразу шесть учебных курсов, изучая попутно материалы из области геометрии, топологии, дифференциальных уравнений, групп Ли, комбинаторики, теории чисел и теории вероятностей. Эти занятия удерживали меня в аудитории с 8:00 до 17:00 ежедневно, едва оставляя время на обед. Оставшееся время я проводил в математической библиотеке, ставшей для меня вторым домом. Я читал почти каждую книгу, которая попадала мне в руки. Поскольку в более молодом возрасте я не мог позволить себе покупать книги, то теперь, прохаживаясь между стеллажами, я ощущал себя ребенком, попавшим в магазин сладостей. По окончании обязательных занятий я часто оставался в библиотеке вплоть до момента закрытия, заработав себе репутацию человека, постоянно уходящего из читального зала последним. Конфуций как-то сказал: «Однажды я провел в размышлениях целый день без еды и целую ночь без сна, но я ничего не добился. Было бы лучше посвятить то время учению». И хотя тогда мне эта цитата еще не была знакома, я, тем не менее, полностью следовал именно этому образу мыслей.

Так почему же из всех областей математики именно геометрия заняла центральное место в моих мыслях и мечтах? Прежде всего потому, что она произвела на меня впечатление математической дисциплины, находящейся ближе всего к природе и, следовательно, ближе всего к ответам на те вопросы, которые заботили меня более всего.

Кроме того, я нахожу полезным, сталкиваясь со сложными понятиями, представлять себе их наглядные изображения, что весьма редко удается сделать во многих трудных для понимания областях алгебры и теории чисел. Плюс ко всему, геометрией в Беркли занималась совершенно потрясающая группа людей, в числе которых были профессора Черн и Чарльз Морри и некоторые из более молодых представителей факультета, такие как Блейн Лоусон, а также аспиранты, такие как будущий обладатель медали Филдса Уильям Тёрстон, зародившие во мне желание приобщиться к их азарту и надежду стать одним из них.

Наконец, существовало и гораздо большее сообщество людей, не только из других университетских кампусов, но и со всего мира, и — как мы уже успели убедиться в этой главе, живших на протяжении всей человеческой истории, — которые прокладывали путь в ту плодородную область, в которую мне посчастливилось войти. Это что-то сродни ньютоновской сентенции о том, что ему посчастливилось «стоять на плечах гигантов», хотя Ньютон и сам по себе был одним из таких гигантов, на плечах которого мы сейчас стоим.

Примерно в то же время, когда я впервые начал размышлять об общей теории относительности Эйнштейна и кривизне абсолютно пустого пространства, мой руководитель Черн вернулся из поездки на восточное побережье весьма взбудораженным, поскольку он только что услышал от известного принстонского математика Андре Вейля о том, что так называемая гипотеза Римана, проблема, сформулированная еще столетие назад, возможно, скоро будет решена. Эта гипотеза относится к вопросу о распределении простых чисел, которое, как казалось до этого, не подчиняется никакому закону. Однако Риман предположил, что на самом деле частота появления простых чисел описывается сложной функцией, так называемой дзета-функцией Римана. В частности, он высказал предположение, что частота появлений простых чисел соответствует расположению нулей соответствующей дзета-функции. Утверждение Римана подтверждено для более чем миллиарда нулей дзета-функции, но строгого доказательства до сих пор так и не было получено.

Впрочем, несмотря на то, что эта проблема является одной из важнейших в математике — и если бы мне посчастливилось ее решить, это не только принесло бы мне бесчисленные предложения работы, но и прославило бы мое имя на всю оставшуюся жизнь, — я совсем не испытывал особого энтузиазма от предложения Черна. Гипотеза Римана не волновала меня, а для того чтобы решить столь грандиозную задачу, поставившую в тупик так много талантливых ученых и требующую многих лет на ее завершение, необходимо по крайней мере быть ею взволнованным. Отсутствие у меня страсти к решению проблемы, естественно, заметно уменьшало мои шансы на ее решение, поэтому если бы я работал над доказательством гипотезы Римана, то вполне возможно, что и спустя много лет мне нечего было бы сказать по этому вопросу. Помимо этого, мне слишком нравятся наглядные изображения. Мне нравятся математические структуры, на которые можно каким-либо образом взглянуть, именно за это я и люблю геометрию. Да и вдобавок мне уже были известны некоторые области геометрии, в которых я мог достигнуть определенных результатов — хотя, возможно, и не столь впечатляющих.

Это чем-то похоже на рыбалку. Если тебе достаточно и маленькой рыбки, ты получишь удовольствие, если поймаешь хоть что-то. А вот если ты собираешься поймать самую большую из рыб, которую когда-либо ловили, — эдакое мифическое создание, существующее только в легендах, — то, скорее всего, придешь домой с пустыми руками. Уже прошло тридцать пять лет, а гипотеза Римана по-прежнему остается недоказанной. Как говорят математики: то, что доказано на 90 процентов, — на самом деле не доказано.

Так я рассуждал, отвергая предложение Черна. Но на самом деле все было гораздо серьезнее. В то время, как я уже говорил, я был полностью поглощен общей теорией относительности, пытаясь понять, какие из особенностей нашей Вселенной возникают вследствие взаимодействия гравитации, искривления пространства и геометрии. Я не знал, когда мои мысли повернулись в этом направлении, однако я предчувствовал, что нахожусь в начале великого похода, собирая воедино все силы геометрии, чтобы двинуться в сторону истины.

Будучи ребенком, появившимся на свет в более чем стесненных обстоятельствах, я никогда не имел возможности увидеть большую часть мира. Моя страсть к геометрии родилась у меня еще в раннем возрасте из желания нанести на карту страну, столь большую, как Китай, и путешествовать по морю, не имеющему конца. Мне посчастливилось совершить куда более дальнее путешествие — эту возможность мне предоставила геометрия. Только теперь вместо одной страны передо мной была вся Земля, а вместо моря — Вселенная. Ну а маленькую соломенную сумку, которую я собирался всюду возить за собой, заменил небольшой портфель с линейкой, циркулем и транспортиром.

14. Georg Friedrich Bernhard Riemann, “On the Hypotheses Which Lie at the Foundations of Geometry,” lecture, Gottingen Observatory, June 10, 1854.

15. E. T. Bell, Men of Mathematics (New York: Simon & Schuster, 1965), p. 21.

16. Leonard Mlodinow, Euclid's Window (New York: Simon & Schuster, 2002), p. xi.

17. Edna St. Vincent Millay, “Euclid Alone Has Looked on Beauty Bare,” quoted in Robert Osserman, Poetry of the Universe (New York: Anchor Books, 1995), p. 6.

18. Andre Nikolaevich Kolmogorov, Mathematics of the 19th Century (Birkhauser, 1998).

19. Deane Yang (Polytechnic Institute of New York University), e-mail letter to author, April 20, 2009.

20. Mlodinow, Euclid's Window, p. 205.

21. Brian Greene, The Elegant Universe (New York: Vintage Books, 2000), p. 231.

22. C. N. Yang. “Albert Einstein: Opportunity and Perception,” speech, 22nd International Conference on the History of Science, Beijing, China, 2005.

23. Chen Ning Yang, “Einstein’s Impact on Theoretical Physics in the 21st Century,” AAPPS Bulletin 15 (February 2005).

24. Greene, The Elegant Universe, p. 72.