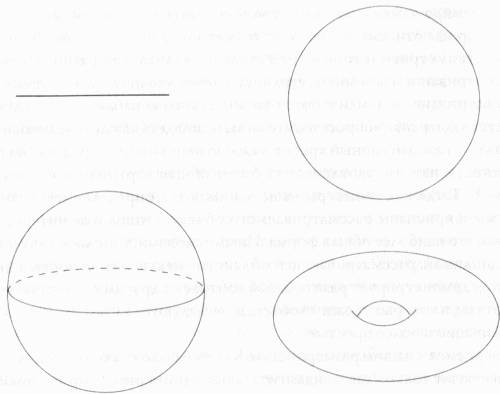
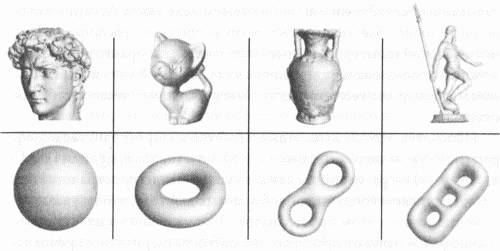
Глава 1. Вселенная где-то рядом

Изобретение телескопа и последующее его усовершенствование на протяжении многих лет помогло подтвердить факт, ставший сегодня азбучной истиной: есть многое во Вселенной, что недоступно нашим наблюдениям. Действительно, согласно имеющимся на сегодняшний день данным, почти три четверти материального мира существует в загадочной, невидимой форме, называемой темной энергией. Большая часть из оставшегося, за исключением только четырех процентов, приходящихся на обычную материю (и в том числе на нас с вами), носит название темной материи. Оправдывая свое название, эта материя может считаться «темной» во всех смыслах: ее трудно увидеть и не менее трудно понять.

Доступная наблюдению область космического пространства представляет собой шар радиусом порядка 13,7 миллиарда световых лет. Эту область часто называют объемом Хаббла, что, разумеется, не предполагает, будто Вселенная ограничена ее пределами. Согласно современным научным данным, Вселенная безгранична, так что прямая линия, проведенная из точки, в которой мы находимся, в любом заданном направлении, вытянется в бесконечность.

Правда, существует вероятность, что пространство искривлено настолько, что Вселенная все же конечна. Но даже если это и так, то кривизна эта настолько мала, что, согласно некоторым теориям, доступный нашему наблюдению объем Хаббла представляет собой не более чем одну из тысячи подобных ему областей, существующих во Вселенной.

А недавно выведенный на орбиту космический телескоп «Планк» уже в ближайшие годы, возможно, покажет, что космическое пространство состоит из не менее чем миллиона объемов Хаббла, только один из которых нам когда-либо будет доступен.^[5] В целом я согласен с астрофизиками, хотя и понимаю, что некоторые из приведенных выше чисел могут быть спорными. Бесспорно только то, что мы видим лишь верхушку айсберга.

С другой стороны, микроскопы, ускорители частиц и различные устройства, предназначенные для получения данных о микромире, продолжают открывать «миниатюрную» Вселенную, освещая ранее недоступный для непосредственного исследования мир клеток, молекул, атомов и еще более мелких объектов. Впрочем, сейчас эти исследования перестали кого-либо удивлять. Более того, мы вправе ожидать, что наши телескопы проникнут еще глубже в космическое пространство, а микроскопы и другие приборы вынесут на свет еще больше объектов невидимого мира.

Впрочем, за последние десятилетия благодаря ряду достижений теоретической физики, а также некоторым успехам геометрии, к которым мне посчастливилось быть причастным, мы смогли осознать нечто еще более удивительное: Вселенная не только больше, чем мы способны увидеть, но и, возможно, содержит также большее (или даже много большее) число измерений, чем те три пространственных измерения, с которыми мы привыкли иметь дело.

Высказанное мною утверждение трудно принять на веру, поскольку если и есть что-то, что мы можем с уверенностью сказать об окружающем нас мире, что-то, что говорят нам наши ощущения, начиная с первого сознательного момента и первых осязательных опытов, — то это число измерений. И это число — три. Не «три плюс-минус один», а именно три. По крайней мере, так казалось на протяжении очень длительного времени. Но все же, возможно (только лишь возможно), что помимо этих трех существуют и некие дополнительные измерения, настолько малые, что мы просто до настоящего времени не обращали на них внимания. И, несмотря на их небольшой размер, они могут играть столь важную роль, значение которой мы едва ли можем оценить, находясь в нашем привычном трехмерном мире.

Возможно, с этим нелегко смириться, но прошедшее столетие научило нас тому, что всякий раз, когда мы выходим за рамки повседневного опыта, интуиция начинает нас подводить. Специальная теория относительности утверждает, что если мы будем двигаться достаточно быстро, то время для нас станет течь медленнее, и это никак не соотносится с нашими повседневными ощущениями. Если мы возьмем чрезвычайно маленький объект, то, согласно требованиям квантовой механики, не сможем точно сказать, где он находится. Например, если мы захотим экспериментально определить, за дверью А или за дверью В находится объект, то обнаружим, что он ни там, ни тут, — в том смысле, что он в принципе не имеет абсолютного местоположения. (Возможна также ситуация, когда объект оказывается в обоих местах одновременно!) Другими словами, многие странные явления в нашем мире не только возможны, но и вполне реальны, и, быть может, крошечные скрытые измерения представляют собой как раз одну из таких реальностей.

Если эта идея верна, то должно существовать нечто вроде скрытой Вселенной, представляющей собой существенный фрагмент объективной реальности, находящейся за пределами наших ощущений. Это был бы настоящий научный переворот сразу по двум причинам. Во-первых, существование дополнительных измерений — главная тема научной фантастики более чем ста последних лет — само по себе столь потрясающе, что достойно занять почетное место в ряду величайших открытий в истории физики. А во-вторых, подобное открытие стало бы не завершением физической теории, а, напротив, отправной точкой для новых исследований. Ибо как генерал получает более четкую картину боя, наблюдая за ходом сражения с какого-нибудь возвышенного места, используя тем самым преимущества, которые дает ему дополнительное вертикальное измерение, так и законы физики могли бы приобрести более наглядный вид и, следовательно, стать более простыми для понимания, если смотреть на них с позиции более высоких размерностей.

Нам привычны перемещения в трех основных направлениях: север-юг, запад-восток, вверх-вниз. (Или, если читателю удобнее: вправо-влево, вперед-назад, вверх-вниз.) Куда бы мы ни шли и ни ехали — будь то поездка в бакалейный магазин или полет на Таити, — наше перемещение всегда представляет собой суперпозицию перемещений в этих трех независимых направлениях. Существование именно трех измерений настолько привычно, что даже попытка представить себе некое дополнительное измерение и понять, куда оно может быть направлено, видится тщетной. В течение долгого времени казалось, что то, что мы видим, то и имеем. Фактически именно это утверждал более двух тысяч лет назад Аристотель в своем трактате «О небе»: «Величина, делимая в одном измерении, есть линия, в двух — плоскость, в трех — тело, и, кроме них, нет никакой другой величины, так как три измерения суть все измерения».^[6] В 150 году нашей эры астроном и математик Клавдий Птолемей попытался строго доказать, что существование четырех измерений невозможно, аргументируя тем, что нельзя построить четыре взаимно перпендикулярные прямые. Четвертый перпендикуляр, согласно его утверждению, должен был бы быть «совершенно неизмеримым и неопределимым».^[7] Его аргументация, однако, представляла собой не столько строгое доказательство, сколько отражала нашу неспособность представить и изобразить что-либо в четырех измерениях.

Для математиков каждое измерение суть «степень свободы» — независимое направление перемещения в пространстве. Муха, летающая над нашими головами, способна перемещаться в любом разрешенном в небе направлении. Если на ее пути нет препятствий, то она имеет три степени свободы. Представим теперь, что муха где-нибудь на автомобильной парковке завязла в свежем гудроне. Пока она временно лишена возможности двигаться, число ее степеней свободы равно нулю, и она полностью ограничена в своих перемещениях одной точкой — миром с нулевой размерностью. Но это создание упорно, и не без борьбы оно все же выбирается из гудрона, хотя и повреждает при этом крыло. Лишенная возможности взлететь, муха теперь имеет только две степени свободы и может разве что ползать по парковке. Почувствовав приближение хищника — например, проголодавшейся лягушки, — героиня нашего повествования ищет убежище в ржавой выхлопной трубе. Теперь у мухи только одна степень свободы, по крайней мере в течение того времени, пока ее движение ограничено одномерным (линейным) миром узкой трубы.

Но все ли варианты перемещения мы рассмотрели? Муха может летать в воздухе, прилипнуть к гудрону, ползти по асфальту или перемещаться внутри трубы — можно ли представить что-нибудь еще? Аристотель или Птолемей сказали бы «нет», что, может быть, и верно с точки зрения не особо предприимчивой мухи, однако для современных математиков, не находящих убедительных причин останавливаться на трех измерениях, этим дело не ограничивается. Напротив, они убеждены, что для правильного понимания таких геометрических концепций, как кривизна или расстояние, их следует рассмотреть во всех возможных размерностях от нуля до n, причем n может быть очень большим числом. Охват рассматриваемой концепции будет неполным, если мы остановимся на трех измерениях, — суть в том, что если какое-либо правило или закон природы работают в пространстве любой размерности, то такие правила и законы являются более сильными и, скорее всего, более фундаментальными, чем утверждения, справедливые только в частных случаях.

Даже если задача, над которой вы бьетесь, относится только к двух- или трехмерному случаю, возможно, ключом к решению окажется рассмотрение задачи в других размерностях. Вернемся к нашему примеру с мухой, летающей в трехмерном пространстве и имеющей три возможных направления движения, или три степени свободы. Теперь представим себе еще одну муху, которая свободно перемещается в том же пространстве; для нее, как и для первой мухи, тоже существуют ровно три степени свободы, но система в целом имеет уже не три, а шесть измерений — шесть независимых направлений для перемещения. Если количество мух, беспорядочно кружащихся в пространстве и движущихся независимо друг от друга, станет еще больше, то соответственно возрастут и сложность системы, и ее размерность.

Одним из преимуществ перехода к системам с более высокой размерностью является возможность предугадывать закономерности, которые невозможно было бы увидеть в более простой модели. В следующей главе, например, мы обсудим тот факт, что на сферической планете, полностью покрытой огромным океаном, вся вода не может одновременно течь в одном направлении, например с запада на восток, в каждой точке. В таком океане будут существовать особые точки, в которых вода вообще не будет двигаться. И хотя это правило применимо к двухмерной поверхности, оно может быть получено только путем исследования системы с большим числом измерений, в которой рассматриваются все возможные конфигурации, а именно все возможные перемещения малых порций воды по поверхности планеты. По этой причине мы постоянно переходим к более высоким размерностям, чтобы увидеть, к чему это может привести и что мы можем узнать. Несомненно, введение дополнительных измерений приводит к усложнению системы. В топологии, где объекты классифицируются в терминах формы в наиболее общем смысле этого слова, имеется два вида одномерных пространств: линия (кривая с двумя концами) и окружность (замкнутая кривая). Других просто не существует. Вы справедливо заметите, что линия может быть волнистой, а замкнутая кривая может иметь вытянутую форму, но эти вопросы относятся к области геометрии, а не топологии. Разница между геометрией и топологией столь же велика, как разница между рассматриванием земной поверхности через увеличительное стекло и рассматриванием Земли с борта космического корабля. В этом случае следует задать себе вопрос: хотите ли вы разглядеть каждую мельчайшую деталь — каждый горный хребет, каждую неровность и трещину на поверхности или вас удовлетворит более общая картина («огромный шар»)? Тогда как геометры чаще занимаются определением точной формы и кривизны рассматриваемого объекта, топологов интересует только его наиболее общая форма. Иными словами, топология является дисциплиной, рассматривающей объект как некую целостность, а этот подход демонстрирует разительный контраст с другими областями математики, в которых сложные объекты исследуются путем разбиения их на меньшие и более простые.

Вернемся к нашим размерностям. Как уже было сказано, в топологии существуют только две фундаментальные одномерные формы: прямая линия, которая идентична любой волнистой линии, и окружность, которая идентична любой петле — вытянутой, волнистой или даже имеющей форму квадрата — любой, какую только можно себе представить. Двухмерные пространства также можно разделить на два фундаментальных типа: это либо сферы, либо бублики. Тополог рассматривает любую двухмерную поверхность как сферу в том случае, если в ней нет дырок, при этом включая в эту категорию такие привычные нам геометрические тела, как кубы, призмы, пирамиды и даже похожие на дыни объекты, которые носят название эллипсоидов.

Вся разница между бубликом и сферой состоит исключительно в наличии дырки в первом и отсутствии ее во второй: неважно, насколько сильно вы деформировали сферу, — пока вы не проделаете в ней дырку, вы ни за что не получите из нее бублик, и наоборот. Другими словами, нельзя проделать ни одной новой дырки в объекте или разорвать его каким-то другим образом, не изменив при этом его топологию. И наоборот, тополог считает две формы функционально эквивалентными, если, вылепив их из пластичной глины или пластилина, можно трансформировать одну в другую, только сжимая и растягивая, но не разрывая ее.

Рис. 1.1. В топологии существуют два вида одномерных пространств, принципиально отличных друг от друга: линия и окружность. Можно преобразовать окружность в петлю любой формы, но превратить окружность в линию, не разрезая ее, невозможно. Двухмерные поверхности, являющиеся ориентируемыми, — что означает, что они, подобно мячу, имеют две поверхности, а не одну, как лента Мёбиуса, — могут быть классифицированы по их роду, грубо говоря, по количеству дырок в данной поверхности. Так, сфера, имеющая род 0, в которой нет дырок, принципиально отлична от бублика, имеющего род 1 и, соответственно, одну дырку. Как и в случае с окружностью и прямой, невозможно превратить сферу в бублик, не проделав в ней дырку

Бублик с одной дыркой называется тором, но бубликоподобные поверхности могут иметь любое число дырок. Двухмерные поверхности, которые являются одновременно компактными (замкнутыми и ограниченными в пространстве) и ориентируемыми (имеющими две стороны), можно классифицировать по числу дырок в них, или по роду. Объекты, имеющие различный вид в двух измерениях, считаются топологически идентичными, если они относятся к одному и тому же роду.

Сделанное выше утверждение о существовании только двух возможных двухмерных форм — бублика и сферы, справедливо лишь в случае, когда мы ограничиваемся ориентируемыми поверхностями, а именно о таких поверхностях мы в основном и будем говорить в этой книге. Мяч, например, имеет две стороны — внутреннюю и внешнюю, и то же самое справедливо в отношении велосипедной камеры. Но существуют и более сложные поверхности — односторонние, или «неориентируемые», такие как бутылка Клейна или лента Мёбиуса, для которых указанное утверждение не верно.

Рис. 1.2. В топологии сфера, куб и тетраэдр (как и многие другие геометрические тела) рассматриваются как эквивалентные, поскольку они могут быть получены друг из друга путем деформации, растяжения или сжатия без разрывов и разрезов

Рис. 1.3. Поверхности нулевого, первого, второго и третьего рода; термин «род» означает число дырок

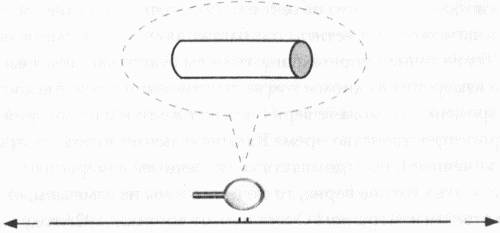
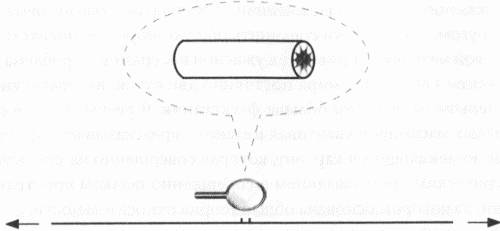
Когда количество измерений превышает два, число возможных форм резко возрастает. Рассматривая пространства с большим числом измерений, мы должны допускать движения в тех направлениях, которые мы не в состоянии наглядно себе представить. Замечу, что речь идет не о тех направлениях, которые лежат, скажем, между направлением на север и направлением на запад (например, на северо-запад) и даже не о направлениях типа «к северу через северо-запад». Речь о таких направлениях, которые можно указать, только выйдя за пределы привычной нам системы координат, держа путь вдоль оси, которую только предстоит нарисовать.

Один из первых крупных прорывов на пути к изображению многомерных пространств был совершен в XVII веке великим Рене Декартом, французским математиком, философом, ученым и писателем. Впрочем, для меня он в первую очередь — геометр. В числе прочих вкладов в науку Декарт показал, что мышление на языке координат гораздо продуктивнее геометрических построений.

Система координат, которую он создал и которая сейчас носит название декартовой, объединила алгебру и геометрию. В узком смысле Декарт показал, что, построив три оси (x, y и z), перпендикулярные друг другу и пересекающиеся в одной точке, можно точно указать положение любой точки в трехмерном пространстве, используя три числа: x, y и z, называемые координатами. Но на самом деле вклад Декарта гораздо шире — одним блестящим жестом он значительно расширил область исследований геометрии. Применение системы координат сделало возможным использование алгебраических уравнений для описания сложных многомерных геометрических фигур, которые нелегко себе представить.

Используя этот подход, можно работать с пространством любой размерности — не обязательно (x, y, z), но и (а, b, с, d, e, f) или (j, k, l, m, n, о, p, q, r, s) — размерность каждого конкретного пространства определяется числом координат, необходимых для того, чтобы указать положение точки в этом пространстве. Вооружившись такой системой, можно рассматривать пространства любой размерности и проводить в них различные вычисления, не заботясь о том, как эти пространства изобразить.

Через два столетия после Декарта эту идею подхватил и развил великий немецкий математик Георг Фридрих Бернхард Риман. В 1850-х годах, работая над геометрией искривленных (неевклидовых) пространств — этой темы мы еще коснемся в следующей главе, — Риман установил, что такие пространства не ограничены в смысле количества измерений. Он также показал, как можно в этих пространствах точно рассчитывать расстояние, кривизну и другие характеристики. В 1854 году при соискании должности экстраординарного профессора Риман сделал доклад «О гипотезах, лежащих в основах геометрии». Изложенные в нем принципы известны с тех пор как риманова геометрия. В этом докладе Риман задался вопросом о размерности и геометрии Вселенной как целого. Помимо этого, еще не достигнув тридцатилетнего возраста, Риман начал работу над математической теорией, способной связать воедино электричество, магнетизм, свет и гравитацию, — предвосхитив тем самым задачу, которая по сей день не дает покоя ученым.

Хотя Риману и удалось освободить пространство от ограничений евклидовой плоскости и трех измерений, физики в течение десятилетий не обращали внимания на его идеи. Отсутствие какого-либо интереса с их стороны можно объяснить отсутствием каких-либо экспериментальных доказательств, позволяющих сделать вывод об искривленности пространства или о существовании дополнительных измерений, помимо трех. Таким образом, новаторские математические построения Римана настолько опередили физику того времени, что потребовалось еще почти пятьдесят лет, чтобы физики (или, по крайней мере, один из физиков) смогли воспользоваться его идеями. Этим физиком стал Альберт Эйнштейн.

При разработке специальной теории относительности, которая была впервые представлена в 1905 году и в последующие годы развита в общую теорию относительности, Эйнштейн обратил внимание на идею немецкого математика Германа Минковского, состоящую в том, что время неразрывно связано с тремя пространственными измерениями, образуя с ними новую геометрическую конструкцию, известную как пространство-время. Так неожиданно время обрело статус четвертого измерения, которое еще десятилетиями ранее было включено Риманом в его элегантные уравнения.

Любопытно, что британский писатель Герберт Джордж Уэллс предвосхитил ту же идею десятью годами ранее в своем романе «Машина времени». Как объясняет путешественник по времени, главный герой романа: «И все же существуют четыре измерения, из которых три мы называем пространственными, а четвертое — временным. Правда, существует тенденция противопоставить три первых измерения последнему».^[8]

Практически ту же самую мысль повторил Минковский в своей речи, произнесенной в 1908 году, за исключением разве что того факта, что он смог привести математическое обоснование своего претенциозного заявления: «Отныне время само по себе и пространство само по себе становятся пустой фикцией, и только единение их сохраняет шанс на реальность».^[9] Разумное обоснование того, что эти два понятия (пространство и время) были соединены чем-то вроде брачного союза — если, конечно, заключение брачного союза вообще нуждается в обосновании, — состоит в том, что любой объект движется не только через пространство, но и через время. Поэтому для того, чтобы описать какое-либо событие в четырехмерном пространственно-временном континууме, нужно не три, а четыре координаты — три пространственные и одна временная: (x, y, z, t).

Хотя эта идея и может показаться немного пугающей, ее легко проиллюстрировать наглядным примером. Предположим, что вы собираетесь встретиться с кем-либо в торговом центре. Вы запомнили, где находится здание — например, на углу Первой улицы и Второй авеню, — и договариваетесь встретиться на четвертом этаже. Так вы задаете свои пространственные координаты x, y и z. Теперь остается только установить четвертую координату — принять решение о времени встречи. Когда все координаты, наконец, заданы, вашу встречу можно считать полностью подготовленной, за исключением разве что каких-либо непредвиденных обстоятельств, которые могут вмешаться в дело. Однако если вы хотите представить описанную выше ситуацию, пользуясь терминологией Эйнштейна, нельзя считать, что вы отдельно договариваетесь о месте и отдельно о времени встречи. На самом деле вы договариваетесь о расположении этого события в пространственно-временном континууме.

Так в начале XX века концепция пространства, в котором обитало человечество с античных времен, в один момент превратилась из уютного трехмерного уголка в эзотерическое царство четырехмерного пространства-времени. Концепция пространственно-временного континуума стала краеугольным камнем построенной Эйнштейном теории гравитации — общей теории относительности. Но является ли она тем самым концом пути, о котором мы уже говорили ранее? Станет ли представление о четырех измерениях окончательным или наше знание о пространстве-времени будет развиваться дальше? Возможный ответ на этот вопрос неожиданно нашелся в рукописи, присланной на рецензию Эйнштейну малоизвестным в то время немецким математиком Теодором Калуцой.

В теории Эйнштейна пространство-время задается десятью числами, позволяющими точно описать действие гравитации в четырех измерениях. Для более краткой записи уравнений гравитационного поля принято помещать эти десять чисел в матрицу 4×4, более известную как метрический тензор, — квадратную таблицу, играющую в многомерных пространствах роль «линейки». В нашем случае метрика имеет 16 компонентов, но только 10 из них являются независимыми. 6 чисел из 16 повторяются, потому что гравитация наряду с другими фундаментальными взаимодействиями является по своей природе симметричной.

Рис. 1.4. Поскольку мы не знаем, как нарисовать четырехмерное изображение, этот рисунок представляет собой весьма грубое, умозрительное отображение четырехмерного пространства-времени. В основе концепции пространства-времени лежит предположение, что три пространственных измерения нашего мира (представленные здесь в виде осей x, y и z) полностью равноправны с четвертым измерением — временем. Мы представляем себе время как постоянно изменяющуюся непрерывную переменную, и на данном рисунке представлены моментальные снимки координатных осей, сделанные в различные моменты времени: t1, t2, t3 и т. д. Таким способом мы попытались показать, что в целом существуют четыре измерения: три пространственных и еще одно, представленное временем

В своей статье Калуца взял за основу общую теорию относительности Эйнштейна и добавил еще одно дополнительное измерение, расширив матрицу 4×4 до размера 5×5. Расширив пространственно-временной континуум до пяти измерений, Калуца сумел объединить две известные на тот момент физические силы — гравитацию и электромагнетизм — в одну единую силу. Для наблюдателя, находящегося в пятимерном мире, который вообразил Калуца, эти силы абсолютно идентичны, что, собственно, и понимается под объединением. А вот в четырехмерном мире они не сольются в одну, а, напротив, будут полностью независимы друг от друга.

Можно сказать, что это происходит потому, что обе силы просто не умещаются в одной матрице 4×4. В то же время дополнительное измерение предоставляет достаточно свободного места в матрице для обеих сил, позволяя им быть составляющими одной более всеобъемлющей силы.

Рискуя навлечь на себя неприятности, все же скажу, что, по моему мнению, только математик обладает достаточной смелостью, чтобы считать, что переход к пространствам более высокой размерности позволит проникнуть в суть явления, которое до тех пор безуспешно пытались исследовать в пространствах более низкой размерности. Я так считаю потому, что математики все время имеют дело с дополнительными измерениями. Нам настолько удобно ими пользоваться, что мы уже не обращаем на них особого внимания. Вполне возможно, что мы способны манипулировать дополнительными измерениями даже ночью, не выходя из фазы быстрого сна.

Впрочем, хотя я и убежден, что только математик способен на столь смелый шаг, в данном случае математик в своей работе опирался на работу физика, Эйнштейна. В свою очередь другой физик, Оскар Клейн, о котором мы вскоре поговорим, построил свою работу на фундаменте, заложенном математиком Калуцой. По этой причине я предпочитаю говорить, что я работаю на стыке двух наук — математики и физики, где происходят процессы сродни перекрестному опылению в ботанике. Именно благодаря тому, что я с 1970-х годов блуждаю по этой плодородной области, мне удалось стать причастным ко многим захватывающим открытиям.

Вернемся к провокационной идее Калуцы. Люди в те времена задавались вопросом, который не утратил своей актуальности и по сей день. И, несомненно, этим же вопросом задавался и Калуца: если действительно существует пятое измерение — абсолютно новое направление движения в знакомом нам четырехмерном мире, — почему его никто до сих пор не видел?

Очевидное объяснение состоит в том, что это измерение чрезвычайно мало. Но где же оно может находиться? Представьте себе нашу четырехмерную Вселенную как одну линию, которая простирается бесконечно в обоих направлениях. Основная идея заключается в том, что три пространственных измерения чрезвычайно (либо бесконечно) велики. Допустим, что время также можно представить в виде бесконечной линии, хотя это допущение и может быть спорным. В любом случае, каждая точка w на том, что мы представили себе как линию, на самом деле обозначает определенную точку (x, y, z, t) в четырехмерном пространстве-времени.

В геометрии линии имеют только длину, но не имеют толщины. Рассмотрим, однако, возможность того, что наша линия все же имеет какую-то толщину, увидеть которую можно лишь через очень мощное увеличительное стекло. С этой точки зрения линия, которую мы себе представили, — на самом деле не линия, а очень узкий цилиндр, что-то вроде садового шланга. Теперь, если мы разрежем наш шланг в каждой точке w, в сечении этого разреза мы получим крошечную окружность, которая, как уже говорилось выше, является одномерной кривой. Таким образом, эта окружность представляет собой дополнительное пятое измерение, которое в определенном смысле «прикреплено» к каждой точке четырехмерного пространства. Измерение, скрученное в крошечную окружность, в научном языке называется компактным (или компактифицированным). Значение слова «компактное» легко понять интуитивно: физики иногда говорят, что объект или пространство является компактным, если вы можете поместить его в багажник своего автомобиля. Существует и более точное определение: если вы будете двигаться вдоль компактного измерения в одном и том же направлении в течение достаточно долгого времени, то сможете вернуться в ту же точку, из которой вышли. Пятимерное пространство-время Калуцы включает в себя как протяженные (бесконечные), так и компактные (конечные) измерения.

Но если эта картина верна, то почему же мы не замечаем, что ходим кругами в пятом измерении? Ответ на этот вопрос в 1926 году дал шведский физик Оскар Клейн, развив тем самым идею Калуцы. Опираясь на квантовую теорию, Клейн рассчитал размер компактного измерения и получил число, которое действительно было крошечным — близким к так называемой планковской длине, величине настолько малой, насколько только можно себе представить — порядка 10^-30см в окружности.^[10] Этим и объясняется то, что пятое измерение существует, оставаясь при этом ненаблюдаемым. Мы не способны ни увидеть это крошечное измерение, ни зафиксировать движение в его пределах.

Теория Калуцы-Клейна, как ее теперь называют, замечательно иллюстрировала роль дополнительных измерений в демистификации тайн природы. После размышлений над статьей Калуцы, длившихся на протяжении более двух лет, Эйнштейн написал в рецензии, что эта идея ему «чрезвычайно»^[11] понравилась. И понравилась она ему настолько, что в ближайшие двадцать лет он постоянно возвращался к ней (иногда в сотрудничестве с физиком Питером Бергманом). Но, в конце концов, теория Калуцы-Клейна была отвергнута. Отчасти это произошло потому, что эта теория предсказывала существование элементарной частицы, которая так никогда и не была обнаружена, отчасти — из-за того, что попытки использовать теорию для расчета отношения массы электрона к его заряду привели к неверным результатам. К тому же Калуца и Клейн — так же, как и Эйнштейн после них, — пытались объединить только электромагнетизм и гравитацию, поскольку ничего не знали ни о слабом, ни о сильном взаимодействии, природа которых была непонятна вплоть до второй половины XX столетия. По этой причине их попытки объединить все силы в одну были с самого начала обречены на провал, так как в колоде, которой они играли, недоставало пары важных карт. Но, по-видимому, основной причиной, по которой теория Калуцы-Клейна была отброшена, стало то, что ее создание пришлось как раз на то время, когда начинала набирать обороты квантовая революция.

Рис. 1.5. Попробуем представить бесконечное, четырехмерное пространство-время в виде линии, неограниченно простирающейся в обоих направлениях. Линия, по определению, толщины не имеет. Но если бы мы посмотрели на эту линию через увеличительное стекло, то, как предполагается в теории Калуцы-Клейна, увидели бы, что линия все же имеет некоторую толщину. Это и есть то самое дополнительное скрытое измерение, и его размер ограничивается диаметром окружности сечения нашей линии

Тогда как Калуца и Клейн в центр своей физической модели поставили геометрические идеи, квантовая теория не только не основывается на геометрии, но и, напротив, вступает в противоречие с привычными геометрическими представлениями (этому вопросу посвящена четырнадцатая глава). В результате переворота, произведенного квантовой теорией, вихрем пронесшейся по физике XX века, и того сверхъестественно плодотворного периода, который последовал за этим, об идее дополнительных измерений вновь вспомнили лишь спустя почти пятьдесят лет.

Основанная на геометрии общая теория относительности, опубликованная Эйнштейном в 1915 году и представляющая собой квинтэссенцию современного понимания гравитации, также нашла огромный отклик в среде ученых, неизменно получая подтверждение в каждом последующем эксперименте, проводимом для ее проверки. В свою очередь квантовая теория прекрасно описывает три из четырех известных взаимодействий: электромагнитное, слабое и сильное. Фактически, это наиболее точная из всех существующих и, по словам гарвардского физика Эндрю Строминджера, «возможно, наиболее тщательно проверенная теория за всю историю человеческой мысли».^[12] К примеру, предсказания поведения электрона в электрическом поле совпадают с экспериментальными данными с точностью до десятого знака после запятой.

К сожалению, эти две надежнейшие теории полностью несовместимы друг с другом. Все попытки соединить общую теорию относительности с квантовой механикой приводят к ужасной несуразице. Проблема в том, что объекты квантового мира постоянно движутся, или флуктуируют, и чем меньше размер, тем больше флуктуация. В результате для случая сверхмалых масштабов квантовая механика предсказывает бурную, постоянно изменяющуюся картину, которая совершенно не согласуется с геометрическим представлением о совершенно гладком пространстве-времени, на котором основана общая теория относительности.

В квантовой механике все основано на вероятностях, и когда в квантовую модель пытаются ввести общую теорию относительности, расчеты часто приводят к появлению бесконечных вероятностей. Возникновение при расчетах бесконечных значений является сигналом, что в них допущена какая-то ошибка. Едва ли можно радоваться такому положению дел, когда две наиболее удачные теории — одна, описывающая огромные объекты, такие как планеты и галактики, а вторая — крошечные, такие как электроны и кварки, при объединении дают полную ахинею. Решение оставить квантовую механику и общую теорию относительности в виде двух отдельных теорий тоже нельзя счесть удовлетворительным хотя бы потому, что существуют такие места (например, черные дыры), где очень большое и очень малое сходятся вместе, и ни одна из теорий сама по себе не в состоянии прояснить их природу. «Там уже не будет законов физики, — утверждает Строминджер. — Там будет только один закон, и он будет прекраснейшим из всех существующих».^[13]

Подобное утверждение — будто Вселенную можно описать при помощи «единой теории поля», которая соединяет все силы природы в единое целое, — является не только эстетически привлекательным, но и напрямую связано с представлением о рождении Вселенной в результате Большого взрыва. В тот момент плотность энергии Вселенной была столь велика, что все силы действовали как одна единая сила. Калуце и Клейну, точно так же, как и Эйнштейну, не удалось построить теорию, которая вобрала бы в себя все наши физические знания. Но сейчас, когда у нас больше деталей мозаики, среди которых, будем надеяться, есть все важные элементы, возникает соблазн: а не попробовать ли снова построить единую теорию поля и на этот раз достичь успеха там, где не удалось великому Эйнштейну?

Рис. 1.6. Теория струн взяла на вооружение старую идею Калуцы-Клейна о скрытом «дополнительном» измерении и значительно расширила ее. Если мы внимательно посмотрим на четырехмерное пространство-время, представленное на рисунке в виде линии, то увидим, что на самом деле оно скрывает в себе шесть дополнительных измерений, скрученных в замысловатое, хотя и крошечное геометрическое пространство, известное как многообразие Калаби-Яу. (Более подробно эти пространства будут обсуждаться далее, поскольку они являются основной темой книги.) Какой бы участок линии вы ни вырезали, вы все равно найдете в нем скрытое многообразие Калаби-Яу, и все многообразия, полученные таким способом, будут идентичными

Именно это и пытаются сделать создатели теории струн — захватывающей, хотя и до сих пор не нашедшей экспериментального подтверждения попытки объединить различные взаимодействия путем замены точечных объектов физики элементарных частиц на протяженные (хотя и крошечные) физические объекты, называемые струнами. Как и теория Калуцы-Клейна, теория струн предполагает, что наличие дополнительных измерений помимо тех трех (или четырех), с которыми мы ежедневно сталкиваемся, является необходимым условием для объединения всех сил природы в одну. Большинство вариантов теории струн предполагают существование десяти или одиннадцати (с учетом времени) измерений, необходимых для осуществления Великого объединения.

Но дело не только в том, чтобы ввести несколько дополнительных измерений и надеяться на лучшее. Чтобы теория получила практическое применение, этим измерениям следует поставить в соответствие определенные размеры и формы (вопрос о том, какие именно размеры и формы, — пока остается открытым). Иными словами, геометрия играет в теории струн особую роль, и многие ее сторонники подтвердят, что именно геометрия дополнительных измерений во многом определяет вид той Вселенной, в которой мы живем, обусловливая свойства всех наблюдаемых (а также по тем или иным причинам ненаблюдаемых) в природе физических сил и элементарных частиц.

Начиная с шестой главы мы займемся теорией струн более подробно. Но прежде чем углубиться в сложную математику, лежащую в ее основе, следует более подробно изучить основы геометрии. (Мой, хотя и предвзятый, опыт говорит, что такая методика является удачной.) Поэтому мы отступим на несколько шагов назад от XX и XXI столетий и заглянем в историю этой почтенной науки, чтобы понять, какое место она занимает в существующем порядке вещей.

И если говорить о том месте, которое она занимает, то лично для меня геометрия всегда была чем-то вроде скоростной полосы на автобане истины — наиболее коротким путем из точки, в которой мы находимся, в точку, в которой мы хотим оказаться. Это неудивительно, если принять во внимание, что большая часть геометрических исследований посвящена как раз указанной проблеме — нахождению расстояния между двумя точками. Поэтому запаситесь терпением, если путь от математики Древней Греции к сложнейшим построениям теории струн покажется вам несколько запутанным и извилистым. Порой самый короткий путь — вовсе не самый прямой, в чем мы скоро и убедимся.

5. Max Tegmark (MIT), interview with author, May 16, 2005. (Note: All interviews were conducted by Steve Nadis unless otherwise noted.)

6. Aristotle, On the Heavens, at Ancient Greek Online Library, http://greektexts.com/library/Aristotle/On_The_Heavens/eng/print/1043.html.

7. Michio Kaku. Hyperspace (New York: Anchor Books, 1995), p. 34.

8. H. G. Wells, The Time Machine (1898), available at http://www.bartleby.com/1000/1.html.

9. Abraham Pais, Subtle Is the Lord (New York: Oxford University Press, 1982), p. 152.

10. Oskar Klein, “From My Life of Physics,” in The Oskar Klein Memorial Lectures, ed. Gosta Ekspong (Singapore: World Scientific, 1991), p. 110.

11. Leonard Mlodinow, Euclid’s Window (New York: Simon & Schuster, 2002), p. 231.

12. Andrew Strominger, “Black Holes and the Fundamental Laws of Nature,” Lecture, Harvard University, Cambridge, MA, April 4, 2007.

13. То же.