Глава 10. Дальше за Калаби-Яу

Создание удачной теории похоже на бег с препятствиями. Как только вы преодолеваете один барьер, перепрыгнув его, обойдя вокруг или даже пробежав под ним, оказывается, что впереди еще много барьеров. И даже если вы успешно расчистили себе путь, оставив преграды позади, вы не знаете, как много их еще впереди и не остановит ли вас навсегда какой-либо высокий барьер. Вот так и с теорией струн и многообразиями Калаби-Яу, где нам известно по крайней мере одно препятствие, которое туманно маячит где-то впереди, но, будучи достаточно большим, может оказаться непреодолимым для блестяще выстроенной теории.

Я говорю о проблеме модулей, которая является предметом многих дискуссий и статей, а также источником неприятностей и разочарований. Как мы увидим, относительно простая на первый взгляд задача может увести нас очень далеко от стартовой точки, порой не оставляя никаких ориентиров в поле зрения.

Размер и форма любого многообразия с дырками определяются параметрами, которые называются модулями. Например, двухмерный тор во многих отношениях определяется двумя независимыми петлями, или окружностями, из которых одна обходит вокруг дырки, а вторая идет через нее. Модули, по определению, измеряют размер окружностей, которые, в свою очередь, управляют как размером, так и формой многообразия. Если окружность, проходящая через дырку, меньше второй окружности, то вы получаете тонкое кольцо; если больше, то вы получаете толстое кольцо с относительно маленькой дыркой в середине. Третий модуль описывает степень скрученности тора.

Так обстоят дела с тором. Многообразие Калаби-Яу, как мы уже отмечали, может иметь до пяти сотен дырок, множество многомерных окружностей и, следовательно, характеризуется большим числом модулей — от десятков до сотен. Обычно его представляют как поле в четырехмерном пространстве-времени. Поле для модуля размера присваивает число каждой точке в обычном пространстве, соответствующее размеру (или радиусу) невидимого многообразия Калаби-Яу. Поле такого сорта, которое полностью характеризуется единственным числом в каждой точке пространства, без направления, называется скалярным полем. Примеры скалярных полей вокруг нас: температура, влажность, атмосферное давление и т. д.

Ловушка состоит в том, что если ничто не ограничивает размер и форму многообразия, то вы полностью погружаетесь в вышеупомянутую проблему модулей, которая похоронит вашу надежду вытянуть реальную физику из геометрии. Мы столкнулись с этой проблемой, выяснив, что скалярные поля, связанные с размером и формой многообразия, являются безмассовыми полями, то есть для их изменения не требуется энергия. Другими словами, их можно беспрепятственно изменять. Попытка расчета Вселенной в этих постоянно меняющихся обстоятельствах напоминает «соревнования по бегу, где финишная черта все время движется в дюйме перед вами», — заметил физик Гэри Шуй из Висконсинского университета.^[180]

Но проблема еще серьезнее: мы знаем, что такие поля не могут существовать в природе. Поскольку если бы они существовали, то представляли бы собой все виды модульных безмассовых частиц, связанных со скалярными (модульными) полями, летающих вокруг со скоростью света. Эти модульные частицы взаимодействовали бы с другими частицами примерно с той же силой, как гравитоны (частицы, являющиеся переносчиками силы гравитации), и тем самым сеяли бы хаос в теории гравитации Эйнштейна. Но из того, что эта теория в том виде, в каком она описана в общей теории относительности, работает достаточно хорошо, мы можем сделать вывод, что этих безмассовых полей и частиц не существует. Помимо того что существование таких полей несовместимо с известными законами гравитации, оно еще и приводит к существованию пятой силы и, вероятно, других дополнительных сил, которые никто никогда не наблюдал.

Рис. 10.1. Потоки можно рассматривать как силовые линии, не отличающиеся от показанных здесь линий магнитного поля, хотя теория струн включает и более экзотические поля, которые указывают на шесть компактных, невидимых для нас направлений

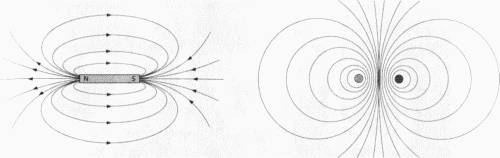
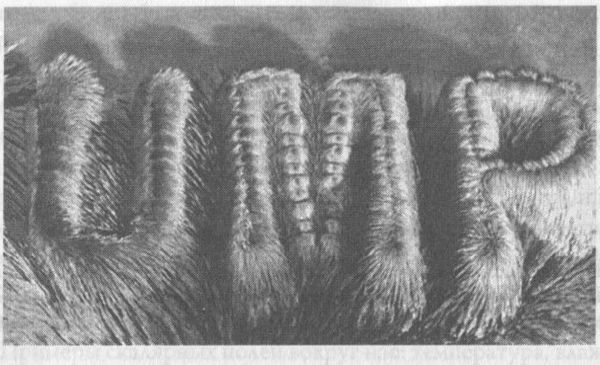
И это является камнем преткновения. Учитывая, что сегодня большая часть теории струн базируется на компактификации многообразий Калаби-Яу, содержащих эти модули со скалярными полями и безмассовыми частицами, которые, скорее всего, не существуют, не означает ли это, что теория струн сама по себе обречена?

Необязательно. Возможно, существует способ обойти указанную проблему, если учесть другие элементы теории, о которых мы уже знаем, но которые не принимали во внимание, чтобы упростить вычисления.

Если включить эти элементы в расчеты, то ситуация будет выглядеть совершенно по-другому. Эти дополнительные компоненты включают в себя элементы, называемые потоками, представляющими собой поля, подобные электрическим и магнитным, хотя новые поля из теории струн не имеют ничего общего ни с электронами, ни с фотонами.

Давайте снова рассмотрим двухмерный тор, и в частности текучее кольцо, форма которого постоянно меняется, и кольцо становится то тонким, то толстым. Мы можем стабилизировать этот тор, зафиксировав его форму путем оборачивания проволоки сквозь дырку и вокруг нее. Здесь существенную роль играет поток. Многие из нас видели аналогичный эффект, когда после включения магнитного поля железные опилки, рассеянные беспорядочным образом, образуют правильный узор. Поток удерживает опилки на месте до тех пор, пока приложенная к ним дополнительная энергия не заставит их двигаться. Точно так же наличие потоков в нашем случае означает, что для изменения формы многообразия требуется дополнительная энергия, поскольку скалярные безмассовые поля становятся скалярными полями с массой.

Рис. 10.2. Так же как мы можем фиксировать и стабилизировать расположение железных опилок путем приложения к ним магнитного потока, мы, в принципе, можем стабилизировать форму и размер многообразия Калаби-Яу, включив разные потоки в теорию струн (фото любезно предоставлено TechnoFrolics, www.technofrolics.com)

Конечно, шестимерные многообразия Калаби-Яу сложнее, так как они имеют намного больше «дырок», чем «бублик», и сами дырки могут иметь более высокую размерность (до шести измерений). Это означает, что здесь больше внутренних направлений, в которых может течь поток, что приводит к увеличению количества возможных путей прохождения линий поля через дырки. Теперь, когда у нас есть все потоки, проходящие через ваше многообразие, мы можем рассчитать, какое количество энергии запасено в сопутствующих полях. Стэнфордский физик Шамит Качру объяснил, что для расчета энергии необходимо взять интеграл от квадрата напряженности поля «по точной форме компактифицированных измерений», или по поверхности Калаби-Яу. Итак, вы делите пространство на бесконечно малые участки, определяете квадрат напряженности поля на каждом участке, складываете все значения, делите на число участков и получаете среднее значение, или интеграл. «Поскольку форма меняется, то изменяется и значение общей энергии поля, — говорит Качру, — многообразие выбирает такую форму, чтобы минимизировать энергию потока этого поля».^[181] Вот так, путем включения потоков в картину можно стабилизировать форму модулей и таким образом стабилизировать форму самого многообразия.

Но это только часть истории, ведь мы забыли об одном важном аспекте процесса стабилизации. Подобно магнитному и электрическому полю, потоки в теории струн квантуются, то есть принимают только целые значения. Вы можете добавить одну единицу потока или две единицы потока, но не можете добавить 1,46 единицы потока. Когда мы говорим, что потоки стабилизируют модуль, мы подразумеваем, что они накладывают на значения модуля определенные ограничения. Вы не можете присвоить модулю любое выбранное значение, а только те значения, которые соответствуют дискретным потокам. В результате набор возможных форм многообразия Калаби-Яу оказывается дискретным.

В предыдущей главе мы уделили много времени гетеротической версии теории струн, но оказывается, что ввести потоки в гетеротические модели довольно сложно. К счастью, в теории струн типа II (категории, включающей оба типа — IIA и IIB), которая иногда является дуальной по отношению к гетеротической теории, это сделать гораздо проще.

Я немного остановлюсь на анализе 2003 года, выполненном в теории струн типа IIB, который заметно выделяется из других типов.

Мы только что обсудили стабилизацию модуля формы для многообразия с потоками. Впервые последовательный способ стабилизации всех модулей Калаби-Яу, как модулей формы, так и модулей размера, был представлен в статье Шамита Качру, Ренаты Каллош, Андрея Линде (все из Стэнфорда) и Сандипа Триведи из Института фундаментальных исследований в Индии; предлагаемый подход авторы статьи назвали KKLT — по первым буквам своих фамилий. Стабилизация размера является решающим фактором для любого типа теории струн, основанной на многообразиях Калаби-Яу, потому что в противном случае нет ничего, способного удержать шесть скрытых измерений от развертывания до бесконечно большого размера, то есть до того размера, который мы предполагаем для основных четырех измерений. Если маленькие, невидимые измерения неожиданно распрямятся и расширятся, то мы с вами будем жить в пространстве-времени из десяти больших измерений, с десятью независимыми направлениями для движения или для поиска наших потерянных ключей, а мы знаем, что наш мир не похож на десятимерный (что дает нам слабую надежду найти потерянные ключи). Что-то удерживает эти измерения от развертывания и что-то, согласно авторам подхода KKLT, является D-бранами.^[182]

Стабилизацию шестимерного Калаби-Яу бранами можно сравнить с ограничением размера автомобильной камеры путем надевания на нее армированной стальным кордом шины. Подобно тому как шина удерживает камеру, когда вы закачиваете в нее воздух, так и браны удерживают многообразия от расширения.

«Говорят, что форма и размер объекта стабилизированы, если вы пытаетесь изменить его, но что-то противодействует вашим попыткам, — объясняет физик Раман Сандрам из Университета Джона Хопкинса. — Наша задача заключалась в создании компактного, стабильного пространства-времени, и подход KKLT показал нам, как это сделать, причем не одним, а множеством разных способов».^[183]

Стабильные объем и размер крайне важны для объяснения такого явления, как космическая инфляция, суть которой состоит в том, что все свойства наблюдаемой нами сегодня Вселенной являются результатом краткого, но ускоренного, экспоненциального расширения ее в начальный период Большого взрыва. Это ускоренное расширение в соответствии с теорией черпало энергию из так называемого инфляционного поля, которое снабжало Вселенную положительной энергией, приводившей в действие процессы расширения. «В теории струн мы предполагаем, что положительная энергия должна возникать из определенного вида десятимерных источников, обладающих тем свойством, что по мере того как компактное [Калаби-Яу] пространство становится больше, связанная с ним энергия становится меньше», — говорит Лиам Макаллистер из Корнеллского университета. Если предоставить природу самой себе, то все поля будут пытаться раздуться и стать разреженными. «По сути это означает, что система “счастливее”, когда внутреннее пространство больше, а энергия — меньше, — говорит он. — Система может уменьшить свою энергию путем расширения и свести ее к нулю, расширившись до бесконечности».^[184] Если ничто не сдерживает внутреннее пространство от расширения, то так и будет.

Когда это происходит, то энергия, которая в иных обстоятельствах запускает инфляцию, рассеивается так быстро, что процесс расширения остановится раньше, чем начнется. По сценарию KKLT браны обеспечивают возможный механизм для образования Вселенной, которую мы видим, — Вселенной, на которую инфляция оказала достаточно сильное влияние.

В нашу задачу не входило воспроизведение Стандартной модели или подробное обсуждение физики элементарных частиц, но скорее широкое представление качественных характеристик нашей Вселенной, включая аспекты космологии, которая сейчас, вероятно, является самой всеобъемлющей дисциплиной из всех.

Дело в том, что в конце нашего обсуждения мы хотим получить теорию, которая работает на всех масштабах — и в физике элементарных частиц, и в космологии. В дополнение к предположениям KKLT относительно того, как инфляция может работать в теории струн, в 2002 году была опубликована статья Качру, Стива Гиддингса и Джозефа Полчински (последние двое из университета Калифорнии в Санта-Барбаре), в которой показано, как теория струн может объяснить очевидную слабость гравитации, которая в триллион триллионов триллионов раз слабее электромагнитных сил. Согласно теории струн это можно объяснить отчасти тем, что гравитация пронизывает все десять измерений, которые «разбавляют» ее силу. Но в сценарии Гиддингса-Качру-Полчински (Giddings-Kachru-Polchinski, GKP) этот эффект ослабления экспоненциально усилен за счет геометрического деформирования, которое мы позже обсудим в данной главе. Объяснение построено на искривленной геометрической модели, впервые описанной в теории поля Лайзой Рэндалл из Гарварда и Раманом Сандрамом и позже введенной в теорию струн GKP, а также в последующую работу KKLT.

Продолжив исследования, авторы KKLT показали в рамках теории струн, как наша Вселенная могла снабжаться положительной энергией вакуума, иногда называемой темной энергией, существование которой стало очевидным благодаря измерениям, проводимым с конца 1990-х годов. Мы не можем дать детальное описание технически сложного механизма передачи энергии, который подразумевает помещение объекта, называемого антибраной (антивещество, противоположное бране) в деформированную область Калаби-Яу, например, на вершину конифолда — некомпактного, конического по форме выступа, простирающегося от «тела» многообразия. Во всяком случае, точные детали не столь важны, так как их исследование никогда не предполагало нахождения окончательного ответа на любой из этих вопросов. Качру пояснил, что «цель KKLT заключалась в создании “игрушечной” модели, с помощью которой теоретики могли бы изучить явление, хотя здесь возможны и другие конструкции».^[185]

Суть в том, что если работа по стабилизации модулей и исследования в области физики элементарных частиц успешно продвигаются вперед, то потенциально, согласно Макаллистеру, физики могут «иметь все. Если вы возьмете многообразие Калаби-Яу и бросите в него D-браны и потоки, то вы можете получить все ингредиенты для получения Стандартной модели, инфляции, темной энергии и другие вещи, с помощью которых мы можем объяснить наш мир».^[186]

В конце концов, авторы статьи KKLT, объяснив, как можно стабилизировать модули, показали, как можно ограничить само многообразие Калаби-Яу до четкого набора стабильных или квазистабильных форм. Это означает, что вы можете выбрать многообразие Калаби-Яу конкретного топологического типа, найти способы снабдить его потоками и бранами и точно рассчитать возможные конфигурации. Беспокоит то, что, когда вы произведете все расчеты, результат может устроить не всех, потому что число возможных конфигураций будет абсурдно большим, до 10⁵⁰⁰.

Эта цифра далеко не точная, она призвана обеспечить приблизительное представление о числе возможных вариантов, которые вы можете получить для многообразия Калаби-Яу со множеством дырок. Давайте снова рассмотрим тор с потоком, навитым сквозь дырку с целью его стабилизации. Поскольку поток квантуется, в дальнейшем мы будем предполагать, что он может принимать целые значения от 0 до 9, что эквивалентно существованию десяти стабильных форм для тора. Если бы у нас был тор с двумя дырками и через каждую из них мог проходить поток, то тор имел бы 10², или 100 стабильных форм. Очевидно, что шестимерное многообразие Калаби-Яу предлагает намного больше вариантов. «Число 10⁵⁰⁰ получено путем математического расчета, где учитывали максимальное возможное число дырок в многообразии (порядка пятисот) и предполагали, что через каждую дырку можно провести поля или потоки, которые могут находиться в одном из десяти возможных состояний, — объясняет Полчински, один из тех, кому обязано появлением это число. — Расчет действительно грубый. Число может быть намного больше или намного меньше, но оно не бесконечно».^[187]

Что это за цифра и что она означает? Во-первых, это означает, что в силу топологической сложности многообразий Калаби-Яу уравнения теории струн имеют большое количество решений. Каждое из этих решений соответствует многообразию Калаби-Яу со своей геометрией, что, в свою очередь, подразумевает разные элементарные частицы, разные физические постоянные и т. д. Кроме того, поскольку многообразия Калаби-Яу по определению являются решениями уравнений Эйнштейна для вакуума, каждое из этих решений, которое включает различные способы введения потоков и бран, соответствует вселенной с разным вакуумным состоянием и, следовательно, различной энергией вакуума.

И вот парадокс: многие теоретики верят, что все эти вселенные действительно могут существовать.

Что же за картина вырисовывается? Представьте себе мяч, катящийся без трения по огромной ровной поверхности. Для мяча не существует предпочтительного положения — он может катиться в любом направлении без затрат энергии. Это похоже на ситуацию с нестабилизированным модулем и безмассовыми скалярными полями. А теперь давайте представим, что эта поверхность не совсем гладкая, а имеет несколько углублений, в которые мяч может попасть и застрять, не имея энергии, чтобы выбраться из ямки. Подобная ситуация имеет место, когда модули стабилизированы; каждое из углублений на поверхности соответствует различному решению теории струн — отдельному Калаби-Яу, занимающему отдельное вакуумное состояние. Поскольку мы имеем большое число возможных решений, такой «ландшафт», содержащий различные вакуумные состояния, огромен.

Конечно, это понятие, называемое ландшафтом теории струн, является чрезвычайно противоречивым. Одни ученые принимают картину с множеством вселенных, другие отрицают, а некоторые (включая меня) считают это понятие спекулятивным. Иногда возникает вопрос о практической ценности данной теории, которая предлагает больше решений, чем мы можем классифицировать. Следом возникает еще вопрос: а существует ли какой-либо способ обнаружить все эти возможные вселенные, разбросанные по всему ландшафту? Больше беспокоит то, что идея ландшафта становится тесно связанной с так называемыми антропными аргументами.

Космологическая константа для нашей Вселенной, рассчитанная из данных последних астрономических наблюдений, по-видимому, должна быть очень маленькой, примерно в 10¹²⁰ раз меньше, чем значение, предсказанное лучшими физическими теориями. Никто не может объяснить это расхождение или тот факт, что константа имеет чрезвычайно маленькое значение. Но что, если все 10⁵⁰⁰ или примерно столько вакуумных состояний в ландшафте действительно где-то реализованы и каждое представляет собой отдельную вселенную или подвселенную со своей внутренней геометрией (или Калаби-Яу) и своей космологической константой? Среди всех этих вариантов, по крайней мере, одна из подвселенных обязательно имеет низкую космологическую постоянную, как у нас. И поскольку мы должны где-то жить, то это и есть там, где мы и обитаем. Но это не бессмысленная удача, потому что мы не можем жить во вселенной с большой космологической постоянной, так как в этом случае расширение происходило бы так быстро, что звезды, планеты и даже молекулы никогда не смогли бы образоваться. Вселенная с большой отрицательной космологической постоянной быстро сжалась бы в ничто или до сильной сингулярности. Другими словами, мы живем во вселенной такого вида, в которой мы можем жить.

Рис. 10.3. Энергия пустого пространства, также называемая энергией вакуума, может принимать огромное число возможных значений, которые представляют стабильные или полустабильные решения уравнений теории струн. Понятие ландшафта теории струн было придумано, в частности, для того, чтобы наглядно показать, что теория имеет много возможных решений, соответствующих многим вакуумным состояниям, или ложным вакуумом, — каждое из которых может представлять другую вселенную. Стабильное состояние ложного вакуума на этом рисунке представлено впадинами, или долинами, куда могут попасть и остаться там шары, которые скатываются вниз с горы в разных направлениях. Высота этих впадин соответствует энергии вакуума, принятой для каждого участка ландшафта. Некоторые теории предполагают, что может быть порядка 10500 решений, каждое из которых соответствует своему многообразию Калаби-Яу и, следовательно, своей геометрии для компактных измерений. Пространства Калаби-Яу являются неотъемлемой частью этой картины, так как, по мнению ученых, суммарная вакуумная энергия поддерживает шесть дополнительных измерений теории струн, свернутых в таких пространствах, не позволяя им расширяться до бесконечности (изображения пространства Калаби-Яу любезно предоставлены Эндрю Дж. Хансоном (Andrew J. Hanson), Университет Индианы)

Физик Дэвид Гросс сравнил антропные аргументы такого рода с тараканами, которых необходимо уничтожать. «Если вас одолели тараканы, вы не можете избавиться от них», — пожаловался он на космологической конференции.^[188]

Стэнфордский физик Бартон Рихтер говорит, что энтузиасты ландшафта, такие как его стэнфордский коллега Леонард Зюскинд «отказались от этой идеи. Для них путешествие, которое завело физиков так далеко, подошло к концу, — пишет Рихтер в New York Times. — Поскольку они верят в эту идею, я не могу понять, почему они не возьмутся еще за что-нибудь, например за макраме».^[189]

«Нам не удается избавиться от множества решений теории струн, — замечает Зюскинд, — поэтому нравится вам это или нет, ландшафт остается». Поскольку это так, то лучше с ним заключить мир и проверить, есть ли что-нибудь полезное, что можно из него извлечь. «Дорога физики усеяна трупами упрямых стариков, которые не знали, когда пора сдаваться», — пишет он в своей книге «Космический ландшафт» (The Cosmic Landscape), осознавая, что он также может быть «упертым стариком, сражающимся до конца».^[190]

Справедливости ради следует сказать, что споры возникали постоянно. Я никогда не принимал участия в дискуссии, от которой, вероятно, получил бы удовольствие будучи математиком. Мне не приходится давать материал, который угрожает подорвать сообщество физиков. Вместо этого я имею возможность сидеть в стороне и задавать обычные вопросы типа: как математика может пролить свет на эту ситуацию?

Некоторые физики вначале надеялись на то, что только одно многообразие Калаби-Яу может характеризовать скрытые измерения теории струн, но скоро стало понятно, что существует большое число таких многообразий, каждое из которых имеет свою уникальную топологию. В рамках каждого топологического класса существует непрерывное, бесконечно большое семейство многообразий Калаби-Яу. Это положение, вероятно, легче всего проиллюстрировать с помощью торов. Тор представляет собой топологический эквивалент прямоугольника. Если скатать прямоугольный лист в цилиндр и соединить концы, то получится тор. Прямоугольник определяется высотой и шириной, которые могут принимать бесконечное число возможных значений. Все эти прямоугольники и соответствующие им торы являются топологически эквивалентными.

Они представляют собой часть одного и того же семейства, но их может быть бесконечное множество. То же справедливо для многообразий Калаби-Яу. Мы можем взять многообразие, модифицировать его «высоту», «ширину» и другие параметры и получить бесконечное семейство многообразий одного и того же топологического типа. Таким образом, KKLT и связанная с ним концепция ландшафта не меняет эту ситуацию. В лучшем случае, наложение ограничений из физики, то есть обязательное квантование потоков, привело к очень большому, но конечному, а не бесконечному, числу многообразий Калаби-Яу. Я полагаю, что это уже можно считать прогрессом.

Рис. 10.4. Две стороны, представляющие спор о ландшафте: а — физик Дэвид Гросс из Санта-Барбары и б — физик Леонард Зюскинд из Стэнфорда (фото Зюскинда предоставила Анна Воррен (Anne Warren))

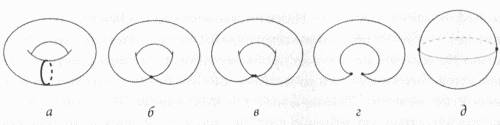
Лично я далек от мысли, что существует одно «данное богом» многообразие Калаби-Яу или только несколько. Я всегда допускал, что все гораздо сложнее. В конце концов, еще никто не говорил, что достичь дна Вселенной и наметить ее внутреннюю геометрию легко.

Итак, что мы можем сделать с идеей ландшафта, которая так тревожит некоторых ученых? Я полагаю, что можно просто проигнорировать ее, так как ничего нельзя установить и доказать. Одни физики считают концепцию полезной, в то время как другие не видят в ней никакой пользы. Поскольку само понятие ландшафта теории струн возникло из рассмотрения бесчисленного количества состояний, многие из которых, если не все, связаны с многообразиями Калаби-Яу, то если мы вообще придаем какое-то значение этой идее с ландшафтом, нам необходимо лучше разобраться в многообразиях Калаби-Яу.

Я сознаю, что мое заявление звучит несколько наивно. Существует множество возможных решений для теории струн и множество возможных геометрий, исходя из которых можно компактифицировать дополнительные измерения, и многообразия Калаби-Яу представляют только верхушку айсберга. Я хорошо понимаю ситуацию и даже работаю над некоторыми из этих новых областей физики. Тем не менее большей части успехов, достигнутых в теории струн, и большей части гипотез мы обязаны использованием многообразий Калаби-Яу как модели. Кроме того, часть альтернативных геометрий, которые сейчас исследуются, такие как не-кэлеровы многообразия, получают путем деформирования или искривления многообразий Калаби-Яу. Не существует прямого и быстрого пути к не-кэлеровым геометриям, поэтому мы должны разобраться в многообразиях Калаби-Яу прежде, чем приступить к изучению таких вещей, как не-кэлеровы многообразия. Это обычная стратегия для всех областей исследования: вы ставите базовый лагерь, который служит знакомой точкой отправления, а затем отправляетесь в неизвестное.

Примечательно, что, несмотря на количество исследований в этой области с момента, как я доказал существование этих многообразий в 1976 году, появилось много простых, даже шокирующее простых вопросов, на которые мы не можем дать ответ, например сколько всего топологически различных многообразий Калаби-Яу? Их число конечно или бесконечно? И связаны ли между собой многообразия Калаби-Яу? Начнем с первого вопроса: сколько существует топологически различных видов или семейств многообразий и входит ли в них Калаби-Яу? Скажем кратко: мы не знаем, хотя попытки ответить на этот вопрос были. Более чем 470 миллионов трехмерных Калаби-Яу были созданы с помощью компьютера. Для них мы построили более чем 30 000 ромбов Ходжа, то есть по крайней мере 30 000 разных топологий. (Ромбы Ходжа, как вы помните из седьмой главы, представляют собой массивы размером 4×4, которые суммируют основную топологическую информацию о трехмерном многообразии.) Однако число может быть значительно больше, чем 30 000, так как два многообразия могут иметь один и тот же ромб Ходжа, но отличаться по топологии.

«Никаких систематических попыток не было сделано для оценки количества топологических типов главным образом потому, что пока не удается однозначно провести различия между такими трехмерными многообразиями, — объясняет физик Гарвардского университета Тристан Хабш. — Мы все еще не имеем четкого “идентификационного номера” для многообразия Калаби-Яу. Мы знаем, что ромб Ходжа является частью его, но он не определяет многообразие однозначно. Он больше похож на регистрационный номер автомобиля».^[191]

Мы не только не знаем, действительно ли число многообразий Калаби-Яу чуть больше или намного больше, чем 30 000, но мы даже не знаем, конечное это число или нет. В начале 1980-х годов я выдвинул гипотезу, что это число — конечное, но математик Майлз Рид из Университета Варвика придерживается противоположной точки зрения, утверждая, что оно бесконечно. Было бы неплохо узнать, кто из нас прав. «Я полагаю, что для физиков, которые надеются, что многообразий Калаби-Яу очень мало, обнаружение того факта, что это число является бесконечным, только усугубит ситуацию, — говорит Марк Гросс из Калифорнийского университета, Сан-Диего. — С математической точки зрения это не имеет значения. Мы же хотим знать ответ. Мы хотим осознать все количество многообразий Калаби-Яу. Предположение о том, что их число конечно, правильное оно или неправильное, служит своего рода мерилом нашего понимания».^[192] А с чисто практической точки зрения, если набор многообразий является конечным, независимо от его величины, вы всегда можете взять среднее значение. Но мы не знаем, как взять среднее значение бесконечного числа объектов, и это усложняет характеристику этих объектов.

До сих пор не выдвинуто аргументов против моей гипотезы. Вероятно, все известные нам методы построения многообразий Калаби-Яу ведут только к конечному числу многообразий. Важно найти другие способы построения многообразий, но после двух десятков лет поисков никто не представил новый метод, ведущий к бесконечному набору многообразий. В 1993 году Марк Гросс ближе всех подошел к решению этой задачи. Он доказал, что если рассматривать Калаби-Яу как четырехмерную поверхность с двухмерными бубликами, присоединенными к каждой из ее точек, то получается только конечное число поверхностей. «Подавляющее большинство известных многообразий Калаби-Яу попадают в эту категорию, которая оказывается конечным множеством», — говорит Гросс. Это главная причина, по которой он поддерживает «конечную» гипотезу. С другой стороны, Гросс отмечает, что множество многообразий не попадают в эту категорию, и мы безуспешно пытаемся доказать что-либо в отношении них.^[193] Так что вопрос остается открытым.

Эта не разрешенная до конца проблема подводит нас ко второму, также нерешенному вопросу, впервые поставленному Ридом в 1987 году: существует ли способ, с помощью которого можно связать все многообразия Калаби-Яу? Или в постановке Рида: «Все эти разновидности Калаби-Яу обладают всеми видами топологических характеристик. Но если посмотреть на проблему шире, то можно заметить, что все это, возможно, одно и то же. Конечно, это безумная идея, которая, вероятно, неверна. Тем не менее…» Фактически, Рид считал идею настолько странной, что он никогда не называл ее гипотезой, предпочитая говорить вместо этого «фантазия». Но он все еще верит, что кто-то, может быть, докажет ее.^[194]

Рид допускал, что все многообразия Калаби-Яу можно связать посредством чего-то, названного им конифолдным переходом. Идея, разработанная в 1980-е годы математиками Хербом Клеменсом из Университета Юты и Робертом Фридманом из Колумбийского университета, описывает, что происходит с многообразиями Калаби-Яу при перемещении их через особый вид сингулярности. Как всегда, концепцию легче показать на двухмерном торе. Вспомним, что тор всегда можно представить как множество окружностей, присоединенных к окружности, представляющей дырку. Теперь возьмем одну из множества окружностей и сожмем ее в точку. Мы получим сингулярность, потому что любое другое место на поверхности является гладким. Итак, на этом крошечном участке, так называемой конифолдной сингулярности, два маленьких конуса сходятся вместе. Далее вы должны проделать операцию, которую математики называют хирургической и которая включает вырезание проблемной точки и замену ее двумя другими точками. Затем мы можем разделить эти две точки, разведя их так, чтобы получилась фигура, имеющая форму рогалика. Далее, мы изменим топологию рогалика, превратив его в топологический эквивалент — сферу. И на этом не будем останавливаться. Предположим, что на следующем этапе мы вытягиваем сферу так, что она снова становится похожей на рогалик. Затем мы соединяем концы рогалика с получением тора, но при этом дополнительно перекручиваем сферу. Таким образом, мы получаем тор с другой топологией и двумя дырками вместо одной. Если мы будем продолжать этот процесс неопределенно долгое время, включая дополнительные перекручивания или дырки, то мы, в конце концов, получим все возможные двухмерные торы. Следовательно, конифолдный переход представляет собой способ связывания топологически разных торов через промежуточную форму (в нашем случае сферу) и эта общая процедура работает и для других нетривиальных видов многообразий Калаби-Яу.

Рис. 10.5. Конифолдный переход представляет собой процесс изменения топологии. В этом сильно упрощенном примере мы начинаем с бублика, сделанного из маленьких окружностей, и сжимаем одну из них в точку. Эта точка представляет собой вид сингулярности, где две формы, напоминающие конусы, сходятся вместе. Конусовидная сингулярность этого рода называется конифолд. Посредством математической версии хирургической операции мы заменяем эту сингулярную точку двумя точками и затем разводим их в стороны, чтобы бублик превратился в рогалик. Затем мы расширяем рогалик, чтобы получить объект, подобный сфере. Таким образом, мы перешли от бублика к топологически другому объекту — сфере

Рис. 10.6. Здесь представлен другой способ конифолдного перехода. Мы начинаем наши действия с многообразия Калаби-Яу, расположенного слева. Это шестимерный объект, потому что он имеет пятимерную основу, будучи декартовым произведением двухмерной сферы (S2) и трехмерной сферы (S3), плюс одно дополнительное измерение для высоты. Эта поверхность Калаби-Яу — элегантная и гладкая, потому что на вершине находится двухмерная сфера (S2). Если сжать поверхность до точки, то мы получим промежуточное изображение — пирамиду. Точка на самом верху пирамиды представляет собой сингулярность — конифолд. Если мы выровняем верхушку, раздув точку в трехмерную сферу (S3), а не в двухмерную (S2), с которой мы начали, то мы придем к третьей модели — многообразию М. Суть идеи в том, что конифолдная сингулярность служит своего рода мостиком от одного многообразия Калаби-Яу к другому (перенесено, с разрешения, с рисунка Тристана Хабша)

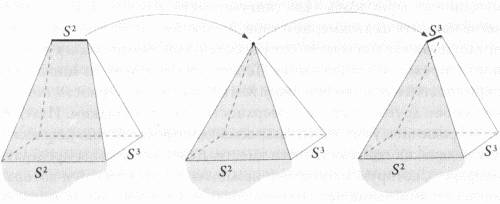
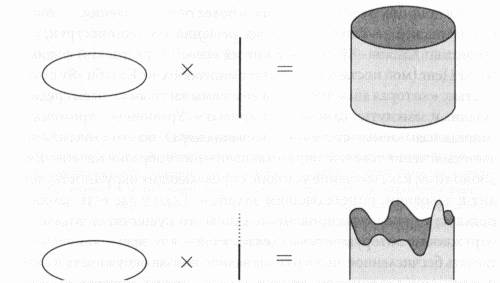
Шестимерные многообразия Калаби-Яу не так просты. На нашем рисунке конифолдного перехода, предложенного Клеменсом, вместо сжатия окружности до точки мы сжали двухмерную сферу. Мы допускаем, что каждое компактное многообразие Калаби-Яу имеет по крайней мере одну двухмерную сферу особого рода, расположенную внутри. Японский математик Сигефуми Мори доказал, что кэлеровы многообразия с позитивной кривизной Риччи имеют, по крайней мере, одну такую подповерхность, и мы ожидаем, что это условие также применимо к многообразиям Калаби-Яу с риччи-плоской метрикой. Каждое известное нам многообразие Калаби-Яу имеет двухмерную сферу, так что наша интуиция нас не подвела. Но у нас все еще нет доказательства для многообразий Калаби-Яу с риччи-плоской метрикой. После сжатия нашей двухмерной сферы в точку мы можем заменить эту точку сжатой трехмерной сферой, которую затем можно снова расширить.

Если наше предыдущее допущение верно, то после такой операции многообразие больше не является кэлеровым, поскольку оно больше не имеет двухмерной сферы и, следовательно, не может быть многообразием Калаби-Яу. Это уже что-то другое — не-кэлерово многообразие. Продолжая конифолдный переход, мы можем взять не-кэлерово многообразие, вставить другую двухмерную сферу (где мы предварительно вставили трехмерную сферу) и получить другое многообразие Калаби-Яу.

Хотя не Рид придумал конифолдный переход, он первым увидел, как его можно использовать для установления связи между всеми многообразиями Калаби-Яу. Важно, что конифолдный переход состоит в получении из одной поверхности Калаби-Яу другой, причем геометрия должна пройти через промежуточную стадию, на которой переходная форма представляет собой не-кэлерово многообразие. Неужели все не-кэлеровы многообразия связаны в том смысле, что из одного можно вылепить другое посредством сжатия, растяжения или вытягивания? Да, действительно, в этом и есть суть гипотезы Рида. Представьте себе гигантский кусок швейцарского сыра с бесчисленными крошечными дырками, или пузырьками. Алан Адамс говорит, что если вы живете в одном пузырьке, то вы не уйдете далеко, не столкнувшись с границей. «Но если вы не возражаете идти через сыр, то сможете попасть из одного пузырька в другой. Рид выдвинул гипотезу, что конифолдный переход может провести вас через сыр (не-кэлерову часть) в другой пузырек», кэлерову часть, которая и представляет собой многообразие Калаби-Яу.^[195]

Проведем еще одну аналогию с сыром, где основное пространство заполнено собственно сыром и немного места оставлено для крошечных пузырьков, разбросанных тут и там. Эти маленькие пузырьки похожи на маленькие кусочки кэлеровых пространств, рассеянных среди намного большего не-кэлерова пространства. В результате мы имеем огромное число не-кэлеровых пространств, где кэлеровы многообразия составляют крошечное подмножество.

Общая стратегия, лежащая в основе гипотезы Рида, придает смысл идеям Марка Гросса. Он говорит, что не-кэлеровы многообразия представляют значительно больший набор объектов и «если вы хотите видеть взаимосвязь вещей, то легче это сделать, согласившись, что они являются частью значительно большего не-кэлерова набора».^[196]

Ситуация напоминает игру «Шесть шагов до Кевина Бэйкона», участники которой должны не более чем за шесть переходов найти связь между загаданным актером и Кевином Бэйконом через актеров, вместе с которыми они снимались. Игра основана на теориях «тесного мира» и «шести рукопожатий». Адамс говорит, что аналогичную ситуацию мы наблюдаем с многообразиями Калаби-Яу. «Неужели они все соседи? Можно ли превратить одно в другое путем деформирования? Конечно, нет. Но гипотеза Рида говорит, что каждое многообразие Калаби-Яу можно деформировать во что-то еще (не-кэлерово многообразие), если знать все другие многообразия Калаби-Яу. Адамс добавляет, что можно провести аналогию с группой людей, между которыми вы пытаетесь найти что-то общее. «Нам только надо показать, что все они знают одного общительного парня и в таком случае все они являются частью одной группы — группы знакомых этого парня».^[197]

Согласуется ли предположение Рида о связанности многообразий Калаби-Яу с реальностью? В 1988 году Тристан Хабш и математик Мерилендского университета Пол Грин доказали, что гипотеза Рида применима к примерно 8000 многообразий Калаби-Яу, которые включали большую часть известных на тот момент многообразий. Последующее обобщение этой работы показало, что более чем 470 миллионов конструкций Калаби-Яу, почти все известные трехмерные многообразия, связаны между собой способом Рида.^[198]

Конечно, мы не можем утверждать, что гипотеза справедлива во всех случаях, пока мы это не доказали. И более чем через двадцать лет после того, как Рид выдвинул свою гипотезу, ее доказательство представляет большую трудность. Я полагаю, что большая часть проблемы заключается в том, что не-кэлеровы многообразия не слишком понятны с точки зрения математических стандартов. Мы сможем получить шанс доказать гипотезу Рида, когда лучше поймем эти многообразия. Сейчас мы не можем с уверенностью сказать, что эти многообразия (не-кэлеровы) реально существуют или математически жизнеспособны. У нас нет четкого доказательства их связи со всеми многообразиями Калаби-Яу, а только с несколькими отдельными случаями.

Если мы намерены детально изучить многообразия, в связи с которыми возникла сложнейшая головоломка с ландшафтом и сопутствующий ей космологический пазл, то целесообразно установить, действительно ли все многообразия Калаби-Яу связаны между собой. Ключ к ответу на эти вопросы может лежать в новой пограничной области, касающейся не-кэлеровых многообразий. Эти многообразия вызывают интерес не только потому, что они могут пролить свет на многообразия Калаби-Яу, но и потому, что с их помощью может быть предложена компактификация геометрии, необходимая для расчета масс элементарных частиц в Стандартной модели, которую мы упустили из виду, пока физики увлекались стратегиями, опирающимися исключительно на многообразия Калаби-Яу.

Мой коллега Мелани Бекер, физик Техасского аграрно-технического университета, полагает, что не-кэлеров подход может дать ответ. «Получить структуру и массы элементарных частиц, — говорит Бекер, — можно только через компактификацию не-кэлеровых многообразий». Это может оказаться та геометрия, которая приведет нас к обетованной земле Стандартной модели. Чтобы понять точку зрения Бекера, вернемся в начало этой главы. Струнные теоретики ввели потоки, чтобы избавиться от безмассовых скалярных полей и таким образом стабилизировать размер и форму многообразия Калаби-Яу. Но включение этих мощных полей, или потоков, может исказить геометрию самого многообразия, изменив метрику так, что это уже будет не кэлерово многообразие. «Когда вы включаете поток, ваше многообразие становится не-кэлеровым — это совершенно другая игра в мяч, — говорит Бекер. — Проблема заключается в том, что это действительно целый новый раздел математики. Многое из математики, что применяют к многообразиям Калаби-Яу, неприменимо к не-кэлеровым многообразиям».^[199] С точки зрения теории струн многообразия, независимо от того, являются они многообразиями Калаби-Яу или не-кэлеровыми, важны возможностью компактификации, то есть редукцией десяти измерений теории струн до четырех измерений нашего мира.

Самый легкий способ разбиения пространства заключается в расщеплении его на четырехмерные и шестимерные компоненты. Это, по сути, подход Калаби-Яу. Мы обычно считаем эти два компонента полностью раздельными и не взаимодействующими между собой. Таким образом, десятимерное пространство-время является декартовым произведением его четырех- и шестимерных частей, и, как мы видим, вы можете визуализировать его с помощью модели Калуцы-Клейна, которую мы обсуждали в первой главе: в этой модели наше бесконечное четырехмерное пространство-время похоже на бесконечно длинную линию, за исключением того, что эта линия имеет толщину — крошечный круг, в котором находится дополнительное измерение. Поэтому все, что мы действительно имеем, так это декартово произведение круга и линии, другими словами — цилиндр. В случае не-кэлерова многообразия четырех- и шестимерные компоненты не являются независимыми.

В результате десятимерное пространство-время получается не прямым, а, скорее, кривым произведением, часто называемым в русскоязычной литературе искривленным произведением, означающим, что эти два подпространства взаимодействуют.

Короче говоря, на расстояния в четырехмерном пространстве-времени, которые постоянно увеличиваются или искривляются, влияет шестимерная часть. Степень расширения или сжатия четырехмерного пространства-времени зависит от коэффициента искажения, и в некоторых моделях искажение представляет собой экспоненциальную функцию.

Обратимся к нашему примеру с цилиндром. Давайте представим шестимерное пространство при помощи круга. Четырехмерная часть представляет собой линию, перпендикулярную к этому кругу и мы изобразим ее отрезком линии, а не бесконечной линией, чтобы показать, как шестимерное пространство влияет на расстояния. Если искажение отсутствует, то, по мере того как вы перемещаете отрезок линии, проходя все точки круга, вы будете вычерчивать правильный сплошной цилиндр.

Однако из-за искажения длина отрезка может варьировать в процессе путешествия по кругу. В одной точке она может быть равна 1, в другой 1/2, еще в другой 1 1/2 и т. д. В результате вы получите неровный, волнистый цилиндр, который деформирован искажением. В 1986 году физик Эндрю Строминджер выразил все это через набор уравнений.

Рис. 10.7. Так называемое декартово произведение круга и отрезка линии аналогично присоединению этого же линейного сегмента к каждой единичной точке на круге. В результате получаем цилиндр. Искривленное произведение выглядит по-другому. В этом случае длина линейного сегмента не должна быть постоянным числом; она может варьировать в зависимости от ее положения на круге. Таким образом, в этом случае мы получаем не настоящий цилиндр, а объект, который можно назвать волнистым, иррегулярным цилиндром

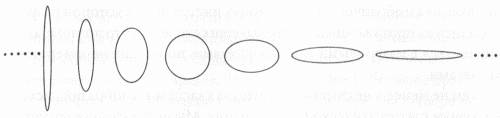
Строминджер отмечает, что в более ранней статье 1985 года, написанной им вместе с Канделасом, Горовицом и Виттеном, где представлена первая серьезная попытка компактификации Калаби-Яу, они сделали упрощающее допущение о том, что четырехмерная и шестимерная геометрии являются независимыми. «И мы нашли решения, в которых они являются независимыми, хотя теория струн не требует этого. Годом позже я решил уравнения, которые получаются без этих допущений». Это так называемые уравнения Строминджера, которые касаются ситуации, где включаются потоки, а четырех- и шестимерные пространства взаимодействуют. «Возможность независимого существования обеих геометрий вызывает интерес, потому что из этого положения вытекает несколько действительно важных следствий», — добавляет Строминджер. Самое выдающееся из этих следствий заключается в том, что искажение может объяснить проблему иерархии масс, то есть почему масса бозона Хиггса настолько меньше планковской массы и почему гравитация настолько слабее других сил.

Уравнения Строминджера, которые применяют к не-кэлеровым многообразиям, описывают более широкий класс решений, чем уравнения, приведенные в статье 1985 года, которые применимы только к многообразиям Калаби-Яу. «Чтобы понять способы реализации теории струн в природе, необходимо понять более общие решения, — говорит Строминджер. — Важно понять все решения для теории струн, а пространство Калаби-Яу не содержит их все».^[200] Гарвардский физик Ли-Шенг Ценг (мой постдок) сравнивает многообразия Калаби-Яу с окружностью, «которая является самым красивым частным случаем среди всех гладких и замкнутых одномерных кривых». Уравнения Строминджера (иногда называемые системой Строминджера), по его словам, «включают смягчение условия, определяющего многообразия Калаби-Яу, подобно тому, как смягчение условий, определяющих окружность, приводит к условиям, определяющим эллипс». Если у вас есть замкнутая петля из струны фиксированной длины, то существует только одна окружность, которую можно сделать из нее, в то время как вы можете сделать бесчисленное число разных эллипсов, взяв окружность и сжимая или раздвигая ее в разной степени. Из всех кривых, которые вы можете сделать из этой петли, окружность является единственной, которая остается инвариантной к поворотам вокруг центра.

Для того чтобы убедиться, что окружность является частным случаем эллипса, нам необходимо посмотреть на уравнение, которое определяет эллипс в декартовой системе координат (x, y): x²/a²+y²/b²=1, где a и b — положительные, действительные числа.

Кривая будет являться окружностью только при условии, что a=b. Кроме того, необходимы два параметра а и b, чтобы определить эллипс, и только один параметр (так как а=b), чтобы определить окружность. Это условие делает эллипс несколько более сложной фигурой, чем окружность, как и система Строминджера (не-кэлерова) является более сложной, чем многообразия Калаби-Яу, которые можно описать меньшим числом параметров.

Хотя переход от окружности к эллипсу и от многообразия Калаби-Яу к не-кэлерову многообразию можно считать шагом назад с точки зрения симметрии и красоты, Ценг отмечает: «очевидно, что природа не всегда выбирает самую симметричную конфигурацию. Например, подумайте об эллиптических орбитах планет. Поэтому вполне возможно, что внутренняя шестимерная геометрия, описывающая нашу естественную Вселенную, может быть не полностью симметричной, как Калаби-Яу, а чуть менее симметричной, как система Строминджера».^[201]

Рис. 10.8. Если у вас есть петля фиксированной длины, то вы можете сделать бесконечное число эллипсов, одни более вытянутые, другие — более округлые, но вы можете сделать только одну окружность заданной длины. Другими словами, ослабив свойства, которые определяют окружность, вы можете получить любое число эллипсов. Аналогично многообразие Калаби-Яу, которое имеет кэлерову симметрию, по определению является (как и окружность) более частным случаем, чем не-кэлерово многообразие, которое удовлетворяет менее жестким условиям и охватывает более широкий класс объектов

Система, предложенная Строминджером, отнюдь не сахар, поскольку она состоит из четырех дифференциальных уравнений, которые должны быть решены одновременно, причем каждое из них может быть кошмаром для решения. Эта система состоит из двух эрмитовых уравнений Янга-Миллса, которые предназначены для калибровочных полей (см. девятую главу). Еще одно уравнение гарантирует, что вся геометрия является суперсимметричной, а последнее предназначено для устранения аномалий, что существенно для обеспечения согласованности теории струн.

Как будто и без того задача не оказывается достаточно сложной, так вдобавок каждое из четырех уравнений фактически представляет собой систему уравнений, а не одно уравнение. Каждое из них можно записать как тензорное уравнение, но так как сам тензор содержит много переменных, то можно разделить одно уравнение на отдельные уравнения для компонентов.

По этой же причине известное уравнение Эйнштейна, которое содержит в себе всю общую теорию относительности, фактически представляет собой набор из десяти уравнений поля, описывающих гравитацию как кривизну пространства-времени, вызванную наличием вещества и энергии, несмотря на то что его можно записать как одно тензорное уравнение. При доказательстве гипотезы Калаби решение уравнений Эйнштейна в вакууме сводится к одному уравнению, хотя и довольно впечатляющему. С не-кэлеровыми многообразиями работать тяжелее, чем с многообразиями Калаби-Яу, потому что здесь наблюдается меньшая симметрия и, следовательно, больше переменных, каждая из которых ведет к увеличению числа уравнений, подлежащих решению. Кроме того, на данный момент у нас фактически нет математических инструментов для решения этой проблемы. В случае с Калаби-Яу, мы привлекли алгебраическую геометрию, инструменты которой разрабатывались на протяжении двух предыдущих столетий, что позволило нам справиться с кэлеровыми многообразиями, но не с их не-кэлеровыми коллегами.

Тем не менее я не считаю, что эти два класса многообразий настолько разные с математической точки зрения. Мы использовали геометрический анализ для построения многообразий Калаби-Яу, и я убежден, что эти инструменты помогут нам построить не-кэлеровы многообразия, допуская, что сначала мы должны решить уравнения Строминджера или, по крайней мере, доказать, что решения существуют. Физикам необходимо знать, действительно ли не-кэлеровы многообразия могут существовать и если да, то удовлетворяют ли всем четырем уравнениям сразу, поскольку, если это невозможно, то люди, работающие над этой задачей, просто даром теряют время. Я занимаюсь ею почти двадцать лет с тех пор, как Строминджер выдвинул свою идею, и не могу найти решение. То есть решение без сингулярностей, так как Строминджер нашел несколько решений с сингулярностями, но они оказались чрезвычайно сложными. И люди начали верить, что решений без сингулярностей не существует.

Затем произошел небольшой прорыв. Я и несколько моих коллег обнаружили решения без сингулярностей для пары специальных случаев. В первой статье, которую я завершил в 2004 году вместе с математиком из Стэнфорда Юном Ли (моим бывшим аспирантом), мы доказали, что класс не-кэлеровых многообразий математически возможен. Фактически для каждого известного многообразия Калаби-Яу мы доказали существование целого семейства не-кэлеровых многообразий, которые достаточны похожи по структуре, чтобы входить в одно семейство. Таким образом, впервые существование этих многообразий было подтверждено математически.

Хотя решение уравнений Строминджера является чрезвычайно трудным делом, мы с Ли сделали самое легкое, что можно было сделать в этой области. Мы доказали, что эти уравнения можно решить для частного случая, когда не-кэлерово многообразие очень близко к многообразию Калаби-Яу. Фактически, мы начали с многообразия Калаби-Яу и показали, как его деформировать, чтобы геометрия или метрика уже не были кэлеровыми. Хотя многообразие все еще могло поддерживать метрику Калаби-Яу, его метрика уже была не-кэлеровой, что сделало возможными решения системы Строминджера.

Вероятно, важнее то, что Ли и я обобщили теорему DUY (о которой упоминалось в девятой главе и название которой является аббревиатурой фамилий ее авторов — Дональдсона, Уленбека и Яу), чтобы охватить все не-кэлеровы многообразия. Теорема DUY имеет большое практическое значение, потому что она автоматически берет на себя решения двух из четырех уравнений Строминджера, связанных с эрмитовой теорией Янга-Миллса, и позволяет решить уравнения суперсимметрии и устранения аномалий.

Учитывая, что DUY является инструментальным средством для компактификаций Калаби-Яу (с точки зрения воспроизведения калибровочных полей), мы надеемся, что она также пригодится для не-кэлеровых компактификаций.

Одним из перспективных способов получения не-кэлеровых многообразий, подразумеваемый гипотезой Рида, является применение конифолдного перехода к уже известному многообразию Калаби-Яу. Я недавно рассматривал эту возможность с Юном Ли и Джи-Хианом Фу, бывшим своим гарвардским аспирантом, сейчас работающим в Фуданьском университете в Шанхае. Исходное многообразие, с которого мы начали, предложил Херб Клеменс, один из архитекторов конифолдного перехода, но он обеспечил нас только общей топологией, то есть многообразием без метрики и, следовательно, без геометрии. Фу, Ли и я пытались придать этому многообразию некоторую форму, показав существование метрики, которая будет удовлетворять уравнениям Строминджера.

Эти уравнения представляются уместными здесь, потому что они применимы не только к не-кэлеровым многообразиям, но также к многообразиям Калаби-Яу, которые представляют собой частный случай. Кроме того, гипотеза Рида включает процедуру, которая позволяет перейти от многообразий Калаби-Яу к не-кэлеровым многообразиям и обратно.

Таким образом, если вам нужен набор уравнений, которые охватывают обе геометрии, то формулировки Строминджера — возможно, именно то, что вы искали. Мы с коллегами доказали, что многообразие Клеменса удовлетворяет трем из четырех уравнений Строминджера, но пока мы не нашли решение для самого трудного из всех уравнений — уравнения устранения аномалий. Я все еще убежден, что искомое многообразие существует. В конце концов, если наши усилия увенчались решением трех уравнений — это уже хорошо. Но пока мы не решим последнее уравнение, у нас не будет необходимого доказательства.

Фу и я пошли дальше, показав, как построить класс, топологически отличный от не-кэлеровых многообразий, который удовлетворяет уравнениям Строминджера. Если вести построение с нуля, а не путем модифицирования известных многообразий Калаби-Яу, то получаемые многообразия, по сути, являются не-кэлеровыми. Они состоят из поверхностей K3 (четырехмерные многообразия Калаби-Яу) с двухмерными торами, присоединенными к каждой точке. Решение уравнения Строминджера в этом случае включает решение уравнения Монжа-Ампера (класс нелинейных дифференциальных уравнений, который мы обсуждали в пятой главе), которое сложнее, чем то, которое мне пришлось решать для доказательства гипотезы Калаби. К счастью, мы с Фу смогли оттолкнуться от наших ранних работ. Наш метод, как и в случае с доказательством гипотезы Калаби, включал априорное оценивание, то есть мы должны были предсказать диапазон значений разных параметров.

Мы с Фу нашли особый метод, позволивший нам решить не одно, а все четыре уравнения. В то время как в случае гипотезы Калаби я смог получить все возможные решения уравнения Монжа-Ампера, на этот раз мы получили лишь подмножество целого класса решений. К сожалению, мы не достаточно хорошо понимали систему, чтобы определить, насколько большим или маленьким является это подмножество. Но, по крайней мере, мы сделали несколько предварительных шагов.

Большинство физиков, которые начинали работать с не-кэлеровыми компактификациями, допускают, что уравнения Строминджера можно решить, не беспокоясь о доказательстве этого. Ли, Фу и я показали, что эти уравнения можно решить в отдельных случаях, которые мы пока не определили, но это еще один способ доказать, что специфические многообразия, то есть какая-то часть всех не-кэлеровых многообразий, действительно существуют. Это явилось всего лишь отправной точкой для решения более существенной задачи: нахождение метрики, удовлетворяющей системе Строминджера и всем ее уравнениям. Несмотря на то что пока никто и близко не подошел к решению этой проблемы и все признаки указывают на то, что проблема дастся физикам нелегко, мы с коллегами нашим небольшим вкладом, по крайней мере, подняли вопрос о его возможности.

Бекер утверждает, что, если все удастся, то это будет важнее, чем доказательство гипотезы Калаби. Может быть, она права, но об этом рано говорить. Пока я не доказал гипотезу Калаби, я не понимал ее полной значимости. И даже после ее доказательства физики еще восемь лет не осознавали его важности и значения сопутствующей теоремы. Но я продолжал изучать пространства Калаби-Яу, потому что для меня они выглядели привлекательно. Пространства, описываемые системой Строминджера, также имеют определенный шарм. Сейчас мы уже увидели, что дело пошло.

Тем временем мы с Фу предложили многообразия, которые мы создали для наших друзей-физиков, сотрудничая с Мелани Бекер, Катрин Бекер, Ценгом и, можно сказать, даже со Строминджером, если причислить его к нашим единомышленникам. Затем наша группа построила еще больше примеров исходной модели Фу-Яу. В отличие от гетеротической компактификации теории струн, описанной в последней главе, наша команда не смогла получить правильные характеристики частиц или три поколения частиц из Стандартной модели. «Что мы имеем, — говорит Мелани Бекер, — так это стабилизованные модули, что является необходимым предварительным условием ко всему, а также реальным способом вычисления масс».^[202]

На данном этапе трудно сказать, что получится из усилий физиков, играющих с не-кэлеровыми компактификациями и многими другими альтернативами многообразий Калаби-Яу (в том числе в области под названием не-геометрические компактификации), исследование которых ведется в настоящее время. Справедливости ради стоит поставить вопрос: действительно ли компактификации Калаби-Яу являются верным описанием нашей Вселенной или только простейшей моделью, из которой мы черпаем знания, — фантастический эксперимент, дающий возможность узнать, как работает теория струн и как мы можем объединить суперсимметрию, силы и прочее в «окончательной» теории.

В конце концов, это исследование может привести нас к совершенно иному виду геометрии.

А сейчас мы просто пытаемся изучить некоторые из многих возможностей, лежащих перед нами на ландшафте теории струн. Но даже среди всех этих возможностей мы пока живем только в одной Вселенной, и эту Вселенную все еще можно описать геометрией Калаби-Яу. Я лично думаю, что многообразия Калаби-Яу являются самой элегантной конструкцией, построенной до настоящего времени, из всех вакуумных состояний теории струн. Но если наука приведет нас к какому-либо другому виду геометрии, я охотно последую за ней.

«За последние двадцать лет мы обнаружили много решений теории струн, включая не-кэлеровы, — говорит Джо Полчински. — Но самые первые и самые простые решения — многообразия Калаби-Яу, — похоже, ближе всего к природе».^[203]

Я склонен согласиться с ним, хотя многие первоклассные ученые думают по-другому. Мелани Бекер, например, является чемпионом по не-кэлеровому подходу. Строминджер, который внес основной вклад как в область Калаби-Яу, так и в область не-кэлеровых многообразий, не считает, что пространства Калаби-Яу когда-то устареют. «Но мы хотим использовать все, с чем мы сталкиваемся, как трамплин для прыжка на следующий уровень понимания, — говорит он, — и многообразия Калаби-Яу стали нашими подспорьем во многих направлениях».^[204]

Надеемся, что вскоре мы будем лучше понимать, куда они нас могут привести. Несмотря на свою привязанность к многообразиям Калаби-Яу, любовь к которым не стала меньше за прошедшие тридцать с лишним лет, я пытаюсь сохранить восприимчивый ум, присоединяясь к сентенции Марка Гросса: «Мы просто хотим знать ответ».

Если окажется, что не-кэлеровы многообразия имеют большее значение для теории струн, чем многообразия Калаби-Яу, я соглашусь с этим, поскольку эти менее изученные многообразия обладают своеобразным очарованием сами по себе. И я ожидаю, что в процессе дальнейших напряженных исследований я оценю их еще больше.

Физик Пенсильванского университета Бёрт Оврут, пытающийся реализовать Стандартную модель через компактификации Калаби-Яу, сказал, что он не готов сделать радикальный шаг к не-кэлеровым многообразиям, для работы с которыми нам пока не хватает математических знаний: «Это повлечет за собой гигантский прыжок в неизведанное, но пока мы не понимаем, что эти альтернативные конфигурации представляют собой на самом деле».^[205] Несмотря на то что я согласен с заявлением Оврута, я всегда готов к решению новых задач, и меня не беспокоит погружение в неведомые воды. Но так как нам часто советуют не пускаться в плавание одному, я не прочь втянуть в него нескольких своих коллег.

180. Gary Shiu, quoted in Adrian Cho, “String Theory Gets Real — Sort Of” Science 306 (November 26, 2004): 1,461.

181. Shamit Kachru (Stanford University), e-mail letter to author, December 6, 2008.

182. Shamit Kachru, Renata Kallosh, Andrei Linde, and Sandip Trivedi, “De Sitter Vacua in String Theory,” Physical Review D 68 (2003).

183. Raman Sundrum (Johns Hopkins University), interview with author, February 22, 2007.

184. Liam McAllister (Cornell University), interview with author, November 12, 2008.

185. Kachru, interview with author, September 8, 2007.

186. Liam McAllister (Princeton University), interview with author, February 20, 2007.

187. Joe Polchinski (University of California, Santa Barbara), interview with author, February 6, 2006.

188. David Gross, quoted in Dennis Overbye, “Zillions of Universes? Or Did Ours Get Lucky?” New York Times, October 28, 2003.

189. Burton Richter, “Randall and Susskind,” letter to editor, New York Times, January 29, 2006.

190. Leonard Susskind, The Cosmic Landscape (New York: Little Brown, 2006), pp. 354–355.

191. Tristan Hubsch (Howard University), interview with author, November 7, 2008.

192. Mark Gross (Stanford University), interview with author, October 31, 2008.

193. Gross, interview with author, September 19, 2008.

194. Miles Reid (University of Warwick), interview with author, August 12, 2007.

195. Allan Adams (MIT), interview with author, October 31, 2008.

196. Gross, interview with author, October 31, 2008.

197. Adams, interview with author, October 31, 2008.

198. Tristan Hubsch, e-mail letter to author, December 15, 2008.

199. Melanie Becker (Texas A&M University), interview with author, February 1, 2007.

200. Andrew Strominger (Harvard University), interview with author, February 7, 2007.

201. Li-Sheng Tseng (Harvard University), interview with author, December 17, 2008.

202. Becker, interview with author, February 1, 2007.

203. Polchinski, interview with author, January 29, 2007.

204. Strominger, interview with author, August 1, 2007.

205. Burt Ovrut (University of Pennsylvania), interview with author, February 2, 2007.