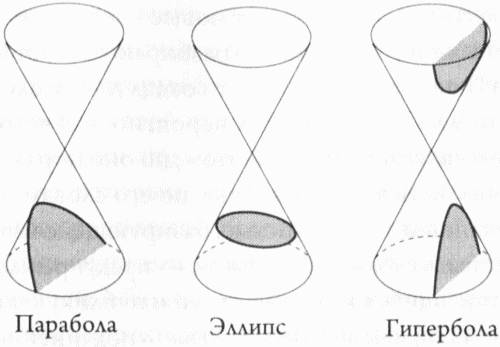
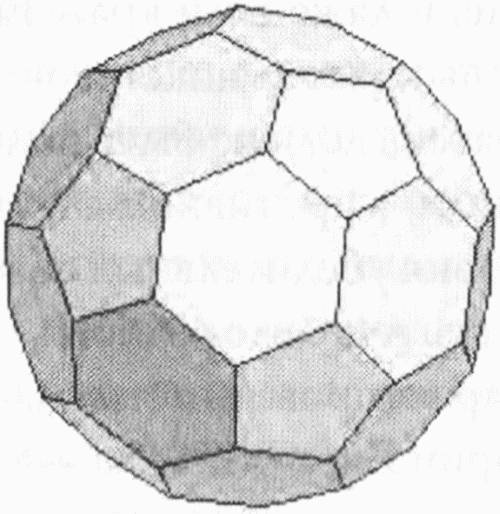
Глава 13. Истина, красота и математика

Насколько далеко могут зайти исследователи в своих попытках изучить скрытые измерения Вселенной при отсутствии физических доказательств? Аналогичный вопрос можно задать и струнным теоретикам, пытающимся создать всеобъемлющую теорию природы, не опираясь на обратную связь с экспериментом. Это похоже на исследование огромной темной пещеры с помощью только колеблющегося пламени свечи. Хотя некоторым исследования в таких обстоятельствах могут показаться чистым безумием, подобная ситуация далеко не беспрецедентна в истории науки. На ранних этапах создания теории периоды блуждания во тьме — скорее правило, чем исключение, особенно когда речь идет о развитии и продвижении широкомасштабных идей. На подобных этапах, когда нет экспериментальных данных, на которые можно опереться, математическая красота — это все, что может служить нам путеводной нитью.

Поль Дирак «называл математическую красоту единственным критерием для выбора пути движении вперед в теоретической физике», — писал физик Питер Годдар.^[251] Иногда такой подход полностью себя оправдывает, как это было в случае прогноза Дирака о существовании позитрона (как электрона с положительным зарядом), что стало возможным только потому, что математическое рассуждение навело его на мысль, что такие частицы должны существовать. Действительно, спустя несколько лет позитрон был открыт, подтвердив тем самым его веру в математику.

Действительно, мы снова и снова открываем для себя, что идеи, которые опираются на математику и соответствуют критерию простоты и красоты, обычно являются теми идеями, которые мы, в конце концов, наблюдаем реализованными в природе. Совершенно непостижимо, почему это происходит. Например, физик Юджин Вигнер пребывал в недоумении от «необоснованной эффективности математики в естественных науках», то есть остается загадкой, как чисто математические конструкции, не имеющие видимой связи с миром природы, тем не менее описывали этот мир с такой точностью.^[252]

Физик Чженьнин Янг тоже удивился, обнаружив, что уравнения Янга-Миллса, описывающие взаимодействия между частицами, уходят своими корнями в физические калибровочные теории, обладающие удивительным сходством с идеями теории расслоения, которую математики начали разрабатывать тридцатью годами раньше и, по словам Янга, «без ссылки на физический мир». Когда он спросил геометра Ч. Ш. Черна, как такое возможно, что «математики выдумали эти понятия из ниоткуда», Черн запротестовал: «Нет, нет. Эти понятия не выдуманы. Они естественны и реальны».^[253]

Конечно, нет недостатка в абстрактных идеях, пришедших к математикам чуть ли не из воздуха, которые, как обнаруживалось впоследствии, описывают природные явления. Не все они, между прочим, были продуктами современной математики. Считается, что конические сечения — круг, эллипс, парабола и гипербола — кривые, получаемые при сечении конуса плоскостью, были открыты греческим геометром Менехмом примерно в 300 году до нашей эры и широко использовались столетие спустя Аполлонием Пергским в его трактате «Коники». Однако эти формы не находили широкого научного применения до начала XVII века, когда Кеплер обнаружил, что орбиты планет Солнечной системы являются эллипсами.

Аналогично фуллерены или бакминстерфуллерены, новая форма углерода, содержащая 60 атомов углерода, соединенные в сфероподобную структуру с пятиугольными и шестиугольными гранями, была открыта химиками в 1980-е годы. А форма этих молекул была описана Архимедом более двух тысяч лет назад.^[254] Теория узлов, раздел чистой математики, сформулированная в конце XIX века, нашла свое применение спустя более чем столетие в теории струн и в исследованиях ДНК.

Трудно сказать, почему математические идеи находят подтверждение в природе. Ричард Фейнман находил в той же степени сложным и объяснение, почему «каждый из наших физических законов может быть представлен чисто математической формулировкой». Ключ к разгадке, как он считал, может таиться в связи между математикой, природой и красотой. «Тем, кто не знает математики, — считал Фейнман, — сложно ощутить красоту, глубочайшую красоту природы».^[255]

Но если красота и является ориентиром, позволяющим выбрать верный путь, по крайней мере пока у нас нет более объективных критериев, следует оставить все попытки дать ей какое бы то ни было определение, предоставив это поэтам. Хотя математики и физики рассматривают концепцию красоты несколько иначе: в обеих дисциплинах мы называем красивыми, как правило, те идеи, которые, с одной стороны, могут быть изложены четко и лаконично, а с другой — обладают чрезвычайной мощью и широким охватом. Тем не менее для такого субъективного понятия, как красота, большую роль неизбежно играет и личный вкус. Я вспоминаю тост, произнесенный на свадьбе старого холостяка, который остепенился сравнительно поздно, после многих лет холостяцкой жизни. Его знакомые гадали, какая девушка сумеет заставить этого парня связать себя узами брака? Старого холостяка это тоже интересовало. «Ты узнаешь, когда увидишь ее», — неоднократно говорил ему друг задолго до того, как холостяк нашел свою единственную.

Я знаю, что он имел в виду. У меня были аналогичные ощущения, когда я встретил свою будущую жену в математической библиотеке Беркли много лет назад, хотя сложно передать словами чувства, охватившие меня в тот момент. Не хочу обидеть свою жену, но похожее неуловимо трепетное чувство эйфории я испытал, когда доказал гипотезу Калаби в середине 1970-х годов. Закончив доказательство гипотезы после месяцев напряженных усилий, растянувшихся на годы, я, наконец, смог расслабиться и насладиться комплексными многомерными пространствами, открытыми мною. Можно сказать, что это была любовь с первого взгляда, хотя после работы над задачей, мне кажется, что я уже хорошо знал эти объекты, даже когда впервые увидел их. Может быть, моя уверенность была неуместной, но тогда я чувствовал (и чувствую до сих пор), что эти пространства, возможно, будут каким-то образом играть чрезвычайно важную роль в физическом мире. Теперь все зависит от струнных теоретиков или, возможно, от исследователей в других, не связанных с ними областях науки, которые покажут, была ли моя догадка правильной.

Рис. 13.1. Конические сечения — это три фундаментальные кривые, которые получаются при пересечении конуса плоскостью (или фактически двух конусов, прикрепленных друг к другу острыми концами). Эти три кривые: парабола, эллипс (в частном случае — окружность) и гипербола

Рис. 13.2. В то время как правильный икосаэдр состоит из двадцати треугольных граней, показанный на рисунке усеченный икосаэдр состоит из двадцати шестиугольных и двенадцати пятиугольных граней, причем никакие два пятиугольника не имеют общей стороны. В отличие от правильных икосаэдров, которые относятся к Платоновым телам, усеченные икосаэдры относятся к архимедовым телам, названным в честь греческого математика, исследовавшего эти фигуры более двух тысяч лет назад. Эта форма напоминает футбольный мяч и один из вариантов так называемых фуллеренов — молекулярной структурированной формы углерода, состоящей из шестидесяти атомов, открытой в 1985 году химиками Гарольдом Крото и Ричардом Смэлли. Термин фуллерен является сокращением от бакминстерфуллерена, класса молекул, названного в честь архитектора Ричарда Бакминстера Фуллера, изобретателя геодезического купола похожей формы

По утверждению математика Майкла Атья, струнным теоретикам должно быть приятно, «что то, с чем они “играют”, если даже это невозможно измерить экспериментально, может оказаться очень богатой… математической структурой, которая не только согласуется с теорией, но фактически открывает новые двери, дает новые результаты и т. д…. Очевидно, они кое в чем разбираются. Остается выяснить, является ли это “кое-что” тем, что Бог создал для Вселенной. Но если Бог создал это не для Вселенной, то, вероятно, для чего-то еще».^[256]

Я не знаю, чем является это «кое-что», но оно поражает меня слишком сильно, чтобы быть ничем. Но Атья, по его словам, также осознает риск быть убаюканным элегантностью, базирующейся на зыбкой почве. «Красота может быть скользкой вещью», — предупреждает Джим Холт, скептически относящийся к теории струн и публикующий свои статьи в «New Yorker».^[257] Или, как выразился Атья: «подчинение физики математике таит в себе опасность, поскольку может завести нас в область измышлений, воплощающих математическое совершенство, но слишком далеких от физической реальности или даже не имеющих с ней ничего общего».^[258]

Безусловно, слепое следование математической красоте способно ввести нас в заблуждение, и даже если красота указывает нам верное направление, то одна лишь красота никогда не сможет привести нас к цели. В конце концов, красота должна быть подкреплена чем-то еще — чем-то более существенным, в противном случае наши теории никогда не выйдут за пределы уровня убедительных спекуляций, независимо от степени их обоснованности и правдоподобия.

«Красота не может гарантировать истины, — утверждал физик Роберт Миллс, соавтор теории Янга-Миллса. — У нас нет никаких логических оснований утверждать, что истина должна быть прекрасной, но наш опыт постоянно подсказывает, что следует ожидать красоту в самой сути вещей и использовать это ожидание в качестве руководства в поисках более глубокого теоретического понимания фундаментальных структур природы». И наоборот, добавляет Миллс, «если предложенная теория неэлегантна, мы считаем ее сомнительной».^[259]

Итак, где же заканчивается математика и начинается теория струн? Физик из Корнеллского университета Генри Тай считает, что «теория струн слишком красива, богата, креативна и утонченна, чтобы ее не использовала природа. Это было бы слишком расточительно»^[260]. Только этого недостаточно, чтобы сделать теорию струн верной, а такие критические трактовки, как «The Trouble with Physics» и «Not Even Wrong», сеют сомнения в общественном сознании в тот момент, когда сама эта теория находится в некотором упадке. Даже такой энтузиаст, как Брайан Грин, автор книги «The Elegant Universe» («Элегантная Вселенная»), признает, что физическая теория не может быть оценена только на основании элегантности: «Вы судите о ней на основании того, может ли она делать предсказания, которые будут подтверждены экспериментом».^[261]

Во время написания этой книги я имел возможность обсуждать ее содержание со многими людьми, имеющими образование в соответствующей области, которым, по моему мнению, было бы интересно читать о подобного рода вещах. Когда они слышали, что книга связана с математическими основами теории струн, то часто их реакция была примерно следующей: «Подождите минуту. Разве с теорией струн что-нибудь не так?» Их вопросы предполагали, что написание книги о математических основах теории струн — это примерно то же, что книга о фантастических инженерных разработках, которые легли в основу строительства «Титаника». Мой коллега-математик, которому, вероятно, виднее, даже публично заявил, что поскольку «суд присяжных по теории струн еще не состоялся», нечего судить о математической базе, связанной с теорией струн.

Такое заявление подразумевает фундаментальное заблуждение о природе математики и ее отношении к эмпирическим наукам. В то время как окончательным доказательством в физике считается эксперимент, в математике это не так. Можно иметь миллиард частных свидетельств о том, что что-то является верным, но миллиард первое опрокинет все здание. До тех пор пока что-то полностью не доказано при помощи чистой логики, оно остается гипотезой.

В физике и других эмпирических науках истинность любого утверждения всегда является предметом ревизии. Теория тяготения Ньютона продержалась более двух столетий, но из-за присущих ей ограничений в конце концов была заменена теорией Эйнштейна, имеющей собственные ограничения, которые когда-нибудь приведут к замене ее теорией квантовой гравитации, например теорией струн. В то же время математика, на которой базируется ньютоновская механика, является на сто процентов верной и никогда не изменится.

Чтобы сформулировать теорию гравитации, Ньютону пришлось попутно изобрести математический анализ. Когда теория гравитации Ньютона оказалась бессильной объяснить новые эксперименты из-за присущих ей ограничений и была разработана общая теория относительности, мы не отказались от математического анализа. Мы держимся за математику, которая является не пустым звуком, но жизненной необходимостью, понимая, что ньютоновская механика представляет собой удивительно хороший инструмент для большинства ситуаций, хотя ее и нельзя применять в предельных случаях.

Теперь перейдем к более современным вещам, которые ближе моему сердцу. Тридцать с лишним лет назад я доказал существование пространств, которые сегодня называются многообразиями Калаби-Яу. И их существование вовсе не зависит от того, окажется ли теория струн всеобъемлющей теорией природы. Следует признать, что в доказательстве могут быть обнаружены слабые места и все аргументы могут рассыпаться, как карточный домик. Но в случае гипотезы Калаби доказательство было проверено столько раз, что вероятность найти ошибку, по существу, равна нулю. Не только пространства Калаби-Яу остались в физике, но и методы, которые я использовал для решения задачи, применяются с большим успехом для многих других математических задач, в том числе и для задач алгебраической геометрии, которые не имеют явных связей с исходной гипотезой.

Действительно, полезность пространств Калаби-Яу в физике в некотором смысле не имеет отношения к вопросу о важности математики. Рискуя показаться нескромным, я мог бы добавить, что в 1982 году я получил медаль Филдса, одну из самых почетных наград в математике, главным образом за доказательство теоремы Калаби. Вы можете заметить, что эту награду мне вручили за несколько лет до того, как физики узнали о многообразиях Калаби-Яу и до появления на карте самой теории струн.

Что касается теории струн, то математика, лежащая в ее основе, или вытекающие из нее следствия, являются абсолютно верными, независимо от того, какое окончательное решение примет суд присяжных в отношении самой теории. Я пойду дальше: если математическая теория, лежащая в основе теории струн, является веской и строго доказанной, то она будет прочно стоять на ногах, независимо от того, живем ли мы на самом деле в десятимерной Вселенной, состоящей из струн и бран.

Что это может означать для физики? Как я уже упоминал, поскольку я математик, не мне судить о справедливости теории струн, но я выскажу некоторые идеи и замечания. Конечно, теория струн остается не только недоказанной, но и непроверенной. Тем не менее главным инструментом проверки работы физиков остается математическая последовательность теории, и пока теория струн выдержала этот экзамен с честью. Последовательность в данном случае означает отсутствие противоречий. Это означает, что если то, что вы вставляете в уравнения теории струн, является корректным, то и то, что вы получите с помощью этих уравнений, тоже должно быть корректным. Это означает, что когда вы делаете расчеты, результаты не расходятся и не стремятся к бесконечности. Функции остаются разумными и не превращаются в тарабарщину. Хотя этого далеко не достаточно, чтобы удовлетворить суровых критиков, но это важная отправная точка. На мой взгляд, в этой идее есть доля истины, даже если природа и не играет по такому сценарию.

Эдвард Виттен, похоже, разделяет эту точку зрения. Он утверждает, что математическая непротиворечивость «была одним из самых надежных проводников для физиков в минувшем столетии».^[262]

Учитывая, насколько трудно разработать эксперимент, который мог бы проникнуть в физику планковских масштабов, и насколько дорогим он может быть, если нам когда-нибудь удастся его придумать, то все, что мы, вероятно, сможем сделать, это именно проверка теории на непротиворечивость, которая, тем не менее, по словам математика из Беркли Николая Решетихина, «может быть очень мощной». «Именно поэтому вершина теоретической физики все больше становится математической. Если ваши идеи не являются математически непротиворечивыми, то их можно сразу же отбросить».^[263]

Теория струн не только математически непротиворечива, но и, вроде бы, соответствует всему, что мы знаем о физике элементарных частиц, а также предлагает новые пути для решения проблем пространства и времени — гравитации, черных дыр и других головоломок. Мало того, что теория струн согласуется с устоявшейся, хорошо проверенной физикой квантовых теорий поля, но, похоже, и неразрывно связана с этими теориями. «Никто не сомневается, что, например, такие калибровочные теории, как теория Янга-Миллса для описания сильного взаимодействия, дают фундаментальное описание природы, — утверждает Роберт Дикграаф, физик из Амстердамского университета. — Но калибровочные теории фундаментально связаны со струнами». Это следует из принципа дуализма, который декларирует эквивалентность теории поля и струнной теории, демонстрируя взгляд на одну и ту же задачу с разных точек зрения. «Невозможно доказать принадлежность теории струн к физике, поскольку она неразрывно связана со всеми вещами, которые нам дороги, — добавляет Дикграаф. — Поэтому мы не можем избавиться от теории струн, независимо от того, описывает она нашу Вселенную или нет. Это всего лишь еще один инструмент для осмысления фундаментальных свойств физики».^[264]

Теория струн также стала первой непротиворечивой теорией квантовой гравитации — самого больного вопроса современной физики. Но она пошла еще дальше. «Теория струн обладает прекрасной предсказательной силой в отношении гравитации», — утверждает Виттен. Под этим он подразумевает, что теория струн делает больше, чем просто описывает гравитацию. «Этот феномен встроен в рамки теории, и тот, кто ничего не знает о гравитации, мог бы открыть ее, как естественное следствие самой теории».^[265] В дополнение к квантованию гравитации теория струн подошла к решению таких задач, как проблема энтропии черной дыры, которую не удается решить другими средствами. В этом смысле теорию струн уже можно считать успешной теорией на определенном уровне, даже если она не станет окончательной теорией физики.

Хотя этот вопрос вынесен на обсуждение, можно не сомневаться, что теория струн приведет к бесценному кладу новых идей, новых инструментов и новых направлений в математике. Например, открытие зеркальной симметрии привело к появлению «семейных предприятий» в области алгебраической и исчислительной геометрии. Зеркальная симметрия, то есть идея, что большинство пространств Калаби-Яу имеют зеркального партнера с другой топологией, но соответствующего той же физике, была открыта в контексте теории струн, а ее справедливость подтверждена математикой. Это, как мы видели, делается по типичной схеме: теория струн может дать понятия, намеки и подсказки, а математики в большинстве случаев обеспечивают доказательство.

Одна из причин, по которой зеркальная симметрия представляет такую ценность для математики, заключается в том, что сложные вычисления для одного пространства Калаби-Яу могут оказаться намного проще для его зеркального партнера. В результате, исследователи смогли в короткие сроки решить многовековые проблемы математики. Гомологическая зеркальная симметрия и теория Строминджера-Яу-Заслоу (Strominger-Yau-Zaslow — SYZ, СЯЗ), которую разрабатывают с середины 1990-х годов, вскрыли неожиданные, но полезные связи между симплектической геометрией и алгебраической геометрией — двумя разделами математики, которые ранее рассматривались отдельно. Хотя зеркальная симметрия была открыта при исследовании теории струн, истинность ее математического фундамента не зависит от теории струн. «Это явление, — отмечает Эндрю Строминджер, — можно описать так, что оно вообще не будет включать теорию струн, [но] прошло бы много времени, пока бы мы его обнаружили, если бы у нас не было теории струн».^[266]

Приведу другой пример: в работе 1996 года я и мой бывший аспирант Эрик Заслоу использовали идею из теории струн для решения классической задачи алгебраической геометрии, связанной с вычислением количества так называемых рациональных кривых на четырехмерной поверхности K3. Напомню, что термин K3 относится к целому классу поверхностей — не к одной, а к бесконечному их числу. «Кривые» в данном случае являются двухмерными римановыми поверхностями, определяемыми алгебраическими уравнениями, и представляют собой топологические эквиваленты сфер, встроенных в эту поверхность. Количество этих кривых, оказывается, зависит только от количества узлов, расположенных на кривой, или точек, указывающих, где кривая пересекает саму себя. Например, цифра «восемь» имеет один узел, тогда как у круга количество узлов равно нулю.

Рассмотрим еще один пример с узлами, который связан с нашим предыдущим обсуждением конифолдных переходов (в десятой главе): если взять двухмерный бублик и сжать одну из окружностей, проходящих сквозь дырку, до точки, то получим что-то похожее на рогалик с соединенными концами. Если разделить эти два конца и разорвать поверхность, то получится топологический эквивалент сферы. Таким образом, можно считать такой «прищипнутый» бублик или «соединенный рогалик» сферой с одним узлом (или пересечением). Точно так же можно перейти к поверхностям более высокого рода и посмотреть на бублик с двумя дырками: сначала сожмем в точку окружность на «внутренней стенке» между двумя дырками, затем проделаем аналогичную операцию где-нибудь на «наружной стенке» бублика. Объект с такими двумя точками сжатия фактически является сферой с двумя узлами, поскольку, если мы разделим эти две точки и разорвем поверхность, то получим сферу. Дело в том, что если начинать с поверхности более высокого рода, скажем, с двумя, тремя или более дырками, то можно получить кривую или сферу с большим количеством узлов.

Позвольте мне переформулировать задачу в алгебраической геометрии, которую мы пытались решить вначале: для поверхности K3 мы хотим определить количество рациональных кривых с g узлами, которые можно расположить на этой поверхности, для любого значения g (положительного целого числа). Используя обычные методы, математики придумали формулу, которая хорошо работает для кривых с шестью или меньшим количеством узлов, но не с большим. Заслоу и я приступили к решению более общей задачи, то есть к кривым с произвольным количеством узлов. Вместо обычного метода мы взяли теорию струн и рассмотрели задачу с точки зрения бран внутри пространства Калаби-Яу.

В соответствии с теорией струн существуют браны, связанные с поверхностью K3, которая состоит из кривых (или двухмерных поверхностей, как мы определили ранее), а также так называемого плоского линейного расслоения, присоединенного к каждой кривой. Чтобы получить представление о таком линейном расслоении, представим человека, идущего по экватору с палкой произвольной длины — пусть даже бесконечно длинной, — держа ее перпендикулярно экватору и касательно к поверхности сферы. В конце концов, палка опишет цилиндр, который называют тривиальным линейным расслоением. Если человек во время ходьбы перевернет палку на 180 градусов, то палка опишет ленту Мёбиуса. Кстати, оба этих линейных расслоения являются «плоскими», то есть они обладают нулевой кривизной.

Заслоу и я заметили, что если взять пространство всех бран, содержащих кривые фиксированного рода g, которые связаны с данной поверхностью K3, и затем вычислить эйлерову характеристику этого пространства, то полученное число будет точно равняться числу рациональных кривых с g узлами, которые вписываются в эту поверхность K3.

Таким образом, я и мой коллега переформулировали исходную задачу в другом виде, показав, что все сводится к получению эйлеровой характеристики пространства бран. Затем мы использовали дуализм теории струн, разработанный Кумруном Вафа и Виттеном, для вычисления эйлеровой характеристики. Таким образом, теория струн дала новый инструментарий для решения задачи, а также новый способ формализации проблемы. Ранее алгебраические геометры не могли решить эту задачу, поскольку они не рассматривали браны: им никогда не приходило в голову решить ее в терминах пространства модулей, включающего в себя совокупность всех возможных бран данного типа.

Хотя мы с Заслоу набросали общий подход, полное доказательство было получено только спустя несколько лет другими учеными — Джимом Брайаном из Университета Британской Колумбии и Найчунгом Конаном Лойнгом из Университета Миннесоты. В результате теперь у нас есть математическая теорема, которая является истинной безотносительно к истинности теории струн.

Рис. 13.3. Если вы идете по экватору и все время удерживаете палку параллельно земле по касательной к поверхности, то опишете цилиндр. Если, огибая земной шар, вы перевернете палку на 180 градусов, то опишете более сложную поверхность, имеющую одну, а не две стороны, называемую лентой Мёбиуса

Кроме того, формула, которую мы вывели для расчета рациональных кривых на поверхностях K3, дает функцию для генерирования всех чисел, которые вы получаете для рациональных кривых с произвольным количеством узлов. Оказывается, эта функция по существу воспроизводит знаменитые тау-функции, которые были введены в 1916 году индийским математиком и гением-самоучкой Шринивасой Рамануджаном.^[267] С тех пор наша функция в сочетании с высказанными Рамануджаном предположениями привела ко многим важным открытиям в области теории чисел. Насколько мне известно, наша работа впервые помогла установить серьезную связь между исчислительной геометрией (предметом расчета кривых) и тау-функцией.

Эта связь была закреплена последними работами Юйонг Дзена, молодого математика, недавно приглашенного работать в Гарвард, которого обучал мой бывший студент Юн Ли. Дзен показал, что не только рациональные кривые на поверхности КЗ связаны с тау-функцией, но расчет любых кривых произвольного рода на любой алгебраической поверхности связан с тау-функцией. И Дзен сделал это, доказав гипотезу, высказанную немецким математиком Лотаром Гёттше, который обобщил так называемую формулу Яу-Заслоу для рациональных кривых на поверхностях K3.^[268] Новая обобщенная формула, справедливость которой доказал Дзен, носит имя Гёттше-Яу-Заслоу. Несколькими годами ранее бывший мой аспирант А. К. Лью опубликовал доказательство формулы Гёттше-Яу-Заслоу.^[269] Но его доказательство, выполненное с помощью сугубо технического, аналитического метода, не дает объяснения в том виде, который устроил бы алгебраических геометров. Таким образом, статья Лью не рассматривается в качестве окончательного подтверждения этой формулы. Доказательство Дзена, основанное на аргументах алгебраической геометрии, получило более широкое признание.

Таким образом, благодаря выводу, изначально вытекающему из теории струн, мы поняли, что связь между исчислительной геометрией и тау-функцией Рамануджана, вероятно, глубже, чем предполагалось. Мы всегда ищем похожие связи между различными разделами математики, поскольку эти неожиданные связи часто могут привести нас к новому пониманию обоих разделов. Я подозреваю, что со временем будет открыто больше связей между исчислительной геометрией и тау-функцией.

В качестве яркого примера обогащения математики теорией струн приведем разработанную в 1990-х годах Виттеном и Натаном Зайбергом из Университета Ратджерса систему уравнений, получившую название Зайберга-Виттена (см. третью главу), которая ускорила исследование четырехмерных пространств. Эти уравнения оказались проще для использования, чем существующие методы, что привело к взрывному росту количества новых идей в работе с четырьмя измерениями, главной из которых является попытка классифицировать и систематизировать все возможные формы. Хотя уравнения Зайберга-Виттена первоначально были получены в теории поля, вскоре было показано, что они также могут быть выведены из теории струн. Кроме того, использование этой идеи в контексте теории струн значительно расширило наши представления о ней. «В ряде случаев, — говорит мой коллега, — Виттен обычно советовал математикам: вот, возьмите эти уравнения, они могут оказаться полезными. И действительно, они оказывались полезными». «Теория струн стала таким благом для математики, таким огромным источникам новых идей, что даже если она окажется несостоятельной как теория природы, она уже сделала для математики больше, чем любой вид человеческой деятельности, который я могу вспомнить», — говорит мой давний сотрудник Бонг Лиан из Университета Брандейса.^[270] Хотя сам я об этом сказал бы более сдержанно, чем Лиан, но, в принципе, я согласен с ним, потому что выигрыш оказался неожиданно огромным. Нашу точку зрения разделяет и Атья: «Теория струн трансформировала, обновила и революционизировала крупные разделы математики… в тех областях, которые кажутся далекими от физики». Многие из областей математики — «геометрию, топологию, алгебраическую геометрию и теорию групп — похоже, смешали в один коктейль, причем способом, глубоко связанным с их основным содержанием, и не по касательной, а прямо в сердце математики».^[271]

Хотя в прошлом другие области физики обеспечивали математику информацией, теория струн проникла гораздо глубже во внутреннюю структуру математики, способствуя новым концептуальным прорывам. По иронии судьбы, появление теории струн привело к гармоничному сотрудничеству внутри самой математики, поскольку теория струн потребовала многого от математиков, работающих в самых разных областях, включающих дифференциальную геометрию, алгебраическую геометрию, теорию групп Ли, теорию чисел и другие. Непостижимым образом наши надежды в отношении единой теории физики содействовали объединению математики.

Несмотря на красоту теории струн и ее глубокое влияние на математику, остается открытым вопрос: как долго мы должны ждать внешнего подтверждения какой-нибудь связи, любой связи теории с реальным миром? Брайан Грин считает, что следует набраться терпения, учитывая, что «мы пытаемся ответить на самые трудные, самые глубокие вопросы в истории науки. [Даже] если мы не получим на них ответы через 50 или 100 лет, мы должны идти вперед».^[272] Шон Кэрролл, физик из Калифорнийского технологического института, соглашается: «Глубокие идеи не появляются в короткие сроки».^[273] Иначе говоря, куда спешить, в конце концов?

Здесь, возможно, будет полезным напомнить исторический прецедент. «В XIX веке вопрос, почему вода кипит при температуре 100 градусов Цельсия, оставался без ответа, — отмечает Виттен. — Если бы вы сказали физику XIX века, что в XX веке вы сможете вычислить температуру кипения, то это показалось бы ему сказкой».^[274]

Нейтронные звезды, черные дыры, гравитационные линзы — плотные концентрации вещества, которые действуют, как линзы в небе, — были бы также отвергнуты, как полнейшая фантазия, если бы их на самом деле не увидели астрономы. «История науки полна суждений о том, что та или иная идея не является практической и никогда не будет проверена», — добавляет Виттен. Но история физики также показывает, что «хорошие идеи выдерживают проверку».^[275] Благодаря новым технологиям, о которых даже не догадывалось предыдущее поколение, идеи, которые, казалось бы, выходят за рамки разумного, превращаются из научной фантастики в научные факты.

«Чем важнее вопрос, тем больше упорства следует проявить при его проверке», — утверждает физик Массачусетского технологического института Алан Гут, один из создателей инфляционной теории, согласно которой наша Вселенная прошла через короткий период быстрого неудержимого расширения в первые моменты Большого взрыва. «Когда мы работали над инфляцией, я даже не думал, что ее будут проверять при моей жизни, — говорит Гут. — Это было бы невероятное везение, если бы нам удалось проверить инфляцию, и нам повезло. Хотя это была не столько удача, сколько потрясающее мастерство исследователей. То же может произойти и с теорией струн. И, возможно, нам не придется ждать сотни лет».^[276]

Несмотря на то, что теорию струн следует рассматривать как гипотезу, в этом нет ничего плохого. Такие гипотезы в математике, как гипотеза Калаби, являются ничем иным, как предположениями, основанными на математической теории. Они абсолютно необходимы для прогресса в моей области. И мы не достигли бы никаких существенных успехов в физике и не продвинулись бы в понимании многих вещей, если не учились бы на гипотезах — это лучше, чем бездействие. Тем не менее слово «гипотеза» подразумевает некоторую степень сомнения, и ваша реакция на него зависит от вашего склада характера, а также от вашего персонального вклада в задачу. Что касается теории струн, то одни ученые настраивают себя на длинный путь в надежде, что их усилия, в конце концов, оправдаются. Другие, кому не нравятся долго решаемые задачи, выдвигают свои сомнения на первый план и размахивают метафорическими плакатами с надписью «Остановитесь! Вы совершаете большую ошибку».

Было время (не так давно — каких-то несколько веков назад), когда людей предупреждали об опасности плавания под парусом вдали от родных берегов, пугая тем, что судно вместе с пассажирами на борту может упасть с края земли. Но некоторые бесстрашные путешественники, тем не менее, ставили паруса, и вместо того, чтобы упасть с края света, открыли Новый Свет.

Возможно, то же происходит и сегодня. Я из лагеря сторонников движения вперед, вместе с математиками. Мы продолжаем работать. И мы будем делать это, невзирая на наличие или отсутствие какого-либо вклада со стороны внешнего мира или экспериментальных данных, сохраняя высокую результативность.

Хотя лично я считаю полезным взять на заметку и физику. Ведь я потратил большую часть своей карьеры, работая на стыке математики и физики, отчасти из-за своего убеждения, что взаимодействие между двумя областями науки имеет решающее значение для углубления нашего понимания Вселенной. В общем, на протяжении десятилетий эти взаимодействия были в основном гармоничными. Иногда ученые развивали идеи в математике раньше, чем находили им применение в физике, как это произошло с великими работами Майкла Атья, Эли Картан, Ч. Ш. Черна, И. М. Зингера, Германа Вейла и других. Но иногда физика опережала математику, как в случае с открытием зеркальной симметрии. Но, возможно, мне не следует характеризовать текущие взаимоотношения между математиками и физиками как полностью безоблачные. По утверждению Брайана Грина, между двумя областями науки «наблюдается сильная, но обычно здоровая конкуренция», и я считаю это верной оценкой.^[277] Конкуренция это не всегда плохо, поскольку она обычно способствует прогрессу.

В различные исторические времена разделение между областями науки или его отсутствие существенно менялось. Такие ученые, как Ньютон и Гаусс, конечно, без труда лавировали между математикой, физикой и астрономией. Гаусс, который был одним из величайших математиков всех времен и народов, служил профессором астрономии в Геттингенской обсерватории в течение почти пятидесяти лет, вплоть до смерти.

Внедрение максвелловских уравнений электромагнетизма и последующие разработки в квантовой механике вбили клин между математикой и физикой, который сохранялся на протяжении большей части столетия. В 1940-е, 1950-е и 1960-е годы многие математики особо не задумывались о физиках и не сотрудничали с ними. С другой стороны, многие физики также с высокомерием относились к математике и мало ее использовали. Когда пришло время для математики, они поняли, что смогли бы ее использовать для решения своих задач.

Физик из Массачусетского технологического института Макс Тегмарк интерпретирует эту ситуацию, ссылаясь на «культурный разрыв» между двумя областями науки. «Некоторые математики, задрав нос, смотрят на физиков из-за их небрежности и отсутствия строгости в выкладках, — говорит он. — Квантовая электродинамика является примером чрезвычайно успешной теории, которая математически строго не сформулирована». Некоторые физики, добавляет он, пренебрежительно относятся к математикам, считая, что «вы, ребята, тратите целую вечность на то, что мы получаем за считанные минуты. И если бы вы обладали нашей интуицией, то поняли бы, что все это лишнее».^[278]

После выхода на сцену теории струн, когда физики-теоретики стали все больше полагаться на высшую математику, этот культурный разрыв начал сокращаться. Математика, которую применяют в теории струн, настолько сложна и является настолько неотъемлемой частью этой теории, что физики не только нуждаются в помощи, но и приветствуют ее. Несмотря на то что математики заинтересовались пространствами Калаби-Яу раньше физиков, последние, в конце концов, пришли к ним, в свою очередь продемонстрировав несколько интересных трюков. Сейчас мы находимся на этапе «повторной конвергенции», по выражению Атья, и это хорошо.

Я не могу сказать, преодолеет ли когда-нибудь теория струн свое самое серьезное испытание — сделать проверяемое предсказание и показать, что теория действительно дает правильный ответ. Математическая часть, как я уже говорил, стоит на более твердой почве. Тем не менее я считаю, что лучший шанс для разработки успешной теории заключается в объединении ресурсов математиков и физиков, сочетании преимущества двух дисциплин и их различных подходов к миру. Мы можем работать параллельно, иногда пересекаясь и переходя на другую сторону для пользы обеих сторон.

Клифф Таубс, мой коллега-математик из Гарварда, подытожил различия между этими дисциплинами. Таубс полагает, что, хотя инструментарий математики и физики может быть одним и тем же, они преследуют разные цели. «Физика — это изучение мира, а математика — изучение всех возможных миров».^[279]

Это одна из причин, по которой я люблю математику. Физики высказывают догадки о других мирах и других Вселенных, как и мы. Но в конце дня они должны вернуться в наш мир и думать о том, что реально. Я вынужден думать, возможно, не только о «всех возможных мирах», как выразился Клифф, но более широко — обо всех возможных пространствах. На мой взгляд, это наша работа. Хотя физики, по большому счету, как правило, смотрят только на одно пространство и видят то, что оно может рассказать нам о природе, а мы, математики, должны смотреть на совокупность всех пространств, чтобы найти общие правила и принципы, применимые к самым интересным случаям.

Рис. 13.4. Эта карикатура физика Роберта Дикграафа показывает взаимосвязь между математиками и физиками (изображение любезно предоставлено Робертом X. Дикграафом)

Тем не менее пространства не созданы равными, и некоторые привлекают мое внимание больше, чем другие, особенно те пространства, в которых, как полагают, находятся дополнительные размерности природы. Перед нами стоит задача выяснить форму этого скрытого мира, который, согласно теории, содержит оба вида материи, наблюдаемые нами из космоса, и все виды физических явлений, которые мы также наблюдаем. Некоторое время я всецело был поглощен этой задачей, и похоже, что в ближайшее время мне от нее не отделаться.

Хотя я занят различными проектами, я время от времени возвращаюсь к этой задаче. И несмотря на мой интерес к другим областям математики и физики, я постоянно возвращаюсь к геометрии. Если спокойствие достигается через понимание, то геометрия является моей попыткой достичь некоего подобия внутреннего спокойствия. Или в более широком смысле, геометрия — это мой способ попытаться разобраться в нашей Вселенной и понять таинственные скрытые пространства, названные, в том числе, в мою честь.

251. Peter Goddard, ed., Paul Dirac: The Man and His Work (New York: Cambridge University Press, 1998).

252. Eugene Wigner, “The Unreasonable Effectiveness of Mathematics in the Natural Sciences,” Communications in Pure and Applied Mathematics 13 (February 1960).

253. Chen Ning Yang, S. S. Chem: A Great Geometer of the 20th Century (Boston: International Press, 1998), p. 66.

254. Robert Osserman, Poetry of the Universe (New York: Anchor Books, 1996), pp. 142–143.

255. Richard P. Feynman, The Character of Physical Law (New York: Modern Library, 1994), p. 50.

256. Michael Atiyah, quoted in Patricia Schwarz, “Sir Michael Atiyah on Math, Physics and Fun,” The Official String Theory Web site, http://www.superstringtheory.com/people/atiyah.html.

257. Jim Holt, “Unstrung,” New Yorker, October 2, 2006, p. 86.

258. Michael Atiyah, “Pulling the Strings,” Nature 438 (December 22–29, 2005): 1,081.

259. Robert Mills, “Beauty and Truth,” in Chen Ning Yang: A Great Physicist of the 20th Century, ed. Shing-Tung Yau and C. S. Liu (Boston: International Press, 1995), p. 199.

260. Henry Tye (Cornell University), e-mail letter to author, December 19, 2008.

261. Brian Greene, interview by Ira Flatow, “Big Questions in Cosmology,” Science Friday, NPR, April 3, 2009.

262. К. C. Cole, “A Theory of Everything,” New York Times Magazine, October 18, 1987.

263. Nicolai Reshetikhin (University of California, Berkeley), interview with author, June 5, 2008.

264. Robbert Dijkgraaf (University of Amsterdam), interview with author, February 8, 2007.

265. Brian Greene, The Elegant Universe (New York: Vintage Books, 2000), p. 210.

266. Andrew Strominger (Harvard University), interview with author, August 1, 2007.

267. S. Ramanujan, “On Certain Arithmetic Functions,” Transactions of the Cambridge Philosophical Society 22 (1916): 159–184.

268. Lothar Goettsche, “A Conjectural Generating Function for Numbers of Curves on Surfaces,” November II, 1997, arXiv.org, Cornell University archives, http://arxiv.org/PS_cache/alg-geom/pdf/9711/9711012vl.pdf.

269. Ai-Ko Liu, “Family Blowup Formula, Admissible Graphs and the Enumeration of Singular Curves, I,” Journal of Differential Geometry 56 (2000): 381–579.

270. Bong Lian (Brandeis University), interview with author, December 12, 2007.

271. Michael Atiyah, “Pulling the Strings,” Nature 438 (December 22–29, 2005): 1,082.

272. Glennda Chui, “Wisecracks Fly When Brian Greene and Lawrence Krauss Tangle Over String Theory,” Symmetry 4 (May 2007): 17–21.

273. Sean Carroll, “String Theory: Not Dead Yet,” Cosmic Variance blog, Discover online magazine, May 24,2007, http://cosmicvariance.com.

274. Edward Witten, quoted in К. C. Cole, “A Theory of Everything,” New York Times Magazine, October 18, 1987.

275. То же.

276. Alan Guth (MIT), interview with author, September 13, 2007.

277. Brian Greene, The Elegant Universe (New York: Vintage Books, 2000), p. 261.

278. Max Tegmark (MIT), interview with author, October 23, 2007.

279. Faye Flam, “Getting Comfortable in Four Dimensions,” Science 266 (December 9, 1994): 1, 640.