Глава 9. Добро пожаловать в реальный мир

В книге «Удивительный волшебник из Страны Оз» при встрече с волшебницей Глиндой Дороти подробно рассказывает историю о том, «как ураган перенес ее в страну Оз, как она нашла друзей и какие удивительные приключения выпали на ее долю. «Но сейчас, — добавляет она, — мое самое большое желание — вернуться в Канзас».^[154]

Когда вы будете слушать этот рассказ, в котором часто будут появляться «Добрый доктор» Виттен и другие и из которого вы узнаете об удивительных приключениях в Стране Калаби-Яу — с ее скрытыми измерениями, зеркальными партнерами, суперсимметрией и исчезающими первыми классами Черна, то некоторым из вас, как Дороти, вероятно, захочется вернуться к более привычной обстановке. Вопрос, как всегда, заключается в следующем: можем ли мы получить одно из другого? Может ли сочетание теории струн и многообразий Калаби-Яу раскрыть секреты скрытой и многомерной области — теоретического эквивалента страны Оз, которую можно только представить, но нельзя пощупать, и в то же время рассказать нам нечто новое о более конкретной физической реальности, так сказать, Канзасе?

«Можно создавать физические теории, которые интересны математикам, но в конечном счете, мне хотелось бы понять реальный мир», — говорит Фолкер Браун, физик из Дублинского института перспективных исследований.^[155] В нашей попытке связать теорию струн и многообразия Калаби-Яу с реальным миром очевидной точкой сравнения является физика элементарных частиц.

Стандартная модель, которая описывает частицы материи и частицы — переносчики взаимодействий, движущиеся между ними, является одной из самых успешных теорий всех времен, но она не является учением о природе по ряду отношений. Во-первых, эта модель имеет около двадцати свободных параметров, таких как массы электронов и кварков, которые модель не способна предсказать. Эти величины необходимо вводить «вручную», что ставит многих ученых-теоретиков в тупик. Мы не знаем, откуда берутся эти числа, и ни одно из них, похоже, не находит логического математического обоснования. Струнные теоретики надеются найти математическое обоснование с единственным свободным параметром, кроме напряжения струн или линейной плотности энергии, который был бы связан с геометрией пространства. Силы и частицы при выборе геометрии должны быть полностью зафиксированы. Вышеупомянутая статья 1985 года Филиппа Канделаса, Гари Горовица, Эндрю Строминджера и Эдварда Виттена (см. шестую главу) «показывает, что можно свести все ключевые моменты воедино и получить мир, который выглядит, по крайней мере, в первом приближении, как Стандартная модель», — утверждает Канделас. — «Тот факт, что вы можете это сделать в теории, которая включает гравитацию, вызвал большой интерес к теории струн».^[156] Один из успехов модели Канделаса и других ученых заключается в том, что она вводит понятие хиральных фермионов — особенности Стандартной модели, в соответствии с которой каждая материальная частица обладает своего рода «доминированием одной из рук»: леворукая версия отличается от ее праворукого зеркального отображения. Как мы видели ранее, эта модель также подразделяет элементарные частицы на четыре семейства, или поколения, а не на три, как Стандартная модель. Хотя эти числа и отличаются на единицу, Канделас утверждает, что «главное было показать, что можно получить различные поколения, то есть повторяемую структуру, наблюдаемую в Стандартной модели».^[157] Строминджер придерживался тех же оптимистических взглядов, называя новаторские компактификации Калаби-Яу «важным скачком от базовых принципов теории струн до чего-то близкого к миру, в котором мы живем. Это похоже на игру в баскетбол, когда мяч, брошенный игроком с противоположного конца поля, попадает в корзину, — отмечает он. — Мы вплотную приблизились к пространству всех явлений, которые, возможно, могли бы произойти во Вселенной. Но нам хочется большего: нам хочется найти нечто не просто более-менее верное, а безусловно верное».^[158] Примерно через год Брайан Грин с коллегами сделали шаг вперед, создав модель, которая давала три поколения, так необходимые для наших теорий, хиральные фермионы, правильное значение суперсимметрии, которое мы обозначаем, как N = 1, нейтрино с некоторой массой (что хорошо), но не слишком большой (что еще лучше); в ней также получались поля, связанные с взаимодействиями Стандартной модели (сильным, слабым и электромагнитным). Возможно, самым большим недостатком этой модели являлось наличие некоторых нежелательных дополнительных частиц, которые не были частью Стандартной модели и от которых следовало избавиться тем или иным способом. Что касается плюсов, то я был поражен простотой метода: фактически все, что надо было сделать авторам модели, — это «выбрать» многообразие Калаби-Яу, причем именно то, которое подведет нас вплотную к получению Стандартной модели. Хотя за прошедшие десятилетия наблюдается значительный прогресс в ряде областей, теория струн и струнные теоретики все еще до конца не поняли Стандартную модель. Даже с высоты наших сегодняшних познаний мы не уверены, может ли теория струн воспроизвести Стандартную модель.

В настоящее время, несмотря на сложность задачи, ее приверженцы надеются, что теория струн не только впишется, но фактически выйдет за рамки Стандартной модели, которая находится там, куда, по их мнению, мы должны прийти. Мы уже знаем, что Стандартная модель не является последним словом в физике. За последнее десятилетие ее неоднократно изменяли или расширяли на основе экспериментальных данных, например, в 1998 году обнаружили, что нейтрино, которые считались безмассовыми, на самом деле обладают некоторой массой. Более того, мы столкнулись с темной материей и темной энергией — двумя таинственными формами, составляющими примерно 96% Вселенной, о которых Стандартная модель ничего не сообщает. Мы ожидаем новых открытий, объясняющих это: или будут обнаружены суперсимметричные частицы — возможные кандидаты на роль темной материи, или будет обнаружено что-то совершенно неожиданное, например с помощью Большого адронного коллайдера, разгоняющего встречные пучки протонов с высокими энергиями. И хотя Канделас с сотрудниками и Грин с сотрудниками не смогли воспроизвести Стандартную модель, их компактификации опередили ее, по крайней мере в одном аспекте, так как они открыли дорогу к достижению минимальной суперсимметричной Стандартной модели (МССМ). МССМ является расширенной версией традиционной модели, куда ввели суперсимметрию, что означает включение всех суперсимметричных партнеров, которые не включены в саму Стандартную модель. Последующие успехи реализации Стандартной модели на основе теории струн, которые мы обсудим позже, также включают суперсимметрию.

Тем, кто считает, что суперсимметрия должна стать частью теории о природе, а в этот список, вероятно, войдут (хотя он и не окончательный) большинство струнных теоретиков, конечно, одной Стандартной модели недостаточно. Существует другой крупный недостаток, который неоднократно будет упоминаться на страницах этой книги, а именно: Стандартная модель, теория физики элементарных частиц, ничего не говорит о гравитации, поэтому она никогда не сможет дать полное описание Вселенной. Гравитация выпадает из этой модели по двум причинам.

• Во-первых, она намного слабее, чем другие силы — сильные, слабые и электромагнитные, и является совершенно несущественной при изучении взаимодействий частиц при малых расстояниях. Сила гравитационного взаимодействия между двумя протонами примерно в 10³⁵ раз слабее, чем электромагнитное взаимодействие. Например, магнит размером с пуговицу способен за счет электромагнитного взаимодействия оторвать от земли канцелярскую скрепку, преодолевая при этом силу гравитации всей планеты Земля;

• Во-вторых, несмотря на широкое обсуждение, пока никто не знает, как связать гравитацию, которая описывается общей теорией относительности, и другие силы в одну цельную теорию. Если теории струн удастся воспроизвести Стандартную модель, введя в нее гравитацию, то мы будем намного ближе к полной теории природы. В таком случае мы получим не только Стандартную модель с гравитацией, но и суперсимметричную Стандартную модель с гравитацией.

Физики пытаются использовать различные методы для реализации такой Стандартной модели, включая орбифолды («орбитальные многообразия», похожие на многообразия в плоском пространстве), пересекающиеся браны, расположенные друг над другом браны и аналогичные вещи, достигнув значительного прогресса на многочисленных фронтах. Однако в нашей дискуссии будет сделан акцент только на одной области, а именно Е8×Е8 гетеротической теории струн, являющейся одной из пяти вариаций этой теории. Мы сделали такой выбор не потому, что считаем ее самой перспективной (я не могу об этом судить), но из-за того, что усилия, приложенные в этом направлении, тесно связаны с геометрией, то есть дисциплиной, которая, бесспорно, имеет наиболее длинную историю попыток перехода от геометрии Калаби-Яу к реальному миру.

Я не подыгрываю геометрии из-за того, что она является во многих отношениях главной темой этой книги. Она жизненно важна для попытки, о которой идет речь. Во-первых, мы не можем описать силы — важную часть Стандартной модели и любой предполагаемой теории природы — без геометрии. Как сказал Кумрун Вафа, «все четыре взаимодействия имеют под собой геометрическую основу, а три из них — электромагнитное, слабое и сильное — связаны между собой симметрией»^[159]. Стандартная модель объединяет вместе три силы и связанные с ними группы (или калибровки) симметрии: специальную унитарную группу 3 или SU(3), которая соответствует сильным взаимодействиям; специальную унитарную группу 2 или SU(2), которая соответствует слабым взаимодействиям, и первую унитарную группу или U(1), которая соответствует электромагнитным взаимодействиям. Симметричная группа состоит из множества всех операций, таких как вращение, которые можно выполнять с объектом, чтобы он при этом оставался неизменным. Вы берете объект и применяете к нему симметричную операцию один или столько раз, сколько хотите, и в конце объект будет выглядеть так же, как в начале. Фактически, вы не можете сказать, производились ли с этим объектом какие-либо манипуляции.

Возможно, самой простой группой для описания является группа U(1), которая включает все вращения, которые вы совершаете с кругом на плоскости. Это одномерная симметричная группа, поскольку вращения происходят вокруг одной одномерной оси, перпендикулярной кругу и проходящей через его центр. SU(2) связана с вращениями в трех измерениях, а более абстрактная SU(3) включает вращения в восьми измерениях. В этом случае эмпирическое правило состоит в том, что любая группа SU(n) обладает симметрией размерности n²-1. Размерности трех подгрупп являются аддитивными, это означает, что общая симметрия Стандартной модели является двенадцатимерной (1 + 3 + 8 = 12).

В качестве решений уравнений Эйнштейна многообразия Калаби-Яу определенной геометрии могут помочь нам произвести расчет гравитационной части нашей модели. Но могут ли эти многообразия учитывать другие силы, входящие в Стандартную модель, и если да, то каким образом? Для ответа на этот вопрос, боюсь, нам придется выбрать окольный путь. На сегодняшний день физика элементарных частиц — это квантовая теория поля, что означает, что все силы, а также все частицы представлены полями. Зная поля, пронизывающие четырехмерное пространство, мы можем вывести связанные с ними силы. Эти силы, в свою очередь, могут быть представлены в виде векторов, обладающих направлением и длиной, это означает, что в каждой точке пространства объект будет испытывать притяжение и отталкивание в определенном направлении и с определенной силой. Например, в произвольной точке Солнечной системы сила тяготения, приложенная к такому объекту, как планета, вероятно, будет направлена к Солнцу, а величина этой силы будет зависеть от расстояния до Солнца. Электромагнитная сила, действующая на заряженную частицу, находящуюся в данной точке, точно так же будет зависеть от ее положения относительно других заряженных частиц.

Стандартная модель является не просто теорией поля, но специальным видом теории поля, называемой калибровочной теорией и получившей широкое распространение в 1950-е годы благодаря работе физиков Чжэньнин Янга и Роберта Миллса (впервые упомянутых в третьей главе). В основе этой теории лежит идея о том, что Стандартная модель объединяет различные симметрии в сложную группу симметрий, которую обозначают как SU(3)×SU(2)×U(1). Эти симметрии являются калибровочными, что делает их специфическими и непохожими на обычные симметрии. Можно взять одно из разрешенных преобразований симметрии, например вращение на плоскости, и применить его по-разному в различных точках пространства-времени, выполнив поворот, скажем, на 45° в одной точке, на 60° в другой и на 90° в третьей. Несмотря на неоднородность применения симметрии, «уравнения движения», которые управляют динамической эволюцией полей, не изменятся, как и вся остальная физика. Вообще ничего не изменится.

Симметрии, как правило, не работают таким образом, если они не являются калибровочными симметриями. Фактически Стандартная модель имеет четыре «глобальные» симметрии, связанные с частицами вещества и сохранением заряда, которые не являются калибровочными. Эти глобальные симметрии действуют на материальные поля Стандартной модели, которые мы обсудим позже. В Стандартной модели и вообще в теории поля существует еще одна глобальная симметрия, которая не является калибровочной. Эта симметрия называется симметрией Пуанкаре. Она включает простые переносы, такие как перемещение всей Вселенной на один метр вправо или проведение одного и того же эксперимента в двух разных лабораториях, и вращения, когда конечный результат выглядит аналогично исходному.

Однако если требуется, чтобы некоторые симметрии были калибровочными, то из расчетов Янга и Миллса следует, что для этого необходимо ввести в теорию нечто дополнительное, некий внешний фактор. Этим «нечто» могут быть калибровочные поля. В Стандартной модели калибровочные поля соответствуют калибровочным симметриям SU(3)×SU(2)×U(1), это означает по ассоциации, что калибровочные поля соответствуют трем взаимодействиям, которые включены в состав модели: сильному, слабому и электромагнитному. Между прочим, Янг и Миллс не были первыми, кто разработал калибровочную теорию U(1), описывающую электромагнетизм, — это было сделано за десятилетие до них. Но они были первыми, кто разработал калибровочную теорию для SU(2), которая показала путь разработки SU(n) теорий, для любого n больше двух, включая SU(3).

Введение калибровочных полей позволило получить теорию с калиброванными симметриями, что в свою очередь позволяет сохранять инвариантность физики, даже когда операции симметрии применяют раздельно. Физики создали Стандартную модель такой не потому, что она поразила их своей элегантностью и эстетической привлекательностью, а потому, что из экспериментов следовало, что так работает природа. Иными словами, Стандартная модель является калибровочной теорией по эмпирическим, а не эстетическим причинам.

Хотя физики обычно рассуждают в терминах калибровочных полей, математики часто выражают те же идеи в терминах расслоений, что является математическим способом представления полей, связанных с тремя взаимодействиями. Струнные теоретики стирают границу между физикой и математикой, а расслоения играют роль гетеротических конструкций, которых мы кратко коснемся.

Рис. 9.1. Чжэньнин Янг и Роберт Миллс, авторы теории Янга-Миллса (Правила Янга)

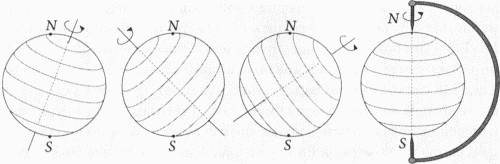
Перед тем как перейти к ним, необходимо объяснить, каким образом многообразия Калаби-Яу связаны с калибровочными полями, которые математики называют расслоениями. Поля, которые мы видим, — четырехмерная гравитация и калибровочные поля SU(3)×SU(2)×U(1), связанные с другими тремя силами, бесспорно, существуют в четырехмерной области, в которой, если верить нашим наблюдениям, обитаем и мы. Калибровочные поля фактически существуют в десяти измерениях, которые описывает теория струн. Компонент, лежащий в шести компактифицированных измерениях Калаби-Яу, дает начало четырехмерным калибровочным полям нашего мира и приводит к сильному, слабому и электромагнитному взаимодействиям. Правильнее было бы сказать, что внутренняя структура Калаби-Яу фактически рождает эти взаимодействия, — собственно, это и следует из теории струн.

До сих пор мы говорили о симметрии без упоминания проблемы, с которой столкнулись создатели модели, а именно с тем, что называют нарушением симметрии. В гетеротической версии теории струн мы обсуждали десятимерное пространство-время, с которого мы начинаем, содержащее нечто, что мы называем Е8×Е8-симметрией. Е8 — это 248-мерная группа симметрии, которую можно считать, в свою очередь, калибровочным полем с 248 компонентами (подобно тому как вектор, указывающий некоторое произвольное направление в трехмерном пространстве, имеет три компоненты, обозначаемые x, y и z). Е8×Е8 — это более обширная группа из 496 компонентов (248 + 248), но для практических целей можно игнорировать второе Е8. Конечно, даже 248 симметричных измерений составляют проблему для вывода Стандартной модели, которая имеет только двенадцать симметричных измерений. Значит, нам нужно каким-то способом «отломать» лишние измерения у 248-мерной Е8-группы, уменьшив их количество до двенадцати.

Давайте вернемся к нашему примеру двухмерной сферы, или шара, обладающей вращательной симметрией в трех измерениях и принадлежащей к симметричной группе SO(3). Здесь термин «SO» — это сокращение от «special orthogonal group» (специальная ортогональная группа), поскольку она описывает вращение вокруг взаимно перпендикулярных осей. Можно взять сферу и начать вращать ее вокруг любой из трех осей — x, y и z, — и она всегда будет оставаться той же самой сферой. Но можно нарушить симметрию, если потребовать, чтобы одна точка всегда отображалась сама на себя. На нашей планете можно было бы в качестве такой точки выбрать Северный полюс. После этого у нас останется только один набор преобразований поворота, а именно повороты относительно оси, проходящей через Северный и Южный полюсы, которые оставляют точку Северного полюса неподвижной. В результате трехмерная симметрия шара нарушается и превращается в одномерную симметрию U(1).^[160]

Для того чтобы перейти к четырем измерениям и Стандартной модели с ее 12-мерной симметричной группой, следует найти аналогичный способ нарушения симметрии калибровочной группы Е8. Например, можно нарушить симметрию путем выбора определенной конфигурации, включающей или выключающей отдельные компоненты 248-компонентного калибровочного поля. В конце концов, мы найдем способ оставить включенными только двенадцать полей, по аналогии с тем, как, зафиксировав Северный полюс, мы оставили только одно из трех направлений вращения на сфере. Но это не могут быть произвольные двенадцать полей: это должны быть правильные поля, чтобы вписаться в симметричные группы SU(3)×SU(2)×U(1). Другими словами, когда вы закончите разрушать массивную группу Е8, то оставите в четырех измерениях только калибровочные поля Стандартной модели.

Рис. 9.2. Благодаря полной симметрии сфера остается без изменений при вращении вдоль любой оси, проходящей через ее центр. Однако можно нарушить симметрию, если потребовать, чтобы при повороте северный полюс оставался неподвижным. Теперь вращение разрешено только относительно одной оси, проходящей через северный и южный полюсы. Следование этому условию нарушает или ограничивает полную вращательную симметрию сферы

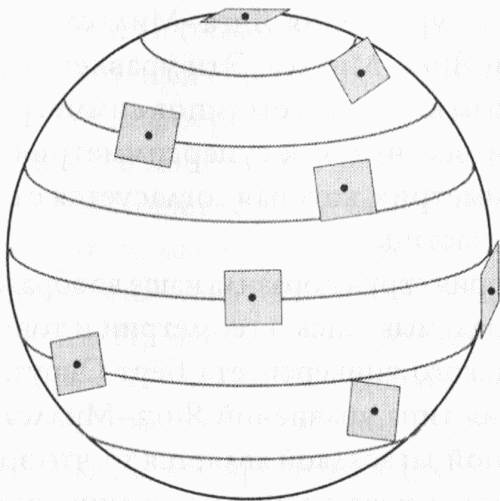
Остальные поля, соответствующие нарушенным симметриям, полностью не исчезают. Они будут проявлять себя только в области очень высоких энергий, что делает их недоступными для нас. Можно сказать, что дополнительные симметрии Е8 спрятаны в Калаби-Яу.

Тем не менее одно лишь многообразие Калаби-Яу само по себе не способно породить Стандартную модель. Здесь и вступают в игру расслоения, которые являются в буквальном смысле расширениями многообразия. Расслоениями называют группы векторов, прикрепленные к каждой точке многообразия. Самый простой тип расслоения известен под названием касательное расслоение. Каждое многообразие Калаби-Яу имеет такое расслоение, но поскольку касательное расслоение Калаби-Яу является более сложным для представления, чем даже само многообразие, то давайте вместо него рассмотрим касательное расслоение обычной двухмерной сферы. Если выбрать точку на поверхности этой сферы и построить два вектора, касательных поверхности сферы в этой точке, то такие векторы определят плоскость или диск в пределах плоскости, если ограничить векторы определенной длиной. Если сделать то же самое в каждой точке поверхности и объединить все эти плоскости или диски вместе, то таким коллективным объектом и будет расслоение. Следует отметить, что расслоение обязательно включает само многообразие, поскольку в расслоение входит, по определению, каждая отдельная точка на поверхности многообразия. По этой причине касательное расслоение двухмерной сферы является четырехмерным пространством, поскольку касательная к поверхности обладает двумя степенями свободы, или двумя независимыми направлениями движения, а также сама по себе сфера, будучи частью расслоения, добавляет еще две степени свободы, которые сами не зависят от касательного пространства.

Рис. 9.3. В каждой точке поверхности сферы существует касательная плоскость, пересекающая сферу только в этой точке и больше нигде. Касательное расслоение для сферы состоит из плоскостей, касательных к каждой точке этой сферы. Поскольку, по определению, касательное расслоение включает каждую точку на сфере, оно также должно включать и саму сферу. Невозможно изобразить касательное расслоение с его бесконечным количеством касательных плоскостей, поэтому мы покажем сферу с кусками касательных плоскостей в нескольких показательных точках

Касательное расслоение шестимерного многообразия Калаби-Яу представляет собой соответственно 12-мерное пространство с шестью степенями свободы в касательном пространстве и шестью степенями свободы в самом многообразии.

Расслоения имеют решающее значение в попытках струнных теоретиков сформулировать физику элементарных частиц в терминах теории Янга-Миллса, где калибровочные поля описываются набором дифференциальных уравнений, называемых, как нетрудно догадаться, уравнениями Янга-Миллса.

Наш следующий шаг состоит, в частности, в поиске решений уравнений для калибровочных полей, живущих на трехмерном многообразии Калаби-Яу. Поскольку основной причиной появления многообразий Калаби-Яу в теории струн было удовлетворение требованиям суперсимметрии, калибровочные поля также должны подчиняться суперсимметрии. Это означает, что мы должны решать специальные суперсимметричные уравнения Янга-Миллса, называемые эрмитовыми уравнениями Янга-Миллса. Эти уравнения дают суперсимметрию с минимальным количеством типов симметрии, которое только можно получить, известную как суперсимметрия N = 1, и это единственная суперсимметрия, которая согласуется с современной физикой элементарных частиц.

«До того как теория струн поразила наше воображение, большинство физиков особо не задумывались о геометрии и топологии, — говорит физик Пенсильванского университета Бёрт Оврут. — Мы просто записывали уравнения типа уравнений Янга-Миллса и пытались их решить». Единственной загвоздкой является то, что эрмитовы уравнения Янга-Миллса являются существенно нелинейными дифференциальными уравнениями, которые никто не может решить. «До сегодняшнего дня, — говорит Оврут, — нет ни одного известного [явного] решения эрмитовых уравнений Янга-Миллса в шестимерном многообразии Калаби-Яу. Следовательно, мы должны были бы остановиться на достигнутом, если бы не работа некоторых геометров, показавших нам иной путь».^[161]

Расслоения предлагают нам обходной путь для этого нелинейного дифференциального барьера, поскольку мы можем считать расслоение, прикрепленное к многообразиям Калаби-Яу, альтернативным описанием калибровочных полей, определяемых уравнениями Янга-Миллса. Как это сделать, описывает теорема DUY(ДУЯ), название которой составлено из первых букв фамилий Саймона Дональдсона (Simon Donaldson) (Королевский колледж), Карена Уленбека (Karen Uhlenbeck) (Техасский университет) и моей (Yau).

Идея, лежащая в основе теоремы, заключается в том, что эрмитовы уравнения Янга-Миллса определяют поле, которое может быть представлено векторным расслоением. Мы доказали, что если построить расслоение на Калаби-Яу, которое удовлетворяет конкретному топологическому условию, а именно является устойчивым или технически — с более устойчивым углом наклона (крутизной), то такое расслоение допускает существование уникального калибровочного поля, которое автоматически удовлетворяет этим уравнениям. «Это не имеет смысла, если вы меняете одну чрезвычайно сложную проблему на другую крайне трудную, — отмечает Оврут. — Но вторая проблема создания устойчивого расслоения намного проще, в результате не надо вообще решать эти ужасные дифференциальные уравнения».^[162]

Иными словами, мы нашли геометрическое решение проблемы, которую не могли решить другими способами. Мы показали, что не стоит волноваться о полях или дифференциальных уравнениях. Все, о чем следует беспокоиться, это о построении устойчивого расслоения. Что означает выражение «расслоение с устойчивым наклоном»? Когда мы говорили о наклоне кривой, мы отметили, что это число, связанное с кривизной, а устойчивость наклона расслоения в данном случае связана с кривизной расслоения. Проще говоря, «наклон выражает чувство равновесия, — объясняет математик Рон Донаги из Пенсильванского университета. — Он указывает, что кривизна в одном направлении не может быть намного больше, чем кривизна в другом направлении. Независимо от выбранного пути, ни одно направление не может быть слишком экстремальным относительно других направлений».^[163] Любое расслоение можно разделить на более мелкие части или субрасслоения, а требование устойчивости означает, что наклон любого из этих субрасслоений не может быть больше наклона расслоения как единого целого. Если это требование выполняется, то такое расслоение является расслоением с устойчивым наклоном, а калибровочные поля удовлетворяют эрмитовым уравнениям Янга-Миллса. В результате условие суперсимметрии будет выполнено.

В некотором смысле идея устойчивости наклона, являющаяся центральной для теоремы DUY, представляет собой следствие теоремы Калаби-Яу, поскольку эта теорема выдвигает определенные требования кривизны к многообразию Калаби-Яу, гарантируя, что касательное расслоение будет обладать устойчивым наклоном. А тот факт, что уравнения Калаби-Яу и эрмитовы уравнения Янга-Миллса одинаковы для касательного расслоения, когда в основе лежит метрика Калаби-Яу, является еще одним следствием доказательства гипотезы Калаби, которое заставило меня подумать о взаимосвязи между устойчивостью наклона и эрмитовыми уравнениями Янга-Миллса. Возникшая у меня идея заключалась в том, что расслоение будет удовлетворять этим уравнениям тогда и только тогда, когда оно устойчивое.

По сути, Дональдсон доказал это в своей части теоремы DUY, опубликованной им в 1985 году, конкретно относящейся к особому случаю двух комплексных размерностей. Уленбек и я работали независимо от Дональдсона, и в работе, вышедшей в свет через год, мы доказали, что аналогичный результат применим к любой комплексной размерности и соответственно к любому пространству с четным количеством реальных размерностей. Я считаю DUY одной из самых сложных теорем, которые я когда-либо доказывал или — в данном случае — доказал совместно с другим ученым. В настоящее время наш труд вместе с работой Дональдсона называется DUY.

Эта теорема очень похожа на доказательство гипотезы Калаби, поскольку в обоих случаях мы стремились свести задачу, включающую систему неприятных нелинейных уравнений, с которыми мы не умеем работать, к геометрической задаче, которую мы умеем решать. В случае Калаби я никогда не решал соответствующие дифференциальные уравнения в явном виде. Я только показал, что если многообразие удовлетворяет определенным условиям (компактное, кэлерово, с исчезающим первым классом Черна), что можно проверить с помощью стандартных процедур алгебраической геометрии, то должно существовать решение таких уравнений в форме риччи-плоской метрики. DUY работает аналогичным образом, предполагая наличие такого расслоения, точнее, устойчивости наклона, чтобы решения эрмитовых уравнений Янга-Миллса всегда существовали. В алгебраической геометрии также разработаны методы для оценки устойчивости расслоения, хотя это оказалось намного сложнее, чем проверить, является первый класс Черна для многообразия исчезающим или нет.

Некоторые люди, в том числе и физики, не знакомые с этой областью математики, находят DUY удивительным, поскольку на первый взгляд условия расслоения не имеют ничего общего с дифференциальными уравнениями, которые вы надеетесь решить.

Но для меня эта теорема не была удивительной, поскольку, если уж на то пошло, она казалась мне естественным продолжением гипотезы Калаби. Все доказательство теоремы Калаби посвящено многообразию Калаби-Яу, тогда как теорема DUY вся посвящена расслоению. Вы ищете метрику расслоения, но метрика многообразия уже дана вам как часть исходной информации. По желанию можно выбрать любую лежащую в основе метрику, включая метрику Калаби-Яу.

Пункт пересечения между гипотезой Калаби и теоремой DUY представляет собой касательное расслоение. И вот почему: когда вы докажете существование многообразий Калаби-Яу, то получите не только эти многообразия, но также их касательные расслоения, так как каждое многообразие имеет расслоение. Поскольку касательное расслоение определяется многообразием Калаби-Яу, оно наследует свою метрику от родительского многообразия — в данном случае от многообразия Калаби-Яу. Другими словами, метрика касательного расслоения должна удовлетворять уравнениям Калаби-Яу. При этом оказывается, что для касательного расслоения эрмитовы уравнения Янга-Миллса те же, что и для уравнений Калаби-Яу, при условии, что фоновая метрика, выбранная вами, является метрикой Калаби-Яу. Следовательно, если касательное расслоение удовлетворяет уравнениям Калаби-Яу, оно также автоматически удовлетворяет эрмитовым уравнениям Янга-Миллса. В результате получается, что касательное расслоение фактически является первым частным случаем теоремы DUY — первым решением, несмотря на то что доказательство гипотезы Калаби было получено за десять лет до теоремы DUY.

Рис. 9.4. Карен Уленбек (фото любезно предоставлено Техасским университетом в Остине)

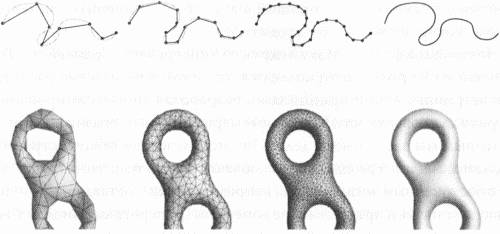
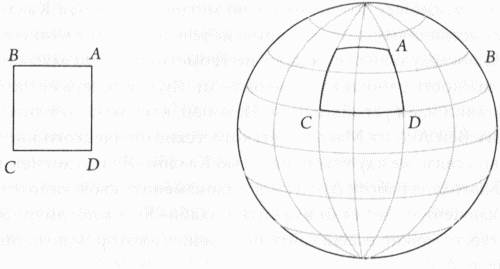
Однако это не самое интересное в DUY. Истинная сила DUY состоит в предписании условий (снова в отношении устойчивости), которым должны удовлетворять другие расслоения (а не только касательное расслоение), чтобы решения эрмитовых уравнений Янга-Миллса существовали.

Еще до выхода нашего труда в 1986 году я говорил Эдварду Виттену, что теория Янга-Миллса, похоже, естественным образом согласуется с многообразиями Калаби-Яу и поэтому должна быть важна для физиков. Виттен вначале не понял актуальности теоремы, но примерно через год, продолжив работу, он пошел еще дальше, показав, как этот подход можно использовать в компактификациях Калаби-Яу. Когда вышел труд Виттена, то благодаря его авторитету в этой области применением DUY к теории струн стали интересоваться и другие исследователи, что служит еще одним примером того, как геометрия взяла инициативу в свои руки, несмотря на то что она не всегда шла этим путем.

Теперь давайте посмотрим, как можно использовать эту геометрию и топологию для получения физики элементарных частиц из теории струн. Первый шаг заключается в выборе многообразия Калаби-Яу, но подходит не всякое многообразие. Если мы хотим использовать определенные методы, которые в прошлом доказали свою эффективность, нам необходимо выбрать неодносвязное многообразие, то есть многообразие с нетривиальной фундаментальной группой. Я надеюсь, вы помните, — это означает, что вы можете найти в таком пространстве петлю, которую нельзя стянуть в точку. Другими словами, многообразие должно быть больше похоже на тор, а не на сферу, и иметь, по крайней мере, одну дырку. Наличие дырки, цикла или петли, бесспорно, оказывает влияние на геометрию и топологию самого расслоения, что, в свою очередь, влияет на физику.

Второй шаг заключается в построении расслоения, которое даст не только калибровочные поля Стандартной модели, но также устранит аномалии — отрицательные вероятности, нежелательные бесконечности и другие раздражающие свойства, которые были присущи самым первым версиям теории струн. Когда Майкл Грин и Джон Шварц проиллюстрировали способ устранения аномалий в своей знаменитой работе 1984 года, их аргумент был сформулирован в терминах калибровочных полей. Выражая аналогичную идею в геометрических и топологических терминах, можно сказать, что расслоение будет удовлетворять требованию устранения аномалий, если его второй класс Черна равен второму классу Черна касательного расслоения.

Мы уже обсуждали понятие класса Черна — метода классификации топологических пространств и грубого определения различия между ними (см. четвертую главу). Как уже указывалось, первый класс Черна исчезает (или равен нулю), если можно ориентировать все касательные векторы на многообразии в одном и том же направлении. Это похоже на задачу расчесать густые волосы, не оставив торчащего чуба. Это невозможно на двухмерной сфере, но можно избежать чуба на поверхности двухмерного тора. Поэтому мы говорим, что тор обладает исчезающим первым классом Черна, тогда как первый класс Черна для сферы является неисчезающим.

Второй класс Черна можно на пальцах определить аналогичным образом, за исключением того, что нам необходимо рассмотреть на некотором многообразии два векторных поля, а не одно. Векторные поля, о которых мы здесь говорим, являются комплексными, то есть координаты отдельного вектора описываются комплексными числами. Если принять, что эти два векторных поля являются независимыми, то в большинстве точек на многообразии векторы, вероятно, будут иметь различные направления. Но в определенных точках векторы из каждого поля могут иметь одно и то же комплексное направление или оба стремиться к нулю. На самом деле, может существовать целый набор точек, где это условие будет выполняться. Такой набор точек образует замкнутую двухмерную поверхность в пределах нашего шестимерного многообразия, а вместе эти точки представляют второй класс Черна.

Каким образом это связано с устранением аномалий? Грин и Шварц показал, что независимо от того, насколько плохими могут оказаться аномалии, если удастся заставить их компенсировать друг друга и тем самым устранить, то, возможно, в конце концов, получится жизнеспособная теория. Один из способов избавления от таких надоедливых аномалий заключается в том, чтобы убедиться, что выбранное вами расслоение имеет тот же второй класс Черна, что и касательное расслоение.

Что касается вопроса, почему это должно работать, мы должны помнить, что расслоения, о которых идет речь, являются, в некотором смысле, эрзацами фоновых полей — гравитационных и калибровочных, из которых можно вывести реальные силы, существующие в природе. Например, касательное расслоение Калаби-Яу является хорошим слепком гравитационного поля, так как Калаби-Яу, характеризуемое специальной метрикой, позволяет решить уравнения гравитационного поля Эйнштейна. Другими словами, гравитация в некотором роде зашифрована в его метрике. Но метрика также связана с касательным расслоением, потому что метрика, как говорилось ранее, предоставляет нам функцию для вычисления расстояния между любыми двумя точками А и В на многообразии. Мы берем все возможные пути между А и В и разбиваем каждый путь на много крошечных касательных векторов; объединенные вместе касательные векторы образуют касательное расслоение. Вот почему в случае попытки удаления аномалий можно использовать касательное расслоение Калаби-Яу, чтобы построить гравитационную часть теории.

Затем мы выбираем дополнительное векторное расслоение с целью воспроизведения калибровочных полей Стандартной модели. Теперь у нас есть два расслоения, одно дает нам гравитационное поле, второе — калибровочные поля. К сожалению, каждое поле неизбежно будет иметь аномалии, которых невозможно избежать, но Грин и Шварц показали, что нет причины для отчаяния. По мнению Донаги, они продемонстрировали, «что аномалия, являющаяся результатом гравитационного взаимодействия, обладает противоположным знаком по отношению к аномалии калибровочного поля. Поэтому если удастся сделать так, чтобы они имели одинаковые абсолютные значения, то они уничтожат друг друга».^[164]

Чтобы выяснить, работает ли наша теория, мы возьмем второй класс Черна как касательного расслоения Калаби-Яу, так и расслоения калибровочного поля. Ответ, который мы получаем для каждого расслоения, зависит от тех особых точек, где векторные поля совпадают или исчезают. Однако невозможно просто вычислить количество таких точек, поскольку на самом деле их количество бесконечно. Вместо этого можно сравнить кривые (единичной комплексной размерности), которые вычерчивают эти точки. Кривые, которые относятся к каждому из этих расслоений, не должны быть одинаковыми, чтобы не соответствовать второму классу Черна, но они должны быть гомологичными.

Гомология является тонким понятием, которое лучше всего объяснить на примере, я постараюсь подобрать наиболее простой пример — крендель. Каждая дырка вырезается по кругу, одномерному объекту, но каждый круг ограничивает дырку, которая является двухмерным объектом. В данном случае примером гомологии будут два круга нашего кренделя. Таким образом, мы называем две кривые, или два круга, гомологичными, если они имеют одну и ту же размерность и ограничивают поверхность или многообразие, имеющее на одно измерение больше. Мы используем термин класс Черна, чтобы указать на наличие целого класса кривых, которые связаны через гомологию. Мы ставим эту концепцию на первое место, потому что если кривые для наших двух расслоений являются гомологичными (касательное расслоение, представляющее гравитацию, и второе расслоение — калибровочные поля), то этим расслоениям будет соответствовать второй класс Черна. В результате, как ни странно, аномалии теории струн исчезнут, чего мы и добивались.

Когда ученые впервые начали проверку этих идей, как это сделали в своем труде Канделас, Горовиц, Строминджер и Виттен в 1985 году, они использовали касательное расслоение как единственное, известное на тот момент. Если использовать касательное расслоение, то второй класс Черна вашего расслоения не может не соответствовать второму класса Черна касательного расслоения. Таким образом, ваш выбор будет правильным, но касательное расслоение также будет удовлетворять условию стабильности, что, как уже указывалось ранее, является прямым следствием доказательства гипотезы Калаби. Тем не менее исследователи считали, что если другие расслоения соответствуют вышеуказанным требованиям, включая стабильность, то можно найти и более гибкие с точки зрения физики варианты. Канделас говорит, что даже в далеком 1985 году «мы уже поняли, что должны существовать более общие способы решения задач, а именно что существуют иные расслоения, кроме касательного, которое мы используем. Хотя мы знали, что это возможно, но еще не знали, как это сделать практически».^[165]

Тем временем с наступлением второй струнной революции в середине 1990-х годов исследователи поняли, что существует возможность смягчить ограничения по расслоениям, в связи с чем открывалось много новых возможностей. В М-теории существовала дополнительная размерность, что давало исследователю свободу и простор для размещения дополнительных полей, которые соответствовали бранам — важным новым компонентам, введенным М-теорией. После введения браны в общую картину второй класс Черна калибровочного поля уже больше не должен быть равным второму классу Черна касательного расслоения: он мог быть меньше или равен.

Все это стало возможным потому, что сама брана или кривая, вокруг которой она обернута, имеет свой собственный второй класс Черна, который можно сложить со вторым классом Черна калибровочного расслоения, чтобы соответствовать касательному расслоению и таким образом обеспечить устранение аномалии. В результате сегодня физики могут работать с более широким разнообразием калибровочных расслоений.

«Каждый раз, когда вы ослабляете условия (в данном случае меняя равенство на неравенство), у вас появляется больше примеров», — объясняет Донаги.^[166] Обратившись снова к нашему примеру со сферой или к большому надувному мячу для игры на пляже, заметим, что вместо присоединения касательной плоскости или ее части к каждой точке на поверхности мяча можно присоединить обычное расслоение с векторами, направленными от поверхности. Существует много других расслоений, которые можно создать, присоединив определенное векторное пространство к различным точкам на многообразии и затем объединив все эти векторные пространства для получения расслоения.

Хотя новая степень свободы «от М-теории» позволила ученым исследовать широкий спектр расслоений, они до сих пор не придумали примеры, которые бы действительно работали. Первый шаг снова заключается в выборе расслоения, которое является устойчивым и избавленным от аномалий. Из теоремы DUY мы знаем, что такое расслоение может дать вам калибровочные поля или взаимодействия Стандартной модели.

Конечно, Стандартная модель посвящена не только взаимодействиям. Это теория физики элементарных частиц, поэтому ей есть что сказать и об элементарных частицах. Тогда поставим вопрос следующим образом: как элементарные частицы связаны с многообразиями Калаби-Яу? Существуют два вида элементарных частиц, о которых будет идти речь: частицы, которые мы можем потрогать (материальные частицы), и частицы-переносчики взаимодействий (полевые частицы), в число которых входят фотоны, переносящие свет, а также другие, невидимые для нас частицы — слабые бозоны и глюоны.

Частицы силовых полей в некотором смысле легче извлечь, поскольку если вы правильно получили все калибровочные поля на предыдущем этапе со всеми группами правильной симметрии, то вы уже имеете все эти частицы. Они являются в буквальном смысле частью силовых полей, а количество симметричных размерностей в каждом калибровочном поле соответствует количеству частиц, передающих взаимодействие. Например, сильное взаимодействие, связанное с восьмимерной симметрией SU(3), обеспечивается восемью глюонами; слабое взаимодействие, связанное с трехмерной симметрией SU(2), передается тремя бозонами: W⁺, W^- и Z; а электромагнитное взаимодействие с одномерной симметрией U(1) передается одной частицей — фотоном.

Мы можем изобразить эти частицы в движении довольно легко. Представим, как два парня едут на роликах параллельно друг другу и один из них бросает волейбольный мяч другому. Парень, бросающий мяч, отклоняется в противоположном от летящего мяча направлении, а парень, ловящий мяч, отклоняется в том же направлении, в каком летит мяч. Если наблюдать это взаимодействие из самолета, летящего достаточно высоко, чтобы не был виден мяч, то может показаться, что на этих двух людей действует сила отталкивания. Но если посмотреть на действие отталкивающей силы с очень близкого расстояния, где эта сила «квантована», то можно увидеть, что движения роллеров вызваны дискретным объектом — волейбольным мячом, а не каким-то невидимым полем. Квантование полей, и материальных, и калибровочных, означает, что среди всех возможных флуктуаций или вибраций вы выбираете только определенные. Каждая специально выбранная флуктуация соответствует волне с конкретной величиной энергии и, следовательно, частотой.

«Именно это наблюдается в Стандартной модели, — говорит Оврут. — Материальные частицы похожи на парней на роликах, а силовые частицы — фотоны, глюоны и бозоны (W⁺, W^- и Z) — на волейбольные мячи, которые они перекидывают».^[167]

Поговорим еще немного о материальных частицах. Все обычные материальные частицы, такие как электроны и кварки, обладают спином -1/2. Спин — это внутренняя, квантованная механическая характеристика всех элементарных частиц, связанная с внутренним моментом импульса частицы. Эти частицы со спином -1/2 являются решениями уравнения Дирака, которое обсуждалось в шестой главе. В теории струн следует решать это уравнение в десяти измерениях. Но когда в качестве геометрии, лежащей в основе, выбирается многообразие Калаби-Яу, уравнение Дирака можно разбить на шести- и четырехмерные компоненты. Решения шестимерного уравнения Дирака делятся на две категории: тяжелые частицы, которые во много триллионов раз тяжелее всех частиц, наблюдаемых при экспериментах на ускорителях с высокими энергиями, и обычные частицы, масса которых настолько мала, что можно считать ее равной нулю.

Независимо от массы частицы чрезвычайно сложно найти решения для уравнений с такими компонентами. К счастью, геометрия и топология снова могут помочь нам избежать решения сложнейших дифференциальных уравнений. В этом случае нам необходимо вычислить когомологию касательного расслоения, как это показали исследователи из Университета Пенсильвании, включая Брауна (ранее работал у Пенна), Донаги, Оврута и Тони Пантева. Когомология тесно связана с гомологией и, как гомология, имеет дело с возможностью трансформирования одного объекта в другой. Две концепции, как считает Донаги, представляют различные способы отслеживания одних и тех же свойств.^[168] Когда вы определяете когомологический класс расслоения, то можно использовать его для нахождения решений уравнения Дирака и получения материальных частиц. «Это отличный математический метод», — утверждает Оврут.^[169]

Используя этот и другие методы, Винсент Бушар из Университета Альберта и Донаги, а также Оврут с коллегами разработали модели, которые, как оказалось, дали много полезного. Обе группы ученых утверждают, что получили верную калибровочную группу симметрии, правильную суперсимметрию, хиральные фермионы и правильные спектры частиц — три поколения кварков и лептонов плюс отдельную частицу Хиггса, и никаких экзотических частиц типа экстра-кварков или лептонов, не входящих в Стандартную модель.

Но разгорелись серьезные дебаты о том, насколько близко эти научные группы подошли к Стандартной модели. Например, были подняты вопросы о методологиях и таких феноменологических деталях, как наличие модульных частиц, которые будут обсуждаться в следующей главе. Физики, с которыми я разговаривал, имеют различные точки зрения на этот вопрос. Лично я пока не в восторге от этой работы, а если быть откровенным, то и от любой попытки на сегодняшний день реализовать Стандартную модель. Шамит Качру из Стэнфорда считает, что последние шаги в этом направлении являются закреплением успехов Канделаса и Грина с коллегами. «Но пока еще никто, — говорит Качру, — не создал модель, которая попала бы в яблочко».^[170] Майкл Дуглас из Центра Саймона по изучению геометрии и физики в Стоуни-Брук согласен, «что все эти модели являются еще сырыми, ни одна из них пока не может пройти всех испытаний на непротиворечивость реальному миру. Но хотя обе модели являются незавершенными, мы многое узнаем из этой работы».^[171] Канделас доверяет моделям Бушара-Донаги и Оврута с коллегами, поскольку они показывают, как использовать другие расслоения помимо касательного. Он считает, что этот труд со временем укажет путь к другим моделям, отмечая, что «вероятно, существуют и другие возможности. Но пока мы их не реализуем, мы не будем знать, как они работают»^[172]. И работают ли они вообще.

Следующие шаги включают не только получение правильных частиц, но также попытки вычисления их масс, без которых невозможно провести значимые сравнения со Стандартной моделью. До того как мы сможем вычислить массу, мы должны определить значение того, что называется константой взаимодействия Юкавы, описывающей силу взаимодействия между частицами: взаимодействия между материальными частицами Стандартной модели и полем Хиггса, а также его частицей, бозоном Хиггса, являющейся чрезвычайно важной. Чем сильнее взаимодействие, тем больше масса частицы.

Давайте возьмем одну частицу, скажем, d-кварк. Как и в случае других материальных частиц, в описание поля d-кварка входят два компонента: один — соответствующий правосторонней форме этой частицы, а второй — левосторонней. Поскольку масса в квантовой теории поля является результатом взаимодействия с полем Хиггса, мы умножаем два поля для d-кварка (лево- и правосторонние формы) на само поле Хиггса. Результат умножения в этом случае соответствует этому взаимодействию, то есть величина произведения, а точнее величина смешанного произведения, показывает, насколько сильным или слабым является взаимодействие d-кварка и поля Хиггса.

Но это только первая часть сложной процедуры. Следующая сложность возникает из-за того, что величина смешанного произведения может меняться по мере перемещения по «поверхности» Калаби-Яу. С другой стороны, константа взаимодействия Юкавы не является переменной величиной, зависящей от месторасположения на многообразии. Это глобальная величина номер один, а способ вычисления этой величины состоит в интегрировании произведения d-кварка и полей Хиггса по всему многообразию.

Следует помнить, что интегрирование фактически является процессом усреднения. У вас есть некоторая функция (в нашем случае произведение трех полей), которая принимает различные значения в разных точках на многообразии, а вам необходимо получить ее среднее значение. Это необходимо сделать, поскольку константа взаимодействия Юкавы является числом, а не функцией, тогда как масса частицы также является числом. Поэтому следует разбить многообразие на мелкие участки и определить значение функции на каждом участке. Затем сложить все значения и разделить на количество участков, получив среднее значение.

Хотя этот метод может показаться довольно простым, он не даст точного правильного ответа. Проблема состоит в том, что многообразие Калаби-Яу, с которым мы работаем, обладает кривизной, и если взять крошечную «прямоугольную» заплатку, допустив на мгновение, что мы находимся в двухмерном пространстве размером dx×dy, то размер такого участка будет изменяться в зависимости от того, насколько велика его кривизна. Вместо этого следует взять значение функции в точке, где находится заплатка, и затем умножить это значение на весовой коэффициент, зависящий от размера заплатки. Другими словами, необходим способ измерения размера заплатки. А для этого необходима метрика, которая подробно описывала бы геометрию многообразия. Но здесь имеется одна загвоздка, о которой мы уже неоднократно упоминали: пока еще никто не смог предложить метод вычисления метрики Калаби-Яу явно, то есть точно.

Здесь вас может ждать ловушка: без метрики невозможно получить массу, а без массы невозможно узнать, насколько близка имеющаяся модель к Стандартной модели. Но существуют несколько математических методов, а именно численные методы, реализуемые с помощью компьютера, которые можно использовать для приближенного вычисления метрики. Затем возникает вопрос, достаточно ли хороша использованная аппроксимация для получения приемлемого ответа.

В настоящее время применяют два основных метода, и оба в некоторой степени опираются на гипотезу Калаби. Эта гипотеза гласит (как уже отмечалось неоднократно), что если многообразие удовлетворяет определенным топологическим условиям, то оно обладает риччи-плоской метрикой. Не создав саму метрику, я не мог бы доказать, что такая метрика существует. При доказательстве был применен так называемый аргумент деформации, это означает, что если начать с чего-то, скажем, с некой метрики, и деформировать ее определенным образом, то этот процесс в конце концов сойдется к необходимой метрике. Если вы можете доказать, что такой процесс деформации стремится к нужному решению, то существует хороший шанс, что можно найти численную модель, которая также будет сходиться.

Недавно два физика, Мэтт Хедрик из Университета Брандейса и Тоби Вайсман из Королевского колледжа, произвели численные расчеты в соответствии с этими принципами, разработав аппроксимированную метрику для поверхности K3, четырехмерного многообразия Калаби-Яу, с которым мы часто имеем дело. Они использовали общую стратегию под названием дискретизация, заключающуюся в том, чтобы взять объект с бесконечным числом точек, например точки, составляющие непрерывную кривую, и представить ее конечным (дискретным) числом точек, надеясь, что этот процесс, в конце концов, сойдется непосредственно на этой кривой. Хедрик и Вайсман считают, что этот процесс сходится, и хотя полученные ими результаты выглядят обнадеживающе, пока они не смогли доказать наличие сходимости.

Один из недостатков описанного метода, не имеющий отношения к анализу Хедрика и Вайсмана, связан с ограничениями современной техники: нынешним компьютерам просто не хватает мощности, чтобы рассчитать подробную метрику для шестимерных многообразий Калаби-Яу. Вычисление в шести измерениях требуют неимоверно больше операций, чем решение четырехмерной задачи. Несомненно, компьютеры продолжают совершенствоваться, и, возможно, они вскоре станут достаточно мощными, чтобы выполнять вычисления и для шести измерений.

Между тем, существует другой метод, который меньше зависит от вычислительных ограничений. Его начало было положено еще в 1980-е годы, когда я предположил, что риччи-плоскую метрику всегда можно аппроксимировать, поместив (или, говоря техническим языком, — «вложив») многообразие Калаби-Яу в опорное пространство очень высокой размерности. Такое опорное пространство называется проективным пространством, и оно напоминает комплексный вариант плоского евклидова пространства, за исключением того, что оно компактно. При размещении, например, многообразия в большем пространстве, подпространство автоматически наследует метрику (которая называется индуцированной метрикой) из опорного пространства. Аналогичная ситуация наблюдается, если поместить сферу в обычное евклидово пространство — сфера примет метрику опорного пространства. Если следовать похожей аналогии, то можно также считать, что дырка в швейцарском сыре встроена в более крупное пространство.

Рис. 9.5. С помощью процесса дискретизации можно аппроксимировать одномерную кривую и двухмерную поверхность конечным числом точек. Такая аппроксимация, естественно, будет точнее при увеличении количества точек

Если мы знаем, как измерить расстояние в более крупном пространстве (большом сыре), то мы также будем знать, как измерить размер дырки. В этом смысле вложенное пространство, или дыра, наследует метрику из «сырного» опорного пространства, в котором она находится. В 1950-е годы Джон Нэш доказал, что если поместить римановы многообразия в пространство с достаточно большим количеством измерений, то можно получить любую желаемую индуцированную метрику. Но теорема Нэша о вложении, являющаяся одной из самых великих работ этого знаменитого математика, применима к действительным многообразиям, помещенным в действительное пространство. В общем случае, комплексный вариант теоремы Нэша неверен. Но я считал, что комплексная версия этой теоремы может быть верной при определенных обстоятельствах. Например, я аргументировал, что большой класс кэлеровых многообразий может быть вложен в проективное пространство высокой размерности таким образом, что индуцированная метрика будет сколь угодно близка к исходной метрике при условии, что индуцированная метрика соответствующим образом масштабирована или «нормализована», то есть все ее векторы умножены на константу. Будучи специальным случаем кэлеровых многообразий, многообразия Калаби-Яу с риччи-плоской метрикой удовлетворяют этому топологическому условию. Это означает, что можно всегда индуцировать риччи-плоскую метрику, и ее можно всегда аппроксимировать путем вложения многообразия в опорное или проективное пространство со значительно большей размерностью.

Рис. 9.6. В геометрии часто говорят о «вложении» объекта или пространства в «опорное пространство» высокой размерности. В данном случае мы вложили квадрат, то есть одномерный объект, поскольку он состоит из изогнутого несколько раз отрезка прямой, в двухмерное опорное пространство — сферу

Ганг Тиан, будучи в то время моим аспирантом, доказал это в статье, вышедшей в 1990 году, которая фактически была его диссертационной работой. С тех пор к моему исходному утверждению было добавлено несколько важных уточнений, включая диссертацию еще одного моего аспиранта Вей-Донг Руана о том, что возможна более точная аппроксимация риччи-плоской метрики. Главное уточнение было посвящено способу вложения многообразия Калаби-Яу в опорное пространство. Нельзя сделать это бессистемно. Идея состоит в том, чтобы выбрать соответствующее вложение так, чтобы индуцированная метрика была наиболее близка к риччи-плоской метрике. Для этого следует поместить многообразие Калаби-Яу на возможно лучшее место, так называемую сбалансированную позицию, которая является той позицией среди всех возможных, где наследуемая метрика приближается вплотную к риччи-плоской.

Понятие сбалансированной позиции ввели в 1982 году Петер Ли и я для случая подмногообразия (или подповерхностей) на сфере, находящейся в действительном пространстве. Затем мы пошли дальше — к общему случаю подмногообразия в сложном опорном (или проективном) пространстве со множеством измерений. В те годы Жан-Пьер Бургиньон, являющийся в настоящее время директором Института высших научных исследований, начал с нами сотрудничество, которое вылилось в 1994 году в совместную статью по этой теме.

Ранее на конференции по геометрии в Калифорнийском университете в Лос-Анджелесе я предположил, что каждое кэлерово многообразие, допускающее риччи-плоскую метрику, включая Калаби-Яу, является устойчивым, но такое понятие устойчивости сложно определить. На последующих семинарах по геометрии я продолжал подчеркивать важность работы Бургиньона-Ли-Яу, как теперь ее называют, в отношении идеи устойчивости. Наконец, несколько лет спустя мой аспирант Вей Луо из Массачусетского технологического института установил связь между устойчивостью Калаби-Яу и условием равновесия. Благодаря работе Луо я смог видоизменить свою гипотезу, придя к заключению, что если вложить Калаби-Яу в многомерное пространство, то можно всегда найти положение, в котором позиция будет равновесной.

Саймон Дональдсон доказал, что эта гипотеза является верной. Его доказательство также подтвердило суть этой новой схемы аппроксимации: если вложить Калаби-Яу в высокоразмерное опорное пространство и выполнить условие равновесия, то метрика будет значительно ближе к риччи-плоской. Дональдсон доказал это, показав, что индуцированные метрики образуют последовательность в опорных пространствах увеличивающейся размерности и что эта последовательность сходится, стремясь к идеальной риччи-плоской метрике при стремлении числа измерений к бесконечности. Однако это заявление справедливо лишь постольку, поскольку верна гипотеза Калаби: когда Дональдсон продемонстрировал, что эта метрика сходится к риччи-плоской метрике, его доказательство опиралось на существование риччи-плоской метрики.

Доказательство Дональдсона имело также и практические результаты, поскольку он показал, что существует лучший способ выполнения встраивания — равновесный метод. Разрешение проблемы таким способом дает средства ее решения и возможную стратегию для вычислений. В 2005 году Дональдсон применил этот метод, численно получив метрику для K3-поверхности, а также показав, что не существует фундаментальных препятствий для использования этого метода в случае увеличения числа измерений.^[173] В 2008 году Майкл Дуглас с сотрудниками в своей статье, основанной на работе Дональдсона, получили численными методами метрику для семейства шестимерных многообразий Калаби-Яу — вышеупомянутой квинтики.

В настоящее время Дуглас сотрудничает с Брауном и Оврутом в вопросах вычисления метрики для многообразия Калаби-Яу в их модели. Пока никто не смог вычислить константы связи или массы. Но Оврута привлекает перспектива вычисления масс частиц. «Не существует способа выведения этих величин из самой Стандартной модели, — говорит он, — но теория струн, по крайней мере, предлагает возможность, которой никогда не было ранее». Не все физики согласны с тем, что эта цель достижима, однако Оврут считает, «что дьявол кроется в деталях. Нам еще предстоит вычислить константы взаимодействия Юкавы и массы, которые могут оказаться полностью неверными».^[174]

Канделас считает маловероятным, что современные модели окажутся конечной моделью Вселенной. Он придерживается мнения, что при попытке создать такую модель можно получить «много верных подтверждений. Но если углубиться в эти модели, то рано или поздно окажется, что в них что-то не работает».^[175] Не стоит считать современные модели последним словом, лучше рассматривать их как часть общего процесса изучения природы, в ходе которого разрабатываются важные инструментальные средства. Все сказанное относится и к работам по реализации Стандартной модели, включающей браны, орбиобразия или торы, ни одна из которых не доведена до конца.

Но Строминджер считает, что прогресс налицо. «Люди находят все больше и больше моделей, а некоторые из этих моделей подходят все ближе к тому, что мы наблюдаем вокруг нас. Но мы еще не видели как “баскетбольный мяч летит через всю площадку”. Именно этого мы ждем с нетерпением».^[176] Используя еще одну аналогию со спортом, Строминджер сравнил статью 1985 года о компактификации Калаби-Яу, написанную им совместно с Канделасом, Горовицом и Виттеном, с попаданием мяча для гольфа в лунку, находящуюся на расстоянии двух сотен ярдов. «Было чувство, что необходим еще только один удар, чтобы попасть в лунку. Но прошло уже два десятилетия, а физики все еще пытаются это сделать», — говорит он.^[177]

«Двадцать пять лет — это большой срок для теоретической физики, и только сейчас заметно явное продвижение вперед, — говорит Канделас. — Мы, наконец, достигли стадии, когда люди могут делать что-то практическое с этими новыми идеями».^[178]

Прекрасно осознавая, что исследователи добились значительных успехов, Аллан Адамс (Массачусетский технологический институт) все же считает, что «неправильно предполагать, будто близость к Стандартной модели означает, что мы уже все сделали». «Наоборот, — утверждает он, — сложно понять, как далеко нам предстоит еще идти вперед. Хотя может показаться, что мы уже близки к нашей цели, но все еще существует “большая пропасть” между Стандартной моделью и тем, где мы находимся сейчас».^[179]

В конце своих приключений в Стране Оз Дороти узнает, что у нее с самого начала была возможность вернуться домой. После нескольких десятилетий исследований Страны Калаби-Яу струнные теоретики и их коллеги-математики (даже те, кто вооружен разящей мощью геометрического анализа) считают, что вернуться домой, к реалиям обычной физики, известной как Стандартная модель, а оттуда к физике, которая, как мы знаем, должна находиться еще дальше, все еще очень сложно. Если бы это можно было сделать так же легко, как закрыть глаза, щелкнуть каблуками башмачков и сказать: «Нет лучше места, чем дом»… Но тогда бы мы пропустили все самое интересное.

154. L. Frank Baum, The Wizard of Oz (Whitefish, Mont.: Kessinger, 2004), p. 111.

155. Volker Braun (Dublin Institute for Advanced Studies), interview with author, November 4, 2008.

156. Philip Candelas (Oxford University), interview with author, December 1, 2008.

157. То же.

158. Andrew Strominger (Harvard University), interview with author, February 7, 2007.

159. Cumrun Vafa, “The Geometry of Grand Unified Theories,” lecture, Harvard University, Cambridge, Mass., August 29, 2008.

160. Chris Beasley (Stony Brook University), interview with author, November 13, 2008.

161. Burt Оvrut (University of Pennsylvania), interview with author, July 20, 2008.

162. Ovrut, interview with author, February 2, 2007.

163. Ron Donagi (University of Pennsylvania), interview with author, November 14, 2008.

164. Donagi, interview with author, November 19, 2008.

165. Candelas, interview with author, December 1, 2008.

166. Donagi, interview with author, May 3, 2008

167. Ovrut, interview with author, November 20, 2008.

168. Donagi, interview with author, November 20, 2008.

169. Ovrut, interview with author, November 20, 2008.

170. Shamit Kachru (Stanford University), interview with author, November 4, 2008.

171. Michael Douglas (Stony Brook University), interview with author, August 20, 2008.

172. Candelas, interview with author, December 1, 2008.

173. Simon Donaldson (Imperial College), interview with author, November 29, 2008.

174. Ovrut, interview with author, November 19, 2008.

175. Candelas, interview with author, December 1, 2008.

176. Strominger, interview with author, February 7, 2007.

177. Adrian Cho, “String Theory Gets Real — Sort Of,” Science 306 (November 26, 2004): 1,461.

178. Candelas, interview with author, December 1, 2008.

179. Allan Adams (MIT), interview with author, November 15, 2008.