|
||
|
|
||
| Главная ≫ Инфотека ≫ Разное ≫ Книги ≫ Глава девятая. Пространство-время. Арена действия / Десять великих идей науки. Как устроен наш мир // Питер Эткинз |
Глава девятая. Пространство-время. Арена действия / Десять великих идей науки. Как устроен наш мирПитер Эткинз
Глава девятая. Пространство-время. Арена действияВремя и пространство есть формы, в которых мы мыслим, а не условия, в которых мы живем. Великая идея: вещество искривляет пространство-времяГде находится то, что происходит? Когда мы смотрим вокруг, ответ кажется очевидным. Мы существуем в пространстве и действуем во времени. Но что есть пространство, и что есть время? И здесь наша интуиция спешит предложить готовый ответ. Мы представляем себе пространство как сцену, возможно, нематериальную сцену, но тем не менее некоторого рода сцену. А время? Время позволяет различить последовательные действия, время является свойством Вселенной, дающим нам возможность опознавать настоящее как вечно движущуюся грань между прошлым и будущим. Иными словами, пространство расставляет по местам одновременные события, а время распутывает непредсказуемое будущее и неизменяемое прошлое. Пространство и время вместе распределяют события по местоположениям и порядковой последовательности, делая их умопостигаемыми. Наука проистекает из существования времени, поскольку главный источник науки, причинность — влияние событий на их последовательность — является по существу систематической преемственностью событий во времени: если сейчас это, то потом то.Однако такие интерпретации времени и пространства скорее сродни чувствам, чем подлинному знанию. Они, возможно, являются скорее отправным пунктом для философа, чем конечным пунктом для ученого. Как мы увидим в этой главе, развитие нашего современного взгляда на время и пространство было освобождением от интуитивной точки зрения, что мир является сценой, ареной действия; но в более недавние времена и этот взгляд начал размываться. Некоторые ученые сегодня считают, что они находятся на пороге открытия даже более великой идеи, чем та, которая является предметом настоящей главы. Наша история начинается с человека, решившего измерять поверхность Земли, осознаваемую тогда в качестве арены действия. На самом деле, они начали мерить не Землю, а землю, что оказалось значимым, судя по последствиям. Разумеется, одним из аспектов научного метода является ограничение амбиций в отношении того, что может быть достигнуто: наука откусывает булочки понемногу, а не пытается слопать великие вопросы за один присест. Ключом к пониманию чего бы то ни было является сочетание наблюдения, особенно количественной разновидности наблюдения, которую мы называем измерением, и систематического способа мышления, который мы называем логикой. Первыми из шагов, которые в конце концов привели нас к современному пониманию нашей арены действия, были измерения, проведенные вавилонянами и египтянами, и логика, развитая греками. Вавилоняне владели процедурой, но не имели доказательств: греки внесли доказательства. Вавилоняне, например, знали за тысячу лет до греков, что сумма квадратов сторон прямоугольного треугольника равна квадрату его гипотенузы, но оставили грекам, возможно, математическому коллективу некоего вида, известному нам под именем Пифагора, доказательство того, что эта связь верна для любого мыслимого прямоугольного треугольника. Процедура является основой знания и базой для приложений, но доказательства обостряют интуицию и ведут нас к более глубокому пониманию. Я остановлюсь ненадолго на теореме Пифагора, поскольку в ней заключено несколько важных уроков. Разумеется, мы увидим, что некоторые черты нашего современного понимания пространства и времени были предвосхищены в трудах Пифагора (около 500 лет до н.э.), Эвклида (около 300 лет до н.э.) и Аполлония из Перга (около 200 лет до н.э.). Об этих персонажах мы не знаем практически ничего, и поскольку большинство анекдотов о них было записано спустя века после их смерти, мы не можем полагаться на эти рассказы. Однако уцелело многое из их необычайных мыслей, золотых сокровищ, содержащих доказательства и прозрения в свойства пустого пространства. Мы начнем с байки и представим себе фантастический подход, который мог использовать древний завоеватель Месопотамии, Хаммурапи, когда он обследовал свои новые владения 3500 лет тому назад. Будем считать, что Хаммурапи жил в мире, полном неудобств, не последним из которых было соглашение, что расстояния с севера на юг измеряются в метрах, а расстояния с востока на запад измеряются в ярдах. Когда землемеры Хаммурапи обследовали его свежезавоеванные поля, они измеряли длины их сторон и, по таинственным причинам, связанным с налогообложением, длины их диагоналей, регистрируя последние либо в метрах, либо в ярдах, как им подскажет фантазия. Можно подозревать, что Хаммурапи нашел мало смысла в числах, которые собрали его землемеры. Например, одно поле, вытянутое с севера на юг, имело стороны 120 метров и 130 ярдов и диагональ 169 метров, в то время как другое, вытянутое с востока на запад, имело стороны 131 ярд и 119 метров с диагональю 185 ярдов. Хаммурапи был озадачен, поскольку оба поля выглядели одинаково. Однажды ему в голову пришла мысль. Он решил отвергнуть древнее соглашение о единицах и приказал, чтобы с этого момента все расстояния регистрировались бы в метрах (м). После большой и усердной работы его землемеры представили ему новый список сторон и диагоналей. Внезапно он увидел, что их измерения стали теперь много более полезными. Стороны обоих полей, выглядевших одинаково, были 120 м и 119 м, а их диагонали были по 169 м. Сведя все эти измерения в один ряд путем использования одинаковых единиц, Хаммурапи отделил форму от ориентации: все объекты одинаковой формы имеют одинаковые размеры, независимо от их ориентации. Хаммурапи пришлось продолжить приведение в порядок измерений в своем царстве и дальше. Не все поля в его царстве имели одинаковые размеры, и его землемеры представляли списки сторон и диагоналей, которые, даже выраженные в метрах, выглядели, на его взгляд, не намного отличающимися от случайных. Например, один богатый землевладелец имел поле со сторонами 960 м и 799 м и диагональю 1249 м, а другой, более бедный землевладелец имел поле со сторонами 60 м и 45 м и диагональю 75 м. И тогда наш фиктивный, но блистательный Хаммурапи внезапно вскрикнул (по-шумерски) эврика. Он увидел, что, если для каждого из его полей, безотносительно к размерам, он возведет в квадрат длины его сторон и сложит два квадрата вместе, то результат будет равен квадрату длины диагонали. То есть все измерения, собранные его землемерами, удовлетворяют формуле: расстояние2 = сторона12 + сторона22,где расстояние есть длина диагонали. Будучи экономным правителем, он мог теперь приказать своим землемерам экономить время и заработную плату и измерять только стороны полей, поскольку длину диагоналей он мог узнать сам. Конечно, он понимал, что, даже если они будут настаивать на использовании причудливых единиц этого царства, он все равно сможет узнавать длину диагонали, записав: расстояние2 = (C × сторона1)2 + сторона22,где C — множитель, необходимый, чтобы перевести ярды в метры, одна из глубоко чтимых фундаментальных констант этого царства. Здесь мы можем отступить от нашей мифической версии Хаммурапи, с его формулой, его эффективностью и его налогами. Более важно, что вечная польза, для которой он предназначал эту формулу, заключается в том, что он идентифицировал выражение, некоторым образом передающее свойства пространства Месопотамии. Неизвестный индиец, написавший Сульвасутру (Правила веревок), расчеты для таинственных сакральных церемоний священнослужителей ведической эры (около 500 лет до н.э.), тоже знал эту формулу, поскольку брахманы нуждались в надежно спроектированном и построенном прямоугольном алтаре. Китайцы Чжан Цан и Цин Чоу-чан, составившие в период Хань (начавшийся в 200 г. до н.э.) сборник, содержавший математические сведения, тоже знали ее. Как мы увидим, существование частной формулы для расстояния между двумя точками соответствует существованию геометрии, описанию пространства в терминах точек, линий, плоскостей и объемов, которые могут существовать в нем. Чтобы определить геометрию пространства, в котором мы обитаем, надо определить формулу. Определение геометрии пространства Месопотамии, данное Хаммурапи, потребовало двух шагов. Сначала мы должны определить единицы вдоль различных координатных осей; затем мы должны найти формулу, которая задает расстояние между двумя точками. Из того, что такая же величина C годится для Индии и Китая, следует, что пространство в Индии и Китае имеет ту же геометрию, что и пространство Месопотамии. Доказательство того, что формула Хаммурапи пригодна для любого поля всюду во Вселенной, а не только в Месопотамии, возможно, было сделано Пифагором и его школой, но надежные свидетельства того, что они сделали нечто большее, чем просто использовали ее, отсутствуют. Чтобы найти доказательство этой теоремы, мы должны обратиться к Началам Евклида, написанным примерно 2300 лет назад и с тех пор воспроизводимым, но причин полагать, что ее доказал сам Евклид, не существует. Евклид обнаружил, что он может вывести характеристики пространства, включая дедуктивную формулу Хаммурапи, из пяти простых и кажущихся очевидными утверждений, из своих «аксиом». Это было поистине замечательным достижением. Если бы я писал эту книгу 2000 лет назад, я обязательно включил бы аксиомы Евклида в число великих идей науки, поскольку, если не считать одного маленького дефекта, они удовлетворяют критериям, предъявляемым великой идее: они просты, но содержат неограниченно богатые следствия. Дефект, конечно, заключается в том, что они неверны (в том смысле, что они неточно описывают пространство, в котором мы обитаем); но мы можем ненадолго пренебречь этим и воздать Евклиду почести, которые он заслужил. Евклид сжал свое описание пространства в следующие пять замечаний: 1. Между любыми двумя точками можно провести прямую.(Я несколько упростил эти утверждения, но сохранил их суть.) Пятая аксиома известна как постулат о параллельных прямых. Он ответственен за большее количество бед, чем почти любое другое утверждение в математике, ибо он имеет более сложный вид по сравнению с другими, соблазнительно намекая, что его можно доказать с помощью четырех более простых аксиом. Целые жизни напрасно были растрачены на безуспешные попытки вывести эту аксиому из других. Теперь мы знаем, что она независима от других аксиом и что можно придумать абсолютно приемлемые геометрии, в которых постулат о параллельных прямых заменен другими, таким, например, как: 5'. Для любых данных прямой и точки, не лежащей на ней, нельзя провести через эту точку ни одной прямой, параллельной данной.Или даже: 5''. Для любых данных прямой и точки, не лежащей на ней, можно провести через эту точку бесконечное число прямых, параллельных данной.Описание пространства, использующее постулат Евклида о параллельных прямых, называется евклидовой геометрией; описания, основанные на альтернативных постулатах, называются неевклидовыми геометриями. Пока что мы сосредоточимся на евклидовой геометрии, так как она, безусловно, выглядит подходящей для пространства, в котором мы живем. В тринадцати книгах Евклида показано, что из этих пяти аксиом может быть выведено огромное количество свойств, и эти свойства оказываются верными при их проверке с помощью практических измерений. Одним из следствий этих аксиом, и, в частности, постулата о параллельных прямых, является теорема Пифагора. Поэтому существование нашей мифической формулы Хаммурапи для расстояния вытекает из пяти аксиом Евклида, и геометрия Хаммурапи тоже является евклидовой. Итак, мы сформулировали евклидову геометрию на плоскости, в плоской двумерной области, похожей на поверхность листа бумаги. Однако мы все знаем, или думаем, что знаем, что обитаем в трехмерном пространстве и обладаем свободой движения вверх и вниз так же, как по плоскости. Теорему Пифагора легко распространить на три размерности, включив длину третьей стороны и записав: расстояние2 = сторона12 + сторона22 + сторона32.Мы не обязаны останавливаться на этом. Математики живут ненасытной страстью к обобщениям, и евклидова геометрия является богатой почвой для обобщений. Хотя большинство из нас не может вообразить что-нибудь за пределами наших домашних трех измерений, легко выразить свойства пространств больших размерностей, используя формулы. Так четырехмерная формула Пифагора будет иметь вид: расстояние2 = сторона12 + сторона22 + сторона32 + сторона42.Вы могли бы подумать, что в размышлениях о пространствах с более высокими, чем три, размерностями мало пользы, если не считать интеллектуального удовольствия, но вы были бы неправы. Мы увидим, к примеру, что способность переходить из размерности в размерность является ценным способом изучения структуры нашего мира. Более того, можем ли мы быть уверены, что в нашем реальном мире имеются только три измерения, или есть несколько — даже много — других измерений, которые как-то спрятаны от нас? Мы видели в главе 8, что такой уверенности нет, так как, может быть, мы обитаем в десятимерном пространстве с дополнительным измерением в виде времени. Я утверждал, что наше воображение не может выйти за пределы трех измерений. Это не вполне верно. Некоторые люди, потратившие в жизни много времени на изучение геометрий более высоких размерностей, заявляют, что имеют некоторое отдаленное представление о связях, существующих в четырех, а не в трех измерениях, и создают ошеломляющие компьютерные образы, изображающие трехмерные сечения четырехмерного, мира (рис. 9.1).[45] Я не призываю вас направить ваши умственные способности по этому пути, но для подготовки к тому, что последует дальше, мы нуждаемся в некотором знакомстве с четырехмерными ландшафтами. Чтобы осуществить это, мы должны вновь пройти фрагменты пути интеллектуальной революции, инициированной итальянскими художниками в конце тринадцатого, начале четырнадцатого веков, такими как Джотто ди Бондоне и Пьеро делла Франческа, которые начали передавать три измерения в двух, используя перспективу, математические основы которой заложил в конце восемнадцатого века Гаспар Монж, граф де Пелоуз (1746-1818) в своей Géométrie descriptive (1798). Затем мы должны пойти дальше и увидеть, как четырехмерные объекты могут быть представлены трехмерными изображениями в двумерных проекциях. Все это звучит довольно сложно, ибо это все равно что просить муравья, который всегда был заперт в плоском мире, воспользоваться своим воображением, чтобы представить себе еще и вертикаль. Но мы интеллектуально оснащены лучше, чем муравьи, и можем ожидать, что достигнем некоторого прогресса.
Ноль-мерный куб (0-куб) — это точка. Представьте себе 0-куб как карандашную точку, тогда одномерный куб (1-куб) является линией, которую карандаш рисует, когда его двигают по прямой (рис. 9.2). Двумерный куб (2-куб) является плоской фигурой, порожденной протаскиванием 1-куба в новом направлении, лежащем перпендикулярно первому. Все это легко воспринять с помощью компаса нашего воображения, так же как и воображения смышленого муравья, и легко проделать на листе двумерной бумаги. Трехмерный куб (3-куб), заурядный повседневный куб, порождается протаскиванием плоского 2-куба в направлении, перпендикулярном его плоскости. С тем, чтобы вообразить этот шаг, проблем не возникает, хотя муравей был бы озадачен, поскольку ему не дано понять, как может существовать третье перпендикулярное направление. Не возникает проблем и с представлением 3-куба на 2-странице, обычном листе бумаги, поскольку мы теперь так хорошо знакомы с двумерными представлениями в искусстве, что расшифровываем эти представления без труда.
Чтобы помочь озадаченному муравью, мы можем проделать следующее. Мы осторожно разрежем 3-куб вдоль одной из граней, развернем его, положим на плоскость (рис. 9.3) и расскажем муравью, как нужно сложить грани, чтобы сформировать 3-куб. Муравей будет озадачен тем, каким образом края, которые я пометил жирной линией, могут соприкоснуться, но по крайней мере он будет иметь некоторое отдаленное представление о том, что такое 3-куб, и, возможно, научится интерпретировать наши двумерные представления 3-куба, включая забавную, в чем муравей может поклясться, картинку, на которой мы изображали его шестиугольником.
Мы знаем теперь достаточно, чтобы построить четырехмерный гиперкуб (4-куб). В математике многое делается по аналогии. Так же как мы протаскивали 0-куб, чтобы получить 1-куб, и так далее, мы построим 4-куб, протаскивая 3-куб (обычный куб) в направлении, перпендикулярном трем первым измерениям. Теперь мы оказались озадаченными муравьями, так как мы не понимаем, что такое направление, перпендикулярное нашим трем измерениям. Все же, в точности так, как муравей, не способный постичь третье измерение, мы можем сделать умственный прыжок и, приняв мысль о том, что оно есть — так же, как муравей, — попытаться понять его по аналогии. Чтобы облегчить себе понимание двумерного образа 4-куба, показанного на рис. 9.2, мы могли бы совершить гипердействие и разрезать куб вдоль некоторой грани, а затем развернуть его в трех измерениях (рис. 9.4). Так же как 3-куб разворачивается на шесть 2-кубов, 4-куб разворачивается на восемь 3-кубов (один 3-куб спрятан в центре верхнего креста). Чтобы вообразить, как 4-куб строится из 3-кубов, которые составляют его поверхность, представим себе склеивание. Нам, 3-читателям, аналогам 2-муравьев, кажется невозможным понять, как, например, могут быть соединены две помеченных грани, так же как у 2-муравья есть похожая проблема с тремя измерениями. У 4-читателя никаких трудностей тут нет.
Евклидова геометрия была завершена в семнадцатом столетии, когда, как мы видели в главе 3, Исаак Ньютон (1643-1727), дополнив наблюдения Галилея статическим описанием пространства, данным Евклидом, построил описание движения в этом пространстве. Чтобы проделать это, Ньютон ввел понятие силы, влияния, которое отклоняет движение частиц от прямолинейного и заставляет их двигаться с переменной скоростью. В контексте текущего обсуждения мы можем рассматривать вклад Ньютона как первую достаточно успешную попытку соединить время и пространство. Это пытался сделать еще Аристотель, но он не добился успеха, поскольку недооценивал возможности геометрии для определения путей: он думал, исходя из опыта перемещения по земле, что для поддержания движения частицы по прямой линии необходимо прилагать силу. Ньютон, напротив, ощутил возможности геометрии для определения путей частиц. Он ввел понятие силы, чтобы выразить отклонение от естественного движения, за которое он принял равномерное движение по прямой линии. Для Ньютона, как и 2000 лет назад для Аристотеля, пространство и время были абсолютны, причем пространство было подмостками, которые делили между собой актеры, играющие на сцене, а время было тикающим параметром, общим для всех них: Абсолютное пространство, в своей собственной природе, без связи с чем-нибудь внешним, всегда остается однородным и неподвижным… Абсолютное, истинное и математическое время, само по себе, исходя из своей собственной природы, течет равномерно, без связи с чем-нибудь внешним.Если у меня сегодня четверг, так и у всех четверг, и если у меня на это уходит час, то и у всех на это уходит час. Если для одного наблюдателя две точки удалены друг от друга на километр, то и для всех наблюдателей между ними километр. Другими словами, пространство является фиксированной, абсолютной сценой, а время тикает универсально. Понятие действия на расстоянии, с помощью которого звезды могли бы искривлять путь отдаленных планет в нечто, подобное кругу, было глубоко озадачивающим. Ньютон и сам видел, что в его теории имелся дефект, Но он реалистически относился к своим возможностям и удовлетворился тем, что оставил эту загадку будущим головам: он откусывал понемногу, а не заглатывал. Голова, почти в одиночку разрешившая загадку, принадлежала Эйнштейну, и в оставшейся части этой главы мы увидим, какого грандиозного понимания он достиг. Альберт Эйнштейн (1879-1955) двинул цивилизацию вперед двумя шагами. На первом он привязал пространство ко времени более тесным образом, чем пытался это сделать Ньютон. Осуществив это, он разрушил ньютоновские представления об абсолютном пространстве и времени и перечеркнул универсальное тиканье. На втором шаге он устранил одно из величайших достижений Ньютона, понятие универсального тяготения как силы. Великие загадки часто решаются посредством их устранения, и ученые должны получать удовольствие, отбрасывая главенствующие концепции, включая их собственные. Мы присоединимся к Эйнштейну теми же двумя шагами. Второй шаг, более значительный, не может быть пройден без первого, и нам придется проследовать по этому пути, если мы действительно хотим глубоко понять, «что, где и когда» является местом нашего обитания. Первым достижением Эйнштейна была частная теория относительности (из-за неправильного перевода с немецкого, раньше ее называли специальной теорией относительности). Частная теория относительности является описанием наблюдений, которые производят люди, находящиеся в равномерном относительном движении без ускорения. Центральным замечанием Эйнштейна было замечание о том, что для наблюдателя, находящегося в равномерном движении, невозможно, не выглядывая из окна, определить, движется он или нет. Это заключение Эйнштейн сжато выразил утверждением, что все инерциальные системы отсчета эквивалентны. «Инерциальная система отсчета» — это просто подмостки, движущиеся с постоянной скоростью по прямой линии. У Галилея в начале семнадцатого века возникла та же идея, когда он вообразил путешествие в каюте без окон на лодке, плывущей по спокойному морю: он не смог представить себе никакого эксперимента, позволяющего определить, движется ли лодка. Чтобы найти современный пример инерциальной системы отсчета, мы можем представить себе эксперименты, которые мы проводим в кабине космического аппарата, находящегося в свободном полете: если у нас нет связи с внешним миром, мы не сможем определить, движется ли он. Решающей разницей между Галилеем и Эйнштейном, а также между двумя разделяющими их веками оказалось то, что в распоряжении Эйнштейна была информация об электричестве и магнетизме, так же как о динамике движущихся тел (маятников и так далее). Чтобы понять значение идеи Эйнштейна об эквивалентности инерциальных систем отсчета, представим себе, что вы и я, являемся авторами учебников. Я полагаю, что я неподвижен в лаборатории, где я провожу серию экспериментов; вы думаете, что вы находитесь в лаборатории, движущейся относительно меня по прямой линии со скоростью 1 000 000 000 километров в час (км/ч; эта скорость соответствует примерно 93 процентам от скорости света, путешествие вокруг Земли с этой скоростью заняло бы 0,14 сек.). В отличие от других авторов, которые, чтобы составить свои тексты, полагаются на работы других, мы решили сами выполнить все классические эксперименты — бросание Галилеем камушков с падающей башни в Пизе, открытие Фарадеем электромагнитной индукции, бесплодные поиски Майкельсона и Морли свидетельств движения через эфир и так далее. С точки зрения Эйнштейна, каждый из нас написал бы по существу один и тот же учебник, несмотря на тот факт, что вы путешествуете относительно меня со скоростью 1 000 000 000 км/ч. Наши слова, конечно, были бы различными, но курсы физики, которым мы обучаем, были бы неразличимыми. Если бы мы обменялись учебниками, я смог бы пользоваться вашим, а вы моим. Эквивалентность наших учебников распространяется на всю физику, не только на движущиеся частицы (Галилей), но также на электричество и магнетизм (Эйнштейн). Теперь мы подходим к центральному пункту. Многие уравнения физики, в частности описывающие электричество и магнетизм, зависят от скорости света с. Проблема в следующем. В моих главах, посвященных электромагнетизму, используемые мною выражения требуют некоторого значения с, которое я измерил в моей лаборатории. Выражения, которые используете вы в своей главе, также содержат определенное значение с, и, чтобы я мог преподавать физику по вашему учебнику, значение величины с, которое измерили вы, должно быть в точности тем же самым, что измерил я. Другими словами, когда вы измеряете с, вы получаете то же значение, что и я, хотя вы двигаетесь со скоростью 1 000 000 000 км/ч относительно меня. Только в этом случае ваш учебник будет согласован с моим. Тот факт, что наблюдатели в разных инерциальных системах отсчета (вы и я) получают при измерении одну и ту же скорость света, имеет глубочайшие следствия для нашего понимания пространства и времени. Например, он разрушает понятие универсальной одновременности и уничтожает концепцию пространства как только арены. Поскольку эти замечания разрушают все, во что мы привыкли верить, настает решающий момент для пересмотра нашего понимания природы. Нам необходимо увидеть более точно, что из этого следует. Как это может быть, что вы получаете в измерении то же значение с, хотя вы так быстро двигаетесь относительно меня? Одно объяснение состоит в том, что ваши измерения расстояния и времени отличны от моих. Например, если ваша измерительная линейка короче, чем моя, а ваши часы идут медленнее, то значения, измеренные вами, будут отличаться от моих, хотя мы и наблюдаем одно и то же явление. Таким образом, может быть, что «толчок», который вы даете лучу света, излучаемому из лампы, движущейся на 1 000 000 000 км/ч быстрее моей, гасится этими видоизменениями вашего восприятия пространства и времени. То есть толчок, даваемый свету вашим движением, может быть полностью погашен этим изменением восприятия. Такие видоизменения уже предлагались ранее ирландским физиком Джорджем Фитцджеральдом (1851-1901) и голландским физиком Хендриком Лоренцом (1853-1928) и были известны как сокращение Лоренца-Фитцджеральда. Достижение Эйнштейна заключалось в том, что он дал их чисто ситуационному предположению более твердую и глубокую теоретическую основу, предложив считать его следствием геометрии времени и пространства. Эйнштейн проник в самое сердце материи. Хотя он и не выражал это таким способом, мы можем вообразить, что землемеров Хаммурапи поджимало время, и они производили свои измерения на бегу, пересекая поля. Однако землемеры, бегущие с разными скоростями через одни и те же поля, докладывали бы о разных длинах диагоналей, и формула Хаммурапи для расстояния была бы теперь непригодна, ибо разные землемеры сообщали бы для нее разные величины, зависящие от того, как быстро они бежали и в каком направлении. Вспышка озарения — и наш фиктивный Хаммурапи и наш реальный Эйнштейн объявили, что сообщений о положении точек в пространстве теперь недостаточно: с этого момента землемеры должны докладывать не только о положении точки, но и о моменте времени, в который, согласно показаниям их часов, это положение регистрировалось. Такую пару измерений мы называем событием. Эйнштейн предложил считать, что истинным «инвариантом», величиной, относительно которой согласны все, независимо от скорости их движения, является интервал между двумя событиями. Интервал между двумя событиями, разделенными в пространстве расстоянием (измеренным отдельным землемером) и разделенными во времени временем (измеренным тем же землемером) определяется как: интервал2 = (c × время)2 − расстояние2,где расстояние вычисляется с помощью выражения, которое мы использовали ранее. Поскольку расстояние между положениями двух событий в пространстве, измеренное вами, меньше, чем расстояние, которое измеряю я, а интервал должен быть тем же самым, время между этими двумя событиями для вас тоже должно быть меньше, чтобы сохранить величину разности (c × время)2 − расстояние2. Иными словами, для вас время бежит медленнее, чем для меня. Время, которое каждый из нас измеряет, называется нашим собственным временем: я полагаю, что ваше собственное время бежит медленней моего собственного времени. Поскольку вы считаете, что это я двигаюсь относительно вас, вы тоже полагаете, что мое собственное время бежит медленней вашего. Предложение Эйнштейна требует удивительного пересмотра нашего понимания времени и пространства. Во-первых, оно уничтожает понятие универсальной одновременности: у наблюдателей в разных инерциальных системах отныне нет возможности достичь согласия о том, являются ли два события одновременными. Чтобы оценить это заключение, предположим, что вы находитесь в космическом корабле, который, как вы знаете, имеет длину 100 м. Вы мчитесь мимо меня со скоростью 1 000 000 000 км/ч. Я замечаю положения двух концов космического корабля в данный момент и нахожу, что между ними всего 38 м. Расстояние во времени между моими двумя событиями (двумя измерениями) равно нулю, поскольку они одновременны, поэтому интервал между ними равен измеренному мною расстоянию в пространстве, которое равно 38 м. Вы знаете, что длина вашего космического корабля равна 100 м, поэтому, чтобы интервал был таким же, время между этими двумя событиями, измеренное вами, не может быть нулевым. В действительности вы думаете, что время между двумя моими измерениями равно 0,31 микросекунды (0,31 мс)! Короче, вы не считаете эти два события одновременными. Надежность понятия одновременности исчезла, так как никакие два наблюдателя, равномерно движущиеся друг относительно друга, не могут достичь согласия о том, являются ли два события одновременными. Иными словами, прощай, ньютоновское понимание абсолютного пространства и времени. Второй частью пересмотра привычных понятий является слияние пространства и времени. Давайте сперва приведем в порядок выражение для интервала. Так же как Хаммурапи помог упростить описание Месопотамии, переведя измерения с востока на запад и с севера на юг в одинаковые единицы, и мы можем упростить описание пространства и времени, переведя измерения пространства и времени в одинаковые единицы. Этот перевод является лишь вопросом удобства, но давайте выберем в качестве выражения для измерения времени «метры, пройденные светом», расстояние, которое за это время проходит свет, получаемое умножением времени на c. Тогда 1c будет представлена как 300 000 км, потому что именно столько пролетит свет за 1 с, а «один метр времени» эквивалентен 3×10−11 с (30 пикосекунд, 30 триллионных секунды) в традиционных единицах. Когда вы глядите на вашу руку с часами, отсчитывающими секунды, представьте себе, что каждое тиканье это еще 300 000 км. Такой перевод единиц измерения является не более чем кулинарным приемом, но он упрощает определение интервала до: интервал2 = время2 − расстояние2,так же как Хаммурапи упростил определение расстояния от (С × сторона1)2 + сторона22 до сторона12 + сторона22, настояв на том, чтобы его землемеры докладывали значение стороны1 в метрах. Теперь мы подошли к очень важному моменту. Так же как формула для расстояния, задаваемая теоремой Пифагора, является следствием геометрии двумерного пространства и может быть обобщена на три и более измерения, так и формула Эйнштейна для интервала существенным образом предполагает, что время следует рассматривать как четвертое измерение, перпендикулярное трем измерениям пространства. Такое понимание восходит к замечанию Германа Минковского (1864-1909), сделанному им в 1907 г.: С этого времени пространство само по себе и время само по себе осуждены постепенно растаять в болотных сумерках, и только некий род их объединения сохранится как независимая реальность.Объединение пространства и времени теперь носит название пространство-время. Нам не следует смешивать четырехмерное пространство-время с четырехмерным пространством, так как их геометрии совершенно различны: расстояние в четырехмерном пространстве задается выражением t2 + x2 + y2 + z2, в то время как его аналог в четырехмерном пространстве-времени, интервал, задается выражением t2 − (x2 + y2 + z2) или t2 − x2 − y2 − z2. Мы говорим, что 4-пространство и 4-пространство-время имеют разные сигнатуры метрики: сигнатура метрики 4-пространства (схема знаков в выражении для расстояния) имеет вид (+,+,+,+), в то время как она же для интервала пространства-времени имеет вид (+,−,−,−). Возможно, вы начинаете схватывать суть или, по крайней мере, определение времени: это координата, соответствующая единственному отличному от других знаку в сигнатуре метрики, +, а не −. Мир, в котором сигнатура метрики имеет вид (+,+,−,−), обладал бы двумерным временем, где «сегодня» пришлось бы определять двумя датами. Если бы даже нам пришлось представить себе пространство-время более высоких размерностей, например, пятимерное пространство-время с сигнатурой метрики (+,−,−,−,−), мы бы немедленно определили первую координату как время; мы сталкивались с пространством-временем более высоких размерностей в главе 8, и здесь мы находим основание для решения, является ли дополнительная координата пространственной или временной. На протяжении этой главы под пространством-временем мы будем иметь в виду четырехмерную версию с сигнатурой метрики (+,−,−,−). Я должен признать, что геометрия пространства-времени, называемая геометрией Минковского, труднее для восприятия, чем геометрия только пространства. Однако следующие замечания призваны дать вам впечатление о некоторых чертах пространства-времени и его отличии от пространства как такового. Этот материал не является центральным для того, что последует дальше, поэтому, если он покажется слегка приводящим в недоумение, не беспокойтесь, пусть так и будет. Чтобы создать у вас уверенность в представлениях о предметах этого рода, я воспользуюсь тем же методом, что и прежде: так же как мы обнаружили, что способны уловить проблеск понимания четырехмерного пространства, постепенно увеличивая размерность, мы можем приблизиться к пониманию четырехмерного пространства-времени, начав с меньшего числа измерений. Таких вещей, как нульмерное и одномерное пространство-время, не существует. Различение между пространством и временем (как оно выражено в сигнатуре метрики) значимо только, когда мы переходим к двумерному пространству-времени (2-пространству-времени), с одним измерением для пространства и одним для времени. Более того, 2-пространство-время может быть представлено на плоском графике, с одной осью, означающей пространство, а другой время (рис. 9.5). Линии на диаграмме показывают пути частицы в этом мире и являются тем, что Минковский называл мировыми линиями. Вертикальная мировая линия изображает историю неподвижной частицы: частица остается в той же точке пространства, а время возрастает. Мировая линия, отклоняющаяся вправо, представляет частицу, медленно движущуюся вправо, поскольку положение частицы смещается направо по мере возрастания времени. Мировая линия с наклоном 45° соответствует частице, которая движется направо со скоростью света, проходя расстояние в 1 м за 1 м светового времени (30 триллионных секунды в обычных единицах). Эта линия представляет самое быстрое из возможных движений частицы, поскольку ничто не может двигаться быстрее чем свет, и только безмассовые частицы (такие как фотоны) могут достигать этой скорости. Все возможные мировые линии лежат между линией, наклоненной на 45° влево (частица, движущаяся влево со скоростью света) и линией, наклоненной на 45° вправо (частица, движущаяся вправо со скоростью света).
Сделаем теперь шаг в 3-пространство-время с двумя пространственными измерениями и одним временным (рис. 9.6), где частица при возрастании времени может перемещаться по двумерной плоскости. Поскольку ни одна частица не может двигаться со скоростью, большей скорости света, все мировые линии лежат внутри конуса, образованного вращением линии, наклоненной под углом 45° к вертикали. Этот конус называется световым конусом события, лежащего в его вершине, поскольку мировые линии, образуемые светом, движущимся со скоростью света, лежат на поверхности этого конуса. Вы можете представить себе круговой импульс света, начинающий путь из точки: со временем он распространяется кругами, показанными на плоскости, и отмеченными различными временами на световом конусе.
Обращаясь к 4-пространству-времени, нам следует представить себе четырехмерный вариант конуса, исходящего из точки события, сечением которого в каждый момент является трехмерная сфера (представляющая поверхность распространения сферического импульса света). Изображение его находится полностью за пределами моих возможностей, и я даже не претендую на то, что обладаю способом его представления на бумаге. К счастью, изображение светового конуса для импульса в двух измерениях на рис. 9.6 дает все, что действительно нужно для понимания. Световой конус делит события на два класса. Рассмотрим, например, события A и B на рис. 9.7. Поскольку B лежит внутри светового конуса с вершиной в A, сигналы из A имеют достаточно времени, чтобы достичь B и повлиять на событие B. Рассмотрим теперь события A и C. Событие A не может повлиять на событие C, потому что последнее лежит вне светового конуса с вершиной в A, и никакой сигнал из A не может достичь C, чтобы произвести какое-либо действие. Мы говорим, что A и B (и все другие точки, лежащие внутри светового конуса или на нем) являются причинно связанными, в то время как C (и все другие точки, лежащие вне светового конуса) не связаны причинно с A. Мы уже отмечали, что причинность является становой жилой науки, поэтому тот факт, что световой конус делит пространство-время на области событий, связанных и не связанных причинно, имеет огромную важность для нашего понимания мира. Например, какое бы событие ни произошло в A, например, распад на куски планеты Земля в полдень прошлого воскресенья, оно не может повлиять на событие в C, которое может быть лекцией по истории космоса, читаемой в следующий понедельник на планете около звезды, весьма удаленной от Земли.
Все предшествующее может ощущаться, как довольно-таки знакомый материал, поскольку линии и конусы, которые мы нарисовали, вторят свойствам обычного пространства. Теперь мы подходим к принципиальному различию между евклидовым пространством и пространством Минковского, к самому трудному для интуитивного восприятия свойству. В пространстве прямая линия является кратчайшим расстоянием между двумя точками. В пространстве-времени, с его забавной геометрией Минковского, нам придется привыкнуть к мысли, что прямая линия является самым длинным интервалом между двумя событиями. Следующая ниже притча о Касторе и Поллуксе поможет разъяснить это обстоятельство. Давайте представим себе, что Кастор остался дома. Его мировая линия вертикальна и тянется от его двадцатого дня рождения до двадцать первого дня рождения. Поллукс, отпраздновав свой день рождения вместе с братом, немедленно пускается на космическом корабле в путешествие, которое для Кастора длится 12 месяцев, движется со скоростью 1 000 000 000 км/ч до удаленной точки в межзвездном пространстве и возвращается, прибыв как раз к его, Кастора, двадцать первому дню рождения. По представлениям Кастора, Поллукс пролетел 8,8 триллиона километров. Кастор использовал время отсутствия своего брата для того, чтобы рассчитать, что интервал между началом и концом путешествия составляет 3,30 триллиона километров. Поллукс с этим согласен, так как интервал является инвариантом. Однако, поскольку он не покидал космический корабль и путешествовал вслепую, Поллукс считает, что он нигде не был, поэтому приписывает весь этот интервал течению времени, а не перемещению в пространстве. В обычных единицах 3,30 триллиона километров светового времени соответствует 4,6 месяца (рис. 9.8). Мы видим, что мировая линия, представляющая путешествие, совершенное Поллуксом между событиями, отмечающими дни рождения Кастора, соответствует интервалу более короткому, чем прямая линия между этими двумя днями рождения (соответствующая мировой линии Кастора), даже несмотря на то, что линия, изображающая это путешествие, в наших евклидовых глазах выглядит длиннее. Это заключение подтверждает наше замечание о том, что прямая линия между событиями соответствует более длинному (в действительности самому длинному) интервалу, чем непрямой путь. Это верно и в общем случае. Когда вы смотрите на диаграмму в пространстве-времени, не давайте евклидовым представлениям вас одурачить.
Второе, что следует заметить: Поллукс стал младше Кастора. Поллукс, чей метаболизм шел в соответствии с течением переживаемого им времени, повзрослел только на 4,6 месяца, в то время как Кастор стал старше на год. Итак, чтобы избежать старения, мы должны двигаться очень быстро. Еще одной чертой пространства-времени, отличающей его от пространства, является смысл объема. На некоторой стадии мы не можем избежать необходимости думать о четырех измерениях, но мы можем совершить этот шаг, представляя себе меньшее число измерений, а затем рассуждая по аналогии. Давайте рассмотрим кубический ящик в трехмерном пространстве-времени с двумя пространственными измерениями и одним временным. Как и обычный кубический ящик в трехмерном пространстве, такой ящик имеет шесть квадратных граней (рис. 9.9). Грань, помеченная на иллюстрации буквой A, полностью лежит в двумерном пространстве и соответствует обычной плоскости в заданное время: представим себе ее плоским листом бумаги в определенный момент. Грань, помеченная буквой B, является той же гранью в более поздний момент: представьте себе ее, как тот же лист бумаги пятью минутами позже, лежащий на том же месте. Грань, помеченная буквой C, составленная из вертикальных мировых линий всех точек одного края неподвижного листа бумаги (одного края грани A); таким же образом каждая из других вертикальных граней состоит из вертикальных мировых линий всех точек каждого из трех других краев листа бумаги.
Четыре вертикальных грани суммируют все события, случившиеся на каждом краю листа бумаги за те 5 минут, которые мы рассматриваем. Например, предположим, что муравей вползает на бумагу слева через 2 минуты. Первоначально лист бумаги пуст, значит, поверхность A тоже пуста. Муравей вползает слева и создает свою мировую линию. Он пересекает левый край, поэтому мы видим появившуюся там точку. Затем (предполагаем мы) муравей останавливается в середине листа и остается там. Его мировая линия теперь вертикальна, и через три минуты точка появляется на грани B. Заметим, что разница между поверхностями A (ни одной точки) и B (одна точка) отмечена точкой где-то на одной из вертикальных поверхностей (в данном примере C). При условии, что частица не может просто появиться из ничего, изменение между двумя горизонтальными «пространственно-подобными» поверхностями A и B должно быть отмечено событием на вертикальной «времени-подобной» поверхности (для муравья, C). Теперь затянем покрепче наш интеллектуальный страховочный ремень и сорвемся в четырехмерное пространство-время. А вот и одеяло, чтобы подстелить для создания комфорта: ухватитесь за тот факт, что четыре измерения в точности аналогичны трем, но пространственные поверхности (листы бумаги заменяются пространственными объемами (комнатами). Муравьи, вползающие на бумагу, заменяются людьми, входящими в комнаты. Как мы уже видели, стены 4-куба образуются из восьми 3-кубов (вспомним рис. 9.4). В пространстве-времени два из этих 3-кубов, обозначим их X и Y, являются чисто пространственными и соответствуют трехмерным областям пространства — реальным комнатам — в начальный и конечный моменты рассматриваемого отрезка времени (рис. 9.10, где о событиях, которые я собираюсь описать, говорится несколько более детально), так же как поверхности A и B в трехмерном пространстве-времени соответствуют настоящим листам бумаги в два разных момента времени. Мы называем эти обычные кубы «пространственно-подобными». Каков смысл других шести 3-кубов? Каждый из них имеет грани, лежащие в двух пространственных измерениях, и одно временное измерение, поэтому они суммируют историю, которая происходит на каждой двумерной грани реального ящика, так же как сторона C суммирует то, что случается на краю листа бумаги. Мы назовем эти кубы «времени-подобными». Чтобы понять их смысл, предположим, что наш пространственно-подобный куб представляет комнату, в которой вы сейчас находитесь. Перед тем как вы пришли в эту комнату, она была пустой, поэтому пространственно-подобный куб X пуст. Когда вы вошли в комнату, вы прошли через дверь в стене, поэтому точка, отмечающая место и время вашего входа, появляется на соответствующем времени-подобном кубе, например, кубе Z (точка может отмечать положение вашего носа). Если мы обследуем комнату несколько позже, пока вы еще в ней, мы обнаружим ваше местоположение, отмеченное точкой, в пространственно-подобном кубе Y. Как и в 3-пространстве-времени, любая разница между кубами X и Y должна быть отмечена точкой внутри одного из остальных шести кубов: где именно лежит эта последняя точка, зависит от того, где и когда вы вошли в комнату.
Теперь, чтобы завершить это обсуждение и подготовить вас к тому, что последует дальше, мне необходимо заставить вас думать несколько более обобщенно. Когда мы подойдем к разговору об энергии или массе, мы будем иметь возможность делать построения на этом рисунке. Полная энергия (или масса, согласно формуле E = mc2) в кубе X будет полной энергией в некой области пространства сначала. Полная энергия в кубе Y будет энергией в этой области после того, как прошел заданный период времени. Полная энергия во времени-подобных кубах представляет собой поток энергии внутрь или вовне области через ограничивающие ее стенки, а конечным притоком энергии должна считаться разность между значениями энергии в пространственно-подобных кубах X и Y. О гиперкубах в пространстве-времени на данный момент, вероятно, сказано достаточно. Вы подошли к началу понимания структуры пространства-времени, смысла точек и объемов в нем. Прежде чем мы вместе сделаем следующий шаг, мне надо ознакомить вас еще с одним аспектом частной теории относительности. Этот важный шаг выявит происхождение самого знаменитого выражения во всей физике, E = mc2, или энергия = масса × c2, и покажет нам, что это важное в интеллектуальном, экономическом, коммерческом, военном и политическом отношениях выражение, которое уже возникало перед нами в этой и предшествующих главах, является к тому же еще одним проявлением геометрии пространства-времени. В единицах, в которых время выражается длиной, c = 1, поскольку свет проходит один метр за 1 метр светового времени, и это выражение Эйнштейна принимает менее знакомую, но более простую и показательную форму энергия = масса. Иными словами, разницы между энергией и массой нет. Я не могу избежать использования небольшой толики математики, но это будет необременительный разговор с передышками, и я надеюсь, что вы его преодолеете (или перепрыгнете: но этот результат важен). Мы знаем соотношение между интервалом, временем и расстоянием: интервал2 = время2 − расстояние2.Легко преобразовать это выражение, разделив обе стороны на интервал2 и получить: 1 = (время2 / интервал2) − (расстояние2 / интервал2).Далее, умножим обе стороны на массу2, где масса есть масса некоторой частицы, о которой мы в данный момент думаем (атом урана, лягушка, Юпитер). Этот шаг дает: масса2 = (масса × время / интервал)2 − (масса × расстояние / интервал)2.Поскольку расстояние / интервал напоминает обычное выражение для скорости, а масса, умноженная на скорость, есть определение импульса (глава 3), мы можем подозревать, что второе слагаемое справа является релятивистским выражением для квадрата импульса. Я не буду вдаваться в подробности, но это подозрение подтверждается при рассмотрении столкновения двух частиц, в котором обнаруживается, что полная величина масса × расстояние / интервал при столкновении остается неизменной. Одним из центральных принципов физики, как мы видели в главе 3, является «сохранение импульса», принцип, говорящий о том, что, какие бы сложные события ни происходили при столкновении двух тел, полный импульс остается неизменным, так что для этого отождествления есть основания. Но что означает первое слагаемое справа? Если мы напишем уравнения для столкновения двух частиц, то обнаружим, что величина масса × время / интервал тоже остается неизменной при столкновении, даже если происходит множество сложных индивидуальных событий. Другим великим принципом физики, как мы видели в главе 3, является сохранение энергии. Наблюдения заставляют предполагать, что мы должны отождествить масса × время / интервал с энергией и переписать последнее уравнение в виде: масса2 = энергия2 − импульс2.Отождествление величины масса × время / интервал с энергией также подтверждается демонстрацией того, что, подобно импульсу, она сохраняется при столкновении. Одним следствием из этого выражения, подобно выражению для интервала, является то, что, так же как пространство и время мыслятся объединенными в пространство-время, импульс и энергия должны мыслиться как две стороны комбинированной величины, которую можно назвать, хотя это делают редко, неуклюжим именем импульс-энергия. Масса, согласно этому выражению, вычисляемая из энергии и момента, так же как интервал, вычисляемый из времени и расстояния, является инвариантом, свойством, которое находят одинаковым все наблюдатели, как бы быстро они ни двигались. Теперь мы можем перейти к нашему итоговому заключению. Предположим, что частица неподвижна в нашей инерциальной системе — это может быть кусок железа, который мы держим в руке. Поскольку частица является неподвижной, ее импульс равен нулю; таким образом выражение масса2 = энергия2 − импульс2 превращается в масса2 = энергия2, и мы немедленно заключаем, что масса = энергия, именно то, что мы хотели вывести. Вам следует обратить внимание, что это необычайно важное выражение является прямым следствием геометрии пространства-времени в сочетании с двумя физическими законами сохранения, позволяющими нам отождествить термины. Наше исследование геометрии пространства-времени привело нас к заключению, что масса и энергия эквивалентны. Мы должны заключить, что если из области уходит энергия, то масса в этой области уменьшается. Если энергия втекает в область, то масса в этой области возрастает. На практике разница в массе для обычных объектов вполне пренебрежима. Например, разница в массе 10-килограммового пушечного ядра при комнатной температуре и температуре 1000 К составляет лишь 50 пикограмм (50 миллионно-миллионных грамма), что совершенно невозможно обнаружить (с помощью современных технологий). Изменения энергии, сопровождающие перестройку субатомных частиц, протонов и нейтронов, составляющих атомные ядра, много больше, чем изменения, получаемые простым нагреванием пушечных ядер. Ядерный распад является процессом, в котором ядро атома распадается на два более маленьких ядра, что дает возможность протонам и нейтронам в ядре занять энергетически более выгодные положения и, следовательно, освободить излишек энергии. Когда 10 килограммов урана-235 подвергается распаду, освобождаемая энергия соответствует потере целых 10 граммов массы. Это эквивалентно энергии, выделяемой 30 тысячами тонн угля. Геометрия удивительно могущественна. Значительная часть этой главы до сих пор основывалась на избавлении от фундаментальной константы, скорости света, и на упрощении результирующих выражений. Теперь мы перейдем к избавлению от другой фундаментальной константы и таким путем достигнем еще более глубокого понимания природы (мы наблюдали этот процесс в главе 3, где мы удалили механический эквивалент теплоты и были вознаграждены термодинамическими прозрениями). Я подозреваю, что, если бы мы избавились от всех фундаментальных констант, мы поняли бы Природу в совершенстве! Именно здесь мы подходим к Великой Идее, являющейся сердцем этой главы. У Эйнштейна ушло более десятилетия на переход от частной теории относительности к более общей теории, которую обычно называют общей теорией относительности, теорией гравитации Эйнштейна или, совсем просто, «теорией Эйнштейна». В теории Ньютона гравитация, рассматриваемая как сила, действующая в пустом пространстве, характеризуется универсальной фундаментальной постоянной, гравитационной постоянной, G.[46] Согласно Ньютону, сила тяготения, создаваемая телом, пропорциональна произведению G на массу тела. Эта пропорциональность означает, что на заданном расстоянии от центров Солнца и Земли (и снаружи от них) сила притяжения Солнца, чья масса в 336 тысяч раз больше массы Земли, в 336 тысяч раз больше силы притяжения Земли. Сначала немного кухни. С этого момента мы включаем G в массу и таким образом выражаем массу в единицах длины. Выраженная в единицах длины, масса Земли равна 4,41 мм, а масса Солнца в 336 тысяч раз больше, 1,48 км. Следует заметить, что теперь мы выразили массу, длину и время в единицах длины: мы могли бы выразить их в единицах времени, разделив на с, но получаемые числа были бы тогда более нелепыми и имели бы меньше прямого смысла. Вам также следует обратить внимание на то, что мы устранили таинственную константу G из ньютоновского описания гравитации, а это предполагает, что гравитация есть, в некотором роде, искусственная концепция и что G появляется в физике не потому, что имеет глубокий фундаментальный смысл, а потому, что наши предки выбрали причудливую единицу (например, килограмм) для выражения массы, а не естественную единицу, единицу длины (такую как метр). Но самое глубокое замечание, которое я могу сделать в этой связи и которое вам следует держать в голове, пока я развиваю эту тему, это то, что, выразив все величины в терминах длины, мы движемся к описанию, в котором действие массы на пространство-время становится предметом геометрии. Евклид был бы восхищен, узнав о размахе, на который способен его метод. Теперь мы подошли к делу. Общая теория относительности возникает из замечательного совпадения, замеченного Эйнштейном. Замечательные совпадения в науке, как и в обычной жизни, всегда подозрительны. В обычной жизни они, как правило, указывают на обман; в науке они обычно указывают на открытие. Совпадение, о котором идет речь, состоит в том, что масса, используемая для выражения способности тела сопротивляться действию силы, которая в главе 3 названа «инерционной массой», является той же самой, что и масса, используемая для выражения способности тела создавать гравитационное притяжение, его «гравитационная масса». Эта эквивалентность была подтверждена экспериментально с точностью до одной триллионной, а это заставляет предполагать, что инерционная масса и гравитационная масса есть в точности одно и то же. Это должно показаться вам очень странным. Нет никаких непосредственно видимых причин, по которым сопротивление пушечного ядра моему удару ногой идентично силе гравитационного поля, которое пушечное ядро порождает. Опираясь на это совпадение, Эйнштейн обнаружил еще одно. Предположим, что вы и я едем на одном и том же лифте, но что-то идет не так. Сначала мы обнаруживаем, что застряли на сотом этаже здания. Чтобы скоротать время до нашего спасения, мы перекидываемся мячом. Будучи наблюдательными, мы замечаем, что путь мяча искривляется (рис. 9.11). Если бы кабина лифта находилась в глубоком космосе, вдалеке от гравитационного притяжения звезд и планет, путь мяча был бы прямой линией. Имея это в виду, мы приписываем кривизну траектории мяча гравитации. Будучи учеными и быстро проделав вычисления, мы узнаем также, что путь мяча представляет собой параболу, кривую, получаемую в сечении конуса плоскостью, параллельной одной из его сторон, то есть образующих его прямых линий.
Внезапно спокойствие нарушается. Наш некомпетентный спасатель по неосторожности перерезал кабель, держащий кабину лифта, и одновременно отключил все приспособления, страхующие ее от падения. Мы срываемся вниз в свободное падение. Будучи учеными, мы хладнокровно пользуемся уникальной возможностью, возникшей благодаря нашему попаданию в фатальный переплет, и продолжаем перекидывать мяч друг другу. К нашему великому изумлению, мы вдруг обнаруживаем, что мяч теперь летает между нами по прямой линии, как если бы мы находились в космосе, свободном от гравитации! Если бы наш лифт находился на поверхности Солнца, параболический путь мяча искривлялся бы более круто, но при вхождении нашего лифта в свободное падение он и ускорялся бы быстрее, и это движение все равно разгладило бы нашу параболу в прямую линию. Отсюда урок: где бы мы ни были, мы можем уничтожить влияние гравитации, вступив на платформу, находящуюся в свободном падении. Если бы каждый когда-либо живший ученый был всегда заперт в кабине свободно падающего лифта, концепция гравитации никогда не появилась бы на свет. Эйнштейн открыл это шокирующее обстоятельство и воспользовался им. Сначала он по существу предположил, что все наблюдатели, населяющие свободно падающие кабины лифтов, написали бы одинаковые учебники физики. В этом суть содержания принципа эквивалентности. В частности, наблюдатели, падающие в кабинах, делающие измерения и обменивающиеся их результатами, испытывали бы те же сокращения пространства и времени, которые предсказываются частной теорией относительности. Мы можем выразить это утверждение в более геометрических терминах: геометрия пространства-времени является одинаковой (и является геометрией Минковского) во всех свободно падающих кабинах лифтов. Итак, все, что мы ранее обсуждали касательно частной теории относительности, приложимо к любой такой свободно падающей кабине. Однако величайшим достижением Эйнштейна были его размышления о том, как геометрия в нашей падающей кабине связана с геометрией в другой кабине, которая может падать с другим ускорением. Например, ваш небоскреб может быть построен на астероиде, и вы падаете, ускоряясь очень, очень медленно. Моя кабина может быть расположена на Земле, и ее ускорение будет около 10 м/с2 (так что через 1 с она падает со скоростью 10 м/с, через 2 с падает со скоростью 20 м/с и так далее). Геометрия пространства-времени является плоской — геометрией Минковского — в каждой из наших кабин, но мой маленький кусочек плоской геометрии изгибается и скручивается относительно вашего. Вы можете представить себе попытку покрыть шар монетами (рис. 9.12): каждая малая область является плоской, но одна область лежит под углом к другой области. Вопрос, который поставил и спустя годы напряженной работы ума разрешил Эйнштейн, заключался в том, как связаны друг с другом области плоского пространства-времени в близком присутствии скопления массы, такого как звезда. Если я могу описать мое земное пространство-время с точки зрения вашего астероида, то я на самом деле описываю воздействие, которое ученые обычно называют гравитацией.
Ранее в этой главе мы получили некоторое представление о пространстве-времени. Теперь мы должны перенести этот опыт развития гибкости ума на следующую стадию, на гибкость пространства-времени, и получить представление об искривленном пространстве-времени. Это не так ужасно, как, возможно, звучит, поскольку теперь мы можем отодвинуть геометрию Минковского на задворки сознания и попытаться забыть о ее сложности. На деле многие считают качественные идеи общей теории относительности гораздо проще, чем идеи частной теории относительности, потому что здесь можно представлять себе искривленное пространство (что легко), а не искривленное пространство-время (что нелегко). Это заблуждение, поскольку общая теория относительности относится к искривленному пространству-времени, но это приемлемое заблуждение, поскольку оно делает всю концепцию доступной, поэтому мы будем продолжать изложение, пользуясь им. Итак, сначала мы сосредоточим внимание на искривленном пространстве, потому что эта концепция довольно проста. Как и прежде, концептуально легче урезать число измерений, которые мы должны попытаться вообразить, а потом вновь достроить это число. Однако, чтобы вообразить даже двумерную искривленную поверхность, нам, очевидно, уже необходимы три измерения, чтобы представить себе, «в чем» эта поверхность искривлена. Поэтому, как нетрудно видеть, для того чтобы представить себе четырехмерное искривленное пространство-время, мы нуждаемся в пяти измерениях! Я не буду просить вас проделать это, поскольку не могу сам (и не знаю никого, кто мог бы), но если вы хотите все же визуализовать искривленное пространство-время в полной мере, вот что вам следует попытаться сделать. Техническим термином для представления искривленного пространства в размерности на единицу большей является «вложение» его в пространство на единицу большей размерности. Чтобы представить себе четырехмерное искривленное пространство-время, вам следовало бы вложить его в пространство пяти измерений. Давайте на минуту остановимся на двумерном искривленном пространстве (а не на пространстве-времени). Чтобы представить себе его искривленным, вообразим 2-пространство, поверхность, вложенную в 3-пространство, объем. Представим себе 2-пространство как поверхность 3-сферы (обычной сферы, похожей на идеализированную Землю). Теперь представим себе сцену, в которой я стою на экваторе на нулевом меридиане (это помещает меня в неуютную влажность океана где-то к западу от побережья Африки), а вы стоите на экваторе на долготе 90° (это помещает вас на побережье Эквадора). Свисток, и мы оба начинаем двигаться к северу, проверяя на каждом шагу на протяжении всего пути, что мы не отклонились ни вправо, ни влево. Будучи физиками-теоретиками, мы не обращаем внимания на неудобства при пересечении пустынь, океанов и ледовых шапок. В конечном счете, когда мы достигаем Северного полюса, мы сталкиваемся носами (рис. 9.13). Нам приходится заключить, что параллельные с виду линии пересекаются в пространстве с этой геометрией. О пространстве, в котором все параллельные с виду линии встречаются, если их продолжить достаточно далеко, — или, что эквивалентно, о пространстве, в котором нет по-настоящему параллельных линий — говорят, что оно имеет положительную кривизну. Это пространство дает пример одной из неевклидовых геометрий, о которых я упоминал раньше.
Немедленным следствием существования неевклидовых геометрий является вывод, что геометрия есть наука экспериментальная, а не нечто (как думал Иммануил Кант, о чем мы узнаем в главе 10), справедливость чего можно установить одной лишь интроспекцией. Одна лишь интроспекция никогда не приводит к истине, что так чудесно проиллюстрировал Аристотель; интроспекция в союзе с экспериментом, конечно — темой нашей книги, — является необычайно чудесным и надежным гидом, что так великолепно проиллюстрировал Галилей. Мы стоим перед выбором перспективы для геометрии пространства: быть ли ей евклидовой, как, сидя в своих креслах, целых 2000 лет полагали Евклид и его последователи, или неевклидовой. Чтобы решить этот вопрос, мы должны обратиться к эксперименту и увидеть, например, столкнемся ли мы носами, если будем идти по параллельным путям достаточно далеко. Карл Фридрих Гаусс (1777-1855), один из величайших математиков, имел некоторое представление о том, что у евклидовой геометрии могут быть конкуренты: На самом деле, поэтому я время от времени в шутку выражаю пожелание, чтобы геометрия Евклида была неверна.Однажды этот концептуальный тупик был пробит в наибольшей мере немецким математиком с трагически короткой жизнью, Бернхардом Риманом (1826-1866). В своей выдающейся лекции, прочитанной в 1854 г. по случаю вступления в должность, он дал человеческому уму свободу, достаточную для того, чтобы вообразить себе неевклидовы пространства уже и с отрицательной кривизной. Рисунок 9.14 показывает двумерную поверхность отрицательной кривизны, вложенную в трехмерное пространство. Когда вы сидите в седле, вас поддерживает двумерная поверхность отрицательной кривизны. В этом пространстве через заданную точку можно провести бесконечное число линий, параллельных данной.
Коль скоро мы преодолели интеллектуальный бугор и признали то обстоятельство, что существуют разные типы неевклидовых геометрий, мы способны перейти к представлению о пространстве, геометрия которого может меняться от места к месту. То есть различные области — пространства могут иметь разную кривизну. Например, мы можем представить себе пространство, похожее на гантель, полученное сжатием сферы в области экватора, превращающем его в талию гантели. Это пространство будет иметь положительную кривизну около полюсов и отрицательную кривизну в седлообразной окрестности экватора. Мы могли бы пойти дальше и вообразить более сложные пространства, втыкая пальцы в эту поверхность и создавая небольшие кратеры, испещряющие ее так, чтобы кривизна менялась от места к месту. Вам может понравиться рассматривать повседневные объекты, которые имеют поверхности с кривизной, меняющейся от места к месту (например, вы сами). Когда мы думаем о пространствах, вложенных в пространства более высокой размерности, мы встаем на точку зрения надменного сверхсущества, которое может судить на глазок, имеется ли тут кривизна. Предположим, однако, что мы муравьи, и наше воображение ограничено реальным пространством, в котором мы обитаем: может ли муравей узнать, искривлена ли Земля, можем ли мы определить, искривлено ли наше пространство-время? Ответ уже следует из текущего обсуждения, поскольку путешествия, которые вы и я предприняли, и вопрос о том, столкнемся ли мы с вами нос к носу или нет, можно представить себе имеющими место на поверхности, независимо от того, считаем мы ее во что-то вложенной или нет. Таким образом, если вы и я отправляемся по двум параллельным с виду путям и сталкиваемся носами, то мы знаем, что пространство, в котором мы пребываем, имеет положительную кривизну. Это заключение не зависит от того, можем ли мы вообразить наше пространство вложенным в пространство более высокой размерности или нет. Мы можем развить эту мысль дальше и научиться измерять кривизну пространства количественно. Пойдемте со мной на Северный полюс (рис. 9.15). Теперь, когда мы здесь, давайте вытянем, каждый, по одной руке, указывая ею вниз прямо на юг, на Гринвич, вдоль меридиана 0°. Свисток, и вы отправляетесь на юг и идете, пока не достигнете экватора. Продолжая указывать рукой на юг, вы идете вдоль экватора, пока не достигнете 90° восточной долготы. Из этой точки, все еще показывая рукой на юг, вы возвращаетесь на Северный полюс. Я, в свою очередь, наблюдаю, как вы появляетесь из-за горизонта. Однако, к нашему общему огромному удивлению, мы обнаруживаем, что ваша рука повернута на 90° относительно моей, несмотря на то, что вы педантично указывали ею строго на юг на протяжении всего вашего путешествия! В плоском пространстве направления, наших рук совпадали бы, поэтому мы заключаем, что реальная поверхность Земли плоской не является. Более того, мы можем описать количественную меру «кривизны» как изменение угла, на который повернута ваша рука, деленное на площадь области, ограниченной вашим маршрутом, что дает 1 / радиус2, где радиус является радиусом Земли. Так как радиус Земли равен 6400 км, кривизна ее поверхности составляет 2,4×10−8 км−2. Это очень маленькая кривизна, указывающая на то, что нам придется делать обход очень большой площади, для того чтобы эффект стал заметным. Вот почему землемеры Хаммурапи не замечали ее: поля, которые они измеряли в Месопотамии, имели площади лишь в несколько тысяч квадратных метров, и кривизна Земли просто не могла быть видна. Кривизна футбольного мяча с радиусом 10 см равна 0,01 м−2, так что эта кривизна становится заметной на областях его поверхности, занимающих довольно небольшую площадь. Для сферы кривизна будет оставаться одинаковой, где бы мы ни начали наше путешествие и какую бы площадь мы ни обошли. Кроме того, кривизна на ней всюду положительна. Куриное яйцо также всюду имеет положительную кривизну, но ее значения меняются примерно от 0,2 см−2 на тупом конце до 0,4 см−2 на более круто искривленном остром конце.
У нас нет необходимости совершать путешествия по поверхностям реальной материальной Земли, футбольного мяча или яйца, чтобы вычислить кривизну. Если бы я оставался на месте, а вы бы путешествовали в пустом пространстве по замкнутой петле и в конце вашего путешествия мы увидели бы, что наши руки указывают в одном направлении, мы были бы вправе заключить, что эта область пространства является плоской и евклидовой. Если бы мы увидели, что между нашими руками есть угол, мы заключили бы, что эта область пространства искривлена и поэтому неевклидова. В этом случае относительное положение наших рук показало бы знак и величину кривизны данной области пространства. В общем случае, путешествие по разным областям пространства может давать разные результаты. Мы даже можем обнаружить, что различные ориентации петлеобразных путешествий вокруг одной и той же точки приводят к разным результатам. Это род эксперимента, который мы могли бы проделать, чтобы определить, геометрия какого рода преобладает в данной области пространства. Мы нуждаемся еще в одном понятии, прежде чем получим возможность вполне оценить свойства искривленного пространства. Геодезической называется путь через пространство, который не отклоняется ни вправо ни влево. Геодезической в плоском пространстве является прямая линия. Значительная часть геометрии Евклида касается свойств фигур (таких, как треугольник и четырехугольник), построенных из отрезков геодезических — прямых линий — на плоскости. В некоторых видах пространств кратчайшим расстоянием между двумя точками является длина геодезической, соединяющей эти точки. На поверхности сферы геодезические проходят по большим кругам. Например, если мы путешествуем вдоль линии определенной долготы (такой, как гринвичский меридиан), то мы следуем по геодезической между двумя положениями с одной и той же долготой. Если две точки имеют разные широту и долготу, как Лондон и Нью-Йорк, кратчайшее расстояние между ними проходит по меньшей дуге большого круга, проходящего через них. Вообще говоря, коммерческие авиалинии проходят по геодезическим, соединяющим пункты вылета и назначения. Настало время сделать шаг от искривленного пространства к искривленному пространству-времени. Этот шаг не столь травмирует, как можно было бы ожидать, поскольку большую часть необходимых понятий можно импортировать из нашего обсуждения искривленного пространства. Чтобы вообразить искривленное пространство-время, мы можем представить себе двумерное пространство с одной пространственной размерностью и одной временной, вложенное в трехмерное пространство, точно так же, как мы представляли себе двумерное пространство. Если пространство-время является плоским, геодезические представляют собой прямые линии на двумерной поверхности. Однако из забавной геометрии пространства-времени следует, что геодезическая, соединяющая две точки, соответствует наибольшему расстоянию между ними (вспомним Кастора и Поллукса). Искривленное двумерное пространство-время можно изобразить в виде изогнутого листа в трехмерном пространстве. Так же как в плоском пространстве-времени, геодезические — которые теперь могут извиваться по пространству в зависимости от его локальной структуры — соответствуют самым длинным интервалам между точками, которые они соединяют. Теперь мы подошли к труднейшему месту всего обсуждения. В этой точке мы соединим вместе все предыдущие концепции. Великая идея, высказанная Эйнштейном в 1915 г., звучала так: масса искривляет пространство. Его величайшим достижением стало обнаружение точной связи между детализированной кривизной пространства-времени и распределением массы. У меня нет возможности представить вам точно эту связь, которая является одной из наиболее элегантных, хотя и сложных связей во всей науке. Однако было бы нехорошо с моей стороны, заставив вас столько потрудиться, чтобы дойти до этого места, бросить вас тут на мели. Поэтому я сделаю две вещи. Во-первых, я дам вам отдаленное представление о форме результата Эйнштейна. Затем я расскажу о некоторых его следствиях. Здесь я должен просить вас вообразить куб со слегка искривленными сторонами, как если бы вы взяли куб, сделанный из резины, и встали на него так, что его края выпучились. В дополнение к этому я должен просить вас представить себе, что этот куб находится в пространстве-времени, а не просто в пространстве. Если быть вполне честным, надо отметить, что представление об обычном пространственном кубе является почти достаточным для передачи сути того, что я хочу сказать, поэтому не стесняйтесь, если вы невольно вернетесь к этому образу. Однако имейте в виду, что на самом деле нам следует разговаривать в терминах пространства-времени, а не в терминах пространства. Вспомним четырехмерный куб, обсуждавшийся нами ранее (рис. 9.4). С этого момента мы будем представлять себе ребра, образующие куб, идущими вдоль геодезических линий области пространства, которую мы рассматриваем. Это значит, что мы должны представлять себе грани немного повернутыми и наклоненными, но таким образом, чтобы они правильно соответствовали друг другу при складывании для образования гиперкуба. Представьте себе, что наш тщательно склеенный гиперкуб посещают массы, находящиеся в его окрестности. Смысл кубов остается тем же самым: содержимое времени-подобных кубов (изображающее историю входов и выходов через поверхность реального ящика) представляет втекание и вытекание массы сквозь различные стенки области, находящейся в ящике, а два пространственно-подобных куба (ящики в начале и в конце рассматриваемого временного периода) представляют полную массу, находящуюся в ящике, в начале и в конце. «Полевые уравнения» Эйнштейна «всего лишь» устанавливают, что повороты и наклоны граней восьми кубов, конструирующих гиперкуб, пропорциональны полной массе внутри каждого из них. Это, по сути, и есть общая теория относительности. Полевое уравнение Эйнштейна просто записать (при использовании достаточно богатого символического языка), но исключительно трудно решить. Тем не менее одно решение было найдено в течение нескольких месяцев после его первого появления в печати. Одним из немногих положительных событий во время Первой мировой войны было то, что служивший в России немецкий математик Карл Шварцшильд (1873-1916) нашел решение для области, лежащей снаружи от массы сферической формы, как, например, космическое пространство вокруг звезды или планеты, и решение внутри сферической однородной массы. Он умер несколько месяцев спустя, освобожденный от военной службы и пораженный редким кожным заболеванием, но термины решение Шварцшильда и радиус Шварцшильда дали ему подлинное бессмертие. Еще одно решение было найдено в 1934 г. Х.П. Робертсоном и Д.Г. Уолкером для пространства-времени всех изотропных, однородных равномерно расширяющихся моделей Вселенной. Давайте вообразим движение от центра однородной Земли в наружное пространство и представим себе форму пространства-времени. Чтобы проделать это, представим себе расположение в пространстве шести точек, связанных с углами восьмигранника (рис. 9.16). Внутри Земли кривизна пространства-времени является полностью «сжатой», в том смысле, что шесть точек восьмигранника лежат ближе друг к другу, чем в пустом пространстве. Это как если бы пространство-время внутри Земли сплющивалось.
Такое поведение является проявлением решения Шварцшильда для уравнения Эйнштейна в случае внутренней области сферической однородной массы. Мы можем представлять себе, что линии свободного падения лежат ближе друг к другу внутри Земли, а четырехмерное пространство-время имеет положительную кривизну — как сфера — с одинаковыми значениями на каждой двумерной плоскости с одной пространственной и одной временной осью координат. Кривизна на каждой плоскости в области с однородной плотностью постоянна, и в некоторой степени мы можем представлять себе ее похожей на кривизну листа резины в области вокруг покоящегося на нем тяжелого шара (рис. 9.17).
Когда множество из шести точек прорывается сквозь поверхность Земли и выходит во внешнее пустое пространство, решение Шварцшильда для внутренней области уступает место решению для области внешней. Теперь геометрия пространства-времени является «приливной», в том смысле, что две точки на линии, перпендикулярной к поверхности, движутся друг от друга вдвое быстрее, чем движутся друг к другу четыре точки, лежащие в плоскости, параллельной поверхности, так, что объем, заключенный между ними, остается постоянным. Мы можем представить себе влияние на пространство как растяжение в одном направлении (вдоль направления, указывающего на вносящую искажение массу) и сплющивание в двух перпендикулярных направлениях. Приливным эффектом без сомнения можно пренебречь: приливный эффект на Земле достаточен для того, чтобы исказить сферическую форму весьма неподатливой Луны всего на 1 км. Приливы в наших океанах как раз и являются проявлением влияния Луны на геометрию пространства-времени у поверхности Земли, с проявляющимся дважды в день вспучиванием геометрии на линии Земля-Луна. Поэтому, когда вы стоите на берегу и созерцаете спад и подъем прилива, вы наблюдаете тень геометрии Шварцшильда, пробегающую по поверхности Земли. Король Канут Великий[47] (994?-1035) не смог удержать геометрию в бухте. Мы можем приписать кривизне численное значение. Радиальная кривизна (кривизна плоскости с одной осью вдоль радиального направления, а другой временной) равна −2 × масса / радиус3, где радиус есть расстояние рассматриваемой точки от центра сферической концентрации массы (звезды или планеты, рис. 9.17). Заметим, что эта кривизна является отрицательной (седлообразной), в точности как на листе резины в области вне зоны, где покоится шар. Каждая из двух плоскостей с одной осью вдоль направления, перпендикулярного радиальному, а другой временной, имеют кривизну, равную масса / радиус3. Эта кривизна положительна, поэтому мы можем представлять себе каждую из этих двумерных поверхностей похожей на поверхность сферы. Эти значения кривизны сохраняют объем 3-куба, поскольку растяжение в одном направлении компенсируется более слабым сжатием в двух перпендикулярных направлениях. Более того, кривизна тем меньше, чем больше мы удаляемся от центра Земли, и на больших расстояниях от Земли пространство-время является плоским. Еще одной чертой геометрии Шварцшильда является замедление хода часов, расположенных вблизи массивного объекта. Значение доли замедления по отношению к ходу часов, находящихся далеко от массивного тела, равно масса / расстояние, где расстояние есть расстояние от центра массивного тела. Если бы мы рассматривали влияние массы Земли на часы, помещенные в самолет, мы должны были бы принять в расчет, что они идут быстрее, чем часы на уровне моря (потому что самолет немного дальше от центра Земли, и его область пространства-времени немного меньше искривлена), но время бежит медленнее из-за того, что самолет находится в движении. Масса Земли мала, поэтому влияние движения коммерческих авиалайнеров мало. Тем не менее в кругосветном путешествии на высоте 10 000 м со скоростью 850 км/час гравитационный эффект ускоряет часы примерно на 0,2 микросекунды, в то время как влияние скорости замедляет их только на 0,05 микросекунды. Проверка общей теории относительности, проводимая таким методом, в реальности принимает в расчет влияние посадки и взлета, так же как изменения скорости самолета во время полета. Почему мы уделили так много внимания геодезическим в пространстве-времени? В пустом пространстве частицы движутся по прямым линиям. Другими словами, они движутся по геодезическим плоского пространства-времени. Это наблюдение подчеркивает важность геометрии при определении путей. Когда пространство-время искажается в присутствии массы — при подходе ближе к звезде, — частицы продолжают двигаться по геодезическим, но эти геодезические искривлены. В действительности кривизна пространства-времени в окрестности массивного тела, подобного звезде, может быть столь велика, что геодезические сворачиваются в спираль. Иными словами, по мере течения времени, планета выглядит движущейся вокруг звезды по почти повторяющимся, очень близким путям, почти по эллипсам. То есть планета движется в пространстве-времени по геодезической, описываемой в пространстве почти замкнутой орбитой. Вдалеке от звезды — скорее как возле Плутона, чем возле Меркурия — пространство искривлено меньше, и планете приходится дольше бороздить пространство-время, прежде чем путь почти замкнется. Другими словами, по удаленным орбитам планеты движутся медленнее, чем по орбитам близким к звезде. На самом деле пути планет не являются совершенными эллипсами: они следуют немного иным путем при каждом новом обороте и для наблюдателя, способного видеть лишь пространство, описывают нечто вроде «розетки» вокруг центральной звезды. Объяснение точной формы подобного розетке пути Меркурия — так называемой прецессии перигелия — было одним из первых успехов общей теории относительности (рис. 9.18).
Мы уничтожили гравитацию. Теперь мы понимаем, что движение планет не является реакцией на силу, называемую тяготением, а просто представляет собой естественное движение тела вдоль геодезической пространства-времени. Иначе говоря, движение есть проявление геометрии. В описании пространства-времени, изложенном выше, существует очень большая проблема: в достаточно малом масштабе геометрии, по-видимому, не существует. Одной из грандиозных проблем современной физики является объединение общей теории относительности и квантовой теории (глава 7) в квантовую теорию гравитации. Несмотря на огромные усилия и несмотря на значительный прогресс, ученые еще не создали объединенной теории. В настоящее время такой теории, как «квантовая теория гравитации», не существует: на ее месте располагается множество умозрений, большая часть которых весьма спорна, выраженных с разными степенями математической изощренности. Однако, когда объединение будет достигнуто, все ожидают, что оно произведет революцию в наших представлениях о пространстве и времени, которая, вероятно, будет более мощной по своему воздействию, чем даже революции, вызванные появлением теории относительности и квантовой теории. Однако, несмотря на туманную природу современных научных представлений о квантовой теории гравитации, имеется несколько свойств, которые, как можно ожидать, она будет иметь. Одно свойство проистекает из того факта, что, вопреки кажимости, мы приняли довольно-таки старомодный взгляд на природу пространства-времени, взгляд, в принципе мало отличающийся от ньютоновского понимания пространства как арены. Конечно, мы сделали описание более изощренным, объединив пространство и время и снабдив получившееся пространство-время неевклидовой геометрией, зависящей от присутствия массы. Но здесь все еще присутствует ощущение, что пространство-время является ареной действия, на которой разыгрываются все события, происходящие в мире. В квантовой теории гравитации это ощущение арены рассеется, а события сами по себе будут определять Вселенную. На самом деле, возможно, нет никакой арены: то, что мы принимаем за Вселенную, есть не более чем огромная сеть взаимосвязанных событий. При таком восприятии уравнение Эйнштейна превращается в утверждение о причинной структуре связей между событиями. Вторым свойством квантовой теории гравитации является то, что в достаточно малом масштабе исчезает само понятие пространства-времени. То есть пространство-время больше нельзя рассматривать как континуум (причинно связанных событий), оно оказывается более похожим на пену (рис. 9.19). Наименьшим возможным пространственным промежутком, разделяющим события, является расстояние, которое мы раньше назвали планковской длиной, а наименьшим возможным промежутком времени между ними является тот, который мы назвали планковским временем.
Планковская длина составляет примерно 10−35 м, что на двадцать порядков меньше диаметра атомного ядра, поэтому неудивительно, что мы, существа чудовищного размера, обладающие очень грубыми возможностями восприятия, ошибочно принимаем пространство-время за континуум. Наименьшая поверхность, способная существовать в пространстве-времени, имеет площадь, близкую, к квадрату планковской длины, а наименьшая трехмерная область, которая может существовать, имеет объем, приблизительно равный кубу планковской длины. В общепринятых единицах планковское время соответствует 10−43 с, поэтому никакие два события не могут располагаться во времени ближе друг к другу. Даже процесс, занимающий миллисекунду, должен состоять из 1040 компонент. Никакие часы не могут тикать быстрее, чем 1043 раз в секунду. Так же как существует абсолютный минимум температуры («абсолютный ноль») в обычной физике, квантовая теория гравитации показывает, что существует также и ее абсолютный максимум, около 1032 К. При этой температуре плавится само пространство-время. Большой Взрыв, ознаменовавший начало Вселенной, был, возможно, не столько драматическим огненным фейерверком, сколько космическими заморозками, которые вморозили пространство и время в последовавшее за ним бытие. Геометрия и все то, из чего для нас образуется этот мир, является вмороженным отпечатком причинности событий. 45. Анимированный стереоскопический образ вращающегося гиперкуба вы найдете на сайте: http://dogfeathers.com/java/hyprcube.html. 46. В настоящее время G = 6,67428·10−11 м3·с−2·кг−1. 47. Король Англии (1016-1035), Дании (1018-1035) и Норвегии (1028-1035) — Прим. пер.
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Разное ≫ Книги ≫ Глава девятая. Пространство-время. Арена действия / Десять великих идей науки. Как устроен наш мир // Питер Эткинз |
|
[time: 10 ms; queries: 7]
2 Мар 2026 13:40:59 GMT+3 |


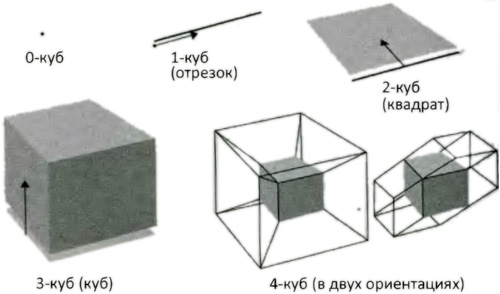

 Рис. 9.4. Теперь мы делаем шаг в следующую размерность и строим гиперкуб из этого набора, содержащего восемь трехмерных кубов (один спрятан прямо под верхним кубом), путем склеивания вместе соседних граней. Нам также нужно склеить две грани, помеченные темными плоскостями и точечной линией. Тем, кто ограничен тремя измерениями, трудно увидеть, как можно выполнить эту операцию, но в четырех измерениях это сделать легко.
Рис. 9.4. Теперь мы делаем шаг в следующую размерность и строим гиперкуб из этого набора, содержащего восемь трехмерных кубов (один спрятан прямо под верхним кубом), путем склеивания вместе соседних граней. Нам также нужно склеить две грани, помеченные темными плоскостями и точечной линией. Тем, кто ограничен тремя измерениями, трудно увидеть, как можно выполнить эту операцию, но в четырех измерениях это сделать легко.
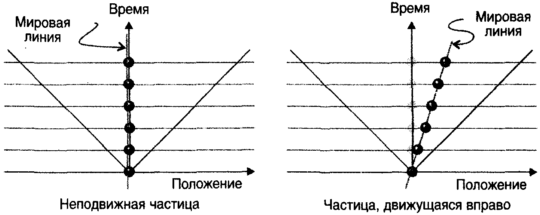
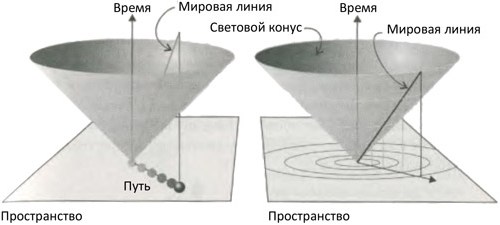
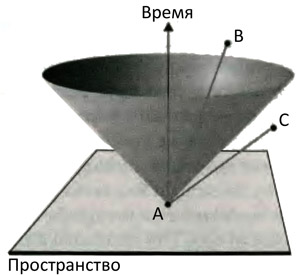
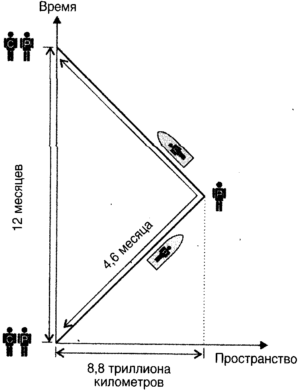
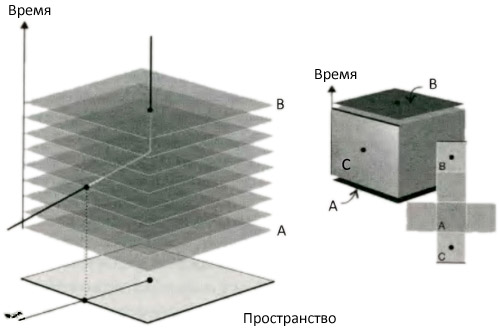
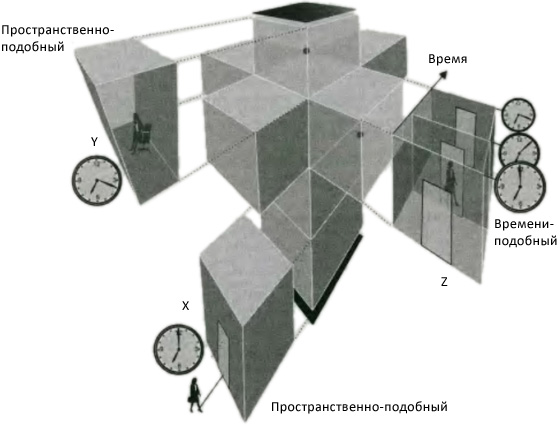
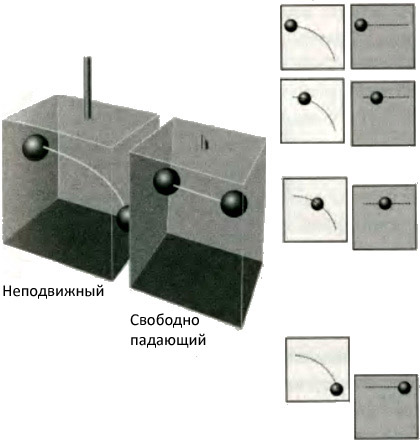
 Рис. 9.12. Локальная геометрия в каждой точке пространства является евклидовой (представлена плоскими кружками, прикрепленными к разным точкам сферы). Однако около тяжелого тела, такого как звезда или планета, пространство искривляется, и локальные евклидовы области изгибаются и скручиваются относительно других локальных областей. Общая теория относительности Эйнштейна показывает, как связать различные локальные системы координат друг с другом.
Рис. 9.12. Локальная геометрия в каждой точке пространства является евклидовой (представлена плоскими кружками, прикрепленными к разным точкам сферы). Однако около тяжелого тела, такого как звезда или планета, пространство искривляется, и локальные евклидовы области изгибаются и скручиваются относительно других локальных областей. Общая теория относительности Эйнштейна показывает, как связать различные локальные системы координат друг с другом.
 Рис. 9.13. Вы стартуете на экваторе и упорно шагаете вверх по гринвичскому меридиану (0° долготы), все время лицом вперед. Я делаю то же самое, но начинаю из точки экватора при 90° западной долготы. Когда мы достигаем полюса, наши носы сталкиваются. Поэтому эти два меридиана не параллельны: в такой геометрии нет параллельных линий. Данная иллюстрация также показывает, как представить себе двумерную поверхность однородной положительной кривизны в виде поверхности трехмерной сферы. Мы говорим, что двумерная поверхность «вложена» в двумерное пространство.
Рис. 9.13. Вы стартуете на экваторе и упорно шагаете вверх по гринвичскому меридиану (0° долготы), все время лицом вперед. Я делаю то же самое, но начинаю из точки экватора при 90° западной долготы. Когда мы достигаем полюса, наши носы сталкиваются. Поэтому эти два меридиана не параллельны: в такой геометрии нет параллельных линий. Данная иллюстрация также показывает, как представить себе двумерную поверхность однородной положительной кривизны в виде поверхности трехмерной сферы. Мы говорим, что двумерная поверхность «вложена» в двумерное пространство.
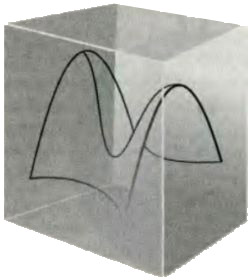
 Рис. 9.15. Кривизну поверхности можно измерить, не прибегая к представлению о вложении ее в пространство более высокой размерности. Наш подход заключается в совершении обхода вокруг точки, в которой измеряется кривизна, и в измерении разницы углов между линиями фиксируемого во время обхода направления. Например, если, как здесь показано, мы стоим на Северном полюсе, а наши руки указывают на юг, и вы идете к экватору по меридиану 90° западной долготы, затем вдоль экватора до гринвичского меридиана и возвращаетесь на Северный полюс, на протяжении всего путешествия держа руку повернутой к югу. Когда вы прибываете, мы обнаруживаем, что ваша рука повернута на 90° относительно моей. Из этого наблюдения мы можем сделать вывод, что кривизна этой поверхности равна 1 / радиус2, где радиус является радиусом сферы.
Рис. 9.15. Кривизну поверхности можно измерить, не прибегая к представлению о вложении ее в пространство более высокой размерности. Наш подход заключается в совершении обхода вокруг точки, в которой измеряется кривизна, и в измерении разницы углов между линиями фиксируемого во время обхода направления. Например, если, как здесь показано, мы стоим на Северном полюсе, а наши руки указывают на юг, и вы идете к экватору по меридиану 90° западной долготы, затем вдоль экватора до гринвичского меридиана и возвращаетесь на Северный полюс, на протяжении всего путешествия держа руку повернутой к югу. Когда вы прибываете, мы обнаруживаем, что ваша рука повернута на 90° относительно моей. Из этого наблюдения мы можем сделать вывод, что кривизна этой поверхности равна 1 / радиус2, где радиус является радиусом сферы.



 Целью этой книги является строгое определение чисел, многочленов и алгебраических дробей и обоснование их свойств, уже известных из школы, а не ознакомление читателя с новыми свойствами. Поэтому читатель не найдет здесь новых для него фактов (за исключением, быть может, некоторых свойств, действительных и комплексных чисел), но узнает, как доказываются вещи, хорошо ему известные, начиная с «дважды два — четыре» и кончая правилами действий с многочленами и алгебраическими дробями. Зато читатель познакомится с рядом общих понятий, играющих в алгебре основную роль.
Целью этой книги является строгое определение чисел, многочленов и алгебраических дробей и обоснование их свойств, уже известных из школы, а не ознакомление читателя с новыми свойствами. Поэтому читатель не найдет здесь новых для него фактов (за исключением, быть может, некоторых свойств, действительных и комплексных чисел), но узнает, как доказываются вещи, хорошо ему известные, начиная с «дважды два — четыре» и кончая правилами действий с многочленами и алгебраическими дробями. Зато читатель познакомится с рядом общих понятий, играющих в алгебре основную роль. Знаменитая Теорема Гёделя о неполноте имеет две версии — синтаксическую (объявленную и доказанную самим Гёделем) и семантическую (чаще всего фигурирующую в популярных рассуждениях о великой Теореме). Семантическая версия утверждает, что какую бы систему формальных доказательств ни придумать, в языке найдутся истинные утверждения, не доказуемые в рамках предложенной системы. Таким образом, семантическая версия исходит из того, что некоторые выражения языка выражают осмысленные утверждения, являющиеся истинными или ложными. Синтаксическая версия не опирается на то, что какие бы то ни было выражения языка имеют какой-то смысл, она смотрит на выражения как на синтаксические конструкции, то есть как на цепочки символов, организованные по определённым правилам.
Знаменитая Теорема Гёделя о неполноте имеет две версии — синтаксическую (объявленную и доказанную самим Гёделем) и семантическую (чаще всего фигурирующую в популярных рассуждениях о великой Теореме). Семантическая версия утверждает, что какую бы систему формальных доказательств ни придумать, в языке найдутся истинные утверждения, не доказуемые в рамках предложенной системы. Таким образом, семантическая версия исходит из того, что некоторые выражения языка выражают осмысленные утверждения, являющиеся истинными или ложными. Синтаксическая версия не опирается на то, что какие бы то ни было выражения языка имеют какой-то смысл, она смотрит на выражения как на синтаксические конструкции, то есть как на цепочки символов, организованные по определённым правилам. Эрвин Рудольф Йозеф Александр Шредингер - австрийский физик-теоретик, лауреат Нобелевской премии по физике. Один из разработчиков квантовой механики и волновой теории материи. В 1945 г. Шредингер пишет книгу "Что такое жизнь с точки зрения физики?", оказавшую существенное влияние на развитие биофизики и молекулярной биологии. В этой книге внимательно рассмотрено несколько важнейших проблем. Основополагающим является вопрос: "Как могут физика и химия объяснить те явления в пространстве и времени, которые имеют место внутри живого организма?" Прочтение этой книги даст не только обширный теоретический материал, но и заставит задуматься над тем, что же в сущности есть жизнь?
Эрвин Рудольф Йозеф Александр Шредингер - австрийский физик-теоретик, лауреат Нобелевской премии по физике. Один из разработчиков квантовой механики и волновой теории материи. В 1945 г. Шредингер пишет книгу "Что такое жизнь с точки зрения физики?", оказавшую существенное влияние на развитие биофизики и молекулярной биологии. В этой книге внимательно рассмотрено несколько важнейших проблем. Основополагающим является вопрос: "Как могут физика и химия объяснить те явления в пространстве и времени, которые имеют место внутри живого организма?" Прочтение этой книги даст не только обширный теоретический материал, но и заставит задуматься над тем, что же в сущности есть жизнь? В отличие от метрической теории алгоритмов, дескриптивная теория не занимается измерением ресурсов (таких как время, объём памяти), затрачиваемых при применении алгоритма к его возможным исходным данным (в другой терминологии — к его входам). Её интересует лишь, возможен алгоритм для решения данной задачи или нет. Начальные понятия дескриптивной теории алгоритмов суть: конструктивный обьект, алгоритм, число шагов алгоритма, вычислимая функция, перечислимое множество, разрешимое множество, сводимость нумераций, главная вычислимая нумерация, вычислимая операция.
В отличие от метрической теории алгоритмов, дескриптивная теория не занимается измерением ресурсов (таких как время, объём памяти), затрачиваемых при применении алгоритма к его возможным исходным данным (в другой терминологии — к его входам). Её интересует лишь, возможен алгоритм для решения данной задачи или нет. Начальные понятия дескриптивной теории алгоритмов суть: конструктивный обьект, алгоритм, число шагов алгоритма, вычислимая функция, перечислимое множество, разрешимое множество, сводимость нумераций, главная вычислимая нумерация, вычислимая операция. Теорема Гёделя, наряду с открытием теории относительности, квантовой механики и ДНК, обычно рассматривается как крупнейшее научное достижение ХХ века. Почему? В чем ее суть? Каково ее значение? Эти вопросы в своей лекции раскрывает Алексей Брониславович Сосинский, математик, профессор Независимого московского университета, офицер Ордена академических пальм Французской Республики, лауреат премии Правительства РФ в области образования 2012 года. В частности, были даны несколько разных ее формулировок, описаны три подхода к ее доказательству (Колмогорова, Чейтина и самого Гёделя), и объяснено ее значение для математики, физики, компьютерной науки и философии.
Теорема Гёделя, наряду с открытием теории относительности, квантовой механики и ДНК, обычно рассматривается как крупнейшее научное достижение ХХ века. Почему? В чем ее суть? Каково ее значение? Эти вопросы в своей лекции раскрывает Алексей Брониславович Сосинский, математик, профессор Независимого московского университета, офицер Ордена академических пальм Французской Республики, лауреат премии Правительства РФ в области образования 2012 года. В частности, были даны несколько разных ее формулировок, описаны три подхода к ее доказательству (Колмогорова, Чейтина и самого Гёделя), и объяснено ее значение для математики, физики, компьютерной науки и философии. Всякая надежда на создание единой математической теории, амбициозного проекта, который был предложен математиком Давидом Гильбертом в 19 веке и продолжил существовать, поддерживаемый многими, в 20 столетии, рухнула. Основы математики были далеко не столь надежными, как того хотел бы Гильберт. А Гëдель своими теоремами ясно продемонстрировал, что любая система аксиом, какой бы обширной она ни была, уязвима для возникновения невосполнимых пробелов. Попытки же восполнить их созданием более полной системы породили бы только бóльшее количество утверждений без доказательств — так что и тут возникнет необходимость в усовершенствовании системы, и так далее до бесконечности. И случилось нечто странное: математики решили не обращать на это внимания. Они посчитали, что неполнота систем не имеет непосредственного влияния на их работу.
Всякая надежда на создание единой математической теории, амбициозного проекта, который был предложен математиком Давидом Гильбертом в 19 веке и продолжил существовать, поддерживаемый многими, в 20 столетии, рухнула. Основы математики были далеко не столь надежными, как того хотел бы Гильберт. А Гëдель своими теоремами ясно продемонстрировал, что любая система аксиом, какой бы обширной она ни была, уязвима для возникновения невосполнимых пробелов. Попытки же восполнить их созданием более полной системы породили бы только бóльшее количество утверждений без доказательств — так что и тут возникнет необходимость в усовершенствовании системы, и так далее до бесконечности. И случилось нечто странное: математики решили не обращать на это внимания. Они посчитали, что неполнота систем не имеет непосредственного влияния на их работу. В научных представлениях о происхождении жизни в последнее десятилетие происходит настоящая революция, и она далеко не завершена. К сожалению, эта информация доступна в основном только на английском языке. Цикл статей, предлагаемый вниманию читателей, отчасти восполнит этот пробел.
В научных представлениях о происхождении жизни в последнее десятилетие происходит настоящая революция, и она далеко не завершена. К сожалению, эта информация доступна в основном только на английском языке. Цикл статей, предлагаемый вниманию читателей, отчасти восполнит этот пробел.