Гипотеза Хорна и соты
Рассмотрим сумму двух эрмитовых матриц A и B. Это снова будет эрмитова матрица. В 1912 году Герман Вейль задался таким вопросом: что можно сказать о ее собственных значениях, если известны собственные значения матриц A и В? Во-первых, ясно, что след A+B будет равен сумме следов исходных матриц; во-вторых, наибольшее собственное значение A+B не превосходит суммы наибольших собственных значений A и B. А какие еще есть ограничения?
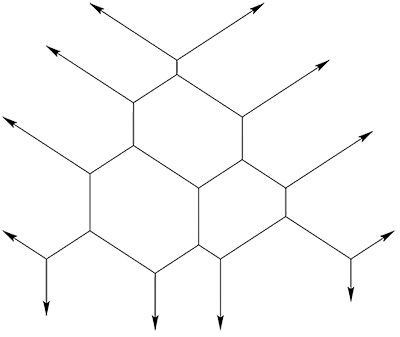
В 1962 году Альфред Хорн выписал ряд неравенств на собственные значения матриц A, B и A+B и сформулировал гипотезу о том, что это полный набор условий. В 1999 году А.А.Клячко свел эту гипотезу к так называемой гипотезе о насыщении, которая вскоре после этого была доказана Алленом Кнутсоном и Терри Тао. Они же предложили описание неравенств Хорна при помощи «сот» — диаграмм вроде той, что изображена на рисунке.
Они также показали, что эти диаграммы — и неравенства Хорна — имеют самое прямое отношение к теории представлений полной линейной группы GL(n), а также к исчислению Шуберта на грассманианах. Они, в частности, позволяют свести задачу о разложении тензорного произведения двух представлений на неприводимые компоненты к чисто комбинаторной задаче подсчета «пазлов» — замощений треугольника элементами мозаики определенного вида.
Курс будет доступен первокурсникам и всем, знающим линейную алгебру в объеме стандартного курса. Знания теории представлений не требуется, все необходимые понятия будут объяснены в ходе лекций.
Смирнов Евгений Юрьевич, кандидат физико-математических наук.
Летняя школа «Современная математика», г. Дубна
24-29 июля 2016 г.
Похожее
-
Иван Оселедец
Возможно ли в линейной алгебре получение новых результатов? Почему в университетах этот курс учат неправильно? Какое матричное разложение является самым важным? Об умножении матрицы на вектор, быстрых алгоритмах и сингулярном разложении. рассказывает доктор физико-математических наук Иван Оселедец.
-
Виктор Викторов
Матрица. Вектор. Сложение векторов и свойства сложения векторов. Геометрическая интерпретация вектора и сложения векторов. Умножение вектора на скаляр и его свойства. Однородная линейная функция вещественных чисел. Геометрическая интерпретация умножения вектора на скаляр. Умножение вектора на матрицу. Зачем нам нужны векторы? Сравнение свойств сложения и умножения вещественных чисел и векторов. Умножение на нулевой вектор. Дистрибутивность. Транспонирование матрицы. Система линейных уравнений. Метод исключения Гаусса-Джордана. Умножение матрицы на матрицу. Обратная матрица. Определитель квадратной матрицы.
-
Алексей Белов
Общая постановка такова. Пусть P(x_1,…,x_n) — некоммутативный многочлен от матриц порядка n. Каким может быть множество его значений? И. Капланский и И. В. Львов поставили вопрос о том, что множество значений полилинейного многочлена есть векторное пространство (в этом случае оно совпадает либо с нулем, либо с пространством всех матриц, либо с пространством бесследовых матриц, либо со скалярными матрицами). Решение проблемы Капланского для матриц второго порядка над квадратично замкнутым полем оказалось весьма нетривиальным и глубоким. Вопросы, связанные с уравнениями в матрицах, помимо прикладного значения имеют отношение к конструкции алгебраически замкнутого тела, к теореме о свободе: если добавить новую некоммутативную переменную и соотношение, где та участвует, то это не приведет к появлению новых соотношений. Имеется ряд глубоких проблем, относящихся к множеству значений слов в группе — в частности, в матрицах второго порядка.
-
Иван Аржанцев
В этом курсе изучается такой замечательный и вполне элементарный объект, как конечномерные коммутативные ассоциативные алгебры над комплексными числами. Здесь достаточно легко доказать первые структурные результаты, но получить полную классификацию едва ли возможно. Мы обсудим различные техники работы с конечномерными алгебрами (максимальные идеалы и локальные алгебры, фильтрации и градуировки, последовательность Гильберта-Самюэля и цоколь) и получим явное описание алгебр малых размерностей. Оказывается, конечномерные алгебры тесно связаны с действиями с открытой орбитой коммутативных групп матриц на аффинных и проективных пространствах. Мы объясним эту связь. В процессе объяснения естественно возникнут такие понятия как экспонента линейного оператора, представление группы и циклический модуль, алгебра Ли и ее универсальная обертывающая.
-
Александр Буфетов, Роман Авдеев
Курс посвящён обобщению понятия вращения евклидова пространства. Оказывается, что с каждым евклидовым пространством можно связать новое пространство, объекты которого называются спинорами. Между исходным пространством и пространством спиноров имеется замечательная связь: всякому вращению исходного пространства можно сопоставить преобразование пространства спиноров, определённое однозначно с точностью до знака. Получаемые таким образом преобразования пространства спиноров образуют группу, называемую спинорной группой.
-
Евгений Смирнов
Группы отражений являются дискретной группой движений пространства постоянной кривизны (сфера, евклидово или гиперболическое пространство), которая порождается множеством отражений. Группы отражений появляются удивительно часто в различных алгебраических задач.
-
Евгений Смирнов
Исчислительная геометрия занимается подсчетом числа геометрических объектов, удовлетворяющих данных условиям. Первой задачей исчислительной геометрии принято считать задачу Аполлония (III в. до н.э.) о числе окружностей, касающихся трех данных окружностей. Как известно всем любителям геометрии, таких окружностей может быть не более восьми, и все их можно построить циркулем и линейкой. С точки зрения проективной геометрии окружности можно рассматривать как коники (кривые второго порядка) на комплексной проективной плоскости, проходящие через две фиксированные бесконечно удаленные точки. Поэтому задача Аполлония есть задача о подсчете числа коник, заданных пятью условиями (прохождение через две точки и касание трех коник). В 1848 году Якоб Штейнер обобщил эту задачу: он предложил найти число коник, касающихся пяти данных коник.
-
Валерий Опойцев
Если что и даёт ясное представление о высшей математике, так это линейная алгебра. Барьер повседневности здесь преодолевается легко и просто. При этом оказывается, что удивительные вещи находятся не в туманной дали, а совсем рядом. В этом курсе: линейные задачи и векторы, линейные преобразования и матрицы, элементарные преобразования, теория определителей, системы уравнений, замена координат, собственные значения и собственные векторы, операторы на комплексной плоскости, спектральная теория, квадратичные формы, сопряжённое пространство, триангуляция Шура, функции от матриц, матричные ряды.
-
Гаянэ Панина
Некоторые комбинаторные схемы дают на выходе интересные выпуклые многогранники, имеющие отношение много к чему из современной математики. Перестановки дают пермутоэдр (перестановочный многогранник). Где он может пригодиться? (Конфигурационное пространство шарнирного многоугольника). Скобочные последовательности дают ассоциэдр (многогранник Сташефа). Зачем он нужен? («Чудесная» компактификация де Кончини–Прочезе.) Вторичный многогранник (secondary polytope Гельфанда–Капранова–Зелевинского) связан с совершенно иной комбинаторной схемой, и при этом обобщает предыдущие примеры.
-
Гаянэ Панина
Как мы узнаем, выпуклые многогранники можно складывать и перемножать между собой. Далее, выпуклые многогранники можно умножать на рациональные числа. И наконец, что несколько неожиданно, для выпуклых многогранников можно определить логарифм и экспоненту. Вооружившись этими умениями, мы построим математически богатый замечательный объект — градуированную алгебру над Q — алгебру многогранников Питера Мак Маллена. С помощью этой алгебры мы докажем теорему об f-векторе выпуклого многогранника. Эта алгебра хорошо «отражается» в теории алгебраических торических многообразий.
Далее >>>
|
|
