Окрошка из кошки

Наталия Гончарук, Юрий Кудряшов

Комментарии: 0

Часть 1

Часть 2

Часть 3

Как приготовить окрошку из кошки? Например, так: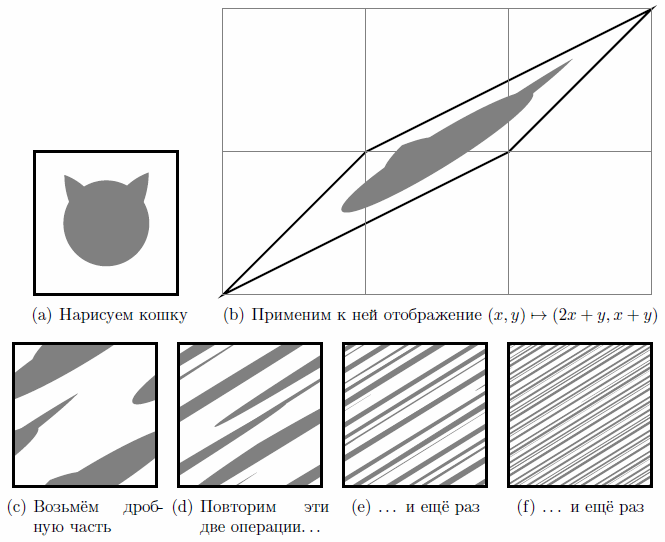

Видно, что с каждой итерацией кошка вытягивается в одном направлении и сжимается в другом. В результате получается «окрошка»: со временем доля кошки в любом маленьком квадратике стремится к одному и тому же числу — доле кошки во всём квадрате!

Если склеить противоположные стороны квадрата, получится тор (поверхность бублика). Если рассматривать отображение (x, y) → (2x+y, x+y) не на квадрате, а на торе, получится непрерывное всюду дифференцируемое отображение, которое тем не менее «размазывает» кошку по тору.

Это отображение — простейший пример диффеоморфизма Аносова. Общее понятие предложил Д. В. Аносов в середине XX века. Грубо говоря, это гладкое отображение, которое растягивает в одних направлениях и сжимает в других.

Про диффеоморфизмы Аносова было сформулировано много гипотез общего характера. Многие из них до сих пор открыты, несмотря на большой интерес, которых они вызывают.

План курса:

На первых двух занятиях мы обсудим различные свойства линейного отображения двумерного тора, заданного формулой (x, y) → (2x+y, x+y): устойчивое и неустойчивое направления, перемешивание, транзитивность, плотность периодических орбит. Кроме того, мы построим марковское разбиение, которое позволяет связать этот диффеоморфизм с цепью Маркова. Эта связь позволяет свести доказательство нетривиальных свойств нашего отображения к стандартным фактам университетского курса теории вероятностей (знание этих фактов от слушателей не требуется).

На третьем занятии мы дадим общее определение диффеоморфизма Аносова и построим пример диффеоморфизма, действующий на более сложном многообразии, чем просто (многомерный) тор.

Последнее занятие будет посвящено открытым вопросам о диффеоморфизмах Аносова и обзору имеющихся результатов.

Гончарук Наталия Борисовна, Кудряшов Юрий Георгиевич

Летняя школа «Современная математика», г. Дубна
28-30 июля 2013 г.

Комментарии: 0

Похожее

Группы Шоттки

Наталия Гончарук, Юрий Кудряшов

Параллельный перенос, поворот, поворотная гомотетия, композиция инверсии и осевой симметрии — частные случаи дробно-линейных отображений комплексной плоскости (в общем случае дробно-линейное отображение плоскости — это отображение, при котором точка z=x+iy переходит в точку (az+b)/(cz+d)). Как известно, инверсия выворачивает круг наизнанку: то, что было внутри, оказывается снаружи, и наоборот. Говорят, что набор дробно-линейных отображений f_1,…,f_g порождает группу Шоттки, если есть набор замкнутых жордановых кривых γ_1,…,γ_g, таких что: 1) Области, ограниченные кривыми γ_j, не пересекаются; 2) Под действием отображения f_j точки внутри γ_{2j-1} оказываются снаружи γ_{2j}, а точки снаружи γ_{2j-1} — внутри γ_{2j}.
О функциях комплексной переменной (вещественный подход к началам комплексного анализа)

Дмитрий Аносов

Из курса математического анализа известно, что если функция имеет n производных, то n-я производная может даже не быть непрерывной; если функция имеет все производные, то она может все-таки не разлагаться в ряд Тейлора: он может расходиться или сходиться к другой функции. Удивительная особенность функций комплексного переменного состоит в том, что одна только дифференцируемость функции во всех точках ее области определения обеспечивает, что функция имеет все производные и разлагается в ряд Тейлора. Этот факт доказывается с использованием интегрального исчисления функций комплексного переменного, хотя по своей форме он относится к дифференциальному исчислению. В лекциях будет предложено другое доказательство того же факта. Оно обходится без специфического комплексного интегрирования и вообще опирается на “вещественные” сведения.
Теорема Римана

Армен Сергеев

Теорема Римана — один из центральных результатов теории функций комплексного переменного. В докладе будет рассказано о месте теоремы в математике и приведена идея ее доказательства, предложенного самим Риманом и основанного на соображениях из гидродинамики.
Новый дискретный вариант комплексного анализа

Сергей Новиков

В совместной работе с И. Дынниковым мы предложили дискретный вариант комплексного анализа, который стартует с решётки правильных треугольников на плоскости. Нам представляется, что этот подход лучше обычного подхода, использующего квадратную решётку.
Теория функций комплексной переменной (ТФКП)

Валерий Опойцев

ТФКП — теория функций комплексной переменной, эквивалент «теории аналитических функций». Математическая дисциплина второго круга образования — не в каждом техническом ВУЗе преподаётся. А жаль. Потому что ТФКП необыкновенно красива и в своей основе достаточно проста. Ибо в римановы пространства и конформные преобразования не обязательно заглядывать без особой надобности. Но и без них в лучах «аналитических функций» многое в нижележащих слоях математики озаряется буквально волшебным светом. Проясняется и упрощается. Вскрываются внутренние механизмы, обнажаются загадки. Поэтому ТФКП, по крайней мере в «данном исполнении», можно рекомендовать для самообразования. Простое изложение может оказаться полезным и при углублённом изучении предмета, когда подробности мешают видеть общую картину.
Удивительный комплексный мир

Дмитрий Аносов

Лекции читает Аносов Дмитрий Викторович, доктор физико-математических наук, профессор, академик РАН. Летняя школа «Современная математика», г. Дубна. 16-18 июля 2002 г.
Двумерная конформная теория поля

Михаил Берштейн

В этой лекции преподаватель магистерской программы «Математическая физика» Сколтеха Михаил Берштейн рассказывает о фазовых переходах и модели Изинга.
Бифуркации векторных полей на плоскости

Наталия Гончарук

В каждой точке плоскости нарисуем вектор. Получилось векторное поле. Будем считать, что по плоскости течёт вода, а векторы — её скорости течения в разных точках. Теперь бросим в воду несколько щепок и нарисуем траектории их движения. Получится фазовый портрет векторного поля. По картинке стало видно, что происходит со щепками: некоторые приближаются к внешнему предельному циклу, от другого цикла все щепки отдаляются. Куда ещё могут накапливаться траектории щепок (теорема Пуанкаре-Бендиксона). Как ещё могут быть устроены фазовые портреты. Также мы обсудим бифуркации: перестройки фазовых портретов, когда векторное поле слегка меняется. Будут свежие результаты и открытые вопросы.
Конструктивная математика

Юрий Кудряшов

Принцип исключенного третьего говорит, что любое утверждение либо истинно, либо ложно. В этом курсе мы откажемся от принципа исключенного третьего. Мы не сможем ни доказывать от противного, ни перебирать случаи. Зато все наши доказательства будут в каком-то смысле конструктивны: доказательство существования объекта всегда можно будет превратить в компьютерную программу, которая строит этот объект. На практике конструктивные доказательства полезнее неконструктивных. Я расскажу о некоторых утверждениях конструктивной математики и о её связи с компьютерными системами доказательств.
Числа, множества, операции

Валерий Опойцев

Комплексные числа: Как возникают и что обеспечивают. Как введение «странных» объектов проливает свет на реальные проблемы. Теория вещественных чисел: Пополнение прямой. Сечения Дедекинда. Зачем это нужно. Системы счисления: Что говорил Плутарх. Позиционная запись чисел. Десятичная система, двоичная. Игра «Ним» на шахматной доске. Двоичный выигрывающий алгоритм. Множества и операции: Наивная теория множеств. Сходство и различия с арифметическими операциями. Булевы структуры. Какими моделями их можно наполнять. Как эти модели перекликаются. Математическая индукция: Аксиома Пеано. Механизм индукции. Примеры.

Далее >>>

∀ x, y, z

Окрошка из кошки

Наталия Гончарук, Юрий Кудряшов

Теги

Похожее