Лекции доктора физико-математических наук, ведущего научного сотрудника сектора математической физики Физического Института им. П.Н. Лебедева РАН, Москва; Directeur de Recherche au CNRS (CNRS — Национальный центр научных исследований) Universite Paris-Sud, Орсэ, Франция Сергея Нечаева, прочитанной 11 апреля 2012 года в рамках проекта «Публичные лекции "Полит.ру"».

Текст лекции

Топология является довольно коварной наукой, потому что хочется всё время апеллировать к кухонным представлениям об узлах, но они оказываются неверными, как правило, и, во всяком случае, не дают возможности решать задачи — как математические, так и физические. Давайте я начну с простого примера с веревкой: скажите, пожалуйста, вот это узел или нет? Хорошо. А вот если я его немножко вот так вот распущу, вот это узел? Ладно, хорошо. Продолжим. Верёвки — это замечательное изобретение человека, так называемое изделие многократного использования, сходное по назначению и устройству с канатами, но используемое именно в тех случаях, когда несколько принижена требовательность к прочности, а также к износостойкости и ещё надежности. С древнейших времён замечено, что веревки по отношению к канатам более гибкие и эластичные. Они великолепно соединяются узлом и практически совсем не пачкают грузы при контакте. Также они используются для подъема и спуска различных грузов, а также отлично подходят для упаковочных, хозяйственных и вспомогательных нужд. Ещё веревки относят к изделиям промышленного текстиля. А вот это узел или нет? Ну, вообще, ни то, ни другое, ни третье не является узлом, потому что узел определён только на замкнутой кривой. Хотя если бы положили на стол вот такую верёвку, вряд ли бы вам пришло в голову назвать её узлом. Тем не менее, это то, что принято называть «тривиальный узел». Чем занимаются математики? они занимаются в основном — не только, но в основном, — классификацией узлов зацепления и построением характеристик, которые зависят только от топологии, то есть не зависят от формы кривой.

Сергей Нечаев. Фото Наташи Четвериковой

Борис Долгин: Так, прошу прошения, прозвучало слово «зацепление», оно не было пояснено.

Сергей Нечаев: Я покажу. Я просто возьму и продену одну петлю в другую, а потом продену ещё. Не очень эстетично, но тем не менее. Вот эта кривая ничем не отличается от той, которая была с самого начала с точки зрения топологии, потому что я непрерывными преобразованиями деформировал исходный узел в этот, не разрывая его. С топологической точки зрения эти кривые одинаковы. Математиков, в первую очередь, интересует вопрос, как строить характеристики, которые зависят только от типа узла, но не от формы, — физиков интересуют другие вопросы, в каком-то смысле более сложные. Давайте представим себе, что мы всё знаем про узлы, и знаем, как их классифицировать. Для того, чтобы понять, какие вопросы интересуют физиков, представьте себе, что у вас есть кусок резины (что это такое? это полимерные цепи, полимерные цепочки, которые сшиты между собой на концах и образуют сетку). Что происходит, если мы деформируем резину, откуда появляется упругость? Если цепи находятся в ненапряжённом состоянии, то у них большое пространство для флуктуаций. Когда мы растягиваем резину в каком-то направлении, пространство для флуктуации цепи уменьшается и, то, как зависит набор допустимых возможностей для флуктуации от степени растяжения, определяет то, насколько резина тянется. Но представьте себе теперь, что помимо таких сшивок, которые возникают на концах из-за того, что это сетка, у нас есть ещё зацепления вот такого рода (топологические). Когда резина не растянута, они не играют никакой роли, но как только мы начинаем растягивать образец, они начинают играть роль дополнительных препятствий уменьшающих конформационный набор состояний цепей в пространстве. Учёт таких явлений – и есть то, что мы хотели бы изучить: с одной стороны, мы должны знать, какое имеется топологическое состояние у цепей, а с другой стороны, мы пытаемся понять, как оно влияет на набор возможных положений цепей в пространстве, когда мы их растягиваем.

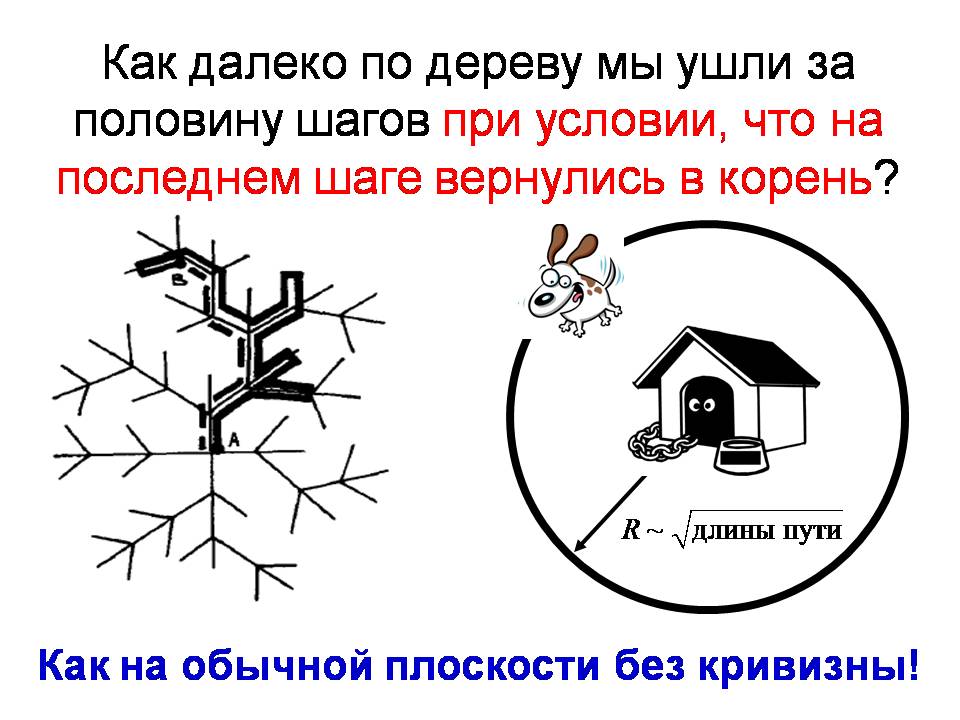
Статистическая топология, или вероятностная топология (она так называется, потому что часто эти задачи формулируются в терминах теории вероятности), является предметом той области, о которой я хотел бы рассказать. Для того, чтобы как-то продвинуться, нужно иметь модель.

Давайте начнём с модели. Представьте себе, что собака бегает вокруг будки. И нас интересует то, как далеко собака отбежит от будки за какое-то количество шагов. Бегает она бегает случайно, кошек нет, и нет никаких костей. Перемещаться собака может как угодно, и если длина цепи, на которую она привязана, – 100 метров, то в среднем она убежит на расстояние 10 метров (корень из 100). Это обычная задача о случайных блужданиях, ограниченных только длиной пути. Давайте теперь поставим другую задачу. Пусть у нас собака бегает в лесу.

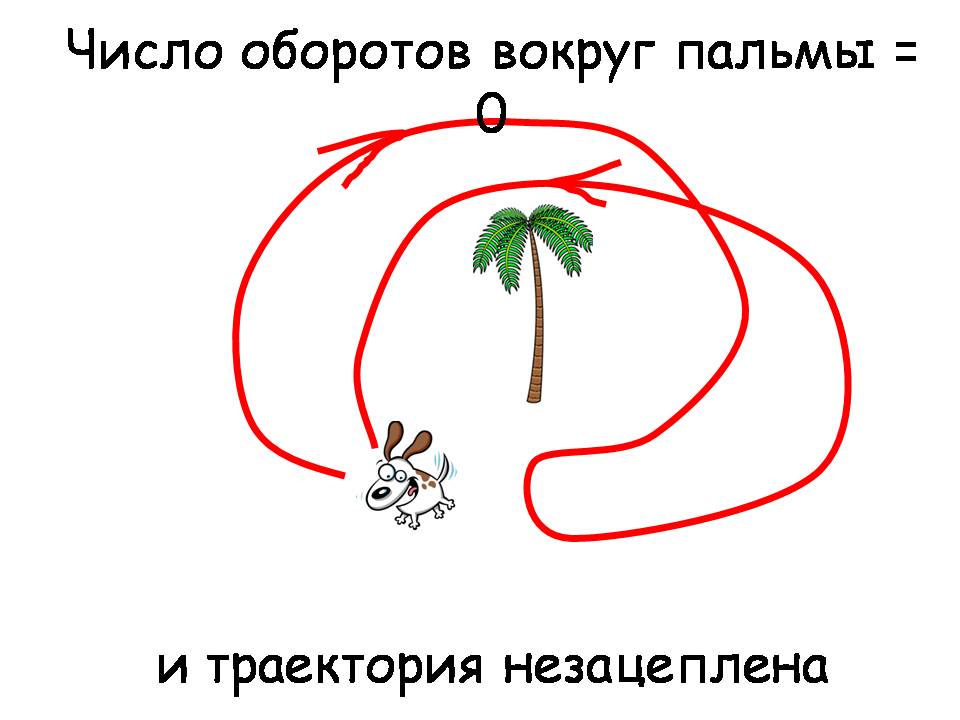
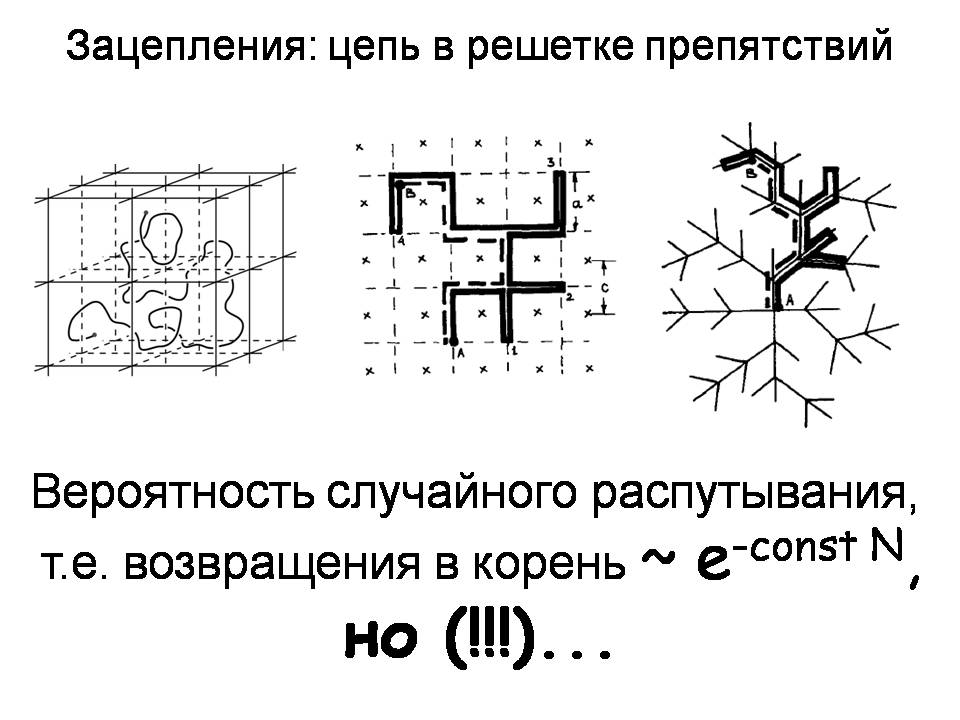
Я только что обнаружил, что на картинке пальмы, а не ёлки, которые я собирался нарисовать. Наверно зима длинная. Вот так собака бегает и возвращается на место. Вот её путь. Вопрос, который мы поставим, звучит так: какова вероятность того, что собака за какое-то количество шагов вернётся в исходную точку, но при этом её цепь не зацепится за эти деревья. Это главная задача, которая объединяет всё то, о чём пойдет речь – топологию и теорию вероятностей. Как обычно, для того, чтобы понять, как её решать, нужно сначала понять, что происходит в простейшем случае, а простейшим случаем является зацепление цепи за одно дерево.

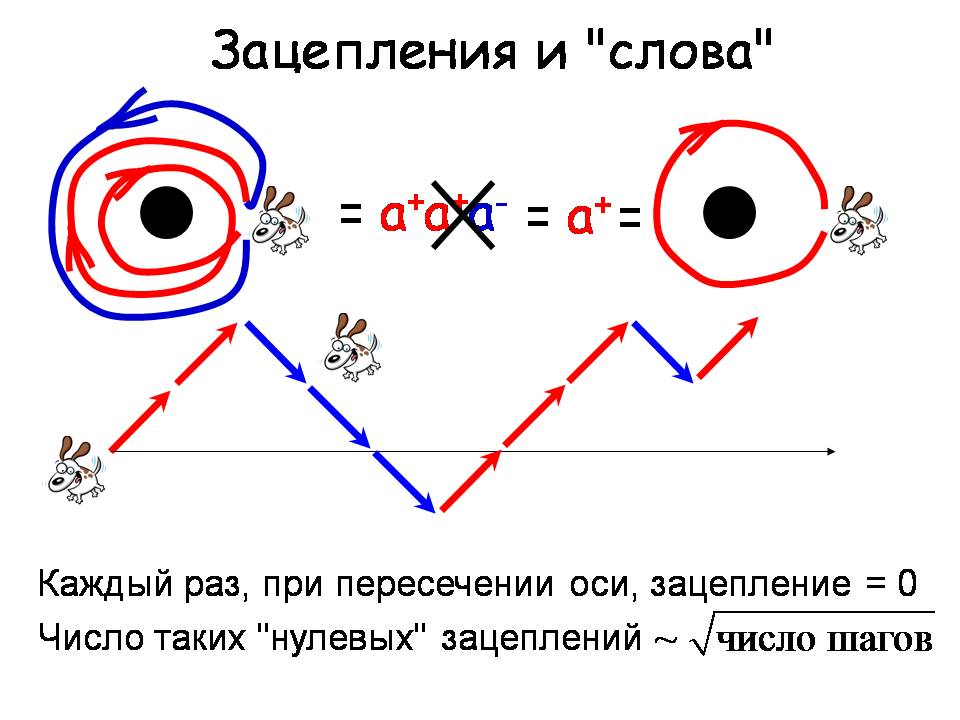
Оказывается, что разница между зацеплением траекторией за одно дерево и за два принципиальная — в то время, как от двух до бесконечности разницы нет, — она, разумеется, есть, но скорее количественная, а не качественная. Как характеризовать, зацепилась ли траектория за дерево или нет? Здесь указано число оборотов, это естественно, потому что собака побежала налево, потом назад направо — и траектория оказалась незацеплена. Давайте посмотрим на такую ситуацию.

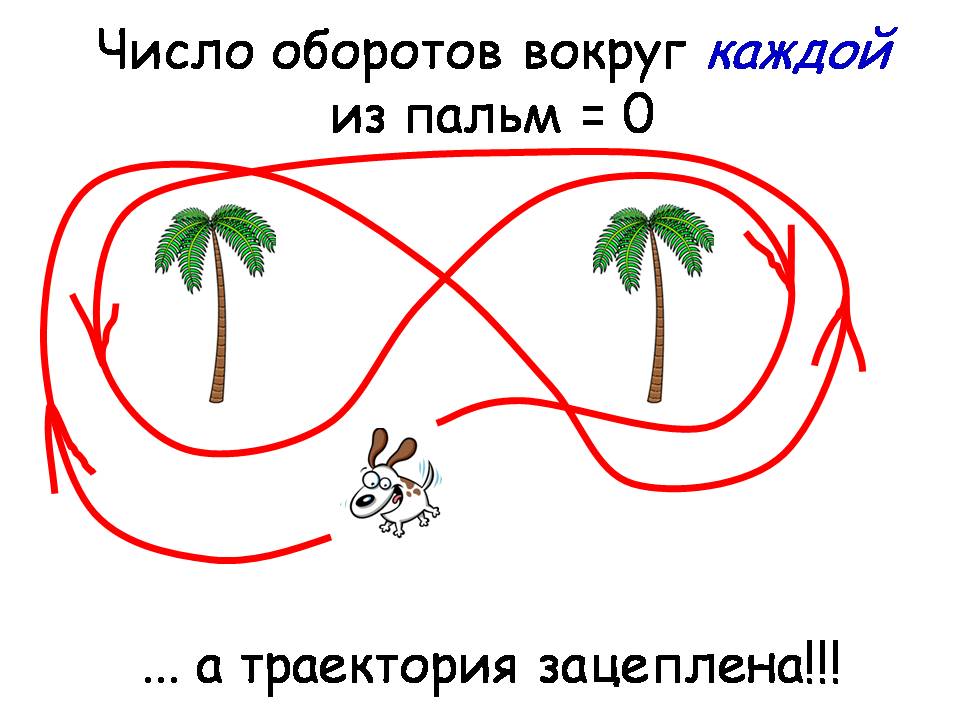
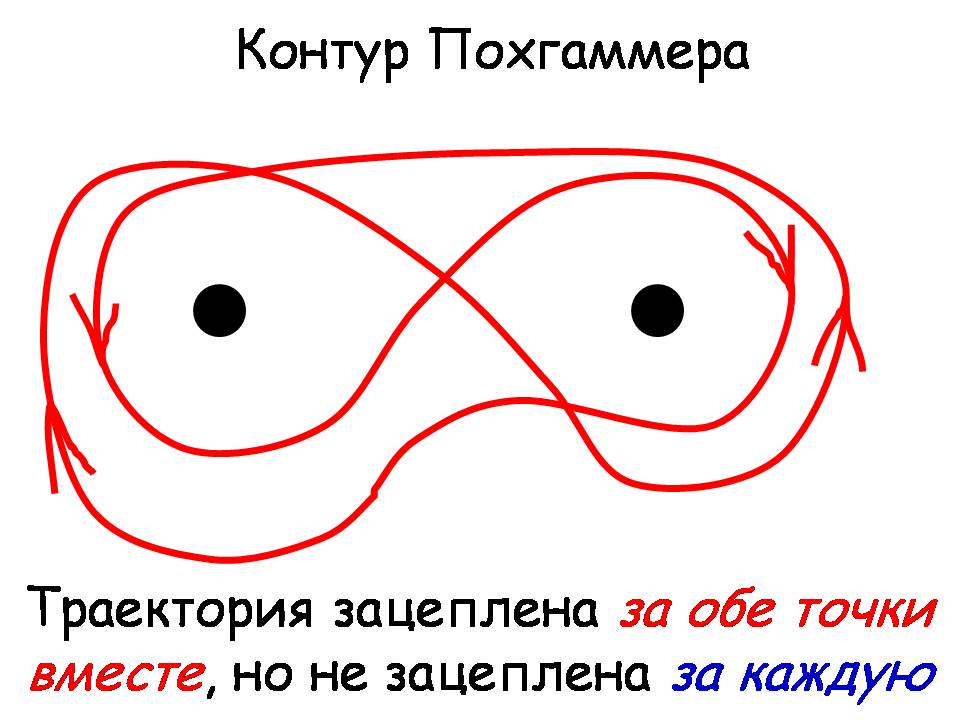
Как раз шаг между предыдущим слайдом и этим является принципиальным – обратите внимание на эту траекторию: допустим, мы начали отсюда: вот собака побежала сюда, по часовой стрелке, потом назад, потом снова назад и вернулась. Я специально нарисовал здесь и здесь стрелочки для того, чтобы показать, что число поворотов, которые она сделала по часовой и простив часовой стрелки вокруг каждого препятствия – ноль. Тем не менее, попробуйте эту траекторию «стащить» с этих особых точек. Не получится! Это пример того, что называется некоммутативность. Теория узлов по своей сути некоммутативна. Как видите, здесь траектория зацеплена, и этот контур имеет название: контур Похгаммера. Устроен он так, что траектория зацеплена за обе особенности (точки) сразу, но не за каждую по отдельности.

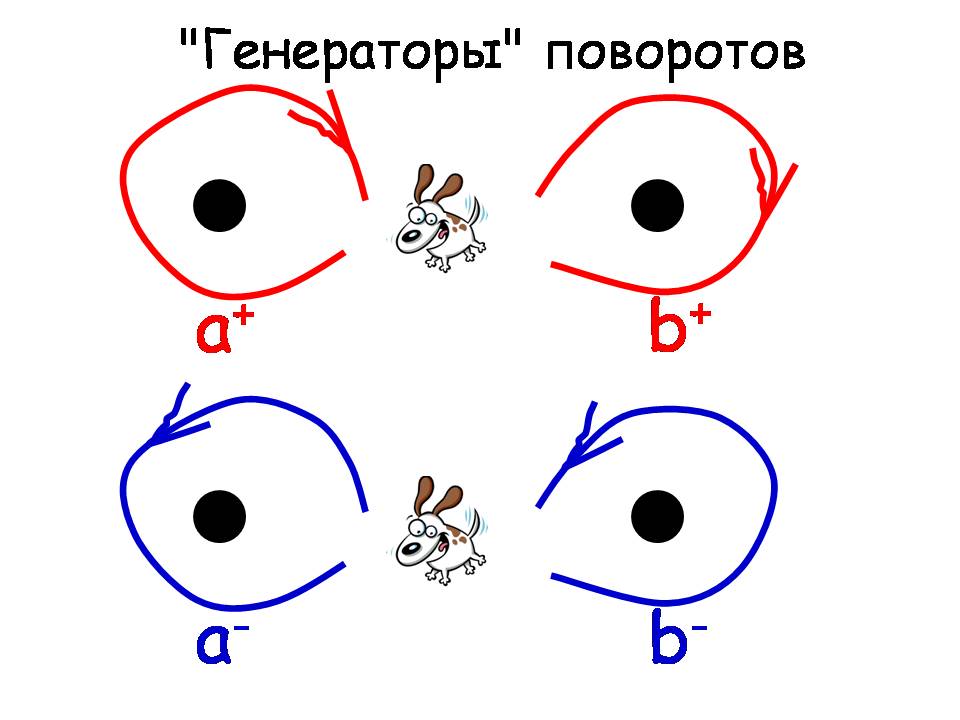
Я хочу показать два простых эксперимента. Фокусами бы я их не назвал. Такой простой демонстрационный эксперимент, мне кажется, будет очень уместен. Смотрите. Я беру нить, и она охватывает стул, дальше я намотаю её вот так — и отпущу. И ясно, что траектория осталась незацепленной. Что было, то и осталось, но вот сделаю ещё раз: вдруг получится что-нибудь другое? Объяснять детали я сейчас не буду. В одном случае я эти две нити держал вместе всё время и синхронно перепутывал и тогда я ничего не могу получить, кроме тривиального зацепления, но в другом случае я одну нить обмотал на один оборот больше, чем другую. Я могу эту веревку зацепить либо за перекладину стула, либо за бесконечно удаленную особенность. Если я покажу вам веревку спрошу: зацеплена она за эту перекладину или нет? В таком положении вы не сможете понять, зацеплена она или нет из-за наличия свободных концов. А вот в следующем эксперименте свободных концов нет. Я сейчас попробую повесить кольцо на цепочку. Вот то же самое: два замкнутых контура, которые между собой не зацеплены. Тем не менее, кольцо весит на цепочке. Если вы сосчитаете, сколько оборотов сделала цепочка вокруг вот этого конца, то получите ноль. Но, тем не менее, зацепление есть. Это типичный пример проявления некоммутативности в топологических задачах.

Давайте пойдём дальше и попробуем сформулировать некоммутативность более чётко в терминах, которые потом помогут решать конкретные задачи, о которых шла речь. У нас есть две особенности, и у нас есть генератор: буква, отвечающая обороту вокруг одной точки, или другая буква, соответствующая обороту вокруг другой точки. Поэтому, имея эту азбуку — я ещё, правда, не сказал, какие правила переставления этих букв, — я могу написать любое слово, идя вдоль траектории.

Скажем, у меня есть путь, который дважды зацеплен и затем пройден в обратном направлении. Я два раза пошёл по красному пути, потом один раз вернулся назад, путь сократился — и получилось вот так.

Совершенно естественная процедура. Я могу это представить в другом виде: стрелочка вверх – это использование буквы «а», а стрелочка вниз – это использование буквы «а-» и тогда расстояние по высоте по горизонтали – это та степень зацепления, которая у нас имеется. Я могу продолжить, и получится так, что если случайным образом я хожу вправо и влево, то время от времени я пересекаю горизонтальную ось и каждый раз, когда я её пересекаю: оказывается, что траектория распутывается. Сосчитать количество пересечений – это всё равно, что решить задачу о случайном блуждании на прямой. И ответ тот же, что и в исходной задаче с собакой: если у меня есть какое-то число шагов, то корень из числа раз я возвращаюсь на горизонтальную линию, и она оказывается распутанной.

Что будет, если у меня есть две особенности? всё то же самое, за одним исключением.

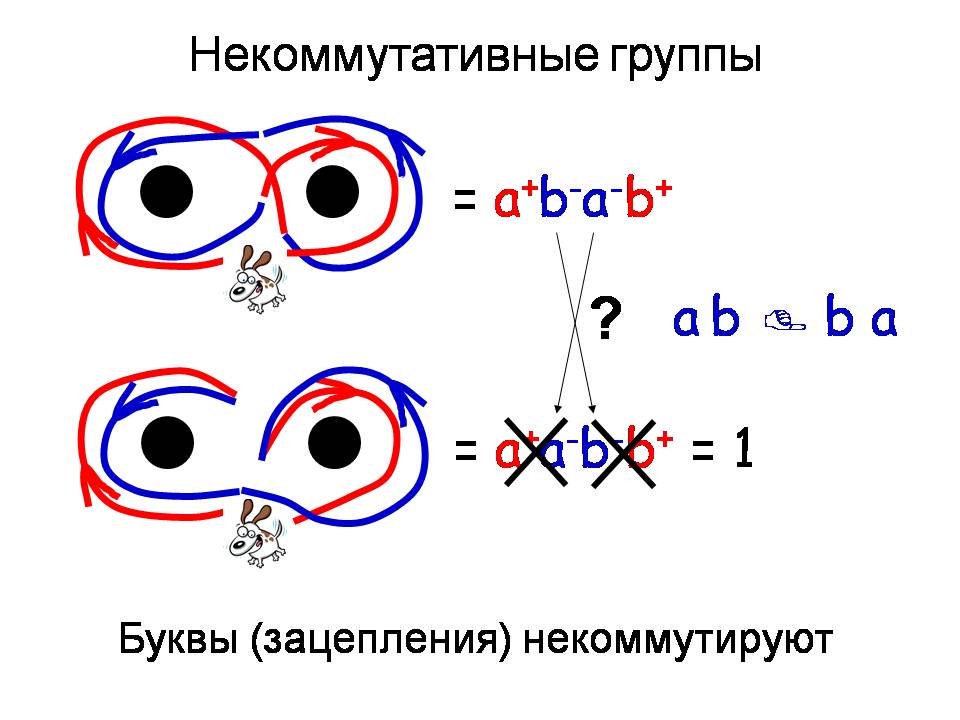
Чем отличается вот эта картинка от нижней? Тем, что я переставил эти буквы. В одном случае я пошёл по красной. Потом я пошёл по синей. А в этом случае я пошёл по красной, потом вернулся, пошёл по синей, потом вернулся. Разница только в последовательности записей, в последовательности букв, но, как вы видите, ситуация принципиальным образом различна, и это как раз то, что математики называют некоммутативностью. Буквы — то есть зацепления, в данном случае, — не коммутируют, я не могу их переставлять. В этом случае, который изображён здесь, всё достаточно просто, поскольку я пошёл по часовой стрелке, потом вернулся, пошёл против часовой стрелки и снова вернулся, в результате я не зацепился. На верхней картинке такого нет.

Давайте суммируем, что у нас есть: у нас есть некоторый граф, решётка, которую мы можем представить себе так: если мы идём по горизонтали, то мы используем букву «а», если мы идём по вертикали, то мы используем букву «b», соответственно, если мы идём вниз, то это обратный шаг и сюда – обратный шаг.

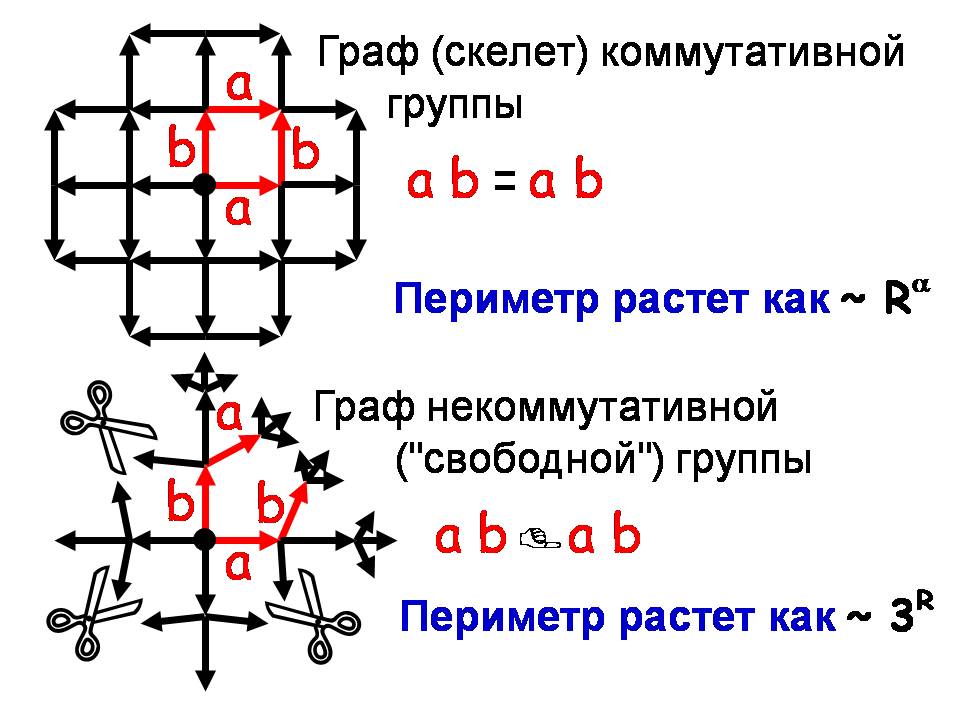
Посмотрите, что получается, если мы посмотрим на граф, то есть на скелет, на эту решётку, то шаги аb приводят в ту же точку, что и bа. Периметр, то есть количество вершин, которое находится на расстоянии от какой-то точки, растёт линейно с ростом радиуса (с удалением от корня дерева). В том случае, когда у нас зацепления не коммутируют, – ситуация другая. Что мы должны сделать? Вот эту точку, которая здесь была одной и той же, мы должны расклеить, как здесь нарисовано.

И это мы должны сделать везде, в любой вершине. В результате мы получим, что вместо решётки, где у нас были циклы, граф, который представляет собой дерево. Теперь периметр, количество вершин, находящихся на каком-то удалении от корня, растёт не как степень, а как экспонента. Это принципиальная разница, между тем, что происходит в нашем обычном евклидовом пространстве и в пространстве, скелет которого является свободной группой (без циклов).

Давайте я покажу вам ещё один опыт. Это тот же самый граф, который был изображён, просто показано, как он строился.

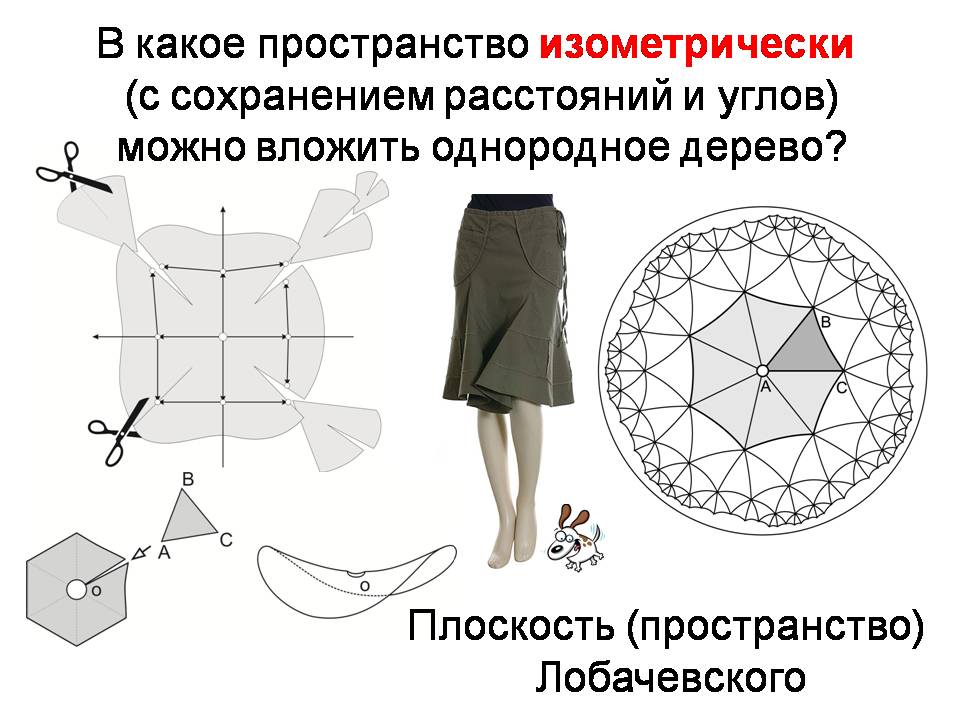
Я взял кусок бумаги и разрезал его по радиусу. Теперь я раздвинул края и вставил туда сектор. Вклеил. Но я это уже сделал дома. Поэтому получился вот такой чипс. Этот чипс не может быть уложен в обычное пространство — в плоскость в данном случае: он будет топорщиться, потому что его периметр растёт быстрее, чем это диктуется правилами роста поверхности в обычном пространстве. Сейчас я найду лист. Лист салата. Мы привыкли к тому, что он так выглядит, но в действительности он объект неевклидовой геометрии. Почему он такой волнистый? Он похож на юбку Годе. Я вернусь к этому слайду.

Это объект, связанный из материи, это не я вязал, это вязал замечательный французский математик Этьен Жис. Во всяком случае, я из взял эту картинку из его статьи. Возвращаясь к листу салата, можно предположить, что клетки, которые находятся на периферии, растут быстрее из-за того, что они больше граничат со свободным пространством. И кажется, что у них есть больше возможности для роста, чем у тех клеток, которые находятся внутри листа. Поэтому получается так, что они растут быстрее, периметр общий растёт быстрее, чем это нужно для того, чтобы лист был плоским, и его можно было бы вложить в плоскость. Это устроено так же, как изображено на рисунке. Схематично то, что я сделал с чипсом, — вот эта картинка? Я взял шестигранник, разрезал, вставил треугольник — и получился правильный семиугольник. Как он выглядит я только что показал на примере из живой природы.

Какое это имеет отношение к тому, о чём шла речь до этого? Вот какое: давайте посмотрим на два рисунка — картинки кажутся сложными, но ничего особенного нет.

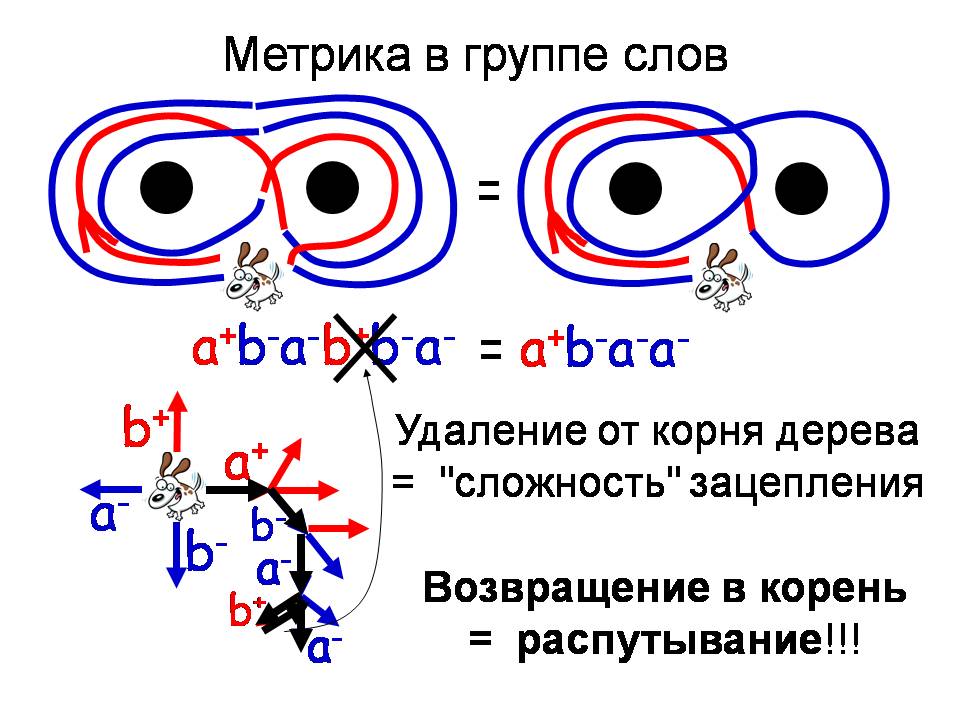
Просто несколько раз я последовательно обходил сначала одну, а потом другую точку. А здесь я упростил эту петлю, которая состоит из куска красной и куска синей. Я её сократил. Но что мы знаем теперь? Мы знаем, что это зацепление может быть изображено в виде букв, слова, которое кодирует последовательность шагов, оборотов. Что я могу сделать? Я могу сократить и получить то, что изображено справа. Но теперь я знаю, что пространство, в котором я могу нарисовать или изобразить это слово, — это дерево, где все вершины расклеены. В результате шаг, а+, он изображен чёрным, потом, следующий. А вот это я сократил, потому что я пошёл назад и пришёл в эту точку. В результате – главное, на что нужно обратить внимание: Я могу связать сложность зацепления с расстоянием по дереву, то есть я могу связать метрику со сложностью зацепления. Возвращение — это распутывание! Теперь понятно, как решать задачу с собакой в лесу. У меня есть случайные шаги, и они происходят на дереве, есть случайные повороты в разной последовательности, для того, чтобы решить задачу, — я должен решить задачу о вывислении вероятности возвращения в корень. Такую задачу решить несложно и она была решена. Я об этом скажу дальше.

Еще несколько образов. Я говорил о том, что салат не помещается в плоскости. А как можно нарисовать дерево так, чтобы оно поместилось на плоскости? Нужно пропорционально удалению от корня уменьшать длину шага. Что здесь изображено?

Здесь изображён пунктирной линией этот же граф (дерево). Вот линии, которые выходят из корня, следующие короче, и каждый раз следующие ещё короче, и каждый раз они уменьшаются в какое-то количество раз. В результате, таким образом, получается, что я могу изобразить граф. Это называется дерево Кейли. Выглядит он примерно вот так. Вот эта конструкция построена таким образом: взят треугольник, но у него сумма углов меньше 180 градусов, поэтому одна сторона у него вогнута. А дальше я строю просто замощение плоскости, отражая треугольники относительно своих сторон. Точно так же, как на плоскости, мы бы вязли кирпич и дальше последовательно брали бы и замащивали поверхность такими прямоугольниками. Мы здесь делаем то же самое, но так как у треугольника одна из сторон вогнута, получается так, что мы приходим к какому-то пределу, и он похож на то, что изображал Эшер, — он это рисовал так

и это один из образов плоскости Лобачевского в интерпретации Мориса Эшера.

И последний слайд на эту тему.

Два изображения: я нашёл в интернете картинку коралла (слева), а справа – картинка, построенная с помощью соображений, которые были частично изложены, на Математике. Мне кажется, что они похожи, во всяком случае, хочется в это верить. Математика и геометрия, которые стоят за этим, похожи на то, что люди знают под названием «филлотаксис». Может быть, я скажу об этом позже, отвечая на вопросы. С этим мы закончим — и вернёмся к исходной задаче о зацеплениях на цепочке, но теперь уже не за две особенности, а за целую решётку. Мы подготовлены и знаем, как ее решать.

Для того чтобы решить такую задачу:

Мы вышли из точки А и как-то блуждали, оказались здесь и траектория не зацеплена за ребра решетки. Для этого, как мы теперь понимаем, нужно вычислить вероятность того, что мы случайно ходим по дереву и вернулись в корень в конце пути. Это очень редкое событие. Понятно, что мы ходим одинаково по каждой ветке, и от корня мы можем уйти по трём путям, а вот вернуться назад можем только по одному. У нас есть поле, которое «тащит» нас от начальной точки. Вероятность того, что мы вернёмся назад, экспоненциально мала. Тут самое главное. Давайте поставим такую задачу — на основе этого слайда всё дальнейшее и построено.

Я на нём остановлюсь подробнее. Пусть мы вернулись на последнем шаге в исходную точку. Как далеко мы ушли за половину шагов? Казалось бы, что ничего особенно не меняется, но самое интересное то, что оказывается, что в результате того, что мы наложили дополнительное условие, что мы на последнем шаге обязательно вернулись в начало, мы не уйдем далеко по дереву! Мы уйдём так же, как и плоскостном случае. Это удивительная вещь. Это достаточно легко сосчитать. Но вот это обстоятельство играет принципиальную роль в укладке, о которой пойдёт речь, которую обнаружили в ДНК.

Я ещё раз сформулирую утверждение: если мы просто ходим по дереву, за какое-то количество шагов мы уходим далеко и редко возвращаемся, но если мы хотим вернуться на последнем шаге, то мы уйдём так же, как, если бы мы ходили не по дереву, а по обычной плоскости. По-другому можно это сформулировать так, что условие возвращения в начальную точку убивает кривизну. Это то, что было сделано на моделях.

Какое это отношение имеет к узлам и ДНК? Давайте рассмотрим то, что называют диаграмма узла.

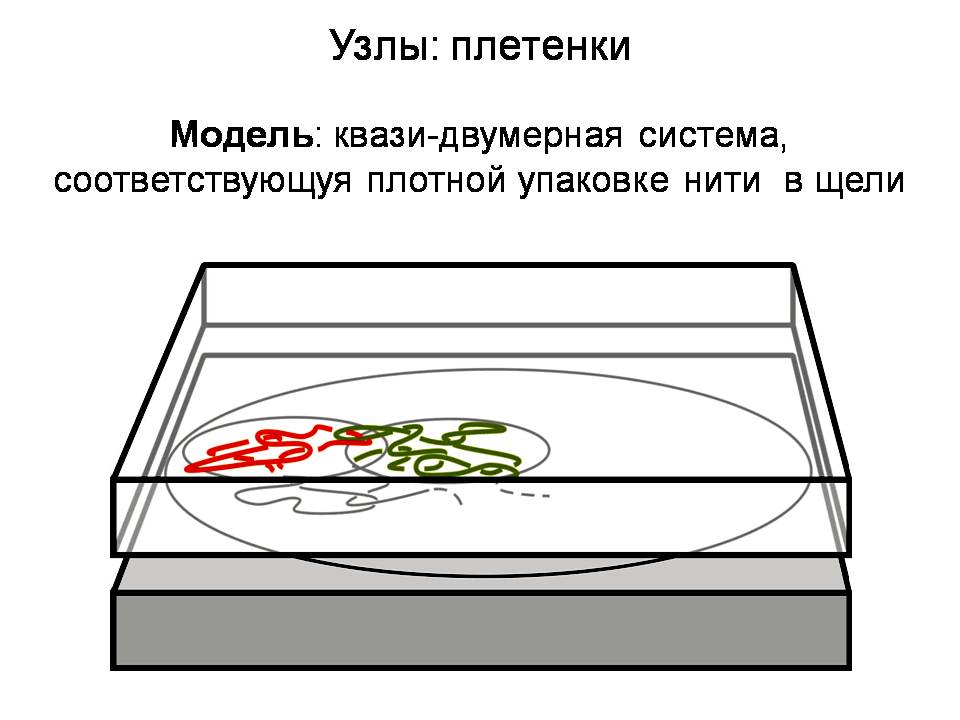
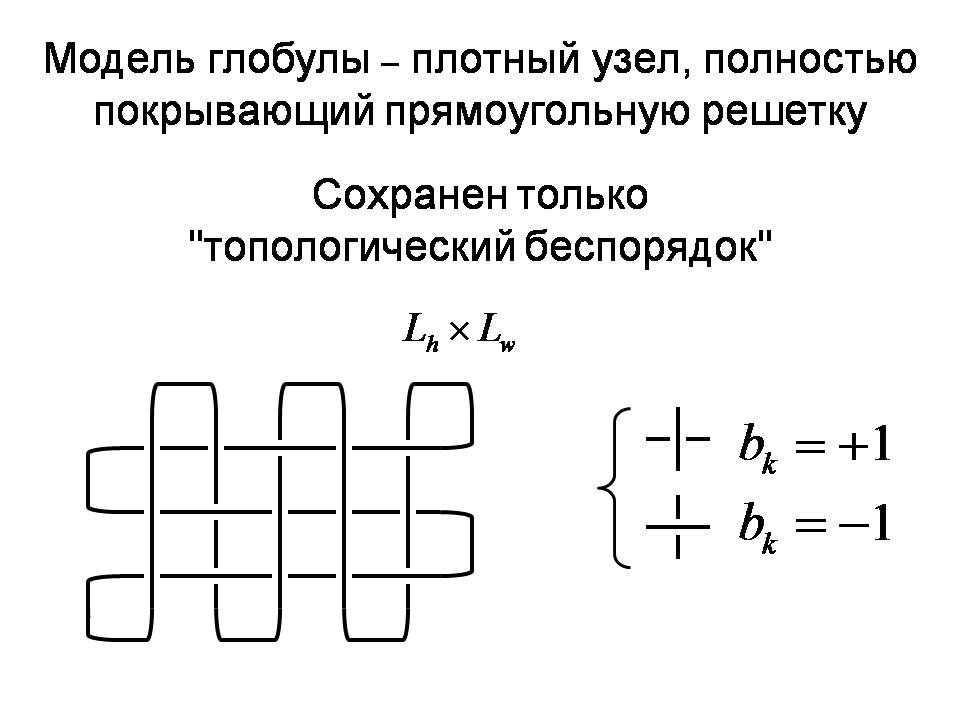
Это плотный узел. Можно себе представлять так, что вы взяли плоскую щель и в ней очень плотно уложили нить. Это плотный узел. Единственная степень свободы, которая тут есть, это такая: кто-то проходит сверху, а кто-то снизу. И понятно, что проход сверху или снизу и определяет, запутана траектория или нет. Какая будет у неё топология. Переменную, которая характеризует прошла нить «сверху» или «снизу», естественно назвать топологическим беспорядком. Мы с какой-то вероятностью выбираем «верхнее» или «нижнее» пересечение и смотрим, что будет с узлом.

Давайте теперь сделаем такую же вещь, как я вам показал раньше на слайде про зацепление.

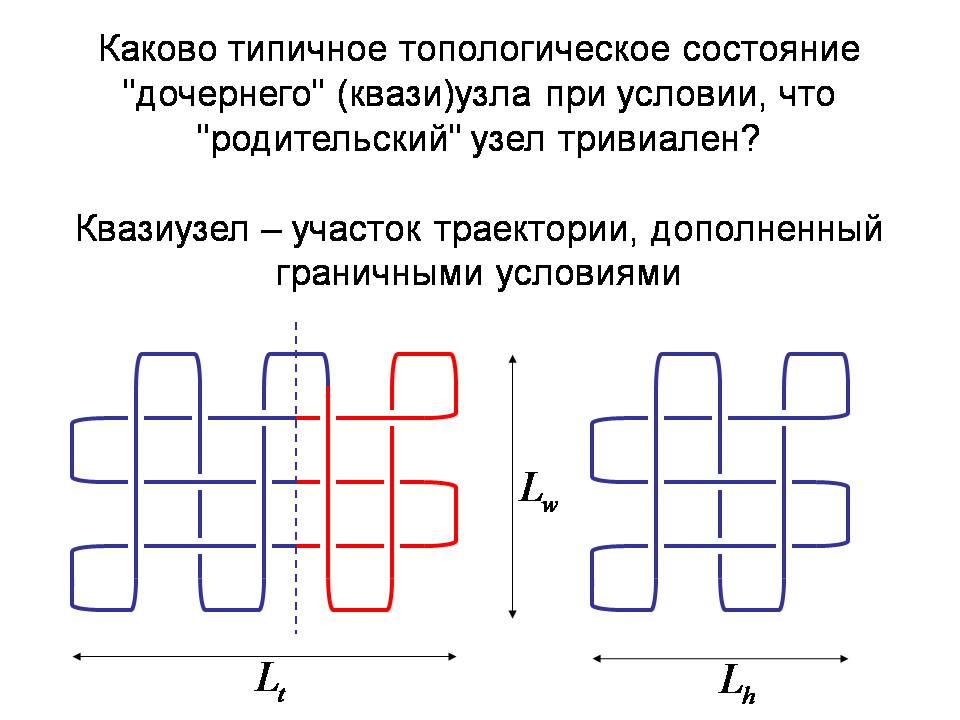
Внимание! Мы знаем, что вся плетёнка — это вот такой тривиальный узел, то есть узел, который распутывается.

Сделаем такую вещь: отрежем часть узла и замкнём то, что осталось, как изображено здесь. Спрашивается: помнит ли кусок, который остался, о том, что он был частью тривиального узла, то есть петли, которая не имела узлов? Это абсолютно такой же вопрос, как вопрос, который мы себе задавали до этого. Если мы вернёмся в исходную точку, зная, что вся траектория не зацеплена, как зацеплена половина траектории? Тут – то же самое, но сформулированное в других терминах, так как здесь речь идёт об узлах. Ответ такой: каждый кусок помнит очень хорошо то, что он является частью тривиального узла! Если бы мы просто поинтересовались, какая сложность у случайно запутанной плетенки, то мы получим ответ, что она очень сильно запутана. Но если мы поставим вопрос об условном распределении: а именно, мы знаем, что целый (родительский) узел – тривиальный, мы отрезали от него любую часть, замкнули и посмотрели на остаток, то оказывается, что любой кусок, какой бы мы ни взяли, всегда помнит о том, что он родительский узел тривиальный!

Давайте теперь думать, как можно в пространстве уложить нить, так, чтобы теперь ее связать тополорию с пространственной укладкой. До этого речь шла только о топологии, о ней мы знаем, что любой кусок не заузлен или слабо заузлен. Как можно уложить в пространстве полимерную цепочку, нить, так, чтобы какой бы кусок от неё мы бы ни взяли, на нём было бы мало узлов? Я вам покажу ответ, как это можно сделать, а потом кое-что постараюсь объяснить. Давайте возьмём кусок длинной цепочки и сделаем на нём маленькие складки. Это изображено на слайде.

Теперь возьмём и сделаем складки из складок. Получим более толстую, более короткую цепочку. Потом проделаем следующий шаг – сделаем складки из складок, состоящих из складок. И так далее. То, что получится, окажется структурой, которая имеет складки на всех масштабах, начиная с некоторого минимального. Вот это её изображение, которое взято из работ, о которых я расскажу. Эта картинка – численный эксперимент, а не просто рисунок, сделанный группой биофизиков и генетиков из MIT-Гарварда, которая занималась укладкой ДНК в хромосоме.

На что надо обратить внимание: то, что я сказал, – это некоторый способ уложить цепочку, но никто не сказал, что если подождать достаточно большое время, то именно такая конфигурация сохранится навсегда, — может быть, она просто является кинетически запертой, и это означает, что пройдёт большое время — и она развалится? Так вот – нет. Такая иерархическая укладка – единственная возможность иметь незаузленную цепочку на всех масштабах. Никаких других не существует. Во всяком случае, мы их не знаем. Это похоже на то, что стоит на столе. Это так называемый Гамильтонов путь в трёхмерном пространстве, вот он. Он устроен именно так, как устроена вот эта кривая Пеано. Посмотрите, как она выглядит. Она имеет складки маленького масштаба, складки маленького масштаба укладываются в складки большого масштаба, и так далее. Я могу взять большой блок и приставить к нему такой же и получить следующий иерархический уровень.

В качестве бонуса коллеги мне принесли этот агрегат, представляющий равновесную глобулу. Здесь семь метров и здесь семь. Это обычная глобула, которая получается из полимерной цепочки, и поместили ли бы ее в такие условия, когда она хочет образовать конденсат, то есть когда взаимодействие между мономерами сильнее, чем между цепочкой и растворителем. Из-за того, что есть свободные концы, она, конденсируясь, пронижет себя петлями, и превратится в такую. Если бы с самого начала мы взяли не разомкнутую, а замкнутую цепочку без узлов и поместили бы ее в условия, в которых ей хочется образовать компактное состояние, то мы бы получили эту кривую Пеано, — и, как вы видите, разница принципиальная. Почему это важно? Почему такая укладка важна?

Это видно даже здесь. Вы посмотрите: она очень мягкая. Достаточно её потянуть чуть-чуть — она прекрасно вытягивается. Она обладает удивительными свойствами упругости. Кроме того попробуйте вытащить участок нити из этой структуры. Я не буду её портить, но вы сами видите, что из-за того, что она сложена в складки и не перепутана, из-за этого вытащить кусок очень легко. Это означает, что для транскрипции очень легко вытаскивать достаточно длинные участки этой цепочки — и потом быстро убирать их назад. Если вы попытаетесь из обычной глобулы вытащить петлю – вам придётся побеспокоить практически все мономеры, потому что она зацеплена очень сильно, если вы вытаскиваете петлю из складчатой глобулы, то это происходит локально. Ответ: надо иметь такую складчатую глобулу. В чём разница? Разница в том, что изображено здесь.

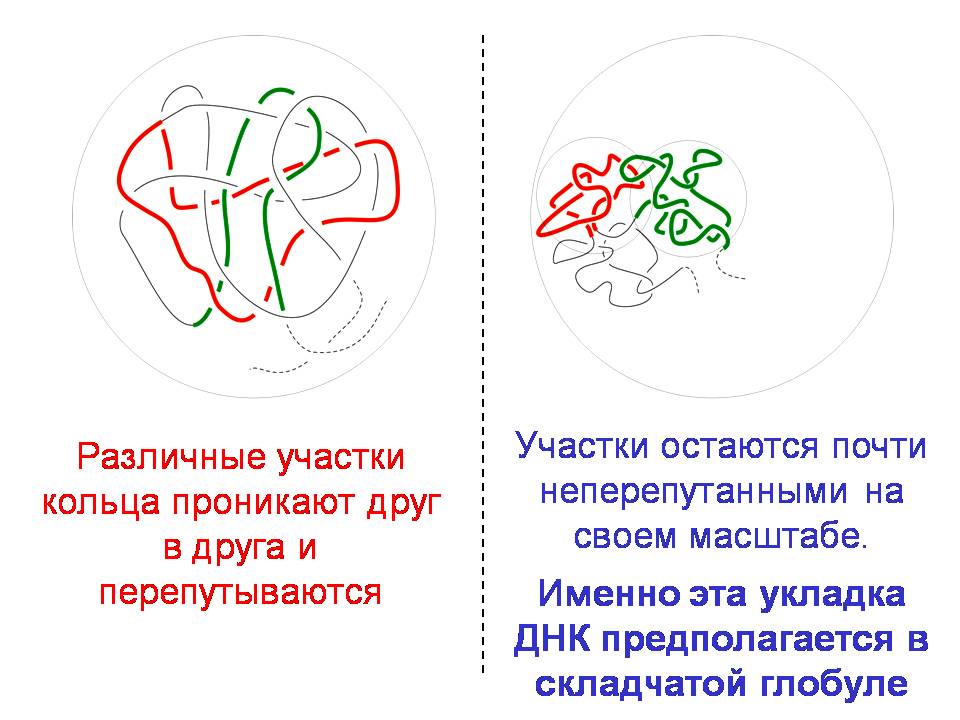
Эта пара имеет разные названия. Это называется кривая Пеано. А вот это то, что люди знали раньше – траектория, которая перепутана на всех масштабах. Разница, как видите, в том, что в случае складчатой глобулы различные участки кольца перепутываются, здесь не перепутываются, и предполагается, что именно это реализуется.

Теперь предпоследний слайд, который объясняет всё то, что сделали, — замечательную, удивительно сложную работу, которая в 2009 году была сделана в группе, в которой принимал участие Леонид Мирный. Он заведует биофизической лабораторией в MIT. Главным, как я понимаю, действующим лицом – экспериментатором, который является одним из основателей этого метода, который называется Hi-C, является американец Йоб Деккер (Job Dekker) из Гарварда.

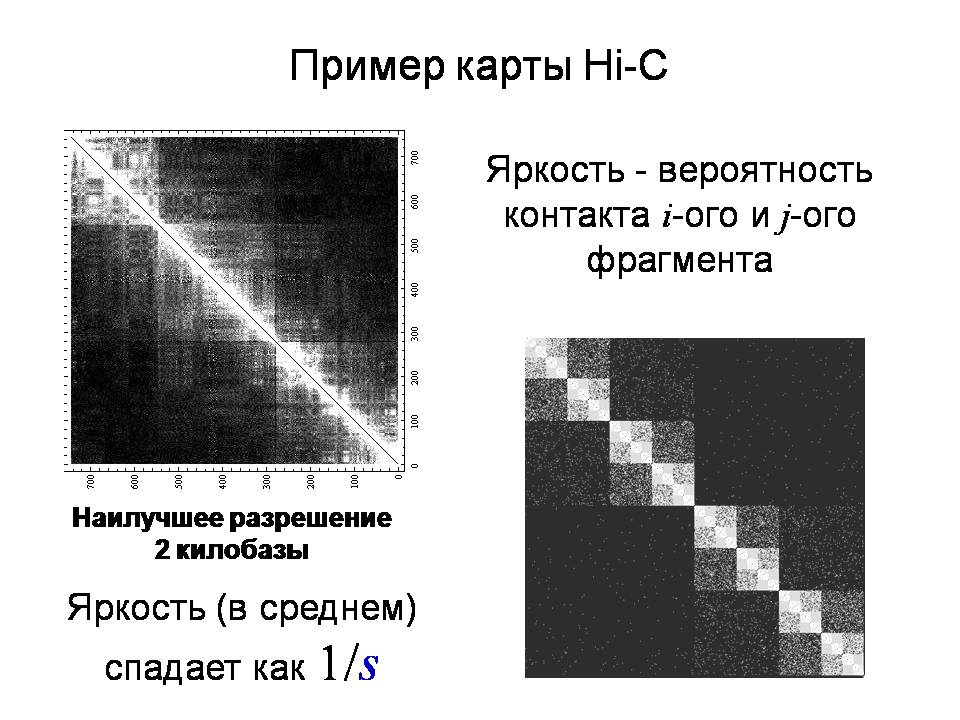
У нас есть гипотеза, как уложена цепь, полученная из топологических представлений. Хотелось бы проверить, правда ли то, что можно придумать какой-либо эксперимент, в котором можно увидеть эту укладку непосредственно? Оказывается, что такой эксперимент может быть осуществлён. Что вычислялось и делалось?

Брался «суп», который представлял собой ансамбль разных молекул ДНК, но с одинаковой последовательностью. Карта, которая здесь изображена, говорит вот о чём. Мы берём ДНК в хромосоме, фиксируем её и в результате мы имеем такую ситуацию, что какие-то два удалённых по цепи участка оказываются рядом в пространстве. Мы замораживаем такое состояние, а потом отрезаем всё то, что находится вокруг. Оставляем только такие сшивки. Мы знаем, какие именно фрагменты ДНК находятся в контакте, кроме того, мы знаем, как далеко они находятся друг от друга вдоль цепи. Таким образом, если в «супе» мы знаем количество таких нарезанных фрагментов, то мы знаем вероятность того, что два удалённых на какое-то расстояние вдоль цепи фрагмента, находятся рядом в пространстве.

Ещё раз. Имеются два фрагмента, которые находятся по цепи на каком-то расстоянии, когда они находятся в пространстве рядом, мы их отрезаем и фиксируем их количество. Из-за того, что мы помним на каком расстоянии они были, мы можем связать вероятность такого контакта с длиной между ними по цепи. Интенсивность цвета на карте — это количество фрагментов, которые находятся в контакте. На пересечении столбца и строки стоит вероятность контакта i-го и j-го фрагментов, поэтому удаление от диагонали есть не что иное, как просто расстояние между фрагментами по цепи. Посмотрите, если мы находимся рядом с диагональю, то i и j — практически одно и то же и фрагменты расположены рядом по цепи. Поэтому чем дальше мы ушли от диагонали, тем больше расстояние между фрагментами, а интенсивность цвета это то, сколько имеется таких фрагментов. Если мы её правильно отнормируем, то получим вероятность контакта. То, что определили американские биофизики – это то, как спадает с удалением от диагонали сигнал, и они увидели, что этот сигнал спадает, как здесь изображено, как 1/S. Это точно соответствует тем предсказаниям, которые могут быть получены исходя из вероятности того, что два конца находятся рядом именно в конфигурации складчатой глобулы, и не в какой иной.

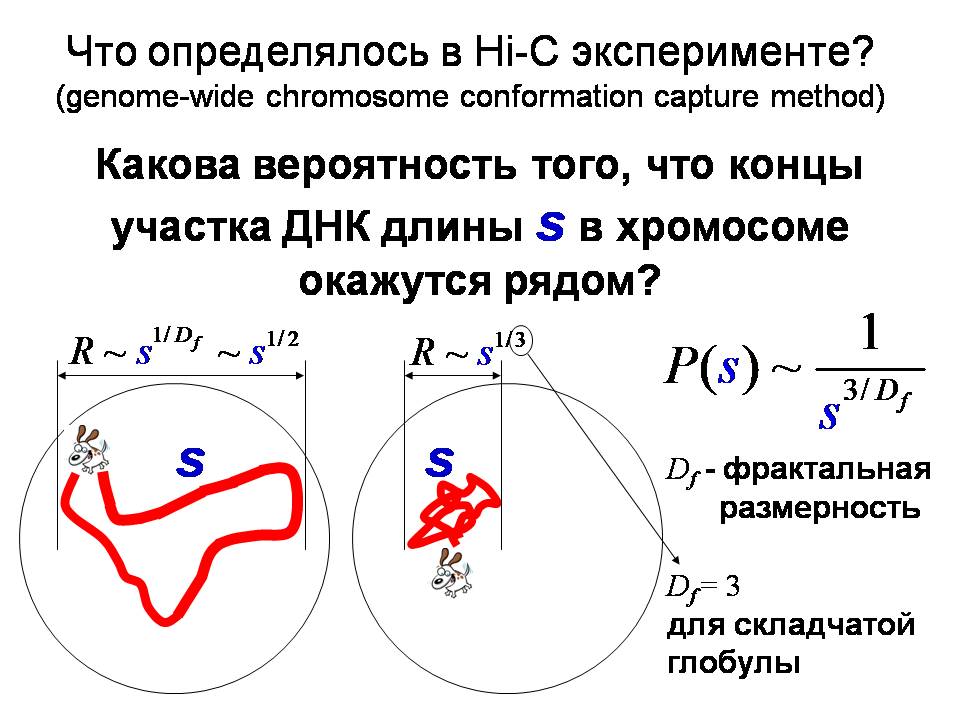
R — размер фрагмента в складчатой глобуле, а s — это количество звеньев во фрагменте. Ну и поскольку кривая плотно уложена в пространстве, то R – это s в степени 1/3, что соответствует максимально плотной упаковке. Такие кривые называются «space-filling curves», кривые, которые плотно укладывается в пространстве. Вот эта «3» — она определяет то, что называется фрактальная размерность, то есть связь того, сколько мономеров находится на отрезке траектории, с пространственным размером этого кусочка. Оказывается, что те кривые, которые получили американцы, в точности совпадают именно с этой укладкой, о которой я сказал. Что является самым важным в этой картинке? Самое важное то, что в этой необычной укладке ближайшие по цепи, то есть те, которые находятся рядом друг с другом, один за другим в химической последовательности, они же являются ближайшими в пространстве, поэтому, если я их вот так вот сложил, то в этом объёме уже не хватает места тем, которые находятся далеко. То есть в каком-то смысле всё самосогласованно. Но есть одна интересная особенность: если вы посмотрите на эту карту, вы увидите, помимо спадания цвета при удалении от главной диагонали, элементы шахматной доски и ещё и элементы блоков, которые выглядят так, что это есть блок, а в нём есть блок ещё более интенсивные (по цвету), и так далее. То есть блочная структура перекликается со структурой, которая подразумевалась как та, которая получается в результате иерархического формирования этой глобулы.

Если делать умозрительные эксперименты и приписать определённые энергии складкам маленьким – одни, тем, которые побольше — и другие, и так далее, и проделать такое же машинное моделирование, как сделали наши американские коллеги, то получится матрица, которая имеет блочно-иерархическую структуру.

Насколько она похожа на то, что получилось реально в эксперименте, трудно сказать наверняка, — это сейчас предмет исследований. Тем не менее, нам кажется, что это достаточно естественная гипотеза, и есть такое представление (верно оно, или нет – это покажет ближайшее будущее), что чем более ярко выражен блок, тем более однозначно выражен фолдинг в ДНК. Что мы видим, глядя на карту контактов одиночной молекулы ДНК? Мы видим сигналы, которые означают, что какие-то мономеры соединились, а между какими-то нет связи… Для того, чтобы получить картину как на слайде, со спаданием цвета, нужно иметь статистику: чем более однозначно воспроизводится фолдинг, тем более ярко высвечивается структура блоков, чем менее однозначен фолдинг, тем более размазанной получается картина. Это сейчас является предметом исследования.

Последний слайд, на котором я хотел бы завершить рассказ, – это фотографии людей, которые в этом принимали участие: Йоб Декер (идеолог Hi-C метода), Леонид Мирный, Hi-C team, который изображён вот здесь, где один из главных действующих лиц – аспирант Максим Имакаев, и мы.

Я должен сказать, что Александру Гросбергу принадлежит идея (задолго до экспериментов американцев), что складчатая глобула, которая родилась в наших работах, имеет отношение к укладке ДНК в хромосомах. Эта идея была опубликована, но до последнего времени была гипотезой. Хочется верить, что данные исследования будут продолжаться. Спасибо.

Обсуждение лекции:

Борис Долгин: Я не до конца понял вашу базовую идентичность. То есть всё-таки вы себя роднее чувствуете где? В физике, в математике, там, где это всё на грани с биологией?

Сергей Нечаев: Физик я. Конечно, потому что математики меня не могут считать своим.

Егор Базыкин: Я не читал интервью, поэтому буду спрашивать ещё раз. У меня несколько вопросов. Во-первых, была картинка про Эшера, на ней был нарисован граф, у которого были циклы, а до и после говорилось о графах, на которых не было циклов.

Сергей Нечаев: Это граф с циклами. Я вам немного наврал. Вот эта картинка имела отношение буквально.

Егор Базыкин: Но тут есть циклы.

Сергей Нечаев: Здесь нет циклов.

Егор Базыкин: Как же?

Сергей Нечаев: Если посмотрите на этот пунктирный скелет и продолжите его, то там дальше не будет циклов.

Егор Базыкин: То есть на сплошные не смотреть?

Сергей Нечаев: Как говорит Миша Тамм: «там рыбу заворачивали».

Егор Базыкин: Понятно, то есть вернуться можно только тем путём, как вышел.

Сергей Нечаев: Хочу вам сказать, что я не совсем врал. Дело в том, что циклы появляются, если мы решаем не буквально эту задачу, а задачу, имеющую отношение к косам. Косы – это объект, с помощью него можно генерировать узлы, там возникает внутренняя структура, возникает группа, в которой есть как возможности образования циклов, то есть как коммутационные соотношения, так и отсутствие их. Это промежуточный объект между графом, где циклов нет, и графом, где они есть, но он ближе по характеристикам к графу без циклов.

Егор Базыкин: Вы берёте глобулу, простую, и проделываете следующую операцию много раз: берёте кусочек и вытягиваете и потом запихиваете обратно. Становится ли она в результате более похожа на складчатую глобулу? Берём глобулу простую, потом начинать брать у неё кусочки и вытягивать, а потом заживлять обратно. Становится ли она больше похожа на ту, которая стоит впереди?

Сергей Нечаев: Дело в том, что распутать обычную глобулу невозможно. Попробуйте ее распутать путём вытаскивания петли — вы её разорвёте. Вам надо её вытаскивать очень хитро. Ответ такой: так, в принципе, можно построить складчатую глобулу. Но надо следить за тем, чтобы вся цепь не была бы заузлена.

Егор Базыкин: Я, наверно, не понял основ. Эта глобула отличается от складчатой тем, что она заузлена?

Сергей Нечаев: Обычная устроена так: у неё есть свободные концы, поэтому вы можете сделать так: можете завязать очень сложный узел, замкнуть цепь и потом заставить ее коллапсировать. Вы никогда не получите складчатую. Складчатую структуру вы получите, только стартуя с тривиального кольца.

Егор Базыкин: Я эволюционист. Мне интересно, как они возникают. Следующая процедура: мы берём глобулу, начинаем от неё отрезать кусочки — и после этого пришиваем их по каким-нибудь правилам таким образом, чтобы оба конца оказались близко друг к другу. Так получится что-то похожее на складчатую глобулу?

Сергей Нечаев: Возможно.

Егор Базыкин: Если это способ, при котором это эволюционирует.

Сергей Нечаев: Я не биолог. Я не могу вам на этот вопрос ответить. Возможно, да.

Егор Базыкин: Вы не можете ответить на вопрос, как это эволюционирует, но можете ответить — получится ли это похоже. Это не биологический вопрос.

Сергей Нечаев: У меня нет визуального образа. Процедура, которая выглядит как кинетический процесс, — вот то, что изображено здесь.

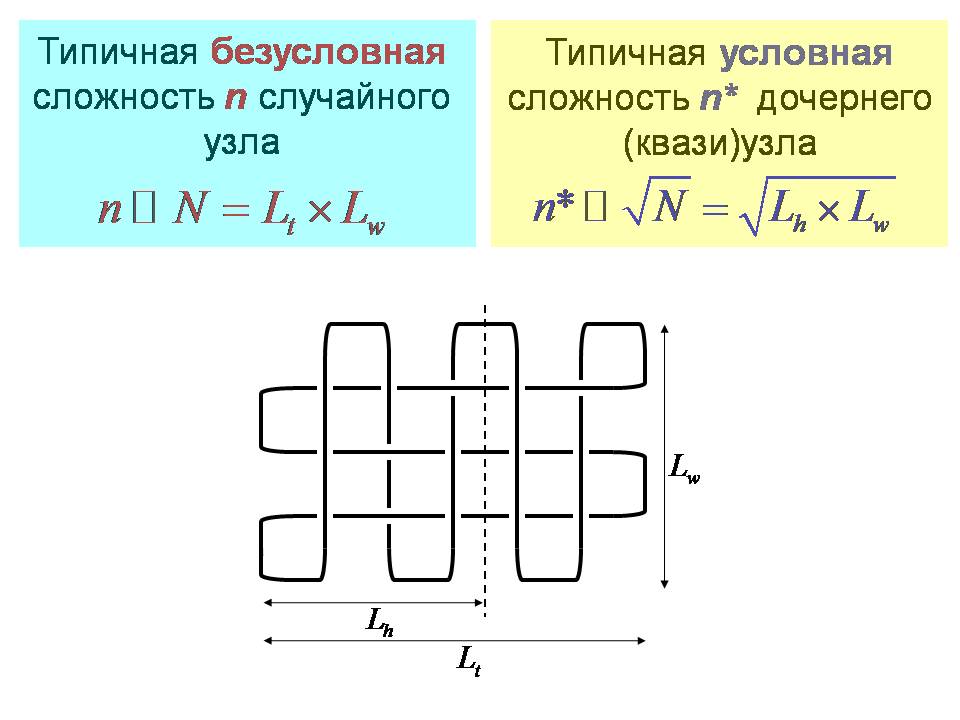
Вы берёте длинную цепочку. Помещаете её в плохой растворитель — и резко понижаете температуру или меняете качество растворителя, в результате она схлопывается. Так как есть вязкость, то она не может схлопнуться как целое. В появляются маленькие складки, затем – побольше, еще побольше... И это естественная кинетика. Можно ли сделать по-другому, путём нарезания? Мне хочется ответить «нет», так как мне кажется, что в моей конструкции возникает иерархия взаимодействия, которая имеет глобальный характер, то есть никакой локальный процесс к построению такой структуры не приведёт. Посмотрите, как была устроена кривая Пеано. Здесь невольно подразумевается, что на каком-то масштабе вы должны оперировать блоками, в которых уже заморожена вся информация о предыстории. Поэтому возможно, что, модифицировав вашу процедуру разрезания такую, что что-то мы разрезали, перекрыли, а потом уже используем это как блок, а потом перекрываем блоки…

Егор Базыкин: Ответ зависит от распределения длин кусочков, которые мы отрезаем?

Сергей Нечаев: Да, возможно.

Егор Базыкин: Может быть, было бы интересно посмотреть на это.

Борис Долгин: Просьба представляться.

Вопрос из зала, Сергей: Эта складчатая глобула представляет собой тривиальный узел. Вопрос: обычная глобула длины n, какой замкнутый принудительными концами, какой сложности узел представляет? Если я начну вытягивать узел, то получится нечто невытягиваемое. Какой сложности получится объект?

Сергей Нечаев: Если мы просто возьмём плотный узел? Давайте сыграем в такую игру: мы берём длинную цепочку и помещаем её в маленький ящик, у цепочки концы разогнуты. И интересуемся вероятностью того, что концы замкнутся, и при этом будет тривиальный узел, e^{- n}.

Сергей: Какая средняя плотность того, что остаётся?

Сергей Нечаев: Типичная сложность узла есть корень из n, в то время как типичная сложность узла в обычной глобуле есть n.

Слайд 22.

Сергей: Это ответ, Егор, на ваш вопрос: так как если корень из n, а n велико, то никаким вытягиванием не отвоюете до тривиального узла.

Сергей Нечаев: На самом деле, когда я говорил про эту игру в «складывание складок», мы спрашивали себя: какая типичная сложность того, что осталось? так вот — она равна корню из n. где n – длина цепочки. А типичная сложность всего — есть n, поэтому корень из n по отношению к n мал, тем не менее, правда относительно небольшая, перепутанность есть.

Вопрос из зала: Я не понимаю одной вещи: ты всё время говоришь о полимерной цепи, которая замкнута в кольцо, но она не имеет концов, потом ты привёл потрясающий пример с ДНК, которая уложена так, как надо в складчатую глобулу, но у неё-то концы не замкнуты. Почему она так долго живёт и не перепутывается? Только не про биологию, а вот всё-таки есть два утверждения: либо концы замкнуты, либо цепь очень длинная. Вот как она должна быть очень длинной, и как тогда складчатая структура становится устойчивой?

Сергей Нечаев: То, с чего я начал: узел определён в двух случаях: либо это кольцо, либо это кусок цепи, концы которого выведены на бесконечность. Я не знаю ответ на вопрос, насколько длинной должна быть цепочка, чтобы складчатость начала реализовываться. Есть численные эксперименты на длинах порядка 100 000 звеньев. где это хорошо видно. Я думаю, что складчатость стабилизируется еще и тем, что всё-таки это объект гетерополимерный, поэтому в принципе помимо топологических взаимодействий есть иные взаимодействия, стабилизирующие структуру, поэтому гидрофобные и гидрофильные взаимодействия таковы, что концы фиксированы на поверхности, но внутри это может быть тривиальный узел.

Реплика из зала: Насколько мне известно, молекула ДНК кольцевая. Бактерии, во всяком случае.

Вопрос из зала: Сергей Константинович, у меня вопрос к вам как к физику. Глобула имеет при определённой упаковке какую-то энергию, можно ли её упаковать её ещё так, чтобы она обладала в 10 раз, в 100 раз меньшей энергией системы? Если взять кусок, оттянуть его и отпустить, он вернётся на старое место, или его конфигурация изменится?

Сергей Нечаев: Я сказал, что эта конфигурация противоестественна. Если мы возьмём эту складчатую глобулу и разрежем в каком-то месте, то она постепенно свернётся в обычную, понизив энергию, так как её плотность станет больше. Складки здесь имеют топологическое отталкивание. В этом смысле энергия её выше. Не разрезая концов, я думаю, что нет способа понизить энергию такой структуры. Это что касается ответа на ваш вопрос. Отвечая на ваш вопрос: если вытащить кусок и отпустить, вернётся ли он на старое место? Для этой модели, думаю, нет. Но в реальных экспериментах возможно, что наличие или отсутствие такой блочной структуры, какую мы видим в Hi-C экспериментах, может свидетельствовать о том, будет это или нет.

Потому что это, как я говорил, блочность связана не с наличием складок, а с однозначностью фолдинга, потому что эти складки можно сложить и по-другому. Грубо говоря, здесь у вас первый контактирует с 10-м, а можно сделать так, что 1-й будет контактировать с 20-м, а всё остальное будет внутри какой-то другой складки. Степень свободы, тем не менее, есть. Наличие внутренней структуры этой карты – это указание на то, стоит думать об однозначности фолдинга, или не стоит.

Вопрос из зала, Юра, биолог: Хотел бы уточнить про ДНК: если упрощать историю, то получается, что изначально организмы простые, у которых была короткая ДНК, тяготели к тому, чтобы ДНК была кольцевой, а потом ДНК становилась длинной и в какой-то момент переставала быть кольцевой и становилась линейной. У нас ДНК разделена на хромосомы и, как вы продемонстрировали, имеет определённые территории в ядре, и я хотел уточнить: согласуется ли эта замечательная математика с тем, что есть некий порог перехода от кольцевой к линейной структуре?

Сергей Нечаев: Я могу ответить с точки зрения физики. Такая структура реализуется на очень длинных цепях; если цепь короткая, то складок не будет видно. Представьте себе, что там распутать обычную петлю просто. Поэтому это всё начинает играть роль тогда, когда длина молекулы намного превосходит, скажем, в 1000 раз превосходит размер минимальной складки.

Кто-то из зала: Прослеживается ли в закономерностях математической теории и геометрии золотое сечение?

Сергей Нечаев: Буквально – нет. Во всяком случае, в биологии этого не видно, но дело в том, что геометрия, которая стоит за построением этих картинок, так или иначе связана с золотым сечением, потому что это цепные дроби. Последовательность, размеры треугольников, которые последовательно уменьшаются, – это геометрическая прогрессия. Никто специально золотое сечение не искал, потому что оно нам не нужно, но оно появляется естественным образом, потому что это та же математика, не буквально, но цепные дроби, двоякопериодические функции, которые здесь возникают, — они растут из одного куста.

Реплика из зала: Комментарий к предыдущему оратору. Мне кажется, дело может быть в том, что если она очень длинная, но не заузленная, существует кинетическая замороженность. То есть если она собралась в такую иерархически складчатую структуру, то время, за которое она найдёт дорогу в такую заузленную глобулу, порядка n в кубе, соответственно, чем длиннее цепь, тем дольше она будет в этом состоянии жить. Такая у меня реакция на ваш вопрос.

Андрей Шмузьков, физик: Первый вопрос: я слышал, есть такой профессор Твердислов, он в МГУ. Они занимаются другой упаковкой, так как ДНК завёрнута, они это складывают, заворачивают в одну сторону, потом в другую, направо, налево и вот так, чередуясь, они приходят к некоторой глобулярной структуре. Вы такие конфигурации не рассматриваете?

Сергей Нечаев: Дело в том, что, как видите, здесь есть, в каком-то смысле, эта модель упрощённая, так как в ней нет жёсткости, но есть топология, которой нет в тех моделях, в которых рассматривается жёсткость. Наверно, в какой-то момент надо будет все срастить, но вопросами, связанными с торсионной упругостью, с образованием узлов, занимался ещё много Франк-Каменецкий.

Андрей Шмузьков, физик: В своей книжке «Самая главная молекула».

Сергей Нечаев: Не только. Вообще я считаю, что Франк-Каменецкий и его группа являются родоначальниками этой науки, статистической топологии, потому что они первыми сделали работы, в которых отошли от представления о коммутативном характере зацеплений. Они делали это с помощью определённых методов алгебраической топологии, так называемых полиномов Александера. Если отвечать на ваш вопрос, то работ Твердислова я просто не знаю, но думаю, что они не имеют отношения к топологии. Имеют ли они какое-то отношение к укладке, о которой шла речь, – трудно сказать, видимо, нет. В контексте нашего обсуждения с коллегами эти работы никогда не всплывали.

Андрей Шмузьков, физик: Он говорил в декабре, что послали работу в журнал. Вопрос по существу: предыдущей на Полит.ру была лекция Юджина Ползика, и он рассказывал о квантовой телепортации, то есть вот здесь вы говорили о классических вещах укладки. Юрий Иванович Манин, знаменитый математик, ещё в 80-м году писал, что если классически представить, как ДНК при репликации разворачивается и заворачивается, то частота будет равна оборотам стиральной машины, но этого не может быть, потому что клетки и ядра повзрывались бы. Вот насколько мы рассматриваем это на данный момент, потому что мы квантовой телепортацией уже занимаемся? Что там с ДНК?

Сергей Нечаев: Я могу вам только ответить, что Наташа, когда делала интервью, спросила меня о тёмной материи. Я сказал, что не могу ответить на этот вопрос. Потому что не могу правильно сформулировать задачу, а раз так…

Андрей Шмузьков, физик: Я понял, вы меня смутили.

Сергей Нечаев: Я просто действительно не знаю.

Егор Базыкин: Я хотел сказать, что с ДНК есть какие-то механизмы, которые упрощают эту историю, потому что есть ферменты, которые вносят разрывы, — и все обороты упрощаются. Никазы и теломеразы решают, то есть существует обходной механизм.

Арсен, биолог: Возможно ли теоретически посчитать, какой диаметр будет этой глобулы, если это когда-нибудь вы это делали? Насколько это совпадает? Толщина цепи ДНК?

Сергей Нечаев: Ну конечно. Картинка – это численный эксперимент, имеющий отношение к настоящим молекулам.

Арсен, биолог: Какой приблизительно размер? Известно, или нет?

Сергей Нечаев: Известно, но ответить не могу: числа не помню, но само число не так важно… Я задумался, потому что, в принципе, мы можем ставить задачу по-разному. Мы можем ставить задачу так, что глобула формируется именно так, как я сказал: мы помещаем цепочку в какие-то условия, при которых внутренние контакты между мономерами оказываются выгоднее, чем контакты с растворителем. Иная постановка такая: мы помещаем петлю в ящик и сжимаем стенки ящика. Возникнет точно такая же структура. В этом случае говорить о каких-то естественных размерах сложно; то, на что мы обращали внимание, – это внутренняя структура. В принципе, размер известен, но я не могу сейчас сказать, надо спросить у ребят, которые делали эксперимент, но поскольку все константы они брали из реальных экспериментов, я думаю, что согласование хорошее, но, повторю, главное, на что мы обращали внимание, – это на структуру складок.

Реплика из зала, Леонид: Я могу прокомментировать вопрос. Когда производилось моделирование, то ДНК рассматривалась как свободно-сочленённая цепь. Персистентная длина ДНК, то есть длина участка, который помнит ориентацию, – это порядка 150 нуклеодных пар, 150 пар, если мы берём ДНК человека, то это где-то 3 нуклеосомы, то есть вот эти линки на участке обеспечивают нам эту длину. Ну, с запасом брали штук 8 этих гистонов как одно звено этой цепи. Здесь некоторые сглаживания ещё осуществляются.

Иван, биолог: Вы показывали картинку с квадратиками.

Здесь видны разные уровни организации. Эти уровни организации рассчитываются из модели? Биологам известно, что это определятся специальными белками, которыми она упаковывается, разными белками. ДНК — не голая верёвка, которая болтается в растворе, это верёвка, которая связана с кучей маленьких, и больших, и разных других катушечек. Эти катушечки — их природа приспособила к тем уровням, которые вытекали просто из статистической модели? Или нет?

Сергей Нечаев: Я не могу ответить на этот вопрос, потому что я не знаю: это вопрос к биологам. Но мы как раз пытаемся подойти к этому вопросу, но, может быть, со стороны других игр разума… Вы говорите о нуклеосомной организации, и есть другие иерархические уровни, может, это скорее вопрос к эволюционному биологу, который тут присутствует?

Иван, биолог: Я думаю так, что природа никогда не идёт против физики: она пытается её использовать, но против неё не идёт. Я не встречал такого, чтобы было сделано против того, что предполагает физика, особенно статфизика. В этом смысле природа могла разными способами на инструментальном уровне — катушечки, белки — использовать то, что в природе без этого может происходить медленно и, вообще говоря, не очень точно. Но с помощью белков и биологических устройств происходит быстро. Точно и однозначно – в этом разница. А так, что иерархическая укладка создавалась против физики, я думаю, что это не так. Может быть, я неправ.

Вопрос из зала: У меня продолжение вопроса про золотое сечение. Как соотносятся разные уровни организации? Какой-то ряд чисел есть или что-то подобное?

Сергей Нечаев: Вы всё время задаёте вопрос про уровни организации.

Кто-то: Они же видны.

Сергей Нечаев: Мы этим занимаемся, и я не могу об этом сказать подробно, так как пока это все – гипотезы.

Реплика из зала: А почему вы думаете, что это уровни организации? Полно в природе всякого. Это ключевой слайд. Но сначала надо понять, что организовано. Вот на этом мы ломаем голову.

Сергей Нечаев: Я думаю, что в действительности здесь идёт игра нескольких вещей. Я не могу сказать, связано ли наличие блоков с какой-то иерархией уровней организации. Но, по-видимому, то, что здесь важно: во-первых, топология, во-вторых, гетерополимерность и наличие замороженной первичной структуры, и, третье, однозначность фолдинга. Эти вещи точно должны присутствовать и быть взаимосвязаны. Связано ли с ними ещё какое-то функционирование, потому что разные уровни организации должны быть связаны с определённой функцией, я не могу ответить.

Вопрос из зала: Узнали мы ещё что-то новое из вашего эксперимента, из вашей модели?

Сергей Нечаев: Пока — только о её укладке. Знание самой первичной структуры ДНК было заложено в этих экспериментах. Дело в том, что если бы мы не знали последовательности нуклеотидов и не знали бы, какой идёт за каким, то мы не могли бы идентифицировать эти куски и их положение в пространстве. Здесь так: карта – 1000 на 1000, а каждая точка 2 килобазы, то есть 2000 единиц, то есть два куска по 1000 единиц, удалённых по цепи, сравнивались, были идентифицированы. Они накладывались в пространстве. Если бы мы не знали структуру в последовательности, то мы не могли бы, в принципе, связать расстояние между фрагментами с их положением в пространстве.

Илья, биохимик: Можно вернуться к слайду, к фрактальной размерности? Вы не могли бы немного пояснить, что фрактальная размерность означает, почему она получилась равной трем? Думаю, что она связана с уровнями организации.

Сергей Нечаев: Думаю, что проще. Смотрите, фрактальная размерность – это вот что такое: вы берёте нить, у вас есть контурная длина, то есть длина вдоль цепи, а так же её пространственный размер, то есть, «радиус инерции» этого куска. Связь между пространственным размером и длиной и есть фрактальная размерность.

Если у вас есть случайное блуждание, вот здесь изображён кусок, который – кусок случайной траектории. Его размер – это корень из длины. Вот так я рисовал как далеко ушла собака от будки. То, что имеем мы эдесь, – это кривая, которая плотно заполняет пространство, то есть это кривая, которая имеет то же самую длину S, но из-за того, что мономеры очень плотно уложены в пространстве, то её размер есть S в степени 1/3, меньше быть не может. Каждый мономер занимает какой-то объём, и это самая плотная упаковка, которая может быть в трёхмерном пространстве, так как объём равен R³. Но это происходит на всех масштабах. Если вы возьмёте кусок длиннее – вы увидите ту же саму закономерность. Эта повторяемость является принципиальной: если бы вы увидели 1/3 только на самом большом масштабе – ничего интересного не было бы. Но из-за того, что это иерархически повторяется везде, — это важно. То, что здесь написано, – это вероятность того, что два куска, разделённые длиной S, окажутся рядом в пространстве, она падает как 1/S. Такая зависимость получается только если это space-filling curve, т.е. кривая, которая плотно заполняет пространство. Именно эта функция изображена на этом графике при удалении от диагонали на карте контакотв: S – это расстояние от главной диагонали. Если бы это отличалось от зависимости 1/S, скажем, это было бы 1/S^3/2, можно было бы обо всём забыть, и я бы сюда не приходил.

Андрей Михайлович, физик: Когда вы изучали складчатую глобулу, вы как-то задавали себе вопрос, сколько она имеет осей симметрии, не напоминает ли вам цифра 3 в коэффициенте фрактальности просто количество осей симметрии, существующих в объёме, тем более, что на слайде 2 это явно плоскость? Это первый вопрос. Второй: иерархическая фрактальность, которую вы обнаружили, раскройте тему.

Сергей Нечаев: Если вы возьмёте обычную траекторию случайного блуждания, ее фрактальная размерность 2.

Андрей Михайлович, физик: Мы говорим об этой глобуле, а не об абстрактной.

Сергей Нечаев: Отвечаю на Ваш вопрос. Здесь написано, что размер порядка корня из расстояния. Это и в трёхмерном пространстве так же. Это не имеет к плоскости никакого отношения. Это просто связано с тем, что у вас шаги некоррелированны, и нет других ограничений. Коэффициент диффузии зависит от размерности пространства, но сама степень от пространства не зависит никак. Это просто свойство случайных блужданий. Поэтому то, что мы имеем здесь, – это немножко другая вещь.

Андрей Михайлович, физик: Там же есть объём — и тройка? А тут тройка и двойка?

Сергей Нечаев: Двойка не имеет отношения к объёму.

Андрей Михайлович, физик: Правильно: тут нет объёма.

Сергей Нечаев: Ответ: плоскость не имеет никакого отношения.

Борис Долгин: Всё, коллеги.

Сергей Нечаев: Я не знаю, что ответить. Если бы собака летала, всё равно бы была бы двойка для фрактальной размерности ее блуждания. Насчёт осей симметрии. Мне трудно сказать про ось симметрии, потому что я не очень понимаю в данном случае, что это – это же не кристалл. Когда мы говорим о случайных структурах – не понятно. что такое ось симметрии.

Андрей Михайлович, физик: Можем говорить о какой-то симметрии?

Сергей Нечаев: В буквальном смысле о симметрии говорить я бы не стал, потому что я не очень понимаю, как ставить эксперимент, чтобы её изучать, но если вы, скажем, говорите о симметрии, когда вы смотрите рассеяние от этой структуры, то это интересный вопрос, и я сейчас не могу на него ответить.

Андрей Михайлович, физик: Вот куб на вашем столе с фрактальной структурой — он имеет некое количество всех симметрий, и их можно посчитать. А вот складчатая глобула сколько имеет осей симметрии? У куба можно посчитать количество симметрий? А вот у складчатой глобулы не считается?

Сергей Нечаев: Я не могу ответить на ваш вопрос. Давайте его опустим.

Реплика из зала: Дело в том, что готовить полимеры таких вот фрактальных структур технически удобнее так, чтобы они были симметричные, поэтому то, что нарисовано на слайде и стоит на столе, – оно симметричное. Реально складчатая структура имеет иерархию масштабов, но в ней нет симметрии, потому что нет механизма, которой создал бы такую симметрию. Ответ: количество симметрий равно нулю.

Иван: Правильно ли я понял, говоря о троечке, что означает, что ДНК уложено максимально плотно на каждом уровне?

Сергей Нечаев: Начиная с некоторого минимального. Потому что есть минимальная складка, которая является блоком, что внутри мы не знаем… точнее, знаем, но это не очень нас в данный момент интересует. А в терминах этих блоков мы начинаем строить наиболее плотную упаковку на всех масштабах.

Иван: То есть это отражение рациональности укладки?

Сергей Нечаев: Кажется, что так, но это некоторая загадка, это является вопросом, который мы пытаемся понять. Настоящий эксперимент (Hi-C) показывает, что именно так она уложена — максимально плотно на всех масштабах. Компьютерный эксперимент с помощью молекулярной динамики на очень длинных цепях показывает, что она немножко перепутывается и участки влезают друг в друга складками. И понять, почему в биологии этот процесс заморожен и не происходит, а здесь он чуть-чуть происходит очень важно… На очень длинных цепях перепутывания не происходит. Но, видимо, есть масштаб, где есть рассогласование численных экспериментов и того, что мы видим из настоящей биологии. Сейчас мы пытаемся это понять и, по-видимому, природа, возможно, именно за счёт наличия дополнительных взаимодействий, кроме топологии, ещё каким-то образом стабилизирует эту структуру.

Иван: Я хотел узнать. Если говорить не о супердлинных цепях, а например, о вирусе папилломы человека, у которого геном кольцевой, и он правит порядка 8000 нуклеотидов, такая у него есть хитрость, и он крадёт человеческие нуклеосомы и свою собственную упаковку ДНК, свою капсиду, он осуществляет тоже за счёт человеческих нуклеосом, и размеры капсида настолько малы, что там действительно внутри никакого места не остаётся вплоть до воды. У меня вопрос такой: можно ли как-то рассчитать количество способов укладки в такую маленькую структуру, и вообще конечно ли оно? Для такой системы?

Сергей Нечаев: Мне было на слух довольно сложно понять, о какой системе идёт речь. Но вообще первые численные эксперименты, которые были ещё до современных на относительно коротких замкнутых цепях, в которых перечислялось количество конфигураций и вероятность заузлевания. На коротких длинах складчатость не видна, но некоторая тенденция есть. Тем не менее, задачу можно поставить; если есть интерес, могу подсказать, с кем можно поговорить для обсуждения.

Альмира, математик: Не могли бы вы сказать, каким методом считался фрактальный размер в данной работе?

Сергей Нечаев: Фрактальный размер здесь считался обычным методом, который называется box counting, то есть вы просто заполняете пространство кубиками и смотрите, сколько в кубик попадает ближайших по траектории мономеров. Я думал, что вы спросите, каким методом считалась топология. Это интересно, потому что мы использовали для этих плетёнок методы алгебраической топологии, так называемые полиномы Джонса. Но в процессе того, как мы пытались решать эту задачу, здесь произошло смешение двух разных типов задач. Математики, если есть такая плетёнка, знают, как по ней построить характеристику, которая скажет, заузлена она или нет. Инварианты Джонса они не являются точными. Но, тем не менее, для статистических задач они достаточны. Мы знаем, что какие-то нити проходят сверху, а какие-то проходит снизу, и эта величина случайна. Вопрос, который задают физики, имеет отношение к неупорядоченной системе типа системы спинов на решетке. Поэтому в действительности в нашей задаче смешались два подхода: с одной стороны — то, что люди использовали для спинов в неупорядоченной системе, а с другой стороны — методы алгебраической топологии. Симбиоз этих двух дисциплин позволил смотреть на узлы как на неупорядоченные системы и дал возможность что-то сосчитать.

Вопрос из зала: Вы очень осторожно говорите о фрактальности, и это похвально, и чувствуется, что вы показываете нечто большее. Раскройте тайну иерархической фрактальности, и почему она похожа на квадрат.

Сергей Нечаев: Она не похожа на квадрат. Просто мы не умеем делать модель из треугольников. Фотография — это тоже не ко мне. Это к Лёне. Ничего я пока не могу сказать вам больше, потому что сам не знаю, но есть некоторая модель, которая, грубо говоря, устроена так: вы строите граф с помощью некоторой иерархической процедуры, а потом смотрите на то, что называется матрица связанности этого графа (матрица, которая указывает кто с кем находится в контакте). В результате вы получаете какой-то набор точек, потому что там, где какие-то два элементы графа сошлись, там есть единица, в противном случае ноль. А после этого мы набираем статистику. По одним и тем же правилам проделываем одну и ту же процедуру и дальше проецируем все карты одну на другую, то что здесь два – это от лукавого. Дробление на два, потому что мы задали такие правила игры. Правильно это или нет, как раз сейчас и обсуждается среди тех, кот этим занимается. Достаточно просто понять, какие правила игры могут привезти к иерархии в матрице контактов. И что нужно сделать, чтобы её разрушить. Ничего больше я пока сказать не могу

Вопрос из зала: А что там по осям?

Сергей Нечаев: По осям? Так. Номера мономеров по цепи. У вас есть цепь. Точка – это две килобазы.

Борис Долгин: По-моему, сегодняшний наш доклад – доказательство того, что комфортно жить между домами. Я имею виду не страны, а дисциплины. Спасибо большое, Сергей.

Сергей Нечаев: Спасибо.

31 мая 2013
Полит.ру