Глава 1. Начальные стадии эволюции

• 1.1. Основной закон эволюции
• 1.2. Химическая эра
• 1.3. Кибернетика
• 1.4. Дискретные и непрерывные системы
• 1.5. Надежность дискретных систем
• 1.6. Информация
• 1.7. Нейрон
• 1.8. Нервная сеть
• 1.9. Простой рефлекс (раздражимость)
• 1.10. Сложный рефлекс

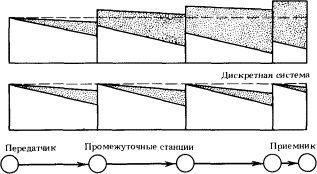
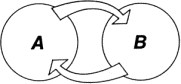
1.1. Основной закон эволюции

В процессе эволюции жизни, насколько нам известно, всегда происходило и происходит сейчас увеличение общей массы живого вещества и усложнение его организации. Усложняя организацию биологических образований, природа действует по методу проб и ошибок. Существующие образования воспроизводятся во многих экземплярах, которые, однако, не вполне тождественны оригиналу, а отличаются от него наличием небольших случайных вариаций. Эти экземпляры служат затем материалом для естественного отбора. Они могут выступать и как отдельные живые существа — тогда отбор приводит к закреплению полезных вариаций, и как элементы более сложного образования — тогда отбор направлен также и на структуру нового образования (например, при возникновении многоклеточных организмов). И в том и в другом случае отбор является результатом борьбы за существование, в которой более жизнеспособные образования вытесняют менее жизнеспособные.

Этот механизм развития жизни, открытый Чарльзом Дарвином, можно назвать основным законом эволюции. В наши цели не входит обоснование или обсуждение этого закона с точки зрения тех законов природы, которые можно было бы провозгласить более фундаментальными. Будем принимать основной закон эволюции как нечто данное.

1.2. Химическая эра

Историю жизни до появления человека можно разбить на два периода, которые мы назовем «химической» эрой и «кибернетической» эрой. Границей между ними служит появление животных с четко оформленной нервной системой, включающей органы чувств, нервные волокна для передачи информации и нервные узлы для ее преобразования. Такая терминология не означает, конечно, что понятия и методы кибернетики неприменимы к жизни «химической» эры; просто животное «кибернетической» эры является классическим объектом кибернетики, на котором она возникла и оформилась как научная дисциплина.

Историю и логику эволюции в докибернетическом периоде мы рассмотрим лишь бегло, ссылаясь на воззрения современных биологов¹. В этом периоде можно выделить три этапа.

На первом этапе закладываются химические основы жизни, образуются макромолекулы нуклеиновых кислот и белков, обладающие свойством редупликации — снятия копий, «отпечатков», когда одна макромолекула служит матрицей для синтеза из элементарных радикалов подобной ей макромолекулы. Основной закон эволюции, который вступает в действие на этом этапе, приводит к тому, что матрицы, обладающие большей интенсивностью воспроизведения, получают преимущество перед матрицами с меньшей интенсивностью воспроизведения, в результате чего образуются все более сложные и активные макромолекулы и системы макромолекул. Биосинтез требует свободной энергии. Первичным ее источником является солнечное излучение. Продукты частичного распада живых образований, непосредственно использующих солнечную энергию (фотосинтез), также содержат некоторый запас свободной энергии, который может быть реализован с помощью уже имеющейся химии макромолекулы. Он и реализуется специальными образованиями, для которых продукты распада служат вторичным источником свободной энергии. Так возникает расслоение жизни на растительный и животный миры.

Второй этап эволюции — возникновение и развитие у животных двигательного аппарата.

В характеристике доступа к источнику энергии есть существенное различие между растениями и животными. При данной освещенности интенсивность поглощения солнечной энергии зависит только от величины поверхности растения, но никак не от того, движется оно или покоится. Совершенствование растений пошло по пути создания выносных светоуловителей — зеленых листьев, крепящихся на системе опор и стрел — стеблей, веток и т. п. Конструкция эта отлично работает, обеспечивая медленное перемещение зеленых поверхностей к свету, отвечающее медленному изменению освещенности.

Совсем другое положение у животного, в частности, у самого примитивного животного, например, амебы. Источник энергии — пища — заполняет среду вокруг него. Приток энергии определяется скоростью диффузии пищевых молекул через оболочку, отделяющую пищеварительный аппарат от внешней среды. Скорость диффузии зависит не только — и даже не столько — от величины поверхности пищеварительного аппарата, сколько от движения этой поверхности относительно среды, дающего возможность выедать пищу из различных ее участков. Поэтому даже простое хаотическое движение в среде или, напротив, движение среды относительно организма (так делают, например, губки, прогоняя через себя воду с помощью ресничек) имеет большое значение для примитивного животного и, следовательно, появляется в процессе эволюции. Возникают специальные образования (внутриклеточные — у одноклеточных организмов и содержащие группы клеток — у многоклеточных), основной функцией которых является производство движения.

На третьем этапе эволюции движения животных становятся направленными, и у них появляются зачатки органов чувств и нервной системы. Это также является естественным следствием основного закона. Животному выгоднее двигаться в том направлении, где концентрация пищи выше, а чтобы осуществить это движение, надо иметь датчики, характеризующие состояние внешней среды в различных направлениях (органы чувств), и информационные каналы связи между этими датчиками и двигательным аппаратом (нервная система). Вначале нервная система чрезвычайно примитивна. Органы чувств различают лишь несколько ситуаций, на которые животное должно реагировать по-разному. Объем информации, который передает нервная система, ничтожен. Специальный аппарат для обработки информации отсутствует. С течением времени органы чувств усложняются и поставляют все больше информации о внешнем мире. Одновременно совершенствуется двигательный аппарат. Это предъявляет все увеличивающиеся требования к пропускной способности нервной системы. Появляются специальные образования — нервные узлы, которые перерабатывают информацию, поступающую от органов чувств, в информацию, управляющую органами движения. Начинается новая — «кибернетическая» эра.

1.3. Кибернетика

Анализ эволюции в кибернетический период, вскрытие законов, по которым происходит усложнение организации живых существ этого периода — мы будем для краткости называть их «кибернетическими животными», — требует введения некоторых фундаментальных понятий и законов кибернетики.

Сам термин «кибернетика« ввел, как известно, Норберт Винер, определив его описательно как учение о связях и управлении в живом организме и машине. Чтобы более точно дать определение кибернетики, как и всякой научной дисциплины, мы должны ввести ее основные понятия. Собственно говоря, ввести основные понятия — это и значит уже определить данную науку, ибо остается только добавить: описание мира с помощью этой вот системы понятий и есть данная конкретная наука.

В основе кибернетики лежит прежде всего понятие системы как некоторого материального объекта, состоящего из других объектов, называемых подсистемами данной системы. Подсистема некоторой системы, в свою очередь, может рассматриваться как система, состоящая из подсистем. Поэтому, если быть точным, смысл введенного нами понятия заключается не в термине «система» самом по себе, т. е. не в приписывании некоторому объекту свойства «быть системой», что довольно бессодержательно, ибо каждый объект может считаться системой, а в связи между терминами «система» и «подсистема», отражающей определенное отношение объектов.

Второе важнейшее понятие кибернетики — понятие состояния системы (подсистемы). Подобно тому как понятие системы непосредственно опирается на нашу пространственную интуицию, понятие состояния непосредственно опирается на нашу интуицию времени, и его невозможно определить иначе, как сославшись на опыт. Когда мы видим, что объект в чем-то изменился, мы говорим, что он перешел в другое состояние. Как и понятие системы, понятие состояния является скрытым отношением — отношением между двумя моментами времени. Если бы мир был неподвижным, понятие состояния не могло бы возникнуть, и в тех дисциплинах, где мир рассматривается статически, например, в геометрии, понятие состояния отсутствует.

Кибернетика изучает организацию систем в пространстве и времени, т. е. то, каким образом связаны подсистемы в систему и как влияет изменение состояния одних подсистем на состояние других подсистем. Основной упор делается, конечно, на организацию во времени, которая в случае, когда она целенаправленна, называется управлением. Причины связи между состояниями системы и вытекающие отсюда особенности ее поведения во времени часто называют заимствованным из физики термином динамика системы. Этот термин в применении к кибернетике неудачен, так как, говоря о динамике системы, мы склонны рассматривать ее как нечто целое, в то время как в кибернетике главным является исследование воздействия друг на друга подсистем, образующих данную систему. Поэтому мы предпочитаем говорить об организации во времени, употребляя термин динамическое описание только тогда, когда его нужно противопоставить статическому описанию, учитывающему лишь пространственные отношения между подсистемами.

Кибернетическое описание может иметь различный уровень детализации. Одну и ту же систему можно описывать либо в общих чертах, разбив ее на несколько крупных подсистем, «блоков», либо более детально, описав строение и внутренние связи каждого блока. Но так или иначе кибернетическое описание всегда имеет какой-то конечный уровень, глубже которого оно не распространяется. Подсистемы этого уровня рассматриваются как элементарные, не разложимые на составные части. Реальная физическая природа элементарных подсистем кибернетика не интересует, ему важно только, как они связаны между собой. Два физических объекта могут радикально отличаться друг от друга по своей природе, но если на каком-то уровне кибернетического описания они организованы из подсистем одинаково (с учетом динамического аспекта!), то с точки зрения кибернетики их можно считать — на данном уровне описания — тождественными. Поэтому одни и те же кибернетические соображения могут быть применимы к таким разным объектам, как радиотехническая схема, программа для вычислительной машины или нервная система животного.

1.4. Дискретные и непрерывные системы

Состояние системы определяется через совокупность состояний всех ее подсистем, т. е. в конечном счете элементарных подсистем. Элементарные подсистемы бывают двух типов: с конечным и бесконечным числом возможных состояний. Подсистемы первого типа называют также подсистемами с дискретными состояниями, второго типа — с непрерывными состояниями. Примером подсистемы с дискретными состояниями может служить колесико арифмометра или счетчика в такси. Нормально это колесико находится в одном из десяти положений, соответствующих десяти цифрам от 0 до 9. Время от времени оно поворачивается и переходит из одного состояния в другое. Этот процесс поворота нас мало интересует. Правильная работа системы (арифмометра, счетчика) зависит только от того, как связаны между собой «нормальные» положения колесиков, а как происходит переход из одного положения (состояния) в другое — несущественно. Поэтому мы и можем рассматривать арифмометр как систему, элементарные подсистемы которой могут находиться только в дискретных состояниях. Современная быстродействующая цифровая вычислительная машина также состоит из подсистем (триггерных схем) с дискретными состояниями. Все, что мы знаем в настоящее время о нервной системе животных и человека, указывает на то, что решающую роль в ее работе играет взаимодействие подсистем (нейронов) с дискретными состояниями.

С другой стороны, человек, катящийся на велосипеде, или аналогичная вычислительная машина дают нам примеры систем, которые описываются как состоящие из подсистем с непрерывными состояниями. В случае велосипедиста таковыми являются все движущиеся друг относительно друга части велосипеда и человеческого тела: колеса, педали, руль, ноги, руки и т. д. Их состояния — это их положения в пространстве, описывающиеся координатами (числами), которые могут принимать непрерывные множества значений.

Если система состоит исключительно из подсистем с дискретными состояниями, то и сама она может находиться лишь в конечном числе состояний, т. е. является системой с дискретными состояниями. Такие системы мы будем называть просто дискретными системами, а системы с непрерывным множеством состояний — непрерывными. Дискретные системы во многих отношениях проще для анализа, чем непрерывные. В частности, пересчет числа возможных состояний системы, который играет важную роль в кибернетике, требует в дискретном случае лишь знания элементарной арифметики. Пусть дискретная система A состоит из двух подсистем a₁ и a₂, причем подсистема a₁ может иметь n₂, а подсистема a₂ — n₂ возможных состояний. Допуская, что каждое состояние системы a₁ может сочетаться с каждым состоянием системы a₂, мы находим, что число N возможных состояний системы A есть n₁n₂. Если система A состоит из m подсистем a_i, где i = 1, 2, …, m, то

N = n₁n₂…n_m.

В дальнейшем мы будем рассматривать только дискретные системы. Кроме того прагматического соображения, что они принципиально проще, чем непрерывные системы, существует еще два довода в пользу целесообразности такого ограничения.

Во-первых, все непрерывные системы можно, в принципе, рассматривать как дискретные системы с чрезвычайно большим числом состояний. В свете тех знаний, которые дала нам квантовая физика, такой подход даже следует рассматривать как теоретически более правильный. Причина, по которой непрерывные системы все же не исчезают из кибернетики, — это наличие весьма совершенного аппарата — математического анализа и, в первую очередь, дифференциальных уравнений для рассмотрения таких систем.

Во-вторых, самые сложные кибернетические системы, как возникшие естественным путем, так и созданные руками человека, неизменно оказываются дискретными. Особенно наглядно это видно на примере животных. Относительно простые биохимические механизмы, регулирующие температуру тела, содержание в крови различных веществ и т. п., являются непрерывными, но нервная система устроена по дискретному принципу.

1.5. Надежность дискретных систем

Почему же, когда необходимо выполнять сложные функции, дискретные системы оказываются предпочтительнее, чем непрерывные? Потому что они отличаются более высокой надежностью. В кибернетическом устройстве, основанном на принципе дискретных состояний, каждая элементарная подсистема может находиться лишь в небольшом числе возможных состояний, поэтому она, как правило, игнорирует малые отклонения от нормы различных физических параметров системы, восстанавливая «в первозданной чистоте» одно из своих допустимых состояний. В то же время в непрерывной системе малые возмущения непрерывно накапливаются и, если система слишком сложна, она перестает правильно работать. Конечно, и в дискретной системе всегда существует возможность сбоя, ибо небольшие изменения физических параметров все-таки приводят к конечной вероятности перехода подсистемы в «неправильное» состояние. И все-таки преимущество, бесспорно, на стороне дискретных систем. Покажем это на следующем простом примере.

Пусть нам надо передать сообщение с помощью электрического провода на расстояние, скажем, 100 км. И пусть через каждый километр провода мы имеем возможность поставить автоматическую станцию, которая будет усиливать сигнал до той мощности, которую он имеет на предыдущей станции, и — если нужно — как-то преобразовывать его (рис. 1.1).

Рис. 1.1. Передача сигнала в непрерывной и дискретной системах. Затенением показана область неопределенности сигнала

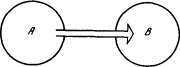
Допустим, что максимальная величина сигнала, который позволяет послать наша аппаратура, составляет 1 В и что среднеквадратичное искажение сигнала при передаче от станции к станции (помеха) равно 0,1 В.

Рассмотрим сначала непрерывный способ передачи информации. Тогда содержанием сообщения будет величина напряжения, приложенного к проводу у его начала. Величина напряжения на другом конце провода — принятое сообщение — будет из-за помех отличаться от начального напряжения. Как велико будет это отличие? Считая помехи на различных участках линии независимыми, мы находим, что после прохождения ста станций среднеквадратичная величина помехи составит 1 В (складываются средние квадраты помех). Таким образом, помеха в среднем равна максимальному сигналу, поэтому ясно, что никакой полезной информации мы фактически не получим. Значение принятого напряжения может совпадать со значением переданного напряжения разве что случайно. Если, например, нас устраивает точность в 0,1 В, то вероятность такого совпадения равна примерно ¹/₁₀.

Теперь рассмотрим дискретный способ передачи. Определим два «осмысленных» состояния начального участка провода: когда приложенное напряжение равно нулю и когда оно максимально (1 В). На промежуточных станциях установим автоматические устройства, которые в одном случае, если принято напряжение меньше 0,5 В, передают дальше нулевое напряжение, а если оно больше 0,5 В, посылают нормальный сигнал в 1 В. Следовательно, в данном случае за один раз (одним сигналом) передается информация вида «да» или «нет» (такое количество информации — единица информации — называется 1 бит). Какова вероятность получения правильной информации? Она сильно зависит от закона распределения вероятности для величины помехи. Как правило, помехи подчиняются так называемому нормальному закону. Приняв этот закон, можно найти, что вероятность ошибки при передаче от предыдущей станции к следующей (равная вероятности того, что помеха превысит 0,5 В) равна 0,25×10^-6. Следовательно, вероятность ошибки при передаче на всю длину линии есть 0,25×10^-4. Чтобы передать то же сообщение, что и в предыдущем случае, т. е. значение с точностью до 0,1 некоторой величины, лежащей в пределах от 0 до 1, нам достаточно послать четыре сигнала вида «да» или «нет». Вероятность того, что хотя бы в одном из сигналов будет допущена ошибка, равна 10^-4. Итак, полная вероятность ошибки при дискретном способе составляет 0,01% против 90% при непрерывном способе.

1.6. Информация

Начав описывать конкретную кибернетическую систему, мы невольно употребляем термин информация, который в своем разговорном, неформальном значении хорошо знаком и понятен каждому культурному человеку. Теперь мы введем кибернетическое понятие информации, имеющее точный количественный смысл.

Представим себе две подсистемы A и B (рис. 1.2), связанные между собой таким образом, что изменение состояния системы A влечет изменение состояния системы B. Это можно выразить такими словами: подсистема A воздействует на подсистему B.

Рис. 1.2. Связанные подсистемы

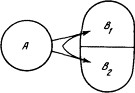
Рассмотрим подсистемы B в некоторый момент времени t₁ и в более поздний момент времени t₂. Первое обозначим через S₁, второе — через S₂. Cостояние S₂ зависит от состояния S₁. Однако оно не определяется состоянием S₁ однозначно, а зависит от него вероятностным образом, ибо мы рассматриваем не идеализированную теоретическую систему, подчиняющуюся детерминистическому закону движения, а реальную систему, состояния которой S суть результаты опытных данных. При таком подходе тоже можно говорить о законе движения, понимая его в вероятностном смысле, т. е. как условную вероятность состояния S₂ в момент t₂ при условии, что в момент t₁ система имела состояние S₁. Теперь забудем на минуту о законе движения. Обозначим через N полное число возможных состояний подсистемы B и будем представлять себе дело таким образом, что в любой момент времени подсистема B может с равной вероятностью принять любое из N состояний независимо от того, какое состояние она имела в предыдущий момент. Попытаемся количественно выразить степень (или силу) причинно-следственного влияния подсистемы A на такую безынерционную и «беззаконную» подсистему B. Пусть B под действием A переходит в некоторое совершенно определенное состояние. Ясно, что «сила влияния», которая требуется для этого от A, зависит от числа N и тем больше, чем больше N. Если, например, N = 2, то система B, даже будучи совершенно не связана с A, под действием каких-то случайных причин может с вероятностью ¹/₂ перейти в то самое состояние, которое «рекомендует» система A. Если же N = 10⁹, то, заметив такое совпадение, мы вряд ли усомнимся во влиянии A на B. Следовательно, мерой «силы влияния» A на B в данном единичном акте, т. е. по существу мерой интенсивности причинно-следственной связи между двумя событиями — состоянием подсистемы A в интервале времени от t₁ до t₂ и состоянием подсистемы B в момент t₂ — должна служить какая-то монотонно возрастающая функция N. В кибернетике эта мера называется количеством информации, переданной от A к B между моментами времени t₁ и t₂, а монотонно возрастающей функцией служит логарифм. Итак, в нашем примере количество информации I, переданное от A к B, равно log N.

Выбор логарифмической функции определяется тем ее свойством, что

log N₁ N₂ = log N₁ + log N₂.

Пусть система A действует на систему B, состоящую из двух независимых подсистем B₁ и B₂ с возможным числом состояний N₁ и N₂ соответственно (рис. 1.3). Тогда число состояний системы B есть N₁×N₂, а количество информации I, которое надо передать системе B, чтобы она приняла одно определенное состояние, есть благодаря указанному свойству логарифма сумма

I = log N₁ N₂ = log N₁ + log N₂ = I₁ + I₂,

где I₁ и I₂ — количества информации, потребные подсистемам B₁ и B₂. Благодаря этому свойству информация принимает определенные черты субстанции, она распределяется по независимым подсистемам подобно жидкости, разливающейся по сосудам. Мы говорим о слиянии и разделении информационных потоков, об информационной емкости, о переработке информации и ее хранении.

Рис. 1.3. Воздействие на две независимые подсистемы

Вопрос о хранении информации связан с вопросом о законе движения. Выше мы мысленно отключили закон движения, чтобы определить понятие передачи информации. Если мы теперь рассмотрим закон движения с новой точки зрения, то он сводится к передаче информации от системы B в момент времени t₁ к той же самой системе B в момент t₂. Если состояние системы не меняется с течением времени, то это и есть хранение информации. Если состояние S₂ однозначно определяется состоянием S₁ в предыдущий момент времени, то систему называют полностью детерминированной. Если имеет место однозначная зависимость S₁ от S₂, то систему называют обратимой; для обратимой системы можно, в принципе, по заданному состоянию вычислить все предыдущие состояния, поэтому потери информации не происходит. Если система необратима, информация теряется. Закон движения в сущности есть нечто, регулирующее поток информации во времени от системы к ней самой.

Рис. 1.4. Канал связи

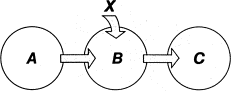
На рис. 1.4 изображена схема передачи информации от системы A к системе C через систему B. Эта последняя носит название канала связи. На состояние B может влиять не только состояние системы A, но еще какой-либо не поддающийся контролю фактор X, называемый помехой. Конечное состояние системы C в этом случае зависит не только от состояния A, но и от фактора Х (искажение информации). Еще одна важная схема обмена информации изображена на рис. 1.5. Это так называемая схема обратной связи. Состояние системы A в момент времени t₁ влияет на состояние B в момент времени t₂, а это последнее влияет на состояние системы A в момент времени t₃. Путь информации замыкается.

Рис. 1.5. Обратная связь

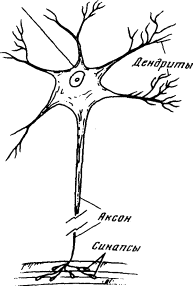
На этом мы пока ограничим наше знакомство с общими понятиями кибернетики и вернемся к эволюции жизни на Земле.

1.7. Нейрон

Внешний вид нервной клетки (нейрона) показан схематически на рис. 1.6. Нейрон состоит из довольно крупного (до 0,1 мм) тела, от которого отходят несколько отростков — дендритов, дающих начало все более и более тонким отросткам, подобно ветвям дерева. Кроме дендритов, от тела нервной клетки отходит еще один отросток — аксон, напоминающий длинный тонкий провод. Аксоны бывают очень длинны — до метра — и заканчиваются, подобно дендритам, древовидным разветвлением. На концах веточек, отходящих от аксона, можно видеть маленькие пластинки или луковички. Луковички одного нейрона близко подходят к различным участкам тела или дендритов другого нейрона, почти прикасаясь к ним. Эти контакты носят название синапсов; через них нейроны взаимодействуют друг с другом. Число луковичек, подходящих к дендритам одного нейрона, может исчисляться десятками и даже сотнями. Таким образом, нейроны очень тесно связаны друг с другом; они образуют нервную сеть.

Рис. 1.6. Схема строения нейрона

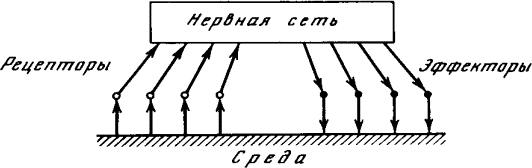
С точки зрения физико-химических свойств, в первую очередь распределения электрического потенциала по поверхности клетки, нейрон может находиться в одном из двух состояний, которые называют состояниями покоя или возбуждения, и время от времени нейрон под воздействием других нейронов или ка­ких-либо внешних факторов переходит из одного состояния в другое. Этот процесс, конечно, занимает некоторое время, так что исследователь, изучающий, например, динамику электрического состояния нейрона, рассматривает его как систему с непрерывными состояниями. Однако, сведения, которыми мы располагаем в настоящее время, указывают на то, что для работы нервной системы в целом существенным является не характер переходных процессов, а самый факт нахождения тех или иных нейронов в спокойном или возбужденном состоянии. Поэтому можно считать, что нервная сеть — это дискретная система, состоящая из элементарных подсистем — нейронов — с двумя состояниями.

Когда нейрон возбуждается, волна электрического потенциала бежит по аксону и доходит до луковичек на его разветвленных концах. С луковичек через синапсы возбуждение передается на соответствующие участки клеточной поверхности других нейронов. Поведение нейрона зависит от состояния, в котором находятся его синапсы. Простейшая модель функционирования нервной сети исходит из предположения, что состояние нейрона в каждый момент времени есть однозначная функция состояния его синапсов. Экспериментально установлено, что возбуждение одних синапсов способствует возбуждению клетки, другие синапсы, напротив, будучи возбуждены, препятствуют возбуждению в клетке. Наконец, некоторые синапсы могут вовсе не проводить возбуждение от луковичек и, следовательно, не влиять на состояние нейрона. Установлено также, что проводимость синапса увеличивается после первого прохождения через него возбуждения и нескольких следующих прохождений. Происходит как бы замыкание контакта. Это объясняет, каким образом без изменения положения нейронов друг относительно друга может меняться система связей между нейронами и, следовательно, характер функционирования нервной сети.

Представление о нейроне как о мгновенном переработчике информации, поступающей от синапсов, является, конечно, сильно упрощенным. Нейрон, как и всякая клетка, — сложная машина, работа которой еще мало изучена. Эта машина обладает большой внутренней памятью, поэтому ее реакции на внешнее воздействие могут отличаться большим разнообразием. Однако, чтобы понять общие закономерности работы нервной системы, мы можем отвлечься от этих сложностей (у нас, собственно говоря, нет другого выхода!) и исходить из очерченной выше простой модели.

1.8. Нервная сеть

Общая схема нервной системы «кибернетического животного» в его взаимодействии с внешней средой представлена на рис. 1.7. Чувствительные нервные клетки, возбуждающиеся под действием внешних факторов, носят название рецепторов (т. е. получателей), ибо они служат первичным приемником информации о состоянии внешней среды. Эта информация поступает в нервную сеть и перерабатывается ею. В результате возбуждаются некоторые из нервных клеток, называемых эффекторами. Разветвления эффекторных клеток пронизывают те ткани организма, на которые нервная система оказывает непосредственное влияние. Возбуждение эффектора вызывает сокращение соответствующей мышцы или стимулирует деятельность соответствующей железы. Состояние всех рецепторов в некоторый момент времени назовем ситуацией в этот момент. (Точнее было бы говорить «результат воздействия ситуации на органы чувств», но это слишком длинно.) Состояние всех эффекторов назовем действием. Следовательно, роль нервной сети сводится к преобразованию ситуации в действие.

Рис. 1.7. Нервная система «кибернетического животного»

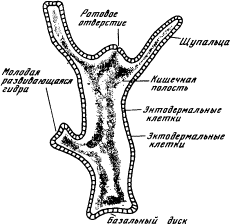
Под «средой» на рис. 1.7 удобно понимать не только предметы, окружающие животное, но также и его костно-мышечную систему и вообще все то, что не входит в состав нервной системы. Это снимает необходимость изображать на схеме отдельно тело животного и «не тело», тем более что никакого принципиального значения для деятельности нервной системы это разграничение не имеет. Важно лишь то, что возбуждение эффекторов приводит к определенным переменам в «среде». При том общем подходе к проблеме, который лежит в основе нашего рассмотрения, нам достаточно квалифицировать эти изменения как «полезные» или «вредные» для животного, не вдаваясь в дальнейшие подробности.

Какова задача нервной системы? Способствовать выживанию и размножению животного. Нервная система работает хорошо, когда возбуждение эффекторов приводит к полезным с этой точки зрения изменениям состояния среды, и плохо — в противном случае. Совершенствуясь в процессе эволюции, нервная система выполняет эту задачу все лучше и лучше. Каким образом это удается? Каким законам подчиняется процесс ее совершенствования?

Мы попытаемся ответить на эти вопросы, выделив в эволюции нервной системы животных несколько этапов, четко отличающихся между собой с кибернетической точки зрения, и показав, что из основного закона эволюции следует неизбежность перехода от каждого предыдущего этапа к каждому последующему. Так как в кибернетическую эру эволюция живых существ — это прежде всего эволюция их нервной системы, периодизация развития нервной системы дает периодизацию развития жизни в целом.

1.9. Простой рефлекс (раздражимость)

Простейший вариант нервной сети — это вообще ее отсутствие. В этом случае рецепторы непосредственно связаны с эффекторами и возбуждение с одного или нескольких рецепторов передается на один или несколько эффекторов. Такую прямую связь между возбуждением рецептора и эффектора мы назовем простым рефлексом.

Этот этап — третий по нашей сквозной нумерации этапов эволюции — является пограничным между химической и кибернетической эрами. Тип кишечнополостных представляет животных, застывших на уровне простого рефлекса. Возьмем, например, гидру, которую изучают в школе как типичного представителя кишечнополостных. Тело гидры (рис. 1.8) имеет вид удлиненного мешочка. Его внутренность — кишечная полость — сообщается с внешней средой через ротовое отверстие, окруженное несколькими щупальцами. Стенки мешочка состоят из двух слоев клеток: внутреннего (энтодерма) и внешнего (эктодерма). И в эктодерме, и в энтодерме много мышечных клеток, содержащих волоконца, которые могут сокращаться, приводя тело гидры в движение. Кроме того, в эктодерме есть и нервные клетки, причем клетки, расположенные ближе всего к поверхности, — это рецепторы, а клетки, заложенные глубже, среди мышц, — эффекторы. Если к гидре прикоснуться иглой, она сжимается в комочек. Это простой рефлекс, вызванный передачей возбуждения от рецепторов к эффекторам.

Рис. 1.8. Строение гидры

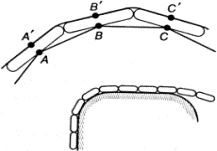
Но гидра способна и к гораздо более сложному поведению. Захватив добычу, она подтягивает ее щупальцами к ротовому отверстию и заглатывает. Такое поведение тоже можно объяснить совокупным действием простых рефлексов, связывающих эффекторы и рецепторы локально — в пределах большого участка тела. Например, следующая модель щупальца объясняет его способность обвиваться вокруг падающих предметов (рис. 1.9). Представим себе некоторое количество звеньев, соединенных между собой шарнирами (для простоты рассматриваем плоскую картину). Точки A и B, A' и B', B и C, В' и C' и т. д. соединены между собой тяжами, которые могут сокращаться (мышцы). Все эти точки являются чувствительными, возбуждаясь от прикосновения к предмету (рецепторы). Возбуждение каждой точки приводит к сокращению двух соседних с нею тяжей (рефлекс).

Рис. 1.9. Модель щупальца

1.10. Сложный рефлекс

Простая рефлекторная связь между возбудимой и мышечной клетками естественно возникает в процессе эволюции по методу проб и ошибок: если оказывается, что корреляция между возбуждением одной клетки и сокращением другой полезна для животного, то эта корреляция устанавливается и закрепляется. При механическом копировании связанных клеток в процессе роста и размножения природа получает систему параллельно действующих простых рефлексов, подобную щупальцу гидры. Но когда в ее (природы) распоряжении оказывается множество рецепторов и эффекторов, связанных попарно или локально, у нее «возникает искушение» усложнить систему связей путем введения промежуточных нейронов. Выгодность этого следует из того, что при наличии системы связей между всеми нейронами становятся возможными такие формы поведения, которые невозможны при ограничении парными или локальными связями. Последнее утверждение можно доказать простым подсчетом всевозможных способов преобразования ситуации в действие при том и другом способах связи. Пусть, например, у нас есть n попарно связанных рецепторов и эффекторов. Связь в каждой паре может быть либо положительная (возбуждение вызывает возбуждение, покой — покой), либо отрицательная (возбуждение вызывает покой, покой — возбуждение). Следовательно, всего возможно 2ⁿ вариантов связи, т. е. 2ⁿ вариантов поведения. Если же предположить, что система связей может быть произвольная, т. е. состояние возбуждения или покоя каждого эффектора может произвольным образом зависеть от состояния всех рецепторов, то подсчет всевозможных вариантов поведения приводит к числу 2⁽²ⁿ⁾ⁿ, неизмеримо большему, чем 2ⁿ. Совершенно такой же расчет приводит к заключению, что объединение любых подсистем, связывающих независимо друг от друга группы рецепторов и эффекторов в единую систему, всегда приводит к огромному возрастанию числа возможных вариантов поведения. Поэтому на протяжении всей истории жизни эволюция нервной системы проходит под знаком увеличения централизации.

Однако централизация централизации рознь. Если связать все нейроны в один бессмысленно запутанный клубок, то, несмотря на крайнюю «централизованность» такой системы, она вряд ли будет иметь шансы выжить в борьбе за существование. Централизация ставит следующую проблему: как из всех мыслимых способов соединения многих рецепторов с многими эффекторами (с помощью промежуточных нейронов, если потребуется) выбрать такой способ, который будет каждой ситуации сопоставлять правильное, т. е. полезное для выживания и размножения, действие? Ведь подавляющее большинство способов соединения не обладает этим свойством.

Мы знаем, что каждый новый шаг на пути усложнения живых структур природа делает по методу проб и ошибок. Посмотрим, что дает непосредственное применение метода проб и ошибок к нашей проблеме. Рассмотрим для примера небольшую систему из ста рецепторов и ста эффекторов. Допустим, что в нашем распоряжении сколько угодно нейронов для создания промежуточной нервной сети и что мы умеем легко определять, дает ли данный способ соединения нейронов правильную реакцию на каждую ситуацию. Будем перебирать все мыслимые способы, пока не натолкнемся на нужный. При n = 100 число функционально различных нервных сетей между n рецепторами и n эффекторами есть

2⁽²ⁿ⁾ⁿ ≈ 10⁽¹⁰³²⁾.

Число это невообразимо велико. Перебор такого числа вариантов недоступен не только нам, но и нашей матушке-природе. Если бы каждый атом во всей видимой нами части Вселенной занимался просмотром вариантов и перебирал бы их со скоростью миллиард штук в секунду, то и за миллиард миллиардов лет (а наша Земля существует не более десяти миллиардов лет) не была бы просмотрена и миллиардная доля общего числа вариантов.

Между тем как-то ведь происходит формирование эффективно работающей нервной сети! Причем число рецепторов и эффекторов у высших животных исчисляется не сотнями и не тысячами, а миллионами.

Разгадка кроется в иерархическом строении нервной системы.

Здесь нам снова необходим экскурс в область общекибернетических понятий. Четвертый этап эволюции мы назовем этапом сложного рефлекса, но дать определение этому понятию сможем лишь после того, как познакомимся с некоторыми фактами об иерархически устроенных нервных сетях.

¹ Мы следуем в основном докладу С.Э.Шноля «Сущность жизни. Инвариантность общего направления биологической эволюции» (Диалектика и современное естествознание: Матер. семинара. Дубна, 1967)