|
||
|
|
||
| Главная ≫ Инфотека ≫ Кибернетика, когнитивистика ≫ Занимательный компьютер: О разуме, машинах и метафизике // Дьюдни А. К. |
Занимательный компьютер: О разуме, машинах и метафизикеДьюдни А. К.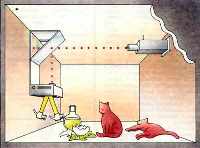
«Подчиняется ли разум физическим законам?
Да и что такое физические законы?» РОДЖЕР ПЕНРОУЗ «Новый ум императора»
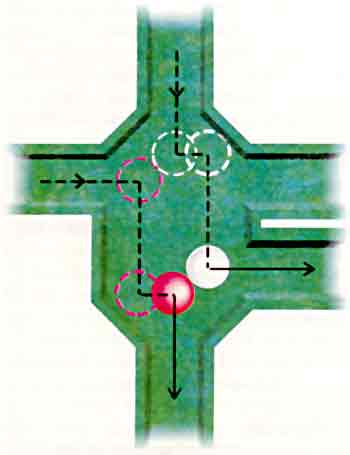
ЧЕЛОВЕЧЕСКИЙ разум превосходит системы искусственного интеллекта, потому что использует физические законы на квантовомеханическом уровне. К такому не бесспорному утверждению склоняется в своей новой книге Роджер Пенроуз, известный ученый, работающий в области математической физики. Хотя (как признает Пенроуз) это утверждение в настоящее время не может быть строго доказано, некоторые интригующие аргументы, содержащиеся в его книге «Новый ум императора», дают достаточно серьезные основания усомниться в справедливости философских положений, которые лежат в основе искусственного интеллекта. Ниже мы рассмотрим аргументы Пенроуза, но поскольку в данной рубрике мы пользуемся своим компасом, совершая плавание по неизведанным морям, я подвергну критике некоторые его выводы, а некоторые его идеи попробую развить. В частности, вопрос «Как же все-таки люди думают?» я поставлю в более широком плане и сформулирую его так: «Получат ли люди когда-нибудь достаточно знаний, чтобы ответить на такой вопрос?» Если структура Вселенной бесконечна, то люди, вероятно, никогда не смогут ответить на этот вопрос в полной мере. С другой стороны, бесконечная регрессия структуры позволяет подойти к ответу на поставленный вопрос расчетным путем. Но прежде чем погрузиться в рассматриваемую проблему, я приглашаю читателей вместе со мной исследовать глубины «Нового ума императора». Сначала мы посетим знаменитую китайскую комнату, чтобы узнать, понимают ли «разумные» программы, что они делают. Затем нанесем короткий визит в бильярдный зал, где увидим бильярдный стол, на котором с учетом законов классической физики об упругих столкновениях могут совершаться практически любые вычисления. Перейдя в лабораторию Эрвина Шредингера, мы справимся о здоровье его кошки, чтобы проанализировать отношение между классической физикой и квантовой механикой. И наконец, достигнув пункта назначения, мы рассмотрим компьютер с бесконечным интеллектом, способный решать такие задачи, которые ни один обыкновенный конечный компьютер никогда не сможет одолеть. Несколько лет назад внимание Пенроуза привлекла телевизионная передача, в которой сторонники искусственного интеллекта позволили себе, с его точки зрения, неосторожное заявление. Они утверждали, что компьютеры, принципиально не очень отличающиеся от существующих, через какое-то время смогут проявить себя не менее разумными, чем люди, - а может быть, и превзойти их. Пенроуз был раздражен этим заявлением. Каким образом все тонкости человеческого интеллекта, в особенности его творческие способности, могут возникнуть из алгоритма, «щелкающего» в электронном мозге компьютера? Эти невероятные утверждения заставили его заняться исследованиями, которые, в свою очередь, привели к появлению книги «Новый ум императора». Методично изучив теорию вычислений, Пенроуз подверг критике одно из ее ключевых положений - тест Тьюринга. Многие специалисты принимают этот тест в качестве критерия, с помощью которого можно отличить разумную программу от неразумной. Тест заключается в следующем. Человек-экзаменатор печатает сообщения двум скрытым от него субъектам, одно человеку, другое компьютеру, запрограммированному так, чтобы разумно отвечать на вопросы. Если в ходе достаточно продолжительного эксперимента экзаменатор не сможет отличить ответы человека от ответов компьютера, то программа успешно проходит тест Тьюринга. Пенроуз отмечает, что тест дает лишь косвенное свидетельство наличия разума. В конце концов, то, что иногда кажется разумным, на самом деле может оказаться пародией, точно так же, как предмет и его зеркальное отображение, которые внешне, хотя и выглядят одинаково, все же различаются во многих других аспектах. Пенроуз утверждает, что прямой метод измерения разума может потребовать значительно большего, чем простой тест Тьюринга. Чтобы подкрепить свою аргументацию, Пенроуз прибегает к так называемой «китайской комнате», своеобразной вариации на тему теста Тьюринга, которая была предложена философом Дж. Сирле. Человек-экзаменатор стоит перед дверью в комнату, через которую могут входит и выходить лишь письменные сообщения. Экзаменатор пишет некую историю, а также ряд относящихся к ней вопросов и передает сообщение в комнату. При этом необходимо соблюдать одно необычное требование: сообщения, как входящие, так и выходящие, должны быть написаны китайскими иероглифами. Чтобы ситуация выглядела еще более необычной, человек, находящийся в комнате, выполняет программу, которая реагирует на представленную ей историю, отвечая на прилагаемые к ней вопросы. Этот человек полностью заменяет собой компьютер. Его работа была бы скучной и утомительной, но после того, как он овладевает правилами работы машины, у него уже не возникает никаких сложностей. Гарантией неведения человека-компьютера служит то, что он не знает китайского языка. Тем не менее то, что (или кто) находится в китайской комнате, кажется, прекрасно понимает рассказ и разумно отвечает на вопросы. Этот мысленный эксперимент, по мнению Пенроуза, приводит нас к выводу, что «простой факт выполнения удачного алгоритма еще не свидетельствует о наличии какого бы то ни было понимания». Этот вывод, разумеется, справедлив по отношению к тому, кто выполняет программу, будь то человек или компьютер. В конце концов, в принципе, выполняется ли программа человеком или компьютером, не имеет значения для взаимодействия этой программы с внешним миром. Но именно по этой причине человек в китайской комнате - это что-то вроде соломенного чучела. Никто не станет придираться к программе лишь на том основании, что выполняющая ее аппаратура ничего в ней не понимает. С еще большей строгостью можно сказать, что никому и в голову не придет критиковать поведение нейрона за то, что он не понимает смысла в тех импульсах, которые воздействуют на него и которые он сам вырабатывает. Это справедливо, независимо от того, выполняет нейрон лишь часть алгоритма или решает значительно более сложные задачи. Таким образом, любое свидетельство о наличии разума в искусственном интеллекте должно содержаться в самом алгоритме. Именно здесь Пенроуз наносит свой следующий удар. Мир алгоритмов по существу сводится к миру вычислимых задач. По словам Пенроуза, алгоритмы представляют собой «лишь очень узкую и ограниченную часть математики». Пенроуз верит (так же, как я и многие другие математики), что математические объекты обладают своеобразной платонической реальностью. Одно из свидетельств существования таких объектов заключается в нашей полной неспособности изменить их. Они просто даны нам, как горы или океаны. В качестве примера Пенроуз приводит множество Мандельброта. Оно не было «изобретено» Бенуа Б. Мандельбротом, известным исследователем из фирмы IBM, оно было им открыто. Подобно планете Нептун, множество существовало задолго до того, как его увидели люди и поняли его значение. Множество Мандельброта несет в себе важное сообщение тем, кто считает его созданием компьютера. Это вовсе не так. Множество Мандельброта даже невозможно вычислить! Не слышу ли я возгласов возмущения? Строго говоря, Пенроуз прав. Множество Мандельброта, хотя оно является лишь одним из объектов платонического мира, находится довольно далеко от сферы интересов людей, которые занимаются исследованием алгоритмов. Читатели, наверное, помнят, что внутреннюю часть множества можно найти с помощью итерационного процесса: комплексное число с возводится в квадрат, затем результат, z1, возводится в квадрат и прибавляется к с, затем второй результат, z2 возводится в квадрат и складывается с с и т. д. Если последовательность значений z, полученных таким образом, никогда не уходит в бесконечность, то с принадлежит внутренней части множества. Однако здесь возникает трудный вопрос. Как долго следует продолжать процесс, чтобы убедиться, что последовательность остается ограниченной? По существу правильный ответ - бесконечно долго! На практике вычисления прерываются на некотором этапе. При этом неизбежно во множество оказываются включенными несколько точек, не принадлежащих ему, поскольку для них должно пройти больше времени, прежде чем проявится неограниченность соответствующих последовательностей. Трудности, возникающие при вычислении множества Мандельброта, ничтожны в сравнении с другими ограничениями, присущими алгоритмам. Например, математика сама по себе формально считается построенной из аксиоматических систем. Предложите небольшой набор аксиом, определите одно-два правила вывода - и у вас есть математическая теория. Концептуальный алгоритм, называемый «алгоритмом британского музея», генерирует все возможные теоремы, которые доказуемы в рамках формальной системы аксиом и правил вывода. К сожалению, полученные таким образом теоремы необязательно содержат в себе все истины данной системы. Это открытие, сделанное математиком Куртом Геделем, сокрушило надежды на то, что вся математика может быть механизирована. Пенроуз пользуется знаменитой теоремой Геделя как свидетельством, что человеческий интеллект способен превзойти возможности алгоритмического метода: «... из теоремы Геделя со всей очевидностью следует, что понятие математической истины не может быть заключено в рамки какой бы то ни было формальной схемы». Но тогда возникает вопрос: «Как может сама теорема Геделя быть результатом алгоритма?» Я не могу дать ответа на этот вопрос, хотя мне известно, что он уже обсуждался. Возможно, что теорему Геделя можно вывести из других аксиом и правил вывода и, следовательно, ее можно получить при помощи алгоритма. Теорема может быть лишь частью нескончаемого потока метатеорем. Я был бы благодарен знающим читателям, которые помогли бы разобраться в этом вопросе. Однако, каким бы ни было наше мнение на этот счет, «Новый ум императора» атакует претензии искусственного интеллекта на другом фронте: со стороны физики вычислений. Пенроуз склонен считать, что вычислительные процессы в значительно большей мере «чувствуют себя как дома» в ощутимом мире классической физики, нежели в непостижимом царстве квантовой механики. Современный компьютер является детерминированной системой, которая главным образом просто выполняет алгоритмы. В несколько шутливой манере Пенроуз выбирает бильярд, так часто служащий в качестве примера при изучении классических столкновений, как подходящую среду для компьютера, работающего в классическом стиле. Если изменить конфигурацию бортиков бильярдного стола, то можно построить своеобразный компьютер, в котором бильярдные шары действовали бы в качестве носителей сигналов, а их взаимодействие играло бы роль логических операций. Бильярдный компьютер был впервые сконструирован несколько лет назад исследователями из Массачусетского технологического института Э. Фредкином и Т. Тоффоли. О простоте и эффективности бильярдного компьютера читатели могут судить сами, рассмотрев диаграмму, приведенную внизу. На диаграмме представлено бильярдное логическое устройство. Два входных канала принимают движущиеся шары в специальную камеру, которая имеет три выходных канала. Если в камеру через один из входных каналов входит только один шар, он покинет ее либо по нижнему, либо по верхнему правому выходному каналу. Однако если в камеру одновременно входят два шара, то один из них покинет ее через выходной канал, расположенный справа внизу. Присутствие или отсутствие шара в данном выходном канале представляет результат известной логической операции, выполняемой вентилем И. На выходе шар появляется тогда и только тогда, когда один шар поступает в первый входной канал и другой шар - во второй канал.
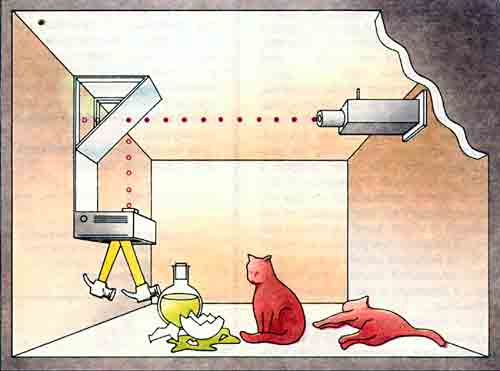
Компьютер можно построить, пользуясь вентилями только что описанного типа и еще одного типа, представляющего собой камеру, которую шар покидает по определенному каналу тогда и только тогда, когда по другому каналу не входит шар. Читателям, наверное, будет интересно сконструировать камеру такого типа, имея в виду, что полезную роль в этом устройстве могут сыграть дополнительные шары. Нам всем нравится наблюдать за плавными, классическими движениями бильярдных шаров. У них есть и другие желательные свойства, о которых мы едва ли задумываемся. Например, никому и никогда не приходило в голову, что бильярдный шар может оказаться сразу в двух местах в один и тот же момент времени. Однако в квантовой механике такие явления вполне допустимы. Квантовомеханические системы, такие как в знаменитом эксперименте с двумя щелями, допускают, возможность одновременного присутствия фотона в двух местах (см. Э. Шимони. Реальность квантового мира, «В мире науки», 1988, № 3). В нескольких словах: когда фотоны проходят через двойную щель, их можно рассматривать как волны, интерферирующие сами с собой. На экране позади щелей появляется интерференционная картина, если только мы не установим по детектору у каждой щели. Сам акт наблюдения как бы заставляет фотон решиться, через какую щель ему пройти! Это явление называется коллапсом вектора состояния. Эксперимент можно расширить для щелей, отстоящих друг от друга на километр (и даже на расстояние, равное световому году). Как утверждают многие физики, фотон может лишь в том случае решить, через какую щель ему пройти, если он по существу находится в обоих местах одновременно. В какой точке бесконечного множества масштабов, от атомного до галактического, квантовомеханическая система становится классической? Эта дилемма иллюстрируется знаменитой кошкой Шредингера. В воображаемом эксперименте ученый, не страшащийся активистов движения в защиту животных, помещает кошку и сосуд с ядовитым газом в камеру, содержащую лазер, наполовину посеребренное зеркало, фотодетектор и молоточек. После того как дверь в камеру заперли, лазер испускает фотон по направлению к зеркалу. Если фотон проходит через него насквозь, кошке не причиняется никакого вреда. Если же фотон отражается от зеркала, он попадает в фотодетектор; последний приводит в действие молоточек, который ударяет по сосуду с газом и разбивает его; ядовитый газ убивает кошку. Находясь снаружи, мы не можем узнать, жива кошка или нет.
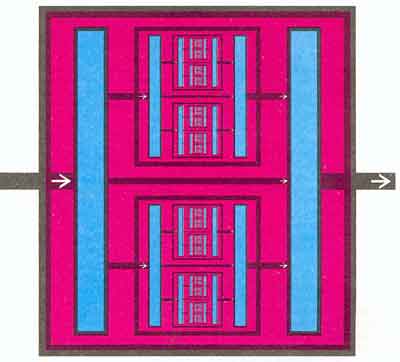
В мире квантовой механики два возможных события могут сосуществовать как суперпозиция двух реальностей. В классическом же мире может произойти либо одно, либо другое событие. Вектор состояния (а с ним, возможно, и жизнь кошки) должен претерпеть коллапс. По мнению Пенроуза, в современной теории отсутствует переходная область между классической физикой и квантовой механикой. Теория как бы расщепляется на две части, вместо того чтобы плавно переходить от одного масштаба к другому на всем их протяжении. Возможно, желаемый синтез будет получен с помощью теории квантовой гравитации. Теперь вернемся, наконец, к человеческому разуму. Пенроуз полагает, что в человеческом сознании присутствует неалгоритмическая компонента. На квантовом уровне возможно сосуществование взаимоисключающих, альтернативных вариантов реальности. Одно квантовое состояние может в принципе состоять из большого количества различных, одновременно проходящих явлений. Может быть, человеческий мозг каким-то образом использует такие явления? Едва ли мне удастся проанализировать эту кажущуюся такой необычной возможность так же хорошо, как это делает Пенроуз. Поэтому я советую заинтересованным читателям приобрести и прочитать его книгу. Однако у меня возникло желание рассмотреть другой вопрос, имеющий некоторое отношение к затронутой теме. Могут ли люди количественно оценить возможности своего интеллекта во Вселенной, которая обладает бесконечной структурой? В самом деле, существование какого-то определенного предела в структуре материи, будь то одна элементарная частица или набор таких частиц, кажется невероятным. При этом я имею в виду не только частицы, но вообще любую структуру, скажем энергетическую или чисто информационную, лежащую в основе обсуждаемых явлений. Мне представляется, что физика сама по себе может оказаться бесконечной наукой по той простой причине, что, как только будет открыта какая-то предельная «элементарная» структура, сразу же возникнет проблема объяснения предельных элементарных законов и самого факта их существования. Во всяком случае, я предпочитаю жить во Вселенной, обладающей бесконечной структурой. Во-первых, наш разум мог бы лучше понять такую Вселенную по сравнению со Вселенной, которая обладает конечной структурой. Компьютеры конструируются таким образом, чтобы исключить влияние любого физического процесса, протекающего на уровне, масштабы которого меньше определенного порога. Алгоритм должен быть защищен от «ошибок». Возможно, наш мозг структурирован так же, но, возможно, что и не так, считает Пенроуз. Не исключено, что физические явления, протекающие на атомарном уровне, играют важную роль в процессе нашего мышления. Что касается молекулярного уровня, то это определенно так. Достаточно лишь вспомнить о влиянии молекул нейротрансмиттеров на поведение нервных клеток. Более того, хорошо известно, что природа обладает свойством использовать физические возможности, ставя их на службу для реализации биологических операций. Если физические структуры простираются до определенного уровня, то имеем ли мы какие-то априорные основания полагать, что мозг не может воспользоваться явлениями, протекающими на этом уровне? А что, если мозг способен пользоваться всеми уровнями структуры в бесконечно структурированной Вселенной? Чтобы продемонстрировать в самой грубой форме потенциальные возможности бесконечного мозга, я построил схему бесконечного компьютера, который пользуется в своей работе структурами всех уровней. В целях удобства демонстрации я буду условно считать, что во всех масштабах физические структуры обладают классическими свойствами. Мой бесконечный компьютер по существу представляет собой квадрат, содержащий два прямоугольника и два других квадрата меньшего размера. Входная линия подведена слева к большому квадрату, и войдя в него, она сразу идет к первому прямоугольнику. Последний представляет собой устройство обработки сигналов, которое я назову модулем подстановки. От модуля подстановки отходит по одной линии к каждому из меньших квадратов, а также к другому прямоугольнику, который мы будем ниже называть модулем сообщения.
Структура этого компьютера обладает свойством бесконечной регрессии. Каждый из меньших квадратов является точной копией большего квадрата, но имеет вдвое меньшие размеры. Когда сигнал распространяется по проводникам и модулям вдвое меньшего размера, ему требуется вдвое меньше времени для прохождения соответствующего пути, поэтому модули подстановки и сообщения срабатывают в два раза быстрее соответствующих модулей внешнего уровня. Бесконечный компьютер решает знаменитую задачу о преобразовании слов, изобретенную математиком Акселем Туэ. В этой задаче даны два слова и словарь допустимых подстановок. Можно ли, пользуясь только допустимыми подстановками, получить второе слово из первого? Рассмотрим задачу на следующем примере: предположим, первое «слово» представлено цепочкой 100101110, а второе - 01011101110. Возможно ли прийти от первого слова ко второму, пользуясь подстановками 010 вместо 110, 10 вместо 111 и 100 вместо 001? Пример был выбран совершенно произвольно, и я специально не буду пытаться решить его. Может случиться так, что ни одна последовательность подстановок не приведет к преобразованию первой цепочки во вторую. В то же время такая последовательность существует. В процессе применения подстановок могут возникнуть очень длинные промежуточные слова. В этом и заключается проблема. Так же, как и в отношении некоторых точек множества Мандельброта, мы по существу не можем прийти к ответу. Не существует алгоритма решения этой задачи, поскольку любой алгоритм (по определению) должен когда-то остановиться. Опасность состоит в том, что алгоритм может остановиться прежде, чем будет получен ответ. По этой причине о задаче Туэ говорят как о неразрешимой. Ни одна компьютерная программа, даже в принципе, не сможет решить всех частных случаев этой задачи. Введем условие задачи в бесконечный компьютер. Слово, к которому нужно прийти, вводится в компьютер через его главную входную линию. За четверть секунды оно попадает в первый подстановочный модуль. Затем слово передается этим подстановочным модулем двум другим подстановочным модулям следующего уровня. Однако теперь передача данных потребует уже только 1/8 секунды. Пересылки на следующие уровни потребуют соответственно 1/16, затем 1/32 с и т.д. Время, которое потребуется, чтобы загрузить все подстановочные модули вторым словом, составит, таким образом, половину секунды. Потом в ходе аналогичного процесса, протекающего с той же скоростью, в компьютер вводятся три (или сколько угодно) подстановочные формулы. Однако на этот раз различные подстановочные модули на разных уровнях запрограммированы так, чтобы воспринимать только определенные подстановки из вводимой последовательности. Каждый подстановочный модуль, согласно содержащейся в нем программе, должен всегда пытаться проводить определенную подстановку в определенной позиции слова, которое поступает в него из внешнего уровня. Подробное описание схемы распределения подстановок и позиций в слове по различным модулям, наверное, утомило бы читателя, поэтому я опускаю его. Однако это не должно помешать тем, кто любит анализировать бесконечные процессы, представить себе, каким образом можно все устроить. Вычисление начинается, когда мы посылаем первое слово в компьютер. Первый подстановочный модуль пытается провести свою подстановку на отведенной для нее позиции введенного слова. Если подстановка не может быть выполнена в требуемом месте, слово передается следующему подстановочному модулю, принадлежащему более низкому уровню машины; если ему удается провести подстановку, он посылает преобразованное слово в квадрат более высокого уровня. Если подстановка оказывается успешной и полученное в результате слово совпадает со вторым заданным словом, хранящимся в памяти подстановочного модуля, то последний посылает сигнал модулю сообщения: «успешно». Каждый квадрат каждого уровня работает в соответствии с только что описанным алгоритмом. Как уже говорилось выше, всегда можно распределить подстановки (и позиции, в которых их следует применять) по бесконечному компьютеру таким образом, чтобы задача преобразования слов успешно решалась. Ответ будет выдан не позднее чем через одну секунду: половина секунды потребуется, чтобы провести вычисления на всем пути до бесконечно малых модулей, и половина секунды на то, чтобы сообщение «успешно» достигло главной выходной линии компьютера. Если подходящей последовательности подстановок не существует, то отсутствие сообщения по истечении одной секунды можно принять как ответ «нет». Читателям, возможно, будет интересно поразмыслить над бесконечным компьютером, воспользовавшись при этом многочисленными (а может быть, и бесконечным числом) структурами своего собственного мозга. В МИРЕ НАУКИ. (Scientific American. Издание на русском языке) 1990 №2. стр. 82-86
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Кибернетика, когнитивистика ≫ Занимательный компьютер: О разуме, машинах и метафизике // Дьюдни А. К. |
|
[time: 7 ms; queries: 7]
8 Мар 2026 02:54:04 GMT+3 |


 Некоторые специалисты, работающие в областях, не связанных с искусственным интеллектом, говорят, что компьютеры по своей природе не способны к сознательной умственной деятельности. Мы публикуем две статьи из журнала Scientific American. В статье Дж.Р.Сирла утверждается, что компьютерные программы никогда не смогут достичь разума в привычном для нас понимании. В то же время в другой статье, написанной П.М.Черчлендом и П. С.Черчленд приводится мнение, что с помощью электронных схем, построенных по образу и подобию мозговых структур, возможно удастся создать искусственный интеллект. За этим спором по существу скрывается вопрос о том, что такое мышление. Этот вопрос занимал умы людей на протяжении тысячелетий. Практическая работа с компьютерами, которые пока не могут мыслить, породила новый взгляд на этот вопрос и отвергла многие потенциальные ответы на него. Остается найти правильный ответ.
Некоторые специалисты, работающие в областях, не связанных с искусственным интеллектом, говорят, что компьютеры по своей природе не способны к сознательной умственной деятельности. Мы публикуем две статьи из журнала Scientific American. В статье Дж.Р.Сирла утверждается, что компьютерные программы никогда не смогут достичь разума в привычном для нас понимании. В то же время в другой статье, написанной П.М.Черчлендом и П. С.Черчленд приводится мнение, что с помощью электронных схем, построенных по образу и подобию мозговых структур, возможно удастся создать искусственный интеллект. За этим спором по существу скрывается вопрос о том, что такое мышление. Этот вопрос занимал умы людей на протяжении тысячелетий. Практическая работа с компьютерами, которые пока не могут мыслить, породила новый взгляд на этот вопрос и отвергла многие потенциальные ответы на него. Остается найти правильный ответ. На лекции мы обсудим вторую весну искусственного интеллекта в цифрах и фактах, ключевые работы в области искусственного интеллекта и машинного обучения в 2017 году. Поговорим о распознавании изображений, речи, обработке естественного языка и о других направлениях исследований; обсудим новые модели и оборудование 2017 года. Также поговорим о применении ИИ и машинного обучения в бизнесе, медицине и науке, а также обсудим, чего мы ждем от искусственного интеллекта и машинного обучения в 2018 году.
На лекции мы обсудим вторую весну искусственного интеллекта в цифрах и фактах, ключевые работы в области искусственного интеллекта и машинного обучения в 2017 году. Поговорим о распознавании изображений, речи, обработке естественного языка и о других направлениях исследований; обсудим новые модели и оборудование 2017 года. Также поговорим о применении ИИ и машинного обучения в бизнесе, медицине и науке, а также обсудим, чего мы ждем от искусственного интеллекта и машинного обучения в 2018 году. В своей лекции я сначала вкратце расскажу об истории, об эволюции искусственного интеллекта, что под ним понимается, в каком состоянии он сегодня. Затем попытаюсь кратко проанализировать текущее состояние и, возможно, предложить что-то для будущего искусственного интеллекта. Эта лекция будет в основном посвящена тому, как делать искусственный интеллект и что он из себя представляет, но в основной части я не буду затрагивать вопрос, нужен ли он, и к каким последствиям создание искусственного интеллекта может привести. В нескольких словах этого вопроса я коснусь в самом конце лекции. И потом постараюсь ответить на все ваши вопросы.
В своей лекции я сначала вкратце расскажу об истории, об эволюции искусственного интеллекта, что под ним понимается, в каком состоянии он сегодня. Затем попытаюсь кратко проанализировать текущее состояние и, возможно, предложить что-то для будущего искусственного интеллекта. Эта лекция будет в основном посвящена тому, как делать искусственный интеллект и что он из себя представляет, но в основной части я не буду затрагивать вопрос, нужен ли он, и к каким последствиям создание искусственного интеллекта может привести. В нескольких словах этого вопроса я коснусь в самом конце лекции. И потом постараюсь ответить на все ваши вопросы. Если живые существа уподобить часовым механизмам, то создавший их часовой мастер, по мнению Р.Докинза, биолога из Оксфорда, автора книги «Эгоистичный ген» (The Selfish Gene), должен быть слепым. В конце концов эволюцией управляют слепые физические силы. Докинз присоединился к полемике между креационистами и эволюционистами, поддерживая последних, о чем свидетельствует написанная им недавно другая книга - «Слепой часовой мастер» (The Blind Watchmaker). Чтобы проиллюстрировать одно из главных положений своей книги, Докинз написал компьютерную программу, которая позволяет пользователю моделировать эволюционный процесс, придумывая и графически изображая свои собственные формы жизни, абстрактные организмы, которые Докинз называет биоморфами.
Если живые существа уподобить часовым механизмам, то создавший их часовой мастер, по мнению Р.Докинза, биолога из Оксфорда, автора книги «Эгоистичный ген» (The Selfish Gene), должен быть слепым. В конце концов эволюцией управляют слепые физические силы. Докинз присоединился к полемике между креационистами и эволюционистами, поддерживая последних, о чем свидетельствует написанная им недавно другая книга - «Слепой часовой мастер» (The Blind Watchmaker). Чтобы проиллюстрировать одно из главных положений своей книги, Докинз написал компьютерную программу, которая позволяет пользователю моделировать эволюционный процесс, придумывая и графически изображая свои собственные формы жизни, абстрактные организмы, которые Докинз называет биоморфами. Недавно на сайте Geektimes вышла статья «Искусственные нейронные сети простыми словами». Мы побеседовали с ее автором о развитии искусственного интеллекта и нейронных сетей. Юрий работает сейчас в небольшой фирме РСПК, изучает чат-ботов.
Недавно на сайте Geektimes вышла статья «Искусственные нейронные сети простыми словами». Мы побеседовали с ее автором о развитии искусственного интеллекта и нейронных сетей. Юрий работает сейчас в небольшой фирме РСПК, изучает чат-ботов.