Чары гипотезы Пуанкаре / The Spell of the Poincare Conjecture
Гипотеза Пуанкаре была сформулирована в Париже, в 1904 году. Сто лет математики бились над попытками доказать эту гипотезу. Каждый из них считал, что он находится в шаге от разгадки, однако это было не так. Многим из выдающихся математиков гипотеза Пуанкаре осложнила и жизнь вне работы... Лишь в 2002 году российскому ученому Григорию Перельману удалось доказать ее весьма нетривиальным и лаконичным способом. Целых три года понадобилось ученым всего мира, чтобы проверить истинность доказательства. И вот, наконец, 2006 год, Мадрид. Эпохальное достижение удостоено медали Филдса, которую называют «нобелевской премией» математиков. Однако происходит невероятное. Григорий Перельман отказывается принять награду. Он уединяется в своей квартире в Санкт-Петербурге и отказывается общаться с внешним миром...
Оригинальное название: The Spell of the Poincare Conjecture
Год выпуска: 2008
Производство: NHK, Япония
Похожее
-
Он доказал гипотезу Пуанкре – одну из самых загадочных геометрических задач ХХ века. Возможно, что это осталось бы сенсацией лишь для узких научных кругов, но он отказался от награды в миллион долларов. А почему? Этого он никому не сказал. Впервые на отечественном экране о Перельмане рассказывают люди, которые узнали его задолго до всей этой истории, которые знают истинную цену его характеру и его интеллекту. Этот фильм - попытка разобраться, что движет удивительным человеком и талантливым ученым Григорием Перельманом. Что значит его открытие для русской и мировой науки? А на вопрос, почему же Перельман не взял свой миллион, зрители ответят сами…
-
Сергей Дужин
Последним великим достижением чистой математики называют доказательство петербуржцем Григорием Перельманом в 2002–2003 годах гипотезы Пуанкаре, высказанной в 1904 году и гласящей: «всякое связное, односвязное, компактное трехмерное многообразие без края гомеоморфно сфере S3». В этой фразе имеется несколько терминов, которые я постараюсь объяснить так, чтобы их общий смысл стал понятен нематематикам (я предполагаю, что читатель закончил среднюю школу и кое-что из школьной математики еще помнит).
-
Доказательство гипотезы Пуанкаре принесло Перельману мировое признание. В 2006 году он стал лауреатом «Медали Филдса», в 2010 году институт Клэя подтвердил присуждение Перельману премии за решение одной из проблем тысячелетия. Однако математик отказался принять эти награды. Григорий Перельман о своем отказе от премии: «Я отказался. Вы знаете, у меня было очень много причин и в ту, и в другую сторону. Поэтому я так долго решал. Если говорить совсем коротко, то главная причина — это несогласие с организованным математическим сообществом. Мне не нравятся их решения, я считаю их несправедливыми. Я считаю, что вклад в решение этой задачи американского математика Гамильтона ничуть не меньше, чем мой».
-
Сергей Дужин
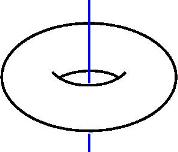
1 февраля 2015 года не стало талантливого математика, докт. физ.-мат.наук, старшего научного сотрудника Санкт-Петербургского отделения Математического института РАН Сергея Васильевича Дужина. Публикуем расшифровку его лекции «Гриша Перельман, яблоко и бублик», с которой он выступил 22 сентября 2011 года.
-
Рено де ля Тай
Теория относительности, открытая в 1904 году, была признана научным сообществом, начиная с 1915 года. Никакая Нобелевская премия никогда за эту теорию присуждена не была. Причина понятна: тот, кто первым сформулировал принцип относительности, умер в 1912 году. Это был Анри Пуанкаре.
-
Сильвия Насар, Дэвид Грубер
Нью Йоркер
Перспектива получения Филдсовской медали заставила Григория Перельмана окончательно порвать с математикой. "Пока я оставался незаметным, у меня был выбор", объяснил Перельман. "Либо крепко всем насолить" (поднять шумиху по поводу нечистоплотных методов в науке), "либо промолчать и терпеть отношение к себе как к домашней собачке. Теперь, когда я превратился в очень заметную персону, я не смогу и дальше молчать. Вот почему я был вынужден уйти".
-
Владимир Успенский
В курсе будет изложена история гипотезы Пуанкаре — с точными определениями и формулировками, но без полных доказательств. Будут объяснены понятия, необходимые для понимания различных версий (топологическая, гладкая, кусочно-линейная) гипотезы Пуанкаре: многообразие, гомотопическая эквивалентность, фундаментальная группа. Слушатели узнают о классификации двумерных компактных многообразий («сферы с ручками и пленками Мебиуса»), об экзотических гладкостях на сферах и на R^4 и о том, что одна из версий гипотезы Пуанкаре (гладкая 4-мерная) остается открытой. Мы обсудим также различные версии проблемы Шенфлиса: ограничивает ли вложенная (n–1)-мерная сфера в R^n вложенный n-мерный шар? Некоторые из этих версий остаются открытыми проблемами.
-
Каким образом появились числа и как они повлияли на развитие человечества – эти вопросы в центре внимания 5-серийного проекта. В эпизодах, которые пронесут нас сквозь время и пространство, мы увидим, что математика играла важную роль в Древнем Египте и Греции, Индии, Средневековой Европе и продолжает играть сейчас в нашем современном мире.
-
Сергей Рукшин
О том, как строить работу с одаренными детьми, на каких принципах удается воспитывать столь одаренных математиков как Григорий Перельман, Станислав Смирнов и другие, мы побеседовали с Сергеем Рукшиным, заслуженным учителем РФ, канд. физ.-мат. наук, членом Общественного совета при Министерстве образования и науки, основателем и директором Санкт-Петербургского городского математического центра для одаренных школьников, доцентом РГПУ им. А.И. Герцена. Беседовала Наталия Демина.
-
Сергей Ландо
Когда топология стала самостоятельным разделом математики? В чем различия между топологией и геометрией? Какое применение топология нашла в физике? И каковы перспективы исследований в этой области? Об этом рассказывает доктор физико-математических наук Сергей Ландо.
Далее >>>
|
|
