|
||
|
|
||
| Главная ≫ Инфотека ≫ Математика ≫ Видео ≫ «Гриша Перельман, яблоко и бублик» // Сергей Дужин |
«Гриша Перельман, яблоко и бублик»Сергей Дужин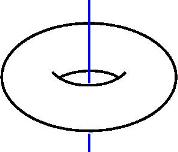
1 февраля 2015 года не стало талантливого математика, докт. физ.-мат.наук, старшего научного сотрудника Санкт-Петербургского отделения Математического института РАН Сергея Васильевича Дужина. Публикуем расшифровку его лекции «Гриша Перельман, яблоко и бублик», с которой он выступил 22 сентября 2011 года.
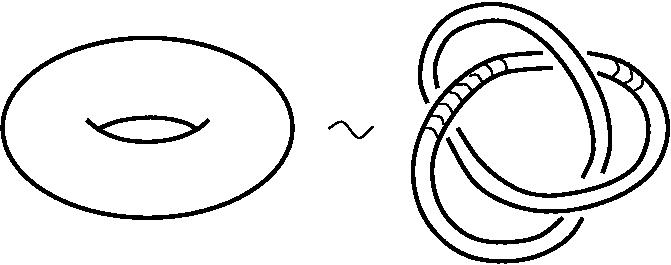
Борис Долгин: Мы давно думали о том, как нам начать разговор о математике. Нельзя сказать, что у нас на лекциях не было математиков. Они были, но разговор шел не о математике. Мы очень рады согласию нашего сегодняшнего лектора поговорить именно о математике. Текст лекции:Сергей Дужин: Хотя эта лекция происходит на «Полит.ру» и фигура Григория Перельмана в значительной степени политизирована, вопреки его собственным воззрениям, о политике я ничего говорить не собираюсь, а собираюсь говорить собственно о математике. Моя лекция будет состоять из двух частей: о гипотезе Пуанкаре и о более общей гипотезе геометризация Тёрстона. Начнём с формулировки гипотезы Пуанкаре, данной великим математиком в 1904 году, когда он построил контрпример к своей предыдущей ошибочной гипотезе. Эта гипотеза буквально гласит: всякое связное, односвязное, замкнутое трёхмерное многообразие (или «просто три-многообразие») гомеоморфно сфере S3. Я постараюсь пояснить все употребленные мною непонятные слова, так что суть вопроса должна стать понятной домохозяйкам с образованием 10 классов. Разумеется, до известной степени. Речь у нас пойдет о топологии. Что такое топология? Главную идею проще всего объяснить на примере этих двух предметов (показывает публике кружку и бублик). Их можно рассматривать либо как сплошные тела с внутренностью, либо только как поверхности. И в том, и в другом случае эти два объекта гомеоморфны. В данном случае это понятие можно пояснить так. Вы берете этот бублик. Представьте себе, что он сделан из пластилина, и, глядя на эту кружку, начнёте так вот нажимать, лепить, вылеплять, в одном месте вы сделаете вот такое тело кружки, а тут у вас останется ручка этой кружки. Так, из бублика получится кружка. В этом смысле они гомеоморфны. Такой гомеоморфизм, который делается руками в пространстве, – это частный случай гомеоморфизма, который можно назвать изотопией. Гомеоморфными могут быть и предметы как бы более «удалённые» друг от друга. Например, если я возьму тор, я его нарисую условно так (рисует на доске тор), он похож на тот же бублик. И я возьму теперь бублик, который заузлен. Сейчас я его нарисую (рисует заузленный тор). Представьте себе бублик, который испечён так хитро, что он вот таким вот образом закручивается в пространстве.
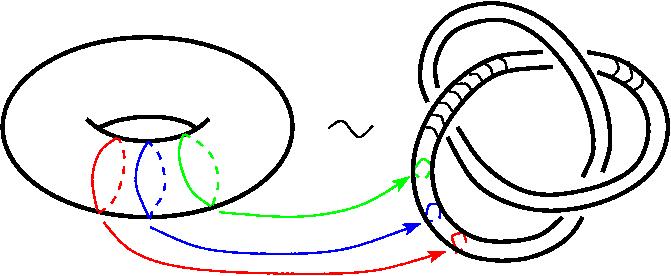
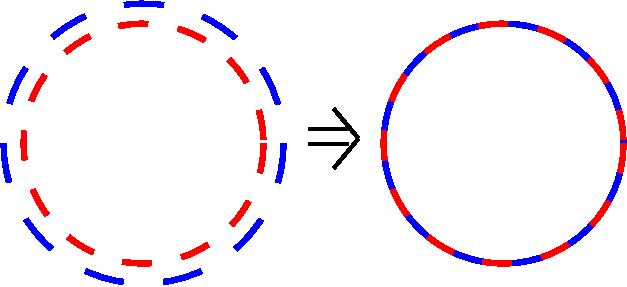
Так вот эти бублики гомеоморфны, хотя они не изотопны. (Ред. Речь идет о двух разных пониманиях топологической эквивалентности: изотопии и гомеоморфизме). То есть если взять такой пластилиновый бублик и начать его деформировать, и что самое главное – без разрывов и склеек, то из этого бублика другой руками в пространстве вы не получите, вам придётся всё-таки где-то делать разрывы и склейки. Топологическая эквивалентность в смысле изотопии не допускает разрывов и склеек, только деформации. Но они между собой гомеоморфны, то есть топологически эквивалентны в более слабом, но гораздо более принятом в топологии смысле. Топология их не различает, почему? Объяснение таково: давайте устроим между ними взаимно-однозначное и взаимно непрерывное соответствие – возьмём где-нибудь на первом бублике окружность, отобразим ее на поверхность второго бублика, соседнюю окружность отобразим в соседнюю окружность, следующую здесь – в следующую там и так далее.
Теперь, когда мы пройдём вокруг первого бублика, то если двигаться с должной скоростью, то мы пройдём и вокруг второго бублика тоже, и замкнёмся в той же точке. В этом смысле эти два топологических тела, как их двумерные поверхности, так и полнотория (то, что внутри тел вместе с поверхностью), – между собой гомеоморфны. Таким образом я попытался объяснить, что означает слово «топология» и самое главное в ней слово «гомеоморфно». Борис Долгин: А если попробовать дать определение? Что такое гомеоморфность? Сергей Дужин: Гомеоморфность двух топологических пространств – это наличие взаимно-однозначного взаимно непрерывного отображения между ними. Что такое «топологическое пространство», я объяснять не буду, я попытаюсь объяснить, что такое многообразие. Это важный частный случай топологических пространств, который более-менее можно объяснить нематематикам. Многообразие – это объект, который склеен, состоит из дисков, является объединением дисков, которые перекрываются тоже по дискам. Одномерные диски – это вот такие открытые интервалы, вот если вот так вот несколько интервалов между собой подклеить, то у вас получится, допустим, окружность – это топологическое одномерное многообразие.
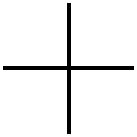
Примером пространства, не являющегося многообразием, может служить, например, крест (пара пересекающихся линий).
Потому что у точки пересечения двух линий любая окрестность является крестом, у нее нет окрестности, которая была бы сама по себе просто такой палочкой (интервалом, или одномерным диском).
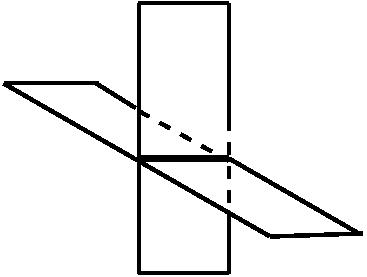
Или, например, в двумерном случае, если взять две пересекающиеся плоскости, то в точках линии пересечения такая конструкция многообразием не является. Впредь мы будем рассматривать только многообразия. Борис Долгин: Это уже трёхмерный случай…. Сергей Дужин: Это двумерный случай. Размерность считается как? Мы берём кусок этого объекта и смотрим, сколько здесь измерений – здесь можно пойти в двух взаимно перпендикулярных направлениях, имеется ширина и глубина, поэтому этот объект двумерный, хотя он вложен в трёхмерное пространство. Вот это самое главное, научиться понимать, что многообразие может жить само по себе, о нём можно мыслить как о независимом объекте, никуда не вложенном. Самое главное, что я попытаюсь объяснить – это что значит трёхмерная сфера S3, которую в наше трёхмерное пространство вложить никак нельзя. Ну, для начала я объясню более простые слова. «Связное» – это понятно, состоит из одного куска. Вот это объект связный, ну, а объект, скажем, состоящий из кружочка и палочки, – не связный; это понятно.
Понятие «односвязности» сложнее. Его лучше всего демонстрировать при помощи такого реквизита (берет в руки яблоко). Представим себе, что это яблоко – идеальный шар и рассмотрим его поверхность, то есть кожуру, – математически, сферу. Если вы здесь расположите любым способом замкнутую кривую, то её всегда можно плавно, не отрывая от поверхности, стянуть в точку. Эта сфера называется двумерной, потому что на ней, на самой её поверхности два измерения: в одну сторону и перпендикулярно. Третьего измерения нет – она вложена в трёхмерное пространство, но сама поверхность двумерная. Двумерная сфера обладает тем свойством, что если вы в неё вложите любую замкнутую кривую (роль кривой изображает обычная резинка на яблоке), то, как бы вы ни старались, как-нибудь так или так, в любом случае, её всегда можно постепенно стянуть в точку, не сползая с поверхности. Теперь если вы возьмете, допустим, бублик (берет в руки бублик), и попытаетесь приложить эту окружность к бублику (использует для демонстрации резинку и бублик), скажем так, как я пытаюсь сделать, вдоль параллели. Тогда как бы вы ни катали её по поверхности, не отрывая от поверхности, вы её в точку никогда не стянете, для этого её нужно будет обязательно оторвать от поверхности. Вот этот, что называется цикл, нетривиальный – эта кривая не стягивается. В этом смысле бублик, то есть поверхность бублика, или тор, является неодносвязным многообразием. (Кстати, и полноторие, то есть бублик с внутренностью, также неодносвязен.) Можно себе представить ещё другую резинку, которая идёт вот так, что называется по меридиану. Эту резинку я не могу сюда так нацепить, это понятно, но если бы у меня она уже была надета, я бы её катал-катал, но снять бы никак не смог. Итак, понятие односвязности я продемонстрировал на примерах. Кстати, вот это многообразие S1 – одномерная сфера или окружность – не односвязна, потому что если я возьму эту свою резинку и нацеплю вдоль этой окружности, то как бы я ни двигал её вдоль окружности, не отцепляя от окружности, я её в точку не стяну.
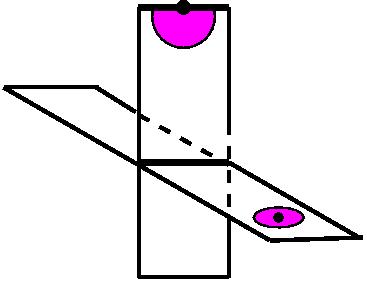
Ещё есть понятие «замкнутое». Замкнутое – по-научному это означает «компактное» и «без края». Понятие края легко объяснить, вот, к примеру, на этой картинке двух кусков пересекающихся плоскостей, если плоскости представлять себе конечными такими прямоугольниками – вот это край. У точек края нет окрестности, которая была бы диском, у неё есть окрестность только в виде половинки диска. Вот точка и вот половинка диска, второй половинки нет. Это край. Мы будем разговаривать о поверхностях без края. Примером такой поверхности, такого многообразия является, например, окружность – это одномерное многообразие без края.
Двумерным примером является обычная сфера, то есть поверхность яблока, как поётся в известной песне: «Да вот – мешала эта, / ах, круглая планета,/ где край света – нету, / и некуда идти», ну, нет у него края, то есть куда бы вы ни шли, вы можете продолжать движение по поверхности дальше – вы не упираетесь ни в какой край. Это понятие края в одномерном и двумерном случаях. В трёхмерном случае совершенно аналогично. Вот, например, то физическое пространство, в котором мы живём или, так скажем, представляем себе, что живём – оно без края, куда бы вы ни пошли – вы в принципе можете продолжать движение вперед, по крайней мере, на уровне наших сегодняшних обывательских представлений о космосе. Компактность означает, грубо говоря, ограниченность. Например, двумерная сфера компактна, но она ограничена. А, скажем, бесконечная математическая плоскость, если эту доску продолжить до бесконечности, – это не компактное многообразие. Или наше трёхмерное пространство, в котором мы как бы живём, – не компактно, оно не ограничено. Итак, что утверждает гипотеза Пуанкаре. Она утверждает то, что явления, которые мы наблюдаем на яблоке, оно, разумеется, имеет место и на трёхмерной сфере. Я объясню, что это такое. Но имеет место и обратное утверждение, что если у вас есть многообразие, на котором любая кривая по поверхности стягивается в точку, то оно обязательно будет сферой. В двумерном случае оно будет двумерной сферой, в трёхмерном случае оно будет трёхмерной сферой. Кстати, эта гипотеза имеет обобщения на любую размерность. Я скоро расскажу, что такое S3 и тогда будет более-менее понятно, что такое сфера любой размерности. Так вот, существует аналог гипотезы Пуанкаре – точно такое же утверждение, только вместо тройки стоит буква N (любое натуральное число). При N>5 это утверждение было доказано Стивеном Смейлом в 1961 году. Виктор Васильев: Больше и равно. Сергей Дужин: Да, больше или равно. Спасибо, Витя. А в случае N=4 оно было доказано в 1982 году Майклом Фридманом. В случае N≤2 это утверждение более-менее очевидно. Я чуть позже приведу список вообще всех замкнутых многообразий размерности 2, он нам понадобится для гипотезы геометризации, и вы увидите, что это очевидно. Единственный сложный случай – это N=3, в гипотезе Пуанкаре именно он оказался самым трудным и был решён только в 2003 году, а человечество убедилось в истинности этого доказательства только в 2006. Три года три различные группы математиков: одна Кляйнер и Лотт, по-моему, вторая – под руководством Джона Моргана, с которым я знаком, и третья из двух китайцев – опубликовали три толстенные книги страниц по 500, в которых были заполнены все детали доказательства Григория Перельмана 2003 года, после чего доказательство было официально признано верным. Итак, я перехожу к объяснению того, что такое собственно трёхмерная сфера. Я стираю всю эту ерунду (стирает с доски). Как понять, что такое трёхмерная сфера? Это объект не физический, его в реальном мире представить себе наглядно, так же вот, как, допустим, поверхность яблока, невозможно, поэтому к нему нужен особый подход. У меня намечено три различных объяснения, что такое S3: координатное, через надстройки и через одноточечную компактификацию. Слова, может быть, страшно звучат, но они довольно понятны. Давайте мы эту доску разделим условно на 4 вертикальные части. 0, 1, 2, 3 – это размерности. Под каждой цифрой я буду писать комментарий, что такое сфера соответствующей размерности. Первый подход – координатный. Координатный подход – это, на самом деле, по существу единственный научный, строго математический подход к исследованию многомерных объектов.
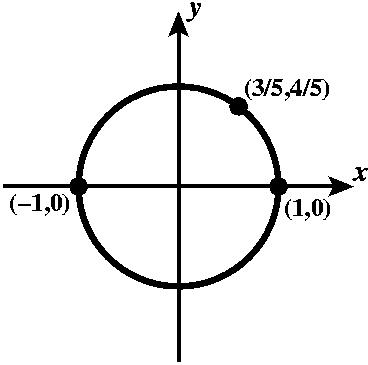
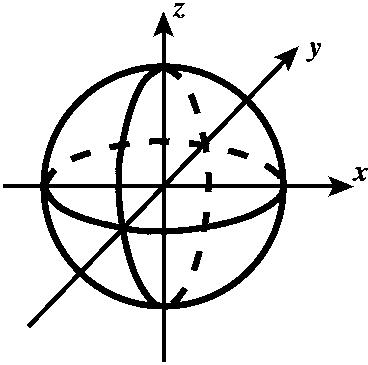
Давайте я начну с одномерной сферы S1. Те, кто окончил 10 классов, знает, что уравнение x2+y2 = 1 – задаёт на координатной плоскости с координатами x и y окружность радиуса 1 с центром в точке 0. Это уравнение окружности. Что здесь имеется в виду? Если я возьму любые два числа x и y, которые удовлетворяют этому уравнению, например ( ±1, 0), то есть ( 1, 0) или ( -1, 0), то они лежат на этой окружности, потому что они удовлетворяют такому уравнению. Или, скажем, для точки (3/5, 4/5), мы точно так же имеем: (3/5)2 + (4/5)2 = 1. Если аккуратно её нарисовать, то она попадёт ровно на окружность. Это уравнение очевидным образом обобщается на любое количество переменных. В приведенном примере у меня две переменных, то есть речь идёт о плоскости, а в плоскость вложена одномерная окружность. Если вместо двух переменных я возьму одну переменную, три переменных или четыре переменных, то получатся соответствующие сферы других размерностей, а именно, 0, 2 и 3. Давайте попробуем написать уравнение нульмерной сферы S0. Что это такое? Уравнение x2=1. Его решения: x=±1. Это две точки: -1, 1. то есть нульмерная сфера – это совокупность двух отдельно лежащих точек. Двумерная сфера S2 ( x2+y2 + z2 = 1) это множество всех точек в обыкновенном трёхмерном пространстве с координатами x, y, z. Здесь x – координата в длину, y в ширину, z в высоту. Если вы возьмёте все тройки точек, которые удовлетворяют такому соотношению, у вас получится объект, который я уже неоднократно рисовал, ну, как-то так его принято изображать – вот это начало координат, вот координатные оси… Например, вы можете проверить, например, что точка (1/3, 2/3, 2/3) лежит на этой сфере. Если вы отложите 1/3 по одной координате, 2/3 по второй и 2/3 вверх – вы попадёте в точности на поверхность этой сферы. Почему? Потому что сумма квадратов этих трёх чисел равна единице. Это примеры наглядные и понятные.
S3 задаётся уравнением x2+y2 + z2 + t2 = 1 (сумма квадратов четырёх букв равна единице). Значит, здесь я имею в виду чисто математический объект. Я рассматриваю четвёрки чисел и считаю их точками четырёхмерного пространства. Физическое пространство–время, которое обычно представляют в качестве четырёхмерного пространства, никакого прямого отношения к этому не имеет – это лишь одна из моделей четырёхмерного пространства. Я говорю чисто о математическом, арифметическом пространстве. Рассмотрим, например, четвёрки чисел (±1/2, ±1/2, ±1/2, ±1/2), где плюсы и минусы можно выбирать как угодно – всего получится 16 вариантов. Все эти 16 точек удовлетворяют выписанному уравнению и, следовательно, располагаются на поверхности трехмерной сферы в четырёхмерном пространстве. Нарисовать её так же понятно, как S2, я затрудняюсь. Значит, я нарисую ее условно, вот таким вот образом (рисует нечто округлое и невнятное). Это трёхмерная сфера.
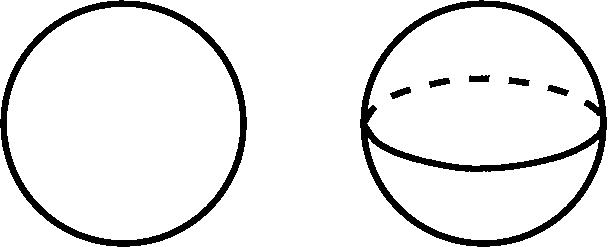
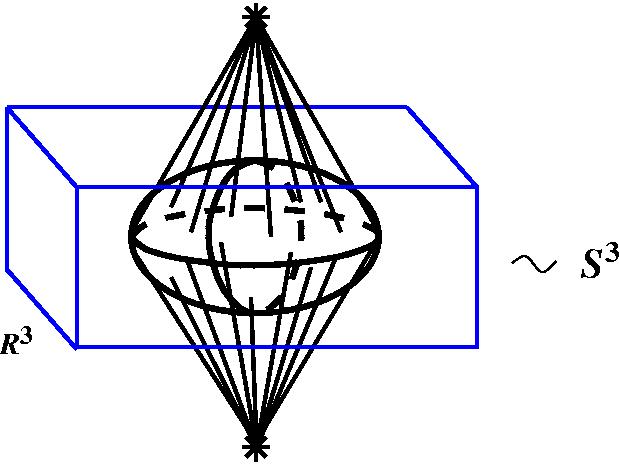
Каким она обладает свойством? Если я возьму в четырёхмерном пространстве трёхмерное подпространство (я его изображаю таким параллелепипедом, обозначается оно R3), то в пересечении этого R3 и этого невнятного объекта, вот здесь у нас вылезет обычная такая круглая двумерная сфера, может быть её каким-то другим цветом нарисовать, но у нас с фломастерами как-то не очень.
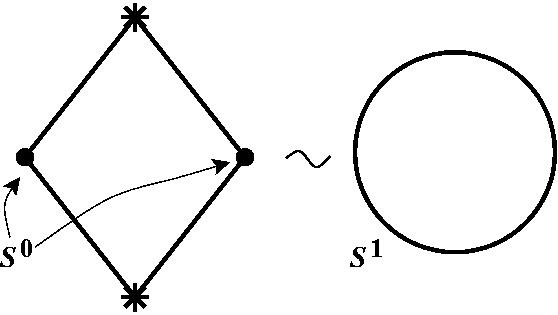
Значит, красный фломастер рисует белым по чёрному, но, тем не менее, здесь возникает в пересечении двумерная сфера. Точно также в предыдущих размерностях имеются простые аналоги, если вы возьмёте здесь (показывает рисунок двумерной сферы в трехмерном пространстве) горизонтальную координатную плоскость, то при пересечении получается окружность, то есть одномерная сфера. Здесь (на плоскости) точно так же: если я возьму координатную прямую, скажем, вертикальную – в пересечении со сферой , то есть с окружностью S1 – возникает две точки, а две точки – это S0. То есть у нас имеется способ уменьшать размерность посредством пересечения. Это первый подход к определению трёхмерной сферы. Второй подход через надстройки. Здесь движение будет происходить в обратную сторону. Я из сфер меньшей размерности буду строить сферы большей размерности. Смотрите, как это делается. Я беру нульмерную сферу S0 – две точки. Конструкция надстройки состоит в следующем: вы взяли нечто, в данном случае 2 точки, неважно. И потом пририсовали ещё 2 точки, я их звёздочками обозначил. Допустим, с разных стороны: сверху и снизу для наглядности, и потом я соединяю эти новые точки со всеми точками старыми, каждую с каждой. Смотрите, что у меня получилось. У меня получился некий четырёхугольник. Но это ведь с точки зрения топологии всё равно, что четырехуголник, что окружность – это сфера S1. Получается, что из сферы S0 посредством надстройки я получил сферу S1.
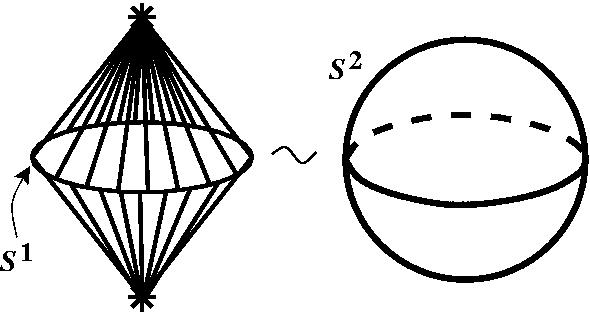
Теперь давайте возьмём сферу S1, расположим её в горизонтальной плоскости, вот так, и применим к ней конструкцию надстройки. Я добавляю две точки, опять же сверху и снизу для наглядности, хотя чисто абстрактно я мог бы их мыслить как бы вообще нигде не находящимися, а просто две абстрактные точки, ну, для наглядности я их рисую. И соединяю каждую из этих добавленных точек со всеми точками уже имеющегося у нас многообразия. Ну, и там сзади тоже такие. Но я их не буду рисовать. Получится такой двойной круглый конус, поверхность этого конуса с точки зрения топологии от сферы ничем не отличается, правда же?
Вопрос из зала: А если б две точки с одной стороны бы были? Это принципиально, чтоб с разных? Сергей Дужин: Если бы две точки были с одной стороны, то тогда пересечения мы бы считали мнимыми, то есть как бы они существуют только при вложении в трёхмерное пространство. На самом деле, эта конструкция чисто абстрактная. Я беру две каких-то точки и беру объединения всех отрезков, которые начинаются в этих точках и кончаются в точках исходного многообразия, при этом эти отрезки все считаются непересекающимися. В данном случае я могу это реализовать просто физически, поэтому я так и делаю. Если вы возьмёте такую резиновую штуку, надуете её – у вас получится круглая сфера, так или нет? S2. Точно так же, чтобы получить S3, что мы должны сделать? Мы должны взять сферу S2 (я её немножко сплющу в виде эллипсоида) и поместить её в некую трёхмерную коробочку, трёхмерное пространство, это у меня R3, потом сверху добавить точку, находящуюся вне трёхмерного пространства, но в четырёхмерном, и ещё одну такую же, и посоединять эти точки со всеми точками сферы, какие есть. Вот то, что у меня получится, вот это, если все эти отрезки считать непересекающимися, то есть они пересекаются только в добавленных точках, в звездочках, и в точках самой сферы, из которых выходит по два отрезка. Все остальные точки у них разные. Этот объект с точки зрения топологии гомеоморфен трёхмерной сфере.
Ну, и наконец, последний способ конструкции сфер – по-научному это называется одноточечная компактификация. Что здесь имеется в виду? Если у вас есть какой-то открытое многообразие, открытое – то есть без края и неограниченное, например, плоскость или внутренность круга (все его внутренние точки, кроме точек границы, то есть кроме точек окружности), то к нему можно применить операцию одноточечной компактификации. Как это делается? Я беру прямую, это бесконечная прямая или что то же самое – конечный отрезок, только без концевых точек, это всё равно, потому что с точки зрения топологии его можно растянуть до бесконечности, на миллион километров – он от этого никак не изменится. Я к нему добавляю одну точку и я её добавляю так, что она приклеивается к его концам: вот так и вот так. То есть два конца этой прямой сходятся и склеиваются между собой.
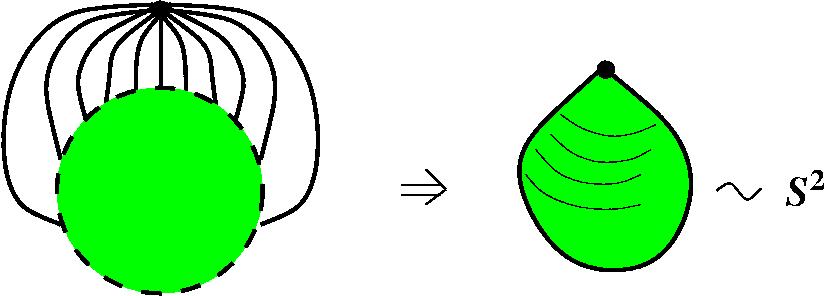
Из R1 (это прямая) у нас получается S1. Подобным же образом, если я возьму бесконечную плоскость, я буду её мыслить как внутренность диска, пунктир означает, что граничные точки мы в расчет не берём, просто точки внутри диска. И добавлю сюда ещё одну точку, и я её как бы отождествлю со всеми точками границы, со всеми, сколько их есть. Что это значит? Ну, мысля по-другому, я должен взять этот кружок, допустим, резиновый, и как бы свернуть его в кулёк, все точки границы стянуть в одну точку, получится нечто вот такое – вот это точка, а это то, что раньше было диском, такая груша получится, ну, эта груша – это всё равно, что двумерная сфера с точки зрения топологии.
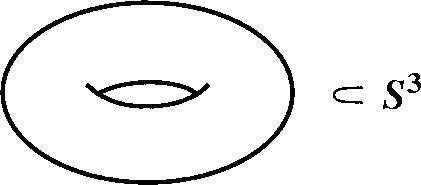
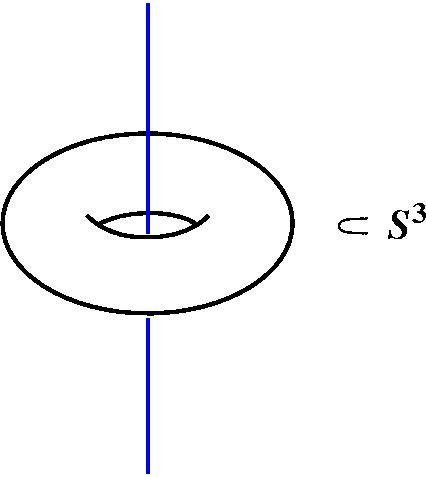
Уточнение из зала: Это яблоко. Сергей Дужин: Да, груша – это яблоко фактически, точнее не яблоко, а его кожура. Самое интересное, как из трёхмерного пространства сделать трёхмерную сферу, вот что нас интересует больше всего. Перед нами трёхмерное пространство, вот оно. Вы его ощущаете. Теперь представим себе, что где-то на бесконечности к нему добавлена ещё одна точка и это значит, что куда бы вы ни двигались в любом направлении – вы идёте, идёте и в конце концов попадаете в эту точку. Пошли в другом направлении, шли, шли, шли, опять в ту же точку попали. Куда бы вы ни шли, вы попадаете в одну и ту же точку, она приклеена к нашему миру извне сразу со всех сторон, она его замыкает, делает компактным – это конструкция трёхмерной сферы. Я хочу её проиллюстрировать на одном полезном примере, который, может быть, поможет многим из вас понять смысл этой конструкции. Я сейчас объясню, что получается из трёхмерной сферы при выбрасывания из неё полнотория. Представьте себе, что это бублик, полноторие – полный бублик, а вокруг него не обычное пространство, а компактифицированное, то есть пространство с дополнительной точкой – трёхмерная сфера.
Что тогда будет дополнением к этому полноторию? То, что останется от трёхмерной сферы, когда выкинуть это полноторие, что это за объект? Это объект очень нам известный – это тоже полноторие. Чтобы это понять, сейчас я проделаю необходимые объяснения: давайте возьмём центральную ось этого полнотория, я имею в виду бесконечную линию. Что представляет собой эта бесконечная линия, находящаяся в трёхмерной сфере? Она представляет собой окружность, потому что этот конец уходит в приклеенную точку и тот конец уходит в ту же самую приклеенную точку, это окружность. Очень хорошо.
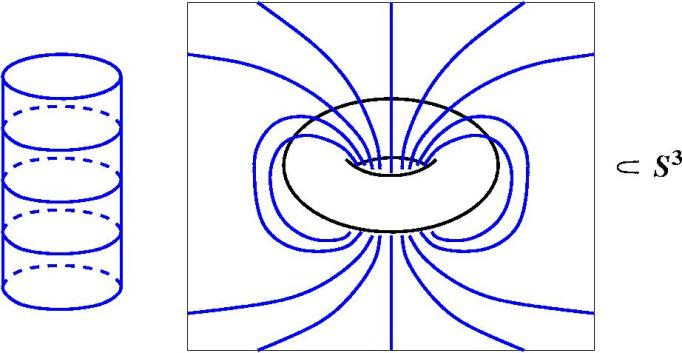
Теперь я возьму какую-нибудь плоскость и начну на ней выписывать круги. Вот это имеется в виду круг такого большого-большого радиуса, потом, значит, круг радиуса поменьше, потом ещё поменьше и так далее. Каждая такая плоскость вне нашего полнотория представляет из себя совокупность окружностей, однопараметрическую совокупность окружностей, значит, она состоит из окружностей, которые начинаются вот здесь, а заканчиваются вот здесь, то есть это как бы цилиндр. Да? Значит, у нас имеется такой цилиндр.
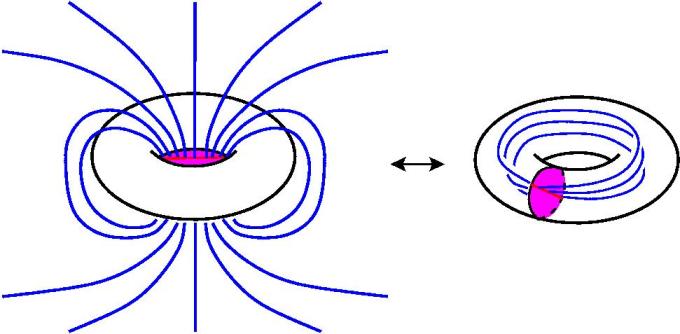
Теперь я хочу объяснить, что совокупность всех этих синих кругов, на самом деле, гомеоморфно полноторию, давайте я опишу явное соответствие между ними. Эта центральная прямая, которая на самом деле окружность, это будет центральная окружность полнотория. Эту прямую я отождествляю с этой окружностью. Дальше у меня имеется такое сечение у полнотория, которое из себя представляет диск, так вот этот диск – это вот этот вот диск, который здесь – через каждую точку этого внутреннего диска моей баранки, я выпускаю какую-то окружность: из центра я выпускаю вертикальную – она окружность, а из любой другой точки – окружность какого-то радиуса. Радиус зависит от расстояния от центра, но всё пространство заполняется такими окружностями именно таким способом, так что семейство окружностей параметризовано диском. Здесь тоже имеется семейство окружностей, параметризованное диском. И мы вот этот диск отождествляем с этим диском, а каждая окружность, которая проходит через точку диска, соответствующей окружности здесь.
Это соответствие, как легко проверить, будет взаимно-однозначным и взаимно непрерывным, таким образом, трёхмерная сфера представляет собой объединение двух полноториев, то есть S3=U+U, где буквой U я обозначаю полноторие. Если этот пример понять, то он помогает немножко въехать в то, что значит вообще трёхмерная топология, потому что этот пример существенно использует тот факт, что у нас есть добавленная точка на бесконечности, что это не в пространстве R3 происходит, а это именно в сфере S3 происходит. Я бы мог привести такое же разложение и в координатном варианте, но это не так поучительно. Это тоже легко пишется, но приведенный наглядный пример я всем очень рекомендую. Итак, будем считать, что я объяснил вам, что такое трёхмерная сфера, тем самым гипотеза Пуанкаре приобретает некий смысл. Да, нужно привести еще какие-то другие трёхмерные компактные и связные многообразия, чтобы был некий простор для воображения. Я приведу ещё два примера. Первый – пример трёхмерного тора. Трёхмерный тор T3, по-научному он пишется как произведение S1 на S1 на S1, а построить его можно следующим образом. Я расскажу, как его можно построить и как ощущать физически.
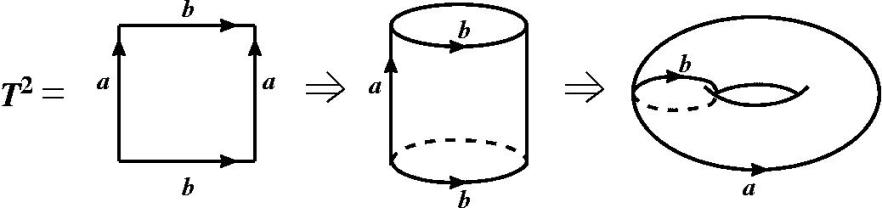
Возьмём такой куб… Извините, давайте я сначала то же самое сделаю для двумерного тора. Двумерный тор можно построить так: нужно взять квадрат на плоскости, обозначить две его противоположные стороны буквой a с направлением (указывает направление стороны стрелкой на стороне квадрата). А другие, например, буквой b с направлением. И сейчас что я делаю? Я склеиваю стороны a в соответствии со стрелками, то есть верх с верхом, тогда у меня получится вот такая примерно вещь, вот это будет a, которое уже склеилось, здесь будет b и здесь будет тоже b. … теперь я приклеиваю b и b в соответствии с ориентацией. Это вот, то что было b – оно склеилось, а то, что было a – идет по кругу. Получится, очевидно, тор. Если всё было резиновое, то можно так согнуть, приклеить и получить такую замкнутую трубку – тор.
Это стандартное представление тора, которое показывает, кстати, что тор имеет плоскую геометрию, об этом мы будем говорить чуть позже в гипотезе геометризации, потому что его можно сделать из обычного плоского квадрата. Хотя тор при стандартном вложении в R3 – как мы его обычно рисуем – он искривленный. На самом деле это вложение неудачное. Двумерный тор лучше всего рисовать в четырёхмерном пространстве – там он и рисуется более естественно, и плоским оказывается без вопросов, но для этого нужен более высокий уровень абстракции.
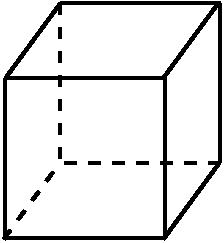
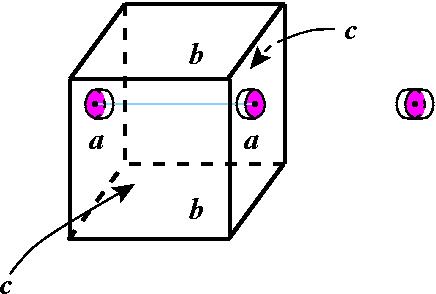
Теперь давайте рассмотрим трёхмерный куб. В нём имеется три пары граней: a-a, b-b, это верхняя и нижняя, ну, и передняя – задняя, скажем, c-c. Я буду делать то же самое, что и на предыдущем шаге. Я отождествляю точки граней a и a посредством параллельного переноса, вот так. То есть я могу, конечно, его и вытянуть вот так вот и так вот заклеить в полноторие, но давайте пока рассуждать абстрактно. Я чисто абстрактно отождествляю вот эти вот точки. Потом я также абстрактно отождествляю точки b и b и так же абстрактно точки граней c и c между собой. После таких отождествлений у этого объекта границы не останется – это получится замкнутое многообразие. Почему? Потому что, например, в этой точке, точка на границе исходного многообразия, вот эта точка – это та же самая точка, у этой точки окрестностью здесь вот является такая полусфера, которая внутрь идёт, а у этой точки является полусфера, которая идёт внутрь с той стороны. Но поскольку грани склеиваются, то вот эти два полушара склеиваются в шар, то есть диск, и окрестностью этой точки является обычный трёхмерный диск, то есть кусок трёхмерного пространства, то есть это многообразие, без края, края у него нет. Это то, что называется трёхмерный тор. Как его себе представить в физическом пространстве? Для этого нужно представить себе такую вещь. Допустим, вы выбрали 3 направления: вперёд, влево и вверх. Если я иду вперёд, иду достаточно долго, я возвращаюсь себе в спину. Если я иду влево, то я через некоторое время вернусь себе в правый бок. Если я полетел вверх, я вернусь себе в ноги. Есть ещё некоторые направления, которые обладают таким же свойством. То есть я могу в некотором рациональном направлении полететь и тоже вернуться себе в соответствующее место, только через более долгое время – это свойство целочисленных решёток, но это неважно. Главное, что трехмерный тор можно себе представлять физически вот таким вот способом. Вот пошёл и вернулся сзади, ну, как в фантастических рассказах. Вопрос из зала: Он – замкнутый… Сергей Дужин: Да, он – замкнутый, это замкнутое трёхмерное многообразие. Прекрасно. Причём на нём есть нестягиваемые пути, а именно, есть этот самый путь, когда я пошёл вперёд и вернулся себе в спину. Вот этот путь, скажем, из этой точки вот в эту точку – это замкнутый путь, потому что его начало совпадает с его концом – он замкнутый. Но его нельзя стянуть, потому что если вы начнёте его как-то стягивать – внутреннюю-то верёвочку можно как хочешь деформировать, а вот эти две точки-концы могут елозить по этим краям только вместе. Они отождествляются между собой только по горизонтали и поэтому снять их нельзя. Это нетривиальный цикл.
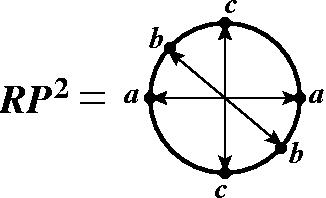
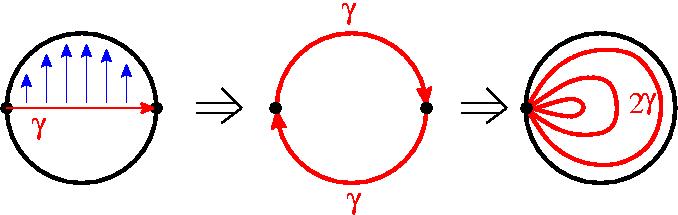
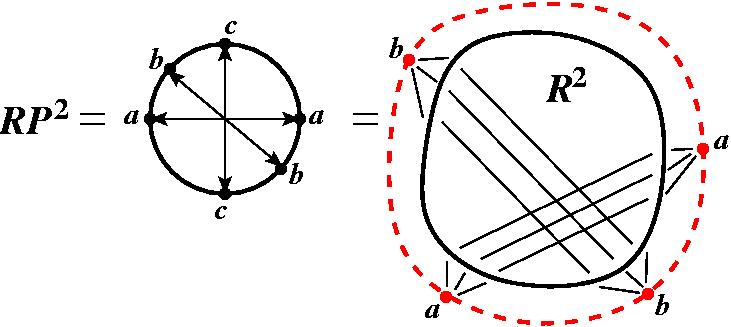
То есть это такая резинка, которая с трёхмерной сферы слезает, а с тора не слезает, также как и с бублика, потому что это собственно есть трёхмерное обобщение бублика. Ну, и ещё один пример я приведу – это трёхмерное проективное пространство RP3. Опять же давайте я сначала нарисую, что такое двумерное проективное пространство RP2. Я беру диск и я в нём отождествляю все пары диаметрально противоположных точек, все пары… Эти точки считаются одинаковыми. Эта точка a и эта a, эта b и эта b… (показывает на чертеже пары диаметрально противоположных точек окружности) и так все-все точки. Физически сделать такое склеивание сделать не получится, то есть я могу, конечно, точки a и a склеить, потом всё подвернуть и b к b приклеить, потом ещё с и c. Но если вы постараетесь, взяв диск из резины, склеить все пары противоположных точек, то у вас ничего не получится, в трёхмерное пространство этот объект без самопересечения не вкладывается. Его можно погрузить в пространство R3 с самопересечениями (это называется поверхность Боя), можно вложить в четырёхмерное пространство и так далее, но рассуждать о проективной плоскости проще всего прямо в таких терминах по определению. Это просто диск, причём все точки внутри диска – это разные точки, а на границе точки склеены попарно и каждая пара считается за одну точку. Это пространство обладает таким уникальным свойством – у него есть цикл, замкнутый путь, скажем, от a до a…. Этот путь от a до a – это ведь окружность, замкнутая кривая, потому что начинается в точке a и заканчивается в точке a – это одна и та же точка, но стянуть его нельзя, потому что как только вы начнёте его стягивать – внутри опять же кривая может делать что хочет, как угодно деформироваться, но концы её обязаны быть противоположными точками края – с края её сдёрнуть нельзя. Потому что если мы её сдёрнем с края, то другой конец сдёрнется с края, и уже из окружности получится отрезок, то есть произойдёт разрыв, а мы должны кривую иметь постоянно замкнутой. То есть это нестягиваемая кривая, давайте обозначим ее буквой γ.
А представьте себе, что будет, если я эту кривую γ проведу дважды. Я утверждаю, что кривая 2γ (то есть я прохожу γ и прохожу по ней ещё раз), стягиваемая. Чтобы это понять, давайте сделаем небольшую деформацию – первый проход из этой точки сюда я пройду вот так вот, мне ничего не мешает – я могу её плавно деформировать в эту сторону, пожалуйста. А второй проход из этой точки обратно я проделаю вот так вот. И у меня получится 2γ – это вот такая кривая. И эту кривую совершенно преспокойно можно стянуть через внутренность этого диска. При этом разрывов не происходит – там происходил разрыв, потому что я отрывался от края, здесь я отрываюсь от края, но кривая у меня идёт не так, а вдоль края. Теперь при деформации кривая везде плавно отходит от края, при этом остаётся замкнутой, разрывов не происходит, и кривая вот так стягивается в точку.
Так вот эта модель RP2 очень поучительна, чтобы понять сущность абстрактной топологии. Вдумайтесь в этот пример – что бывает кривая сама по себе не стягиваемая, но дважды пройденная – уже стягиваемая. Это кажется поразительным, но это факт.
Как представить себе RP3? Да, кстати, по-другому, проективную плоскость RP2 можно себе представлять вот как. Можно взять просто плоскость R2, такую огромную, и считать, что к ней добавлена бесконечно удалённая линия, обладающая таким свойством, что все прямые, параллельные между собой, идут в одну и ту же точку. Эти в точку a, например, а эти в какую-то точку b. Для каждого направления прямых имеется замыкающая их точка на бесконечности, причём с обеих сторон одна и та же. Нетрудно понять, что эта конструкция равносильна предыдущей. Так вот трёхмерное проективное пространство, здесь вот, в физическом пространстве (показывает на зал, где проходит лекция), можно себе представить себе так. Мы живём в обычном пространстве, но оно обладает таким удивительным свойством, что если 2 человека двинутся из разных мест строго параллельно, то где-то там далеко они попадут в одну точку, даже если один пошёл вперёд, а второй назад (смеется). Это ориентируемое, кстати, многообразие (а RP2 - неориентируемое, но об этом я говорить не собирался, это так к слову), неодносвязное, потому что имеются нестягиваемые кривые, трёхмерное многообразие, замкнутое без края. Прекрасно. Теперь пару слов о гипотезе геометризации и о потоках Риччи. Гипотеза геометризации (1982) принадлежит Уильяму Тёрстону (William Paul Thurston). (У него еще есть сын Дилан, тоже выдающийся математик). Философский смысл этой гипотезы такой. Ранее я вам попытался объяснить, что такое топология. Топология - это такая резиновая геометрия, где неважна конкретная форма предмета, не важны расстояния, углы, важна лишь общая форма, есть ручка или нет ручки, например, – вот это важно. Склеивать, разрывать нельзя, а деформировать по-разному можно. Кроме топологии, есть ещё собственно геометрия. Скажем, дифференциальная геометрия, или метрическая геометрия, где всё жёстко определено. Между любыми двумя точками можно измерить расстояние, между любыми двумя прямыми можно измерить угол, как бы всё жёстко, как положено, как в евклидовой (школьной) геометрии. Так вот оказалось, по Тёрстону, что если мы возьмём топологическое многообразие, я сейчас говорю очень грубо, если возьмём топологическое многообразие, то среди всех его возможных форм, модификаций, можно выбрать такую форму, на которой существует единственная, совершенно точно определённая геометрия из конечного списка заранее описанных геометрий. Это гипотеза геометризации. Частным случаем является гипотеза Пуанкаре, которая гласит, что если вы возьмёте топологический класс замкнутых многообразий, обладающий одним дополнительным свойством – односвязностью, то тогда среди них, среди всех этих кривых сфер, можно выбрать ровно одну кругленькую сферу, у которой, что называется, постоянная кривизна. Она круглая и определена однозначно с точностью до растяжения, которое не существенно. В этом классе имеется такой чёткий геометрический объект с постоянной кривизной. Так вот формально формулировка гипотезы геометризации гласит… Обычно она формулируется для ориентируемых многообразий, потому что для не ориентируемых она сложнее. Гипотеза Пуанкаре, кстати, не требует ориентированности, потому что у не ориентируемых многообразий не бывает тривиальной фундаментальной группы, то есть у не ориентируемого многообразия всегда есть цикл, который не стягивается, вот как на проективной плоскости. Поэтому это упоминать не надо, если известно, что таких циклов нет, то мы автоматически можем устроить ориентацию. А в гипотезе Пуанкаре это как раз предполагается. Ориентируемое простое трёхмерное многообразие, простое замкнутое (мы только о замкнутых говорим), можно разрезать торами, так, что любой кусок имеет геометрическую структуру конечного объёма. И геометрических структур известно всего восемь. Таким образом, эта гипотеза (сейчас я детали поясню) в целом объясняет строение всех трёхмерных многообразий, а именно, что их можно разбить на разумные куски, в которых имеется жёсткая геометрия. Вот что утверждается. Что значит разрезать торами? Дело в том, что, скажем, двумерные многообразия можно разрезать на части окружностями, если у вас есть, допустим, крендель, такой объект (рисует) – это поверхность кренделя, да? Тогда можно провести такую окружность (рисует) и ножницами разрезать поверхность на две части. Каждая часть – это тор с дыркой.
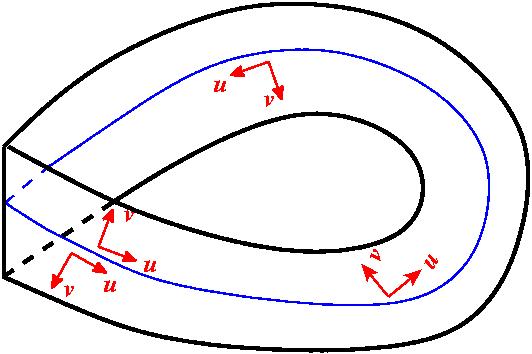
А трёхмерное многообразие можно резать, во-первых, двумерными сферами S2, двумерная сфера – это аналог одномерной сферы. Если вы возьмёте 2 трёхмерных многообразия, из каждого вырежете шарик, у каждого шарика границей будет сфера, и эти сферы между собой склеите, то эти два многообразия сольются в одно, точно также как здесь. Смотрите, я взял два тора, вот это у меня был тор, да. Я в нём проделал дырочку, вырезал кружок, и слева тоже был тор – я проделал в нем дырочку, вырезал кружок, а потом эти кружки по краям склеил. Кружок в трёхмерном случае – это диск, трёхмерный шар, а граница его уже не окружность, а двумерная сфера. Это означает склеивание по двумерным сферам, то есть прямая (связная) сумма 3-многообразий. Это очень простая операция, поэтому Тёрстен от неё сразу открещивается – он говорит только о простых трёхмерных многообразиях, простое – это такое, которое нельзя разложить в связную сумму путём разрезания по двумерным сферам. Но в трёхмерном случае можно резать ещё и по торам, в чём вы убедились, когда я вам демонстрировал, как можно разрезать трёхмерную сферу двумерным тором, да? Я её разрезал на два полнотория. Полноторие или более общий объект – такое тело с ручками типа внутренность вот такого кренделя – это аналог полнотория. Или можно взять три таких дырки, тоже заполнить, будет такое полное тело рода 3, что называется. Оказывается, любое трёхмерное многообразие можно составить из максимум двух таких вот полных тел, это называется диаграмма Хегора – это такая специальная наука, особый подход к изучению трехмерных многообразий. Но во всяком случае по тору многообразие резать можно. Его можно разрезать торами так, что любой кусок будет иметь совершенно определённую геометрическую структуру конечного объёма. А структуры вот какие…. Геометрическая структура – есть два определения, одно через риманову геометрию, одно через группы Ли. Давайте я попробую объяснить в терминах римановой геометрии. Имеется понятие «модельная геометрия», модельная геометрия – это полное однородное риманово многообразие. В общем-то всё. А геометрическая структура, давайте ее обозначим буквой M – это факторпространство этого многообразия по дискретной группе, действующей свободно. Здесь слишком много математики, пожалуй, поэтому я, наверное, полное объяснение давать не буду. Я приведу только примеры геометрических структур. Геометрическими структурами, в смысле модельными геометриями, являются: S3 – трёхмерная сфера, E3 – трёхмерное евклидово пространство, обычное, в котором мы как бы живём, Н3 – это гиперболическое трёхмерное пространство или пространство Лобачевского. Эти три пространства не только однородны, но и изотропны. В самом деле, в нашем пространстве нет никакой разницы, куда идти, правильно? Влево, вправо, вверх или вниз, с точки зрения математика разницы никакой нет (смеется). Точно так же дело обстоит на трёхмерной сфере и в трёхмерном пространстве Лобачевского. Кроме этого, есть две модельные геометрии, которые являются произведениями, а именно S2 умножить на R и H2 умножить на R (здесь H2 – плоскость Лобачевского). И имеются ещё три более хитрые модельные геометрии, которые я, пожалуй, толком пояснить не смогу. Это многообразие SL2(R) с волной – универсальная накрывающая группы Ли матриц 2 x 2 с определителем единица. Ещё имеются многообразие, точнее модельная геометрия Nil – Nil-геометрия, которая реализуется группой Гейзенберга из матриц 3 на 3. Ещё имеется Solv-геометрия, которая обозначаются Sol и которую я не стану вообще комментировать. Эти объекты обладают такими свойствами – они не изотропны. Например, что значит S2 умножить на R? У вас имеется двумерная сфера, у которой положительная кривизна. По поводу кривизны сейчас я пару слов скажу. Попросту говоря, она внутрь загнута во всех местах – это считается положительная кривизна. Теперь эта сфера просто утолщается. Умножить на R – это значит добавить лишний параметр перпендикулярно поверхности. То есть у яблока кожура не тонкая, а толстая, причём открытая с обеих сторон. Такая толстая кожура, открытое такое многообразие, на нём можно задать метрику, оно станет римановым однородным и полным многообразием. Но оно не изотропно. В направлении сферы у него кривизна положительная, а в направлении прямой у него кривизна 0. Точно также и здесь (указывает на доске на формулу H2 x R). В направлении плоскости Лобачевского H2 – это двумерная гиперболическая плоскость или плоскость Лобачевского – кривизна отрицательна, а здесь кривизна 0, а в случае других модельных геометрий происходят всякие комбинации этих явлений. Чтобы это понять, я, пожалуй, приведу двумерный пример. А потом расскажу немножко про потоки Риччи – собственно, средство доказательства этих обеих гипотез. Как обстоит дело в двумерном случае? Если мы зададимся вопросом: а какие бывают замкнутые, ну, пускай ориентируемые…. Иосиф Красильщик: Ты ни разу не сказал, что такое ориентируемые. Сергей Дужин: Ни разу не сказал, сейчас скажу. Давайте я прямо сейчас и скажу. Ориентируемые – это вот что значит. Это понятие из области научной фантастики. Наше трёхмерное пространство является ориентируемым, если, как бы вы ни ходили, ни летали по космосу, вернувшись в исходную точку, у вас левая рука останется левой, а правая – правой. Это называется свойством ориентируемости. Если существует такой обход, при котором человек отражается относительно собственной оси, то наше пространство не ориентируемо. Иосиф Красильщик: Лист Мёбиуса. Сергей Дужин: Да, разумеется. Простейшим наглядным примером является лист Мёбиуса. Это вот такая штука. Вы берёте длинный лист бумаги, перекручиваете на 180 градусов и склеиваете концы.
Он обладает таким свойством. Возьмём парочку взаимноперпендикулярных векторов, скажем u и v, и будем её непрерывно перемещать по этому листу. Вот этот вектор u, а вот у вас будет v. И когда вы придете в эту точку, у вас будет u смотреть сюда, а v сюда. То есть любая картинка, которая здесь берётся, при обходе переворачивается. Это свойство называется неориентируемостью. Я хотел в качестве затравки привести классификацию всех двумерных замкнутых ориентируемых многообразий. Это классификация состоит из одного бесконечного списка объектов, которые нумеруются натуральным числом. Начинается список со сферы. Сфера. Потом идёт тор. Потом идёт крендель с двумя ручками. Потом идёт крендель с тремя ручками, ну и так далее. Это полный список ориентируемых замкнутых двумерных многообразий. Характеристика, которая их отличает, называется род, обозначается буквой g от слова genus и имеет такие значения: g=0, g=1, g=2, g=3 (количеству ручек) и так далее.
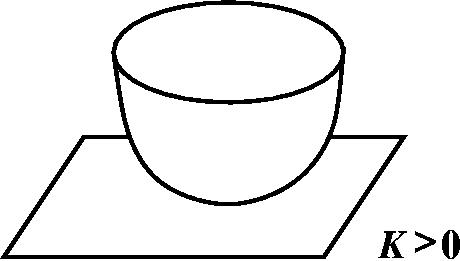
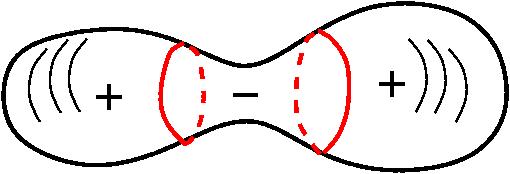
Замечательно вот что: что гипотеза геометризации Тёрстона в двумерном случае гласит, что здесь (показывает на сферу) есть метрика кривизны постоянной больше нуля. Здесь (показывает на тор) есть метрика кривизны 0, а дальше (указывает остальные фигуры из списка) есть метрика кривизны меньше нуля, тоже постоянная. Откуда это берётся и каковы модельные геометрии в этом случае? В этом случае (показывает на рисунок сферы) модельная геометрия – это сама сфера S2. Да, что означает метрика положительная или отрицательная (в смысле кривизна положительная или отрицательная)? Если у вас есть окружность, допустим радиуса ½, то её кривизна равна двум. Кривизна – это величина, обратная радиусу окружности, которая наиболее плотно касается данной кривой. Если кривая – это просто окружность, то ее кривизна – это величина, обратная радиусу. Если вы возьмёте радиус 10, кривизна будет равна 1/10, а если возьмёте прямую, то радиус кривизны будет бесконечность, а кривизна будет равна 0. Это исходное определение кривизны для кривой, вложенной в евклидово пространство. Здесь речь идёт о поверхностях. Они, конечно, вложены у нас в трёхмерное пространство. Но о них можно мыслить и абстрактно, и по-другому, и как о факторпространствах и так далее, но давайте посмотрим на то, что мы здесь наблюдаем. Давайте я нарисую иллюстрацию на тему «кривизна». Если я возьму, например, такую гантель, такую круглую штуку, две сферы, соединённые таким перешейком, то у этого объекта, вообще у двумерных поверхностей под кривизной, о которой я здесь говорю, понимается Гауссова кривизна. Гауссова кривизна определяется при помощи кривизны кривых, которую я объяснял. Нужно взять в точке на поверхности два перпендикулярных направления, взять нормаль, то есть перпендикуляр к поверхности, провести две секущие плоскости через нормаль и через каждое из этих двух выбранных направлений. На поверхности будет высечены две кривые. Эти кривые могут идти либо в одну и ту же сторону по отношению к плоскости, то есть вот так и вот так (показывает руками), в этом случае знак кривизны обеих кривых один и тот же и их произведение положительно – это называется положительная гауссова кривизна. Это бывает, если поверхность устроена как чашечка (рисует). В этом случае гауссова кривизна больше нуля.
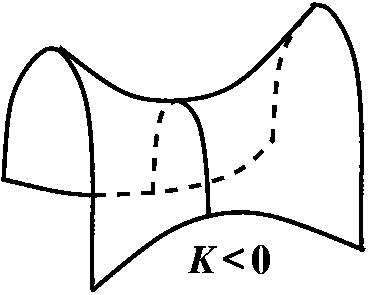
Если поверхность устроена так, что в одном направлении выпуклость сюда, а в перпендикулярном направлении выпуклость туда, это трудно изобразить – имеются в виду две взаимно перпендикулярные плоскости. Вот такое седло, например (рисует).
Здесь у нас в этом сечении направление выпуклости вниз, а в перпендикулярном направлении – выпуклость в другую сторону. В этой точке Гауссова кривизна отрицательна. Если в каком-то направлении кривая получается практически прямая, то она имеет кривизну 0. Так вот, если мы пойдём по видимому краю этой гантели, то здесь, видите, я иду, поворачиваю вправо. А в какой-то момент начинаю поворачивать влево. Так вот, в тот момент, когда меняется направление поворота – в этот момент кривизна будет ровно 0. И она будет 0 на всей такой окружности. И здесь точно такая же будет окружность нулевой кривизны. В точках справа и слева, там, где гантель похожа на сферу, кривизна положительна, потому что она выпукла в одну сторону, а здесь она ведёт себя как седло, здесь кривизна отрицательная.
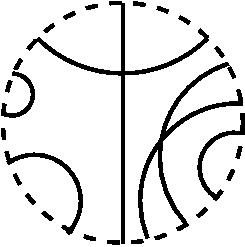
Так вот оказывается, что для тора можно найти модельную геометрию, а именно евклидову плоскость, только эту евклидову плоскость E2 нужно профакторизовать по группе Z2. Что это значит? Это значит, что мы на плоскости считаем одинаковыми точки, которые отличаются друг от друга переносом на целочисленные векторы – по вертикали или по горизонтали, это всё как бы одна и та же точка. То есть мы получаем, если лишнее выкинуть – оставить один квадрат, то у него опять же нужно склеить стороны: верхнюю с нижней, левую с правой – получится та модель тора, которая уже фигурировала. Е2 – это плоская геометрия, это плоскость. Модельная геометрия для тора плоская, поэтому на торе можно задать метрику нулевой кривизны, а именно вот таким способом (показывает на доске прямоугольную решетку, то есть чертеж факторизации Е2/Z2).Что же касается поверхностей более высокого рода, они получаются из плоскости Лобачевского. Ну, плоскость Лобачевского – это отдельный разговор. Все в мире знают, что на плоскости Лобачевского параллельные линии пересекаются. Кто это знает, поднимите руки! О, есть такие люди. На самом деле всё обстоит наоборот. Плоскость Лобачевского задаётся аксиомой, что если в ней дана прямая и точка вне прямой, то существует, по крайней мере, две прямых линии, которые с данной прямой на пересекаются. А не пересекаются, это по определению значит параллельны: параллельные линии не пересекаются – это тавтология. Они пересекаться никак не могут по определению. Параллельность – означает отсутствие общих точек. Так вот в геометрии Лобачевского этих параллельных данной прямой может быть несколько. Одна из моделей плоскости Лобачевского – это модель в круге, модель Пуанкаре, в которой точки окружности не входят в плоскость. Плоскость у нас неограниченная. Прямыми считаются, во-первых, диаметры этой окружности, во-вторых, дуги разных окружностей, перпендикулярные границе. Граница называется абсолют – она не входит в геометрию. Вот это прямые.
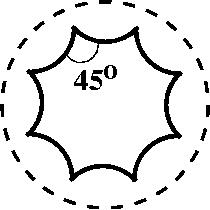
Вот у вас дана прямая, вот точка, мне ничего не стоит нарисовать сколько хочешь прямых, которые будут как бы прямыми в смысле, которые я определил, прямыми Лобачевского и не пересекаться с данной. Вот через эту точку я нарисовал две дуги, которые перпендикулярны абсолюту и которая с данной дугой не пересекаются. Это такая замечательная геометрия, она самая содержательная во всей гипотезе геометризации Тёрстона, гиперболические многообразия далеко не исследованы полностью, речь идёт о том, чтобы изучить дискретные группы движений пространства Лобачевского, о которых написано сотни работ, они изучаются. Но принципиально вопрос решён. Так вот, например, крендель можно получить вот так: я возьму плоскость Лобачевского и здесь я нарисую такой специальный восьмиугольник. Восьмиугольник я нарисую на таком расстоянии от центра, чтобы все углы были по 45 градусов. Восьмиугольник можно рисовать, ну, я имею в виду, центрально симметричный восьмиугольник с центром в центре круга, на разном расстоянии от этого центра. Чем дальше я его оттягиваю к краю – тем меньше становятся углы, чем ближе, тем больше. Рядом с центром геометрия почти что плоская, поэтому восьмиугольник будет с углами как у плоского восьмиугольника (135 градусов). А подальше – будет стремиться к нулю, если на абсолюте взять точки, то будут просто равны нулю. Но есть такое положение, где углы по 45 градусов.
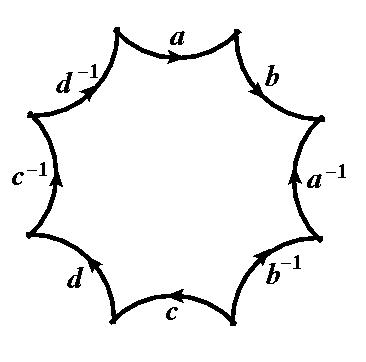
Так вот оказывается, что эти вот дуги (стороны восьмиугольника) – это куски прямых Лобачевского, т.е. если их продолжить, это будут дуги, перпендикулярные абсолюту, относительно них можно сделать отражение – можно отразить этот восьмиугольник в восемь сторон, потом каждый из полученных (они станут меньше, визуально) ещё отразить и таким образом замостить всю внутренность этого круга копиями этого восьмиугольника. Если все эти копии поотождествлять, то у вас получится отождествление на сторонах восьмиугольника по схеме: a, b, a-1, b-1, c, d, c-1, d-1, где знак означает изменение направления склейки. Если c сюда, то c в минус первой – сюда (рисует стрелки на сторонах восьмиугольника). Они склеиваются вот так вот. Если так склеить, то получится такой крендель. И постоянная кривизна у него будет ровно минус один. Так вот это гипотеза геометризации в двумерном случае, а в трёхмерном для этого используется поток Риччи.
Поток Риччи придумал Ричард Гамильтон (Richard Hamilton), в 1981 году. И пытался использовать его для доказательства гипотезы Пуанкаре и гипотезы геометризации. У него, правда, ничего не вышло, но сама идея была правильной. Её-то Гриша Перельман и довёл до ума.
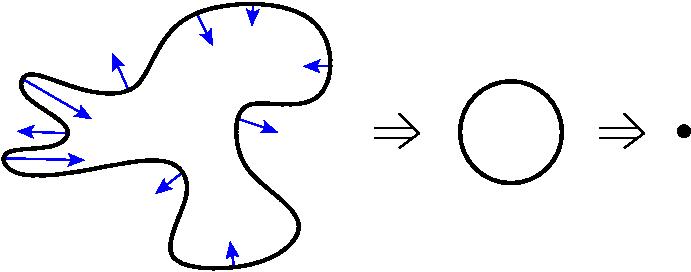
Берём многообразие, замкнутое, допустим, ориентируемое, трёхмерное, какое надо, и добавляем к нему любую метрику. Метрика, с точки зрения обывательской – это способ измерять расстояния и углы, ну, а с точки зрения более математической – это некий дифференциально-геометрический объект с индексами. Не будем вдаваться в подробности. Теперь он что делает? Он делает эволюцию метрики по потоку Риччи. Чтобы это понять, я дам простейший пример. Он не очень адекватный, но зато предельно ясный. Что такое поток Риччи на кривой, вложенной в плоскость? Это значит, что мы в каждой точке рисуем вектор. Там, где кривизна, ну, радиус кривизны снаружи, мы рисуем вектор наружу. Там, где радиус, то есть соприкасающаяся окружность, внутри, мы рисуем вектор внутрь. Где кривизна маленькая – вектор маленький. Где побольше – там побольше. Где ещё больше, ещё больше. И вот так, значит, мы рисуем такие векторы и начинаем двигать эту кривую сразу вдоль этих векторов с той скоростью, какова их длина.
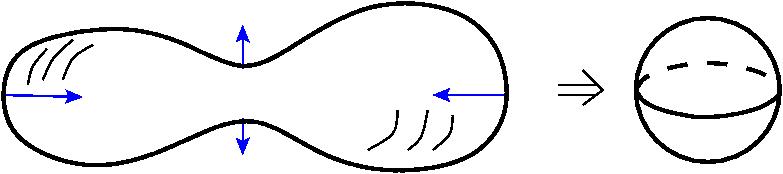
Оказывается, что при этом любая кривая постепенно распрямляется и, в конце концов, превращается в маленькую-маленькую окружность и схлопывается в точку. Но если ещё при этом сделать нормировку так, чтобы кривую увеличивать каждый раз, чтоб она была гомотетична самой себе, а площадь сохранялась, то тогда она просто станет круглой окружностью в конце концов. Вот это как бы простейший пример доказательства гипотезы Пуанкаре, что любое одномерное замкнутое многообразие гомеоморфно окружности. При помощи потока Риччи. Это же работает и в двумерном случае. Если вы возьмёте вот эту гантелю, например, и что такое поток Риччи я уже не объясняю, но это значит некая эволюция метрики, внутренней метрики. Здесь я говорю о внешней метрике для наглядности. Но на самом деле в работах Перельмана речь идёт о внутренней метрике многообразия, которое никуда, вообще говоря, не вложено. Так вот если мы возьмём гантелю, то поток Риччи увеличивает места отрицательной кривизны и уменьшает места положительной кривизны и тоже загоняет всё в сферу. Ну если эта штука была гомеоморфна сфере – получается круглая сфера.
В трёхмерном случае возникает такой объект – в трёхмерном случае возникают перетяжки вида, например, S2 умножить на S1. Это вместо того, что вот здесь находится (показывает окружность на перетяжке «гантели»). Такие куски, где S2, ну, умноженное на R (можно написать). Вот такие вот кусочки возникают. И в этих местах при эволюции этого потока Риччи многообразие перестаёт быть многообразием. Оно становится примерно таким вот. Два таких вот куска, а здесь – особая точка. Вот и с этим ничего не мог поделать Гамильтон.
А Перельман в серии работ 2002-2003 годов смог построить модификацию потока Риччи в окрестности таких особенностей, так, чтобы обходить особенности и чтобы при этом топология многообразия не менялась. При этом полностью доказывается гипотеза геометризации – многообразие, которое идёт по потоку Риччи с поправками Перельмана, в конце концов, превращается в многообразие, которое торами режется на геометрические куски, на каждом из которых имеется одна из восьми геометрий Тёрстона. Я закончил. Борис Долгин: Спасибо большое. (Бурные аплодисменты).
Обсуждение лекцииБорис Долгин: Эту расшифровку надо будет сопровождать рисунками. Ефим Островский: У меня такой вопрос от лица всех домохозяек. Вот что, вот это всё, что вы нам рассказали, значит для домохозяйки непосредственно? Сергей Дужин: Непосредственно для домохозяйки это ничего не значит. Ефим Островский: Так… (аплодисменты). А тогда к чему вы это всё вели? Сергей Дужин: Я рассказывал для интересующихся домохозяек. Я имел в виду, что если человек, имеющий образование в объёме средней школы, хочет узнать, чем занимался, допустим, Перельман, что это вообще за шумиха такая была в мире? Ну, я вот об этом на таком уровне и пытался рассказать. Для интересующихся домохозяек, не для всех. Борис Долгин: Стоп. Вопрос был видимо в том, а нельзя как-нибудь это сразу приложить для домохозяйки, чтобы у неё котлета как-то быстрее жарилась? Ефим Островский: Потому что единственный вывод, который я услышал, что нет разницы, иду ли я влево, или вправо, всё равно я прихожу в какую-то точку, которую вы обозначили. Борис Долгин: Нет, это не дай Бог вам сделать этот вывод из сказанного. Ефим Островский: Это не то, что я делаю этот вывод, это то, что я услышал из сказанного. Сергей Дужин: Я так не говорил. Я сказал, что существует такая математическая конструкция, в которой это верно. Ефим Островский: Посмотрите по расшифровке, вы же сказали «и в самом деле…». Ведь нет разницы, ведь так? Борис Долгин: При определенных условиях. Сергей Дужин: Я сказал, для математика нет разницы. Борис Долгин: Спасибо. Здесь я должен, видимо, пояснить, что публичная лекция ни в коем случае не ставит задачу рассказать исключительно о том, что имеет непосредственно прикладной характер, иначе это был бы совсем другой проект. Вопрос из зала: У меня вопрос-дополнение к лекции. Вы не успели рассказать про 8 геометрических структур Тёрстона, если я не ошибаюсь основных, не могли бы вы кратко пояснить, что это? И второй вопрос, я наверное по-другому сформулирую, то, что хотел спросить молодой человек – эта геометрия – она чисто теоретическая или она где-то применима на практике? То есть, условно говоря, до какой степени мы это можем изобразить – представить, а в какой степени это нечто такое совершенно на научных выкладках, где пересекаются параллельные прямые и так далее? Сергей Дужин: В настоящий момент – это чистая математика. Но, вообще говоря, не исключены её приложения к физике, потому что никто на самом деле не знает, как устроена Вселенная, в которой мы живём. Она вполне может оказаться трёхмерной сферой, например. Если мы достаточно далеко её изучим. Или ещё чем-нибудь. Каким-то трёхмерным многообразием, науке пока не известным. Поэтому приложение такого характера возможно, но пока что об этом речь не идёт. Просто решена столетняя, очень важная проблема чистой математики. Я говорю о чистой математике без всяких приложений. Борис Долгин: Да, собственно, если вы когда-либо учились в вузе, вы, наверное, сталкивались с тем, что одни люди хорошо читают лекции, другие хорошо ведут семинары. Третьи нередко занимаются исследованиями лучше, и так далее. Пытаться от одного и того же человека требовать и совершить исследование и придумать приложение или и совершить исследование в одной сфере и придумать, как она накладывается на другую – это некоторая чрезмерность. Вопрос из зала: А вот про 8 геометрических структур… почему не говорите… Борис Долгин: Ну, если останется время, мы спросим о 8-ми геометрических структурах. Сергей Дужин: Ну, давайте я одну структуру поясню, раз уж два раза спросили. Это не сложно. Значит одна из 8-ми структур. Давайте я одну поясню. Допустим, Nil. Nil– это группа Гейзенберга. Она состоит из матриц вот такого вида с обычным умножением.
Это однородное риманово многообразие, там можно ввести метрику и так далее. Пожалуйста, конкретный пример. Более подробно я не имею возможности рассказывать обо всех этих геометриях. Могу дать ссылку на литературу, пожалуйста. Борис Долгин: Да, если можете назвать пару книжек, где просто внятно можно с нуля более-менее, то есть с 10 класса об этом прочитать…
Сергей Дужин: В интернете лежит книга самого Тёрстона, которая до сих пор не дописана до конца. Есть книжка Скотта, даже на русском языке, переводил её мой коллега Сергей Ландо в свое время – Питер Скотт «Геометрии на трехмерных многообразиях». Я не помню, как его зовут, этого Скотта. Там эти геометрии, 8 штук очень подробно изучаются. Есть, в конце концов, Википедия, в которой можно получить первоначальные сведения. Значит там есть соответствующая статья, эти геометрии, по крайней мере, им дано определение. Борис Долгин: Вы, наверное, говорите об англоязычной Википедии. Или в русскоязычной адекватные сведения? Сергей Дужин: В англоязычной я видел. Может быть в русскоязычной есть. Я не знаю. Егор Елизаров: Я не математик. Я хотел уточнить. Есть что-то аналогичное теореме Пуанкаре, которая сейчас тоже ожидает доказательства и в ближайшее время будет решена, что-то в таком духе, какая-то очередная сенсация? Сергей Дужин: Ну, во-первых, никто не ожидал в 2002-2003 году, что она будет решена. Егор Елизаров: Я понимаю. Просто не так раскручена, грубо говоря. Сергей Дужин: Есть проблема нулей функции Римана. Есть функция Римана – дзета-функция, которая задаётся формулой ζ(z)=Σn=1...∞ n-z , где z – комплексное число. У этой функции есть нули, и есть гипотеза, что все они находятся на одной прямой. Эта гипотеза открыта – она связана ещё с вопросом распределения простых чисел в натуральном ряду, как это ни странно на первый взгляд. Виктор Васильев: P-NP? Сергей Дужин: Да, есть проблема P-NP, но я, честно говоря, ничего не понимаю в теории сложности, поэтому…. Такая проблема есть. Есть классы сложности P и NP. Если будет доказано, что P=NP, то многие алгоритмы упростятся. Ну, не знаю, сам скажи... Виктор Васильев, академик РАН: Описывать эти классы сложности я тоже не буду, но могу на пальцах объяснить. Раньше, когда мы в школе писали выпускные экзамены, мы решали уравнения. Была такая задача – решить какое-то уравнение. А теперь вместо этого нам дают на выбор 4 ответа. Надо проверить, удовлетворяют ли эти ответы нашему уравнению. Фактически задача состоит в том, чтобы подставить эти ответы, и проверить, удовлетворяют ли они этому уравнению или нет?
Проблема P=NP состоит в следующем: эта задача в бесконечное количество раз проще исходной для настоящих проблем или все-таки не бесконечно проще, а сравнимо. Сложность задачи – это сколько нужно действий для ее решения. Конечно, для одной конкретной задачи проверка ответа не может быть бесконечно проще исходной: сложности и того и другого – конечные числа, и их частное конечно. Но бывают серийные задачи, зависящие от параметра: решить любую систему уравнений от t переменных, или упорядочить по росту t человек, или оптимизировать трафик в городе с t перекрестками, или разобраться в экономической задаче с t видами ресурсов, или разгадать шифр с кодом длины t . При росте t усложняется и исходная задача и проверка решения. Проблема (грубо говоря) состоит в том, насколько быстрее усложняется исходная задача (из некоторого класса таких задач) по сравнению с решением при наличии подсказки. Борис Долгин: Спасибо. Александр: Можно ещё раз уточнить, правильно ли я понял, что основная заслуга Григория Перельмана – в том, что он смог разобраться с геометрией в этих точках перегиба или в этих точках сингулярности? Сергей Дужин: Да, он преодолел, смог обойти сингулярности в потоке Риччи. Александр: Метод, которым он обходил эти сингулярности, применим только здесь или это применимо и для других сингулярностей, скажем, тех, которые возникают в физических проблемах? Сергей Дужин: Вряд ли. Там довольно специфические были у него вычисления. Я присутствовал на его докладах на семинарах покойной Ольги Александровны Ладыженской, когда он впервые об этом рассказывал – это семинар по дифференциальным уравнениям – там такая суровая аналитическая работа с параболическими дифференциальными уравнениями, специфического вида. Дифференциальные уравнения в разных местах все разные, редко встречаются одинаковые. Александр: Правильно ли я понял, что общий смысл доказательства – что в данной сингулярности можно построить какие-то геометрии, которые будут… Сергей Дужин: Ну, да, он, вместо того, чтобы идти через точку сингулярности, он в этом месте часть эволюции вырезает и заменяет другой, при которой топология сохраняется. Александр: Это касается только этого типа пространств? Или это может, если мы говорим о физическом пространстве… Сергей Дужин: Ну, физическое пространство – оно тривиально, это R3 – по крайней мере, я его себе так ощущаю. Здесь же речь идёт о любых трёхмерных многообразиях. Борис Долгин: Если я правильно понимаю вопрос, если его чуть-чуть расширить. Первая его часть – это вообще может ли этот метод быть как-то экстраполирован на другую проблематику, второе – может ли эта проблематика найти какие-то аналоги в собственно физических проблемах? Сергей Дужин: Мне неизвестно никаких применений этой методики в других работах – это раз, и неизвестно применение чего бы то ни было такого в физике. По крайней мере, до сих пор. Что же касается нашего физического пространства, то для него поток Риччи является тождественным – он его не меняет, потому что кривизна равна нулю и тензор Риччи равен нулю. Он работает только для «кривых» многообразий. Константин Иванович: Возвращаясь к школе. Ваше мнение, уровень математического преподавания в школе улучшается – ухудшается, какие к вам приходят специалисты и какие учителя работают в школах? Ваше мнение. Спасибо! Сергей Дужин: Я про школу ничего не знаю. Лично ко мне приходят отличные студенты из Санкт-Петербургского государственного университета. С одним из них – третьекурсником Мишей мы в этом году решили проблему Пшитыцкого (J.Przytycki), которая простояла 24 года. Так что талантливые школьники по-прежнему к нам приходят, хотя общий уровень образования, конечно, снижается. Владимир: Владимир, школьный учитель. Борис Долгин: Учитель математики? Владимир: Да. Сергей Васильевич, Вы говорите о параболических уравнениях, а там вполне возможно, что параболические уравнения они ж описывают сохранение тепла. И вполне возможно, что вот эти схлопывания – это какая-то тепловая катастрофа, которую можно как-то обойти… Сергей Дужин: Модельным параболическим уравнением является уравнение теплопроводности, да. Но здесь уравнение гораздо более сложное. Владимир: Там какая-нибудь неоднородная структура, бла-бла-бла. Коэффициент теплопроводности зависит от пространства. Там такого нет? Это один вопрос. Сергей Дужин: Нет, я бы сказал, там просто не уравнение теплопроводности. Оно параболического типа, но оно другое! Владимир: Хорошо, да, и была книжка Тёрстона на русском языке – там про эти 8 структур не написано? МЦНМО издавало... Сергей Дужин: В книжке Тёрстона про 8 структур, по-моему, будет написано во втором томе, который готовится к изданию на русском языке. В первом томе есть отдельно про евклидову геометрию и гиперболическую – это точно, а перечисление всех 8 типов – я там не помню. Владимир: Я тоже не помню, поэтому спросил. Борис Долгин: Так, еще коллеги? Владимир Карманов, пенсионер: Меня интересует инструментарий, который использовал Перельман, в данном случае – потоки Риччи, но в итоге дифференциальные уравнения. А вот топологическими методами как-то, чисто топологическими, можно? Сергей Дужин: Не получилось! Не получились! Пытались люди. Владимир Платонов: То есть сам Пуанкаре пытался это сделать? Сергей Дужин: Да. Владимир Карманов: То есть в этом предел? Сергей Дужин: У меня есть список лиц, которые пытались это решить топологическими методами. Первым был Уайтхед (John Henry Constantine Whitehead). В 1930-е годы он пытался решить эту проблему, даже сказал, что решил, нашёл ошибку, но при этом построил замечательное многообразие Уайтхеда. Потом Р. Бинг, В. Хакен, Э. Мойз и Х. Папакирьякопулос (R. H. Bing, W. Haken, E. Moise, Ch. Papakyriakopoulos) – 50-60-е годы. Все они публиковали работы, которые впоследствии оказывались ошибочными. В 1980-90-е годы было ещё несколько работ, не опубликованных уже. Уже народ не стал их публиковать, пока не разберётся. Я не знаю точно, кто это был. Топологические попытки продолжались вплоть до последнего времени, пока не стало ясно, что ни у кого не получается. Конечно, это некрасиво. Точнее, с одной стороны это красиво, с другой – мне лично хотелось бы и чисто топологического доказательства. Но его нет. Вопрос из зала: Это вопрос одной сингулярности? Сергей Дужин: Нет, это при данном подходе. У нас подход какой? Мы берём топологическое многообразие. Кладём на него метрику совершенно произвольную и эту метрику начинаем деформировать, она начинает эволюционировать под действием потока Риччи – это такой специальный метод. Не знаю, как он в голову вообще пришёл, может быть из этих примеров, который я здесь приводил. Потому что это тоже от Гамильтона – я читал его статьи в своё время. Этот метод приводит к сингулярностям, с которыми нужно разбираться методами дифференциальных уравнений. Иначе никак. Возможно, существуют другие методы, о которых никто ничего не знает. Борис Долгин: Я позволю себе более простой вопрос: как бы вы обозначили вообще место топологии в современной математике и в науке в целом, потому что понятно, что топологией пользуются за пределами математики? Сергей Дужин: Ну, топология в математике и в современной математической физике – это теория струн, топологическая квантовая теория поля и так далее, занимают одно из центральных мест наряду с алгебраической геометрией. Две таких области математики, которые сейчас бурно развиваются и находят применение в современной теоретической физике. Это, кстати от приложений ещё тоже далеко, хотя это физика. Но это теоретическая физика. Но все мы знаем, что уравнения Максвелла были написаны совершенно абстрактно в середине XIX-го века, а теперь, грубо говоря, на их основе лампочки горят. Максим: Я не математик, но мне интересно: есть ли какая задача на подходе, которая может быть решена, которая в принципе перевернёт наше представление о мире, и все мы будем очень удивлены? Сергей Дужин: Виктор Анатольевич Васильев здесь рассказал о такой задаче, которая называется задача P=NP. Эта задача, безусловно, перевернёт криптографию, банковское дело, работу ФБР, ФСБ, ЦРУ и так далее. Максим: Почему? Сергей Дужин: Пускай он лучше ответит. Виктор Васильев: Я не знаю, почему это моя задача, это задача, о которой я рассказал. Сергей Дужин: Почему эта задача имеет практические применения? Ты можешь сказать или нет? Потому что я… Виктор Васильев: Но ты всё правильно сказал, там она могла бы применяться, только надежды мало, что решат, конечно. Но может и решат! Борис Долгин: Да, я чувствую после этого комментария воспоследуют большие вливания средств в решение одной определённой задачи (Смех). Виктор Васильев: Скорее всего, она будет решена негативно… Сергей Дужин: И никто миллиона не получит! Виктор Васильев: Нет, почему? Нет-нет. Сергей Дужин: Потому что миллион дают только за положительные решения. (Ну так мне А.М. Вершик говорил: я был у Джаффе….). (Артур Джаффе – председатель фонда в Институте Клэя, который назначает миллионные премии за решение семи задач тысячелетия). Виктор Васильев: Я думаю, что за любое, за любое из трех. 1) За доказательство, что они равны, 2) за доказательство того, что они не равны и 3) за доказательство того, что доказать невозможно ни то ни другое. Я думаю, что за любое из этих трёх исходов дадут миллион.
Сергей Дужин: Про гипотезу Пуанкаре я слышал такое, что если бы её доказали в отрицательном смысле, то никому не положено было бы миллиона (смеются). За что купил, за то и продаю. Я –тополог. Виктор Васильев: Не знаю. Константин: Добрый вечер, Константин, Москва. Я хотел спросить, применительно к нашей Вселенной с точки зрения космологии. Наше пространство – у него какая кривизна? Нулевая, положительная? Отрицательная? Сергей Дужин: Есть такая наука – общая теория относительности Эйнштейна, в которой считается, что массы создают кривизну. Но я-то занимаюсь топологией многообразий в целом. Про топологию в целом это ничего не говорит – ну там у какой-то звезды чего-то покривилось. Ну, ладно, бывает. То есть к проблеме геометризации это прямого отношения, на самом деле, не имеет. Я не большой специалист в физике, просто знаю, что есть общая теория относительность Эйнштейна, в которой есть кривизна, но в обычном пространстве R3 (или R4, если добавить время), это глобально ничего не меняет, вот и всё. Вопрос из зала: Там гравитацией определяется. Сергей Дужин: Ну, я и говорю, гравитацией – массой. Дмитрий, Хабаровск: Исходя из лекции, понятно, что это некая популяризация очень сложных вещей. Мы знаем Якова Перельмана с его «Популярной физикой», которая живет уже сто лет. Вот эти материалы будут как-то переложены? Они будут доступны в печатном виде, в электронном? За пределами лекции, или с расширением сферы? Сергей Дужин: Я над этим работать не собираюсь, но представители «Полит.ру», которые здесь присутствуют, что-то говорили о какой-то публикации видеозаписи с картинками. Борис Долгин: Да, конечно. Видеозапись, с расшифровкой, с картинками. Да, конечно. Сергей Дужин: Я отредактирую, пускай ради Бога оно выйдет. Борис Долгин: Наверное, всё-таки речь идёт о том, не собирается ли кто-нибудь так уж совсем томов на пять это популярно изложить? Сергей Дужин: Нет, ну подробное изложение есть! Борис Долгин: Подробное изложение с нуля? Сергей Дужин: С нуля это изложить невозможно, потому что нужно по дороге пройти пять томов дифференциальной геометрии Спивака. Пройти, допустим, там какого-нибудь Спеньера алгебраической геометрии такой талмуд и так далее… Это всё нужно знать, нужно пройти теорию дифференциальных уравнений на очень хорошем уровне. Изложить это с нуля в пяти томах так, чтобы кто-то это смог прочитать – невозможно. Потому что человек, который начинает с нуля – он дойдёт максимум до конца первого тома. А человек, который первый том знает, он может прочесть второй, допустим. И так далее. Я считаю этот проект невозможным. Борис Долгин: То есть иными словами популяризировать современную математику становится тяжелее, чем математику, условно говоря, рубежа XIX и XX веков? Принципиально тяжелее? Сергей Дужин: Ну, это зависит ещё от той математики, которой человек занимается. Например, свою собственную математику, вот то, что я, например, делаю, скажем, в этом году я решил некую проблему, которая простояла не 99 лет, как проблема Пуанкаре, а 24 года. Вот эту задачу – она не имеет такой фундаментальной важности в науке и, в общем-то, она ерундовская, тем не менее, она была известна. Её решали известные люди, в том числе Джон Конвей пытался решить и не смог. Эту задачу я мог бы объяснить популярно вот этой же публике. Борис Долгин: Да, понятно.
Сергей Дужин: Потому что я занимаюсь элементарной математикой. Существует математика высшая, которая занимается, точнее, занимался Перельман – это высшая математика. Я всех деталей его доказательства не знаю, хотя я был и на его докладах, я слушал курс лекций Моргана, который разбирался в этом всём. Я читал его препринты и так далее, но я не понимаю деталей доказательства, потому что там такие дифференциальные уравнения, от которых у меня уши отваливаются. Борис Долгин: Вы полагаете, что именно занимался, а не занимается? Сергей Дужин: Я полагаю, что он прекратил занятия математикой. Но я на политические темы разговаривать не собираюсь. Борис Долгин: Хорошо, спасибо большое! Я надеюсь, что мы математическую линию обязательно продолжим. Правда, кажется, что это достаточно трудная задача и ей занимаются недостаточно.
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Математика ≫ Видео ≫ «Гриша Перельман, яблоко и бублик» // Сергей Дужин |
|
[time: 12 ms; queries: 7]
22 Фев 2026 08:35:01 GMT+3 |






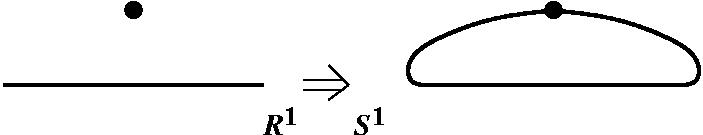
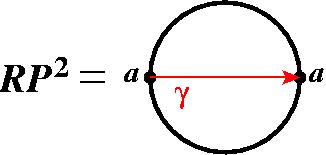









 Последним великим достижением чистой математики называют доказательство петербуржцем Григорием Перельманом в 2002–2003 годах гипотезы Пуанкаре, высказанной в 1904 году и гласящей: «всякое связное, односвязное, компактное трехмерное многообразие без края гомеоморфно сфере S3». В этой фразе имеется несколько терминов, которые я постараюсь объяснить так, чтобы их общий смысл стал понятен нематематикам (я предполагаю, что читатель закончил среднюю школу и кое-что из школьной математики еще помнит).
Последним великим достижением чистой математики называют доказательство петербуржцем Григорием Перельманом в 2002–2003 годах гипотезы Пуанкаре, высказанной в 1904 году и гласящей: «всякое связное, односвязное, компактное трехмерное многообразие без края гомеоморфно сфере S3». В этой фразе имеется несколько терминов, которые я постараюсь объяснить так, чтобы их общий смысл стал понятен нематематикам (я предполагаю, что читатель закончил среднюю школу и кое-что из школьной математики еще помнит). Доказательство гипотезы Пуанкаре принесло Перельману мировое признание. В 2006 году он стал лауреатом «Медали Филдса», в 2010 году институт Клэя подтвердил присуждение Перельману премии за решение одной из проблем тысячелетия. Однако математик отказался принять эти награды. Григорий Перельман о своем отказе от премии: «Я отказался. Вы знаете, у меня было очень много причин и в ту, и в другую сторону. Поэтому я так долго решал. Если говорить совсем коротко, то главная причина — это несогласие с организованным математическим сообществом. Мне не нравятся их решения, я считаю их несправедливыми. Я считаю, что вклад в решение этой задачи американского математика Гамильтона ничуть не меньше, чем мой».
Доказательство гипотезы Пуанкаре принесло Перельману мировое признание. В 2006 году он стал лауреатом «Медали Филдса», в 2010 году институт Клэя подтвердил присуждение Перельману премии за решение одной из проблем тысячелетия. Однако математик отказался принять эти награды. Григорий Перельман о своем отказе от премии: «Я отказался. Вы знаете, у меня было очень много причин и в ту, и в другую сторону. Поэтому я так долго решал. Если говорить совсем коротко, то главная причина — это несогласие с организованным математическим сообществом. Мне не нравятся их решения, я считаю их несправедливыми. Я считаю, что вклад в решение этой задачи американского математика Гамильтона ничуть не меньше, чем мой». Гипотеза Пуанкаре была сформулирована в Париже, в 1904 году. Сто лет математики бились над попытками доказать эту гипотезу. Каждый из них считал, что он находится в шаге от разгадки, однако это было не так. Многим из выдающихся математиков гипотеза Пуанкаре осложнила и жизнь вне работы... Лишь в 2002 году российскому ученому Григорию Перельману удалось доказать ее весьма нетривиальным и лаконичным способом. Целых три года понадобилось ученым всего мира, чтобы проверить истинность доказательства. И вот, наконец, 2006 год, Мадрид. Эпохальное достижение удостоено медали Филдса, которую называют «нобелевской премией» математиков. Однако происходит невероятное. Григорий Перельман отказывается принять награду. Он уединяется в своей квартире в Санкт-Петербурге и отказывается общаться с внешним миром...
Гипотеза Пуанкаре была сформулирована в Париже, в 1904 году. Сто лет математики бились над попытками доказать эту гипотезу. Каждый из них считал, что он находится в шаге от разгадки, однако это было не так. Многим из выдающихся математиков гипотеза Пуанкаре осложнила и жизнь вне работы... Лишь в 2002 году российскому ученому Григорию Перельману удалось доказать ее весьма нетривиальным и лаконичным способом. Целых три года понадобилось ученым всего мира, чтобы проверить истинность доказательства. И вот, наконец, 2006 год, Мадрид. Эпохальное достижение удостоено медали Филдса, которую называют «нобелевской премией» математиков. Однако происходит невероятное. Григорий Перельман отказывается принять награду. Он уединяется в своей квартире в Санкт-Петербурге и отказывается общаться с внешним миром... Он доказал гипотезу Пуанкре – одну из самых загадочных геометрических задач ХХ века. Возможно, что это осталось бы сенсацией лишь для узких научных кругов, но он отказался от награды в миллион долларов. А почему? Этого он никому не сказал. Впервые на отечественном экране о Перельмане рассказывают люди, которые узнали его задолго до всей этой истории, которые знают истинную цену его характеру и его интеллекту. Этот фильм - попытка разобраться, что движет удивительным человеком и талантливым ученым Григорием Перельманом. Что значит его открытие для русской и мировой науки? А на вопрос, почему же Перельман не взял свой миллион, зрители ответят сами…
Он доказал гипотезу Пуанкре – одну из самых загадочных геометрических задач ХХ века. Возможно, что это осталось бы сенсацией лишь для узких научных кругов, но он отказался от награды в миллион долларов. А почему? Этого он никому не сказал. Впервые на отечественном экране о Перельмане рассказывают люди, которые узнали его задолго до всей этой истории, которые знают истинную цену его характеру и его интеллекту. Этот фильм - попытка разобраться, что движет удивительным человеком и талантливым ученым Григорием Перельманом. Что значит его открытие для русской и мировой науки? А на вопрос, почему же Перельман не взял свой миллион, зрители ответят сами… В курсе будет изложена история гипотезы Пуанкаре — с точными определениями и формулировками, но без полных доказательств. Будут объяснены понятия, необходимые для понимания различных версий (топологическая, гладкая, кусочно-линейная) гипотезы Пуанкаре: многообразие, гомотопическая эквивалентность, фундаментальная группа. Слушатели узнают о классификации двумерных компактных многообразий («сферы с ручками и пленками Мебиуса»), об экзотических гладкостях на сферах и на R^4 и о том, что одна из версий гипотезы Пуанкаре (гладкая 4-мерная) остается открытой. Мы обсудим также различные версии проблемы Шенфлиса: ограничивает ли вложенная (n–1)-мерная сфера в R^n вложенный n-мерный шар? Некоторые из этих версий остаются открытыми проблемами.
В курсе будет изложена история гипотезы Пуанкаре — с точными определениями и формулировками, но без полных доказательств. Будут объяснены понятия, необходимые для понимания различных версий (топологическая, гладкая, кусочно-линейная) гипотезы Пуанкаре: многообразие, гомотопическая эквивалентность, фундаментальная группа. Слушатели узнают о классификации двумерных компактных многообразий («сферы с ручками и пленками Мебиуса»), об экзотических гладкостях на сферах и на R^4 и о том, что одна из версий гипотезы Пуанкаре (гладкая 4-мерная) остается открытой. Мы обсудим также различные версии проблемы Шенфлиса: ограничивает ли вложенная (n–1)-мерная сфера в R^n вложенный n-мерный шар? Некоторые из этих версий остаются открытыми проблемами. Перспектива получения Филдсовской медали заставила Григория Перельмана окончательно порвать с математикой. "Пока я оставался незаметным, у меня был выбор", объяснил Перельман. "Либо крепко всем насолить" (поднять шумиху по поводу нечистоплотных методов в науке), "либо промолчать и терпеть отношение к себе как к домашней собачке. Теперь, когда я превратился в очень заметную персону, я не смогу и дальше молчать. Вот почему я был вынужден уйти".
Перспектива получения Филдсовской медали заставила Григория Перельмана окончательно порвать с математикой. "Пока я оставался незаметным, у меня был выбор", объяснил Перельман. "Либо крепко всем насолить" (поднять шумиху по поводу нечистоплотных методов в науке), "либо промолчать и терпеть отношение к себе как к домашней собачке. Теперь, когда я превратился в очень заметную персону, я не смогу и дальше молчать. Вот почему я был вынужден уйти". Каким образом появились числа и как они повлияли на развитие человечества – эти вопросы в центре внимания 5-серийного проекта. В эпизодах, которые пронесут нас сквозь время и пространство, мы увидим, что математика играла важную роль в Древнем Египте и Греции, Индии, Средневековой Европе и продолжает играть сейчас в нашем современном мире.
Каким образом появились числа и как они повлияли на развитие человечества – эти вопросы в центре внимания 5-серийного проекта. В эпизодах, которые пронесут нас сквозь время и пространство, мы увидим, что математика играла важную роль в Древнем Египте и Греции, Индии, Средневековой Европе и продолжает играть сейчас в нашем современном мире. Лекция математика Алексея Владимировича Савватеева в СУНЦ МГУ про великие математические революции и нерешенные задачи, многие из которых уже решены, а некоторые — ждут своих героев. Для старших и "продвинутых" школьников, интересующихся математикой.
Лекция математика Алексея Владимировича Савватеева в СУНЦ МГУ про великие математические революции и нерешенные задачи, многие из которых уже решены, а некоторые — ждут своих героев. Для старших и "продвинутых" школьников, интересующихся математикой. О том, как строить работу с одаренными детьми, на каких принципах удается воспитывать столь одаренных математиков как Григорий Перельман, Станислав Смирнов и другие, мы побеседовали с Сергеем Рукшиным, заслуженным учителем РФ, канд. физ.-мат. наук, членом Общественного совета при Министерстве образования и науки, основателем и директором Санкт-Петербургского городского математического центра для одаренных школьников, доцентом РГПУ им. А.И. Герцена. Беседовала Наталия Демина.
О том, как строить работу с одаренными детьми, на каких принципах удается воспитывать столь одаренных математиков как Григорий Перельман, Станислав Смирнов и другие, мы побеседовали с Сергеем Рукшиным, заслуженным учителем РФ, канд. физ.-мат. наук, членом Общественного совета при Министерстве образования и науки, основателем и директором Санкт-Петербургского городского математического центра для одаренных школьников, доцентом РГПУ им. А.И. Герцена. Беседовала Наталия Демина.