|
||
|
|
||
| Главная ≫ Инфотека ≫ Математика ≫ Григорий Перельман |
Григорий Перельман
Григорий Яковлевич Перельман (54 года) родился 13 июня 1966 года в Ленинграде. Отец его был инженером-электриком, мать — преподавателем математики в ПТУ. Когда отец Григория Перельмана получил возможность уехать на постоянное жительство в Израиль, мать отказалась ехать с ним и осталась с Григорием и старшей дочерью в Ленинграде. Учась в школе, Григорий Перельман занимался в математическом кружке городского дворца пионеров и успешно участвовал в школьных математических олимпиадах. В 1982 году на Международной математической олимпиаде в Будапеште Перельман был награжден золотой медалью, получив за решения каждой из предлагавшихся семи задач максимально возможный балл. После окончания 239-й физико-математической школы Григорий Перельман был без экзаменов зачислен на математико-механический факультет Ленинградского государственного университета. Окончив университет, Перельман учился в аспирантуре Ленинградского отделения Математического института им. В. А. Стеклова, защитил кандидатскую диссертацию и стал работать старшим научным сотрудником этого института. В начале 1990-х несколько лет работал в США, в Курантовском институте математических наук, Университете штата Нью-Йорк в Стоуни-Брук и Калифорнийском университете в Беркли. Затем вернулся в Математический институт имени Стеклова. В 2002 — 2003 годах опубликовал на сайте препринтов arXiv.org три статьи, посвященные доказательству проблемы Пуанкаре, которые сразу привлекли внимание ученых. Перельман был приглашен в ряд университетов США, где выступил с докладами о своих работах. В 2006 году доказательство Перельмана было признано верным. В декабре 2005 года Григорий Перельман уволился с должности ведущего научного сотрудника лаборатории математической физики и объявил, что прекращает занятия наукой. После этого вел замкнутый образ жизни, игнорируя прессу. Жил в Санкт-Петербурге в Купчино вместе матерью на ее пенсию и сбережения, оставшиеся от зарубежных поездок. В отделение Математического института им. Стеклова, откуда уволился автор доказательств гипотезы Пуанкаре, на его имя до сих пор приходит почта, но Перельман сказал, что забирать ее не будет: «С наукой покончено». В сентябре 2011 года стало известно, что математик отказался принять предложение стать членом Российской академии наук. В 2014 году Григорий Перельман получил шведскую визу сроком на 10 лет. В Стокгольме давно живёт родная сестра учёного Елена. Позднее сообщалось, что он переехал жить в Швецию, где местная частная фирма, занимающаяся научными разработками, предложила ему высокооплачиваемую работу. Наибольшую известность Григорию Перельману принесло осуществленное им доказательство гипотезы Пуанкаре — одной из знаменитых задач в области математической топологии. Гипотеза была сформулирована выдающимся французским математиком Анри Пуанкаре еще в 1904 году. Она связана с понятием гомеоморфизма — возможности изменить форму объекта при помощи непрерывной трансформации, но так, чтобы он не утратил своих топологических свойств. Например, бублик и чашка с ручкой гомеоморфны: если мы представим бублик из пластилина, то из него, не делая разрывов, можно вылепить чашку. Предположение Пуанкаре касалось односвязных поверхностей, то есть таких, на которых можно провести замкнутую кривую, которая не делила бы их на части. В общем виде гипотеза Пуанкаре звучит так: «любая односвязная трехмерная поверхность гомеоморфна трехмерной сфере». Следует помнить, что трехмерные поверхности относятся к четырехмерному пространству, так, трехмерная сфера — это поверхность четырехмерного шара. Для отдельных частных случаев гипотезу успел доказать сам Пуанкаре. Затем над этим работали другие математики. Одно из доказательств в 1930-е годы предложил выдающийся английский математик Генри Уайтхед, но оно оказалось ошибочным, зато благодаря ему Уайтхед стал основоположником нового раздела топологии — топологии малых размерностей. Работа Уайтхеда стимулировала интерес ученых к гипотезе Пуанкаре. В 60-70-е годы гипотеза была доказана для поверхностей с числом измерений большим или равным пяти. В 1982 году Майкл Фридман доказал ее для четырехмерных поверхностей. Но общее доказательство не поддавалось математикам. Хотя было опубликовано несколько работ, авторы которых считали, что добились успеха, в их доказательствах обнаруживались ошибки. В 2000 году Математический институт Клэя включил доказательство гипотезы Пуанкаре в число семи «проблем тысячелетия», за решение любой из которых была обещана премия в один миллион долларов. В тот момент специалисты понимали, что существующими методами доказательства получить не удастся и для успеха необходимо применение принципиально новых подходов. Григорий Перельман использовал в своей работе идеи Ричарда Гамильтона, которые связывают топологические проблемы с системами дифференциальных уравнений в частных производных, известными под названием «потоки Риччи». Также Перельман доказал и более общее утверждение о свойствах трехмерных поверхностей — гипотезу геометризации Тёрстона. В 2006 году журнал Science назвал доказательство Перельманом гипотезы Пуанкаре научным «прорывом года». Популярное изложение сути работ Григория Перельмана можно прочитать в тексте лекции «Гриша Перельман, яблоко и бублик», прочитанной старшим научным сотрудником Санкт-Петербургского отделения Математического института РАН Сергеем Дужиным в рамках проекта «Публичные лекции Полит.ру». Доказательство гипотезы Пуанкаре принесло Перельману мировое признание. В 2006 году он стал лауреатом «Медали Филдса», в 2010 году институт Клэя подтвердил присуждение Перельману премии за решение одной из проблем тысячелетия. Однако математик отказался принять эти награды. В дальнейшем Перельман прекратил научную деятельность и отказался от общения с прессой. Другая громкая история была связана с попыткой группы китайских математиков заявить, что они выполнили более полное доказательство гипотезы Пуанкаре, тогда как доказательство Перельмана, по их словам, было неполным. Чжу Сипин и Цао Хуайдун из Лихайского университета входили в числе трех независимых групп ученых, которые проверяли доказательство Перельмана, возглавлял эту группу видный китайско-американский математик Яу Шинтан. В 2006 году в журнале «Нью-Йоркер» вышла статья Сильвии Назар и Дэвида Грубера «Manifold Destiny», об истории доказательства гипотезы Пуанкаре. В ней Яу Шинтан обвинялся в неоднократных нарушениях научной этики. В ответ китайский математик обвинил авторов статьи в клевете. Редакция журнала поддержала авторов, объявив, что изложенные в статье факты были тщательно проверены, а изложению позиции Яу Шинтана было уделено достаточное место. Григорий Перельман о своем отказе от премии: «Я отказался. Вы знаете, у меня было очень много причин и в ту, и в другую сторону. Поэтому я так долго решал. Если говорить совсем коротко, то главная причина — это несогласие с организованным математическим сообществом. Мне не нравятся их решения, я считаю их несправедливыми. Я считаю, что вклад в решение этой задачи американского математика Гамильтона ничуть не меньше, чем мой». Сергей Рукшин о своем ученике: «Гриша начал очень много работать в девятом классе, и у него оказалось очень ценное для занятий математикой качество: способность к очень длительной концентрации внимания без особых успехов внутри задачи. Все-таки человеку нужна психологическая подпитка, нужны психологические успехи, чтобы заниматься чем-то дальше. Фактически гипотеза Пуанкаре — это почти девять лет без знания того, решится задача или не решится. Понимаете, там даже невозможны были частичные результаты. Не доказалась теорема в полном объеме — иной раз можно опубликовать даже двадцатистраничную статью, по тому, что все-таки получилось. А там — или пан, или пропал. Либо доказана гипотеза Пуанкаре, либо нет… Частичных результатов и до него получали много. Вот такая вот длительная концентрация внимания без надежды на успех — это замечательное качество Перельмана!» Сергей Рукшин о причинах ухода Перельмана из науки: «Первый фактор — это длительное и очень сильное перенапряжение головного мозга и нервной системы, это было непросто. Второе — это конфликт с математическим сообществом. Гриша очень ригористичен. Он ригорист, его моральные требования завышены. Ну, например, он поссорился с моим другим учеником, Антоном Петруниным, с которым они занимались совместной научной работой, и перестал с Петруниным общаться, остались незавершенные работы, результаты, которые ни тот, ни другой не опубликовали. Один не публиковал, потому что без Гриши нельзя, а другой — потому то он с Антоном не общается. А поссорились они из-за того, что кто-то кого-то где-то не процитировал, что в устном докладе не считалось никогда грехом, можно было бы и забыть, и не сослаться на то, что такой-то результат кому-то принадлежит, а просто им воспользоваться: "Есть известный результат, что… Ссылаясь на него, получаем…" А Гриша считает, что это было неуместно. Всё. Гриша рассорился и перестал с Антоном общаться».
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Математика ≫ Григорий Перельман |
|
[time: 13 ms; queries: 7]
4 Мар 2026 02:51:02 GMT+3 |


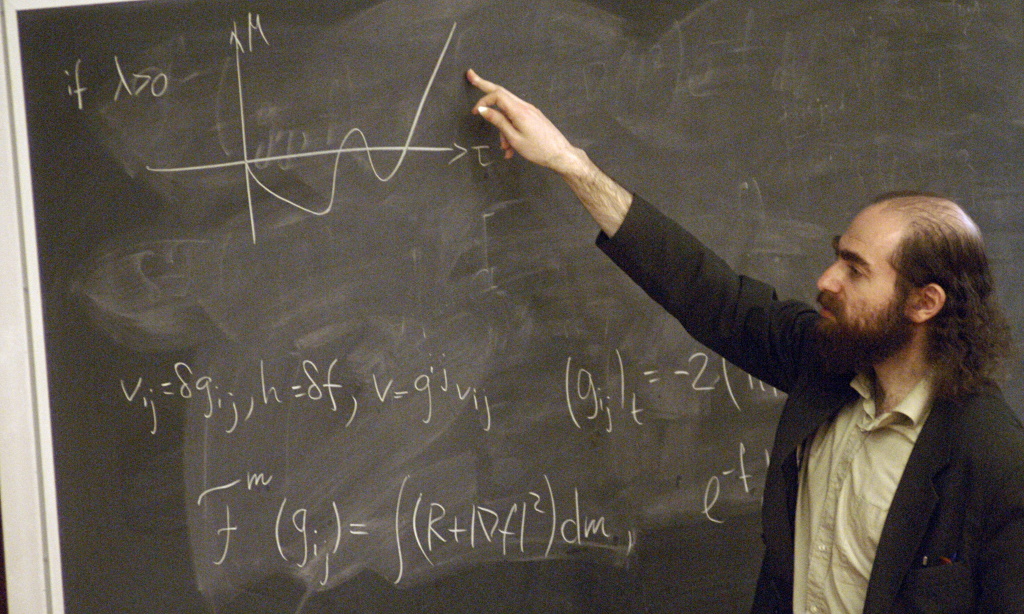
 Он доказал гипотезу Пуанкре – одну из самых загадочных геометрических задач ХХ века. Возможно, что это осталось бы сенсацией лишь для узких научных кругов, но он отказался от награды в миллион долларов. А почему? Этого он никому не сказал. Впервые на отечественном экране о Перельмане рассказывают люди, которые узнали его задолго до всей этой истории, которые знают истинную цену его характеру и его интеллекту. Этот фильм - попытка разобраться, что движет удивительным человеком и талантливым ученым Григорием Перельманом. Что значит его открытие для русской и мировой науки? А на вопрос, почему же Перельман не взял свой миллион, зрители ответят сами…
Он доказал гипотезу Пуанкре – одну из самых загадочных геометрических задач ХХ века. Возможно, что это осталось бы сенсацией лишь для узких научных кругов, но он отказался от награды в миллион долларов. А почему? Этого он никому не сказал. Впервые на отечественном экране о Перельмане рассказывают люди, которые узнали его задолго до всей этой истории, которые знают истинную цену его характеру и его интеллекту. Этот фильм - попытка разобраться, что движет удивительным человеком и талантливым ученым Григорием Перельманом. Что значит его открытие для русской и мировой науки? А на вопрос, почему же Перельман не взял свой миллион, зрители ответят сами… Последним великим достижением чистой математики называют доказательство петербуржцем Григорием Перельманом в 2002–2003 годах гипотезы Пуанкаре, высказанной в 1904 году и гласящей: «всякое связное, односвязное, компактное трехмерное многообразие без края гомеоморфно сфере S3». В этой фразе имеется несколько терминов, которые я постараюсь объяснить так, чтобы их общий смысл стал понятен нематематикам (я предполагаю, что читатель закончил среднюю школу и кое-что из школьной математики еще помнит).
Последним великим достижением чистой математики называют доказательство петербуржцем Григорием Перельманом в 2002–2003 годах гипотезы Пуанкаре, высказанной в 1904 году и гласящей: «всякое связное, односвязное, компактное трехмерное многообразие без края гомеоморфно сфере S3». В этой фразе имеется несколько терминов, которые я постараюсь объяснить так, чтобы их общий смысл стал понятен нематематикам (я предполагаю, что читатель закончил среднюю школу и кое-что из школьной математики еще помнит).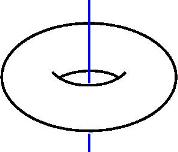 1 февраля 2015 года не стало талантливого математика, докт. физ.-мат.наук, старшего научного сотрудника Санкт-Петербургского отделения Математического института РАН Сергея Васильевича Дужина. Публикуем расшифровку его лекции «Гриша Перельман, яблоко и бублик», с которой он выступил 22 сентября 2011 года.
1 февраля 2015 года не стало талантливого математика, докт. физ.-мат.наук, старшего научного сотрудника Санкт-Петербургского отделения Математического института РАН Сергея Васильевича Дужина. Публикуем расшифровку его лекции «Гриша Перельман, яблоко и бублик», с которой он выступил 22 сентября 2011 года. Гипотеза Пуанкаре была сформулирована в Париже, в 1904 году. Сто лет математики бились над попытками доказать эту гипотезу. Каждый из них считал, что он находится в шаге от разгадки, однако это было не так. Многим из выдающихся математиков гипотеза Пуанкаре осложнила и жизнь вне работы... Лишь в 2002 году российскому ученому Григорию Перельману удалось доказать ее весьма нетривиальным и лаконичным способом. Целых три года понадобилось ученым всего мира, чтобы проверить истинность доказательства. И вот, наконец, 2006 год, Мадрид. Эпохальное достижение удостоено медали Филдса, которую называют «нобелевской премией» математиков. Однако происходит невероятное. Григорий Перельман отказывается принять награду. Он уединяется в своей квартире в Санкт-Петербурге и отказывается общаться с внешним миром...
Гипотеза Пуанкаре была сформулирована в Париже, в 1904 году. Сто лет математики бились над попытками доказать эту гипотезу. Каждый из них считал, что он находится в шаге от разгадки, однако это было не так. Многим из выдающихся математиков гипотеза Пуанкаре осложнила и жизнь вне работы... Лишь в 2002 году российскому ученому Григорию Перельману удалось доказать ее весьма нетривиальным и лаконичным способом. Целых три года понадобилось ученым всего мира, чтобы проверить истинность доказательства. И вот, наконец, 2006 год, Мадрид. Эпохальное достижение удостоено медали Филдса, которую называют «нобелевской премией» математиков. Однако происходит невероятное. Григорий Перельман отказывается принять награду. Он уединяется в своей квартире в Санкт-Петербурге и отказывается общаться с внешним миром... Перспектива получения Филдсовской медали заставила Григория Перельмана окончательно порвать с математикой. "Пока я оставался незаметным, у меня был выбор", объяснил Перельман. "Либо крепко всем насолить" (поднять шумиху по поводу нечистоплотных методов в науке), "либо промолчать и терпеть отношение к себе как к домашней собачке. Теперь, когда я превратился в очень заметную персону, я не смогу и дальше молчать. Вот почему я был вынужден уйти".
Перспектива получения Филдсовской медали заставила Григория Перельмана окончательно порвать с математикой. "Пока я оставался незаметным, у меня был выбор", объяснил Перельман. "Либо крепко всем насолить" (поднять шумиху по поводу нечистоплотных методов в науке), "либо промолчать и терпеть отношение к себе как к домашней собачке. Теперь, когда я превратился в очень заметную персону, я не смогу и дальше молчать. Вот почему я был вынужден уйти". В курсе будет изложена история гипотезы Пуанкаре — с точными определениями и формулировками, но без полных доказательств. Будут объяснены понятия, необходимые для понимания различных версий (топологическая, гладкая, кусочно-линейная) гипотезы Пуанкаре: многообразие, гомотопическая эквивалентность, фундаментальная группа. Слушатели узнают о классификации двумерных компактных многообразий («сферы с ручками и пленками Мебиуса»), об экзотических гладкостях на сферах и на R^4 и о том, что одна из версий гипотезы Пуанкаре (гладкая 4-мерная) остается открытой. Мы обсудим также различные версии проблемы Шенфлиса: ограничивает ли вложенная (n–1)-мерная сфера в R^n вложенный n-мерный шар? Некоторые из этих версий остаются открытыми проблемами.
В курсе будет изложена история гипотезы Пуанкаре — с точными определениями и формулировками, но без полных доказательств. Будут объяснены понятия, необходимые для понимания различных версий (топологическая, гладкая, кусочно-линейная) гипотезы Пуанкаре: многообразие, гомотопическая эквивалентность, фундаментальная группа. Слушатели узнают о классификации двумерных компактных многообразий («сферы с ручками и пленками Мебиуса»), об экзотических гладкостях на сферах и на R^4 и о том, что одна из версий гипотезы Пуанкаре (гладкая 4-мерная) остается открытой. Мы обсудим также различные версии проблемы Шенфлиса: ограничивает ли вложенная (n–1)-мерная сфера в R^n вложенный n-мерный шар? Некоторые из этих версий остаются открытыми проблемами. Каким образом появились числа и как они повлияли на развитие человечества – эти вопросы в центре внимания 5-серийного проекта. В эпизодах, которые пронесут нас сквозь время и пространство, мы увидим, что математика играла важную роль в Древнем Египте и Греции, Индии, Средневековой Европе и продолжает играть сейчас в нашем современном мире.
Каким образом появились числа и как они повлияли на развитие человечества – эти вопросы в центре внимания 5-серийного проекта. В эпизодах, которые пронесут нас сквозь время и пространство, мы увидим, что математика играла важную роль в Древнем Египте и Греции, Индии, Средневековой Европе и продолжает играть сейчас в нашем современном мире. О том, как строить работу с одаренными детьми, на каких принципах удается воспитывать столь одаренных математиков как Григорий Перельман, Станислав Смирнов и другие, мы побеседовали с Сергеем Рукшиным, заслуженным учителем РФ, канд. физ.-мат. наук, членом Общественного совета при Министерстве образования и науки, основателем и директором Санкт-Петербургского городского математического центра для одаренных школьников, доцентом РГПУ им. А.И. Герцена. Беседовала Наталия Демина.
О том, как строить работу с одаренными детьми, на каких принципах удается воспитывать столь одаренных математиков как Григорий Перельман, Станислав Смирнов и другие, мы побеседовали с Сергеем Рукшиным, заслуженным учителем РФ, канд. физ.-мат. наук, членом Общественного совета при Министерстве образования и науки, основателем и директором Санкт-Петербургского городского математического центра для одаренных школьников, доцентом РГПУ им. А.И. Герцена. Беседовала Наталия Демина.