|
||
|
|
||
| Главная ≫ Инфотека ≫ Математика ≫ Видео ≫ Полтора // Михаил Тихонов |
ПолтораМихаил Тихонов
Бывают объекты непрерывные, а бывают дискретные. Например, размерность пространства. Она дискретна: пространства бывают одномерные, двумерные, трехмерные… А вот размерности «полтора» не бывает. Или бывает? Оказывается, дискретные объекты иногда можно обобщить до непрерывных, и на первой половине курса мы разберем несколько конкретных примеров. Начав с совсем тривиальной арифметики, мы быстро дойдем до таких «странных» вещей, как дробные производные, а на второй лекции разберем красивый пример из алгебраической геометрии. Эти примеры проиллюстрируют один общий рецепт нетривиальных обобщений: если суметь переговорить привычные понятия на другом языке, то «сложные» операции могут стать простыми, и наоборот. А во второй половине я расскажу, как этот рецепт позволяет подступиться к очень глубокой проблеме современной… биологии. За последние 10 лет в микробиологии произошла настоящая революция, и по мере того, как мы все больше узнаем о микроорганизмах, привычные дискретные понятия «вида» и «организма» становятся все более размытыми. Биология не знает, как правильно обобщить эти понятия до непрерывных, причем вопрос отнюдь не праздный: сегодня эта проблема особенно остро встает при изучении микробных сообществ, представляющих прямой медицинский интерес. Следуя нашему «рецепту», мы попробуем придумать «другой язык» для описания динамики экосистемы. А именно, вместо численности популяций и количества видов мы задумаемся о свойствах «спектра релаксации» (предварительно определив, что это такое). Мы увидим, что экосистему с двумя видами можно непрерывно перевести в такую, где видов уже три. Причем сделать это можно разными способами, один из которых на промежуточном этапе похож на «два с половиной вида», а другой совсем не похож. Первые три лекции будут доступны всем. На последней лекции мне придется использовать слова «собственный вектор» и «собственное значение», а также написать пару простых дифференциальных уравнений. Тем не менее, я надеюсь, что на некотором интуитивном уровне происходящее будет понятно и школьникам. План курса: 1. Арифметика, алгебра, анализ: дробные числа, дробные степени, дробные производные; 2. Алгебраическая геометрия: может ли точек быть больше одной, но меньше двух; 3. Проблема «вида» и «организма»; примеры из биологии, заставляющие задуматься; 4. Экосистема из «полутора» видов. Гладкая интерполяция между одним организмом и двумя. Тихонов Михаил Андреевич Летняя школа «Современная математика» г. Дубна, дом отдыха «Ратмино» 20-26 июля 2017 г.
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Математика ≫ Видео ≫ Полтора // Михаил Тихонов |
|
[time: 7 ms; queries: 7]
19 Фев 2026 07:43:58 GMT+3 |


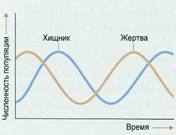 Иногда простая математическая модель хорошо описывает сложную биологическую систему. Примером этого служат долговременные отношения между видами хищника и жертвы в какой-либо экосистеме. Математические расчеты роста популяции отдельно взятого вида показывают, что пределы плотности популяции можно описать простыми уравнениями, которые на выходе дают характерную S-образную кривую. Это — кривая численности популяции, которая растет экспоненциально, пока она небольшая, а затем выравнивается, когда она достигает пределов возможности экосистемы поддерживать ее. Простое продолжение этой концепции позволяет нам понять экосистему, в которой взаимодействуют два вида — хищник и жертва.
Иногда простая математическая модель хорошо описывает сложную биологическую систему. Примером этого служат долговременные отношения между видами хищника и жертвы в какой-либо экосистеме. Математические расчеты роста популяции отдельно взятого вида показывают, что пределы плотности популяции можно описать простыми уравнениями, которые на выходе дают характерную S-образную кривую. Это — кривая численности популяции, которая растет экспоненциально, пока она небольшая, а затем выравнивается, когда она достигает пределов возможности экосистемы поддерживать ее. Простое продолжение этой концепции позволяет нам понять экосистему, в которой взаимодействуют два вида — хищник и жертва. Я давно хотела попасть в Летнюю школу «Современная математика» возле Дубны, которую вот уже 12-й год проводят Московский центр непрерывного изучения математики и Математический институт РАН. Как-то не получалось. В 2009 году я собрала отклики преподавателей и организаторов о Школе, которые говорили о том, как там здорово и интересно. Меня туда приглашал один из ее организаторов, человек, без сомнения, бывший душой Школы — Владимир Игоревич Арнольд. В этом году я решила, что надо, наконец, посмотреть, где же математики проводят лучшую часть лета, и, может быть, найти то место, где находится часть души Арнольда.
Я давно хотела попасть в Летнюю школу «Современная математика» возле Дубны, которую вот уже 12-й год проводят Московский центр непрерывного изучения математики и Математический институт РАН. Как-то не получалось. В 2009 году я собрала отклики преподавателей и организаторов о Школе, которые говорили о том, как там здорово и интересно. Меня туда приглашал один из ее организаторов, человек, без сомнения, бывший душой Школы — Владимир Игоревич Арнольд. В этом году я решила, что надо, наконец, посмотреть, где же математики проводят лучшую часть лета, и, может быть, найти то место, где находится часть души Арнольда.