|
||
|
|
||
| Главная ≫ Инфотека ≫ Математика ≫ Видео ≫ Математическое моделирование и вычислительная математика // Александр Шапеев |
Математическое моделирование и вычислительная математикаАлександр Шапеев
Что такое моделирование? Моделирование — это создание модели, то есть отражения реальности, более простого, чем реальность. Либо это упрощение другой, более сложной модели: моделью человека может быть рисунок человека, может быть манекен, может быть мышь. Разные модели в разных случаях могут быть более или менее полезны. Например, если дизайнер сделал новый пиджак и хочет понять, хорош он или плох, он использует манекен в качестве модели человека. Если биолог проверяет новое лекарство, то он использует мышь как первую модель человека. Это примеры нематематических моделей. Интересующей нас математической моделью будет либо трехмерная геометрия человека, если речь идет о дизайне одежды, либо дифференциальные уравнения, которые будут описывать эволюцию концентрации лекарства в организме человека или мыши. С моей точки зрения, человеком, внесшим наибольший вклад в математическое моделирование, был сэр Исаак Ньютон. Он предложил первые модели, которые используются до сих пор и которые похожи на математические модели, используемые сейчас в науке. Например, известные законы движения, когда Ньютон сказал, что, моделируя любое тело как точку, имеющую массу, мы можем посчитать ускорение, если мы знаем силу, которая действует на эту точку. Зная ускорение, мы знаем скорость; зная скорость, мы можем посчитать траекторию. Это были математические модели, очень похожие на те, которые мы используем сейчас. В молекулярном моделировании мы решаем те же самые уравнения Ньютона, которые были придуманы почти 400 лет назад. Также Ньютон придумал математический аппарат, дифференциальные уравнения и описание всех этих явлений гладкими функциями. Давайте рассмотрим пример моделирования упругого материала ― возьмем линейку. Если мы можем сделать модель линейки, мы надавливаем на нее, и тогда линейка будет отклоняться, мы можем предсказывать форму отклонения этой линейки. Линейка описывается обычной функцией отклонения ее от вертикального положения. При этом, если подумать, модель дифференциального уравнения есть упрощение реальности, хотя первокурсники, возможно, со мной не согласятся. Но если мы рассмотрим пластиковую линейку, то она состоит из органических полимеров ― цепочек углерода, водорода, связанных между собой ковалентными связями, и это очень сложно описать. Зато очень просто описать линейку как непрерывную функцию. При этом линейку из любого материала мы можем описывать теми же самыми уравнениями. В линейке из стали металлические связи, ее структура совершенно другая, но описывается она теми же уравнениями упругости. После того как мы написали уравнения, мы написали модель, и на этом наша задача математического моделирования выполнена. Если это простые уравнения, мы их можем решить и точно сказать, что формой линейки будет либо парабола, либо полином третьей степени. Но когда это более сложная система (мост), на нем случайным образом расположены машины, мы уже не можем точно написать формулу, какая у этого моста будет упругая деформация. Но мы все равно хотим предсказать, упадет мост или нет, и это делали еще за 100 лет до возникновения компьютеров. Это делали средствами математического анализа, то есть выписывались уравнения, мы их не могли решить, но доказывали свойства про решение этого уравнения ― например, что напряжения в мосте будут меньше пороговых значений. Пятьдесят лет назад, когда появились первые вычислительные машины, правила игры поменялись. Теперь уравнения, эти математические модели мы можем решать на компьютере, и это дает нам огромные преимущества. Мы можем очень быстро решать для какого-то дизайна моста, какие в нем будут напряжения, и делать выводы о том, хороший это дизайн или плохой. Вернемся к простой модели линейки. Если в математической модели она описывается непрерывной функцией, то в компьютере — системой точек и отрезков между ними. При этом точки оказывают сопротивление изгибам отрезков, за счет чего моделируется упругое сопротивление материала. Когда мы дискретизировали модель, перешли к модели дискретных точек, мы, с одной стороны, несколько усложнили модель. Но с другой стороны, теперь эти точки мы можем представить на компьютере. Если у нас линейку представляют 9 точек, то дифференциальные уравнения становятся системой линейных уравнений 9 на 9, которую мы можем легко решить на компьютере. На современных компьютерах мы можем легко решать системы с миллионом или даже миллиардом неизвестных. Это меняет правила игры в том смысле, что мы теперь проводим не натурные эксперименты моста, а делаем дизайн моста на компьютере, проводим численный эксперимент, дальше смотрим, какие у нас напряжения, и пытаемся что-то оптимизировать. Я упомянул три элемента математического моделирования в вычислительной математике, которые сейчас идут рука об руку: собственно математическое моделирование — построение модели, дискретизация и линейная алгебра, которая позволяет решать дискретные системы уравнений. Четвертая часть — это оптимизация. Методы оптимизации позволяют нам полностью доверить компьютеру, вместо того чтобы руками исправлять дизайн моста, доводить мост до нужных параметров и потом пытаться минимизировать его стоимость. Мы начинаем с того, что делаем дизайн моста, и компьютер нам выдает уже оптимальное решение по напряжениям в мосте и его стоимости. Про вычислительный эксперимент, который я сейчас описал, говорят, что он стал ни много ни мало третьим способом познания мира. Если первыми двумя были теория и эксперимент, которые еще восходят как минимум к древним грекам, то теперь появилось численное моделирование, которое не является, строго говоря, ни тем ни другим. Теория дает нам математическую модель, и мы как будто делаем эксперимент на компьютере. У нас есть ошибки, погрешности, как и в численных экспериментах, есть знания о том, как этот численный эксперимент провести. Те данные, которые мы получаем, лежат между тем и другим, но ни тем ни другим не являются. Численное моделирование становится все более важной частью современных технологий производства. Особенно это касается нового технологического уклада, в котором изделия проектируются за несколько часов на компьютере, а не на бумаге и чертежах, после этого эти изделия можно распечатать на 3D-принтере и тут же отвезти заказчику или проверить, как они работают. Простые изделия вроде украшений или элементов интерьера уже могут разрабатываться дизайнером, который находится в своем доме на курорте Краснодарского края. Утром, пока вода еще не согрелась, он делает дизайн предмета интерьера, на который получил заказ, и отправляет в соответствующий город, в Воронеж, молодым ребятам, которые напечатают его ночью в гараже на 3D-принтере, и уже утром заказчик получит изделие. Вычислительные методы при этом играют следующую роль: тест на прочность или другие тесты можно провести прямо на компьютере у дизайнера автоматически. Для этого не нужно будет изготавливать изделие и его тестировать, и работа идет в этом направлении. Даже с такими сложными изделиями, как машины, вагоны, все равно нужно проводить натурные эксперименты, но сейчас тенденция идет к тому, чтобы большую часть экспериментов по тестированию и сертифицированию проводить на компьютере. Это сокращает время тестирования и производства данных изделий. Задачи, о которых я рассказывал, например проектирование изделий, были в области вычислительной науки, а стали вычислительными технологиями ― вполне стандартной вещью, которой пользуются инженеры. Акцент в научных разработках сместился в соседнюю область. Например, сейчас активно разрабатываются вычислительные методы для uncertainty quantification, численное оценивание неопределенностей. Это направление о том, что даже если все технологические процессы выдержаны, то изделия, которые получаются, все равно разные, и нужно оценивать то, как эти разные изделия повлияют на работу системы в целом, чтобы быть уверенными, что система даже с изделиями, которые чуть-чуть разные и являются элементами этой системы, работает так, как надо. Еще одно направление ― это многомасштабное моделирование, и оно заключается в том, что кроме моделирования изделия в целом мы моделируем его микроструктуру. Опять вернемся к линейке. Если мы точно знаем, из какого полимера она состоит, как волокна этого полимера друг на друга зацеплены, то мы можем узнать упругие свойства этой линейки. В отношении линейки это нам не очень интересно, но для современных композитных материалов это очень важно уметь рассчитывать. В современных производственных технологиях стирается разница между материалом и изделием, у нас уже умеют печатать на 3D-принтере изделия из композитных материалов. Композитный материал — это армирующие волокна, матрица. Если мы посмотрим в микроскоп или даже в увеличительное стекло на материал, то мы увидим там много неоднородностей. Если мы хотим это моделировать классическими способами, то для каждого нового такого материала нужно проводить эксперимент, чтобы узнать, какие параметры нужно вставлять в модель. Но с многомасштабным моделированием мы можем моделировать и рассчитывать эту микроструктуру, после чего сразу рассчитывать поведение изделия в целом. Таким образом, для этих новых материалов нам необязательно проводить много экспериментов. Еще одно направление ― это быстрые солверы, или быстрые алгоритмы решения. В качестве примера можно привести приложение персонализированной медицины. Когда компания Siemens изготавливает аппарат для МРТ головного мозга, она в своем дата-центре рассчитывает его параметры и вместе с этим аппаратом поставляет софт, которым он пользуется, для того чтобы обработать данные МРТ. Софт делается для среднего человека, и он не совсем оптимален. Сейчас существуют подходы, которые, я думаю, появятся через 3–5 лет, когда катушки, которые создают магнитное поле, будут подстраиваться под пациента. Это, например, может сокращать время исследования с 45 минут до 10, что очень здорово. Но для этого нужно рассчитывать, как система с подвинутыми катушками влияет на головной мозг в данном случае. Если у нас будут более быстрые алгоритмы, то мы можем это рассчитывать прямо на ходу. И может быть, даже мы сможем дойти до такого состояния, когда мы можем очень точно составлять карту головного мозга отдельного человека и проводить диагностику его способностей просто по магнитно-резонансной томографии. Александр Шапеев PhD in Mathematics, доцент Центра по научным и инженерным вычислительным технологиям для задач с большими массивами данных Сколковского института науки и технологий (Сколтех)
ТегиПохожее
|
| Главная ≫ Инфотека ≫ Математика ≫ Видео ≫ Математическое моделирование и вычислительная математика // Александр Шапеев |
|
[time: 12 ms; queries: 7]
7 Мар 2026 03:14:17 GMT+3 |


 В 1936 году советский инженер и учёный Владимир Лукьянов создал вычислительную машину, все математические операции в которой выполняла текущая вода. Гидравлический интегратор Лукьянова — первая в мире вычислительная машина для решения дифференциальных уравнений в частных производных — на протяжении полувека был единственным средством вычислений, связанных с широким кругом задач математической физики.
В 1936 году советский инженер и учёный Владимир Лукьянов создал вычислительную машину, все математические операции в которой выполняла текущая вода. Гидравлический интегратор Лукьянова — первая в мире вычислительная машина для решения дифференциальных уравнений в частных производных — на протяжении полувека был единственным средством вычислений, связанных с широким кругом задач математической физики.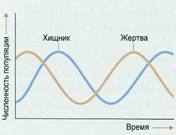 Иногда простая математическая модель хорошо описывает сложную биологическую систему. Примером этого служат долговременные отношения между видами хищника и жертвы в какой-либо экосистеме. Математические расчеты роста популяции отдельно взятого вида показывают, что пределы плотности популяции можно описать простыми уравнениями, которые на выходе дают характерную S-образную кривую. Это — кривая численности популяции, которая растет экспоненциально, пока она небольшая, а затем выравнивается, когда она достигает пределов возможности экосистемы поддерживать ее. Простое продолжение этой концепции позволяет нам понять экосистему, в которой взаимодействуют два вида — хищник и жертва.
Иногда простая математическая модель хорошо описывает сложную биологическую систему. Примером этого служат долговременные отношения между видами хищника и жертвы в какой-либо экосистеме. Математические расчеты роста популяции отдельно взятого вида показывают, что пределы плотности популяции можно описать простыми уравнениями, которые на выходе дают характерную S-образную кривую. Это — кривая численности популяции, которая растет экспоненциально, пока она небольшая, а затем выравнивается, когда она достигает пределов возможности экосистемы поддерживать ее. Простое продолжение этой концепции позволяет нам понять экосистему, в которой взаимодействуют два вида — хищник и жертва. В вычислительной математике обычно ставится конкретная вычислительная задача, которая затем решается с целью получить результат — в точности как типичный сеанс работы в Mathematica. В чистой математике, напротив, берутся некоторые математические объекты, результаты или структуры, формируются некоторые гипотезы относительно них и потом приводятся доказательства верности выдвинутых гипотез. Большое число чистых математиков продолжает делать всё точно также, как это делалось веками — от руки и на бумаге. Как же эффективно привнести технологии в такой рабочий процесс?
В вычислительной математике обычно ставится конкретная вычислительная задача, которая затем решается с целью получить результат — в точности как типичный сеанс работы в Mathematica. В чистой математике, напротив, берутся некоторые математические объекты, результаты или структуры, формируются некоторые гипотезы относительно них и потом приводятся доказательства верности выдвинутых гипотез. Большое число чистых математиков продолжает делать всё точно также, как это делалось веками — от руки и на бумаге. Как же эффективно привнести технологии в такой рабочий процесс?