Перевод поста Стивена Вольфрама (Stephen Wolfram) "Computational Knowledge and the Future of Pure Mathematics". Выражаю огромную благодарность тем, кто помог мне сделать этот перевод: Владиславу Глаголеву (Himura), Илье Марчевскому, Сергею Шевчуку (opckSheff) и Анне Коваленко.


Уже больше века, каждые 4 года в некоторой точке мира проходит Международный конгресс математиков (ICM). В 1900 году, именно на нем Давид Гильберт представил свою знаменитую коллекцию проблем математики, которая по сей день задает направление исследования математикам всего мира.

В этом году ICM проходит в Сеуле, и сегодня я отправляюсь туда. Однажды я уже бывал на ICM — в Киото в 1990 году. Тогда системе Mathematica было всего 2 года, и математики ещё только начинали привыкать к ней. Многие уже повсеместно её использовали, но на ICM были и те, кто говорил «Я занимаюсь чистой математикой. В чем, интересно, мне может помочь система Mathematica?»


24 года спустя большинство специалистов в области чистой математики по всему миру, так или иначе, пользуются системой Mathematica. Но, тем не менее, большое число чистых математиков продолжает делать всё точно также, как это делалось веками — от руки и на бумаге.

С момента посещения конгресса ICM в 1990-м году я не перестаю размышлять о том, каким образом в этот традиционный процесс можно внедрить технологии. И сейчас мне не терпится рассказать о том, что, по-видимому, я начал понимать как это можно осуществить. Хотя нужно отметить: многие детали мне пока еще неведомы. Но чтобы осуществить задуманное, понадобится поддержка и сотрудничество большинства чистых математиков во всем мире. Если все получится — результат обещает быть впечатляющим — он точно заставит чистых математиков изменить методы работы настолько же сильно, насколько система Mathematica (а для молодого поколения, Wolfram|Alpha) изменила всю вычислительную математику. Потенциально, этот результат способен вывести чистую математику в новый золотой век.


В целом данный вопрос весьма сложен. Но для меня одой из важнейших отправных точек является разница в методах, используемых в вычислительной математике и чистой математике. В вычислительной математике обычно ставится конкретная вычислительная задача, которая затем решается с целью получить результат — в точности как типичный сеанс работы в Mathematica. В чистой математике, напротив, берутся некоторые математические объекты, результаты или структуры, формируются некоторые гипотезы относительно них и потом приводятся доказательства верности выдвинутых гипотез.

Как же эффективно привнести технологии в такой рабочий процесс? Есть один простой способ — вспомнить о Wolfram|Alpha. Если ввести 2+2, то Wolfram|Alpha, точно так же, как и Mathematica, выдаст в ответе 4. Но если ввести, скажем, «new york», «2.3363636», или «cos(x) log(x)», то простого «ответа», который можно посчитать не будет. Вместо него, Wolfram|Alpha сгенерирует отчет, содержащий набор «интересных фактов» касательно введенных вами данных.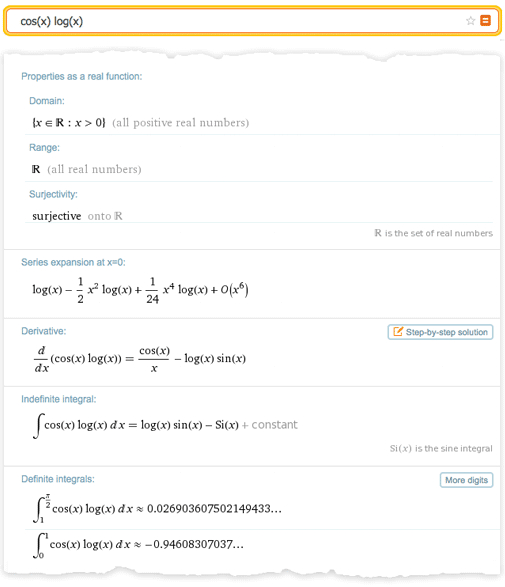


Ответы такого рода отлично вписываются в рабочий процесс чистой математики. Вы вводите какой-нибудь математический объект, результат или структуру, а система пытается рассказать что-нибудь о них, подобно тому, как это мог бы сделать ваш очень мудрый коллега-математик. Если нужно, вы можете рассказать системе, о чём конкретно вы хотите узнать, или даже просто указать некоторое утверждение, которое может быть истинно. Но работа в Wolfram|Alpha всегда похожа на поиск ответа на вопрос вроде «Что ты можешь рассказать мне об этом?», тогда как в Mathematica на вопрос в духе — «Каков ответ на то что я спросил?».

Wolfram|Alpha уже может делать очень многое со всевозможными математическими объектами. Например, введите число, математическое выражение, граф, распределение вероятностей, что угодно — и Wolfram|Alpha будет использовать сложнейшие алгоритмы, пытаясь рассказать о введенных данных какие-нибудь интересные вещи, структурированные в виде подробных отчетов.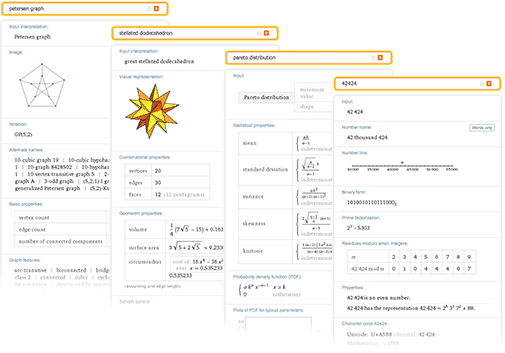


Но для того, чтобы на самом деле быть полезной при работе с чистой математикой, системе Wolfram|Alpha нужно ещё кое что. Помимо работы с конкретными математическими объектами, необходима также возможность работы с абстрактными математическими структурами.

Бесчисленное множество статей по чистой математике начинаются со слов: “Положим, что F — поле с такими-то и такими-то свойствами”. Поэтому нам нужно иметь возможность вводить нечто подобное, чтобы потом система автоматически выдавала нам теоремы и факты о поле F, в сущности, самостоятельно создавая полноценную статью, посвященную полю F.

Итак, что же нам нужно, чтобы создать такую систему? Возможно ли её создать в принципе? Есть несколько составляющих, которые необходимы для такой системы — они сложны и на их создание уйдет куча времени. Но основываясь на моем опыте работы над Mathematica, Wolfram|Alpha и A New Kind of Science (фундаментальная монография о клеточных автоматах и смежных вопросах — “Новый вид науки”), я почти уверен что при правильном руководстве и достаточных усилиях, все они могут быть созданы.

Ключевая составляющая — наличие точного символьного описания математических концепций и структур. Большая её часть уже существует — после более чем четверти века работы над ней — в системе Mathematica. Поэтому в Wolfram Language непосредственно встроены максимально абстрактные пути представления геометрических объектов, уравнений, стохастических процессов, кванторов и пр. Но вот чего в Wolfram Language пока что нет, так это представлений таких концепций чистой математики как, например, биекции, абстрактные полугруппы или декартов квадрат.


На протяжении веков множество математиков изучало самые разные задачи. Но возможно ли расширить Wolfram Language настолько, чтобы охватить весь спектр задач чистой математики и сделать нечто вроде “Mathematica Pura”? Бесспорно, ответ да. решать эту задачу будет потрясающе интересно, но это потребует сложнейшей проработки структуры языка.

Я занимаюсь разработкой структуры такого языка уже 35 лет — и я могу сказать, что это самая сложная интеллектуальная задача из всех, что я встречал. Она требует совмещения ясного мышления с эстетическим и прагматичным подходом. Постоянно приходится разбираться, чтобы достичь наиболее глубокого понимания вещей и как можно сильнее все унифицировать, при этом результатом работы всегда должны быть примитивы, которые самым простым и очевидным образом представляют вещи.

На данный момент, основным способом описания чистой математики (например, в статьях) является смесь математической нотации и естественного языка вместе с небольшим количеством схем. И это должно быть отправной точкой при разработке точного символьного языка для чистой математики.

Можно подумать, что так или иначе, математическая нотация уже решила данную проблему, но на самом деле, существует не такое уж и большое множество конструкций и концепций, которые могут быть выражены хоть сколько-нибудь стандартизованным образом с помощью математической нотации, при этом многие из них уже имеются в Wolfram Language.

Так как же нам продвинуться дальше? Первый шаг — понять какие необходимы примитивы. Весь Wolfram Language на данный момент содержит около 5000 встроенных функций вместе с миллионами встроенных стандартизованных объектов данных. Мне кажется, что для широкой поддержки чистой математики, понадобится еще около тысячи дополнительных продуманных функций, вероятно вместе с несколькими десятками тысяч новых объектов данных или их аналогов, которые дополнят и свяжут существующую структуру.


Рассмотрим такую область, как функциональные пространства. Скорее всего, в этой области должна существовать функция FunctionSpace, задающая пространство функций. Затем понадобятся операции над функциональными пространствами, например, PushForward (образ меры под действием отображения) или MetrizableQ (метризуемое ли пространство). Далее, потребуется определить множество известных функциональных пространств, например, «CInfinity» (пространство бесконечно-дифференцируемых функций) с различными вариантами параметризации.

На низком уровне, всё сводится к символьным выражениям. Но в Wolfram Language в конечном итоге всё сводится к трём способам непосредственного ввода информации, при этом все они необходимы для того, чтобы иметь удобный и читаемый язык. Первый способ — использование краткой нотации — такой, как + или ∀ — в точности также, как в обычной математической нотации. Второй — использование очень тщательно продуманных имен функций, например, MatrixRank или Simplex. И третий — использование свободной формы ввода на естественном языке, например, “trefoil knot” (трилистный узел) или “aleph0” (мощность множества алеф-0).

Мы хотим иметь краткую запись для некоторых наиболее распространённых структурных или соединительных элементов, но при этом нам требуется правильное их количество: не слишком мало (как в LISP) и не слишком много (как в APL). Помимо этого нам хочется, чтобы имена функций были такими, как будто то, что они делают просто написано обычными словами, чтобы можно было легко получить представление о назначении функции, просто прочитав её название по словам.


Но в современном мире Wolfram Language, так же имеется свободная форма ввода на естественном языке. Ключевой момент здесь заключается в том, что используя её, можно эффективно использовать все многообразие удобных (хотя и некрасивых) вариантов записи, которые понимают и используют только настоящие математики. Например, «L2» может в соответствующем контексте интерпретироваться как «Лебегово пространство второй степени». Система распознавания естественного языка позаботится о том, чтобы разрешить неоднозначность трактовки такого запроса и найдёт каноническую символьную форму для него.

В конечном счете, каждая конструкция или концепция чистой математики, имеющая свое имя, должна найти своё место в нашем символьном языке: большинство объектов из более чем 13 тысяч статей на сайте MathWorld, материалы примерно 5600 элементов классификатора понятий математики MSC2010, всё множество тех объектов в любой области, суть которых математики понимают сразу же, как только услышат их название.

Допустим, нам удастся создать точный символьный язык, работающий с концепциями чистой математики. Что же мы сможем делать с помощью него?

Скажем, можно работать в «стиле Wolfram|Alpha»: вы вводите что-нибудь в свободной форме, введённые данные интерпретируются языком, а после того, как будут выполнены все расчёты, вы получите сгенерированный отчёт.

Но можно рассмотреть ещё и такой вариант: если у нас будет такой идеально продуманный символьный язык, то он будет полезен не только компьютерам, но и человеку. По сути, если язык получится достаточно хорошим то, вероятно, люди начнут записывать свои математические выкладки на нём, вместо классической смеси естественного языка и математической нотации.

Когда я программирую на Wolfram Language, то довольно часто получается думать прямо на нём. Я не придумываю, что я хочу сделать на естественном языке с последующим переводом этого в язык Wolfram Language. Я формирую мысли на Wolfram Language изначально и его структура помогает мне формировать эти мысли.

Если у нас получится разработать достаточно хороший символьный язык для чистой математики, это, помимо всего прочего, даст математикам инструмент, который можно использовать напрямую в мышлении. Это хорошо ещё и тем, что если вы можете описать то, что думаете на точном символьном языке, то отпадает возможность любой двусмысленности или разночтений: в документации языка всегда можно найти однозначное описание любого объекта и символа.

При этом, как только чистая математика начинает записываться точным символьным языком, она становится тем, над чем можно производить вычисления. Доказательства можно генерировать и проверять. Можно производить поиски теорем. Можно автоматически находить связи и цепочки предпосылок.

Но хорошо, допустим, у нас есть просто вычислительный аппарат, необходимый для чистой математики. Как мы можем использовать его для реализации рабочего процесса в «стиле Wolfram|Alpha» — когда мы вводим описания вещей, и автоматически получаем всевозможные математические знания о них?

Существует, по видимому, два различных пути решения этого вопроса. Первый — представить абстрактное перечисление возможных теорем о введённых данных, а потом использовать эвристический алгоритм отбора тех из них, которые могут быть интересны. Второй — начать с создания вычисляемых версий тех миллионов теорем, когда-либо опубликованных в математической литературе, а потом понять то, как найти связь между ними и любым введённым запросом.

Каждое из этих направлений, по сути, отражает немного различный взгляд на то, как происходит исследование в области математики. И о каждом направлении есть что рассказать.


Давайте начнём с последовательности теорем. В простейшем случае можно начать с системы аксиом и последовательной формулировки верных теорем на основе этой системы. Существует два основных способа сделать это. Первый — сформулировать гипотетические утверждения и, используя прямые или непрямые доказательства, определить истинные. Второй — перечислить возможные способы доказательств, а затем выяснить возможные способы применения аксиом.

Оба способа просто осуществить, если объектом является, например, булева алгебра. При этом результатом будет последовательность истинных теорем. Но если на них посмотрит человек, то многие из них покажутся тривиальными или неинтересными. Таким образом, появляется вопрос, какие из теорем являются «достаточно интересными» для того, чтобы они были включены в генерируемый отчёт.

Моё первое предположение заключалось в том, что такого автоматического подхода в этом вопросе не существует, а также, что интерес к различным теоремам обязательно зависит от исторического развития соответствующей области математики. Но когда я работал над A New Kind of Science, я провел простой эксперимент в булевой алгебре.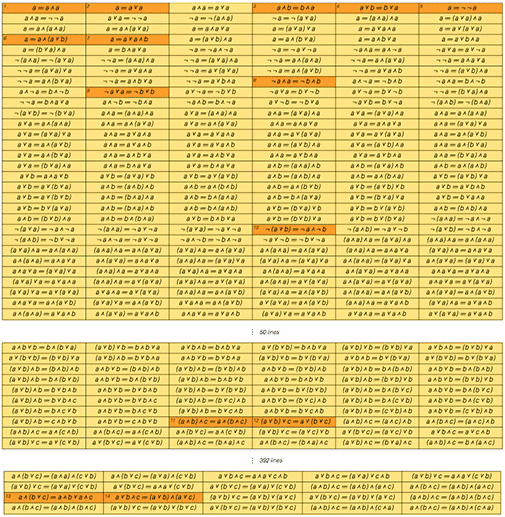


В булевой алгебре есть 14 теорем, которые считаются «достаточно интересными» и им дают в учебниках специальные названия. Я взял все возможные теоремы и перечислил их в порядке усложнения (по количеству переменных, операторов и т. д.) и я обнаружил удивительную вещь — совокупность вышеупомянутых теорем преимущественно относится к тем, которые нельзя доказать непосредственно с помощью предыдущих в списке. Другими словами, теоремы, которым дали названия, в некотором смысле являются минимальными утверждениями, дающими новую информацию о булевой алгебре.

Булева алгебра, конечно, самый простой пример. И к тому же в этом примере построения как только мы получаем теоремы, соответствующие всем аксиомам, можно сделать вывод, что больше нет ни одной «интересной» теоремы, что для многих математических теорий весьма абсурдно. Но я думаю, что этот пример хорошо показывает, как можно на деле автоматически выяснить, какие теоремы стоит «включать в отчет», а какие — «неинтересны» и являются просто лишь “украшениями” отчета.


Конечно, проблема классификации по интересу возникает в Wolfram|Alpha постоянно. В математических примерах это вопросы вроде: «какая область графика наиболее интересна?», «какие альтернативные формы выражений интересны?» и т. д. Даже когда кто-то вводит одно число, можно спросить, «какие замкнутые формы этого числа интересны?» — и для того, чтобы это понять, необходимо классифицировать все виды математических объектов (например, насколько сложней представление 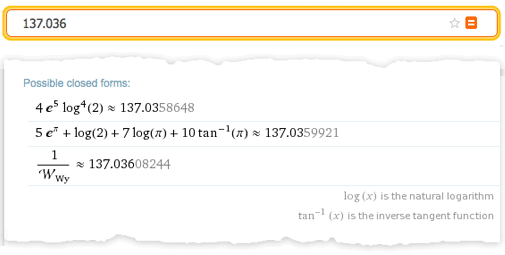по отношению к log(343) и к константе Хинчина и т. д.?)


Итак, в принципе можно представить себе систему, которая генерирует «интересные» теоремы о том, что поступает на вход. Заметьте, что в то время как при обычных вычислениях в Mathematica на вход поступают данные и над ними производятся вычисления “для получения ответа”, здесь о них “генерируются интересные утверждения”.

Характер входных данных также отличается. В случае вычислений вы обычно имеете дело с той операцией, которую нужно выполнить. В случае же работы с чистой математикой в “стиле Wolfram|Alpha” пользователь обычно даёт описание некоторого объекта. В некоторых случаях оно явное, скажем: число определенного типа, конкретное уравнение, граф определенного типа. Но чаще оно неявное, скажем, это может быть просто набор ограничений. Скажем, для вышеупомянутого примера с полем, мы говорим: «Пусть F — поле», и затем задаём ограничения, которым это поле должно удовлетворять.

В каком-то смысле система аксиом также задаёт ограничения: она не утверждает, что такой-то оператор “есть Nand” (штрих Шеффера); просто утверждается, что оператор должен удовлетворять определенным условиям. Мы знаем из теоремы Гёделя, что невозможно, даже для чего-либо наподобие стандартной арифметики Пеано, полностью преодолеть ограничения, — мы никогда не сможем закрепить за знаком “+” в аксиомах конкретную операцию, например простого сложения целых чисел. Конечно, при этом мы можем доказать достаточно много теорем о “+”, в том числе и те, которые используем для отчёта.

Итак, при конкретных входных данных мы можем придумать, как представить их в виде набора ограничений на нашем точном символьном языке. Затем мы сможем сформулировать теоремы, основанные на этих ограничениях и эвристически выбрать из них «самые интересные».

Я уверен, что однажды это занятие станет самой важной частью работы чистого математика. На сегодняшний же день для большинства чистых математиков эта задача покажется чуждой, так как они не привыкли к теоремам “без автора”; они привыкли к теоремам из статей конкретных математиков.

И это приводит нас ко второму подходу, — к автоматической генерации «математических знаний: начать со всей коллекции написанных математических статей, а затем связать её с любыми конкретными входными данными. Так, чтобы можно было сказать, например, «Следующая теорема из статьи Х таким-то образом применима к вашим входным данным» и т. д.


Насколько велик исторический фонд математики? Всего существует около 3 миллионов опубликованных математических статей, или около 100 миллионов страниц и это число увеличивается в среднем на 2 миллиона страниц в год. При этом во всех этих статьях, по-видимому, содержится порядка 5 миллионов различных сформулированных теорем.

Что с этим всем можно сделать? Прежде всего, конечно, простые исследования и обработку. Часто словами в статье описано намного больше материала, чем только лишь математической записью и формулировками теорем. Но с помощью технологии лингвистического распознавания для математических запросов в Wolfram|Alpha не так сложно осуществить хорошую статистическую обработку фонда математических статей.

Но можно ли пойти дальше? Кто-то может подумать о создании тэгов для документов-источников с целью улучшения обзора. Но я полагаю, что такая работа не будет иметь смысла, на что указывает то, что для интернета намного проще и лучше создавать более утонченную и осознанную систему, чем просто добавлять тэги от каждому документу и их группам.

Что было бы безусловно рациональнее, — перевести теоремы в оригинальную вычислимую форму: извлечь теоремы из статей и переписать их на точном символьном языке.

Возможно ли это сделать автоматически? В конце концов, я полагаю, для большей части это будет возможно. Сегодня мы уже можем взять маленькие фрагменты теорем из статей и использовать систему лингвистического распознавания Wolfram|Alpha, чтобы преобразовать их в код на языке Wolfram Language. Но постепенно можно будет переходить к большим фрагментам, и в конце концов прийти к тому, что для перевода типичной теоремы в точную символьную форму понадобится лишь самое незначительное усилие человека.

Итак, давайте представим, что мы организовали все теоремы из математической литературы в вычислимой форме. Что мы сделаем затем? Мы бы, конечно, смогли построить наглядную систему, похожую на Wolfram|Alpha, которая бы была очень полезной на практике для чистой математики.


Однако неминуемо будут существовать некоторые ограничения, которые, фактически, накладывает сама математика. Например, не всегда легко сказать, какую теорему можно применять к какому объекту и даже то, какие теоремы являются эквивалентными. В конце концов, это классические теоретически неразрешимые проблемы — и я подозреваю, что они будут создавать сложности и на практике. По крайней мере, к ним можно применить такой основной процесс как автоматическое доказательство.

Итак, предлагается сочетание двух основных подходов, которые мы обсудили. Сначала берётся весь фонд опубликованных математических работ и рассматривается формально как гигантская 5-миллионная система аксиом, а затем следует процедура последовательной формулировки теорем, т. е. то, что мы назвали «перечислением интересных фактов»


Итак, хорошо, допустим мы создали такую систему. Будет ли она на самом деле решать ключевую задачу поиска новых истин в чистой математике, или же она не справится с этим?

Я думаю, всё зависит от того, что считать сутью чистой математики. Является ли она наукой или искусством? Если это наука, то быстрое создание большего числа теорем конечно очень хорошо. Но если она является искусством, то это не главное. Если работу в чистой математике рассматривать с художественной картиной, то автоматический подход скорее станет контрпродуктивным, поскольку основа этой деятельности — форма самовыражения человека.

Это же имеет отношение и к роли доказательства. Для некоторых математиков важна только теорема: знать, истинно ли утверждение. По сути, доказательство служит только фактом отсутствия ошибки. Но для других математиков доказательство является ключевой частью содержания математики. Для них доказательство является рассказом, который вносит ясность в математические концепции и объединяет их.

Итак, что же происходит, когда мы автоматически генерируем доказательство? У меня был один интересный пример, который я рассмотрел 15 лет назад, когда работал над A New Kind of Science и уже окончил работу над простейшей системой аксиом булевой алгебры (как оказалось, она состоит лишь из одной аксиомы (p◦q)◦r)◦(p◦((p◦r)◦p))==r). Чтобы доказать состоятельность системы аксиом, я применял автоматическую систему доказательства теорем на основе эквациональной логики (которая сейчас встроена в функцию FullSimplify). И я включил сгенерированное доказательство в книгу:


Оно содержит 343 шага и при стандартном размере шрифта займёт, пожалуй, 40 печатных страниц. И, как мне кажется, для человека оно совершенно нечитабельно. Кто-то может подумать, что разбиение доказательства на 81 лемму поможет в понимании. Но как я ни старался, я не смог превратить это автоматическое доказательство в то, что мог бы понять человек. Прекрасно, что существует такое доказательство, но оно само по себе ничего не говорит, кроме как доказывает утверждение.


Проблема здесь, я полагаю, в том, что элементы доказательства не содержат в себе «когнитивной истории». Даже если выбирать набор лемм, как ключевых моментов доказательства, они тоже не несут когнитивных связей и не связаны никакой историей. Они представляют собой просто факты без содержания и связи.

Как же улучшить этот процесс? Если мы сгенерируем большое количество аналогичных доказательств, тогда, может быть, мы станем лучше различать аналогичные леммы, и таким образом они станут более понятными и значимыми. Наверняка, существуют методы визуализации, которые помогут быстро увидеть общую картину доказательства. При этом, конечно же, если мы сможем управлять и иметь в распоряжении базу всех известных в математической литературе теорем, то мы сможем автоматически связать сгенерированные леммы с этими теоремами.

В данный момент ещё не совсем ясно, насколько это будет возможно. В самом деле, на основе существующих примеров доказательств при помощи компьютера, например, теоремы о четырех цветах, гипотезы Кеплера или простейшей универсальной машины Тьюринга — у меня складывается впечатление, что часто сгенерированные автоматически леммы редко соотносятся с теоремами из литературы.

Но не смотря на всё это, я знаю, по крайней мере, один пример, показывающий, что при достаточном количестве усилий можно генерировать доказательства, ход которых будет понятен людям — это система пошаговых решений в Wolfram|Alpha Pro. Миллионы раз в день студенты и другие пользователи вычисляют вещи, такие как интегралы и делают другие расчёты с помощью Wolfram|Alpha, а затем просят эту систему предоставить им пошаговое решение.


Следует отметить, что найти интеграл намного проще, чем показать качественное пошаговое решение. При этом для того, чтобы найти те шаги решения, которые будут понятны и естественны для человека требуются довольно сложные алгоритмы и эвристика. Но пример пошаговых решений в Wolfram|Alpha даёт надежду, что при должных усилиях станет возможной генерация доказательств, которые человек сможет прочесть как “рассказ”, при этом, вероятно, даже удастся сделать их как можно проще и короче («доказательства из самой Книги Бога», как сказал бы Пол Эрдёш).

Конечно, в то время как такого рода автоматические методы могут в конечном счете служить для качественного связывания элементов объекта, такого как, скажем, доказательство, они на самом деле не смогут даже приблизительно связать воедино, не то что определить, всеобъемлющие идеи и мотивы математики. Стоит ли говорить, что современные статьи по чистой математике также очень плохо выполняют эту функцию? Потому что из-за стремления обеспечить строгость и точность, многие статьи пишутся очень формально. В них не выражены глубинные идеи и мотивы автора — в результате чего некоторые важные идеи в математике передаются только устно.

Несомненно, шагом вперёд для чистой математики стала бы возможность объединить воедино всё её содержимое. При этом точный символьный язык чистой математики упростил бы формирование явной записи для некоторых таких важных моментов, которые в настоящий момент нигде не описаны. Одно ясно без сомнений: благодаря такому языку мы смогли бы найти теорему из любого источника, скажем, в виде обычного фрагмента кода на языке Wolfram Language, и вставить её куда угодно для дальнейшего использования.

Но вернёмся к вопросу, имеет ли смысл автоматизация в чистой математике. Я считаю абсолютно очевидным, что наличие “помощника в чистой математике”, который бы имел вид, похожий на Wolfram|Alpha, будет полезно для математиков-людей. Я также полагаю довольно очевидным то, что наличие качественного, точного символьного языка — своего рода языка Mathematica Pura, являющегося продолжением стандартной математической нотации — будет очень полезно и удобно для формулирования, проверки и объединения всех понятий математики.


Что можно сказать о компьютерах, которые просто “погружаются в себя и выполняют математические вычисления сами по себе”? Очевидно, что компьютер может сформулировать набор теорем, и даже использовать эвристические методы для выделения тех, которые могут показаться интересными математику-человеку. Если мы будем обладать всей коллекцией математической литературы, то мы сможем построить обширную «эмпирическую метаматематику», на основе которой мы начнём пробовать выделять теоремы, обладающие определенными характеристиками, возможно, с применением методов теории графов ко всему графу теорем, что позволит найти те из них, которые можно признать “неожиданными” или “мощными”. В этом нет ничего особенно сложного, как и на сайте WolframTones, на котором компьютер применяет эстетические критерии, полученные путем изучения того, что выбирают люди на сайте.

Однако, как мне кажется, истинный вопрос состоит в том, способен ли компьютер создавать новые подходы и новые конструкции — и в конце концов новые математические теории. Конечно, некоторые теоремы полученные перебором будут весьма интересными и их получение будет свидетельствовать о приобретении новых знаний. При этом, конечно, крайне интересным будет то, когда компьютер сможет взять большой набор теорем (не важно — установленных им же, или найденных в литературе) и начнёт обнаружить связи между ними, которые будут задавать некоторый новый объединяющий их принцип. Однако, как я думаю, со временем стоит ожидать того, что компьютеры смогут не только обнаруживать новые конструкции, но также называть и описывать их. Разумеется, только люди могут решать, чем должны занимаются компьютеры, однако во многом их деятельность, как я полагаю, будет неотличима от работы людей, занимающихся чистой математикой.

Все это пока что остаётся в довольно далеком будущем, однако уже сейчас существует прекрасный способ обнаружения математических фактов, который практически не используется в том объеме, в котором мог бы — это экспериментальная математика. Разные люди понимают это понятие немного по-разному. С моей точки зрения это изучение математических систем путем проведения экспериментов над ними. К примеру, если мы хотим узнать что-то о некотором классе клеточных автоматов, нелинейных дифференциальных уравнений в частных производных, числовых последовательностях или о чем-то ещё, мы просто готовим набор возможных частных случаев и рассчитываем их, наблюдая за результатами.

Таким образом можно обнаружить очень много всего. И, разумеется, этот путь может быть весьма плодотворным для формулировки наблюдений и гипотез, которые могут быть исследованы с применением традиционной методологии чистой математики. Однако истинная направленность такого пути и тех результатов, которые могут быть получены, не вписываются в то, что чистые математики обычно понимают под математикой. Это больше похоже на исследования “флоры и фауны”, а также принципов мира всех возможных систем, а не на построение математических конструкций, которые могут быть исследованы и описаны с помощью теорем и доказательств. Именно поэтому — здесь стоит процитировать название моей книги (A New Kind of Science) — мне кажется, что следует считать этот процесс новым видом науки, а не чем-то, являющимся лишь частью существующей математики.

Говоря об экспериментальной математике и “Новом Виде Науки”, следует отметить в некоторой степени удивительную вещь, заключающуюся в том, что чистая математика вообще может работать, поскольку если кто-нибудь начнёт задавать совершенно произвольные вопросы о математических системах, многие из них в конечном итоге останутся неразрешимыми.

Это особенно очевидно, если кто-либо находится в вычисляемой вселенной всех возможных программ, но это также верно и для программ, которые представляют типичные математические системы. Итак, почему же большинство проблем в области обычной чистой математики все же не являются неразрешимыми? Ответ заключается в том, что чистая математика неявным образом стремится выбирать то, что она будет изучать, тем самым избегая неразрешимых проблем. В некотором смысле кажется, что это является следствием истории: чистая математика следовала за тем, что успешно получалось по мере её развития и в конечном счёте она стала ходить вокруг неразрешимых проблем, производя миллионы теорем, которые сформировали совокупность современной чистой математики.

Итак, мы обозначили некоторые вопросы и направления. Однако где мы сейчас находимся на самом деле в вопросе привнесения вычисляемых знаний в чистую математику?


Соответствующие исследования имеют длинную историю. Это работы Пеано, Уайтхеда и Рассела вековой давности, и проблемы Гильберта; разработка теории множеств и теории категорий. В 1960-е годы это — первые компьютерные системы, такие как Automath — для представления структуры доказательств. Затем, начиная с 1970-х годов, системы типа Mizar, в которых предпринимались попытки обеспечить компьютерную основу для доказательств. В настоящее время это набирающие популярность системы «поддержки доказательств», такие как Coq или HOL.

Во всех этих разработках имеется одна существенная особенность: они были задуманы как определения некоторого «языка низкого уровня» для математики. Как и большинство существующих на сегодняшний день компьютерных языков, они содержат ограниченное число базовых конструкций и предполагают, что практически любые необходимые новые объекты должны быть подгружены откуда-то извне, либо конкретным пользователем, либо с помощью готовой библиотеки.

Однако новая идея языка Wolfram Language состоит в том, чтобы иметь язык, основанный на знаниях, в котором насколько возможно большой объём актуальных знаний тщательно внедрён в сам язык. И мне кажется, что как и для вычислений общего назначения, идея языка, основанного на знаниях, окажется исключительно важной для внедрения вычислений в чистую математику наиболее эффективным и широко применимым способом.

Итак, что же должно быть включено в создание Mathematica Pura, которая представляет собой расширение языка Wolfram Language, содержащее современную структуру и объекты чистой математики? На самом низком уровне Wolfram Language оперирует произвольными символьными выражениями, которые могут представлять собой абсолютно что угодно. Однако затем язык использует такие выражения для многих конкретных целей. К примеру, символ x может использоваться для обозначения алгебраической переменной. С учётом этого, в Wolfram Language имеется множество функций для обработки символьных выражений — интерпретируемых как математические или алгебраические выражения — и выполнения различных математических операций над ними.

В математическом аппарате, реализованном в Mathematica и Wolfram Language, сегодня сделан акцент на «практическую», вычислительную математику. На данный момент она покрывает практически всю математику, существовавшую в 19 веке и ранее. Но что можно сказать про более современную математику? Исторически сама математика пережила трансформацию примерно сто лет назад. Как и стиль модерна, захвативший различные области искусства, в математике появилось собственное течение — стали рассматриваться конструкции, которые появились совершенно формально, без связи с окружающим миром.

Этот вид математики, начиная с исследований Бурбаки и позднее, стал основным направлением развития чистой математики в 20-м веке. Неизбежно значительная часть такой математики посвящена созданию абстрактных структур, которые затем будут изучаться. В простейших случаях кажется, что можно было бы представить эти структуры, используя некоторую иерархию типов. Однако эти типы должны быть полностью описаны, и весьма скоро образуются целые алгебры или исчисления типов — в точности так, как и в языке Wolfram Language можно использовать общие символьные выражения с произвольными головными частями, а не просто описания типов.

Как я упоминал ранее в этом посте, планируется использовать все виды новых встроенных функций и стандартизованных объектов данных для того, чтобы реализовать конструкции, необходимые для представления современной чистой математики. Разумеется создание системы, позволяющей работать с чистой математикой, которая имела бы широкие возможности, была бы удобной и понятной, потребует многих лет тщательной разработки. Но в целом нет никаких фундаментальных трудностей в том, чтобы создать символьные конструкции, которые позволили бы работать, скажем, с понятием дифференцируемости ли модулями римановых поверхностей или с чем-либо ещё. Всё это — просто вопросы разработки языка, такие же как, скажем, способы представления трехмерных растровых изображений, реализация удалённых вычислений или же обращение к внешней курируемой базе структурированных данных.

Итак, что же можно сказать о курировании теорем из всей математической литературы? Используя Wolfram|Alpha и Wolfram Language, не говоря уже о, к примеру, Wolfram Functions Site и Wolfram Connected Device Project, мы уже имеем огромный опыт в процессе создания и поддержания в актуальном состоянии огромных баз структурированных данных о самых разных объектах, а также в том, чтобы делать такого рода данные вычисляемыми.


Но чтобы получить ясное представление о том, что собой представляет организация и упорядочивание математических теорем, в течение последних двух лет мы осуществляли наш пилотный проект на базе Wolfram Foundation, поддерживаемый фондом Альфреда Слоуна. Для этого проекта мы выбрали очень конкретный и хорошо разработанный раздел математики: исследование цепных дробей. Цепные дроби непрерывно изучались с античных времён, но достигли пика своей популярности между 1780 и 1910 годами. В общей сложности они описываются примерно в 7000 книг и статей общим объёмом около 150 000 страниц.

Мы выбрали около 2000 документов, а потом приступили к выделению из них теорем и другой математической информации. Результатом работы стали примерно 600 теорем, 1500 основных формул и 10000 производных формул. Формулы были представлены непосредственно в вычисляемом виде, поэтому не составило труда присоединить их к более чем 300000 формул на сайте Wolfram Functions, каждая из которых сейчас внедрена в Wofram|Alpha. Но теоремы мы поначалу рассматривали просто как объекты, обладающие определёнными свойствами, такими, как место первой публикации, автор теоремы и т. д. Причём даже на этом этапе, нам удалось вставить ряд замечательных возможностей в Wolfram|Alpha.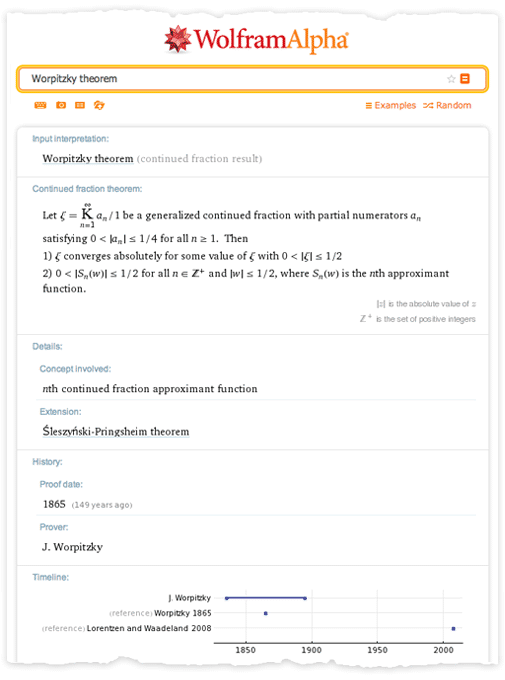


Но также мы начали пытаться перевести содержание теорем в вычисляемую форму. Это потребовало внедрения новых конструкций, таких, как LebesgueMeasure (мера Лебега), ConvergenceSet (множество сходимости) и LyapunovExponent (экспонента Ляпунова). При этом не возникло никаких фундаментальных проблем в том, чтобы создать точные символьные представления теорем. Только благодаря этим представлениям стало возможно производить в Wolfram|Alpha подобные вычисления: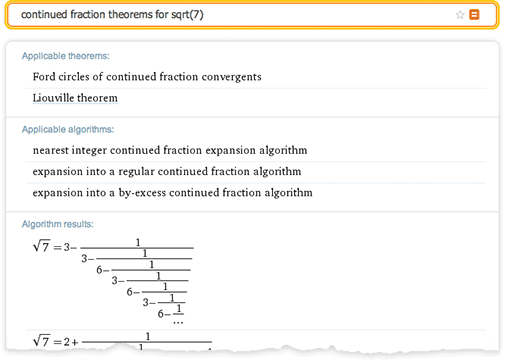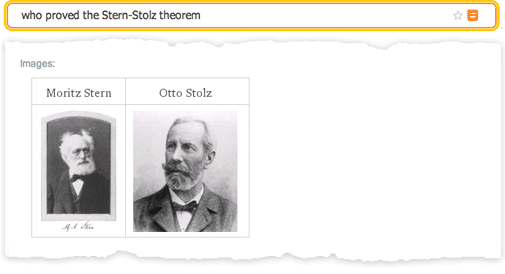




Интересной особенностью проекта о цепных дробях (сокращенно, “eCF”) было то, как процесс упорядочивания информации в действительности вёл к новым открытиям в математике. По завершении исследования более 50 статей о цепных дробях Роджерса и Рамануджана стало ясно, что существуют неучтённые ими случаи, которые теперь можно рассмотреть. Таким образом, результаты расчётов заполнили брешь в данной области исследований, оставленную Рамануджаном, которая не была заполнена никем на протяжении 100 лет.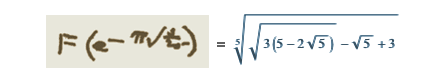


Всегда существует компромисс между курированием знаний и созданием знаний с нуля. Так, например, обстоит дело с сайтом Wolfram Functions, где всегда находилось ядро взаимосвязей между функциями, которые были найдены в справочниках и другой литературе. Но при этом гораздо эффективнее оказалось генерировать и вычислять новые взаимосвязи, чем прочёсывать литературу в их поисках.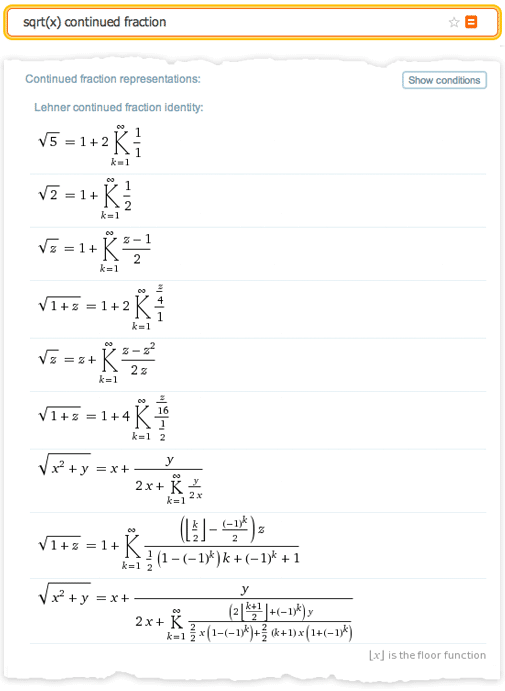


Но что потребуется для анализа всей математической литературы, если целью является именно организация и упорядочивание знаний? В ходе данного проекта перевод каждой теоремы в вычисляемую форму требовал около трёх часов работы математика. Но вся эта работа осуществлялась вручную, и я уверен, что в крупномасштабном проекте большая часть работы могла бы быть выполнена автоматически, не в последнюю очередь благодаря расширениям нашей системы распознавания естественного языка в Wolfram|Alpha.

Конечно, по ходу работы возникают всевозможные практические проблемы. Новые статьи написаны преимущественно в TeX, так что не так сложно выделить из них теоремы со всей математической нотацией. Но более старые статьи необходимо сканировать, что требует систем оптического распознавания математических символов и формул, которые только предстоит разработать.

Также возникают определённые сложности касаемо того, являются ли теоремы, сформулированные в статьях, действительно верными. И даже если 100 лет назад теорема была признана действительной, неизвестно, осталась ли она таковой сейчас. Например, в области цепных дробей существует много теорем, сформулированных до 1950-х, которые в своё время были успешно доказаны, но которые не принимали во внимание точки ветвления и линия разреза многолистных функций комплексного переменного, таким образом, в наши дни их нельзя считать верными.

При этом, в конце концов, конечно же, требуется множество хороших математиков для того, чтобы направлять процесс организации и упорядочивания и для того, чтобы переводить теоремы в вычисляемую форму. Но в некотором смысле такая мобилизация математиков не является чем-то из ряда вон выходящим; подобное объединение учёных потребовалось, когда в 1931 году был основан математический журнал Zentralblatt, или в 1941 году на старте публикации журнала Mathematical Reviews. (Забавно, но основателем и главным редактором обоих журналов был Отто Нейгебауэр, который работал чуть дальше по коридору от меня в Институте перспективных исследований в начале 80-х, про которого я думал, что он не занимается ничем, кроме расшифровки Вавилонских математических трудов, до тех пор, пока не провёл некоторые исследования для этого поста).

Когда всё на самом деле доходит до создания системы для системного описания чистой математики, то есть интересный пример: система Theorema, начало которой положил Бруно Бухбергер в 1995, которая недавно была обновлена до версии 2. Theorema написана на языке Wolfram Language и предоставляет собой среду как для отображения математических формулировок и доказательств, так и для осуществления полноценных вычислительных алгоритмов автоматического доказательства теорем и т. п.


Вне всяких сомнений, эта система станет элементом того, что будет создано в конце концов. Но в целом проект неизбежно окажется достаточно большим — возможно, это первый в мире пример “big math” (“большой математики”). Так возможно ли сейчас довести этот проект до его завершения? Ключевым элементом является то, что теперь у нас есть техническая возможность разработать язык и построить необходимую инфраструктуру. Но помимо этого проекту необходима сильная заинтересованность мирового математического сообщества, как необходимо и участие каждого отдельного математика из всех возможных разделов данной науки. При этом действительность такова, что это видимо не тот проект, который мог бы быть поставлен на коммерческие рельсы, так что около 100 миллионов долларов, необходимых на развитие проекта, должны быть собраны из некоммерческих источников.

Но это серьёзный и важный проект, который обещает стать ключевым для чистой математики. У каждой области есть своя “золотая эпоха”, когда были совершены основные открытия. И чаще всего началом таких “золотых эпох” послужило создание новых методологий или возникновение новых технологий. И именно это, я уверен, произойдёт и с областью чистой математики. Если мы сможем направить наши усилия на организацию и упорядочивание математических знаний и построим систему, которая будет использовать их и на их основе создавать вычисляемые формы знания, тогда мы преуспеем не только в сохранении и распространении огромного наследия чистой математики, но также дадим толчок бурному росту данного раздела науки.

Крупные проекты, подобные этому, нуждаются в надёжном руководстве. И я всегда готов выполнить свою часть работы и привнести базовые технологии, которые потребуются для его реализации. Сейчас для дальнейшего развития проекта требуется заинтересованность всего мирового математического сообщества. У нас есть возможность сделать второе десятилетие двадцатого века по-настоящему значимым периодом во всей многотысячелетней истории чистой математики. Так давайте сделаем это!