Раскраска натуральных чисел от 1 до 7824, удовлетворяющая условию задачи

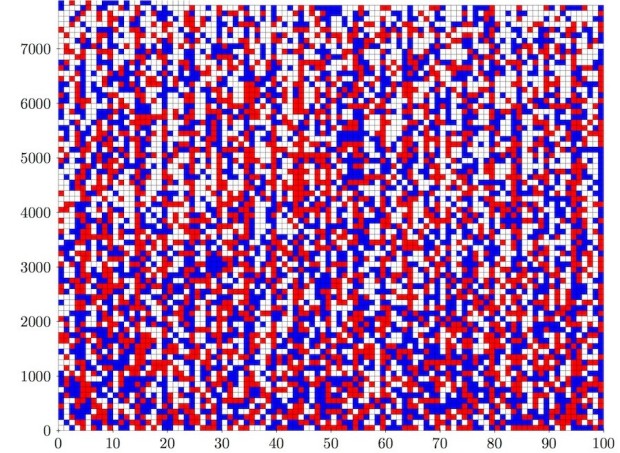
Математики из Университета Техаса в Остине с помощью компьютерных методов решили задачу о булевых пифагоровых тройках. Полная запись решения занимает около 200 терабайт, что делает его самым большим доказательством из существующих. На решение задачи ушло два дня непрерывной работы 800-процессорного суперкомпьютера. Размер предыдущего рекордного доказательства был «всего» в 14 гигабайт. Препринт работы опубликован на сайте arXiv.org, кратко о нем сообщает Nature.

Задача формулируется следующим образом. Существуют тройки натуральных чисел, называемые пифагоровыми, они устроены так, что сумма квадратов двух из них в точности равна квадрату третьего. Можно ли поделить все натуральные числа на две группы таким образом, чтобы ни в одной из них по отдельности не нашлось ни одной пифагоровой тройки?

Иными словами, задача предлагает разделить все числа на «красные» и «синие» таким образом, чтобы ни одна из троек не оказалась одноцветной. К примеру, для классической тройки 3²+4²=5², если 3 и 4, к примеру, «синие», то 5 точно должна быть «красной». Одна из сложностей состоит в том, что количество пифагоровых троек бесконечно велико, причем одно и то же число может входить в разные тройки.

В случае, если это невозможно, математикам необходимо предоставить контрпример — набор натуральных чисел от 1 до N, который так гарантированно нельзя раскрасить. За решение этой задачи Рональд Грэм, математик из Университета Калифорнии, в шутку пообещал вручить приз в 100 долларов.

Авторы показали, что раскраска возможна для наборов чисел вплоть до от 1 до 7824. Однако, как оказалось, набор чисел от 1 до 7825 не удовлетворяет требованию задачи. Для того, чтобы доказать этот факт, в простейшем случае потребовалось бы перебрать огромное число вариантов — 2⁷⁸²⁵. Это число с по меньшей мере 2350 нулями. Воспользовавшись некоторыми наблюдениями, симметриями и приемами теории чисел, авторам удалось сократить перебор до триллиона вариантов.

Ученые отмечают, что несмотря на то, что ответ на задачу найден, компьютерное решение не отвечает на вопрос «почему». В препринте, описывающем доказательство, авторы замечают, что 7825 — «катет» сразу в двух тройках. При попытках раскрасить натуральные числа от 1 до 7824, числа 5865 и 5180, входящие в одну тройку, оказывались другого цвета, чем числа 625 и 7800, входящие в другую.

Как отмечает Nature, Рональд Грэм в начале мая передал чек на 100 долларов одному из авторов доказательства.

Существует более сильная версия этой теоремы, согласно которой для любого заданного количества цветов k найдется такое число N, что набор натуральных чисел от 1 до N нельзя раскрасить в k цветов с сохранением разноцветности всех троек.

Предыдущий рекорд — доказательство объемом 14 гигабайт — относилось к гипотезе Эрдёша о расхождении. Она формулируется следующим образом: для любой бесконечной последовательности из чисел 1 и −1 всегда можно найти такие числа k и d, что взяв каждый k-й член этой последовательности и сложив первые d из них, мы получим число равное по модулю или большее, чем некоторое наперед заданное C. Компьютерными методами двум математикам российского происхождения удалось доказать эту гипотезу для C равного двум.