Москва, концертный зал «Академический», 13 мая 2006 года. Публичная лекция по приглашению фонда «Династия».

Недавно в американской книжке «Законы Мерфи» я нашел четкую классификацию всех наук: «Если воняет, то это химия, когда ничего не работает — физика, а если понять нельзя ни слова — математика».

Я всю жизнь борюсь с этим представлением. По моему мнению, математика — просто часть физики, экспериментальная наука, которая открывает человечеству самые важные и простые законы природы.

Разница между математикой и физикой состоит только в том, что в физике эксперименты стоят миллионы или даже миллиарды долларов, а в математике — единицы рублей или копеек.

Сегодня я намерен показать вам, как с помощью простейших экспериментов можно открывать новые и неожиданные законы природы.

Вслед за Ньютоном и Пуанкаре я считаю лучшие такие открытия важными вехами на пути прогресса человеческой цивилизации. Некоторые современные математики придерживаются противоположной точки зрения.

Например, Харди объяснил слова Гаусса «математика — королева наук» полной бесполезностью обеих. Директор Математического института Макса Планка в Бонне написал (в статье, посвященной 2000-летию Иисуса Христа), что математика — это формализированное переливание из пустого в порожнее, а ее вклад в решение основной проблемы современного постиндустриального человечества состоит, по его мнению, «в отвлечении лучших умов от более опасных, чем математика, занятий».

«Некоторые идиоты считают, — говорит он, — будто математика полезна для физики и техники» (в его статье слова «идиоты» нету, но спорил он именно со мной, я и заказал ему эту статью от имени Международного математического союза, который ее и опубликовал к 2000 году). «Истинная же польза» — по его словам — в том, что если бы вместо проблемы Ферма математики занимались бы усовершенствованием автомобилей или самолетов, то вреда было бы гораздо больше».

Я не собираюсь усовершенствовать ни автомобили, ни самолеты, ни даже криптографию, к которой относится сегодняшний доклад.

Но я всю жизнь следую рецепту Дирака, который учил, как создавать Новую Физику, следующими словами:

«Прежде всего, — говорил Дирак, — нужно отбросить все так называемые "физические представления", ибо они — не что иное, как термин для обозначения устаревших предрассудков предшествующих поколений».

Начинать, по его словам, следует с красивой математической теории. «Если она действительно красива,— говорит Дирак, — то она обязательно окажется прекрасной моделью важных физических явлений. Вот и нужно искать эти явления, развивать приложения красивой математической теории и интерпретировать их как предсказания новых законов физики», — так строится, по словам Дирака, вся новая физика, и релятивистская, и квантовая.

Между прочим, мало кто знает, что за три года до проблем Гильберта и лет за десять до Эйнштейна Пуанкаре сформулировал основную задачу, оставленную XIX веком в наследство двадцатому в области математики. В формулировке Пуанкаре основная задача такова: построение математической теории для релятивистских и квантовых явлений. Ну он, кстати, это и сделал для релятивистского случая — правда, почему-то странным образом Эйнштейн до 1945 года на него забывал ссылаться. В 45-м году упомянул, что Минковский ему посоветовал прочитать, что за десять лет до Эйнштейна напечатал друг Минковского Пуанкаре. Вот.

Еще менее известно, что релятивистские электронные уравнения Дирака возникли у него из древней математической теории кос. А именно: Дирак заметил, исходя из топологии семейства эллиптических кривых в алгебраической геометрии, что в группе сферических кос из четырех нитей существует элемент второго порядка, и интерпретировал это свое открытие в виде теории спина электрона, имеющего 2 значения (это означает, что для того, чтобы частица вернулась в прежнее положение, ей нужно повернуться не на 360 градусов, а 720).

Это было никому не понятно, и поэтому ему не верили. Чтобы убедить физиков в справедливости соответствующей странной математической теоремы (утверждающей, что фундаментальная группа группы SO(3) вращений трехмерного пространства состоит из двух элементов), Дирак продемонстрировал соответствующий эксперимент, изготовив физически свою сферическую косу второго порядка.

Эта коса делается так: берется сфера и другая концентрическая с ней меньшая сфера и соединяются четырьмя веревками. Четыре гвоздя вбиваются в наружную сферу, четыре во внутреннюю, и четыре веревки их соединяют, но так, чтоб эти веревки не по радиусу шли, а переплетались между собой. Вторая, точно такая же, коса (это называется «сферическая коса») — вторая коса, совершенно так же устроенная, соединяет меньшую сферу с еще меньшей.

А теперь, элемент второго порядка — это вот что такое. Это значит, что, если убрать среднюю сферу, получится четыре веревки, связывающие самую большую с самой маленькой. Так вот, они оказывались незапутанными, они были запутаны между большой и средней, запутаны между средней и малой таким же способом. А если среднюю убрать, то между большой и малой их можно непрерывным преобразованием перетащить на радиальные незапутанные. Получается тривиальная коса.

Это и есть та математическая теорема, о которой идет речь, которую Дирак и доказал. Дирак изготовил эти сферы и среднюю сжег. Сферы оказались соединенными незавязанными веревками, и физики поверили в теорию спина. Так он это и доказал.

Между прочим, сейчас ни физики, ни математики этого уже не знают. Может, один я прочитал у Дирака, как это делается и как он это придумал. А в спин физики верят, потому что провозглашено там, дают за это нобелевские премии, значит, что уже это всем известно, что это знаменитая, великая вещь. И все верят, просто потому, что это провозглашено, что это так.

Ну так вот. На самом деле, это открытие Дирака — теория спина — было основано на эксперименте, доказавшем математическую теорему.

Поэтому и я начну сейчас рассказ о своих экспериментах, которые я вам сейчас покажу, но только сделаю одно предварительное замечание о докладе.

Фарадей, который выучился всему самоучкой, первым организовал публичные научные лекции для слабоподготовленных слушателей, и они были замечательными. В результате своих лекций Фарадей пришел к такому выводу: «По-настоящему поучительная лекция никогда не сможет быть популярной, а по-настоящему популярная никогда не достигнет настоящей поучительности».

Я постараюсь опровергнуть эту точку зрения великого физика (теории которого составили основу современной цивилизации после того, как Максвелл записал их математически в виде своей знаменитой системы уравнений).

Математические открытия, о которых я буду сегодня говорить, немножко похожи на теорию Максвелла, которая установила неразрывную связь между совершенно разными на вид явлениями электричества и магнетизма.

Точно так же и математика всегда устанавливает неразрывное единство совершенно разных явлений, которые на первый взгляд не имеют между собой ничего общего.

Но для математиков такая новая наука может оказаться слишком трудной, но менее подготовленные слушатели и даже школьники, которым я рассказывал об этих теориях в Объединенном институте ядерной физики в Дубне в 2005 году и в Международном центре теоретической физики имени Абдуса Салама в Мирамаре месяц назад, не только меня поняли, но даже получили первые новые самостоятельные результаты в этом направлении, где много еще остается сделать, как вы сейчас услышите.

Ну вот теперь я перехожу к делу. Значит, я буду рассказывать про теорию самого общего математического объекта, который только есть. Я его называю для простоты «монадой» по Лейбницу и объясню сейчас вам, что это такое. Значит, монада. Это самый простой математический объект, какой только можно придумать.

Пусть имеется конечное множество — оно там М обозначено. И пусть имеется отображение этого конечного множества в себя. Каждой точке этого конечного множества сопоставляется новая точка. Это и есть монада. Значит, вот, оказывается, существует теория этих монад, и из этой теории вытекают совершенно нетривиальные математические и физические следствия. И я некоторые из этих теорий, некоторые из этих следствий вам сейчас покажу.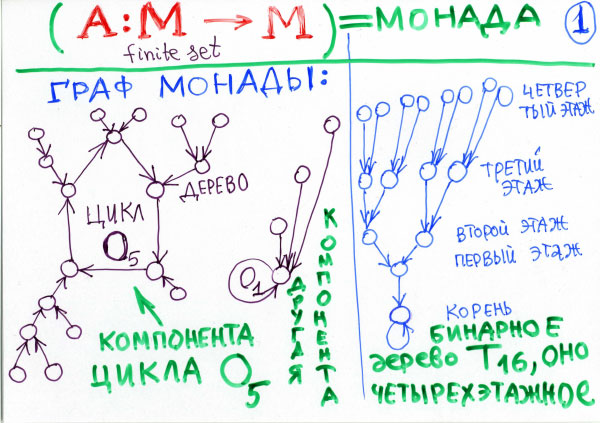

Во-первых. Чтобы понять монаду, мы будем ее изображать в виде графа — картинки. Значит, граф монады строится таким образом: берется конечное множество точек. Это множество монада отображает в себя, то есть для каждой точки x из этого множества монада переводит ее в какую-то другую точку y — y, которое есть А от x, отображение в себя. Так вот, соединим каждую точку x стрелочкой с той точкой, в которую она отображается. Вот y, например, вот эта точка, тоже куда-то отображается. Например, сама в себя. А эта точка отображается, например, вот в эту. Ну, еще осталось тут указать, куда эта точка, ну, например, вот сюда.

Вот монада из четырех точек, и нарисован граф этой монады. Вот как он устроен. Это определение первое, поэтому самое простое понятие. Это вам не суперструна. Это просто.

Теперь рассмотрим теорему первую, простейшую. Теорема: «Каждая монада — граф каждой монады — разбивается на связные компоненты». Вот эта монада связная — одна компонента только. А может быть, тут рядом имеются еще какие-то точки — в этом же множестве М — и монада их тоже переводит друг в друга. Тогда будет несколько компонент связности.

Теорема: «В каждой компоненте связности монады обязательно имеется цикл». Вот здесь имеется — а, у меня нарисовано, давайте нарисуем по-другому, чтобы циклы были разными, а то у меня здесь все циклы одинаковые, это что такое… Вот здесь цикл длины четыре. А здесь цикл длины один. Но это циклы. Компоненты без цикла не бывает. Доказательство: множество точек конечное, поэтому, если мы выйдем и пойдем по стрелочкам, будем идти, идти, идти, когда-нибудь вернемся в точку, где уже были раньше. Потому что их конечное число. Тогда от первого посещения этой точки до второго будет цикл. Конец доказательства.

Второе утверждение: «В компоненте не может быть двух циклов». Доказательство: если бы в какой-нибудь компоненте было два цикла — ну тут где-то точки стоят в каком-то количестве, вот — то, так как это в одной компоненте, между ними была бы связь, тоже из стрелок как-то состоящая. И тогда где-то посередине была бы точка, из которой можно идти по стрелкам и к одному циклу, и к другому. А ведь тут же отображение: из каждой точки выходит только одна стрелка — приходить может много, а выходит только одна. Поэтому связь между двумя циклами невозможна. Не бывает связи между двумя циклами. Вот такая картинка невозможна, потому что из этой точки выходим сюда, а стрелка на этой должна обязательно быть в эту сторону. Значит, из этой вершины идем сюда и сюда, а так не бывает — из каждой вершины в одну сторону. Значит, всё. Цикл только один.

Итак, как же устроена монада? Монада устроена так всегда: имеется цикл, у него имеются вершины, и в каждой из этих вершин имеется аттрактор — что-то, что к нему притягивается. А то, что к нему притягивается, — это дерево, это уже кусок без цикла. Деревья могут быть разные — некоторые деревья большие, некоторые маленькие, у некоторых вершин даже пустые деревья, может и не быть никакого дерева, такое тоже бывает. Но, во всяком случае, всякая монада имеет геометрическое строение, которое весьма просто.

Вот теперь я теорию монад начинаю использовать. Я сейчас использую теорию монад для исследования очень древней, очень важной, очень фундаментальной и нерешенной задачи, которая не знаю, к какой науке относится. Значит, я отношу ее к математике, по привычке, а на самом деле эту задачу можно относить к естествознанию, криптографии, к компьютерной теории и вообще к чему угодно.

Эта задача такая: вот у нас имеется какая-то деятельность, мы что-то решаем, какие-то задачи, какие-то объекты исследуем. Среди этих объектов бывают объекты простые, а бывают объекты сложные. Задача, которую я хочу обсудить, — это такая: как различать, какие объекты простые, а какие сложные? Что такое сложность, что такое сложность объекта?

Конечно, этой задачей много занимались. Например, в теории алгоритмов имеются алгоритмически разрешимые проблемы и алгоритмически неразрешимые, имеется понятие алгоритмической сложности». Но дело в том, что во всех этих теориях рассматриваются бесконечные наборы и рассматривается сложность задач, у которых бесконечное число возможностей. И говорится, что какая-нибудь такая задача, ну, скажем, проблема Ферма (xⁿ + yⁿ = zⁿ)… Вот можно поставить вопрос: разрешима ли она алгоритмически, есть ли алгоритм, который будет решением. Так это значит вот что: ведь если n фиксированное, если x, y, z фиксированные, то проверить, так это или не так, всегда можно, это легко. Задача возникает из-за того, что нету ограничения, что система не ограниченная — бывают очень большие x, y и z, и узнать надо про все сразу, про всё бесконечное множество надо сразу узнать. А я хочу сложность определять не для бесконечных задач, а для конечных.

Вот пусть имеется некоторый конечный объект. Например, программа в машине, скажем. Сложная она или простая? Я сейчас придам точный математический смысл — при помощи монад — понятию «сложности задачи». На я буду рассматривать, конечно, задачи все-таки для примера специального вида.

Я взял самую простую задачу, самый простой объект из математических объектов — последовательность нулей и единиц. Вот, значит, возьмем — бинарные последовательности это называется — возможно брать языки любые, последовательности любые, символы любых алфавитов. Ну я возьму самый простой алфавит, в котором всего есть 0 и 1 и ничего другого. И вот последовательность — это есть несколько нулей и несколько единиц, записанных подряд. Вот: 001001. Вот последовательность длины шесть, из шести элементов. Значит, я их буду писать так. Вот это я буду обозначать x, первый ноль — это x₁, который равен нулю, вот это x₂, вот это вот x_n — тогда последовательность длины n. В моем примере n равно шести. Спрашивается: вот эта последовательность (видно, что довольно простенькая — 001001), а бывает последовательность… — вот видите там есть последовательность 010101 — она простенькая, — а вторая последовательность 010011 — она уже … не так легко продолжать, не так легко догадаться, как она написана, по какому принципу. Но можно до любого n, конечно, такие вещи делать, и мы и будем так делать.

Но вот спрашивается: в каком точном смысле вторая последовательность сложнее первой? Сейчас монады дают ответ на этот вопрос, и вот какой ответ: рассмотрим, значит, все последовательности длины n из символов 01. Таких последовательностей будет 2ⁿ штук. 2⁶, например, длины 6, как у меня тут, — 64 последовательности возможно. И вот я хочу различить из этих 64 последовательностей — какие простые, какие сложные. Значит, это множество всех последовательностей имеет в математике разные названия — в зависимости от области математики вы можете их по-разному называть. Можно называть это… Вот, например, если последовательности длины 2 — 00, 01, 10, 11 — можно говорить, что это квадрат: четыре вершины квадрата. А можно говорить, что это векторное пространство размерности 2, плоскость над коэффициентами — остатками от деления на 2. Вот арифметика по модулю 2, значит… Плоскость там имеет всего четыре точки. Вот эти четыре точки здесь и есть. Вот точно так же в общем случае, значит, если у нас длина n, то это куб в n-мерном пространстве. Если n равно трем (длина 3), то это будет восемь точек, и они образуют кубик вот такой. Так, хорошо.

Так вот, оказывается, каждой точке x вот такого вида — скажем, любой вот такой последовательности —я сейчас сопоставлю монаду. Монада одна будет, а это будет вершина, это будет конечное множество, вот эти вершины куба. Мы построим отображение вершин куба в себя: из каждой вершины куба будет выходить стрелка, которая ведет в какую-то другую вершину. А придумал этот способ Ньютон, который уже рассматривал ту задачу, о которой я буду рассказывать.

Задача у него была такая: дана функция, и нужно определить, простая она или сложная, как написать формулу для этой функции. Ну вот, например, можно считать, что здесь у меня написано как последовательность, но можно считать,что x — это функция, x_i — это функция от i. Значит, это функция, которая определена на дискретном множестве из n точек, конечном множестве от единицы до n и принимает значения либо 0, либо 1 в этих точках. И причем любая вот такая функция.

Как Ньютон исследовал функции, как он исследовал, например, многочлен — функция или нет, — как он это делал? Он предложил: надо рассмотреть разности у этой функции. Вот как Ньютон это делал. Вот, значит, мы начинаем эксперимент… (Это называется доска?.. Вот я слышал — мне рассказывал Виталий Лазаревич Гинзбург, — что у них в институте в ФИАНе не бывает ни мела, ни досок, но, может, он и ошибался, я не знаю. По-видимому, это свойство такое всеобщее. Ну ладно.) Определение у Ньютона было такое: вот если какая-то последовательность есть — вот, скажем, давайте возьмем эту самую 001001, да — то образуем новую последовательность таким образом: возьмем разности соседей в исходной последовательности, первые разности возьмем. Причем это остатки от деления на 2, и мы разности вычитания будем брать по модулю 2. 0 минус 0… (Когда я в Дубне там лекцию читал школьникам, они все кричали с места, сколько это.) Сколько? Ноль. 1 минус 0? Сколько, Митрофанушка? Один! 0 минус 1? Тоже один. По модулю 2. 0 минус 0? Ноль. 1 минус 0? Один. Но чтобы получить последовательность длины 6, а не 5, я буду считать, что после последнего элемента опять идет первый, чтобы она была как бы периодическая такая. Тогда не будет меняться длина. Значит, после этой единицы идет как бы этот ноль, поэтому получится опять единица. Вот из этой последовательности получилась вот такая вот последовательность, а можно брать следующую разность и так далее.

Так вот. Ньютон заметил: если функция была константа, то первые разности будут нули. А если первые разности будут константа, то функция будет многочлен первой степени. А если вторые разности константа, то не больше второй. И так далее. Ну да. У второй вторые разности константа. А третьи нули.

Так вот. Определим оператор А, который действует на последовательность x и определяет последовательность y по такой формуле: y_i = x_i+1 – x_i.

Разности я вам показал, а вот формула для них. Вот и всё. Это операция Ньютона. Мы получили отображение из нашего куба, из множества вот этих самых… Куб наш (M мы его обозначим) — это множество вершин — это, значит последовательности длины n, у которых элементы 0 и 1. И операция: каждой такой последовательности сопоставляем новую — вот операция А. Получается отображение в себя.

А раз получили отображение в себя, то, значит, есть монада. А есть монада, то есть граф. А есть граф, то есть картинка. А есть картинка, то есть циклы и деревья. И вот в терминах этих геометрий, этих монад, и будет дано сейчас скоро очень определение сложности.

Так вот. Я обещал эксперимент — вот он будет сейчас. Мы сейчас просчитаем… Вот я уже дал определение теории, и эта теория трудна и не решена математически и является трудной математической задачей, формулирует трудную и нерешенную в общем виде математическую задачу. Дано число n, найти граф монады операции Ньютона. Какая будет картинка? Это трудная задача, по поводу которой я доказал несколько десятков теорем, открыл несколько очень странных фактов (экспериментально, без компьютеров даже), потом ученики мои проверяли, доказывали, я часть доказал, а многое остается гипотезами.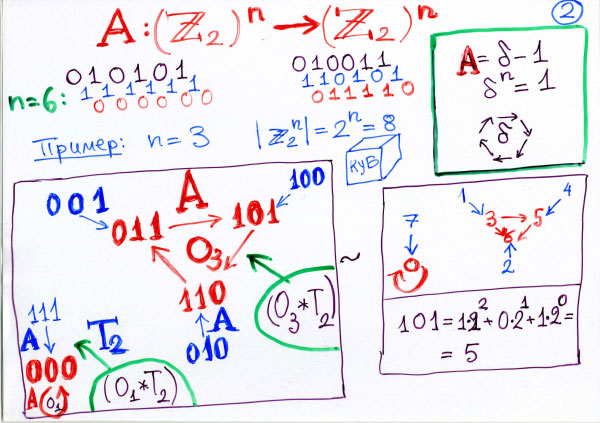

Давайте мы начнем вот с чего. Возьмем n = 3 и просчитаем всё явно. Если n = 3, то точек всего восемь. И для восьми-то точек мы сумеем посчитать разности? Последовательность длины всего 3 — это проще, чем в этом примере, но давайте посмотрим. Какие бывают последовательности нулей и единиц длины 3? Какие последовательности? Вот бывает последовательность 0, 0, 0. Бывают другие длины 3? Бывают. Еще какие? 0, 0, 1? Вот. И возьмем еще… ноль…

Знаете, я-то буду вот что считать. Я буду считать, что у меня тут ученые слушатели, которые знакомы с компьютерами и, значит, с бинарными числами и могут считать: такая последовательность — это просто двоичная запись числа в двоичной системе цифрами. Там две цифры только — 0 и 1.

Значит, вот это вот двоичная запись числа ноль. А вот это двоичная запись какого числа? Один. А поэтому мы возьмем число 2 и его тоже запишем. Как записывается? 0, 1, 0. А теперь возьмем число 3 и его запишем. Как число 3 двоично записать? 0, 1, 1. Бывает еще 4. Четыре — 1, 0, 0. Бывает 5. Пять… что? Я что-нибудь неправильно написал?

Знаете, когда я читал лекции в Московском университете, я привык: надо все формулы писать неправильно. Вот, например, кинетическую энергию надо вместо «mv² пополам» писать «два mv²». Или там где-нибудь в лагранжиане вместо «T минус U» писать «T плюс U». И тогда все просыпаются и начинают участвовать, и начинают говорить. Я привык к этому и сейчас по этой привычке тоже могу написать иногда неправильную двоичную запись. Но, надеюсь, вы меня исправите, да?

Шесть мне надо написать. 6 — это что такое? 4 и 2. 7 — это… Что? 4… Сейчас, погодите, я не пропустил? 0, 1, 2… Ах, 8, это оно и есть. 5, 6, 7, 8. Нет. Ноль… Их всего восемь, восьми нету. Оно будет четырехзначное число. 7 — последнее. Хотя последнее 7, а их восемь, потому что начинается с нуля. Ну вот. Единичка три раза. Вот так. Хорошо!

Теперь давайте считать разности. У последовательности 0, 0, 0 какие разности? Она же сама! Значит, 0 переходит в себя. Вот мы уже начали наш граф строить.

У последовательности 0, 0, 1 какие разности? 0, 1, 1. Теперь, это где стоит? Вот он.

У последовательности 0, 1, 0 разности 1, 1, 0. Это где? Шестерка.

Так. 0, 1, 1 — разности: 1, 0, 1… 1, 0, 1 — пятерка.

Так, теперь здесь. 1, 1, 0 — шестерка. И дальше… Что? Из пятерки шестерка, из шестерки… Что?

Из шестерки: 0, 1, 1. 0, 1, 1 — где это? Вот, тройка.

И из семерки три нуля.

Что-нибудь неверно? А? У тройки? Из тройки две стрелки? Не может быть! Нет, сейчас… из тройки одна стрелка. Что? Пятерка? Это пятерка, правильно? Пятерка: 1, 1, 0 — 1, 1, 0, шестерка. Что неправильно? А? Из четырех?

А, забыл 4, правильно! Тут стерто, и я забыл, правильно. 1, 0, 1… 1, 0, 1 — где это? 1, 0, 1 — пятерка, вот. Правильно, спасибо! Вот, совсем как со школьниками.

Так вот, получается… Получается граф этой монады, который у меня вон там нарисован. Там-то у меня правильно нарисовано. Значит, мы видим: компонент две — один цикл длины 3, а другой цикл длины единица. Цикл длины 3 я обозначаю символом O₃, цикл длины единица я обозначаю символом O₁.

Теперь деревья, которые к этим аттракторам стремятся. Там они длины единица, видите, вот здесь… Этот самый цикл — это кто? Цикл образует 3, 5… Три… Что, 3, 5, 6, да? Вот, возьмем 3, 5, 6. 3, 5, 6, 3 — вот цикл. Да. Но в тройку входят кроме шестерки еще единицы. И так повсюду. Значит, вот эта компонента — она вот такая: просто треугольник, который цикл, и он притягивает — каждая его вершина — притягивает еще дерево, которое из двух вершин всего, очень коротенькое такое. Росток такого дерева, вот так. Вот. Хорошо!

Значит, вот мы проделали этот эксперимент. Решение задачи, о которой я говорил, дальнейшее при других n совершенно такое же. Только вместо восьми точек здесь будет 2ⁿ точек. Вот. И, знаете, я, как маленький, стал делать n равное 4, 5… и дошел до 12-ти. При двенадцати число точек будет два в двенадцатой степени, то есть четыре тысячи. И, значит, они у меня еще уместились, эти точки, на одном листе. И поэтому я мог нарисовать этот граф. А при 13-ти они у меня уже на одном листе не умещались, и поэтому я его не сумел нарисовать, и поэтому я уже не посчитал до конца. Но, правда, ученики у меня потом на компьютере посчитали, так что я знаю сейчас ответы очень далеко, и эти ответы имеют совершенно удивительный вид, и я вам сейчас их покажу, и, глядя на таблицу этих ответов, я придумал несколько десятков теорем, о которых я вам несколько слов скажу. (Пожалуйста, следующий кадр.)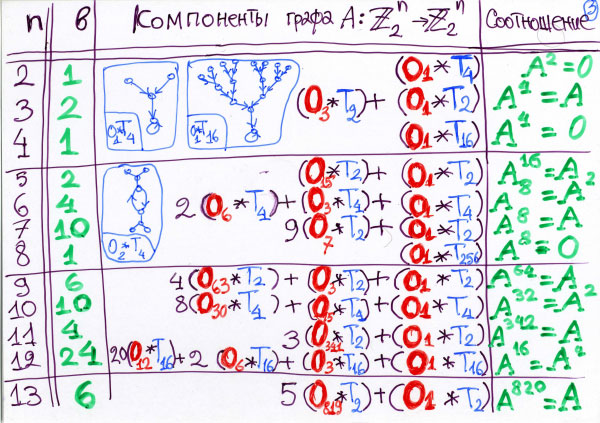

Вот. Вот, значит, здесь вы видите n равное двум — очень простенький ответ: там О₁ * T₄, то есть имеется такое вот дерево высоты четыре… T₄ — это дерево из четырех вершин, вот такое.

А, нет, простите. Простите. Я забыл обозначения. Значит, мне потребуется такое понятие — бинарное дерево. Бинарное дерево — это дерево, у которого в каждой точке ветвления две ветки расходятся. Вот. И при этом они так до самого верхнего этажа, а на верхнем этаже они… Ну, значит, T₄ — это такое дерево. У него 4 вершины — вот они. И вот они устроены таким образом. Ну, при этом, так как он аттрактор, еще имеется цикл. Вот он притягивается к циклу, и T₄ — это вот такое вот дерево, которое вот так просто устроено.

Ну, а T₈ — это, соответственно, будет еще в каждую из этих вершин тоже по две. Тогда их станет 8. 16 — еще больше. И так далее. T₂ в степени n — это значит, будет соответствующее число n этажей. Так вот, в этой таблице — там и указано — оказывается, странным образом, все компоненты имеют такой вид: каждая компонента оснащена лесом из деревьев, и деревья всех вершин компоненты, всех вершин — циклы у деревьев все одинаковые. И притом бинарные всегда. Там загадочное число, какое именно бинарное, из каких именно вершин. Вот, например, если n равно восьми … нет, какой тут странный случай … 11-ти. Если длина последовательности 11, то здесь цикл длиной 341. А если n равно восьми, то дерево T₂₅₆ — это бинарное дерево высоты 8. Значит, восьмиэтажный дом такой вот расцвел. Вот так вот, оказывается.

Ну, теперь, глядя на эту таблицу, можно сделать много-много всяких умозаключений, которые и оказываются математикой. Это и есть открытия, это и есть математические теоремы. Ну вот, например. Последний столбец в этой таблице, в каждом месте последний столбец — это компонента специального вида. Цикл длины один, вот как здесь, вот как у этого дерева. И к нему растет привязано бинарное дерево и ничего другого. Просто бинарное дерево, у которого нижняя вершина переходит сама в себя. Никакого большого цикла там нету.

Теорема: такая компонента есть при любом n и точки вершины x, которые ей принадлежат, — не какие попало, а это очень интересные точки. А вот что это такое: они и только они являются многочленами. Функция x, которую мы исследуем, для которой мы строили дерево, является многочленом, если и только если эта точка в графе попадает на эту последнюю часть, вот на это дерево.

Отсюда следует, что многочлены — вовсе не все функции. Вот, например, при n равном двум все функции многочлены, при n равном трем — нет, при n равном четырем все функции многочлены, при n равном пяти — нет, и так далее.

Мы изучаем пространство функций, функциональное пространство. Но, в отличие от анализа обычного, здесь у нас конечное число точек в этом функциональном пространстве. И мы изучаем комбинаторику этого функционального пространства из конечного числа точек. В нем есть анализ, дифференциальные уравнения, синусы, косинусы, экспоненты… А мы сейчас изучаем многочлены.

Многочлены — это последний столбец, причем интересно: этот последний столбец будет единственным столбцом в каких случаях? Посмотрите: при n равном двум, четырем, восьми… Вот здесь написано, сколько компонент. Одна компонента — когда? Когда n равно двум, четырем, восьми…

Ну, дальше у меня тут нету таких случаев, но если посчитать дальше, то в 16-ти. И мои школьники уже догадывались, и уже в этот момент начинали кричать — в отличие от нобелевских лауреатов, которым я читал тоже такую лекцию, которые ничего не понимали, — но школьники сразу замечали: компонента только одна, если и только если n — степень двойки.

Если число n — степень двойки, то все функции — многочлены. Это кольцо многочленов. Их можно умножать, произведение, сумму многочленов снова в многочлен… Все функции — многочлены для функции на конечном числе точек тогда и только тогда, когда число точек — степень двойки.

Ну вот. Причем сколько там многочленов — тоже можно посчитать, раз только одна компонента. А в других случаях получаются тоже интересные наблюдения, но я не буду уж перечислять — тут много есть интересных открытий, которые кто захочет, тот сделает сам и получит либо какую-нибудь мою теорему, либо мою гипотезу, либо неверное утверждение, которое опровергнуто вычислениями моих учеников, которые сделаны дальше.

Вот я, например, скажу. Одно из открытий, которое я сделал, глядя на это таблицу. Смотрите. Для каждого n имеется самый длинный цикл. Вот самый длинный цикл. Если n = 10, то самый длинный цикл — O₃₀, длины 30. Если n = 9, то самый длинный цикл длины 63. Если n = 13, то самый длинный цикл имеет длину 819. Спрашивается: какая длина у самого длинного цикла?

Мои школьники в Дубне догадывались, в чём тут дело. Ответ: длина самого длинного цикла делится на n. Вот если 10, то 30 — делится, и в частном получается 3. Если 9, то 63 — делится, и в частном получается 7. А какие частные? 3, 7… — что это за числа? А мои школьники догадались. Математика — это экспериментальная наука: можно глядеть на эксперимент и получать ответы. Ответ: частное будет степень двойки без единицы. 7 — это два в кубе без единицы, 3 — это два в квадрате. Даже если вот возьмете там подальше там 819, тоже будет верно — надо разделить только на 13. Это долго, но если вы разделите, то сколько там получится? 819 разделить на 13, да? Это сколько будет? 78, да? И 39. 78 — это 6, 39 — это 3, значит будет 63. Это 64 минус единица. 2⁶ минус единица.

И вот всё время так получается. Это удивительный факт, для которого вот нет доказательства, а есть опровергающий пример. Первое число, для которого… Это всё верно не всегда, а неверный пример нашли мои ученики на компьютере. Оказывается, если n = 23, то это неверно. Если n = 23, оказывается, беда вот в чём. Оказывается, если n = 23, то самый длинный цикл очень длинный, но длина этого цикла уже сама степень двойки минус единица, и делить на n не надо. Она уже степень двойки без единицы.

Ну, в общем, тут получается огромное количество теорем теории чисел, и очень интересные теории чисел, но, конечно, всё рассказать-то невозможно — я только хочу вам показать примеры, что уже самые простые математические эксперименты с самыми простыми математическими объектами уже приводят к интересным результатам. (Можно следующий.)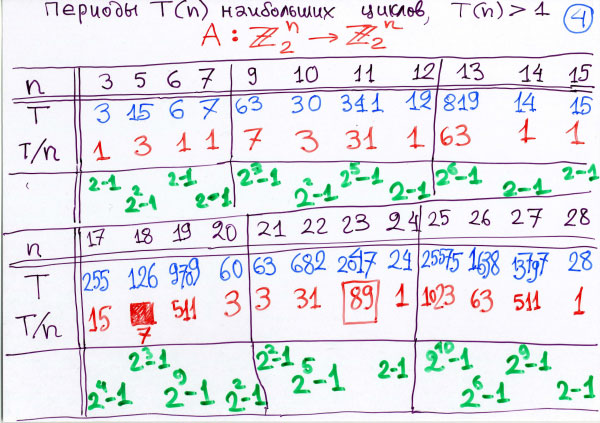

Вот таблица этих самых делений. Вот периоды самые короткие выписаны здесь. При больших n, не только при тех 12-ти, которые я посчитал сам, но и при тех, которые посчитали мои ученики. Вот здесь вот имеется число 23, которое дает период самого короткого цикла 2047. 2047 — если его поделить на n, которое 23, оно делится на 23. Но получится 89, которое ни к какой степени двойки не имеет никакого отношения. Так беда здесь в том, что число 2047 само равно 2048 без единицы. А 2048 — это степень двойки.

Значит, здесь возникает целая наука, я не буду рассказывать вам всё, что по этому поводу известно. Известно много… Но вот, например, даже асимптотика — как ведут себя эти дроби t деленное на n при больших n, насколько часто встречаются исключительные случаи вроде 23-х… Всё по этому поводу имеются гипотезы моих учеников, но нет настоящих теорем, по-настоящему не доказано. (Можно следующий кадр.)

Вот. Теперь вот из вычислений я показываю пример одной из компонент. Значит, есть длина 6 — цикл длины 6, О₆, вот он. И у него деревья оказываются T₄ — значит, деревья из 4-х вершин к нему привязаны. Но я изображаю эти последовательности двоичными числами. Я, например, там пишу 29 или 40, там, написано. Но это имеется в виду последовательность из 4-х нулей и единиц, которая в двоичной записи будет давать это вот. Так вот. Эта последовательность чисел — вот я их посчитал просто, до 12-ти я всё посчитал просто — там не такие уж длинные вычисления, — я всё посчитал эти графы, получил замечательные картинки, и так далее.

Меня интересовал следующий вопрос. Конечно, самая простая функция ноль. Конечно, следующая по простоте — единица. Конечно, вслед за константами идут многочлены первой степени. Потом второй. Потом все многочлены вместе. Вот про них я уже вам рассказал. А как устроены дальше функции? Какая самая сложная функция при данном n?

Значит, определение, кстати: последовательность называется более сложной, если она принадлежит циклу, который имеет большую длину. А если две последовательности имеют циклы одинаковой длины, то сложнее та, которая дальше от цикла. Которая на дереве на высоких ветках. Вот определение сложности.

После этого мы можем действительно реально конечные последовательности — вот например мой вот пример: вот эта последовательность, в которой там были нули и единицы, которые были выписаны. И мы увидим: вот те, которые нам интуитивно кажутся простыми, оказываются действительно в этом смысле строго простые. А те, которые нам кажутся сложными, действительно этому интуитивному понятию сложности совершенно соответствуют.

Хотя, насколько я знаю, до меня в математике не было никакого другого определения, так что нельзя было сравнивать такие вещи. А вот теперь можно, вот я объяснил, как. Геометрия монад позволяет узнавать, какая последовательность сложная, а какая простая.

Я это рассказываю для случая остатков от деления на два, вот для такой простой модели, но между тем эта геометрия распространяется на совершенно общие задачи, гораздо более широкие, и для них тоже все это можно делать, но только это приводит к новым теоремам, к новым результатам… Так вот. Занимаясь всем этим, я наконец нашел самую сложную функцию. И вот я вам, значит, такой, можно сказать, экспериментальный, но главный в каком-то смысле результат, который оказался неожиданным.

Утверждение. Я не называю его теоремой, а причина тут такая: я ее не сумел доказать. Я уверен, что она верна. Но я ее проверил, там, в нескольких сотнях случаев. Какое же это доказательство? Это как такой крупнейший американский математик, филдсовский лауреат Делинь, как-то приезжал в Москву, и мы с ним обсуждали другие мои результаты, и он мне сказал: «Ну какая же это у тебя теорема — ты рассмотрел всего сорок миллионов примеров». А здесь даже до сорока миллионов не доходит. Здесь меньше тысячи примеров. Но все-таки.

Итак, утверждение: самая сложная функция — логарифм. Вот идут константы, потом многочлены малых степеней, потом многочлены более высоких степеней… Можно было бы строить тригонометрию, синусы, спецфункции, можно было бы строить весь анализ тут. Это всё можно сделать. Но логарифм оказывается сложнее всего. Причина мне совершенно непонятна, я этого не предвидел. Но просто посчитал, какая сложность логарифма, — оказалось, что он самый сложный. Вернее, не совсем так. Он либо самый сложный, либо почти самый сложный — я сейчас определю, что это такое, покажу, как это получается. Но прежде всего надо определить, что такое логарифм.

К сожалению, логарифмы… Вот министр Филиппов хотел исключить из средней школы логарифм. И потом там был еще такой представитель Всероссийской школы экономики, такой Ярослав Кузьминов, которому было поручено математику ликвидировать, и он мне сказал: «Логарифмы никому и ни для чего не нужны».

Я ему говорю: ну а как же, например, вот там, имеется, там, закон Планка или параметрическая формула, например, как же так вот… «Да это, — он говорит, — мы экономисты, нам это не нужно». А я ему говорю: а закон Мальтуса как понять без логарифмов? Или, например, сложные проценты? Или, там, я еще сказал несколько такого рода примеров… Так, значит, вот, инфляция без логарифмов не получается. Ничего не получается. И оказалось, что у них там эти экономисты не знают о таких понятиях как сложные проценты, инфляция и закон Мальтуса. Пришлось объяснять. Но знаете, нет, он оказался очень способным учеником. Он оказался очень способным учеником, он через сколько-то недель, не помню, опубликовал в газете: «Мои предыдущие утверждения, что логарифмы не нужны в школе, были ошибочными — логарифмы очень полезны для вычисления сложных процентов». Ну хорошо.

Так вот, и здесь, оказывается… вот, вдохновившись этим своим опытом с логарифмами, которые даже экономистам нужны, я тоже решил опробовать логарифмы, и вот что получилось. Оказалось, что логарифм — самая сложная функция. Но надо определить теперь логарифмы для нашей ситуации. Итак. Мы хотим определить функцию… Аргумент у нас i — это номер члена последовательности. Но как определить логарифм i — ведь это не будет число бинарное? Чтобы это было число, остаток от деления на два надо. Как же это сделать? И вот что я придумал.

Я придумал воспользоваться опытом великого такого юриста. Был такой великий юрист во Франции, до Ньютона еще — Ферма. И, значит, Ферма доказал такую знаменитую теорему Ферма. Это не то, что обычно называют теоремой Ферма, которую он не доказал и которая была его гипотезой. А это так называемая Малая теорема Ферма, которую он действительно доказал. Причем я очень во многом следую во всем этом рассказе как раз его методу.

Он исследовал математические вопросы именно так. Он составлял таблицы величиной в несколько километров и смотрел на них. И обнаруживал факты. Ну, потом искал доказательства. Когда находил, то это теоремы Ферма. Когда не находил, то гипотезы. Потом через несколько сотен лет находится какой-нибудь филдсовский лауреат, который решит там это, докажет это. Так я тоже стараюсь делать таким же образом. Я, что могу, доказываю. Вот здесь я кое-что доказал, а кое-что нет.

Так вот. Определение. Теорема Ферма устроена таким образом. Оказывается… Это теорема о геометрической прогрессии. Ну вот. Давайте я вам покажу сейчас. Геометрические прогрессии исключили уже из школ? Мне нужны теории остатков и теории геометрических прогрессий. Я буду рассматривать остатки по модулю p, а p будет у меня для примера 13 — простое число. Вот. А геометрическую прогрессию я возьму такую: 2^a. a равняется 1, 2 и так далее. Ну, можно даже с нуля начинать, но я предпочитаю с единицы. Вот.

Так вот у этих чисел — степеней двойки — надо брать остатки от деления на 13. Что это будет за последовательность? Ферма проделал первый этот эксперимент. А мы сейчас повторим, мы тоже можем. Смотрите.

При a равном единице какое число? Двойка. Так. Остаток двойки от деления на 13? Двойка. Теперь при a равном двойке. Четверка. Остаток от деления на 13? Четыре. Восемь. Остаток от деления на 13? Восемь. Следующее? Три. Потому что дважды 8 будет 3. Потому что дважды 8 это 16, а остаток от деления 16 на 13 — это 3. 3 на 2? Шесть. 6 на 2? 12. Это еще хорошо — меньше 13-ти. 12 на 2? 11, правильно. 12 это минус 1, поэтому 12 на 2 будет —2. А —2 по модулю 13 — это 11. Правильно. 11 на 2? —4, то есть 9. 9 на 2 — 18, то есть 5. 5 на 2 — 10, 10 на 2 — 20, то есть 7, 7 на 2 — 14, то есть 1. 1 на 2 — 2.

Так вот, заметьте: двойка получилась опять. Мы с нее начинали и к ней пришли. Вывод Ферма: эта последовательность периодическая. И притом, какой у нее период, посчитайте. Смотрите: на какой раз получилась двойка? Раз, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 — на тринадцатом месте. И так будет всегда, период будет p.

То есть, простите, как тринадцатом? Как это может быть? Сейчас. 1-е, 2-е, 3-е, 4-е, 5-е, 6-е, 7-е, 8-е, 9-е, 10-е, 11-е, 12-е. А второй раз двойку считать не надо. Длина периода 12, а не 13. А 12 — заметил Ферма — это 13 минус один. И он доказал, что p минус один — всегда период. Ну, это, может, не наименьший период… В данном случае это наименьший период, но, во всяком случае, всегда есть такое число, для которого период будет p минус один.

А тогда мы напишем вот как. Если a в степени l равняется k (по модулю p) то мы l назовем логарифмом числа k. Это довольно обычно, если кто встречал где-нибудь логарифмы, в школе когда-нибудь… Так и определяется — по модулю a, ну, логарифмы с основанием a. Но. Это число — l — определено по модулю периода, по модулю p минус 1. Поэтому это число l само является остатком от деления на p минус 1. Вот. А k — остаток от деления на p.

Стало быть, у каждого остатка от деления на p имеется логарифм. Вот он определен. Но этот логарифм сам является остатком от деления на p минус 1. Вот беда. А мы хотим, чтобы логарифм имел значения в , то есть имел значения только 0 и 1. А тогда мы сделаем так. Мы это число по модулю p минус 1… Если p было нечетным — простое число, — то p минус 1 будет четным. Поэтому по модулю p минус 1 можно привести по модулю 2. И посмотреть, четное или нечетное число l. Если число l четное, то скажем, что логарифм, приведенный по модулю 2, равен нулю. А если нечетное, то единице. И это и есть определение логарифма.

Арифметический логарифм определяется таким способом. Арифметический логарифм числа равен нулю, если это число является основанием в четной степени (для остатков), а единице — в противном случае. Но в этом случае надо только… смотрите… сколько у нас аргументов? k — это остаток от деления на p, то есть, значит… сколько их бывает? k — это остаток от деления на p, но неравный нулю надо брать, конечно, остаток, иначе не получится. Чтобы он был… Ноль тут не получается, это неравный нулю. То есть их будет p минус 1. Значит n = p — 1.

Для последовательности длины не любой, а p минус 1 мы определили. Двоичные логарифмы определяются вот этим правилом. Между прочим, для знающих теорию чисел, надо сказать, еще это и так можно определить: если вычет k — квадратичный вычет, то 0, а если невычет, то 1, и поэтому этот логарифм был давно известен в теории чисел — называется символом Лежандра.

Так вот. Возьмем теперь этот логарифм и в каждом случае, для каждого нашего n, которое есть p — 1, посчитаем его. Вот если взять n равное шести, которое 7 — 1, то логарифм можно посчитать, и логарифм (вот он написан здесь, вот этот логарифм) — когда мы его посчитаем здесь (надо посчитать значения: логарифм единицы, логарифм двойки, логарифм тройки) — будет последовательность, а эту последовательность можно записать как двоичное число. А это двоичное число можно посчитать, и оно равно в этом случае одиннадцать.

А теперь 11 занимает в нашей диаграмме какое-то место. А вот какое место. Наша диаграмма: цикл длины 6, на котором растет лес из деревьев T₄. А 11 — это верхняя вершина на цикле T₄. А длиннее циклов не бывает при этом значении n. Следовательно, 11 (вот эта точка) — самая сложная точка нашей монады. А это значит, логарифм в этом случае — это двоичный логарифм — самая сложная функция. Вот я вам провел доказательство… Но это в частном случае, этих случаев, я сказал, у меня, там, меньше миллиона, но все-таки много. (Пожалуйста, следующий.)

Вот здесь, например, написаны другие значения, которые тоже… n равно четырем, p равно пяти. Тогда, оказывается, логарифм соответствует целому числу 6, двоичное разложение 6-ти дает. А дерево здесь вот какое. Видите: цикл длины один и дерево — это будет дерево, какое там, — T₁₆. О₁ значит T₁₆.

Но 6 — оказывается, длиннее нету в этом случае — цикл самый длинный. Но логарифм — не самая высокая вершина. На единицу отстоит. И в других примерах у меня так же. Для всех примеров, в которых я считал, логарифм либо самая высокая вершина, он всегда принадлежит самому длинному циклу, и при этом вершина оказывается либо самой высокой, либо предшествующей. Почти самая высокая. Вот здесь, в этом случае, константа двойка, или 13 — они еще сложнее, чем логарифм, но чуть-чуть сложнее.

Я не знаю, что это за функции, надо посмотреть, может быть это какой-нибудь там x логарифм x или что-нибудь в этом роде… или единица делить на логарифм может даже оказаться… Но… не знаю. Вот дальше у меня показан там… еще один пример я показал — логарифм для p равного 11-ти, то есть n равного 10-ти… логарифм соответствует… функция логарифма соответствует числу 285, цикл имеет длину 30, и вот я некоторый кусок этого цикла выписал, из каких чисел он состоит, и видно… И в этом случае логарифм оказывается самой далекой вершиной, на самом длинном цикле, тоже как и в предыдущем случае. Вот я объяснил. (Так, пожалуйста, следующий.)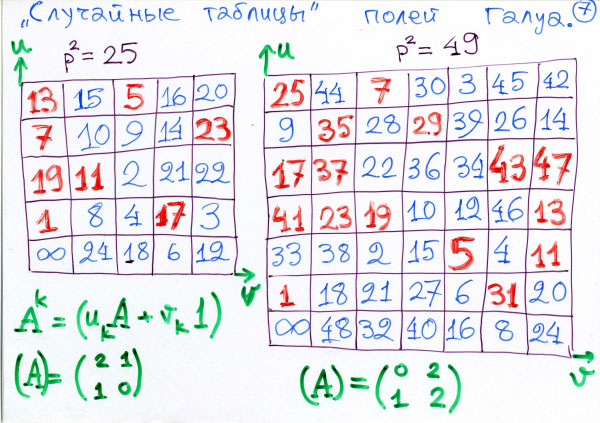

А теперь я уже кончаю доклад, но хочу еще показать несколько интересных вещей. Значит, оказывается, сложность этого логарифма связана с очень странным и загадочным явлением природы. Это явление встречается в разных науках под разными названиями — эргодическая теория, теория хаоса… И вот здесь тоже… Дело вот в чем. Рассмотрим вот, скажем, нашу геометрическую прогрессию, которую мы тут выписывали (а я уже стер ее, но она была), и посмотрим. Какие-то эти остатки как-то там распределены. Как они распределены?

Утверждение состоит в том, что вот этот логарифм или, наоборот, геометрическая прогрессия, обратная функция, — распределены их значения, вообще значения, хаотическим образом. Оказывается… нарисуем график для обычных картинок… ну там вот есть какая-нибудь функция… ну или там логарифм… вот он имеет какой-нибудь гладкий график вот… в обычном случае… А в нашей арифметической задаче оттого что мы берем остатки от всего этого, то оказывается, получается функция, у которой график ведет себя вот так. Безобразный график получается, хаотический. Он не непрерывный, конечно, это конечное число точек, это облако точек некоторое. Но если нарисовать этот график аккуратно, то есть одна точка здесь, одна здесь, получается случайный набор точек на плоскости.

В каком смысле он случайный? Это надо определять. Что такое случайность, что такое случайный набор… Все это можно сделать, проверить, посчитать… Я вот занимался когда-то с Яковом Борисовичем Зельдовичем случайностью распределения галактик и скопления галактик во Вселенной и применял потом здесь, в этой задаче, те же самые критерии, при помощи которых определяли, случайно галактики распределены или нет, можно и к этим точкам. Удовлетворяют всем критериям, по которым Зельдович считал, что галактики случайно в какой-то области распределены… Так и здесь: те же самые критерии можно применить, и получается, что это случайные точки.

Так вот теперь спрашивается: а где брать случайные точки вообще? В криптографии очень нужны случайные точки — для того чтобы код делать случайный… И как их получать? И вот я сейчас хочу рассказать… эта теория, про которую я здесь рассказываю, в частности дает некоторые очень странные алгоритмы построения случайных последовательностей.

Я придумал такие алгоритмы для разных других задач, но все-таки использовал такие два алгоритма. Один алгоритм я взял такой: я взял список академиков Национальной академии наук США и других академий, в которых я состою, значит тоже брал. И брал списки телефонных номеров по алфавитному списку академиков, и брал средние цифры телефонного номера, чтобы не учитывать, что там какой-нибудь там… нули в конце или там какой-нибудь 192 в начале, чтобы не попадали одинаковые, чтобы, несмотря на то, где они там, в Гарварде или в Принстоне, чтобы этот Гарвард не влиял. Получается последовательность, которая, как и галактики, как и эти вычеты, удовлетворяет всем распределениям случайности.

А я сделал еще… второй опыт я сделал такой. Я взял и мимо нашего Математического института имени Стеклова проходящие номера машин списал. Значит, взял несколько сотен машин, списал номера, а потом взял и обработал теми же методами. Опять получается.

Я пробовал некоторые другие вещи — они НЕ получаются. Я знаю, какие последовательности случайные, какие нет. Не все случайные. Но вот одна случайная мне очень нравится, и про нее я хочу сказать вам несколько слов. Она сейчас там уже вот видна. Это даже не последовательность, а это случайные перестановки. Мне нужно было для некоторых целей знать, как выглядит случайная перестановка n элементов.

Так вот, таблицы случайных перестановок доставляет теория полей Галуа. Это как раз перестановки, которые происходят от геометрических прогрессий в полях Галуа, которые ровно такие же, как и здесь. То, что я рассказывал — когда берутся остатки от деления на p — то это как раз поле Галуа и есть. Но поля Галуа всегда имеют число элементов p в какой-нибудь степени. Бывает из p элементов, где p — простое число, p², p³ и так далее. Вот если брать из p² элементов, то получится перестановка p² чисел, и она записывается заполнением таблицы размером p²… Вот у меня нарисовано слева, там, где p равно пяти, 25 клеточек, и в них вписаны числа от единицы до 25. Но на самом деле, до 24-х, и еще бесконечность там есть по некоторым причинам. (Но это, не хочу рассказывать, это, там, связано с теорией полей Галуа, которую обычно как-то скрывают, даже в учебниках по полям Галуа вы этого не найдете.)

Но если посчитать, это сделать — что, конечно, тоже можно выполнить — то получается заполнение такой шахматной доски номерами. Но можно было бы занумеровать, как на шахматной доске, цифрами и буквами или цифрами подряд, а здесь заполнение получается совершенно нерегулярное. Смотрите, у меня там отмечены места, где стоят образующие поле Галуа. Но это не важно, не важно, что там красным, надо смотреть на все заполнения. Вот там…

Можно сказать так, что если знаешь, где стоит, скажем, единица, предсказать, где будет тройка или двойка, уже очень трудно. И вот критерий случайности это тоже выдерживает, так же хорошо, как и номера телефонов академиков и как номера автомобилей, идущих по улице Вавилова. Вот там написаны такие таблицы случайных чисел, случайных перестановок, которые получаются вот таким вот способом.

Значит, вот эта наука, о которой я рассказывал, она дает вот такие самые разнообразные странные приложения, отчасти экспериментальные, отчасти доказанные.

В заключение (пожалуйста, следующий) я сделал еще одну картинку специально для сегодняшнего доклада. Потому что, там, предыдущее я школьникам рассказывал и нобелевским лауреатам. А это для вас специально. Я решил вспомнить такое высказывание математиков общего характера — это у Бурбаки я где-то такое прочитал — такое общее высказывание. Вот какое высказывание: понять теорему можно только таким способом, есть только один способ понять теорему — надо ее обобщить. Чтобы найденные закономерности оказались распространенными на более широкий круг явлений.

Поэтому я не останавливался на рассказанной вам теории бинарных последовательностей, а решил проделать то же самое с тернарными, специально для сегодняшнего доклада. Тернарные — это значит, что остатки не от деления на 2, 0 и 1, как в компьютере, а на 3. Можно любое число брать было бы, но я поленился брать для любого. А для 3-х просчитал.

И вот что у меня получилось — там нарисовано, какие монады получаются, если брать остатки от деления на 3. Значит, вместо бинарных деревьев получаются тернарные. Многочлены образуют тернарное дерево, которое есть всегда. И там теоремы делимости, которые были, тоже имеют аналоги свои… Но я не всё рассказываю, что там просчитал. Здесь забавные такие разбиения этих монад… Вместо куба там будет более сложный такой многогранник, у которого число вершин не 2ⁿ, а 3ⁿ, где n — это длина последовательности.

И вот я очень удивился, когда заканчивал уже вычисления и вычислял для n равного семи. Последовательности длины 7, тернарные последовательности длины 7 какую имеют монаду? И вот это последнее, что я вам хочу показать. Это удивительный результат, который, только благодаря тому что вот «Династия» пригласила меня прочитать этот доклад, был обнаружен. А именно: обнаружилась совершенно удивительная связь этой теории, при n равном семи и при тернарных последовательностях, с астрономией. А эту связь вы сейчас увидите. Значит, 3 в степени 7 — это число точек монады, число вершин, мы сейчас будем граф рисовать с таким числом вершин.

Что такое 3 в степени 7? Не много, не много. Когда я учился в школе, то нас заставляли это решать в уме и говорить сразу, а кто не говорил, тому двойку. Да. 3 в степени 7 — это 3 умножить на 3 в степени 6. А 3 в степени 6 — это 27 в квадрате, или 9 в кубе. Между прочим, 9 в кубе легче всего посчитать. Потому что 9 в квадрате — 81, умножить на 9 — 729.

Мало кто замечает, что эта формула имеет огромное астрономическое значение, а я заметил и сейчас вам расскажу. Что? 3, конечно. Спасибо. Спасибо. Ну я, как всегда, всё путаю нарочно. Так вот. Спасибо, спасибо. Значит слушают, правильно. Теперь замечание, замечание, замечание. Вон там стоят ответы, вот они написаны. Там T₃ стоит — почему T₃? Какое дерево?

Смотрите: самая простая последовательность длины 7 — это 7 семерок, 7 нулей. Ну я ее обозначаю «ноль». Ноль, конечно, переходит в себя. Последовательность разностей из нуля будет ноль. А кто в него еще переходит, какое дерево навешано на этот цикл длины 1? У какой еще функции, кроме нуля, разности 0? Это константа. А какие бывают константы? Нет…. Это же тернарные последовательности. Только две константы — единица и двойка. Ну, 0, конечно, тоже. Они переходят в 0, в 0 переходят три точки. Ноль, единица и двойка. Поэтому тернарное дерево. Спрашивается: а в единицу кто переходит? Многочлены там первой степени…

Но смотрите, в чём дело. Надо по разностям найти функцию, у которой такие разности. Единица. Эта операция называется интегрирование. Но интегрировать константу очень опасно. Потому что получится суммирование (обратная операция к разности). Получится, что интеграл по всему циклу будет 7. Но это тернарные, по модулю 3. Значит, если 7, если была единичка, будет 7, а 7 это 2. Нет, 7 это 1, по модулю 3. Один.

А это значит, что последовательность периодической быть не могла. Потому что через периода она прирастает на единицу. Линейная функция не бывает периодической. А это значит, что никакого другого элемента, кроме единицы и двойки чистой, в ноль не переходит. Дерево только вот такое. А из этого следует, что у всех циклов дерево только вот такое. Это легко уже доказать. Поэтому каждая компонента имеет число элементов, которое делится на 3. Поэтому сумма всех длин всех циклов — 729.

Все компоненты имеют вид: дерево T₃, навешанное на цикл О_n. И сумма этих n — 729. Но одна из компонент — вот она — это компонента нуля. Это цикл длины единица. Поэтому, если брать сумму по n, которые не равны единице, — остальные компоненты — то будет 728. А спрашивается: как разбить на слагаемые? Какие же там циклы? Ну я посчитал вручную, надо сказать, может быть, и можно это догадаться как-нибудь, но я до сих пор не умею хорошо догадываться. Я только, когда такая трудная задача, надо 300 чисел рассмотреть, я их просто все выписываю. Я выписал и получил: компонент две. Оказывается, компонент две, они одинаковые. Имеется два одинаковых цикла, сумма длин которых 728. Трудный вопрос: какая длина каждого цикла? Какая длина каждого цикла? 728 надо разделить пополам. Значит, длина каждого цикла будет 728 пополам — равняется 364.

А теперь мы, во-первых, обращаемся к астрономии. Мы получили длину года без високосного дня. А теперь мы обращаемся к моей теореме. Длина цикла делится на длину последовательности. А длина последовательности была 7. Значит, получаем вывод: 364 делится на 7. А теперь делим: 364 разделить на 7 — что получается? Ну, мои школьники умели. Сколько? 52 — число недель в году. А это равняется: 13 умножить на 4. Следовательно: 364 — год — состоит из 13 месяцев, лунных, по 28 дней в каждом. Что и требовалось доказать.

Благодарю за внимание.

Скачать: Доклад в Московском математическом обществе (pdf 393 KB)