Как выглядел простейший циркуль? Что такое коники Аполлония? По какой траектории летит пушечное ядро? На что похож параболический циркуль Леонардо да Винчи? Почему живописцы прошлого были неравнодушны к эллипсу?

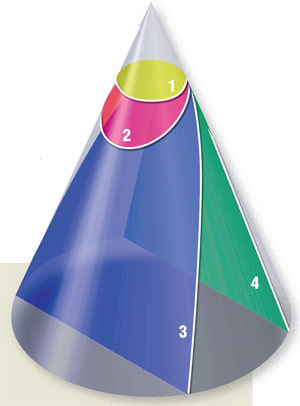
У планетария им. Тихо Браге в Копенгагене крыша эллиптической формы образована сечением здания, построенного в форме кругового цилиндра.

Античные геометры изучали самые разные плоские кривые. Особого их внимания удостоились конические сечения: эллипс, парабола и гипербола. Всё это — линии пересечения прямого кругового конуса плоскостями, не проходящими через его вершину и наклонёнными под разными углами к образующей.

Интерес к коническим сечениям появился у греков в попытках решить знаменитые задачи древности: об удвоении куба, квадратуре круга и трисекции угла. Когда стало ясно, что построением прямых и окружностей дело не ограничится, математики по-пробовали найти решения, определяя точки пересечения кривых. Выбор пал на конические сечения.

Конические сечения: окружность (1), эллипс (2), парабола (3), гипербола (4).

Их открыл в IV веке до н. э. древнегреческий математик Менехм, пересекая разного вида конусы (остроугольный, прямоугольный и тупоугольный) плоскостью, перпендикулярной образующей. В итоге ему удалось свести решение задачи об удвоении куба к нахождению точек пересечения двух парабол. Более столетия конические сечения не имели собственных названий (указывали лишь способ получения кривых, например, эллипс — «сечение остроугольного конуса»). В истории науки они известны также как «триада Менехма».

Свойства эллипса, параболы и гиперболы изучали многие, в том числе Архимед и Евклид. Однако наи-более важных результатов добился Аполлоний Пергский в III веке до н. э. Он разработал общую теорию конических сечений, которую изложил в труде «Коника» (отсюда другое название кривых — коники), в восьми книгах, где рассмотрел почти 400 теорем. Аполлоний впервые получил все три линии как сечения одного и того же конуса. Он же ввёл их современные названия: парабола, гипербола и эллипс. Они происходят от греческих слов «приближение», «избыток» и «недостаток». Кстати, того же происхождения литературные термины: «эллипсис» (пропуск слова во фразе для усиления выразительности речи); «парабола» (иносказательная история) и «гипербола» (образное преувеличение).

Долгое время конические сечения не находили применения, пока ими всерьёз не заинтересовались астрономы и физики. Выяснилось, что эти линии встречаются в природе (пример тому — траектории небесных тел) и графически описывают многие физические процессы (здесь лидирует гипербола: вспомним хотя бы закон Ома и закон Бойля-Мариотта), не говоря уже об их применении в механике и оптике. На практике, чаще всего в технике и строительстве, приходится иметь дело с эллипсом и параболой.


Эллипс и его частный случай — окружность, параболу и гиперболу легко получить экспериментально. На роль конуса вполне подойдёт, например, вафельный рожок для мороженого. Мысленно проводим одну его образующую и разрезаем рожок под разными углами к ней. Задача — сделать всего четыре попытки и получить на срезах все возможные конические сечения. Ещё проще провести опыт с карманным фонариком: в зависимости от его положения в пространстве конус света даст на стене комнаты пятна разной формы. Граница каждого пятна — одно из конических сечений. Поворачивая фонарик в вертикальной плоскости, вы увидите, как одна кривая сменяет другую: окружность вытягивается в эллипс, затем он превращается в параболу, а она, в свою очередь, в гиперболу.

Математик решает ту же задачу теоретически, сравнивая два угла: α — между осью конуса и образующей и β — между секущей плоскостью и осью конуса. И вот результат: при α < β в сечении получится эллипс или окружность, при α = β — парабола, а при α > β — ветвь гиперболы. Если считать образующие прямыми, а не отрезками, то есть рассмотреть неограниченную симметричную фигуру из двух конусов с общей вершиной, станет понятно, что эллипс — замкнутая кривая, парабола состоит из одной бесконечной ветви, а гипербола — из двух.


Простейшее коническое сечение — окружность — можно начертить, воспользовавшись ниткой и гвоздиком. Достаточно привязать один конец нитки к гвоздику, воткнутому в бумагу, а другой — к карандашу и натянуть. Сделав полный оборот, карандаш очертит окружность. А можно воспользоваться циркулем: меняя его раствор, легко нарисовать целое семейство окружностей.

Муза Урания — покровительница астрономии. Римская копия греческой скульптуры. III век до н. э. В её правой руке — циркуль.

Сотворение мира. Миниатюра. XIII век. На ней изображён Бог-творец с циркулем в руках.

По легенде, этот инструмент изобрёл Талос, племянник и ученик Дедала — знаменитого древнегреческого мастера и изобретателя. На самом деле циркуль был известен задолго до греков. Его изображения — не редкость на старинных картинах и фресках, гравюрах и обложках книг. Древнейший из найденных археологами циркулей представляет собой металлическую рогульку (у него фиксированный раствор). С помощью такого циркуля наносили простейший орнамент на изделия из дерева, керамики, кости и т.д. Чтобы хоть как-то разнообразить узор, мастера вполне могли пользоваться набором рогулек. Ещё лучше, если бы под рукой оказался один инструмент, рисующий сразу несколько окружностей разного радиуса.

Задача. Как могла бы выглядеть простейшая конструкция циркуля для рисования окружностей разного радиуса? Как одним раствором циркуля описать окружности разного радиуса? Попробуйте найти несколько решений.


Ещё Аристотель в IV веке до н. э. интересовался траекторией метательных снарядов. Философ полагал, что она состоит из двух отрезков — наклонного и вертикального — и связывающей их дуги окружности. Представления эти, конечно, далеки от истины.

В XVI столетии, в эпоху бурного развития военного дела, тем же вопросом применительно к огнестрельному оружию занимался итальянский учёный-самоучка Никколо Тарталья (tartaglia в переводе с итальянского — заика). Он прославился не только как математик и инженер, но и как автор первых научных трудов по баллистике.

Измерение угла наклона ствола пушки при помощи оружейного квадранта. Старинная гравюра.

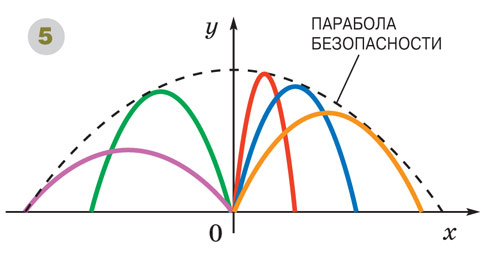
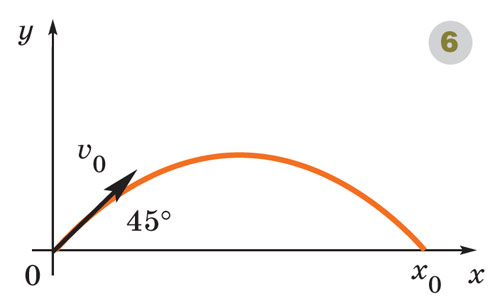
Работая в венецианском арсенале «консультантом по расчётам», Тарталья первый исследовал траекторию ядра и дальность его полёта в зависимости от угла наклона ствола пушки к горизонту. Кстати, он предложил определять этот угол с помощью квадранта, помещённого в ствол орудия. Но способ не прижился: слишком уж уязвимым становился артиллерист-измеритель во время вражеской атаки.

На основе многочисленных наблюдений Тарталья пришёл к выводу, что траектория снаряда — кривая линия, а наибольшая дальность его полёта соответствует углу наклона пушки к горизонту 45°. Правда, строго обосновать этот результат в то время было невозможно. Это удалось сделать лишь сто лет спустя, когда Галилей открыл законы падения тел. Согласно его теории, выпущенный под углом к горизонту снаряд движется по параболе при условии, что сопротивлением воздуха можно пренебречь. Истинная траектория, конечно, от неё отличается.

Пушки с разрывными ядрами. Рисунок Леонардо да Винчи. 1490 год. На нём видны и траектории снарядов (семейство кривых, близких к параболе), и угол наклона ствола пушки.

Задача. Используя результат Галилея, покажите, что дальность полёта ядра будет максимальной, если оно вылетит из пушки под углом 45° к горизонту. Как определить расстояние до точки падения снаряда?


Ответы на вопросы, занимавшие Никколо Тарталью, почти на полвека раньше него дал Леонардо да Винчи. Он изучал различные траектории и виды сложного движения в природе и технике. В записных книжках художника и учёного есть немало набросков, сделанных на основе наблюдений. Полёт птиц, водоворот, распространение света и звука, круги на воде, движение мяча и снаряда… Во всех случаях его особо интересовала геометрия траекторий: углы падения и отражения, кривые и прочие линии, а также зависимость их формы от различных параметров. Неудивительно, что да Винчи предвосхитил результаты Тартальи.

Леонардо да Винчи часто доводилось делать построения и измерения, для которых требовались специальные инструменты. Вот как описывает мастера за работой Дмитрий Мережковский в романе «Воскресшие боги»: «…Стоя на коленях, рядом с Венерой, вынул он циркуль, угломер, полукруглую медную дугу, наподобие тех, какие употреблялись в математических приборах, и, с выражением того же упорного, спокойного и проникновенного любопытства в холодных, светло-голубых глазах и тонких, плотно сжатых губах, начал мерить различные части прекрасного тела…»

Параболический циркуль. Рисунок Леонардо да Винчи. Около 1500 года.

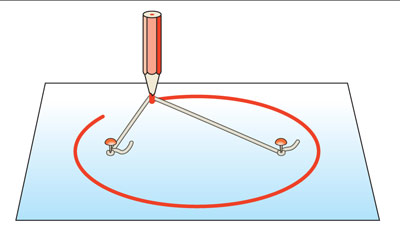
В рукописях Леонардо да Винчи содержатся упоминания о самых разных чертёжных инструментах. Считается, что некоторые из них сконструировал он сам. Одно из его изобретений — устройство для рисования параболы. (Подобный инструмент, известный ещё грекам, описал арабский математик X—XI веков ас-Сиджизи.) Это был совершенный циркуль — с его помощью чертили все виды конических сечений: окружность, эллипс, параболу и гиперболу.

Задача. Попробуйте объяснить принцип работы устройства для рисования параболы, придуманного Леонардо да Винчи, уяснив роль каждой детали и установив, какому элементу конуса она соответствует.


Самый простой способ построения эллипса, безо всяких инструментов, приведённый в одном арабском трактате IX века, сродни способу рисования окружности. Он основан на определении эллипса как множества всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек постоянна. Нужно прикрепить лист бумаги к картону двумя гвоздиками, привязать к ним нитку, длина которой больше расстояния между ними, и натянуть её карандашом. Если провести карандашом по бумаге, сохраняя нитку натянутой, и вернуться в исходную точку, конец его опишет эллипс. Однако такое построение не всегда надёжно и практично. Например, очертить на земле клумбу эллиптической формы, используя колышки и верёвку, или вырезать в доске отверстие, вбив в дерево пару гвоздиков и нарисовав эллипс, можно. А как быть, если требуется изготовить зеркало такой же формы?

Построение эллипса при помощи нитки, гвоздиков и карандаша.

Эллиптический циркуль. При движении ползунов по прорезям точка М описывает эллипс.

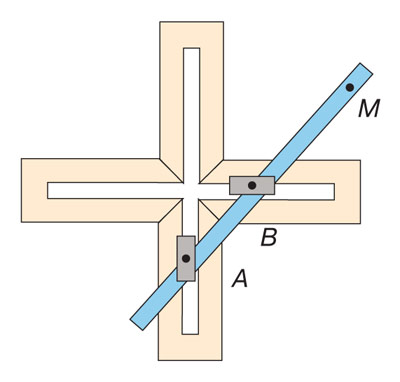
Придётся воспользоваться специальным стеклорезом на присосках. Механизм его работы основан на действии простого чертёжного инструмента, известного как эллиптический циркуль. Устройство состоит из крестовины с двумя одинаковыми перпендикулярными прорезями. По ним перемещаются ползуны А и В (один — по вертикали, другой — по горизонтали), к которым шарнирами прикреплена линейка, а на её конце в точке М закреплён карандаш (в стеклорезе его заменяет режущий ролик). При движении линейки конец карандаша описывает эллипс.


Вообще, с эллипсом мы встречаемся постоянно. Взять, к примеру, работу дизайнеров. Одни выбирают эллиптическую форму для цветников, фонтанов и искусственных водоёмов, другие — для предметов интерьера. Столешница, абажур, рама для картины, рисунок ковра, декоративное блюдо, циферблат часов — и тот может иметь очертания эллипса. Но эллипс образуется в сечении не только конуса, но и прямого кругового цилиндра (достаточно пересечь плоскостью его боковую поверхность, не затрагивая при этом оснований). Этот приём взяли на вооружение современные архитекторы. Пример тому — здание планетария в Копенгагене, носящего имя Тихо Браге — знаменитого датского астронома, учителя Иоганна Кеплера. Здание в форме усечённого цилиндра имеет крышу эллиптической формы. Но чаще встречаются сооружения, представляющие эллипс в плане. Самое известное из них — римский Колизей, грандиозный античный амфитеатр, вмещавший до 70 000 зрителей. Его арена, на которой устраивались состязания и зрелища, также ограничена эллипсом.

Колизей в Риме имеет в плане форму эллипса. Построен в 72—80 годах н. э.

Наконец, с этой кривой имеют дело художники всякий раз, когда изображают окружность в перспективе. Рисуя натюрморт — фрукты, тарелки, вазы и прочие предметы круглой формы, — они решают непростую задачу: строят проекции окружностей на плоскость полотна. Живописцы прошлого использовали эллипс и при создании композиции картины. Сначала мастера придумывали общую геометрическую схему, а затем вписывали в неё различные элементы. За счёт этого им удавалось управлять движением взгляда зрителя, акцентируя внимание на важных деталях.

Завтрак с ветчиной. Художник Питер Клас. 1647 год.

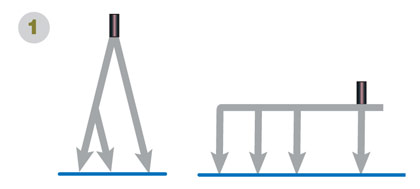
Даже беглое знакомство с коническими сечениями показывает, насколько богата и интересна их история и многообразно их применение. Недаром в разные времена этими сечениями интересовались не только учёные, инженеры, строители, но и представители разных искусств.


Так в истории геометрии назвали задачи на построение: об удвоении куба (построить куб вдвое большего объёма, чем заданный), трисекции угла (разделить произвольный угол на три равные части) и квадратуре круга (построить квадрат, равновеликий данному кругу). Решения всех трёх задач математики искали со времён античности. В XIX веке было доказано, что ни одну из них нельзя решить при помощи только циркуля и линейки. Вместе с тем известно множество таких построений с применением других инструментов и приспособлений. В них используются различные плоские кривые, в частности конические сечения.


Древняя рогулька

Инструмент для построения двух и более окружностей разного радиуса, очевидно, должен представлять собой циркуль с несколькими ножками, число, местоположение и длину которых можно при необходимости изменить. Две простейшие конструкции показаны на рис. 1.

Рис. 1.

Построить окружности разного радиуса циркулем с фиксированным раствором можно так. Сначала следует начертить окружность на бумаге, как обычно, затем приподнять конец циркуля и опереть его, скажем, на кубик, а другим концом описать ещё одну окружность — она будет меньшего размера (рис. 2).

Рис. 2.

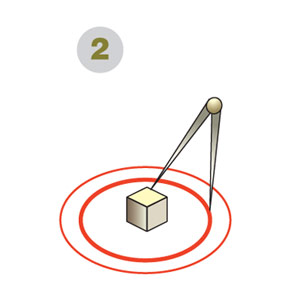
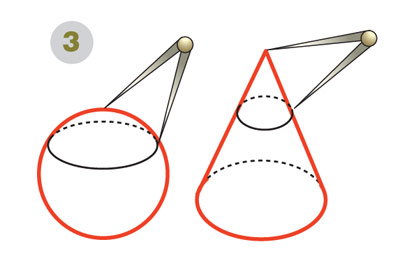
Второй способ — начертить окружность на поверхности фигуры, в сечении которой она может получиться: например на шаре, конусе (рис. 3) или ином подходящем теле вращения.

Рис. 3.

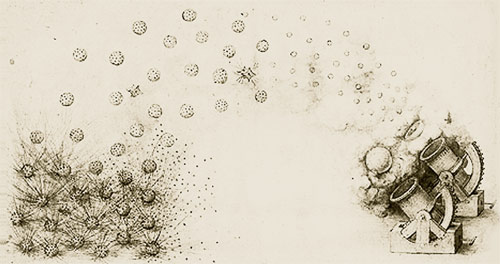
С помощью таких нехитрых приёмов и приспособлений легко нанести рисунок из концентрических или пересекающихся окружностей и дуг, например, на глиняную посуду. Подобные узоры (их называют циркульными) встречаются на многих древних сосудах, на их поверхности видны даже отметки от острия циркуля (фото 4).

Рис. 4.

Догадка Тартальи

При отсутствии сопротивления воздуха ядро, выпущенное из пушки со скоростью ν0 под углом a к горизонту, движется по параболе, ветви которой направлены вниз:

,

где — ускорение свободного падения.

Ордината точки падения ядра , тогда абсцисса этой точки, то есть искомое расстояние

Эта величина достигает наибольшего значения при , или , (рис. 5). Значит, результат, полученный Никколо Тартальей экспериментально, правильный.

Рис. 5.

Добавим, что .

Это означает, что два ядра, выпущенные из пушки под углами, дополняющими друг друга до , например и , попадут в одну точку. И ещё один интересный факт. Если рассмотреть все траектории, которые получаются при начальной скорости ядра и углах , то они будут касаться одной линии — и это тоже парабола! Её называют параболой безопасности (рис. 6). Ни в какой объект, находящийся за пределами ограниченной ею области, снаряд не попадёт.

Рис. 6.

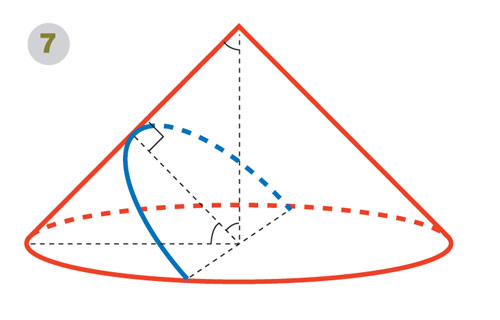
Инструмент да Винчи

Если угол между осью конуса и образующей равен углу между секущей плоскостью и осью конуса, то в сечении получится парабола. Так будет, в частности, при пересечении прямоугольного конуса плоскостью, перпендикулярной образующей (рис. 7). Это свойство подсказывает, как изготовить параболический циркуль. Конструкция должна иметь две ножки: неподвижную, опорную (представляет ось конуса), и вращающуюся, составляющую с ней угол (играет роль образующей, а точнее, её отрезка от вершины конуса до линии сечения). Первая ножка — фиксированной длины, вторая — переменной; по сути, это трубочка, в которой свободно скользит стержень, рисуя параболу. Такова и конструкция Леонардо да Винчи, которую он укрепил на треноге.

Рис. 7.

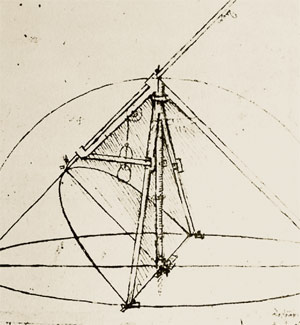
Во Флоренции, в Музее истории науки, представлена действующая модель циркуля, изготовленная в 2001 году по эскизу Леонардо да Винчи (рис. 8). Парабола чертится на листе бумаги на наклонной плоскости, параллельной одной из «ног» треноги, причём в два шага: сначала одна ветвь, затем другая, начиная с вершины. Стержень соскальзывает вниз под тяжестью собственного веса и веса прикреплённого на нитке груза.

Рис. 8.

Добавим, что конструкция совершенного циркуля аналогична той, что придумал Леонардо да Винчи, но более мобильна: она позволяет варьировать углы между осью конуса и образующей и между секущей плоскостью и осью конуса. Иными словами, всегда можно наклонить опорную ножку к плоскости листа под определённым углом и выбрать раствор циркуля так, чтобы начертить то или иное коническое сечение. Однако на практике удобнее пользоваться стационарной моделью и изменять положение секущей плоскости.